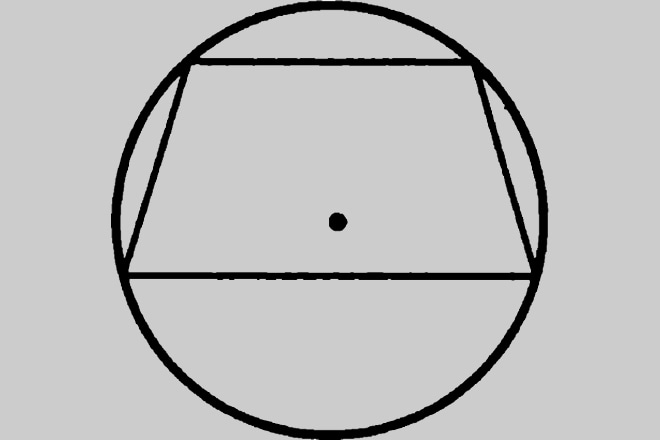
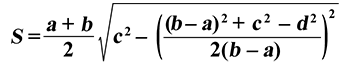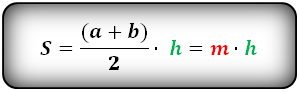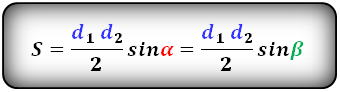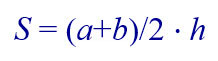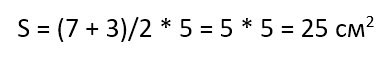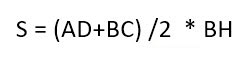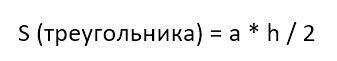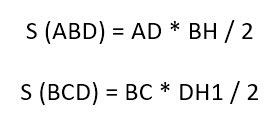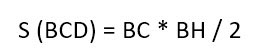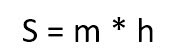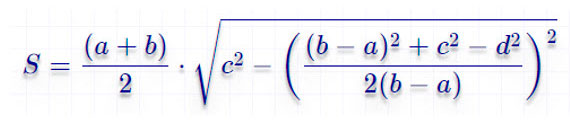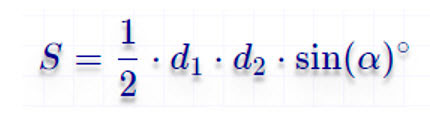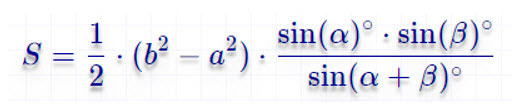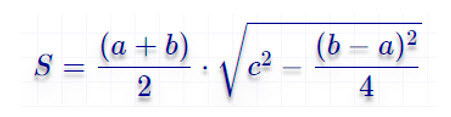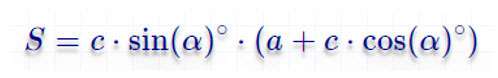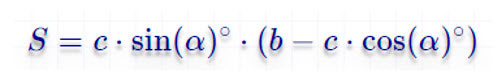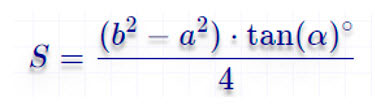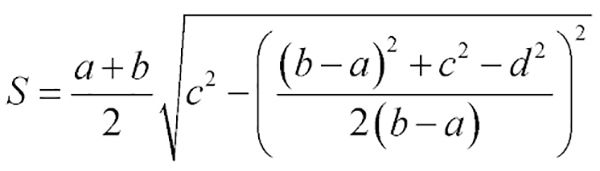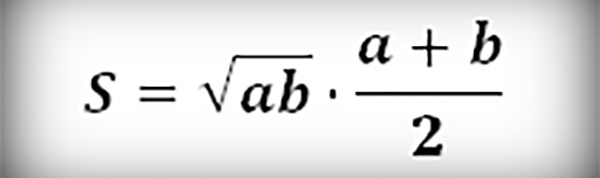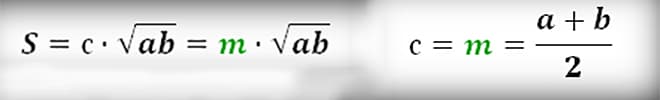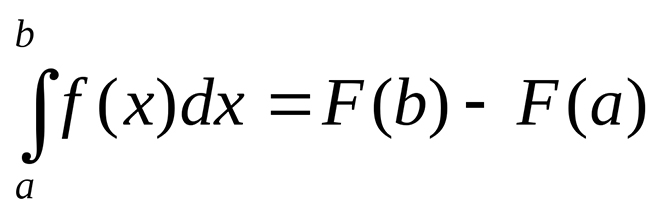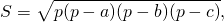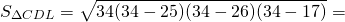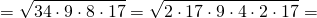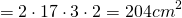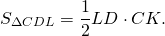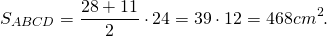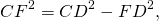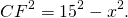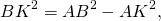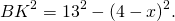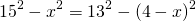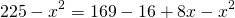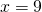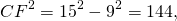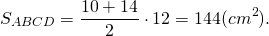Как высчитать площадь трапеции
Как высчитать площадь трапеции
Площадь трапеции
Онлайн калькулятор
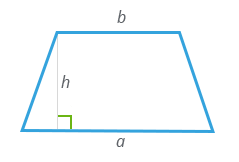
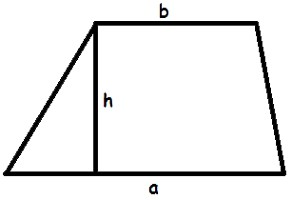
Через длины оснований и высоту

основание a =
основание b =
высота h =
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
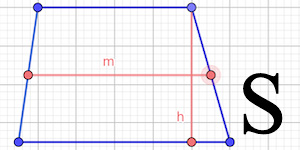
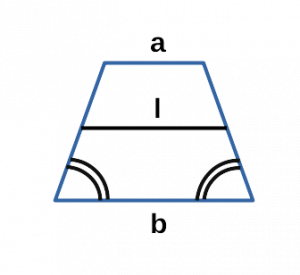
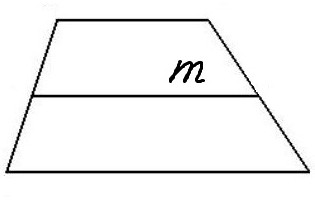
Через среднюю линию и высоту
средняя линия m =
высота h =
Чему равна площадь трапеции если известны средняя линия m и высота h?
Формула
Пример
Если у трапеции средняя линия m = 6 см, а высота h = 4 см, то её площадь:
Через длины сторон и оснований
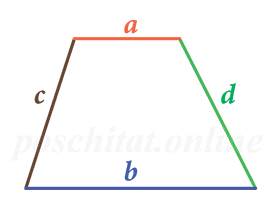
основание a =
основание b =
сторона c = сторона d =
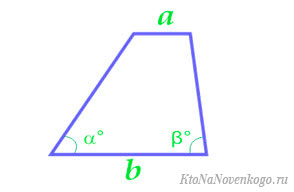
Чему равна площадь трапеции если известны основания a и b, а также стороны c и d?
Формула
Пример
Если у трапеции основание a = 2 см, основание b = 6 см, сторона c = 4 см, а сторона d = 7 см, то её площадь:
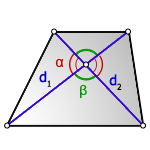
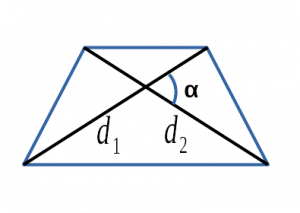
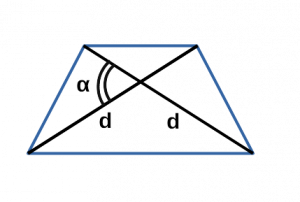
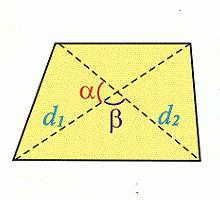
Через диагонали и угол между ними
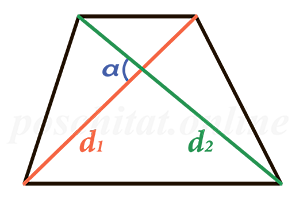
Чему равна площадь трапеции если известны диагонали d1 и d2 и угол между ними α?
Формула
Пример
Если у трапеции одна диагональ d1 = 5 см, другая диагональ d2 = 7 см, а угол между ними ∠α = 30°, то её площадь:
S = ½ ⋅ 5 ⋅ 7 ⋅ sin (30) = 17.5 ⋅ 0.5= 8.75 см²
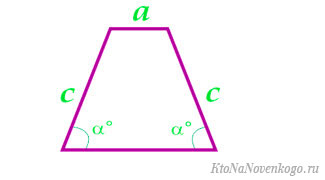
Площадь равнобедренной трапеции
Через среднюю линию, боковую сторону и угол при основании
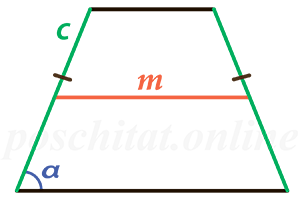
средняя линия m =
сторона c =
угол α =
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формула
Пример
Если у равнобедренной трапеции средняя линия m = 6 см, сторона c = 4 см, а угол при основании ∠α = 30°, то её площадь:
S = 6 ⋅ 4 ⋅ sin (30) = 24 ⋅ 0.5 = 12 см²
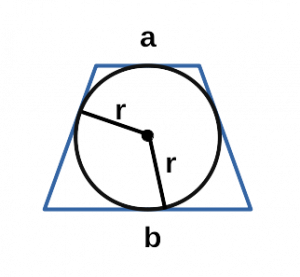
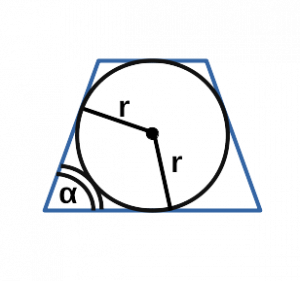
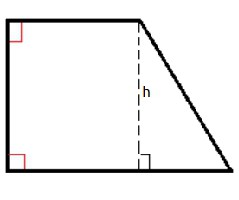
Через радиус вписанной окружности
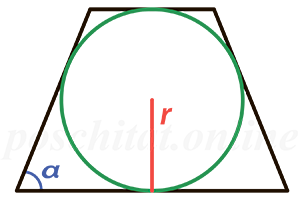
радиус r =
угол α =
Чему равна площадь равнобедренной трапеции если радиус вписанной окружности r, a угол при основании α?
Формула
Пример
Если у равнобедренной трапеции радиус вписанной окружности r = 5 см, а угол при основании ∠α = 30°, то её площадь:
S = 4 ⋅ 5² / sin (30) = 100 / 0.5 = 200 см²
Онлайн калькулятор. Площадь трапеции
Используя этот онлайн калькулятор, вы сможете найти площадь трапеции.
Воспользовавшись онлайн калькулятором для вычисления площади трапеции, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь трапеции
Ввод данных в калькулятор для вычисления площади трапеции
В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.
Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади трапеции
Теория. Площадь трапеции
Формула для вычисления площади трапеции:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Площадь трапеции
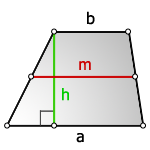
Трапеция – это четырехугольник, у которого две стороны параллельны друг другу. Высотой трапеции называют линию, перпендикулярную основаниями, для удобства ее часто проводят из тупого угла трапеции на большее основание. Средняя линия трапеции – это линия, которая параллельна основаниям, и разделяет боковые стороны ровно пополам. Среднюю линию трапеции можно найти средним арифметическим оснований – сложив их и разделив на два.
Площадь трапеции в самом простом виде – это произведение средней линии на высоту, или если раскрыть формулу средней линии, то произведение полусуммы оснований на высоту.
Доказательством этой формулы будет служить представление площади трапеции, как суммы площадей двух треугольников полученных при проведении диагонали.
Площади этих треугольников будут равны соответственно 

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с помощью метода подстановки.
Площадь трапеции через диагонали и угол между ними считается условным делением трапеции на четыре треугольника, точно также как и площадь любого произвольного четырехугольника.
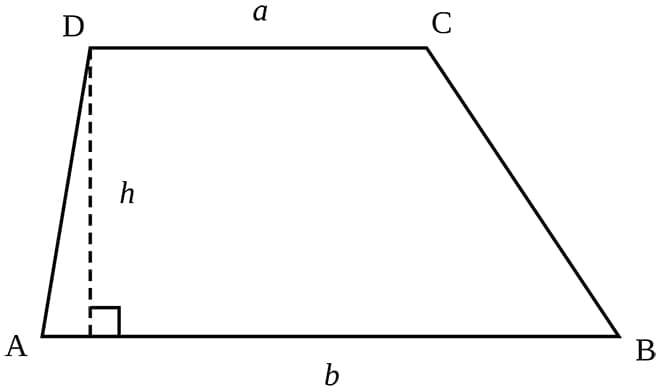
Площадь равнобедренной трапеции можно найти еще одним способом, если даны угол при основании и радиус вписанной окружности. Дело в том, что центр вписанной окружности, откуда берет свое начало радиус, находится точно в центре трапеции, таким образом, приравнивая высоту и диаметр окружности (либо удвоенный радиус). Также одно из свойств трапеции, описанной вокруг окружности – это равенство суммы оснований и суммы боковых сторон, значит, мы сможем найти среднюю линию, зная боковые стороны. Проведя высоту, из прямоугольного треугольника получаем боковую сторону 

Тогда площадь трапеции равна
Все формулы площади произвольной трапеции
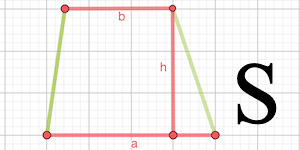
1. Формула площади трапеции через основания и высоту
Формула площади трапеции, ( S ):
2. Формула площади трапеции через диагонали и угол между ними
Формула площади трапеции, ( S ):
3. Формула площади трапеции через четыре стороны
Формула площади трапеции, ( S ):
Как найти площадь трапеции
Что такое площадь трапеции
Трапеция — четырехугольник, две стороны которого, называемые основаниями, параллельны друг другу, а две другие стороны — нет.
Вычисление площади трапеции входит в раздел геометрии, который называется планиметрия и занимается фигурами на плоскости.
Площадь трапеции, как и любой другой геометрической фигуры — это часть плоскости, ограниченная периметром и измеряемая в квадратных единицах.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
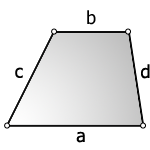
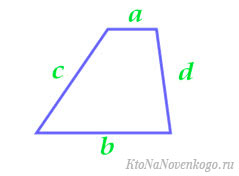
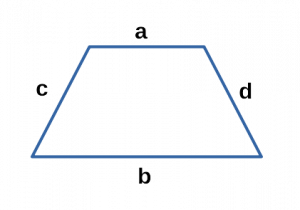
В формулах основания обозначаются буквами a и b, боковые стороны — с и d.
Способы нахождения площади
Существует более двадцати способов вычисления площади трапеции. Выбор способа расчета зависит от известных данных, которые можно подставить в формулу, и от типа самой трапеции: она может быть равнобедренной (равнобокой) или прямоугольной, тогда задача упростится.
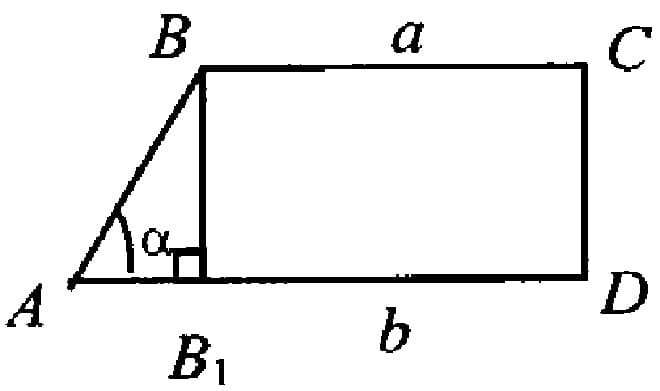
Например, если трапеция равнобедренная, вычислить длину ее сторон можно, разбив ее на прямоугольник и два прямоугольных треугольника.
Если трапеция прямоугольная, легко запомнить соотношение ее сторон, пользуясь формулами для усеченного конуса, который образуется при ее вращении вокруг ее боковой стороны, находящейся под прямым углом к основаниям:
Стороны такой трапеции, наглядно видные на схеме, связаны следующим соотношением:
Но большинство формул подходит и для разносторонних трапеций. Если задача практическая и трапеция имеет материальную форму, основания, боковые стороны, высоту и диагонали легко измерить с помощью линейки.
Формулы для вычисления площади равнобедренной и неправильной трапеций
По длине оснований и высоте
Площадь трапеции равна произведению половины суммы оснований на высоту:
Через длины всех сторон (Формула Герона)
Чтобы посчитать площадь через длины сторон, можно воспользоваться следующей формулой:
Существует более простая формула, известная, как формула Герона. Для облегчения ее запоминания вводится р, полусумма всех четырех сторон:
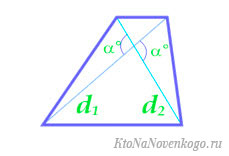
Через диагонали и угол между ними
\(S = \frac<1><2>\times d_ <1>\times d_ <2>\times \sin\alpha.\)
Здесь \(d_<1>\) и \(d_<2>\) — диагонали, а \(\alpha\) — угол, образованный ими.
Через радиус вписанной окружности
Вписать окружность в трапецию можно только тогда, когда сумма ее оснований равна сумме боковых сторон.
Площадь любой трапеции можно найти через радиус вписанной окружности, зная длину оснований:
\(S = (a + b) \times r.\)
Площадь равнобокой трапеции также можно найти через круг, вписанный в нее. Для этого нужно знать радиус этого круга, а также угол \(\alpha\) при основании.
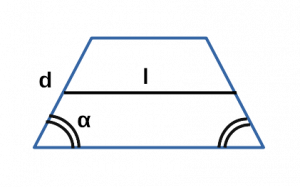
Через среднюю линию, боковую сторону и угол при основании
\(S = m \times c \times \sin\alpha.\)
Примеры решения задач
Найти площадь трапеции, размер одной диагонали которой равен 6 см, второй — 9 см, а угол между ними — \(30^\circ.\)
Подставим известные данные в формулу:
\(S = \frac<1><2>\times d_ <1>\times d_ <2>\times \sin\alpha\)
Получим: \(S = \frac<1><2>\times 6 \times 9 \times \sin30^\circ = 13,5. \)
Параллельные стороны плоской геометрической фигуры равны 9 и 5 см. Расстояние между ними — 7 см. Найти площадь фигуры.
Подставим известные данные в формулу:
\(S = \frac<1> <2>(a+b) \times h\)
\(S = \frac<1> <2>(9+5) \times 7 = 49.\)
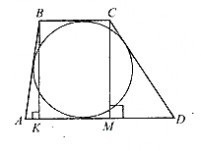
Найти площадь трапеции, если известны длины непараллельных сторон — 13 и 15 см, а также разность длин оснований — 14 см. В трапецию вписана окружность.
Одно из основных свойств трапеции — в нее можно вписать окружность, если сумма оснований равна сумме боковых сторон. Следовательно, если представить две проведенные высоты, как на рисунке, АК + МD = АD — BC = 14.
Поскольку углы К и М являются прямыми, воспользуемся теоремой Пифагора:
\(AB^ <2>= AK^ <2>+ BK^<2>.\)
\(BK^ <2>= AB^ <2>— AK^<2>.\)
\(CD^ <2>= CM^ <2>+ MD^<2>.\)
\(CM^ <2>= CD^ <2>— MD^<2>.\)
\(BK = CM.\)
\(AB^ <2>— AK^ <2>= CD^ <2>— MD^<2>.\)
Подставим числовые значения:
\(13^ <2>— (14 — MD)^ <2>= 15^ <2>— MD^<2>.\)
MD = 9 см.
\(CM^ <2>= CD^ <2>— MD^<2>.\)
Теперь, вычислив высоту, мы можем воспользоваться формулой:
\(S = \frac<1> <2>(a+b) \times h\)
Подставим в нее известные значения, получив:
Площадь трапеции
Трапеция — геометрическая фигура, представляющая собой выпуклый четырёхугольник, у которого основания параллельны, а боковые стороны – нет. Средняя линия трапеции — отрезок, соединяющий середины боковых сторон. Калькуляторы для нахождения площади трапеции находятся внизу страницы.
Формулы нахождения площади
Существует несколько базовых способов нахождения площади трапеции, в зависимости от того, какие исходные данные известны.
Через основания и высоту
Площади трапеции можно определить, если известны значения длин ее оснований и высоты:
где a и b – основания, h – высота.
Через среднюю линию и высоту
где m – средняя линия, h – высота.
Через четыре стороны
Пусть a – верхнее основание, b – нижнее, c и d – боковые стороны трапеции. Тогда формула для нахождения площади:
По диагоналям и углу между ними
где d1 и d2 – диагонали трапеции, α – угол между ними.
Через вписанную в равнобедренную трапецию окружность
где r – радиус окружности, α – угол при основании трапеции.
Расчет площади трапеции через высоту, верхнее и нижнее основание
Расчет площади трапеции через значения ее высоты и средней линии.
Трапеция
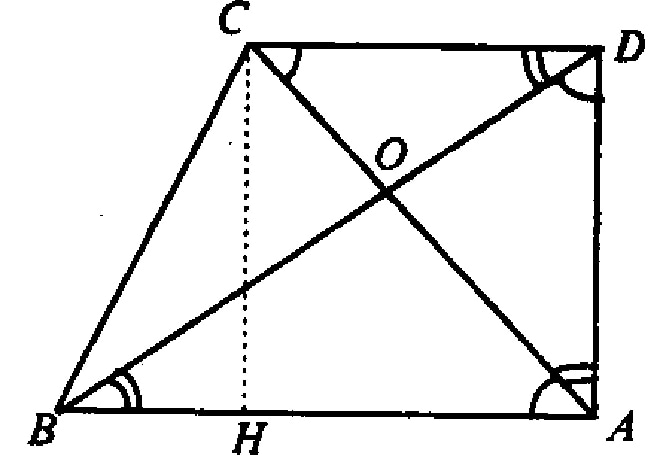
Основные свойства трапеции
AK = KB, AM = MC, BN = ND, CL = LD
BC : AD = OC : AO = OB : DO
d 1 2 + d 2 2 = 2 a b + c 2 + d 2
Формулы определения длин сторон трапеции:
a = b + h · ( ctg α + ctg β )
b = a – h · ( ctg α + ctg β )
a = b + c· cos α + d· cos β
b = a – c· cos α – d· cos β
4. Формулы боковых сторон через высоту и углы при нижнем основании:
| с = | h | d = | h |
| sin α | sin β |
Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
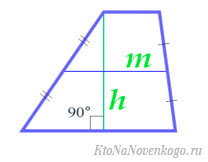
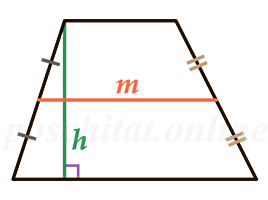
Средняя линия трапеции
Средняя линия – отрезок, соединяющий середины боковых сторон трапеции.
Формулы определения длины средней линии трапеции:
2. Формула определения длины средней линии через площадь и высоту:
| m = | S |
| h |
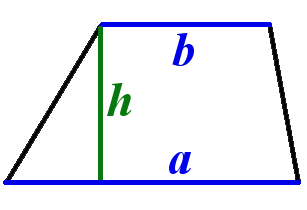
Через длины оснований и высоту
Чему равна площадь трапеции если известны основания a и b, а также высота h?
Формула
Пример
Если у трапеции основание a = 3 см, основание b = 6 см, а высота h = 4 см, то её площадь:
S = ½ ⋅ (3 + 6) ⋅ 4 = 36 / 2 = 18 см²
Площадь трапеции через перпендикулярные диагонали
Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
Таблица с формулами площади трапеции
В зависимости от известных исходных данных и вида трапеции, площадь трапеции можно вычислить по различным формулам.
| эскиз | формула | ||
| Площадь для всех видов трапеции | |||
| 1 | высота и два основания |  | |
| 2 | высота и средняя линия |  | |
| 3 | четыре стороны |  | |
| 4 | диагонали и угол между ними |  | |
| 5 | основания и углы при одном из оснований |  | |
| Площадь равнобедренной трапеции | |||
| 6 | стороны |  | |
| 7 | основание, боковые стороны и угол при основании |  | |
| 8 | основание, боковые стороны и угол при основании |  | |
| 9 | основания и углы при одном из оснований |  | |
| 10 | диагонали и угол между ними |  | |
| 11 | средняя линия, боковые стороны и углы между основанием и боковыми сторонами |  | |
| 12 | радиус вписанной окружности и угол при основании |  | |
| 13 | основания и радиус вписанной окружности |  | |
| 14 | основания и углы при одном из оснований |  | |
| 15 | основания и боковые стороны |  | |
| 16 | основания и средняя линия |  | |
Найти площадь равнобедренной трапеции, зная радиус вписанной окружности и угол
Через среднюю линию, боковую сторону и угол при основании
Чему равна площадь равнобедренной трапеции если средняя линия m, боковая сторона с, a угол при основании α?
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
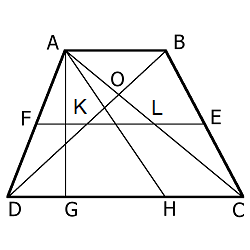
Пусть a и b основания трапеции. доказать что отрезок, соединяющий середины её диагоналей равен 1/2 * | а – б|?
Возьмем трапецию ABCD
Определим точку М как середину диагонали АС, точку N как середину диагонали BD. Тогда средняя линия трапеции KF будет проходить через точки M и N.
Вспомним свойство средней линии трапеции: средняя линия трапеции является параллельной основаниям и равняется полусумме их длин.
Рассмотрим треугольник ACD:
Рассмотрим треугольник BCD
Выразим MN через отрезки MF и NF:
Подставим в формулу значения отрезков MF и NF:
MN = AD/2-BC/2 = (AD-BC)/2
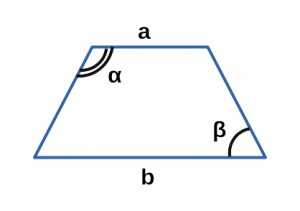
Площадь трапеции через основания и два угла
Как найти площадь трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.
Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.
Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.
Что такое трапеция
Но для начала будет нелишним напомнить, что из себя представляет трапеция.
Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.
Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.
Вот так выглядит трапеция:
А вот так параллелограмм:
Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.
Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.
Что такое площадь
Раз уж мы решили вычислять эту величину, напомним, что она обозначает.
Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве. А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
В нашем случае площадь трапеции – это область, закрашенная синим цветом:
Кстати, в древности вместо термина «площадь» говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.
Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
Главная формула для вычисления площади трапеции
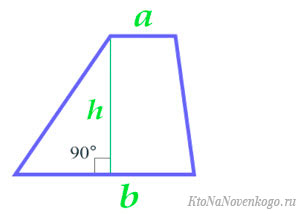
Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.
Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.
Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.
То есть мы имеем вот такие исходные данные:
Здесь «a» и «b» являются основаниями трапеции, а «h» — высотой.
И тогда формула для вычисления площади трапеции выглядит вот так:
Например, если длины сторон и высота равны:
то площадь такой трапеции будет равна:
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.
Доказательство теоремы о площади трапеции
Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.
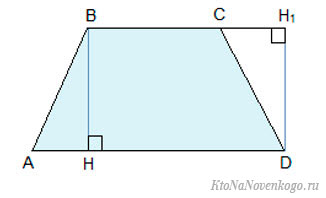
Возьмем для примера трапецию:
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.
И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.
А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту DH1.
Но в случае с трапецией высоты равны, то есть BH = DH1. И тогда формулу площади для второго треугольника можно заменить на:
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:
Как часто говориться на уроках геометрии – что и требовалось доказать!
Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Как еще можно найти площадь трапеции (другие формулы)
На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.
По высоте и средней линии
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:
По четырем сторонам
Тут формула гораздо сложнее:
Площадь трапеции через диагонали
По основанию и углам при нем
Формулы площади для равнобедренной трапеции
Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.
Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.
По четырем сторонам
По малому основанию, боковой стороне и углу у большого основания
По большому основанию, углу при нем и боковой стороне
По основаниям и углам
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.
Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (1)
Теперь любой школьник сможет блеснуть знаниями перед учителем, продемонстрировав несколько способов нахождения площади трапеции. Я уже далеко не школьник, но тоже было интересно.
Площади фигур. Площадь трапеции.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей
одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь
будет равна числу этих квадратов.
Трапецией называется четырехугольник, у которого только две стороны параллельны, а две другие не
Площадь трапеции равна произведению полусуммы ее оснований a и b на высоту h.
Воспользуйтесь нашим калькулятором для расчета площади трапеции.
Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.
Площадь трапеции можно найти по следующим формулам:
1. Формула Герона для трапеции.
2. Формула площади трапеции по длине основ и высоте.
Площадь трапеции равна произведению полусуммы ее оснований на высоту
Калькулятор площади трапеции
Трапеция — специфический вид четырехугольника, две стороны которого параллельны друг другу, а две другие — нет. Несмотря на свой оригинальный вид, трапеция находит широкое распространение в реальности, поэтому расчет площади фигуры становится актуальной задачей не только в школьных упражнениях, но и в повседневности.
Геометрия трапеции
Трапеция и трапеза — однокоренные слова, ведь название фигуры произошло от греческого слова «трапезион», которое в переводе означает «стол». В геометрическом определении трапеция — четырехугольник, у которого две стороны лежат на параллельных прямых (основания фигуры), а две другие — на непараллельных (боковые стороны). Так как у данной фигуры есть две параллельных стороны, прямоугольник и параллелограмм можно считать частными случаями трапеции. Существует несколько видов трапеций:
Грубо говоря, трапецию можно представить как усеченный треугольник, вершина которого отсечена прямой, параллельной основанию. Именно поэтому разнообразие трапеций напоминает разнообразие треугольников.
Трапеция в реальности
Данная фигура встречается не только в геометрии, но и в реальности. Форму трапеции принимают такие реальные объекты, как автомобильные и обычные окна, скаты крыш, столешницы, паруса и даже юбки. Кроме того, название «трапеция» носят спортивный и цирковой снаряды, широкая мышца на спине, упражнение в конном спорте и многое другое. Такое распространение четырехугольника в реальности делает вопрос определения его площади актуальной задачей.
Площадь трапеции
Площадь геометрической фигуры — это числовая характеристика, показывающая, какая часть плоскости ограничена сторонами четырехугольника. Площадь трапеции определяется по простой формуле:
где a и b – основания фигуры, h – ее высота.
Площадь трапеции можно определить пятью способами разной степени сложности, однако в нашем онлайн-калькуляторе используется только два из них, которые оперируют:
Вы можете использовать любой способ в зависимости от того, какую форму имеет трапеция. Для равнобедренной вам понадобится замерить только основания и высоту, а для разносторонней или прямоугольной — все сторону и высоту. Таким образом, для определения площади фигуры вам понадобится измерить 3 или 5 параметров. Рассмотрим пару примеров.
Примеры из реальной жизни
Автомобильное окно
Сегодня в автопроме правят бал обтекаемые формы, однако в советских автомобилях в почете были строгие геометрические фигуры. Дверные окна «Жигулей» имели форму прямоугольной трапеции, поэтому инженеры вычисляли площадь стекла по стандартной формуле. Давайте определим, сколько материала понадобилось бы для застекления одного дверного окна. Стандартное окно имеет приблизительно такие размеры: a = 90 см, b = 40 см, c = 60 см, а d = 50 см. Высота окна при этом составляетh = 50 см. Введем эти данные в форму и получим результат в виде:
Таким образом, приблизительная площадь дверного окна «Жигулей» составляет 3 250 квадратных сантиметров или 0,325 квадратных метров.
Лисель
Лисель — это дополнительный парус в форме трапеции, который ставится с внешней стороны прямого паруса. Несмотря на то, что на современных судах лиселя уже не устанавливаются, мы можем подсчитать размер ткани, который понадобится нам для изготовления такого паруса. Допустим, размеры лиселя составляют a = 120 см, b = 100 см, h = 80 см. Используем эта данные для расчетов и получим
Следовательно, площадь лиселя составляет 8 800 квадратных сантиметров или 0,880 квадратных метров.
Заключение
Трапеция — специфический четырехугольник, тем не менее, он широко распространен в повседневной жизни. Чаще всего с трапециями имеют дело инженеры и проектировщики, которые рассчитывают площади трапециевидных фигур при создании тех или иных изделий. Используйте наш сборник онлайн-калькуляторов для вычисления параметров любых плоских фигур или объемных тел.
Площадь трапеции
Вы будете перенаправлены на Автор24
На данной странице вы можете ознакомиться со всеми формулами для нахождения площади трапеции, как обычной, так и равнобедренной или неправильной. Также здесь есть несколько примеров решения задач по данным формулам, что удобно для нахождения своих ошибок и недочетов. Для экономии времени воспользуйтесь соответствующим онлайн-калькулятором.
Площадь трапеции по высоте и двум основаниям
Формула нахождения площади трапеции по высоте и двум основаниям:
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
Решение:
$S = 8 \cdot 7 = 56$
Площадь трапеции по четырём сторонам
Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
Площадь трапеции через ее основание и углы
Формула нахождения площади трапеции через ее основание и углы при основании:
Площадь равнобедренной трапеции через стороны
Формула нахождения площади равнобедренной трапеции через ее стороны:
Площадь равнобедренной трапеции через малое основание
Формула нахождения площади равнобедренной трапеции через малое основание, боковую сторону и угол при большем основании
$S = c \cdot \sin (α) \cdot (a + c \cdot \cos (α))$, где
Площадь равнобедренной трапеции через большее основание, боковую сторону и угол
Площадь равнобедренной трапеции через основания и угол при основании
Формула нахождения площади равнобедренной трапеции через основания и угол при основании:
Площадь равнобедренной трапеции через диагонали и угол между диагоналями
Формула нахождения площади равнобедренной трапеции через диагонали и угол между диагоналями:
$S = \frac12 \cdot D^2 \cdot \sin (α)$, где
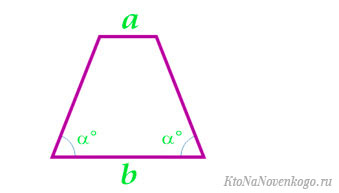
Площадь равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
Формула нахождения площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании:
$S = m \cdot c \cdot \sin (α)$, где
Чтобы проверить правильность своего решения и ответа или найти какие-либо ошибки в действиях необходимо решить пример данной задачи. Для наглядности выполним пример задачи на нахождение равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании.
Решение:
$S = 8 \cdot 10 \cdot \sin (30) = 80 \cdot \frac12 = 40$ см$^2$.
Площадь прямоугольной трапеции: онлайн калькулятор, формула расчета, пример вычисления
Вы будете перенаправлены на Автор24
Ниже вы узнаете, как выглядят формулы для нахождения площади прямоугольной трапеции, а также сможете воспользоваться онлайн-калькуляторами для её расчёта.
Особенность прямоугольной трапеции в том, что её высота равна стороне, расположенной перпендикулярно двум основаниям.
Для того чтобы вычислить площадь прямоугольной трапеции через 3 её стороны, воспользуйтесь нашим онлайн-калькулятором. Для расчёта введите имеющиеся данные в поля для ввода.
Площадь прямоугольной трапеции
Следовательно, формула для вычисления площади прямоугольной трапеции имеет вид:
$S = \frac12 \cdot (a + c) \cdot b$, где
$a$ — малое основание;
$с$ — большее основание;
$b$ — перпендикулярная основаниям сторона.
Задача
Решение:
Воспользуемся приведённой выше формулой:
Проверим ответ с помощью онлайн-калькулятора. Значения совпадают, а значит, решение найдено верно.
Также площадь прямоугольной трапеции можно рассчитать и по другим формулам, общим для всех видов трапеций, например, через среднюю линию и высоту. Высоту в формуле также можно заменить на сторону, перпендикулярную основаниям.
Площадь трапеции по высоте и средней линии
Формула нахождения площади трапеции по высоте и средней линии:
$S = m \cdot h$, где
Другой способ расчёта площади прямоугольной трапеции — через длины оснований и два угла, расположенных при одном основании.
Площадь трапеции через ее основание и углы
Формула нахождения площади трапеции через ее основание и углы при основании:
Также площадь прямоугольной трапеции можно найти через диагонали и угол между ними.
Площадь трапеции по диагонали и углу между диагоналями
Формула нахождения площади трапеции по диагонали и углу между диагоналями:
$S =\frac12 \cdot d1 \cdot d2 \cdot \sin (α)$, где
Задача
Решение:
Вычисленный ответ совпадает с ответом онлайн-калькулятора, а значит, решение — верное.
И наконец, рассмотрим случай когда нет данных о том, какие стороны являются основаниями, а какая сторона расположена под прямым углом, но при этом известны все стороны трапеции.
Площадь трапеции по четырём сторонам
Формула нахождения площади трапеции по четырём сторонам выглядит следующим образом:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Площадь, средняя линия и высота трапеции
Формулы трапеции
Результат округлять до знаков после запятой








Числа на входе должны быть:



трапеция





Площадь трапеции равняется полусумме оснований, умноженную на высоту.

Периметр является суммой длин всех сторон :

Медиана (называемая также средней линией) представляет собой отрезок линии на полпути между двумя основаниями.
Средняя линия трапеции равняется полусумме оснований.
Посмотрев на формулу площади трапеции, а затем на формулу средней линии, мы легко можем заметить, что площадь трапеции также можно найти как среднюю линию, умноженную на высоту.

Высоту трапеции можно найти при известных площади и средней линии трапеции как:
А также при известных площади и двух оснований трапеции следующим образом:
Последняя формула опять же вытекает из формулы средней линии трапеции.

$$S = \frac<6 м + 4 м> <2>* 3 м = 5 м * 3 м = 15 м^2$$.

$$P = a + b + c + d = 5 см + 12 см + 4 см + 15 см = 36 см$$.
Способ 2 : Воспользуемся второй формулой (см. раздел теория)
Формулы трапеции
Для расчёта всех основных параметров трапеции воспользуйтесь калькулятором.
Виды трапеции
Свойства трапеции
Свойства и признаки равнобедренной трапеции
Формулы площади произвольной трапеции
Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через четыре стороны
Формулы площади равнобедренной трапеции

Площадь трапеции через стороны
Площадь трапеции через стороны и угол
Площадь трапеции через диагонали и угол между ними
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
Площадь трапеции если в нее вписана окружность
Формулы сторон произвольной трапеции
Основание через другое основание и среднюю линию
Основание через другое основание, диагонали и угол между ними
Формулы сторон равнобедренной трапеции

Длина основания через диагональ, боковую сторону и другое основание
Длина боковой стороны через диагональ и основания
Длина основания через высоту, другое основание, диагонали и угол между ними
Длина основания через высоту, другое основание и площадь трапеции
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
Длина боковой стороны через площадь трапеции, основания и угол при основании
Формулы сторон прямоугольной трапеции
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
Длина основания через площадь трапеции, другое основание и высоту
Формулы диагоналей произвольной трапеции
Длина диагоналей через четыре стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту
Длина диагоналей через стороны и другую диагональ
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
Формулы диагоналей равнобедренной трапеции

Длина диагоналей через стороны
Длина диагоналей по теореме косинусов
Длина диагоналей через высоту основание и угол при основании
Длина диагоналей через сторону и высоту
Формулы диагоналей прямоугольной трапеции
Формулы средней линии произвольной трапеции
Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и высоту
Формулы средней линии равнобедренной трапеции

Длина средней линии через основания
Длина средней линии через основание, высоту и углы при нижнем основании
Длина средней линии через основания, боковую сторону и высоту
Длина средней линии через диагонали, высоту и угол между диагоналями
Длина средней линии через площадь и боковую сторону
Формулы средней линии прямоугольной трапеции
Длина средней линии через основания, высоту и угол при нижнем основании
Длина средней линии через основания, боковую сторону и угол при нижнем основании
Длина средней линии через основания и боковые стороны
Длина средней линии через диагонали, высоту и угол между диагоналями
Формулы высоты произвольной трапеции
Длина высоты через четыре стороны
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через среднюю линию, диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы высоты равнобедренной трапеции

Длина высоты через по сторонам
Длина высоты через боковую сторону и прилегающий угол к основанию
Длина высоты через основания и прилегающий угол к основанию
Длина высоты через диагонали и углы между ними
Длина высоты через площадь и основания
Длина высоты через площадь и среднюю линию
Формулы боковых сторон прямоугольной трапеции
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
Сторона BC через основания и угол ∠BCD
Сторона BC через Сторону AD
Сторона BC через площадь, среднюю линию и угол ∠BCD
Сторона BC через площадь, основания и угол ∠BCD
Прямоугольная трапеция
Свойства
Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований. (рис.105.1) m=(b+d)/2
Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру. Следовательно, площадь трапеции, которая обычно равна произведению высоты на среднюю линию, преобразуется в произведение боковой стороны на среднюю линию. (рис.105.2) S=hm=am=(a(b+d))/2
Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой. c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )
Периметр такой трапеции вычисляется также как обычной, сложением всех ее сторон. P=a+b+c+d=a+b+d+√(a^2+〖(d-b)〗^2 )
Обе диагонали прямоугольной трапеции являются гипотенузами в прямоугольных треугольниках со стороной, перпендикулярной основаниям. Поэтому вычислить их становится возможным, используя теорему Пифагора. (рис.105.3) d_1=√(a^2+b^2 ) d_2=√(a^2+d^2 )
Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований. r=√bc/2
Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником
Площадь трапеции
Площадь трапеции, формулы расчета, определение,
способы найти площадь, нахождение площади
через величины и примеры площади трапеции.
Все формулы расчета площади трапеции
через основания и угол, периметр, радиус,
синус и две стороны, диагональ,
высоту, среднюю линию.
Площадь трапеции через окружность вписанную можно
найти, зная радиус окружности вписанной в трапецию
и некоторые другие величины.
Формулы площади трапеции
Площадь любых трапеций
Ⅰ. Площадь трапеции через основания и высоту:
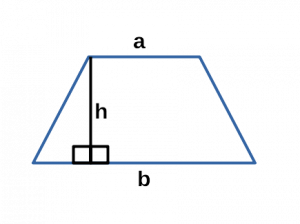
\[ S = \frac
a,b — основания трапеции;
h — высота трапеции;
Ⅱ. Площадь трапеции через высоту и среднюю линию:
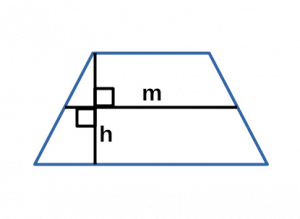
\[ S = mh \]
m — средняя линия трапеции;
h — высота трапеции;
Ⅲ. Площадь трапеции через диагонали и угол между ними:
\[ S =\frac<1><2>d_1d_2 \cdot \sin \alpha \]
\( d_1, d_2 \) - диагонали трапеции;
sin α — синус угла альфа в трапеции;
Ⅳ. Площадь трапеции через периметр, высоту и боковые стороны:
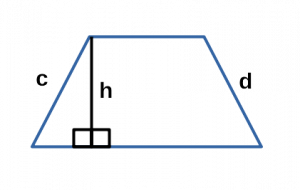
\[ S = \frac
P — периметр трапеции;
c,d — боковые стороны трапеции;
h — высота трапеции;
Ⅴ. Площадь трапеции через основания и боковые стороны:
a,b — основания трапеции;
с,d — боковые стороны трапеции;
Ⅵ. Площадь трапеции через основания и углы:
a,b — основания трапеции;
α — угол при основании a в трапеции;
β — угол при основании b в трапеции;
sin α — синус угла альфа в трапеции;
sin β — синус угла бетта в трапеции;
Площадь равнобедренной трапеции
Ⅰ. Площадь трапеции через синус угла, среднюю линию и боковую сторону:
\[ S = ld \cdot \sin α \]
l — средняя линия равнобедренной трапеции;
d — боковая сторона равнобедренной трапеции;
α — угол альфа при боковой стороне d равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅱ. Площадь трапеции через диагонали и синус угла:
\[ S = \frac
d — диагональ равнобедренной трапеции;
α — угол между двумя диагоналями в равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Ⅲ. Площадь трапеции через радиус вписанной окружности и основания:
r — радиус вписанной окружности равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅳ. Площадь трапеции через основания:
a, b — основания равнобедренной трапеции;
Ⅴ. Площадь трапеции через основания и среднюю линию:
l — средняя линия равнобедренной трапеции;
a, b — основания равнобедренной трапеции;
Ⅵ. Площадь трапеции через синус угла и стороны:
\[ S = c \cdot \sin α \cdot (a-c \cdot \cos α) \]
a — нижнее основание равнобедренной трапеции;
с — боковая сторона равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
cos α — косинус угла альфа в равнобедренной трапеции;
Ⅶ. Площадь трапеции через угол и радиус вписанной окружности:
r — радиус вписанной окружности равнобедренной трапеции;
sin α — синус угла альфа в равнобедренной трапеции;
Определения трапеции
Трапеция — это четырехугольник, у которого две
стороны параллельны а две другие нет.
Зная углы трапеции, можно определить, к какому виду
она относится. Всего различают три вида трапеций:
Площадь равнобедренной, прямоугольной трапеции,
можно найти через формулы площади обычной трапеции.
Формул, с помощью которых, можно найти площадь трапеции
через описанную окружность около трапеции, не существует.
Элементы трапеции
Любая трапеция является четырехугольником,
поэтому у трапеции 4 угла и 4 стороны.
Основание трапеции — это сторона, противолежащая
сторона которой параллельна.
Боковая сторона трапеции — это сторона, противолежащая
сторона которой не параллельна.
Средняя линия трапеции — это отрезок, соединяющий
середины боковых сторон трапеции.
Диагональ трапеции — это отрезок, соединяющий две
вершины, которые лежат в разных концах трапеции.
Высота трапеции — это отрезок, соединяющий меньшее основание с большим,
образуя при этом два угла по 90 градусов на большей стороне.
Основания у трапеции не могут быть никогда равны.
Боковые стороны могут быть равны только,
если трапеция — равнобедренная.
Площадь трапеции — это площадь геометрической фигуры,
у которой четыре стороны и четыре угла, причем только
две стороны параллельны а остальные нет.
Стороны трапеции
Свойства
Трапеция является фигурой с двумя параллельными противоположными сторонами, при этом все четыре стороны могут быть разной длины. Параллельные стороны b и d называются меньшим и большим основанием трапеции, a и c – боковыми сторонами. Зная стороны трапеции, можно найти все характеризующие ее параметры. Периметр трапеции, зная стороны, представляет собой их сумму. P=a+b+c+d
Высота трапеции является перпендикуляром, соединяющим два основания, и может быть проведена в любой их точке, но удобнее всего это делать из вершины углов при меньшем основании, так как тогда образуется прямоугольный треугольник, из которого выводится формула. (рис.103.1) h=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )
Средней линией трапеции называется отрезок, соединяющий середины боковых сторон, и равный полусумме оснований. (рис.103.2) m=(b+d)/2
Площадь трапеции равна произведению ее высоты на среднюю линию. Чтобы найти площадь трапеции через стороны, необходимо развернуть эту формулу до ее истоков, заменив неизвестные переменные. S=hm=√(a^2-(((d-b)^2+a^2-c^2)/2(d-b) )^2 )*(b+d)/2
Если в трапецию можно вписать окружность (а это возможно, если противоположные стороны в сумме дают одно и то же число), то радиус вписанной окружности будет равен половине высоты, или половине квадратного корня из произведения меньшего основания на большее, с учетом условия для окружности. (рис.103.3) r=h/2=√bd/2
Описать окружность можно только вокруг равнобокой трапеции, и если она является таковой, то радиус описанной окружности будет равен радиусу окружности, описанной вокруг треугольника, образованного диагональю. (рис.103.4) R=(abd_1)/√((a+b+d_1)(a+b)(a+d_1)(b+d_1))
Диагонали трапеции рассчитываются по формулам, приведенным через теорему Пифагора в треугольниках, образованных высотой и диагоналями. d_1=√(c^2+db d(c^2-a^2 )/(d-b)) d_2=√(a^2+db (b(c^2-a^2))/(d-b))
Вычисление площади трапеции онлайн
Наш онлайн калькулятор позволяет вычислить площадь трапеции двумя способами: через основания и высоту или через среднюю линию и высоту. Для того чтобы найти площадь трапеции выберите подходящий способ, заполните соответствующие поля и нажмите кнопку «Вычислить», калькулятор покажет ответ и пошаговое решение!
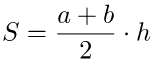
Как найти площадь трапеции
Данный онлайн калькулятор дает возможность быстро и без проблем высчитать площадь любой трапеции. Вам надо знать только один из наборов параметров:
Справка: средняя линия – это линия разделяющая трапецию поперек ровно по центру. Разделите боковые стороны пополам и проведите между ними линию. Это и будет та самая средняя линия, которая потребуется для того, чтобы узнать площадь всей трапеции.
Введите имеющиеся параметры в отдельные окошки и нажмите на кнопку «Вычислить». Теперь вы знаете, как имея на руках 2 значения всего за 2 клика легко и быстро посчитать площадь трапеции.
Копирование материалов с сайта возможно только с разрешения
администрации портала и при наличие активной ссылки на источник.
Площадь трапеции: формулы и методика вычислений
Определяем трапецию
Свойства трапеции
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота – это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d1 d2) на синус угла между ними:
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор. Вот эта формула:
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции – полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
в этой формуле M – количество узлов, т.е. пересечений линий фигуры с линиями клетки на границах трапеции (оранжевые точки на рисунке), N – количество узлов внутри фигуры (синие точки). Удобнее всего пользоваться ею при нахождении площади неправильного многоугольника. Тем не менее, чем больше арсенал используемых методик, тем меньше ошибок и лучше результаты.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Площадь трапеции
Что такое трапеция
Трапеция — это плоская фигура, ее изучают в курсе геометрии 8 класса.
Трапеция — четырехугольник, две стороны которого параллельны, и две другие стороны не параллельны.
Основаниями называются параллельные стороны трапеции. Непараллельные — боковые стороны.
Частный случай трапеции — равнобедренная трапеция, боковые стороны которой равны. Трапеция с углами по 90 градусов, прилежащими к одной боковой стороне, называется прямоугольной.
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон и параллельный основаниям.
ABCD — трапеция, EF — ее средняя линия, BC||EF||AD, BE=CF, AE=DF.
Формулы площади трапеции
Чтобы найти площадь трапеции можно использовать несколько формул. Выбор зависит от данных условия.
Площадь трапеции равна произведению половины суммы ее оснований на высоту.
Площадь трапеции равна произведению ее средней линии на высоту.
Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.
Формула площади равнобедренной трапеции
Площадь равнобедренной трапеции можно рассчитать по тем же формулам. Некоторые из них имеют упрощенный вид.
Площадь равнобедренной трапеции с перпендикулярными диагоналями
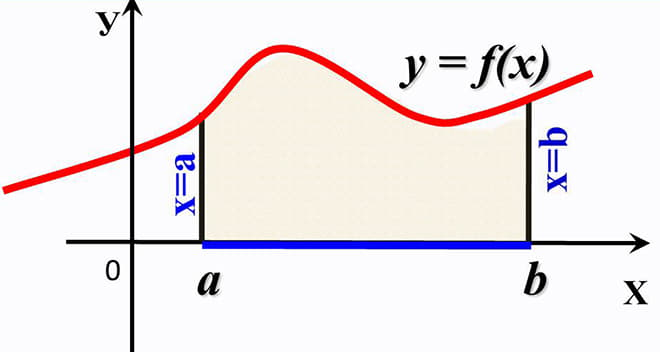
Формула площади криволинейной трапеции
Криволинейная трапеция — это плоская фигура, ограниченная графиком непрерывной и неотрицательной на отрезке [а;b] функции y=f(х), прямыми х=а, x=b и осью абсцисс.
Отрезок [a;b] называют основанием криволинейной трапеции. Отрезки, ограничивающие криволинейную трапецию слева и справа, могут вырождаться в точку. Верхняя граница криволинейной трапеции может быть задана разными формулами на разных частях отрезка.
Формула Ньютона-Лейбница
Нахождение площади криволинейной трапеции рассматривают в 11 классе как пример применения интеграла.
Пояснение на примерах
Найдите площадь трапеции, если ее основания равны 4 и 7 см, а высота — 4 см.
Найдите площадь фигуры под кривой на заданном интервале: f(x)=x3+3, x∈[−1;1].
Площадь трапеции по четырём сторонам
Трапеция – это четырёхугольник, у которого две стороны параллельны. Параллельные стороны называются основаниями, а другие – боковыми сторонами. Если и две другие стороны тоже будут параллельны, то тогда это будет прямоугольник – частный случай трапеции.
Расчёт площади трапеции этот онлайн калькулятор будет производить по четырём сторонам.
Для нахождения площади воспользуемся следующей формулой:
Здесь:
Для вычисления площади трапеции введите значения длин оснований и боковых сторон и нажмите кнопку “Рассчитать”.
Длины оснований, м:
Длины боковых сторон, м:
Площадь трапеции, м²: не рассчитывалось
Если задать основания одинаковой длины (a равно b) – случай, когда у нас прямоугольник, то эта формула не будет работать. Это происходит потому, что при вычислении b-a в результате будет получен 0. И тогда будет деление на ноль! Так что для вычисления площади прямоугольника лучше воспользоваться этим калькулятором.
Площадь трапеции онлайн калькулятор

Площадь трапеции через основания и высоту
Площадь трапеции через среднюю линию и высоту
Трапеция – это геометрическая фигура, которая имеет две параллельные стороны, называющиеся основанием и две не параллельные, имеющие названия боковые стороны трапеции. Линия, соединяющая середины боковых сторон, называется средней линией трапеции.
Как самостоятельно посчитать площадь трапеции?
Для вычисления площади трапеции можно воспользоваться следующими формулами:
1. Через основания и высоту:
Площадь трапеции = Высота * ( Основание А + Основание Б ) / 2
2. Через среднюю линию и высоту:
Площадь трапеции = Высота * Средняя линия
Теперь, у вас всегда есть под рукой удобный и легкий калькулятор для расчетов.
Площадь прямоугольной трапеции
Время чтения: 9 минут
Прямоугольная трапеция особенна тем, что имеет сторону, перпендикулярную двум неравным основаниям фигуры. Важным признаком является и наличие двух прямых смежных углов. Поиск площади прямоугольной трапеции возможен по любой из общих формул, предназначенных для данного вычисления любых трапеций (прямоугольной, равнобедренной, произвольной).
5 способов вычисления:
Вычисление площади трапеции через три её стороны (основания и перпендикулярную сторону) подходит только для прямоугольных трапеций.
Площадь прямоугольной трапеции по трём сторонам
Значение высоты прямоугольной трапеции совпадает со значением её стороны, перпендикулярной основаниям фигуры. Площадь такой фигуры можно найти через три известных стороны.
a – малое основание;
b – перпендикулярная сторона;
c – большое основание;
h – высота.
Рисунок 1. Прямоугольная трапеция. Высота h.
Если половину суммы малого и большого основания умножить на перпендикулярную сторону трапеции или высоту, в результате получается площадь.
Задача.
Найдите площадь прямоугольной трапеции S, если малое основание a составляется 4,84 см, а большое с – 7,88 см, перпендикулярная основаниям высота b равна 4,64 см.
Решение:
Основываясь на данные о трёх её сторонах, по соответствующей формуле найдём площадь.
Ответ: Площадь прямоугольной трапеции равна 29,51 кв.см.
Площадь прямоугольной трапеции по высоте и средней линии
Для расчета площади потребуются данные о высоте трапеции и линии, проведенной посередине фигуры. Произведение этих величин и составит площадь. Рассмотрим рисунок 2.
\[\boldsymbol=\boldsymbol
Задача.
Найдите площадь прямоугольной трапеции S, зная высоту h – 4,64 см и среднюю линию m – 6,36 см.
Решение:
Найдём площадь трапеции путём умножения известных величин.
Ответ: S = 29,51 кв.см.
Вычисление площади по основаниям и углам
Зная значения оснований трапеции и углов при них, для вычисления площади нужно половину разницы квадратов оснований фигуры умножить на частное из произведения синусов углов при основании и синуса суммы этих углов. Рассмотрим рисунок 3.
\[S=\frac<1> <2>*\left(c^<2>-a^<2>\right) * \frac<\sin (y) * \sin (x)><\sin (y+x)>\], где S – площадь; с – большое основание;a – малое основание;
y, x – первый и второй угол при основании.
Задача.
Как узнать площадь прямоугольной трапеции S по формуле оснований и углов, если малое снование a равно 4,84 см, а большое с – 7,88 см, первый угол при основании y прямой, а второй x равен 56,8 о ?
Решение:
Рассчитаем площадь трапеции, используя данные об основаниях и углах при большом основании.
Площадь трапеции: формулы с примерами
Трапеция – четырехугольник у которого две стороны параллельны. Параллельные стороны – это основание, непараллельные стороны – боковые.
Существует несколько основных видов: криволинейная, равнобедренная, произвольная, прямоугольная. Вычисления площади трапеции по формуле разнятся в зависимости от конкретного типа геометрической фигуры.
Что такое трапеция: типы и отличия
Всего существует четыре типа, отличающихся между собой не только вариативностью углов, но и возможным наличием криволинейных отрезков.
Площадь произвольной трапеции
Вариативность расчета площади произвольной трапеции невелика. Ее можно вычислить относительно заданных размеров основания и высоты; посчитать через обозначенные четыре стороны фигуры; решить пример, зная длину средней линии и высоты; по указанным диагоналям и углом между ними; высчитать через основания и два угла.
Формула через основания и высоту
Основная формула расчета данного способа: 
Где а и b – параллельные стороны, а h – высота четырехугольника.
Пример задачи: Дана плоская геометрическая фигура, параллельные стороны которой соответствуют длине 12 и 20 см, а высота равна – 10 см. Как найти площадь?
Решение: Допустимое решение согласно вышеприведенной формуле S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 см².
Формула через высоту и среднюю линию
Зная длину средней линии и высоту плоской фигуры, всегда можно найти площадь трапеции, выполнив буквально одно действие:

Где h – высота четырехугольника, а m – средняя линия (прямая, соединяющая середины боковых сторон).
Пример решения задачи: Дана трапеция, в которой длина средней линии – 28 см, а высота фигуры – 19 см. Какова площадь плоского четырехугольника?
Решение: Используя формулу S = hm, подставляем вместо букв цифровые значения из условия задачки. Получаем S = 28 х 19 = 532 см².
Формула через четыре стороны
Этот метод не так прост, как предыдущие. Здесь взяты за основу основные теоремы геометрии, а потому принцип расчета площади трапеции выглядит следующим образом:

Где a, b, c, d – четыре стороны фигуры, причем сторона b в обязательном порядке должна быть длинней а.
Пример вычисления: Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?
Расчет:
Формула через диагонали и угол между ними
Вычислить площадь трапеции также можно, зная размеры обеих диагоналей и значения угла между ними. 
Обозначения: d₁ и d₂ — первая и вторая диагонали, α – угол между диагоналями.
Пример: Вычислить площадь фигуры при следующих известных значениях — d₁ = 17 см, d₂ = 25 см, α = 35⁰.
Верное решение: S = ½ х 17 х 25 х sin35 = 212,5 х 0,57 = 121,125 см².
Формула через основания и два угла
Еще один вариант вычисления, основанный на расчете площади трапеции посредством длин двух оснований и двух углов.

Значения букв: b, a – длины оснований, α и β – углы.
Как посчитать (пример): Пускай угол α будет равен 67⁰, угол β = 106⁰, длина основания а равно 8 см, размер b = 11 см.
Решение:
Обучающее видео
Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.
Видео «Трапеция: решение задач»
Видео для новичков – доходчиво изложенная информация, содержащая основные формулы вычисления площади трапеции.
Видео «Площадь трапеции»
Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.
Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.
Площадь трапеции: как вычислить, формула
В математике известно несколько видов четырехугольников: квадрат, прямоугольник, ромб, параллелограмм. Среди них и трапеция — вид выпуклого четырехугольника, у которого две стороны параллельны, а две другие нет. Параллельные противоположные стороны называются основаниями, а две другие – боковыми сторонами трапеции. Отрезок, который соединяет середины боковых сторон, называется средней линией. Существует несколько видов трапеций: равнобедренная, прямоугольная, криволинейная. Для каждого вида трапеции есть формулы для нахождения площади.
Площадь трапеции
Чтобы найти площадь трапеции, нужно знать длину ее оснований и высоту. Высота трапеции — это отрезок, перпендикулярный основаниям. Пусть верхнее основание — a, нижнее основание — b, а высота — h. Тогда вычислить площадь S можно по формуле:
т.е. взять полусумму оснований, умноженную на высоту.
Также удастся вычислить площадь трапеции, если известно значение высоты и средней линии. Обозначим среднюю линию — m. Тогда
Решим задачу посложнее: известны длины четырех сторон трапеции — a, b, c, d. Тогда площадь отыщется по формуле:
Если известны длины диагоналей и угол между ними, то площадь ищется так:
S = ½ * d1 * d2 * sin α
где d с индексами 1 и 2 — диагонали. В данной формуле в расчете приводится синус угла.
При известных длинах оснований a и b и двух углах при нижнем основании площадь вычисляется так:
Площадь равнобедренной трапеции
Равнобедренная трапеция — это частный случай трапеции. Ее отличие в том, что такая трапеция — это выпуклый четырехугольник с осью симметрии, проходящей через середины двух противоположных сторон. Ее боковые стороны равны.

Найти площадь равнобедренной трапеции можно несколькими способами.
S = c * sin α * (a + c * cos α)
где а — верхнее основание, с — боковая сторона.
S = c * sin α * (b – c * cos α)
S = ½ * (b2 – a2) * tg α
Пусть боковая сторона — с, средняя линия — m, угол — a, тогда:
Иногда в равностороннюю трапецию можно вписать окружность, радиус которой будет — r.
Известно, что в любую трапецию можно вписать окружность, если сумма длин оснований равна сумме длин ее боковых сторон. Тогда площадь найдется через радиус вписанной окружности и угол при нижнем основании:
Такой же расчет производится и через диаметр D вписанной окружности (кстати, он совпадает с высотой трапеции):
Зная основания и угол, площадь равнобедренной трапеции вычисляется так:
(эта и последующие формулы верны только для трапеций с вписанной окружностью).
Через основания и радиус окружности площадь ищется так:
Если известны только основания, то площадь считается по формуле:
Через основания и боковую линию площадь трапеции с вписанным кругом и через основания и среднюю линию — m вычисляется так:
Площадь прямоугольной трапеции
Прямоугольной называется трапеция, у которой одна из боковых сторон перпендикулярна основаниям. В этом случае боковая сторона по длине совпадает с высотой трапеции.
Прямоугольная трапеция представляет из себя квадрат и треугольник. Найдя площадь каждой из фигур, сложите полученные результаты и получите общую площадь фигуры.
Также для вычисления площади прямоугольной трапеции подходят общие формулы для расчета площади трапеции.
В качестве h (высоты) может выступать боковая сторона с. Тогда формула выглядит так:
или на длину боковой перпендикулярной стороны:
S = ½ * d1 * d2 * sin α
Если диагонали перпендикулярны, то формула упрощается до:
Эта формула действительна для оснований. Если брать длины боковых сторон, то одна из них будет равна удвоенному радиусу. Формула будет выглядеть так:
Площадь криволинейной трапеции
Криволинейная трапеция представляет из себя плоскую фигуру, ограниченную графиком неотрицательной непрерывной функции y = f(x), определенной на отрезке [a;b], осью абсцисс и прямыми x = a, x = b. По сути, две ее стороны параллельны друг другу (основания), третья сторона перпендикулярна основаниям, а четвертая представляет из себя кривую, соответствующую графику функции.
Площадь криволинейной трапеции ищут через интеграл по формуле Ньютона-Лейбница:
Так вычисляются площади различных видов трапеций. Но, помимо свойств сторон, трапеции обладают одинаковыми свойствами углов. Как у всех существующих четырехугольников, сумма внутренних углов трапеции равна 360 градусов. А сумма углов, прилежащих к боковой стороне, — 180 градусам.
Площадь трапеции по средней линии и высоте: онлайн-калькулятор
Есть несколько вариантов решения задачи. Выбор способа зависит от данных, указанных в условии. В этом онлайн-калькуляторе площадь трапеции равна произведению средней линии на высоту. Другие возможные способы собраны в разделе на сайте.
Автоматические расчеты не предполагают регистрации и оплату. Тренироваться можно неограниченное количество раз. Сервис позволяет сэкономить на репетиторах и овладеть материалом самостоятельно.
Материалы, которые помогут вам лучше разобраться в теме:
Как найти площадь трапеции через среднюю линию и высоту
С помощью программы можно быстро найти ответ на задание. Для этого не нужно производить никаких действий вручную. Все переводы выполняются автоматически.
Площадь трапеции рассчитывается по формуле:
Кто и почему использует наш сервис:
Если у вас объемный срочный проект, с которым не получается справиться самостоятельно, обратитесь за платными услугами к консультанту. Наш сотрудник подберет преподавателя, который сможет доходчиво объяснить непонятную тему. На момент контрольной или экзамена мы организуем дистанционное сопровождение, во время которого подскажем решение.
Площадь трапеции по сторонам
Как найти площадь трапеции по 4 сторонам?
Чтобы найти площадь трапеции, нужно знать её основания и высоту. Основания известны, следовательно, задача сводится к нахождению высоты трапеции.
Из вершины тупого угла провести прямую, параллельную боковой стороне.
Найти площадь полученного треугольника по формуле Герона. Зная площадь, найти высоту треугольника, которая является также высотой трапеции.
Найти площадь трапеции, основания которой равны 11 см и 28 см, а боковые стороны — 25 см и 26 см.

AD∥BC, AB=25 см, BC=11 см,
CD=26 см, AD=28 см
1) Проведем через вершину C прямую CL, CL∥AB.

По свойству параллелограмма, AL=BC=11 см, CL=AB=25 см. Следовательно, LD=AD-AL=28-11=17 см.
2) Рассмотрим треугольник CDL. Его площадь найдём по формуле Герона
найдём площадь трапеции ABCD:
Провести из тупых углов трапеции две высоты.
В результате получим прямоугольник и два прямоугольных треугольника.
Один из катетов этих треугольников — высота трапеции. Её можно выразить через другие стороны в каждом из треугольников, затем приравнять полученные равенства.
Найти площадь трапеции, основания которой равны 10см и 14 см, а боковые стороны — 13 см и 14 см.
Дано :ABCD — трапеция,
AD∥BC, AB=13 см, BC=10 см,
CD=15 см, AD=14 см

Четырёхугольник BCFK — прямоугольник (так как у него все углы прямые). Поэтому, KF=BC=10 см.
Пусть FD=x см, тогда AK=AD-KF-FD=14-10-x=4-x см.
Рассмотрим треугольник CDF — прямоугольный. По теореме Пифагора
Аналогично, из треугольника ABK
Приравниваем правые части:
Традиционно трапецию изображают именно в таком виде, как на рисунке 1 — с двумя тупыми углами при меньшем основании.
Но в трапеции также могут быть тупыми противоположные углы — как на рисунке 2.
Для трапеции с противоположными тупыми углами верны все рассуждения, приведенные выше, за одним исключением — в этом случае BC=AF=AK+AF.
В разных вариантах трапеции отрезки FD и AK имеют разную длину, но величина высоты, а значит, и площади, одинакова.
2 Comments
Интересное утверждение в решении задачи 2: ‘Четырёхугольник BCFK — прямоугольник (так как у него все углы прямые). Поэтому, BK=CF=10 см.’
Если этот четырёхугольник — прямоугольник, то это ещё не значит, что он квадрат.
Не согласна с этим объяснением. Прокомментируйте подробнее.