Как высчитать среднее значение
Как высчитать среднее значение
Как правильно вычислить среднее значение?
Средняя зарплата… Средняя продолжительность жизни… Практически каждый день мы с вами слышим эти словосочетания, используемые для описания множества одним единственным числом. Но как ни странно, «среднее значение» — достаточно коварное понятие, часто вводящее в заблуждение обычного, неискушенного в математической статистике, человека.
В чем проблема?
Под средним значением чаще всего подразумевается среднее арифметическое, которое очень сильно варьируется под воздействием единичных фактов или событий. И вы не получите реального представления о том, как именно распределены значения, которые вы изучаете.
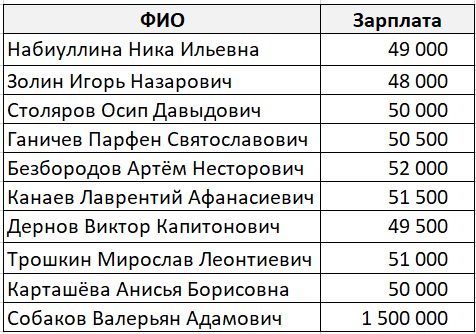
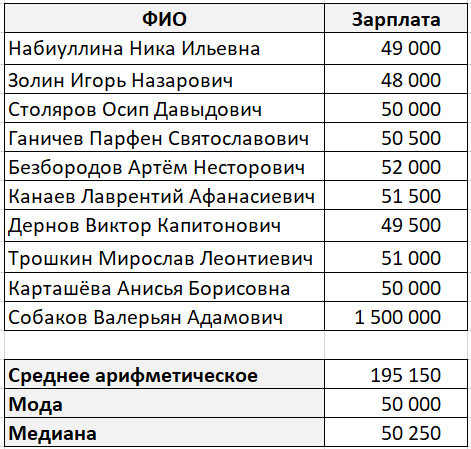
Давайте обратимся к классическому примеру со средней зарплатой.
В какой-то абстрактной компании работает десять сотрудников. Девять из них получают зарплату около 50 000 рублей, а один 1 500 000 рублей (по странному совпадению он же является генеральным директором этой компании).
Средним значением в данном случае будет 195 150 рублей, что согласитесь, неправильно.
Какие способы вычисления среднего бывают?
Первым способом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.
Вторым способом является вычисление моды, то есть наиболее часто встречающегося значения.
Третий способ — это вычисление медианы, то есть значения, которое делит упорядоченную выборку на две половины и находится между ними. А если такого значения нет, то за медиану принимается среднее арифметическое между границами половин выборки.
Мы рассмотрели основные методы нахождения среднего значения, называющиеся мерами центральной тенденции (на самом деле их больше, но это наиболее популярные).
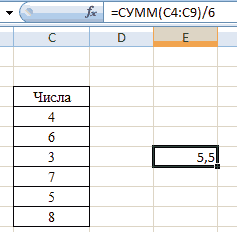
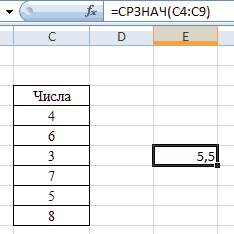
А теперь давайте вернемся к нашему примеру и посчитаем все три варианта среднего при помощи специальных функций Excel:
И вот какие значения у нас получились:
В данном случае мода и медиана гораздо лучше характеризуют среднюю зарплату в компании.
Но что делать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без проблем.
Вычисляем среднее арифметическое на SQL
И чтобы ее использовать достаточно написать вот такой запрос:
Вычисляем моду на SQL
В SQL нет отдельной функции для нахождения моды, но ее легко и быстро можно написать самостоятельно. Для этого нам необходимо узнать, какая из зарплат чаще всего повторяется и выбрать наиболее популярную.
Вычисляем медиану на SQL
Выглядит все это так:
Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Google BigQuery.
Какой способ все-таки использовать?
Из сказанного выше следует, что медиана лучший способ для вычисления среднего значения.
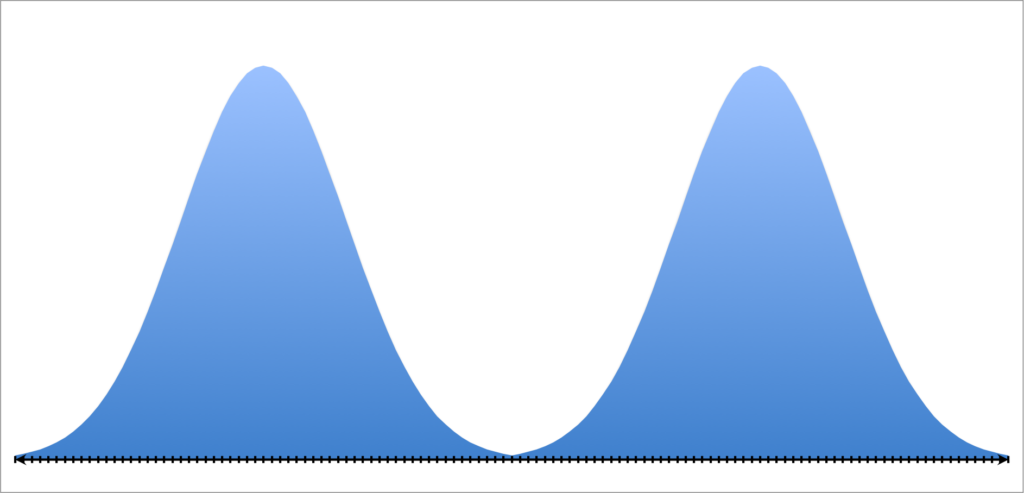
Но это не всегда так. Если вы работаете со средним, то остерегайтесь многомодального распределения:
На графике представлено бимодальное распределение с двумя пиками. Такая ситуация может возникнуть, например, при голосовании на выборах.
В данном случае среднее арифметическое и медиана — это значения, находящиеся где-то посередине и они ничего не скажут о том, что происходит на самом деле и лучше сразу признать, что вы имеете дело с бимодальным распределением, сообщив о двух модах.
А еще лучше разделить выборку на две группы и собрать статистические данные для каждой.
Вывод:
При выборе метода нахождения среднего нужно учитывать наличие выбросов, а также нормальность распределения значений в выборке.
Окончательный выбор меры центральной тенденции всегда лежит на аналитике.
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
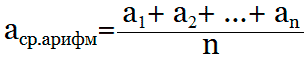
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
Как вычислить среднее арифметическое
Среднее арифметическое — статистический показатель, который демонстрирует среднее значение заданного массива данных. Такой показатель рассчитывается как дробь, в числителе которой стоит сумма всех значений массива, а в знаменателе — их количество. Среднее арифметическое — важный коэффициент, который находит применение в бытовых расчетах.
Смысл коэффициента
Среднее арифметическое — элементарный показатель для сравнения данных и подсчета приемлемого значения. К примеру, в разных магазинах продается банка пива конкретного производителя. Но в одном магазине она стоит 67 рублей, в другом — 70 рублей, в третьем — 65 рублей, а в последнем — 62 рубля. Довольно большой разбег цен, поэтому покупателю будет интересна средняя стоимость банки, чтобы при покупке товара он мог сравнить свои расходы. В среднем банка пива по городу имеет цену:
Средняя цена = (67 + 70 + 65 + 62) / 4 = 66 рублей.
Зная среднюю цену, легко определить где выгодно покупать товар, а где придется переплатить.
Среднее арифметические постоянно используется в статистических расчетах в случаях, если анализируется однородный набор данных. В примере выше — это цена банки пива одной марки. Однако мы не можем сравнить цену на пиво разных производителей или цены на пиво и лимонад, так как в этом случае разброс значений будет больше, средняя цена будет смазана и недостоверна, а сам смысл расчетов исказится до карикатурного «средняя температура по больнице». Для расчета разнородных массивов данных используется среднее арифметическое взвешенное, когда каждое значение получает свой весовой коэффициент.
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Наша программа представляет собой простой и удобный калькулятор для расчета среднего арифметического. Для выполнения расчетов вам понадобится ввести только значения параметров.
Рассмотрим пару примеров
Расчет средней оценки
Многие учителя используют метод среднего арифметического для определения годовой оценки по предмету. Давайте представим, что ребенок получил следующие четвертные отметки по математике: 3, 3, 5, 4. Какую годовую оценку ему поставит учитель? Воспользуемся калькулятором и посчитаем среднее арифметическое. Для начала выберете соответствующее количество полей и введите значения оценок в появившиеся ячейки:
(3 + 3 + 5 + 4) / 4 = 3,75
Учитель округлит значение в пользу ученика, и школьник получит за год твердую четверку.
Расчет съеденных конфет
Давайте проиллюстрируем некоторую абсурдность среднего арифметического. Представим, что у Маши и Вовы было 10 конфет. Маша съела 8 конфет, а Вова — всего 2. Сколько конфет в среднем съел каждый ребенок? При помощи калькулятора легко вычислить, что в среднем дети съели по 5 конфет, что совершенно не соответствует действительности и здравому смыслу. Этот пример показывает, что показатель среднего арифметического важно считать для осмысленных наборов данных.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах. Используйте наши калькуляторы в качестве помощника для решения задач на вычисление среднего арифметического.
Простая формула, чтобы подсчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
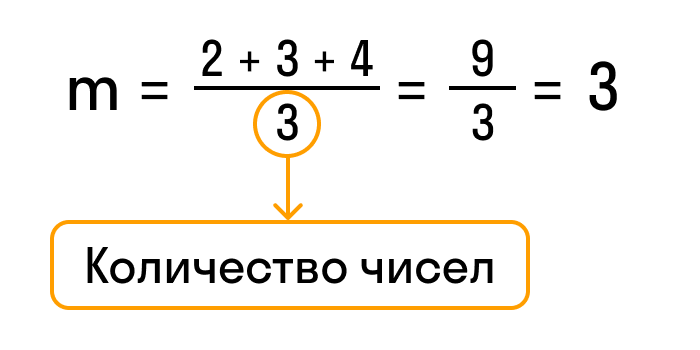
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Расчет среднего значения
В Excel существует несколько способов найти среднее для набора чисел. Например, можно воспользоваться функцией для расчета простого среднего, взвешенного среднего или среднего, исключающего определенные значения.
Чтобы научиться вычислять средние значения, используйте предоставленные образцы данных и описанные ниже процедуры.
Копирование примера данных
Чтобы лучше понять описываемые действия, скопируйте пример данных в ячейку A1 пустого листа.
Создайте пустую книгу или лист.
Выделите приведенный ниже образец данных.
Примечание: Не выделяйте заголовки строк или столбцов (1, 2, 3. A, B, C. ) при копировании данных примера на пустой лист.
Выбор примеров данных в справке
Цена за единицу
Количество заказанных изделий
Среднее качество изделий
Средняя цена изделия
Среднее качество всех изделий с оценкой качества выше 5
Нажмите клавиши 
Выделите на листе ячейку A1, а затем нажмите клавиши 
Расчет простого среднего значения
Выделите ячейки с A2 по A7 (значения в столбце «Качество изделия»).
Расчет среднего для несмежных ячеек
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
На вкладке Формулы щелкните стрелку рядом с кнопкой Автоумма 
Щелкните ячейку, которая содержит только что найденное среднее значение (ячейка A8 в этом примере).
Если используется образец данных, формула отображается в строка формул, =СС00(A2:A7).
В строке формул выделите содержимое между скобками (при использовании примера данных — A2:A7).
Удерживая нажатой клавишу 
Выделенная ссылка на диапазон в функции СРЗНАЧ заменится ссылками на выделенные ячейки. В приведенном примере результат будет равен 8.
Расчет среднего взвешенного значения
В приведенном ниже примере рассчитывается средняя цена за изделие по всем заказам, каждый из которых содержит различное количество изделий по разной цене.
Выделите ячейку A9, расположенную слева от ячейки с текстом «Средняя цена изделия».
На вкладке Формулы нажмите кнопку Вставить функцию, чтобы открыть панель Построитель формул.
В списке построителя формул дважды щелкните функцию СУММПРОИЗВ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СУММПРОИЗВ.
Щелкните поле рядом с надписью массив1 и выделите на листе ячейки с B2 по B7 (значения в столбце «Цена за единицу»).
Щелкните поле рядом с надписью массив2 и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество заказанных изделий»).
В строке формул установите курсор справа от закрывающей скобки формулы и введите /
Если строка формул не отображается, в меню Вид выберите пункт Строка формул.
В списке построителя формул дважды щелкните функцию СУММ.
Выделите диапазон в поле число1, нажмите кнопку DELETE и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество изделий»).
Теперь в строке формул должна содержаться следующая формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).
Нажмите клавишу RETURN.
В этой формуле общая стоимость всех заказов делится на общее количество заказанных изделий, в результате чего получается средневзвешенная стоимость за единицу — 29,38297872.
Расчет среднего, исключающего определенные значения
Вы можете создать формулу, которая исключает определенные значения. В приведенном ниже примере создается формула для расчета среднего качества всех изделий, у которых оценка качества выше 5.
Выделите ячейку A10, расположенную слева от ячейки с текстом «Среднее качество всех изделий с оценкой качества выше 5».
На вкладке Формулы нажмите кнопку Вставить функцию, чтобы открыть панель Построитель формул.
В списке построителя формул дважды щелкните функцию СРЗНАЧЕСЛИ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СРЗНАЧЕСЛИ.
Щелкните поле рядом с надписью диапазон и выделите на листе ячейки с A2 по A7 (значения в столбце «Цена за единицу»).
Щелкните поле рядом с надписью условие и введите выражение «>5».
Нажмите клавишу RETURN.
Такая формула исключит значение в ячейке A7 из расчета. В результате будет получено среднее качество изделий, равное 8,8.
Совет: Чтобы использовать функцию СРЗНАЧЕСЛИ для расчета среднего без нулевых значений, введите выражение «<>0″ в поле условие.
Чтобы научиться вычислять средние значения, используйте предоставленные образцы данных и описанные ниже процедуры.
Копирование примера данных
Чтобы лучше понять описываемые действия, скопируйте пример данных в ячейку A1 пустого листа.
Создайте пустую книгу или лист.
Выделите приведенный ниже образец данных.
Примечание: Не выделяйте заголовки строк или столбцов (1, 2, 3. A, B, C. ) при копировании данных примера на пустой лист.
Выбор примеров данных в справке
Цена за единицу
Количество заказанных изделий
Среднее качество изделий
Средняя цена изделия
Среднее качество всех изделий с оценкой качества выше 5
Нажмите клавиши 
Выделите на листе ячейку A1, а затем нажмите клавиши 
Расчет простого среднего значения
Рассчитаем среднее качество изделий двумя разными способами. Первый способ позволяет быстро узнать среднее значение, не вводя формулу. Второй способ предполагает использование функции «Автосумма» для расчета среднего значения и позволяет вывести его на листе.
Быстрый расчет среднего
Выделите ячейки с A2 по A7 (значения в столбце «Качество изделия»).
Примечание: Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.
Расчет среднего с отображением на листе
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
На панели инструментов Стандартная под названием книги щелкните стрелку рядом с кнопкой 
Результат составляет 8,166666667 — это средняя оценка качества всех изделий.
Расчет среднего для несмежных ячеек
Существует два способа расчета среднего для ячеек, которые не следуют одна за другой. Первый способ позволяет быстро узнать среднее значение, не вводя формулу. Второй способ предполагает использование функции СРЗНАЧ для расчета среднего значения и позволяет вывести его на листе.
Быстрый расчет среднего
Выделите ячейки, для которых вы хотите найти среднее значение. Например, выделите ячейки A2, A4 и A7.
Совет: Чтобы выбрать несмещные ячейки, щелкните их, удерживая 
В приведенном примере результат будет равен 8.
Примечание: Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.
Расчет среднего с отображением на листе
Выберите ячейку, в которой должно отображаться среднее значение, например ячейку A8, которая находится слева ячейки с текстом «Среднее качество изделия» в примере данных.
На панели инструментов Стандартная под названием книги щелкните стрелку рядом с кнопкой 
Щелкните ячейку, которая содержит только что найденное среднее значение (ячейка A8 в этом примере).
Если используется образец данных, формула отображается в строка формул, =СС00(A2:A7).
В строке формул выделите содержимое между скобками (при использовании примера данных — A2:A7).
Удерживая нажатой клавишу 
Выделенная ссылка на диапазон в функции СРЗНАЧ заменится ссылками на выделенные ячейки. В приведенном примере результат будет равен 8.
Расчет среднего взвешенного значения
В приведенном ниже примере рассчитывается средняя цена за изделие по всем заказам, каждый из которых содержит различное количество изделий по разной цене.
Выделите ячейку A9, расположенную слева от ячейки с текстом «Средняя цена изделия».
На вкладке Формулы в разделе Функция выберите пункт Построитель формул.
В списке построителя формул дважды щелкните функцию СУММПРОИЗВ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СУММПРОИЗВ.
В разделе Аргументы щелкните поле рядом с надписью массив1 и выделите на листе ячейки с B2 по B7 (значения в столбце «Цена за единицу»).
В разделе Аргументы щелкните поле рядом с надписью массив2 и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество заказанных изделий»).
В строке формул установите курсор справа от закрывающей скобки формулы и введите /
Если строка формул не отображается, в меню Вид выберите пункт Строка формул.
В списке построителя формул дважды щелкните функцию СУММ.
В разделе Аргументы щелкните диапазон в поле число1, нажмите кнопку DELETE и выделите на листе ячейки с C2 по C7 (значения в столбце «Количество изделий»).
Теперь в строке формул должна содержаться следующая формула: =СУММПРОИЗВ(B2:B7;C2:C7)/СУММ(C2:C7).
Нажмите клавишу RETURN.
В этой формуле общая стоимость всех заказов делится на общее количество заказанных изделий, в результате чего получается средневзвешенная стоимость за единицу — 29,38297872.
Расчет среднего, исключающего определенные значения
Вы можете создать формулу, которая исключает определенные значения. В приведенном ниже примере создается формула для расчета среднего качества всех изделий, у которых оценка качества выше 5.
Выделите ячейку A10, расположенную слева от ячейки с текстом «Среднее качество всех изделий с оценкой качества выше 5».
На вкладке Формулы в разделе Функция выберите пункт Построитель формул.
В списке построителя формул дважды щелкните функцию СРЗНАЧЕСЛИ.
Совет: Чтобы быстро найти функцию, начните вводить ее имя в поле Поиск функции. Например, начните вводить СРЗНАЧЕСЛИ.
В разделе Аргументы щелкните поле рядом с надписью диапазон и выделите на листе ячейки с A2 по A7 (значения в столбце «Цена за единицу»).
В разделе Аргументы щелкните поле рядом с надписью условие и введите выражение «>5».
Нажмите клавишу RETURN.
Такая формула исключит значение в ячейке A7 из расчета. В результате будет получено среднее качество изделий, равное 8,8.
Совет: Чтобы использовать функцию СРЗНАЧЕСЛИ для расчета среднего без нулевых значений, введите выражение «<>0″ в поле условие.
Средние величины и показатели вариации
Понятие и виды средних величин
Существует 2 класса средних величин: степенные и структурные.
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле:
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической простой: (3+4+4+5)/4 = 16/4 = 4.
Средняя арифметическая взвешенная имеет следующий вид:
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Рассчитаем средний балл по формуле средней арифметической взвешенной: (3*1 + 4*2 + 5*1)/4 = 16/4 = 4.
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Средняя арифметическая применяется чаще всего, но бывают случаи, когда необходимо применение других видов средних величин. Рассмотрим такие случаи далее.
Средняя гармоническая
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
Средняя геометрическая
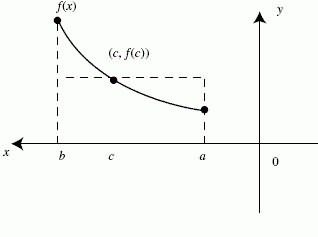
Средняя геометрическая применяется при определении средних относительных изменений, о чем сказано в теме Ряды динамики. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
Средняя квадратическая
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
Главной сферой применения квадратической средней является измерение вариации значений X, о чем пойдет речь позднее в этой лекции.
Средняя кубическая
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
Структурные средние величины
К наиболее часто используемым структурным средним относятся статистическая мода и статистическая медиана.
Статистическая мода
Если X задан дискретно, то мода определяется без вычисления как значение признака с наибольшей частотой. В статистической совокупности бывает 2 и более моды, тогда она считается бимодальной (если моды две) или мультимодальной (если мод более двух), и это свидетельствует о неоднородности совокупности.
Если X задан равными интервалами, то сначала определяется модальный интервал как интервал с наибольшей частотой f. Внутри этого интервала находят условное значение моды по формуле:
где Мо – мода;
ХНМо – нижняя граница модального интервала;
hМо – размах модального интервала (разность между его верхней и нижней границей);
fМо – частота модального интервала;
fМо-1 – частота интервала, предшествующего модальному;
fМо+1 – частота интервала, следующего за модальным.
Если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Статистическая медиана
Если X задан дискретно, то для определения медианы все значения нумеруются от 0 до N в порядке возрастания, тогда медиана при четном числе N будет лежать посередине между X c номерами 0,5N и (0,5N+1), а при нечетном числе N будет соответствовать значению X с номером 0,5(N+1).
Если X задан в виде равных интервалов, то сначала определяется медианный интервал (интервал, в котором заканчивается одна половина частот f и начинается другая половина), в котором находят условное значение медианы по формуле:
где Ме – медиана;
ХНМе – нижняя граница медианного интервала;
hМе – размах медианного интервала (разность между его верхней и нижней границей);
fМе – частота медианного интервала; 
Также как и в случае с модой, при определении медианы если размах интервалов h разный, то вместо частот f необходимо использовать плотности интервалов, рассчитываемые путем деления частот f на размах интервала h.
Показатели вариации
Размах вариации
Размах вариации – это разность между максимальным и минимальным значениями X из имеющихся в изучаемой статистической совокупности:
Недостатком показателя H является то, что он показывает только максимальное различие значений X и не может измерять силу вариации во всей совокупности.
Cреднее линейное отклонение
Например, студент сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4. Рассчитаем среднее линейное отклонение простое: Л = (|3-4|+|4-4|+|4-4|+|5-4|)/4 = 0,5.
Вернемся к примеру про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5. Ранее уже была рассчитана средняя арифметическая = 4 и среднее линейное отклонение простое = 0,5. Рассчитаем среднее линейное отклонение взвешенное: Л = (|3-4|*1+|4-4|*2+|5-4|*1)/4 = 0,5.
Линейный коэффициент вариации
С помощью линейного коэффициента вариации можно сравнивать вариацию разных совокупностей, потому что в отличие от среднего линейного отклонения его значение не зависит от единиц измерения X.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, линейный коэффициент вариации составит 0,5/4 = 0,125 или 12,5%.
Дисперсия
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил оценки: 3, 4, 4 и 5, ранее уже была рассчитана средняя арифметическая = 4. Тогда дисперсия простая Д = ((3-4) 2 +(4-4) 2 +(4-4) 2 +(5-4) 2 )/4 = 0,5.
В рассматриваемом примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию взвешенную: Д = ((3-4) 2 *1+(4-4) 2 *2+(5-4) 2 *1)/4 = 0,5.
Если преобразовать формулу дисперсии (раскрыть скобки в числителе, почленно разделить на знаменатель и привести подобные), то можно получить еще одну формулу для ее расчета как разность средней квадратов и квадрата средней:
В уже знакомом нам примере про студента, который сдал 4 экзамена и получил следующие оценки: 3, 4, 4 и 5, рассчитаем дисперсию методом разности средней квадратов и квадрата средней:
Д = (3 2 *1+4 2 *2+5 2 *1)/4-4 2 = 16,5-16 = 0,5.

Cреднее квадратическое отклонение
Выше уже было рассказано о формуле средней квадратической, которая применяется для оценки вариации путем расчета среднего квадратического отклонения, обозначаемое малой греческой буквой сигма:
Еще проще можно найти среднее квадратическое отклонение, если предварительно рассчитана дисперсия, как корень квадратный из нее:
В примере про студента, в котором выше рассчитали дисперсию, найдем среднее квадратическое отклонение как корень квадратный из нее:
.
Квадратический коэффициент вариации
В примере про студента, в котором выше рассчитали среднее квадратическое отклонение, найдем квадратический коэффициент вариации V = 0,707/4 = 0,177, что меньше критериального значения 0,333, значит вариация слабая и равна 17,7%.
Среднее арифметическое нескольких чисел
Среднее арифметическое множества чисел — число, равное сумме всех чисел множества, делённой на их количество.
Для трёх чисел необходимо сложить их и разделить на 3:
Для четырёх чисел необходимо сложить их и разделить на 4:
Данный онлайн калькулятор поможет вычислить среднее арифметическое ряда чисел.
Вводите каждое новое число в отдельную ячейку. Для добавления ячейки нажмите на кнопку со знаком «+».
Онлайн калькуляторы
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
8.3. Средние величины в статистике
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, являются средние показатели (средняя величина).
Средняя величина – представляет обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Показатель в форме средней величины выражает типичные черты и дает обобщающую характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.
Значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.
Сущность средней заключается, в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.
ВИДЫ СРЕДНИХ ВЕЛИЧИН наиболее часто применяемых на практике:
Выбор средней величины зависит от содержания осредняемого признака и конкретных данных, по которым ее приходится вычислять.
ФОРМУЛЫ СРЕДНИХ ВЕЛИЧИН
Таблица 8.2 – Результаты опроса работников офиса
Как определить подходящую меру центральной тенденции?
Мера центральной тенденции (measure of central tendency) представляет из себя статистическую величину, которая характеризует целый набор данных одним единственным числом. Ее также называют мерой центрального расположения (measure of central location). Она описывает, как выглядит приблизительный центр набора данных.
Но сам по себе термин “центр” может подразумевать немного разные значения в зависимости от конкретной ситуации. Вы можете считать “центром” среднее арифметическое. Вы также можете назвать “центром” данные, которые просто находятся в середине вашей выборки. А еще вы можете рассматривать в качестве “центра” данные, которые повторяются чаще всего. Все эти центры по-своему характеризуют ваши данные.
Поскольку человеческое понимание “центра” может разниться, статистика позаботилась определить каждый вариант. Таким образом мы имеем следующие общепринятые меры центральной тенденции:
В этой статье я расскажу, каким образом распределение вашего набора данных играет роль в выборе подходящей меры центральной тенденции. А объяснять я буду это на примере реальных наборов данных.
1. Среднее арифметическое
Среднее арифметическое — это среднее значение всех элементов в наборе данных. Оно рассчитывается как сумма всех значений, деленная на общее количество значений.
Среднее арифметическое = сумма всех значений / общее количество значений
Когда следует использовать среднее арифметическое?
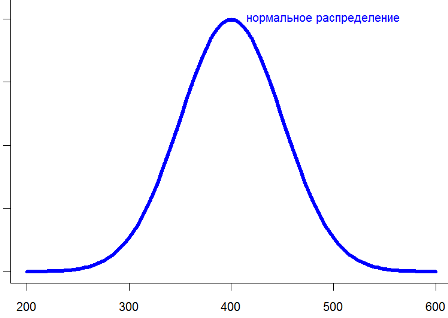
Среднее арифметическое лучше всего использовать для описания данных, которые имеют нормальное распределение. Нормальное распределение — это когда построив график по “значениям” и их “частоте” (количеству появлений каждого значения в наборе данных), вы получаете кривую, по форме напоминающую колокол. Центр этой кривой совпадает со средним арифметическим.
Пример — набор данных с длинами крыльев комнатной мухи
В качестве примера я буду использовать реальный набор данных — это набор данных с длинами крыльев комнатной мухи, который естественным образом имеет нормальное распределение.
Источник набора данных: [Sokal, R.R. and F.J. Rohlf, 1968. Biometry, Freeman Publishing Co., p 109. Original data from Sokal, R.R. and P.E. Hunter. 1955. A morphometric analysis of DDT-resistant and non-resistant housefly strains Ann. Entomol. Soc. Amer. 48: 499-507.]
Набор данных содержит длины крыльев комнатной мухи в миллиметрах. В нем 100 элементов.

Я построил гистограмму (по “значениям” и “количествам повторений этих значений”) этих данных, которую вы можете наблюдать ниже. Если мы проведем по внешним краям столбцов плавную линию, то она образует колоколообразную кривую. Вычислив среднее арифметическое значение этих данных, мы получим 45,5. А теперь давайте поищем на приведенном ниже графике полученное значение 45,5. Он находится прямо по середине.
Колоколообразная кривая со средним значением в центре дает нам четкое понимание, что этот набор данных имеет нормальное распределение.
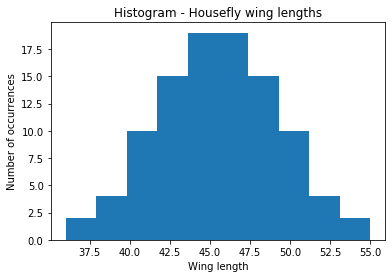
Это хороший пример, наглядно демонстрирующий, что для нормально распределенных данных имеет смысл использовать “среднее арифметическое” как меру центральной тенденции.
Когда НЕ стоит использовать среднее арифметическое?
Хотя среднее арифметическое является одной из основных мер центральной тенденции, иногда (на самом деле очень часто) оно наоборот может ввести вас в заблуждение. Данные из реального мира не всегда имеют нормальное распределение. В подавляющем большинстве случаев есть вероятность, что ваши данные ассиметричны.
Ассиметричные данные — это данные, в которых несколько элементов у верхнего или нижнего пределов имеют заметно отличающийся паттерн по сравнению с остальной частью набора данных.
Пример — набор данных с зарплатами игроков NBA
Давайте посмотрим на набор данных с зарплатами игроков NBA. Этот набор данных содержит зарплаты в долларах США за период с 2017 по 2018 годы.
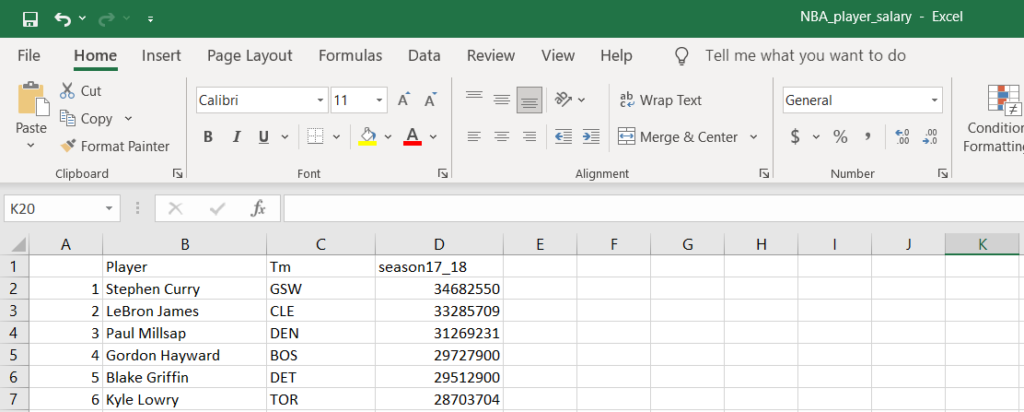
Я построил гистограмму столбца c зарплатой (название столбца “season17_18”).
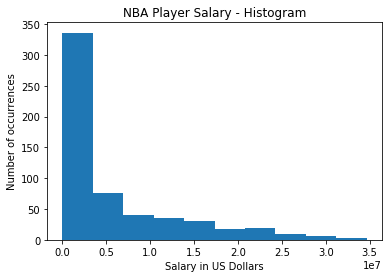
Глядя на приведенное выше распределение, становится очевидным, что данные распределены не нормально. Из 573 игроков более 300 получают зарплату ниже 2,5 миллионов долларов (из графика выше). Но когда мы вычисляем среднее арифметическое заработной платы, оно составляет 5,85 миллиона долларов.
Как вы считаете, годится ли среднее арифметическое в качестве лучшего представления этих данных в целом?
Уж точно нет. Те немногие игроки, которые получали огромные зарплаты, утащили среднее арифметическое далеко от центра. Это называется асимметрией данных.
Не имеет смысла и говорить о том, что среднее арифметическое, которое составляет 5,85 миллиона, является центром, потому что абсолютное большинство из игроков получили зарплату менее 2,5 миллиона долларов.
Таким образом, в случае подобных асимметрий наборов данных среднее арифметическое хорошим выбором для представления данных не является. Здесь нам может помочь медиана.
2. Медиана
Медиана — это значение, которое находится в центре (прямо посередине), если данные расположены в порядке возрастания или убывания.
Если общее количество значений в наборе данных нечетное, то в центральной позиции будет только одно число. Это и будет наша медиана. Если общее количество значений в наборе данных четное, в центральной позиции будет два значения. В этом случае медиана представляет собой среднее значение этих двух значений.
Когда следует использовать медиану?
Если набор данных асимметричен или содержит выбросы, среднее арифметическое — не лучший способ представления данных. В таком случае как меру центральной тенденции можно использовать медиану. Выбросы не портят медиану. Потому что само название “выбросы” означает, что они располагаются снаружи, либо в нижнем, либо в верхнем диапазоне. В таком случае медиана — это среднее значение, не нарушенное выбросами.
Еще раз давайте рассмотрим ассиметричный набор данных с зарплатами игроков NBA. (Который мы рассматривали в предыдущем разделе “Когда НЕ стоит использовать среднее арифметическое?”). Медиана по зарплате составляет 2,38 миллиона долларов.
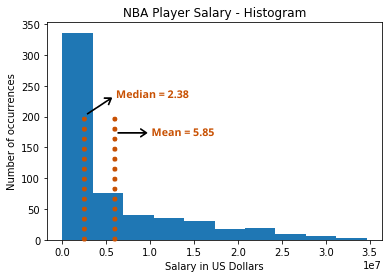
Это значение находится в первой столбце. Обратите внимание, что ось X это 10^7. Итак, первый столбик представляет зарплату до 2,5 миллионов. Таким образом, медианное значение 2,38 миллиона лучше всего представляет эти данные, потому что большинство игроков получают зарплату, близкую к этому показателю.
Когда НЕ стоит использовать медиану?
Если и среднее арифметическое, и медиана одного и того же набора данных не сильно отклоняются, то можно использовать обе эти меры. В любом случае расчет среднего арифметического предполагает учет всех элементов данных и их усреднение. Таким образом, логичнее, что среднее арифметическое является более точной мерой (когда среднее арифметическое и медиана не сильно отклоняются).
Как определить, является ли ваш набор данных асимметричным или содержит выбросы?
Самый банальный способ определить, является ли ваш набор данных асимметричным или содержит выбросы, — это вычислить среднее арифметическое и медиану. Если обе меры не сильно отклоняются, то с вашим набором данных все в порядке. И вы сэкономили время, которое в противном случае было бы потрачено на очистку и преобразование данных.
Если среднее арифметическое и медиана очень сильно отклоняются, ваш набор данных асимметричен или содержит выбросы. Следующий шаг — провести исследование с целью выявить и удалить выбросы, если таковые имеются. Или применить какое-либо преобразование, чтобы уменьшить асимметрию в ваших данных, если таковая имеется.
3. Мода
Мода — это значение, которое чаще всего встречается в наборе данных. В гистограмме мода — это значение с самым высоким столбцом.
Если набор данных имеет более одного значения с одинаковой максимальной частотой появления, набор данных имеет мультимодальное распределение, поскольку он имеет несколько мод. Если в наборе данных нет повторяющихся значений, то и моды у него тоже нет.
Когда стоит использовать моду?
Моду можно использовать для анализа часто встречающихся значений как числовых, так и категориальных данных.
Пример — Простое перечисление
Ниже приведен учебный набор данных, отражающий любимый вид искусства семерых человек. Построим частотный график (гистограмму).
data_art = [‘music’, ‘painting’, ‘pottery’, ‘painting’, ‘dance’, ‘music’, ‘music’]

Во многих областях машинного обучения возникают функции многих переменных и их производные. Такие производные ещё называют «матричными». На открытом уроке мы поговорим про отличие таких производных от обычных, изучаемых в школе, разберём необходимую теорию, научимся такие производные считать, а также посмотрим, где и как матричные производные используются. Регистрация открыта по ссылке для всех желающих.
Как вычислить среднее арифметическое взвешенное
Среднее арифметическое — это статистический показатель, иллюстрирующий среднее значение набора данных, который рассчитывается как сумма всех значений, деленная на их количество. Это важный коэффициент, получивший широкое распространение в прикладных науках.
Что такое среднее арифметическое
Суть данного показателя проще всего продемонстрировать на примере. Торговец продает на рынке яблоки. В понедельник ему удалось продать 54 кг, во вторник — 47 кг, а в среду — 61 кг. Торговец хочет спланировать свои продажи и ему интересно, сколько килограмм фруктов он продает в среднем за день. Вот здесь на сцену и выходит среднее арифметическое. Для его определения необходимо суммировать значения показателей и разделить на их количество.
Среднее = (54 + 47 + 61) / 3 = 54 кг
Торговец выяснил, что в среднем он продает 54 кг яблок в день и может грамотно спрогнозировать свои затраты на покупку товара. Так как килограмм яблок стоит 10 рублей, то в день наш коммерсант зарабатывает в среднем 540 рублей.
Среднее арифметическое широко используется в статистике в случаях, если рассматривается набор однородных данных. В нашем случае это были только яблоки. Однако если торговец расширит свой ассортимент и добавит на прилавки еще и апельсины? Как изменится средняя стоимость одной единицы товара?
Пусть в понедельник торговец реализовал 23 кг апельсинов, во вторник — 28 кг, а в среду — 21 кг. Средний уровень продаж апельсинов составит:
Среднее = (28 + 21 + 23) / 3 = 24 кг.
Так как цена одного килограмма цитрусов составляет 20 рублей, то средний доход от продажи апельсинов составит 480 рублей в день.
Теперь решим простую на первый взгляд задачу. Какова средняя стоимость реализации одного килограмма любого товара? Неискушенный аналитик решит эту задачу как:
Среднее = (20 + 10) / 2 = 15 рублей,
за килограмм апельсинов или яблок. Однако не все так просто. В случае с разнородными данными важно учитывать их вес.
Среднее арифметическое взвешенное
Данный показатель используется при расчете среднего арифметического для разных данных, каждое из которых имеет свой вес. Для определения взвешенного параметра необходимо каждое значение умножить на свой вес, суммировать эти произведения, после чего разделить на сумму весов.
В данном случае у нас есть средний вес каждого вида фруктов и его необходимо учесть для определения средней цены одного килограмма товара. На практике это выглядит так:
Среднее взвешенное = (20 × 24 + 10 × 54) / (24 + 54) = 13,07.
Естественно, 13,07 не сильно отличается от 15, однако чем больше слагаемых и больший разброс весов, тем сильнее отличается среднее взвешенное от простого среднего арифметического. Также очевидно, что если все веса равны единице, то среднее взвешенное становится равным среднему арифметическому.
Что выбрать?
Если требуется найти среднее значение одного элемента из однородного набора, то достаточно отыскать среднее арифметическое. Именно это мы делали при поиске среднего уровня продажи яблок или апельсинов за день. Если требуется найти среднее между разными элементами, принадлежащими к разным группам или отыскать среднее средних, то для расчета используется среднее арифметическое взвешенное.
Наша программа представляет собой калькулятор для расчета среднего арифметического и его взвешенного варианта. В меню калькулятора вы можете выбрать тип искомого параметра. Для расчета среднего арифметического вам понадобится ввести только значения параметров. В случае необходимости вы можете добавить дополнительные ячейки.
Для расчета взвешенного среднего выберите соответствующий пункт в меню калькулятора, укажите значения и их вес. Рассмотрим на примерах, как рассчитывать взвешенное значение.
Примеры из реальной жизни
Подсчет средней зарплаты
Пусть на вашем предприятии числятся сотрудники, каждый из которых получает зарплату в соответчики с должностью. Для рекламного проспекта о поиске персонала вы хотите уточнить, на какую среднюю зарплату может рассчитывать соискатель. Вы знаете, что:
Для вычисления средней зарплаты на предприятии вам потребуется ввести в ячейки значений размер зарплаты, а в ячейки весов — количество сотрудников, которые ее получают. Калькулятор мгновенно выдаст вам результат, что средняя зарплата равна 19 540 рублей. Без учета веса значений среднее арифметическое было бы равно 22 666 рублей, что уже значительно отличается от взвешенного значения.
Средняя скорость автомобиля
Допустим, водитель ехал по городскому проспекту со скоростью 60 км/ч в течение одного часа. Затем он выехал на автомагистраль, увеличил скорость до 120 км/ч и ехал так три часа, после чего свернул на проселочную дорогу и со скоростью 40 км/ч ехал еще два часа. С какой средней скоростью ехал водитель? В этой задаче в качестве веса выступает время езды, а значений — скорость. Выглядит это так:
Введем эти данные в форму калькулятора и получим ответ: средняя скорость автомобиля составляет 83,3 км/ч. Без учета времени средняя скорость была бы равна 73,3 км/ч, что неверно.
Заключение
Расчет среднего арифметического взвешенного широко используется в прикладных науках. Этот параметр популярен не только в статистике, но и в физике, экономике или финансах. Используйте наши калькуляторы в качестве помощника для решения практических и теоретических задач.
Расчет среднего значения в программе Microsoft Excel
В процессе различных расчетов и работы с данными довольно часто требуется подсчитать их среднее значение. Оно рассчитывается путем сложения чисел и деления общей суммы на их количество. Давайте выясним, как вычислить среднее значение набора чисел при помощи программы Microsoft Excel различными способами.
Стандартный способ вычисления
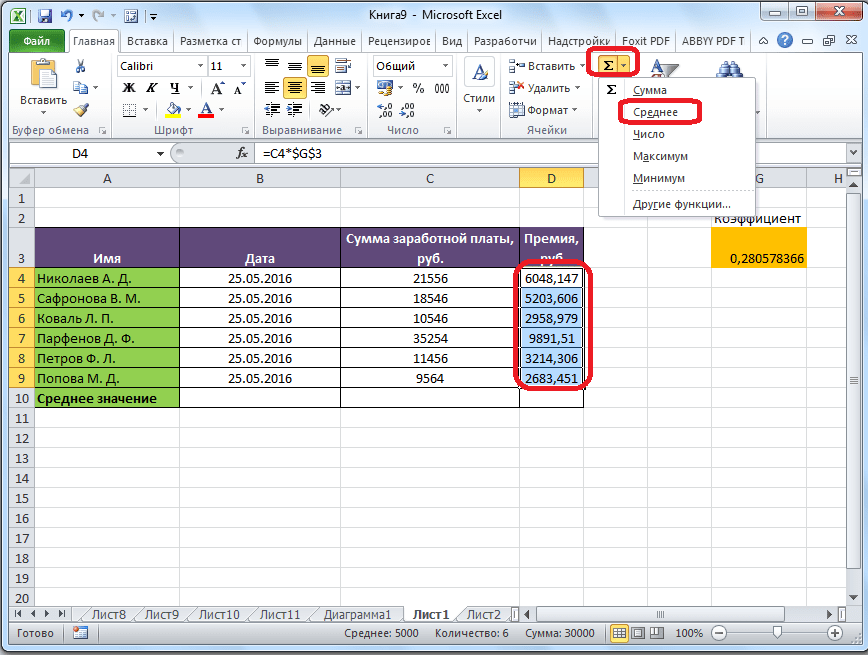
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».
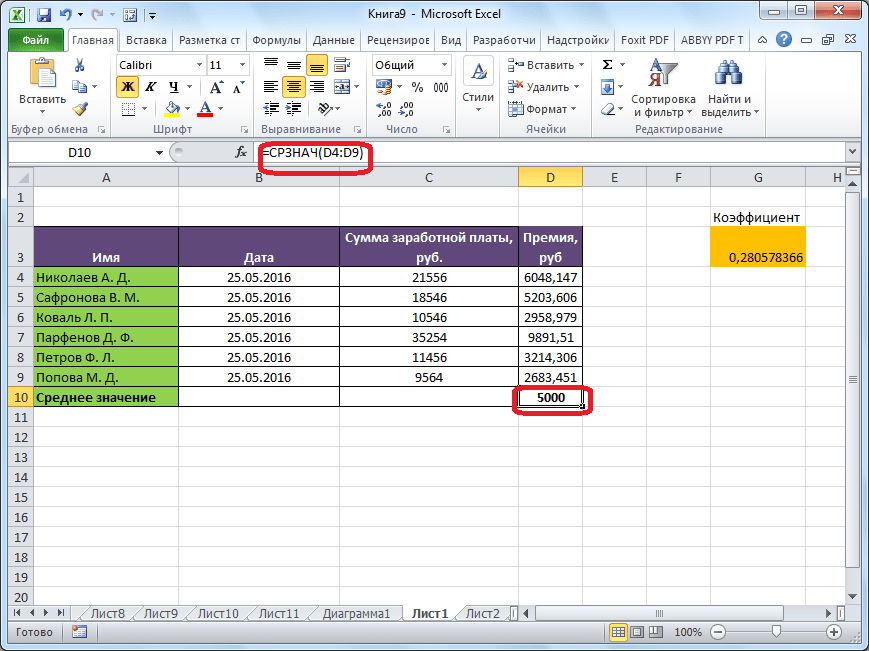
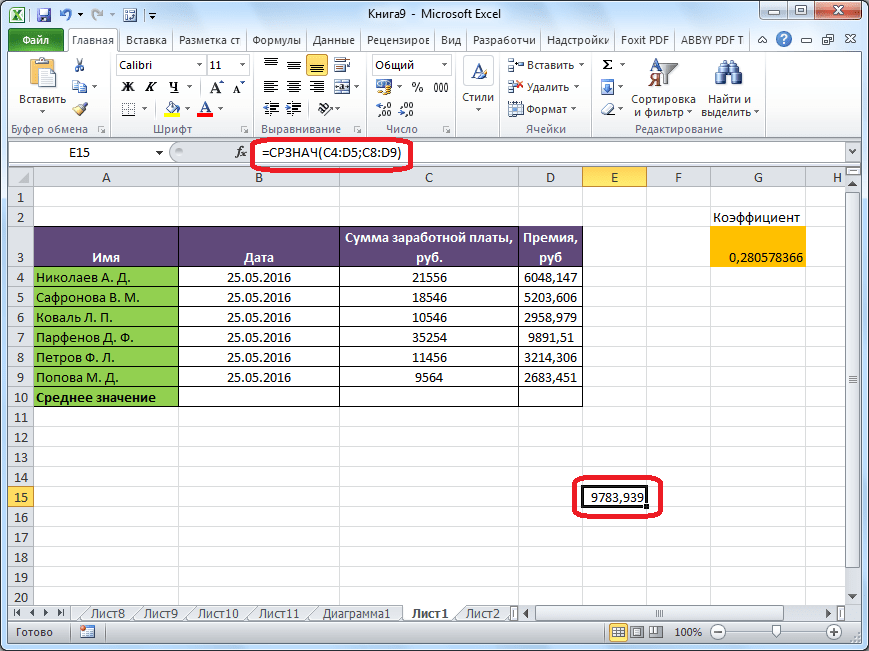
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.
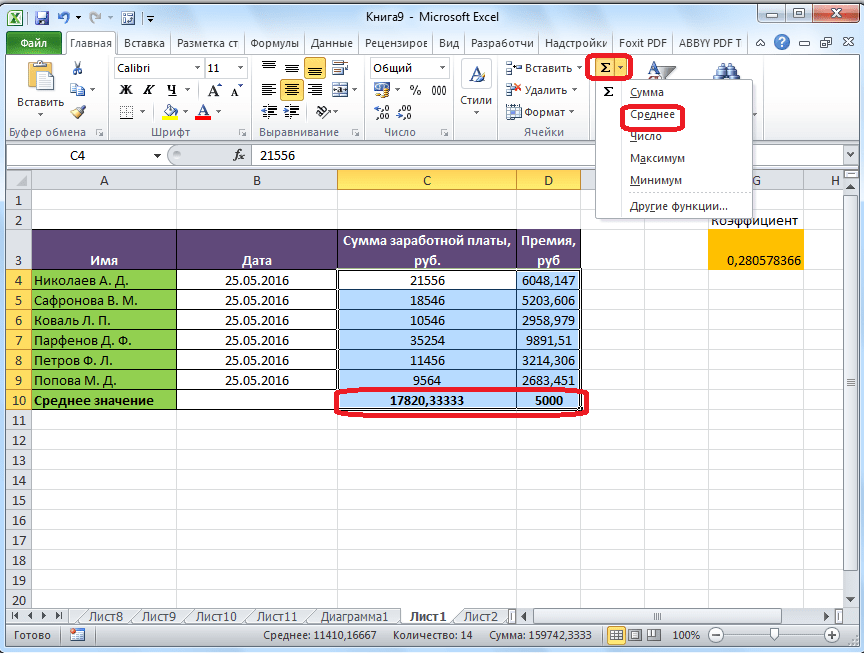
Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.
Вычисление с помощью Мастера функций
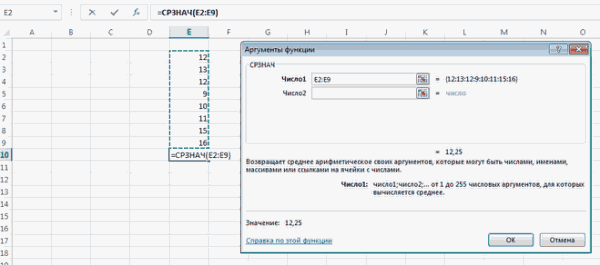
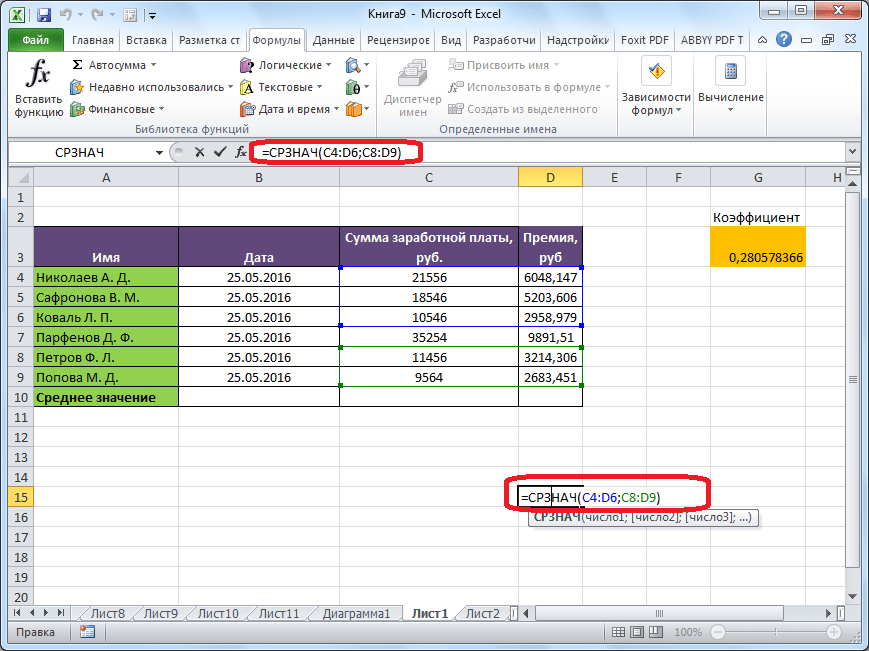
Для случаев, когда нужно подсчитать среднюю арифметическую массива ячеек, или разрозненных ячеек, можно использовать Мастер функций. Он применяет все ту же функцию «СРЗНАЧ», известную нам по первому методу вычисления, но делает это несколько другим способом.
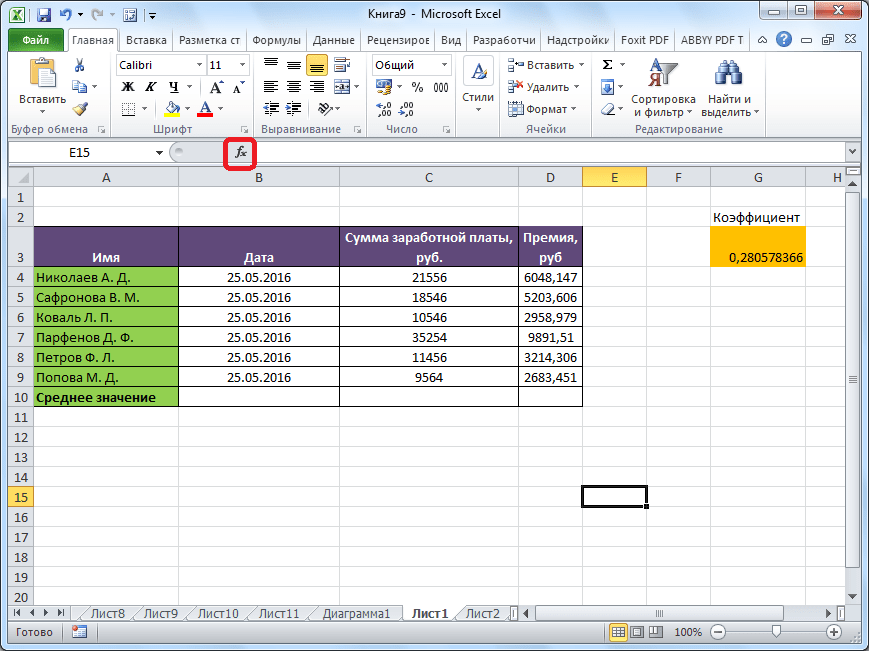
Кликаем по ячейке, где хотим, чтобы выводился результат подсчета среднего значения. Жмем на кнопку «Вставить функцию», которая размещена слева от строки формул. Либо же, набираем на клавиатуре комбинацию Shift+F3.
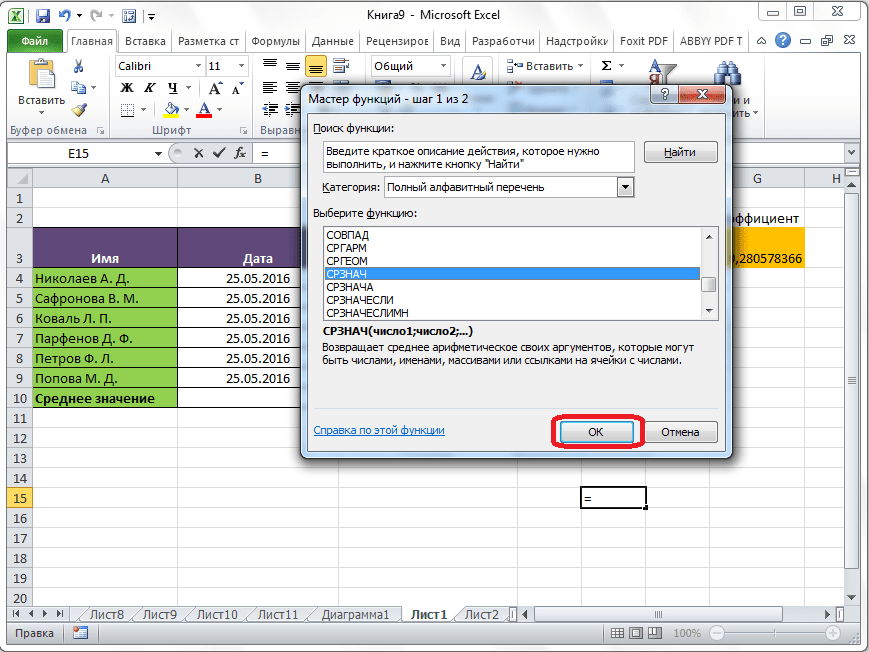
Запускается Мастер функций. В списке представленных функций ищем «СРЗНАЧ». Выделяем его, и жмем на кнопку «OK».
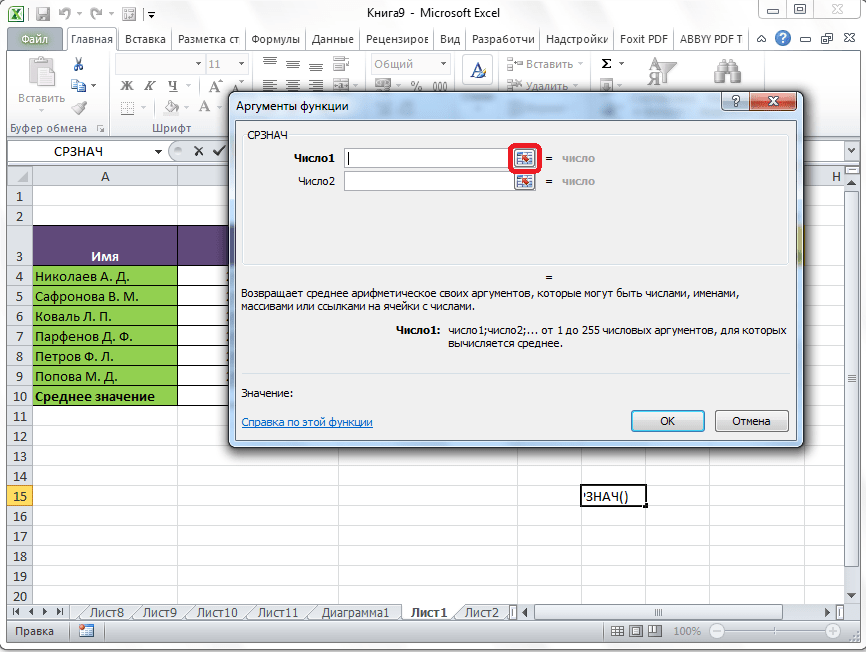
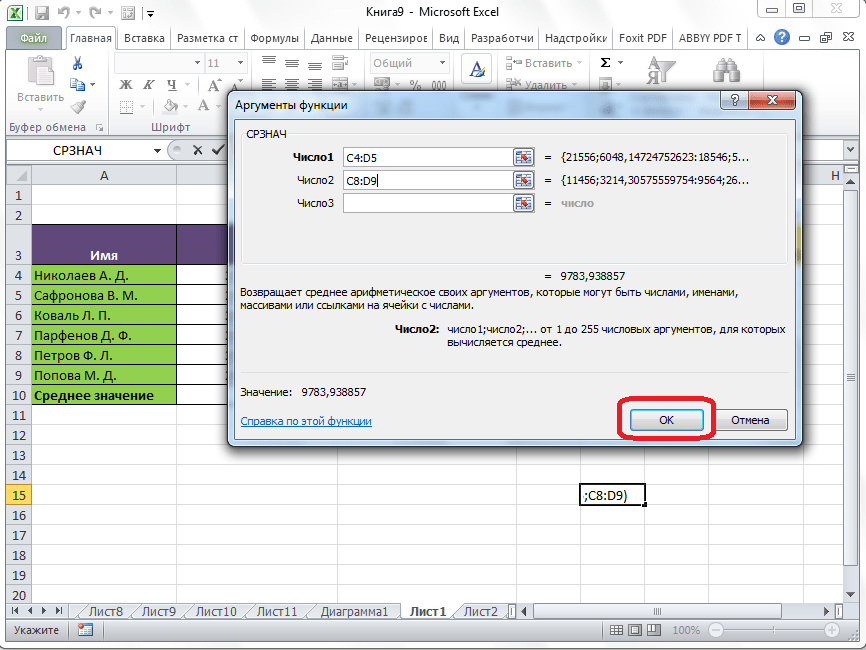
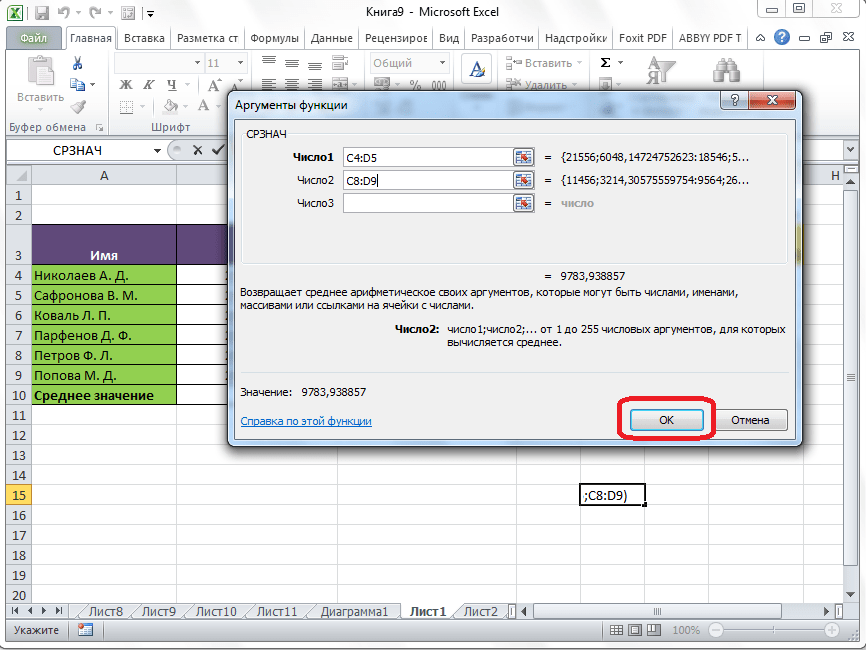
Открывается окно аргументов данной функции. В поля «Число» вводятся аргументы функции. Это могут быть как обычные числа, так и адреса ячеек, где эти числа расположены. Если вам неудобно вводить адреса ячеек вручную, то следует нажать на кнопку расположенную справа от поля ввода данных.
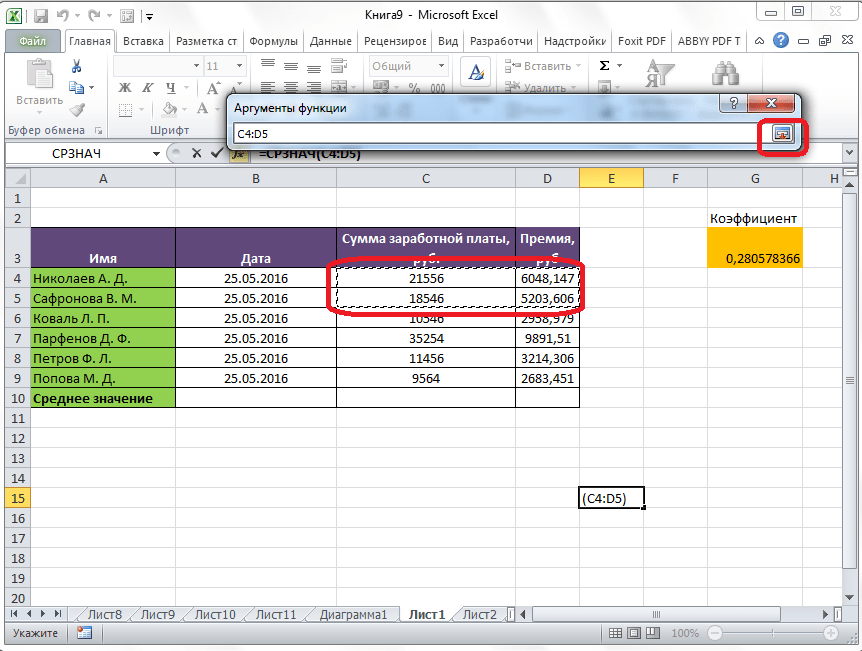
После этого, окно аргументов функции свернется, а вы сможете выделить ту группу ячеек на листе, которую берете для расчета. Затем, опять нажимаете на кнопку слева от поля ввода данных, чтобы вернуться в окно аргументов функции.
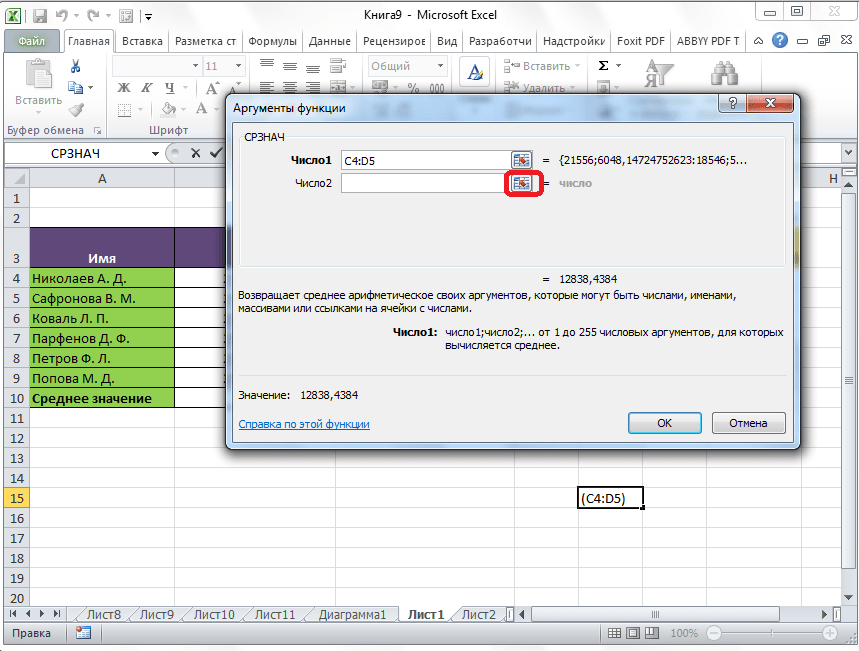
Если вы хотите подсчитать среднее арифметическое между числами, находящимися в разрозненных группах ячеек, то те же самые действия, о которых говорилось выше, проделывайте в поле «Число 2». И так до тех пор, пока все нужные группы ячеек не будут выделены.
После этого, жмите на кнопку «OK».
Результат расчета среднего арифметического будет выделен в ту ячейку, которую вы выделили перед запуском Мастера функций.
Панель формул
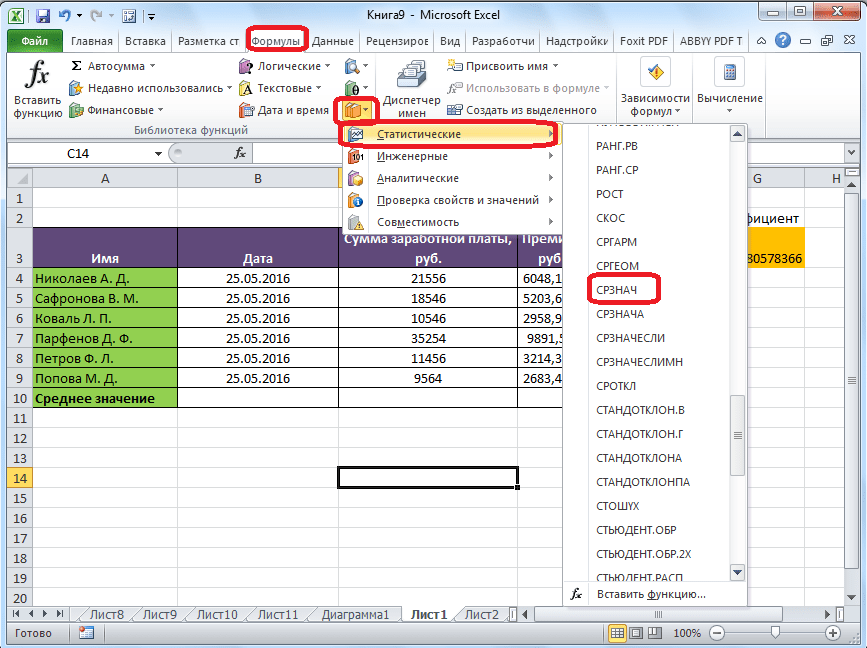
Существует ещё третий способ запустить функцию «СРЗНАЧ». Для этого, переходим во вкладку «Формулы». Выделяем ячейку, в которой будет выводиться результат. После этого, в группе инструментов «Библиотека функций» на ленте жмем на кнопку «Другие функции». Появляется список, в котором нужно последовательно перейти по пунктам «Статистические» и «СРЗНАЧ».
Затем, запускается точно такое же окно аргументов функции, как и при использовании Мастера функций, работу в котором мы подробно описали выше.
Дальнейшие действия точно такие же.
Ручной ввод функции
Но, не забывайте, что всегда при желании можно ввести функцию «СРЗНАЧ» вручную. Она будет иметь следующий шаблон: «=СРЗНАЧ(адрес_диапазона_ячеек(число); адрес_диапазона_ячеек(число)).
Конечно, этот способ не такой удобный, как предыдущие, и требует держать в голове пользователя определенные формулы, но он более гибкий.
Расчет среднего значения по условию
Кроме обычного расчета среднего значения, имеется возможность подсчета среднего значения по условию. В этом случае, в расчет будут браться только те числа из выбранного диапазона, которые соответствуют определенному условию. Например, если эти числа больше или меньше конкретно установленного значения.
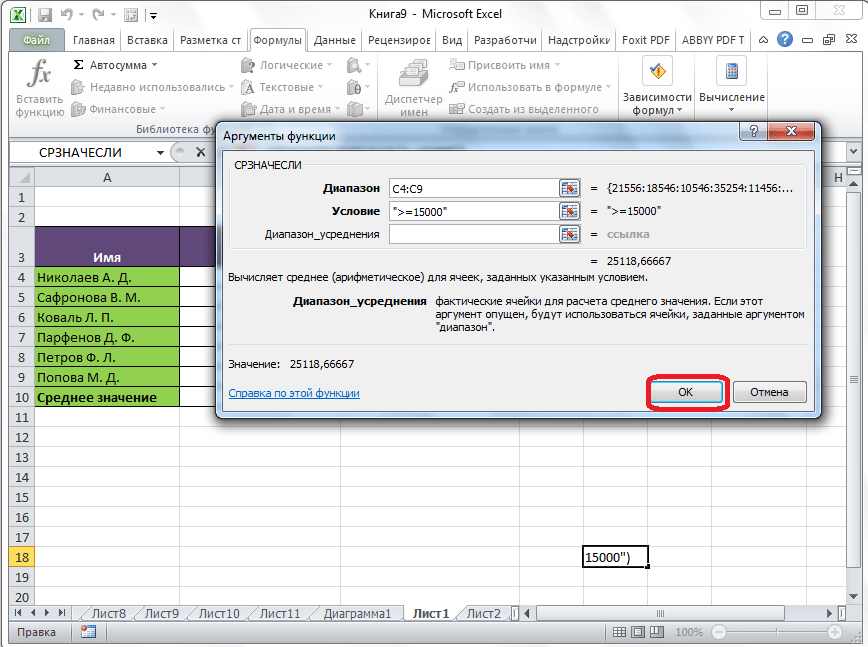
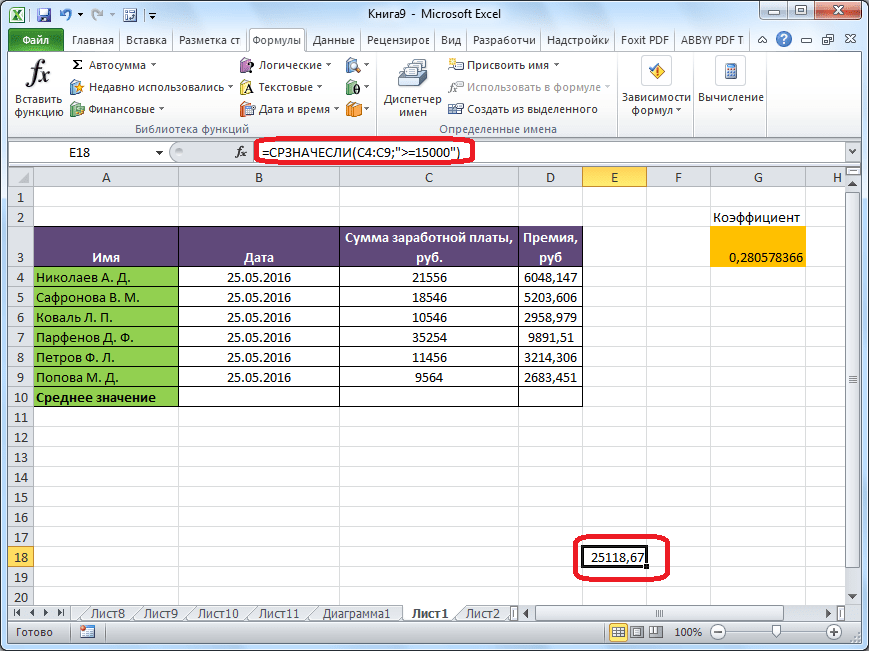
Для этих целей, используется функция «СРЗНАЧЕСЛИ». Как и функцию «СРЗНАЧ», запустить её можно через Мастер функций, из панели формул, или при помощи ручного ввода в ячейку. После того, как открылось окно аргументов функции, нужно ввести её параметры. В поле «Диапазон» вводим диапазон ячеек, значения которых будут участвовать в определении среднего арифметического числа. Делаем это тем же способом, как и с функцией «СРЗНАЧ».
А вот, в поле «Условие» мы должны указать конкретное значение, числа больше или меньше которого будут участвовать в расчете. Это можно сделать при помощи знаков сравнения. Например, мы взяли выражение «>=15000». То есть, для расчета будут браться только ячейки диапазона, в которых находятся числа большие или равные 15000. При необходимости, вместо конкретного числа, тут можно указать адрес ячейки, в которой расположено соответствующее число.
Поле «Диапазон усреднения» не обязательно для заполнения. Ввод в него данных является обязательным только при использовании ячеек с текстовым содержимым.
Когда все данные введены, жмем на кнопку «OK».
После этого, в предварительно выбранную ячейку выводится результат расчета среднего арифметического числа для выбранного диапазона, за исключением ячеек, данные которых не отвечают условиям.
Как видим, в программе Microsoft Excel существует целый ряд инструментов, с помощью которых можно рассчитать среднее значение выбранного ряда чисел. Более того, существует функция, которая автоматически отбирает числа из диапазона, не соответствующие заранее установленному пользователем критерию. Это делает вычисления в приложении Microsoft Excel ещё более удобными для пользователей.
Вычисление среднего значения ряда чисел
Предположим, вам нужно найти среднее количество дней для выполнения задач разными сотрудниками. Или вы хотите вычислить среднюю температуру для определенного дня на основе 10-летнего промежутка времени. Существует несколько способов расчета среднего для группы чисел.
Функция СРЗНАЧ вычисляет среднее значение, то есть центр набора чисел в статистическом распределении. Существует три наиболее распространенных способа определения среднего значения:
Среднее значение Это арифметическое и вычисляется путем с добавления группы чисел и деления на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана Среднее число числа. Половина чисел имеют значения больше медианой, а половина чисел имеют значения меньше медианой. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода Наиболее часто встречается число в группе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. В акосимном распределении группы чисел они могут быть другими.
Выполните действия, описанные ниже.
Щелкните ячейку снизу или справа от чисел, для которых необходимо найти среднее.
На вкладке «Главная» в группе «Редактирование» щелкните стрелку рядом с кнопкой » 
Для этого используйте функцию С AVERAGE. Скопируйте приведенную ниже таблицу на пустой лист.
Среднее значение всех чисел в списке выше (9,5).
Среднее значение 3-го и последнего числа в списке (7,5).
Среднее значение чисел в списке за исключением тех, которые содержат нулевые значения, например ячейка A6 (11,4).
Для этой задачи используются функции СУММПРОИВ И СУММ. В этом примере вычисляется средняя цена за единицу для трех покупок, при которой каждая покупка приобретает различное количество единиц по разной цене.
Скопируйте приведенную ниже таблицу на пустой лист.
Правильное среднее
Существует много видов средних, но в каждой ситуации только одно из них правильное. Только один вид среднего следует использовать в каждом конкретном случае, и ошибка может вам стоить очень дорого.
Дело в том, что в основе такого усреднения лежит закон больших чисел и допущение, что исходная величина распределена нормально. А это подразумевает, что возможные значения сконцентрированы вокруг некоторого наиболее частого значения, а отклонения и в большую, и в меньшую сторону относительно невелики и равновероятны.
В следующих записях я приведу интересные примеры неправильного усреднения, а сейчас перейдем к другим видам среднего.
Сначала, наверное, может показаться, что правильное значение 65 км/ч, потому что (50+80)/2 = 65.
Однако быстро становится понятно, что если бы другой автомобиль двигался со средней скоростью, то он провел бы в пути столько же времени, что и первый. Именно в этом смысл усреднения в данном случае.
И вот тут на помощь приходит среднее гармоническое:
Для нашей задачи искомое среднее равно 2/(1/50+1/80)=61.54 км/ч. И действительно в первом случае автомобиль затратил 2 часа на преодоление 100 км со скоростью 50 км/ч и еще 1.25 часа ему потребовалось на следующие 100 км, потому что скорость возросла до 80 км/ч. Таким образом, всего ушло 3.25 часа.
Если бы автомобиль все 200 км двигался со скоростью 61.54 км/ч, то у него также ушло бы на дорогу 3.25 часа.
Можно предположить, что есть несколько вариантов усреднения. Во-первых, среднее арифметическое: (12+42)/2 = 27%. Во-вторых, сложный процент: 1.12*1.42=1.5904, т.е. 59.04% за 2 года или 28.02% за год.
Но «в среднем» означает, что применив это значение к каждому году, мы получим тот же самый результат, что и при использовании множества исходных значений.
Проверяем. Среднее арифметическое: 1.27*1.27=1.6129 (на 61.29%). Сложный процент: 1.2802*1.2802=1.6389 (на 63.89%). Результаты мало того, что разные, так и оба неправильные, потому что выручка за 2 года выросла на 59.04%.
Среднее геометрическое часто встречается в реальных бизнес-задачах вместе с процентами и долями. Если в вашей задаче что-то растет или падает и вы хотите усреднить динамику показателя, то вам следует применять среднее геометрическое.
Вместо заключения
Повторю главные моменты:
— среднее арифметическое далеко не всегда соответствует смыслу и физической сущности усредняемого показателя;
— существует много видов средних значений, но в каждом конкретном случае есть только один правильный вид среднего, и именно его следует использовать в расчетах.
Как посчитать среднее значение в Excel
Подсчет среднего арифметического
Формула для вычислений предельно проста:
P = (a1 + a2 + … an) / n,
где an – значение величины, n – общее количество значений.
Для чего может использоваться данный показатель? Первое и очевидное его применение — это статистика. Практически в каждом статистическом исследовании используется показатель среднего арифметического. Это может быть средний возраст вступления в брак в России, средняя оценка по предмету у школьника или средние траты на продукты в день. Как уже говорилось выше, без учета весов подсчет средних значений может давать странные или абсурдные значения.
К примеру, президент Российской Федерации сделал заявление, что по статистике, средняя зарплата россиянина составляет 27 000 рублей. Для большинства жителей России такой уровень зарплаты показался абсурдным. Не мудрено, если при расчете учитывать размер доходов олигархов, руководителей промышленных предприятий, крупных банкиров с одной стороны и зарплаты учителей, уборщиков и продавцов с другой. Даже средние зарплаты по одной специальности, например, бухгалтера, будут иметь серьезные отличия в Москве, Костроме и Екатеринбурге.
Как считать средние для разнородных данных
В ситуациях с подсчетом заработной платы важно учитывать вес каждого значения. Это означает, что зарплаты олигархов и банкиров получили бы вес, например, 0,00001, а зарплаты продавцов — 0,12. Это цифры с потолка, но они приблизительно иллюстрируют распространенность олигархов и продавцов в российском обществе.
Таким образом, для подсчета среднего средних или среднего значения в разнородном массиве данных, требуется использовать среднее арифметическое взвешенное. Иначе вы получите среднюю зарплату по России на уровне 27 000 рублей. Если же вы хотите узнать свою среднюю оценку по математике или среднее количество забитых шайб выбранного хоккеиста, то вам подойдет калькулятор среднего арифметического.
Если в массиве есть числа в текстовом формате
В случае, если число введено в ячейку с текстовым форматом (см. ячейку А6 ), то это значение воспринимается функцией СРЗНАЧ() как текст и игнорируется. Поэтому, не смотря на то, что в диапазоне A 5: A 15 11 значений, для функции СРЗНАЧ() их всего 10, т.е. n в этом случае =10. Среднее будет равно 20,4 (см. файл примера ).
Примечание : о вычислении средневзвешенного значения см. статью Средневзвешенная цена в MS EXCEL
Способ стандартный
Первостепенно разберем способ, как посчитать среднее арифметическое в Excel, который подразумевает использование стандартного инструмента для этого. Метод является наиболее простым и удобным для использования, однако у него существуют и некоторые недостатки. Но о них позже, а сейчас перейдем к выполнению поставленной задачи.
Как только вы это сделаете, в ячейке рядом появится результат расчета среднего арифметического выделенных значений. Его расположение будет зависеть от блока данных, если вы выделили строку, то находиться результат будет справа от выделения, если столбец, снизу.
Но как было сказано ранее, у данного метода есть и недостатки. Так, у вас не получится рассчитать значение из диапазона ячеек, или же ячеек, расположенных в разных местах. Например, если в вашей таблице смежно находятся два столбца с числовыми значениями, то, выделив их и произведя вышеописанные действия, вы получите результат для каждого столбца в отдельности.
Способ с помощью Мастера функций
Способов, позволяющих найти среднее арифметическое в Excel, существует много, и естественно, что с их помощью есть возможность обойти ограничения, предполагающие предыдущий способ. Сейчас будет рассказано о произведении вычислений путем использования Мастера функций. Итак, вот что вам необходимо сделать.
По завершении ввода окно Мастера закроется, а в ячейке, которую вы выделяли в самом начале, появится результат вычислений. Теперь вы знаете второй способ, как рассчитать среднее арифметическое в Excel. Но далеко не последний, поэтому двигаемся дальше.
Основная идея
Предположим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые хотят поступить в наш ВУЗ. Оценки по различным предметам у наших кандидатов следующие:
Свободное место, допустим, только одно, и наша задача – выбрать достойного.
Первое, что обычно приходит в голову – это рассчитать классический средний балл с помощью стандартной функции Excel СРЗНАЧ
На первый взгляд кажется, что лучше всех подходит Иван, т.к. у него средний бал максимальный. Но тут мы вовремя вспоминаем, что факультет-то наш называется “Программирование”, а у Ивана хорошие оценки только по рисованию, пению и прочей физкультуре, а по математике и информатике как раз не очень. Возникает вопрос: а как присвоить нашим предметам различную важность (ценность), чтобы учитывать ее при расчете среднего? И вот тут на помощь приходит средневзвешенное значение.
Средневзвешенное – это среднее с учетом различной ценности (веса, важности) каждого из элементов.
В бизнесе средневзвешенное часто используется в таких задачах, как:
Расчет средневзвешенного формулами
Добавим к нашей таблице еще один столбец, где укажем некие безразмерные баллы важности каждого предмета по шкале, например, от 0 до 9 при поступлении на наш факультет программирования. Затем расчитаем средневзвешенный бал для каждого абитурента, т.е. среднее с учетом веса каждого предмета. Нужная нам формула будет выглядеть так:
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в двух указанных диапазонах – оценки абитурента и вес каждого предмета – а затем суммирует все полученные произведения. Потом полученная сумма делится на сумму всех баллов важности, чтобы усреднить результат. Вот и вся премудрость.
Как найти среднее значение в Excel?
Итак, как обычно рассчитывается среднее арифметическое? Для этого нужно сложить все числа и разделить на их общее количество. Для решения очень простых задач этого достаточно, но во всех остальных случаях такой вариант не подойдет. Дело в том, что в реальной ситуации числа всегда меняются, количество этих чисел тоже. К примеру, у пользователя есть таблица, где указаны оценки студентов. И нужно найти средний балл каждого студента. Понятно, что у каждого из них будут разные оценки, а количество предметов на разных специальностях и на разных курсах тоже будет разным. Было бы очень глупо (и нерационально) все это отслеживать и считать вручную. Да и делать это не понадобится, поскольку в Excel есть специальная функция, которая поможет найти среднее значение любых чисел. Даже если они будут изменяться время от времени, программа будет автоматически пересчитывать новые значения.
Можно предположить, что у пользователя есть уже созданная таблица с двумя колонками: первый столбец — название предмета, а второй — оценка по этому предмету. И необходимо найти средний балл. Для этого надо с помощью мастера функций прописать формулу для расчета среднего арифметического. Делается это достаточно просто:
Если теперь, например, изменить какое-то значение по одному из предметов (или вовсе его удалить и оставить поле пустым), то Эксель сразу же пересчитает формулу и выдаст новый результат.
Альтернативные способы расчета среднего значения
Еще один способ найти среднее значение в Excel — с помощью строки формул.
Пример использования функции СРЗНАЧ для расчета среднего значения диапазона ячеек
Также можно прописывать любые формулы и вручную. Для этого нужно в любой выбранной ячейке поставить знак «=», прописать вручную формулу (СРЗНАЧ), открыть скобку, выбрать нужный диапазон ячеек и закрыть скобку. Результат тут же будет отображен.
Вот таким простым способом рассчитывается среднее значение в Microsoft Excel. Аналогичным образом можно считать и среднее арифметическое только для нужных полей, а не для всего диапазона ячеек. Для этого во время выбора диапазона ячеек потребуется лишь зажать клавишу «Ctrl» и поочередно щелкать по каждому нужному полю.
Что возвращает функция
Возвращает число, соответствующее среднему арифметическому от заданного диапазона данных.
Синтаксис
=AVERAGE(number1, [number2], …) – английская версия
=СРЗНАЧ(число1;[число2];…) – русская версия
Стандартный способ вычисления
Самый простой и известный способ найти среднее арифметическое набора чисел — это воспользоваться специальной кнопкой на ленте Microsoft Excel. Выделяем диапазон чисел, расположенных в столбце или в строке документа. Находясь во вкладке «Главная», жмем на кнопку «Автосумма», которая расположена на ленте в блоке инструментов «Редактирование». Из выпадающее списка выбираем пункт «Среднее».
После этого, с помощью функции «СРЗНАЧ», производится расчет. В ячейку под выделенным столбцом, или справа от выделенной строки, выводится средняя арифметическая данного набора чисел.
Этот способ хорош простотой и удобством. Но, у него имеются и существенные недостатки. С помощью этого способа можно произвести подсчет среднего значения только тех чисел, которые располагаются в ряд в одном столбце, или в одной строке. А вот, с массивом ячеек, или с разрозненными ячейками на листе, с помощью этого способа работать нельзя.
Например, если выделить два столбца, и вышеописанным способом вычислить среднее арифметическое, то ответ будет дан для каждого столбца в отдельности, а не для всего массива ячеек.
Синтаксис СРЗНАЧ
=СРЗНАЧ(число1;[число2];…) – русская версия
Аргументы СРЗНАЧ
Для расчета проделайте следующие шаги:
Функция рассчитает среднее значение в указанном диапазоне среди тех ячеек, в которых есть числа.
Как найти среднее арифметическое чисел?
Чтобы найти среднее арифметическое, необходимо сложить все числа в наборе и разделить сумму на количество. Например, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы нашли среднее арифметическое по формуле: =(3+4+3+5+5)/5.
Как это быстро сделать с помощью функций Excel? Возьмем для примера ряд случайных чисел в строке:

Или: сделаем активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).
Теперь посмотрим, что еще умеет функция СРЗНАЧ.
Найдем среднее арифметическое двух первых и трех последних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Результат:
Среднее значение по условию
Условием для нахождения среднего арифметического может быть числовой критерий или текстовый. Будем использовать функцию: =СРЗНАЧЕСЛИ().
Найти среднее арифметическое чисел, которые больше или равны 10.

Третий аргумент – «Диапазон усреднения» – опущен. Во-первых, он не обязателен. Во-вторых, анализируемый программой диапазон содержит ТОЛЬКО числовые значения. В ячейках, указанных в первом аргументе, и будет производиться поиск по прописанному во втором аргументе условию.
Внимание! Критерий поиска можно указать в ячейке. А в формуле сделать на нее ссылку.
Найдем среднее значение чисел по текстовому критерию. Например, средние продажи товара «столы».
Функция будет выглядеть так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон – столбец с наименованиями товаров. Критерий поиска – ссылка на ячейку со словом «столы» (можно вместо ссылки A7 вставить само слово “столы”). Диапазон усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.
В результате вычисления функции получаем следующее значение:
Внимание! Для текстового критерия (условия) диапазон усреднения указывать обязательно.
Среднее значение через формулу в Эксель
Сделать задачу также можно через стандартную формулу для чего прописываем в ячейке:
Через мастер формул
При необходимости нужно выделить нужную ячейку и кликнуть на функции.
Далее в категории «Полный алфавитный перечень» выбираем СРЗНАЧ.
Теперь можно выделить столбец или строку, где нужно произвести вычисление.
Заключение
Расчет среднего арифметического широко используется во многих научных сферах. Этот показатель популярен не только в статистических расчетах, но и в физике, механике, экономике, медицине или финансах.
Как посчитать среднее значение, квадратическое отклонение и погрешность
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 24 человек(а).
Количество просмотров этой статьи: 63 360.
После сбора данных их нужно проанализировать. Обычно нужно найти среднее значение, квадратичное отклонение и погрешность. Мы расскажем вам, как это сделать.
Меры центральной тенденции.
До сих пор мы обсуждали методы, которые мы можем использовать для организации и представления финансовых данных с целью того, чтобы они были более понятными.
Например, частотное распределение доходности класса активов показывает характер рисков, с которыми инвесторы могут столкнуться в конкретном классе активов. Гистограмма годовой доходности S&P 500 ясно показывает, что большие положительные и отрицательные значения годовой доходности являются обычной ситуацией.
Хотя таблицы частотных распределений и гистограммы предоставляют собой удобный способ обобщить серии наблюдений, эти методы являются лишь первым шагом к описанию финансовых данных.
В этом разделе мы обсудим использование количественных показателей, которые объясняют характеристики данных. Наше внимание сосредоточено на мерах центральной тенденции и других показателях (или параметрах), характеризующих положение данных.
Показатель или мера центральной тенденции (англ. ‘measure of central tendency’) указывает, насколько центрированы финансовые данные.
Меры центральной тенденции, вероятно, используются более широко, чем любые другие статистические показатели, потому что их легко рассчитать и применить. Меры положения (англ. ‘measures of location’) включают в себя не только меры центральной тенденции, но и другие показатели, которые иллюстрируют местоположение или распространение данных в рамках распределения.
Среднее арифметическое.
Определение среднего арифметического.
Мы можем вычислить среднее арифметическое как для совокупностей, так и для выборок. Эти показатели известны как среднее по совокупности и выборочное среднее значение соответственно.
Среднее значение для совокупности.
Если мы можем адекватно определить совокупность, то мы можем рассчитать среднее значение для совокупности как среднее арифметическое всех наблюдений или значений в совокупности.
Например, аналитики, изучающие годовой рост продаж крупных оптовых клубов в США за 2013 финансовый год, могут определить интересующую совокупность, включив в нее только три компании: BJ’s Wholesale Club (частная компания с 2011 г.), Costco Wholesale Corporation. и Sam’s Club, входящую в группу Wal-Mart.
В качестве другого примера можно привести портфельного менеджера, специализирующегося на индексе Nikkei 225. Интересующая его совокупность включает 225 акций из первой секции Токийской фондовой биржи, которые формируют индекс Nikkei.
Формула среднего значения для совокупности.
Среднее по совокупности, \( \bf \mu\), является средним арифметическим значением совокупности.
Для конечной совокупности используется следующая формула среднего значения:
\(\large< \mu = <\dsum_
Среднее по совокупности является примером статистического параметра. Среднее значение для совокупности уникально; то есть, данная совокупность имеет только одно среднее значение.
Чтобы проиллюстрировать расчеты по приведенной формуле, мы можем найти среднее по совокупности для доли прибыли в выручке американских компаний, управляющих крупными оптовыми клубами за 2012 год.
В течение года прибыль в процентах от выручки для оптовых клубов BJ, Costco Wholesale Corporation, и Wal-Mart Stores составляли 0,9%, 1,6% и 3,5% соответственно, согласно списку Fortune 500 за 2012 год. Таким образом, среднее значение по совокупности для прибыли в процентах от выручки составило:
\(\mu\) = (0,9 + 1,6 + 3,5)/3 = 6/3 = 2%
Выборочное среднее значение.
Очень часто мы не можем наблюдать каждый элемент множества данных; вместо этого мы наблюдаем подмножество или выборку из генеральной совокупности.
Концепция среднего значения может применяться к наблюдениям в выборке с небольшим изменением обозначений.
Формула выборочного среднего значения.
\(\large < \overline
Формула 3 предписывает суммировать значения наблюдений \(X_i\) и делить эту сумму на количество наблюдений. Например, если выборка коэффициентов прибыли на акцию (P/E) для шести публичных компаний содержит значения 35, 30, 22, 18, 15 и 12, то среднее значение P/E для выборки будет 132/6 = 22. Среднее значение выборки также называется средним арифметическим (англ. ‘arithmetic average’).
Как отмечалось ранее, выборочное среднее значение является статистикой (то есть описательной мерой выборки).
Средние значения можно рассчитывать для отдельных статистических единиц или для временного отрезка.
В качестве примера можно привести рентабельность собственного капитала (ROE) за 2013 год для 100 компаний из FTSE Eurotop 100, индексе 100 крупнейших компаний Европы. В этом случае мы рассчитываем среднее значение ROE за 2013 год в среднем по 100 отдельным статистическим единицам (или элементам множества, от англ. ‘statistical unit’ или просто ‘unit’).
Когда мы изучаем характеристики некоторых статистических единиц в определенный момент времени (например, ROE для FTSE Eurotop 100), мы изучаем перекрестные данные (англ. ‘cross-sectional data’). Среднее этих наблюдений называется перекрестным средним значением (англ. ‘cross-sectional mean’).
С другой стороны, если наша выборка состоит из исторической месячной доходности по FTSE Eurotop 100 за последние 5 лет, то мы имеем дело с данными временного ряда (англ. ‘time-series data’). Среднее значение этих наблюдений называется средним временного ряда (англ. ‘time-series mean’).
Мы рассмотрим специализированные статистические методы, связанные с поведением временных рядов в следующих разделах, посвященных анализу временных рядов.
Ниже мы покажем пример определения выборочной средней доходности для 16 европейских фондовых рынков за 2012 г. В этом случае среднее значение является перекрестным, поскольку мы усредняем доходность по отдельным странам.
Пример вычисления перекрестного среднего значения.
Термин «скорректированный с учетом свободного обращения акций» (англ. ‘free float-adjusted’) означает, что веса компаний в индексе отражают стоимость акций, фактически доступных для инвестиций.
По состоянию на сентябрь 2013 года EAFE состояла из 22 индексов стран развитых рынков, включая индексы для 16 европейских рынков, 2 австралийских рынков (Австралия и Новая Зеландия), 3 дальневосточных рынков (Гонконг, Япония и Сингапур) и Израиля.
Предположим, что мы заинтересованы в показателях динамики местной валюты на 16 европейских рынках EAFE в 2012 году. Мы хотим найти примерную среднюю общую доходность за 2012 год по этим 16 рынкам.
Ряды ставок доходности, представленные в Таблице 8, приведены в местной валюте (то есть доходность указана для инвесторов, проживающих в стране). Поскольку эта доходность не указывается в валюте каждого отдельного инвестора, она не является доходностью, которую мог бы получить отдельный инвестор. Это, скорее, средняя доходность для местных валют 16 стран.

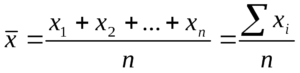
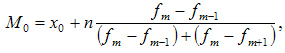
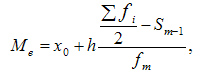

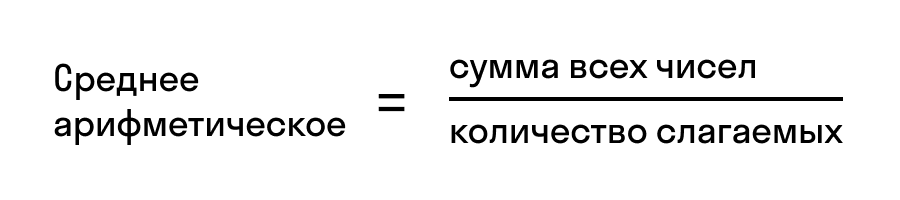






















 .
.








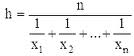

























 В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, как найти среднее арифметическое значение с помощью этой программы.
В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, как найти среднее арифметическое значение с помощью этой программы.