канонические формы уравнений гиперболического параболического и эллиптического типов

30.04.202305.05.2023 admin 0 Комментариев

Дифференциальные уравнения в частных производных¶

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Эллиптические уравнения¶

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

Параболические уравнения¶

Параболические уравнения появляются в нестационарных задачах теплопроводности, диффузии, иногда параболические задачи получаются из гиперболических уравнений (параболическое приближение в оптике) и т. д. Уравнение теплопроводности, например, имеет вид:

В первом слагаемом коэффициенты это плотность и удельная теплоемкость, во втором слгаемом – коэффициент теплопроводности, правая часть – плотность источников тепла.

Гиперболические уравнения¶

Начальные и граничные условия¶

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи. Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.

Источник

6. Основные типы уравнений срп. Уравнения гиперболического, параболического и эллиптического типа.

Для простейшего случая пространственной распределённости по одной координате х, изменяющейся на отрезке (одномерная задача), уравнение (1) записывается в виде:

(4)

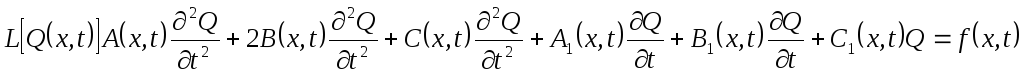
где А, В, С – заданные функции могут быть равны CONST/

В зависимости от значения, дискриминанты Δ, равные (АВВ 2 ), различают уравнения:

— гиперболического типа (Δ 0),

— смешанного типа (Δ меняет знак в области допустимых изменений x и t).

Уравнения гиперболического типа

Уравнения содержат две производные функции состояния, как по t, так и по x, они описывают колебательные процессы различной природы (механические, электромагнитные, звуковые и т.д.), связанные с конечной скоростью V, распространения волновых явлений.

(5)

Уравнение (5) моделирует распространение свободных колебаний (при распространении со скоростью звука пульсации расхода газа в длинном трубопроводе).

При , уравнение (5) записывается в виде:

— описывает вынужденные

колебания под влиянием внешнего воздействия .

2) Уравнение гиперболического типа:

(7)

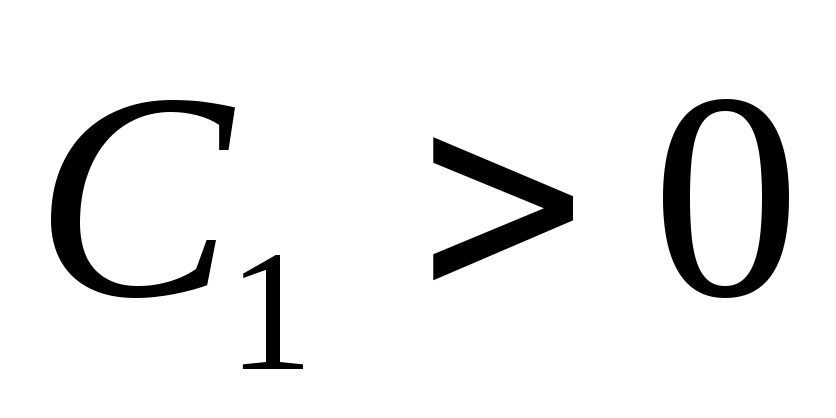
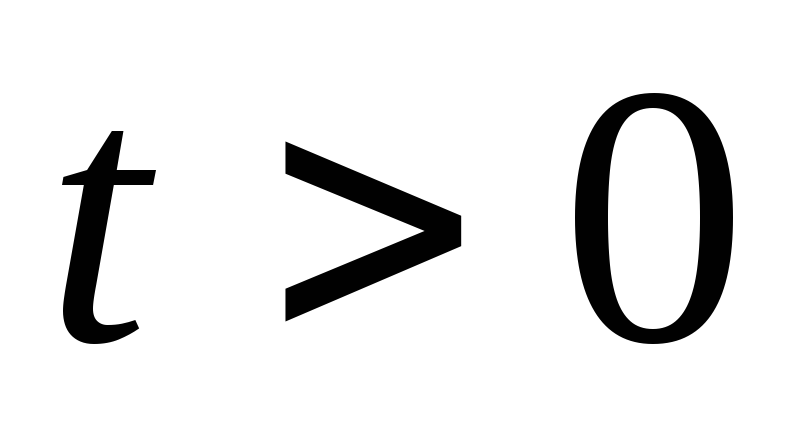
Описывает распределение напряжения тока вдоль длинной электрической линии.

— скорость распределения электромагнитных волн вдоль линии.

При уравнение (7) сводится к волновому уравнению, при и уравнение (7) моделирует процессы механических колебаний в среде сопротивления.

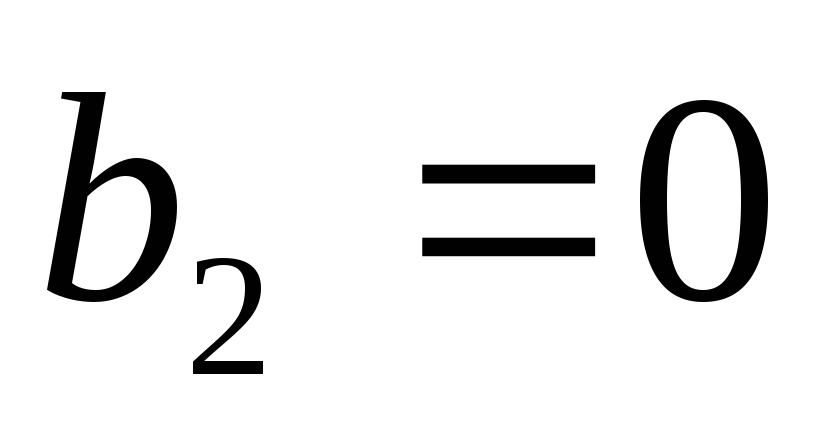
Уравнение параболического типа

Они содержат первую производную и вторую производную по координате t.

Описывает задачи, связанные с процессами теплопроводности, диффузии с распространением электромагнитных волн, с движением вязкой жидкости и т.д.

Уравнение теплопроводности (уравнение Фурье)

(8)

Уравнение (8) – однородное уравнение теплопроводности, описывает температурные поля не стационарной теплопроводности, тепло массы перевода и т.д.

(9)

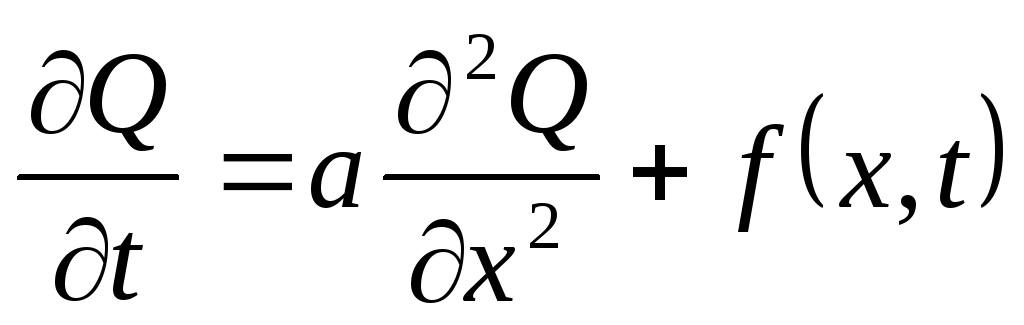
Уравнение (9) – неоднородное уравнение теплопроводности, учитывающее внешнее воздействие от внутренних источников вещества и энергии.

Включив в правой части уравнений (8) и (9) дополнительный член 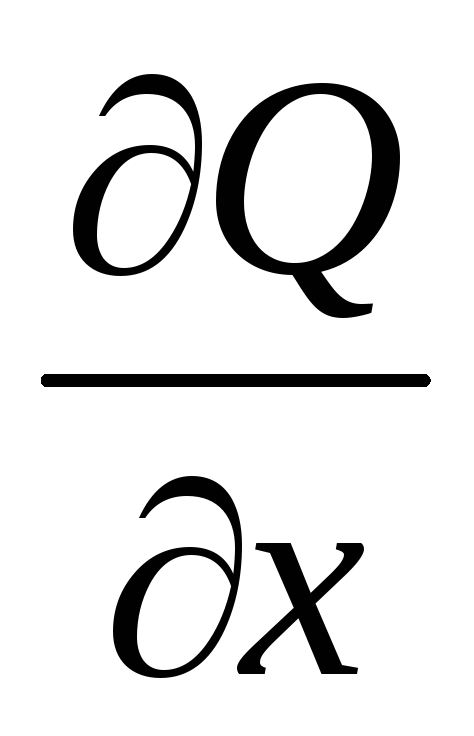, получим уравнение теплопроводности в цилиндрической системе пространственных координат.

Уравнения эллиптического типа

В уравнениях этого типа отсутствует производная от по времени t и описывают стохастическое состояние ОРП.

(10)

(11)

при в уравнении (10)

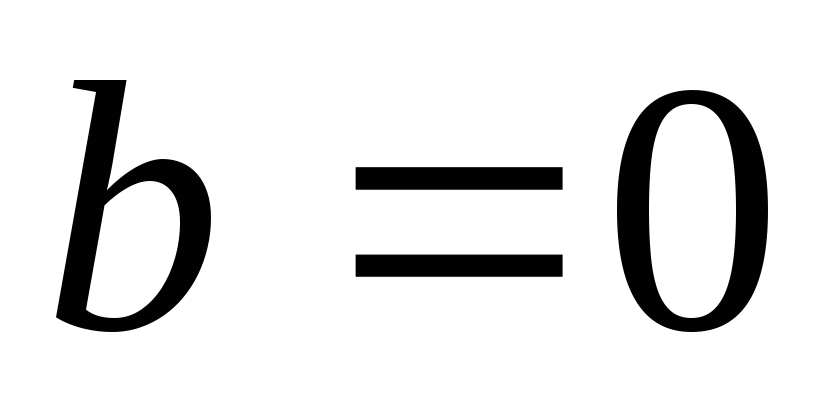
3) Лапласа (эллиптического типа)

При

(12)

Уравнения (11) и (12) моделируют в распространении температуры потенциала скоростей при стационарном течении несжимаемой жидкости потенциал электрического поля в задачах электрической статики и т.д. при отсутствии или наличии внешних воздействий соответственно.

Уравнение (10) описывает многие физические процессы теплопроводности, диффузии в движущихся средах, напряженности поля и т.д.

Источник

Канонические формы уравнений гиперболического параболического и эллиптического типов

С помощью векторов мы ввели понятие пространства и его размерности, в частности трехмерного. Рассмотрим в нем поверхности, которые «похожи» на поверхности, образованные вращением кривой второго порядка вокруг ее оси симметрии. Например, сфера может быть получена вращением окружности вокруг диаметра. Поверхность, описываемая некоторой линией, вращающейся вокруг неподвижной прямой d, называется поверхностью вращения с осью вращения d. Наряду с такими поверхностями мы встретимся и с более сложными случаями.

Пусть в пространстве задана прямоугольная декартова система координат.

Поверхность второго порядка – геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида

в котором хотя бы один из коэффициентов отличен от нуля. Уравнение (2.48) называется общим уравнением поверхности второго порядка.

Уравнение (2.48) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (2.48) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных классов поверхностей: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из этих поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением.

Перечисленные поверхности второго порядка относятся к так называемым нераспадающимся поверхностям второго порядка. Можно говорить о случаях вырождения – распадающихся поверхностях второго порядка, к которым относятся: пары пересекающихся плоскостей, пары мнимых пересекающихся плоскостей, пары параллельных плоскостей, пары мнимых параллельных плоскостей, пары совпадающих плоскостей.

Наша цель – указать канонические уравнения для поверхностей второго порядка и показать, как выглядят эти поверхности.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

2. Эллипсоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно координатных осей,

· плоскостной симметрией относительно начала координат.

3. В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс (см. рис. 2.22).

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

1. Эллиптический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

2. Эллиптический параболоид обладает

Можно получить эллиптический параболоид симметричный относительно оси 0х или 0у, для чего нужно в уравнении (2.50) поменять между собой переменные х и z или у и z соответственно.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Гиперболический параболоид обладает

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

5. Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

Свойства однополостного гиперболоида.

1. Однополостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что z – любое число.

2. Однополостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением

называется двуполостным гиперболоидом (рис. 2.26) .

1. Двуполостный гиперболоид – неограниченная поверхность, поскольку из его уравнения следует, что | z |≥ c и неограничен сверху.

2. Двуполостный гиперболоид обладает

· центральной симметрией относительно начала координат,

· осевой симметрией относительно всех координатных осей,

· плоскостной симметрией относительно всех координатных плоскостей.

Примечание. Если уравнение поверхности в прямоугольной системе координат имеет вид: F ( x 2 + y 2 ; z )=0, то эта поверхность – поверхность вращения с осью вращения 0z. Аналогично: F ( x 2 + z 2 ; y )=0 – поверхность вращения с осью вращения 0у, F ( z 2 + y 2 ; x )=0 – с осью вращения 0х

С учетом данного примечания могут быть записаны уравнения для рассмотренных выше поверхностей вращения, если осью вращения являются оси 0х или 0у.

Цилиндрическая поверхность образуется движением прямой линии, скользящей по некоторой неподвижной замкнутой или незамкнутой кривой и остающейся параллельной своему исходному положению. Множество прямолинейных образующих представляет собой непрерывный каркас цилиндрической поверхности. Через каждую точку поверхности проходит одна прямолинейная образующая. Неподвижная кривая, по которой скользит образующая, называется направляющей. Если направляющая линия является кривой второго порядка, то и цилиндрическая поверхность – второго порядка.

Если уравнение поверхности не содержит в явном виде какой–либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.

Достаточно нарисовать на плоскости х0у направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 0z. Для наглядности следует построить также одно–два сечения плоскостями, параллельными плоскости х0у. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Аналогично поступают, рассматривая направляющую в плоскости х0z или у0z.

Цилиндрическая поверхность является бесконечной в направлении своих образующих. Часть замкнутой цилиндрической поверхности, заключенная между двумя плоскими параллельными сечениями, называется цилиндром, а фигуры сечения – его основаниями. Сечение цилиндрической поверхности плоскостью, перпендикулярной ее образующим, называется нормальным. В зависимости от формы нормального сечения цилиндры бывают:

1) эллиптические – нормальное сечение представляет собой эллипс (рис. 2.27а), каноническое уравнение

2) круговые – нормальное сечение круг, при a = b = r уравнение

3) гиперболические – нормальное сечение гипербола (рис. 2.27б), каноническое уравнение

4) параболические – нормальное сечение парабола (рис. 2.27в), каноническое уравнение

5) общего вида – нормальное сечение кривая случайного вида.

Если за основание цилиндра принимается его нормальное сечение, цилиндр называют прямым (рис. 2.27). Если за основание цилиндра принимается одно из косых сечений, цилиндр называют наклонным. Например, наклонные сечения прямого кругового цилиндра являются эллипсами. Наклонные сечения прямого эллиптического цилиндра в общем случае – эллипсы. Однако его всегда можно пересечь плоскостью, наклонной к его образующим, таким образом, что в сечении получится круг.

Конической поверхностью называется поверхность, производимая движением прямой, перемещающейся в пространстве так, что она при этом постоянно проходит через неподвижную точку и пересекает данную линию. Данная прямая называется образующей, линия – направляющей, а точка – вершиной конической поверхности (рис. 2.28).

Конусом называется тело, ограниченное частью конической поверхности, расположенной по одну сторону от вершины, и плоскостью, пересекающей все образующие по ту же сторону от вершины. Часть конической поверхности, ограниченная этой плоскостью, называется боковой поверхностью, а часть плоскости, отсекаемая боковой поверхностью, – основанием конуса. Перпендикуляр, опущенный из вершины на плоскость основания, называется высотой конуса.

Конус называется прямым круговым, если его основание есть круг, а высота проходит через центр основания. Такой конус можно рассматривать как тело, происходящее от вращения прямоугольного треугольника, вокруг катета как оси. При этом гипотенуза описывает боковую поверхность, а катет – основание конуса.

В курсе геометрии общеобразовательной школы рассматривается только прямой круговой конус, который для краткости называется просто конусом.

Если вершина конуса расположена в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат, то уравнение эллиптического конуса имеет вид:

При а = b конус становится круговым.

Примечание. По аналогии с коническими сечениями (аналогично теореме 2.1) существуют и вырожденные поверхности второго порядка. Так, уравнением второго порядка x 2 = 0 описывается пара совпадающих плоскостей, уравнением x 2 = 1 – пара параллельных плоскостей, уравнением x 2 – y 2 = 0 – пара пересекающихся плоскостей. Уравнение x 2 + y 2 + z 2 = 0 описывает точку с координатами (0;0;0). Существуют и другие вырожденные случаи. Полная теория поверхностей второго порядка рассматривается в курсе аналитической геометрии

Источник

Приведение к каноническому виду линейных уравнений с частными производными второго порядка

Федеральное агентство по образованию

ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Институт математики, экономики и информатики

Кафедра дифференциальных и интегральных уравнений

ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ ЛИНЕЙНЫХ УРАВНЕНИЙ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА

Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными …………………………………………………………………………

1.1. Необходимый теоретический материал………………………..

1.2. Пример выполнения задачи1 (приведение к

1.3. Пример выполнения задачи 2 (приведение к

каноническому виду уравнений параболического типа)

1.4. Пример выполнения задачи 3 (приведение к

1.5. Задачи для самостоятельного решения ………………….….

Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2.1. Необходимый теоретический материал …………………..

2.2. Пример выполнения задачи 4

2.3. Задачи для самостоятельного решения ……………………..

В настоящих методических указаниях изложен теоретический материал и на конкретных примерах разобрано приведение к каноническому виду линейных уравнений с частными производными второго порядка с двумя независимыми переменными для уравнений гиперболического, эллиптического и параболического типов.

Методические указания предназначены для студентов математических специальностей очной и заочной формы обучения.

§1. Приведение к каноническому виду линейных уравнений с частными производными 2-го порядка с двумя независимыми переменными.

Задача. Определить тип уравнения

(1)

и привести его к каноническому виду.

1.1. Необходимый теоретический материал.

I. Тип уравнения (1) определяется знаком выражения :

· если в некоторой точке, то уравнение (1) называется уравнением гиперболического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением эллиптического типа в этой точке;

· если в некоторой точке, то уравнение (1) называется уравнением параболического типа в этой точке.

Уравнение (1) будет являться уравнением гиперболического, эллиптического, параболического типа в области D, если оно гиперболично, эллиптично, параболично в каждой точке этой области.

Уравнение (1) может менять свой тип при переходе из одной точки (области) в другую. Например, уравнение является уравнением эллиптического типа в точках ; параболического типа в точках ; и гиперболического типа в точках .

II. Чтобы привести уравнение к канонического виду, необходимо:

1. Определить коэффициенты ;

2. Вычислить выражение ;

3. Сделать вывод о типе уравнения (1) (в зависимости от знака выражения );

4. Записать уравнение характеристик:

; (2)

5. Решить уравнение (2). Для этого:

а) разрешить уравнение (2) как квадратное уравнение относительно dy:

; (3)

б) найти общие интегралы уравнений (3) (характеристики уравнения (1)):

· (4)

в случае уравнения гиперболического типа;

· , (5)

в случае уравнения параболического типа;

· , (6)

в случае уравнения эллиптического типа.

6. Ввести новые (характеристические) переменные и :

· в случае уравнения гиперболического типа в качестве и берут общие интегралы (4) уравнений (3), т. е.

· в случае уравнения параболического типа в качестве берут общий интеграл (5) уравнения (3), т. е. , в качестве берут произвольную, дважды дифференцируемую функцию , не выражающуюся через , т. е. ;

· в случае уравнения эллиптического типа в качестве и берут вещественную и мнимую часть любого из общих интегралов (6) уравнений (3):

7. Пересчитать все производные, входящие в уравнение (1), используя правило дифференцирования сложной функции:

, (7)

8. Подставить найденные производные в исходное уравнение (1) и привести подобные слагаемые. В результате уравнение (1) примет один из следующих видов:

· в случае уравнения гиперболического типа:

;

· в случае уравнения параболического типа:

;

· в случае уравнения эллиптического типа:

1.2. Пример выполнения задачи 1.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение гиперболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (9)

5. Решим уравнение (9). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy: ;

;

(10)

б) найдём общие интегралы уравнений (10) (характеристики уравнения (9)):

6. Введём характеристические переменные:

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (8) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Ответ. Уравнение (8) является уравнением гиперболического типа на всей плоскости XOY. Канонический вид

где

1.3. Пример выполнения задачи 2.

Определить тип уравнения

и привести его к каноническому виду.

1. Определим коэффициенты . В нашем примере они постоянны:

2. Вычислим выражение :

3. уравнение параболического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (12)

5. Решим уравнение (12). Для этого:

а) разрешаем уравнение (9) как квадратное уравнение относительно dy. Однако в этом случае левая часть уравнения является полным квадратом:

;

(13)

б) имеем только одно уравнение характеристик (13). Найдём его общий интеграл (уравнения параболического типа имеют только одно семейство вещественных характеристик):

6. Введём характеристические переменные: одну из переменных вводим как и ранее

а в качестве берут произвольную, дважды дифференцируемую функцию, не выражающуюся через , пусть

;

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (11) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Функцию, стоящую в правой части уравнения (11) необходимо также выразить через характеристические переменные.

После деления на 25 (коэффициент при ):

Ответ. Уравнение (11) является уравнением параболического типа на всей плоскости XOY. Канонический вид

где

1.4. Пример выполнения задачи 3.

Определить тип уравнения

(14)

и привести его к каноническому виду.

1. Определим коэффициенты :

2. Вычислим выражение :

3. уравнение эллиптического типа во всей плоскости XOY.

4. Запишем уравнение характеристик:

. (15)

5. Решим уравнение (15). Для этого:

а) разрешаем уравнение (15) как квадратное уравнение относительно dy: ; (16)

б) уравнения (16) – это пара комплексно-сопряженных уравнений. Они имеют пару комплексно-сопряженных общих интегралов. (Уравнения эллиптического типа не имеют вещественных характеристик)

(17)

6. Введём характеристические переменные как вещественную и мнимую части одного из общих интегралов (17):

7. Пересчитаем производные, входящие в исходное уравнение.

Используя формулы (7), получим:

Здесь слева написаны коэффициенты уравнения (14) при соответствующих производных.

8. Собирая подобные слагаемые, получим:

Или после деления на 4 (коэффициент при и ):

Ответ. Уравнение (14) является уравнением эллиптического типа на всей плоскости XOY. Канонический вид

где

1.5. Задачи для самостоятельного решения.

Определить тип уравнения и привести его к каноническому виду.

§2. Упрощение группы младших производных

для уравнений второго порядка с постоянными коэффициентами

2. 1. Необходимый теоретический материал

В самом общем виде линейное уравнение с частными производными второго порядка с двумя независимыми переменными имеет вид

(1)

Преобразованием независимых переменных группа старших производных уравнения может быть упрощена. Уравнение (1) приводится к одному из следующих видов

· в случае уравнения гиперболического типа:

; (11)

· в случае уравнения параболического типа:

; (12)

· в случае уравнения эллиптического типа:

. (13)

Если коэффициенты исходного уравнения постоянны, то для дальнейшего упрощения уравнения любого типа нужно сделать замену неизвестной функции

, (14)

где — новая неизвестная функция, — параметры, подлежащие определению. Такая замена не «испортит» канонического вида, но при этом позволит подобрать параметры так, чтобы из трех слагаемых группы младших производных в уравнении осталось только одно. Уравнения гиперболического, параболического и эллиптического типов соответственно примут вид

;

Чтобы реализовать замену (14) в уравнениях (11), (12), (13), необходимо пересчитать все производные, входящие в эти уравнения по формулам

(15)

Подробно рассмотрим этот процесс на примере уравнения гиперболического типа, т. е. уравнения (11). Пересчитаем производные, входящие в это уравнение, используя формулы (15).