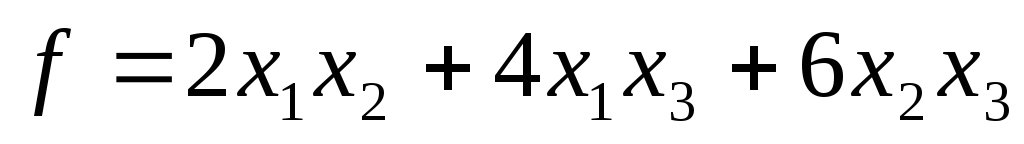канонический вид квадратичной формы метод лагранжа
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Квадратичная форма
Определение
Пример. Функции
Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.
Пример.
Метод Лагранжа приведения квадратичной формы к каноническому виду
Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.
Пример. Привести форму
Пример. Привести форму
Пример. Привести форму
Матричная форма записи квадратичной формы
Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.
Пример. Для приведенной выше квадратичной формы
| $ x_ <1>$ | $ x_ <2>$ | $ x_ <3>$ | |
|---|---|---|---|
| $ x_ <1>$ | $ f_ <11>$ | $ \frac<1><2>f_ <12>$ | $ \frac<1><2>f_ <13>$ |
| $ x_ <2>$ | $ \frac<1><2>f_ <12>$ | $ f_ <22>$ | $ \frac<1><2>f_ <23>$ |
| $ x_ <3>$ | $ \frac<1><2>f_ <13>$ | $ \frac<1><2>f_ <23>$ | $ f_ <33>$ |
Пример. Для
Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.
Пример. Для формы
Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.
Метод Лагранжа и метод Гаусса
Пример. Рассмотрим матрицу квадратичной формы
Формула Якоби
Закон инерции для квадратичных форм
Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.
Ранг квадратичной формы
Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.
Закон инерции
Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.
Доказательство ☞ ЗДЕСЬ.
Доказательство следует из формулы Якоби.
Пример. Найти ранг и сигнатуру квадратичной формы
Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:
Как меняются ранг и сигнатура при непрерывном изменении параметров?
Справедливо и более общее утверждение.
Конгруэнтность квадратичных форм
Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.
Какое преобразование квадратичной формы оставляет ее инвариантной?
Знакоопределенность
Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.
Теорема. Ненулевая квадратичная форма, представленная в правильном виде
Доказательство ☞ ЗДЕСЬ.
К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.
Теорема [Сильвестр]. Квадратичная форма
Доказательство ☞ ЗДЕСЬ.
Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:
Пример. Квадратичная форма
Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?
Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений
Пример. Найти ортогональную замену переменных, приводящую квадратичную форму
Доказательство основано на правиле знаков Декарта.
Геометрия замен переменных
Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.
112. Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции
Теорема 1. Любую квадратичную форму
F(X1, x2,…, Xn) = F(X)= 
H(Y1, Y2,…, Yn) = 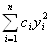
Доказательство. Докажем теорему методом математической индукции по числу N переменных в квадратичной форме F. Пусть N =1. Тогда квадратичная форма F имеет вид F = B11X12 и является квадратичной формой канонического вида.
Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем N переменных, и докажем ее для квадратичной формы F, имеющей N переменных. Рассмотрим два случая.
1. Среди диагональных коэффициентов B11, B22, …, Bnn есть отличный от нуля. Пусть, например, B11 ≠ 0. Рассмотрим квадратичную форму 
Будет квадратичной формой, содержащей только неизвестные X2,…, Xn. Отсюда




И определитель равен B11 ≠ 0. Обратное ему преобразование тоже невырожденное и приводит форму F в форму (4). По индуктивному предположению квадратичную форму G( Y2,…, Yn) невырожденным преобразованием переменных Y2,…, Yn можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная Y1 остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма F приводится к каноническому виду.
2. Все диагональные коэффициенты B11, B22, …, Bnn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, B12 ≠ 0. Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:
Оно невырожденное, так как матрица этого преобразования равна

И определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид
И форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных Z3,…, Zn. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных.
Пример. Методом Лагранжа привести квадратичную форму к каноническому виду

И найти преобразование переменных, приводящую эту форму к каноническому виду.
Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных
Матрица этого преобразования равно
И квадратичная форма преобразуется к виду

Выделим полный квадрат из членов, содержащих X1

Полагаем Y1 =Z1 +(5/2)Z3, Y2 = Z2+(1/2) Z3, Y3 = Z3 приведем квадратичную форму к каноническому виду


Тогда преобразование, переводящее данную квадратичную форму к форме канонического вида имеет матрицу, равную произведению матриц.

Математика
In the coming weeks, this wiki’s URL will be migrated to the primary fandom.com domain. Read more here
Метод Лагранжа приведения квадратичной формы к каноническому виду
Описание
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
есть данная квадратичная форма. Возможны два случая:
В первом случае преобразуем квадратичную форму следующим образом:


где 



С ней поступают аналогичным образом и так далее.
Заметим, что
Второй случай заменой переменных 
Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции.
Теорема 1. Любую квадратичную форму
f(x1, x2,…, xn) = f(x)= 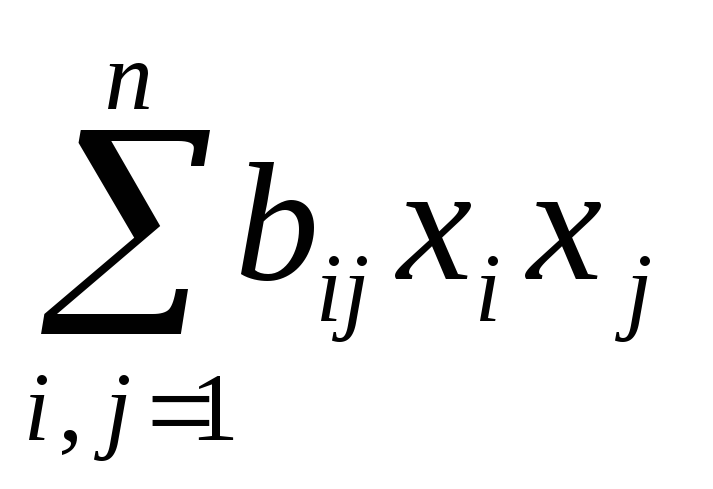
h(y1, y2,…, yn) = 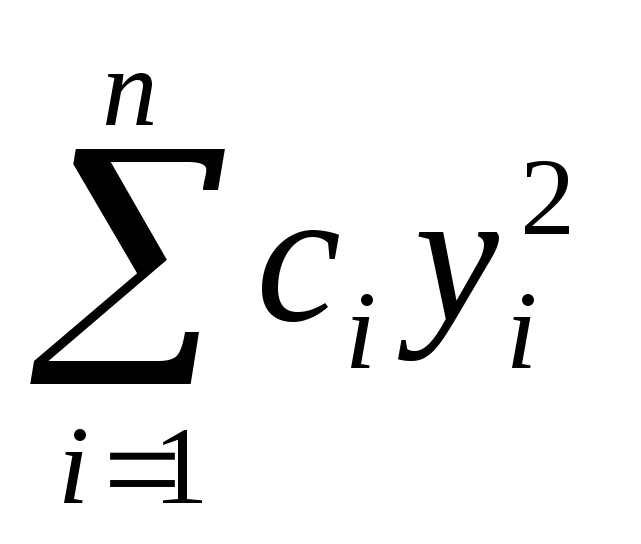
Доказательство. Докажем теорему методом математической индукции по числу n переменных в квадратичной форме f. Пусть n =1. Тогда квадратичная форма f имеет вид f = b11x1 2 и является квадратичной формой канонического вида.
Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем n переменных, и докажем ее для квадратичной формы f, имеющей n переменных. Рассмотрим два случая.
будет квадратичной формой, содержащей только неизвестные x2,…, xn. Отсюда




и определитель равен b11 0. Обратное ему преобразование тоже невырожденное и приводит форму f в форму (4). По индуктивному предположению квадратичную форму g( y2,…, yn) невырожденным преобразованием переменных y2,…, yn можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная y1 остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма f приводится к каноническому виду.
2. Все диагональные коэффициенты b11, b22, …, bnn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, b12 0. Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:
Оно невырожденное, так как матрица этого преобразования равна

и определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид
и форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных z3,…, zn. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных.
Пример. Методом Лагранжа привести квадратичную форму к каноническому виду
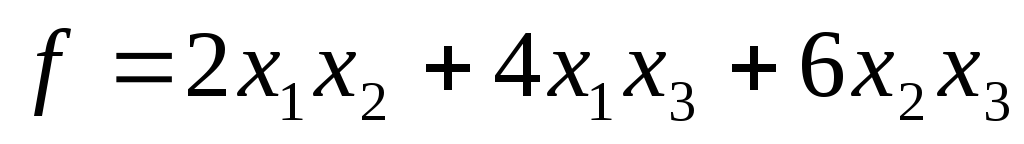
и найти преобразование переменных, приводящую эту форму к каноническому виду.
Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных
Матрица этого преобразования равно
и квадратичная форма преобразуется к виду
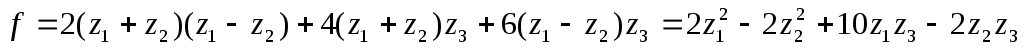
Выделим полный квадрат из членов, содержащих x1




преобразование переменных имеет вид:
Закон инерции квадратичных форм. Квадратичную форму можно привести к каноническому виду различными способами.
Теорема 1. Любую квадратичную форму с действительными переменными невырожденным линейным преобразованием переменных можно привести к нормальному виду.
Доказательство. Приведем сначала квадратичную форму к каноническому виду (2) §3. Можно предположить что в полученной квадратичной форме канонического вида имеется r коэффициентов неравных нулю, среди которых имеется s положительных коэффициентов и t отрицательных коэффициентов. При этом можно неизвестные перенумеровать и форму канонического вида представить в виде:

где 0 s r n и все коэффициенты с1, с2,…, сr положительны. Тогда невырожденное преобразование переменных
приводит форму f к нормальному виду,

Определение 2. Рангом квадратичной формы называется ранг матрицы квадратичной формы.
Теорема 2. При невырожденных линейных преобразованиях переменных ранг квадратичной формы не меняется. Ранг квадратичной формы равен числу ненулевых коэффициентов в форме канонического вида, т.е. rang f = s+ t .
Лемма 1. Ранг произведения AB матриц не превосходит ранга каждого из его сомножителей.
Доказательство. Из определения произведения матриц следует, что столбцы матрицы AB являются линейными комбинациями столбцов матрицы A. Тогда столбцы матрицы AB выражаются через базисные столбцы матрицы A. И максимальное число линейно независимых столбцов матрицы AB меньше ранга матрицы A. Отсюда ранг матрицы AB не больше ранга матрицы A.
Из определения произведения матриц следует, что строки матрицы AB являются линейными комбинациями строк матрицы B. Тогда строки матрицы AB выражаются через базисные строки матрицы B. Отсюда ранг матрицы AB не больше ранга матрицы B.
Лемма 2. Если один из сомножителей A или B квадратная невырожденная матрица, то ранг произведения AB равен рангу другого сомножителя.
Так как форма канонического вида получена из квадратичной формы невырожденным преобразованием переменных, то ранг квадратичной формы равен рангу матрицы квадратичной формы, т.е. равен числу ненулевых коэффициентов в форме канонического вида.
Теорема 3. Число положительных и число отрицательных коэффициентов в форме канонического вида (сигнатура квадратичной формы) не зависит от способа приведения квадратичной формы к каноническому виду.
Доказательство. Допустим, что квадратичная форма f ранга r от n переменных двумя способами приведена к каноническому виду,
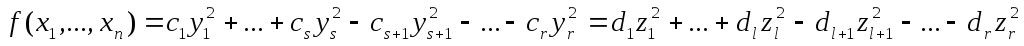
где предполагаем, что все коэффициенты сi и di (i=1,…,n) положительны. Пусть исходные переменные связаны с новыми переменными посредством невырожденных преобразований:
Из представлений (1) в силу указанного выбора значений переменных находим

Мы пришли к противоречию и наше предположение неверно. Следовательно, s = l.
Пример 1. Квадратичная форма