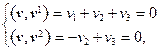канонический вид квадратичной формы ортогональное преобразование

30.04.202305.05.2023 admin 0 Комментариев

Канонический вид квадратичной формы ортогональное преобразование

Существует довольно простой метод (метод Лагранжа) приведения квадратичной формы к каноническому виду. Этот метод, однако, во многих задачах не дает нужного результата. Например, в задачах аналитической геометрии часто требуется привести общее уравнение кривой или поверхности второго порядка к каноническому виду, причем такое приведение требуется осуществить с помощью весьма специального преобразования переменных (а именно ортогонального); метод Лагранжа не всегда обеспечивает это условие. В связи с этим мы укажем способ, основанный на отыскании собственных значений матрицы квадратичной формы.

Теорема 38. Всякая квадратичная форма с матрицей А может быть приведена к каноническому виду

при помощи преобразования переменных с ортогональной матрицей. При этом коэффициенты канонического вида являются корнями характеристического многочлена матрицы каждый из которых взят столько раз, какова его кратность.

Доказательство. Пусть дана вещественная квадратичная форма с матрицей А. По теореме 35 квадратичная форма после выполнения линейного преобразования переменных с матрицей будет иметь матрицу

Отсюда следует, что задача приведения квадратичной формы к каноническому виду равносильна задаче приведения симметрической матрицы А к диагональному виду путем умножения ее слева и

справа соответственно на взаимно транспонированные матрицы

Воспользуемся теоремой 34, утверждающей, что для всякой симметрической матрицы А существует ортогональная матрица такая, что матрица

диагональна. Легко видеть, что матрица решает поставленную задачу, так как вследствие ее ортогональности имеем и потому

Заметим попутно, что (как видно из доказательства теоремы 34) диагональные элементы матрицы В суть корни характеристического многочлена матрицы каждый из которых взят столько раз, какова его кратность. Теорема доказана.

Канонический вид формы можно найти, таким образом, и не находя самого ортогонального преобразования переменных, а зная лишь собственные значения определяемые матрицей А.

Это положение подтверждает важность понятия собственного значения.

Пример. Найти канонический вид, к которому приводится квадратичная форма

посредством ортогонального преобразования, не находя самого этого преобразования.

Решение. Находим корни характеристического многочлена матрицы А данной формы:

Источник

Канонический вид ортогонального преобразования евклидова пространства

Рассмотрим инвариантные подпространства ортогонального преобразования евклидова пространства. По теореме 9.4 линейное преобразование вещественного пространства имеет одномерное или двумерное инвариантное подпространство. Выясним геометрический смысл сужения ортогонального преобразования на инвариантное подпространство.

Поэтому несобственное ортогональное преобразование имеет два одномерных инвариантных подпространства (см. пункт 1).

Теорема (9.9) о каноническом виде ортогонального преобразования

Приведение ортогонального преобразования к каноническому виду

Задача приведения ортогонального преобразования к каноническому виду формулируется следующим образом: требуется найти базис (канонический), в котором матрица ортогонального преобразования имеет канонический вид (9.20). Для приведения ортогонального преобразования к каноническому виду нужно выполнить следующие действия.

Нахождение канонического вида ортогонального преобразования ( первый этап ).

1. Выбрать базис [math]\boldsymbol_1,\ldots, \boldsymbol_n[/math] евклидова пространства [math]\mathbb[/math] и найти матрицу [math]A[/math] преобразования в этом базисе.

2. Составить характеристическое уравнение [math]\det(A-\lambda E)=0[/math] и найти различные его корни [math]\lambda_1,\ldots, \lambda_k[/math] (а также их алгебраические кратности).

3. Записать блочно-диагональную матрицу (9.20) канонического вида ортогонального преобразования:

— каждый действительный корень [math]\lambda_1[/math] кратности [math]n_1[/math] поместить на главной диагонали [math]n_1[/math] раз;

Нахождение канонического базиса ( второй этап ).

1. Собственные векторы ортогональной матрицы, принадлежащие различным собственным значениям, ортогональны.

2. Из пункта 1 следует, что для получения ортонормированного базиса достаточно ортонормировать отдельно каждую группу векторов, получаемых в пункте 4 или пункте 5 алгоритма, причем по свойству 8 столбцы [math]x_j,y_j[/math] в пункте 5 будут ортогональными.

3. Матрицу вида (9.20) можно представить в виде произведения матриц, каждая из которых есть либо матрица [math]\operatorname(1,\ldots,1,-1,1,\ldots,1)[/math] простого отражения относительно гиперплоскости, либо матрица math]\operatorname(1,\ldots,1, R_<\varphi>,1,\ldots,1)[/math] простого вращения двумерной плоскости. Поэтому любое ортогональное преобразование можно представить в виде композиции простых отражений и простых вращений.

Решение. Первый этап. Нахождение канонического вида преобразования.

2. Составляем характеристическое уравнение

Уравнение имеет три простых (кратности 1) корня: один действительный [math]\lambda_1=1[/math] и пару комплексных сопряженных [math]\lambda_<2,3>= \frac<1><2>\pm\frac<\sqrt<3>><2>\,i,

Выделяем действительную и мнимую части:

Нормируя столбцы, поделив координаты вектора [math]\boldsymbol[/math] на его длину

6. Записываем полученные в пункт 4, 5 столбцы [math]s_1,\,s_2,\,s_3[/math] в искомую матрицу перехода

Источник

Инструменты сайта

Основное

Информация

Действия

Содержание

Квадратичная форма

Определение

Пример. Функции

Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.

Пример.

Метод Лагранжа приведения квадратичной формы к каноническому виду

Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.

Пример. Привести форму

Матричная форма записи квадратичной формы

Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.

Пример. Для приведенной выше квадратичной формы

$ x_ <1>$	$ x_ <2>$	$ x_ <3>$
$ x_ <1>$	$ f_ <11>$	$ \frac<1><2>f_ <12>$	$ \frac<1><2>f_ <13>$
$ x_ <2>$	$ \frac<1><2>f_ <12>$	$ f_ <22>$	$ \frac<1><2>f_ <23>$
$ x_ <3>$	$ \frac<1><2>f_ <13>$	$ \frac<1><2>f_ <23>$	$ f_ <33>$

Пример. Для

Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.

Пример. Для формы

Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.

Метод Лагранжа и метод Гаусса

Пример. Рассмотрим матрицу квадратичной формы

Формула Якоби

Закон инерции для квадратичных форм

Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.

Ранг квадратичной формы

Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.

Закон инерции

Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.

Доказательство ☞ ЗДЕСЬ.

Доказательство следует из формулы Якоби.

Пример. Найти ранг и сигнатуру квадратичной формы

Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:

Как меняются ранг и сигнатура при непрерывном изменении параметров?

Справедливо и более общее утверждение.

Конгруэнтность квадратичных форм

Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.

Какое преобразование квадратичной формы оставляет ее инвариантной?

Знакоопределенность

Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.

Теорема. Ненулевая квадратичная форма, представленная в правильном виде

Доказательство ☞ ЗДЕСЬ.

К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.

Теорема [Сильвестр]. Квадратичная форма

Доказательство ☞ ЗДЕСЬ.

Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:

Пример. Квадратичная форма

Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?

Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений

Пример. Найти ортогональную замену переменных, приводящую квадратичную форму

Доказательство основано на правиле знаков Декарта.

Геометрия замен переменных

Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.

Источник

Приведение квадратичной формы к каноническому виду ортогональным преобразованием

Определение 15.2. Квадратичная форма называется канонической (или имеет канонический вид), если все a_ij = 0 при i ¹ j. Таким образом, канонический вид квадратичной формы следующий:

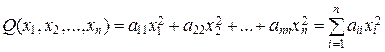
Очевидно, что канонической квадратичной форме соответствует диаго-нальная матрица

= diag (а₁₁, а₂₂,…, а_nn).

Нахождение канонического вида квадратичной формы называется приведением формы к каноническому виду.

Теоремa 15.1. Любая квадратичная форма с помощью ортогонального преобразования может быть приведена к каноническому виду

, (15.3)

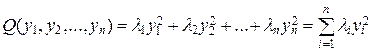
где l₁, l₂,…, l_n – собственные значения матрицы квадратичной формы.

Доказательство. Так как матрица А квадратичной формы является сим-метрической, то в силу теоремы 14.2 для нее существует ортогональная матрица Т, такая, что выполнено равенство L = Т * АТ. Пусть x = Тy, y = (у₁, у₂,…, у_n), где у₁, у₂,…, у_n – это координаты x в новом базисе, состоящем из нормированных собственных векторов матрицы А. Тогда из соотношения (15.2) получаем

Q (x₁, x₂,…, x_n) = (x, Аx) = (Ty, А(Тy)) = (y, (Т * АТ)y) = (y, Ly) =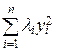, y = Т * x. (15.4)

Таким образом, квадратичная форма в базисе, состоящем из ортонорми-рованных собственных векторов матрицы А, приводится к каноническому виду. Алгоритм приведения ее к каноническому виду заключается, очевидно, в диагонализации симметрической матрицы квадратичной формы и последующей записи квадратичной формы в виде (15.3).¨

Пример 3. Привести к каноническому виду квадратичную форму

Q (x₁, x₂, x₃, x₄) = .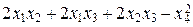

Решение. Составим соответствующую этой форме матрицу

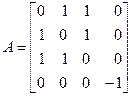
общее решение которой имеет вид

v = ,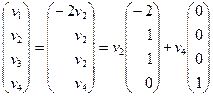

где v₂ и v₄ – произвольные действительные числа.

u 1 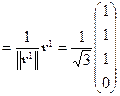, u 2 , u 3 , u 4 ,

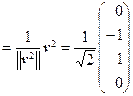
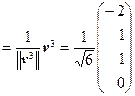
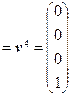
которые являются столбцами матрицы ортогонального преобразования Т, т. е.

Источник

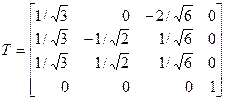
11.6. Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных

Теорема 11.9. Если существует ортогональное преобразование с матрицей С, приводящее действительную квадратичную формуК каноническому виду

То— характеристические числа матрицыКвадратичной формы

Теорема 11.10. Для любой действительной квадратичной формы существует ортогональное преобразование, приводящее ее к каноническому виду.

Теорема 11.11. Для любой, действительной симметрической матрицыСуществует такая ортогональная матрицаЧто— диагональная матрица.

Следствие. Любая действительная симметрическая матрица может быть приведена к диагональному виду.

Теорема 11.12. Если линейное преобразование действительного линейного пространства имеет действительную симметрическую матрицу в некотором ортонормированном базисе, то существует ортонормированный базис, состоящий из собственных векторов этого преобразования.

Из этих теорем следует правило нахождения ортогонального преобразования, приводящего квадратичную форму п переменных к каноническому вицу. Эго правило состоит в следующем: 1) записать матрицу данной квадратичной формы, найти ее собственные значения и п попарно ортогональных собственных векторов, пронормировать их; 2) составить матрицу из ортонормированных собственных вектор-сголбцов; 3) записать искомое ортогональное преобразование с помощью последней матрицы.

Пример 11.3. Найти ортогональное преобразование, приводящее к каноническому виду квадратичную форму двух переменных хи х,,

Найдем собственные векторы, соответствующие полученным собственным значениям. Координаты (л, I) этих векторов определяются из системы уравнений (10.12), которая в данном случае имеет вид

(5-А)« + 2>/бг = 0,0 гЛв + (7-А) 1 = 0.

При А, = 1, А, = 11 имеем две системы

Из этих систем находим собственные векторы и = (- (л/б/2) I, I), V = ((-Уб/з) I, I),

Где 1Ф 0. Положив 1х=—2, 1г =3, получим м= (Л,-2), V = (Л, 3).’ Нормировав эти векторы, запишем их координаты в столбцы, составим матрицу В: