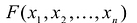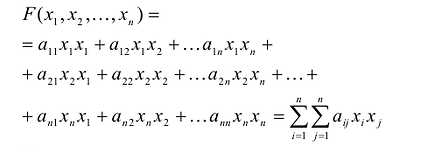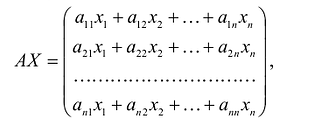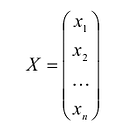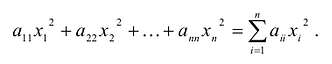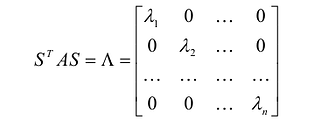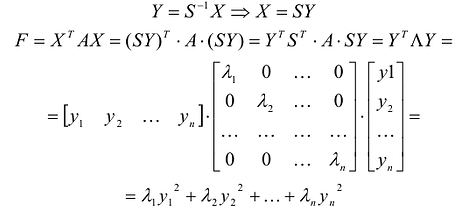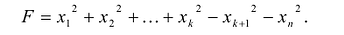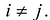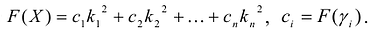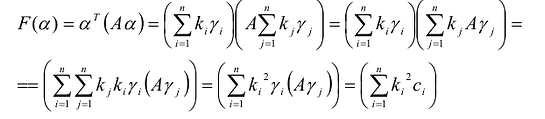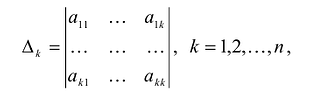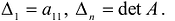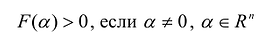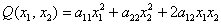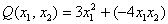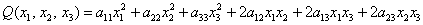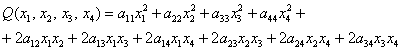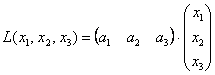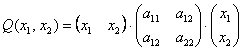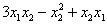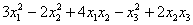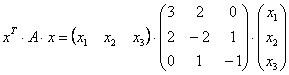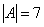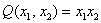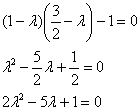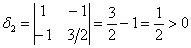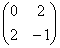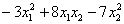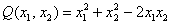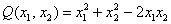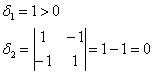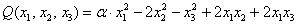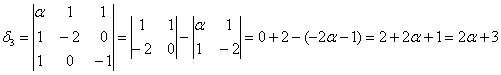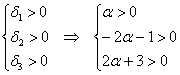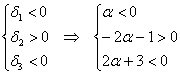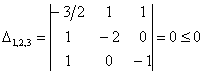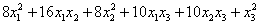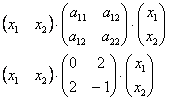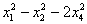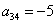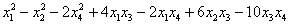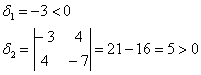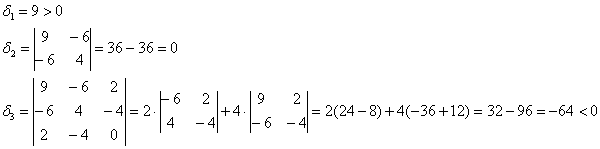каноническое представление положительно определенной квадратичной формы

Содержание:

Первоначально теория квадратичных форм использовалась для исследования кривых и поверхностей, задаваемых уравнением второго порядка, содержащими две или три переменные, Позднее эта теория нашла и другие приложения. В частности, при математическом моделировании экономических процессов целевые функции могут содержать квадратичные слагаемые. Многочисленные приложения квадратичных форм потребовали построения общей теории, когда число переменных равно любому п, а коэффициенты квадратичной формы не всегда являются вещественными числами.

Понятие квадратичной формы

Квадратичной формой

Пример:

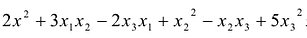
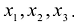
Сумма является квадратичной формой от трех неизвестных .

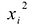
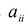
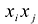
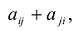
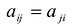
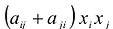
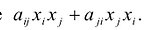
Каждую квадратичную форму можно записать в стандартном виде. Для этого сначала приводятся подобные в квадратичной форме, затем коэффициенты при обозначаются через а коэффициенты при через причем „ Член записывается в виде После этих преобразований квадратичную форму можно записать в виде:

С учетом правила умножения матриц можно вывести матричную форму записи квадратичной формы.

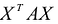
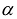
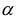
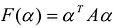
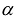
результатом скалярного произведения матриц X и АХ. Матричная форма записи квадратичной формы имеет вид . Если — произвольный n— мерный вектор, то после подстановки в квадратичную форму вместо X получится число , которое называется значением квадратичной формы F(X) на векторе .

Канонический базис квадратичной формы

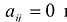
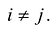
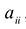
Принято считать, что квадратичная форма F(X) имеет канонический вид, если все коэффициенты при произведениях различных переменных равны нулю, т.е. при . При этом квадратичная форма представляет собой сумму квадратов переменных с соответствующими коэффициентами ,т.е.:

В этом случае матрица квадратичной формы имеет диагональный вид:

Очевидно, что изучение свойств квадратичной формы, записанной в каноническом виде, значительно упрощается. В связи с этим возникает задача приведения произвольной квадратичной формы к каноническому виду. В основе многих известных методов приведения квадратичной формы к каноническому виду лежит следующая теорема.

Теорема. Всякая квадратичная форма с помощью невырожденного линейного преобразования может быть приведена к каноническому виду.

Метод ортогональной матрицы использует особенности собственных значений и собственных векторов симметрической матрицы.

где 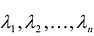-собственные значения матрицы А.

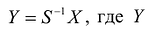
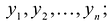
Применим к квадратичной форме линейное преобразование — матрица-столбец новых переменных — матрица, обратная к S.

Таким образом, квадратичную форму всегда можно представить в каноническом виде с коэффициентами, равными собственным значениям матрицы квадратичной формы.

Канонический вид квадратичной формы определяется неоднозначно. В то же время можно доказать, что все канонические формы, к которым приводится данная квадратичная форма, содержат одинаковое число отрицательных, положительных и нулевых коэффициентов при квадратах новых переменных.

Такую запись называют нормальным видом квадратичной формы. В нем общее число квадратов равно рангу r квадратичной формы.

Квадратичная форма может быть приведена к нормальному виду многими различными преобразованиями. При этом справедлива следующая теорема.

Теорема, Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится данная вещественная квадратичная форма вещественным невырожденным линейным преобразованием, не зависит от выбора этого преобразования.

Эту теорему называют законом инерции квадратичных форм.

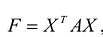
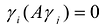
Базис пространства R» называется каноническим базисом квадратичной формы , если в этом базисе квадратичная форма имеет канонический вид, т.е. при

Если канонический базис F(X), то выражение: называется каноническим видом F(X) в базисе где — новый набор неизвестных.

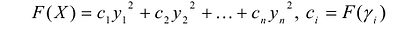
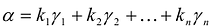
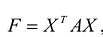
Теорема. Если — разложение вектора а по каноническому базису квадратичной формы то значение F(X) на векторе а вычисляется по формуле

Доказательство:

Эта теорема утверждает, что если известны канонический базис квадратичной формы F(X) и ее канонический вид в этом базисе, то для вычисления значения F(a) квадратичной формы F(X) на векторе а достаточно:

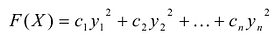
Квадратичная форма имеет много разных канонических базисов. Процесс построения канонического базиса называется приведением квадратичной формы к сумме квадратов.

Наиболее часто используются: канонический базис из собственных векторов матрицы А и канонический базис Якоби.

Канонический базис из собственных векторов матрицы квадратичной формы

Теорема. Ортонормированный базис пространства Rсостоящий из собственных векторов симметрической матрицы , является каноническим базисом квадратичной формы , а выражение — ее каноническим видом в базисе ,

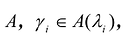
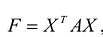
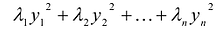
Доказательство:

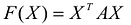
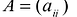
Канонический базис Якоби квадратичной формы . Будем говорить, что матрица удовлетворяет условию Якоби, если определители:

называемые угловыми минорами матрицы А, не равны нулю. Очевидно, что

Обозначим через 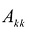матрицу:

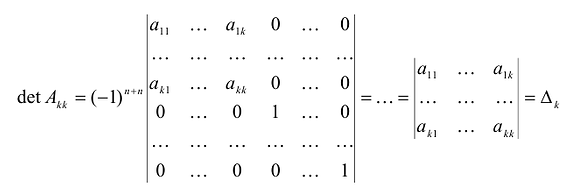
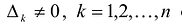
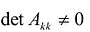
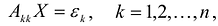
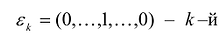
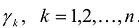
Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д. Из условия следует, что и, значит, каждая система уравнений , где вектор диагональной системы, имеет единственное решение . Система векторов называется системой векторов Якоби матрицы А, которая удовлетворяет условию Якоби.

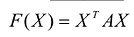
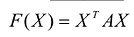
Теорема. матрица А квадратичной формы удовлетворяет условию Якоби, система векторов Якоби матрицы А является каноническим базисом квадратичной формы , а выражение:

ее каноническим видом в базисе .

Положительно и отрицательно определенные квадратичные формы

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Квадратичная форма

Определение

Пример. Функции

Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.

Пример.

Метод Лагранжа приведения квадратичной формы к каноническому виду

Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.

Пример. Привести форму

Пример. Привести форму

Пример. Привести форму

Матричная форма записи квадратичной формы

Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.

Пример. Для приведенной выше квадратичной формы

Пример. Для

Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.

Пример. Для формы

Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.

Метод Лагранжа и метод Гаусса

Пример. Рассмотрим матрицу квадратичной формы

Формула Якоби

Закон инерции для квадратичных форм

Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.

Ранг квадратичной формы

Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.

Закон инерции

Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.

Доказательство ☞ ЗДЕСЬ.

Доказательство следует из формулы Якоби.

Пример. Найти ранг и сигнатуру квадратичной формы

Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:

Как меняются ранг и сигнатура при непрерывном изменении параметров?

Справедливо и более общее утверждение.

Конгруэнтность квадратичных форм

Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.

Какое преобразование квадратичной формы оставляет ее инвариантной?

Знакоопределенность

Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.

Теорема. Ненулевая квадратичная форма, представленная в правильном виде

Доказательство ☞ ЗДЕСЬ.

К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.

Теорема [Сильвестр]. Квадратичная форма

Доказательство ☞ ЗДЕСЬ.

Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:

Пример. Квадратичная форма

Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?

Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений

Пример. Найти ортогональную замену переменных, приводящую квадратичную форму

Доказательство основано на правиле знаков Декарта.

Геометрия замен переменных

Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.

Источник

Квадратичные формы.
Знакоопределённость форм. Критерий Сильвестра

Прилагательное «квадратичный» сразу наталкивает на мысль, что что-то здесь связано с квадратом (второй степенью), и очень скоро мы узнаем это «что-то» и что такое форма. Прямо скороговоркой получилась 🙂

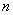
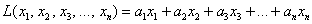
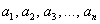
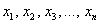
Приветствую вас на своём новом уроке, и в качестве незамедлительной разминки мы рассмотрим форму в полосочку линейную. Линейной формой переменных называют однородный многочлен 1-й степени:

, где:

– какие-то конкретные числа* (предполагаем, что хотя бы одно из них отлично от нуля), а – переменные, которые могут принимать произвольные значения.

* В рамках данной темы будем рассматривать только действительные числа.

С термином «однородный» мы уже сталкивались на уроке об однородных системах линейных уравнений, и в данном случае он подразумевает, что у многочлена нет приплюсованной константы .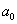

Например: 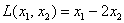– линейная форма двух переменных

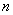
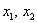
Теперь форма квадратичная. Квадратичной формой переменных называют однородный многочлен 2-й степени, каждое слагаемое которого содержит либо квадрат переменной, либо парное произведение переменных. Так, например, квадратичная форма двух переменных имеет следующий вид:

Внимание! Это стандартная запись, и что-то менять в ней не нужно! Несмотря на «страшный» вид, тут всё просто – двойные подстрочные индексы констант сигнализируют о том, какие переменные входят в то или иное слагаемое:
– в этом слагаемом находится произведение и (квадрат);
– здесь произведение ;
– и здесь произведение .

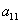
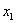
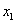
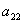
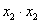
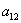
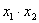
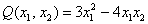
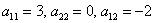
Далее будем полагать, что хотя бы одна из констант не равна нулю, и вот, пожалуйста, «неполный» пример: , в котором:

– сразу упреждаю грубую ошибку, когда теряют «минус» у коэффициента, не понимая, что он относится к слагаемому:

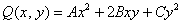
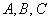
Иногда встречается «школьный» вариант оформления в духе , но то лишь иногда. Кстати, заметьте, что константы нам тут вообще ни о чем не говорят, и поэтому запомнить «лёгкую запись» труднее. Особенно, когда переменных больше.

И квадратичная форма трёх переменных содержит уже шесть членов:

…почему в «смешанных» слагаемых ставятся множители-«двойки»? Это удобно, и скоро станет понятно, почему.

Далее ситуация начинает усугубляться:

и усугублять мы её дальше не будем, т.к. формы с бОльшим количеством переменных встречаются довольно редко.

Однако общую формулу запишем, её удобно оформить «простынёй»:

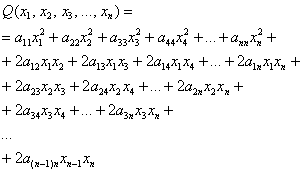
– внимательно изучаем каждую строчку – ничего страшного тут нет!

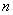
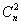
Квадратичная форма содержит слагаемых с квадратами переменных и слагаемых с их парными произведениями (см. комбинаторную формулу сочетаний). Больше ничего – никаких «одиноких иксов» и никакой приплюсованной константы (тогда уже получится не квадратичная форма, а неоднородный многочлен 2-й степени).

Матричная запись квадратичной формы

Как на счёт матриц? 🙂 Знаю, знаю, соскучились. В практических задачах широко распространенная матричная запись квадратичных форм. Объяснения опять начну с формы линейной, например, от трёх переменных: 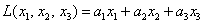. Её можно записать, как произведение двух матриц:

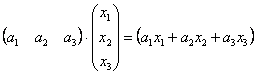
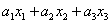
И действительно, выполняя матричное умножение, получаем матрицу «один на один»: , единственный элемент которой можно эквивалентно записать вне матрицы: .

Легко понять, что линейная форма «эн» переменных записывается в виде:

Квадратичная форма представима в виде произведения уже трёх матриц:

, где:

– столбец переменных;

– его транспонированная строка;

– матрица квадратичной формы.

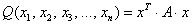
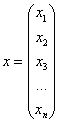
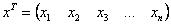
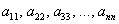
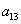
Это так называемая симметрическая матрица, на главной диагонали которой расположены коэффициенты при квадратах неизвестных, а симметрично относительно неё – «смешанные» коэффициенты, причём, строго на «своих местах» (например, – в 1-й строке, 3-м столбце и 1-м столбце, 3-й строке).

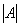
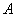
Определитель называют дискриминантом квадратичной формы, а ранг матрицы – рангом квадратичной формы.

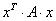
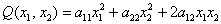
Если перемножить три матрицы , то получится в точности длинная «простыня» из предыдущего параграфа, но разворачивать её мы, конечно, не будем, а посмотрим, как это происходит в элементарном случае . Согласно общей формуле, матричная запись данной формы имеет следующий вид:

И в самом деле: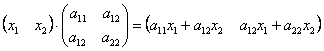

далее: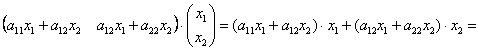

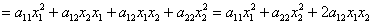
, в чём и требовалось убедиться.

Как вариант, сначала можно было перемножить правые матрицы, и затем первую матрицу умножить на полученный результат.

Вам понравилось так же, как и мне? Ну тогда пример для самостоятельного решения =)

Записать квадратичную форму в матричном виде и выполнить проверку. Определить дискриминант и ранг формы.

…что-то смущает? 😉 Краткое решение и ответ в конце урока! Статьи об определителе и ранге матрицы – в помощь.

После чего разберём аналогичную задачу с формой трёх переменных:

Записать матрицу квадратичной формы, найти её ранг и дискриминант

Решение: сбросим тяжёлую ношу лишних формул, и будем ориентироваться на сами члены:

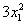
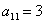
– слагаемое дважды содержит 1-ю переменную, поэтому ;

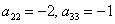
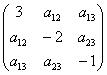
– из аналогичных соображений определяем и сразу записываем результаты на главную диагональ симметрической матрицы: .

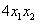
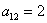
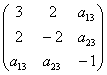
Так как в слагаемое входят 1-я и 2-я переменная, то (не забываем поделить на 2) и данный коэффициент занимает свои законные места: .

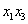
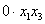
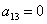
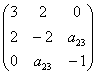
Поскольку в форме отсутствует член с произведением (а точнее, присутствует с нулевым множителем: ), то , и на холст отправляются два нуля: .

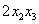
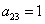
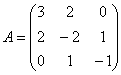
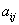
И, наконец, из слагаемого определяем , после чего картина завершена:
– матрица квадратичной формы. Вот так-то оно бывает – мы не только не испугались «страшных обозначений» , но и заставили их работать на себя!

По условию не требовалось записывать матричное уравнение, однако науки ради:

Желающие могут перемножить три матрицы, в результате чего должна получиться исходная квадратичная форма.

Теперь определим ранг формы. Он равен рангу матрицы . Так как в матрице есть хотя бы один ненулевой элемент, например, , то ранг не меньше единицы. Теперь вычислим минор , значит, ранг не меньше двух. И осталось проверить минор 3-го порядка, т.е. определитель всей матрицы. Здесь я ко второму столбцу прибавлю третий и раскрою определитель по 3-й строке:
, значит,

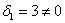
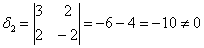
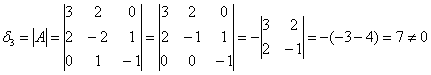
Если не очень понятно, что к чему, обязательно изучите статью о ранге матрицы – это довольно замысловатая задачка, и перед нами оказался лишь простой случай, когда угловые миноры не равны нулю.

Дискриминант квадратичной формы получен автоматом.

Ответ: , ранг равен трём, дискриминант

Следующее задание для самостоятельного решения:

Восстановить квадратичную форму по её матрице

При этом не нужно вспоминать никаких формул! Решение почти устное:

– сначала смотрим на главную диагональ и записываем слагаемые с квадратами переменных;

– затем анализируем симметричные элементы 1-й строки (или 1-го столбца), и записываем все слагаемые, в которые входит 1-я переменная (не забывая удвоить коэффициенты);

– далее смотрим на оставшиеся симметричные элементы 2-й строки (справа от диагонали) либо 2-го столбца (ниже диагонали) и записываем соответствующие парные произведения (с удвоенными коэффициентами!).

– и, наконец, анализируем правую нижнюю пару симметричных чисел.

Подробное решение и ответ в конце урока.

Знакоопределённость квадратичной формы. Критерий Сильвестра

До сих пор мы рассматривали «внешнее устройство» форм и пришло время изучить их функциональное назначение. Да, по существу, они работают, как функции. Вернёмся к простенькой линейной форме .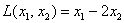

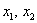
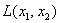
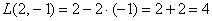
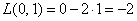
Как отмечалось в начале урока, переменные могут принимать произвольные действительные значения (мы ограничились ими), и каждой такой паре соответствует определённое значение , например:

, и так далее.

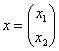
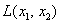
Говоря языком науки, перед нами скалярная функция векторного аргумента, в которой каждому вектору ставится в соответствие определённое число . Обращаю ваше внимание, что сейчас идёт речь не о геометрическом векторе, а о векторе в его алгебраическом понимании.

В зависимости от значений рассматриваемая форма может принимать как положительные, так и отрицательные значения, и то же самое касается любой линейной формы – если хотя бы один из её коэффициентов отличен от нуля, то она может оказаться как положительной, так и отрицательной (в зависимости от значений ).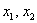

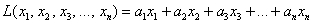
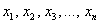
Такая форма называется знакопеременной. И если с линейной формой всё прозрачно, то с формой квадратичной дела обстоят куда более интересно:

Совершенно понятно, что данная форма может принимать значения любого знака, таким образом, квадратичная форма тоже может быть знакопеременной.

– всегда, если только одновременно не равны нулю.

– для любого вектора , кроме нулевого .

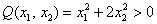
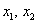
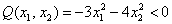
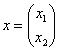
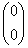
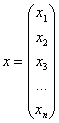
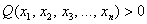
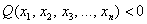
И вообще, если для любого ненулевого вектора , , то квадратичную форму называют положительно определённой; если же – то отрицательно определённой.

Можно предположить, что форма определена положительно, но так ли это на самом деле? Вдруг существуют значения 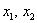, при которых она меньше нуля?

На этот счёт существует теорема: если ВСЕ собственные числа матрицы квадратичной формы положительны*, то она определена положительно. Если все отрицательны – то отрицательно.

* В теории доказано, что все собственные числа действительной симметрической матрицы действительны

Запишем матрицу вышеприведённой формы:
и из уравнения найдём её собственные значения:

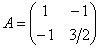
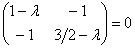
Решаем старое доброе квадратное уравнение: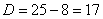

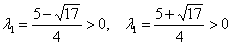
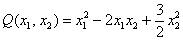
, значит, форма определена положительно, т.е. при любых ненулевых значениях она больше нуля.

Рассмотренный метод вроде бы рабочий, но есть одно большое НО. Уже для матрицы «три на три» искать собственные числа – есть занятие долгое и неприятное; с высокой вероятностью получится многочлен 3-й степени с иррациональными корнями.

Как быть? Существует более простой путь!

Критерий Сильвестра

Нет, не Сильвестра Сталлоне 🙂 Сначала напомню, что такое угловые миноры матрицы. Это определители 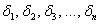которые «разрастаются» из её левого верхнего угла:

и последний из них в точности равен определителю матрицы.

Теперь, собственно, критерий:

1) Квадратичная форма определена положительно тогда и только тогда, когда ВСЕ её угловые миноры больше нуля: .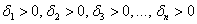

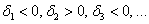
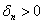
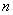
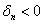
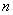
2) Квадратичная форма определена отрицательно тогда и только тогда, когда её угловые миноры знакочередуются, при этом 1-й минор меньше нуля: , , если – чётное или , если – нечётное.

Если в 1-й или 2-й последовательности есть нулевые миноры, то это два особых случая, которые я разберу чуть позже, после того, как мы перещёлкаем более распространённые примеры. При любой другой комбинации плюсов-минусов (и опционально нулей) форма знакопеременна.

Проанализируем угловые миноры матрицы :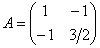

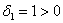
, и это сразу говорит нам о том, что форма не определена отрицательно (отпал пункт 2).

Вывод: все угловые миноры больше нуля, значит, форма 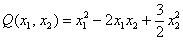определена положительно.

Есть разница с методом собственных чисел? 😉

Запишем матрицу формы 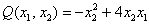из Примера 1:

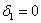
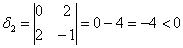
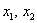
первый её угловой минор , а второй , откуда следует, что форма знакопеременна, т.е. в зависимости от значений , может принимать как положительные, так и отрицательные значения. Впрочем, это и так очевидно.

Возьмём форму 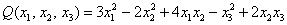и её матрицу из Примера 2:

тут вообще без озарения не разобраться. Но с критерием Сильвестра нам всё нипочём: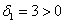
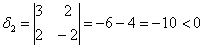
, следовательно, форма точно не отрицательна.

, и точно не положительна (т.к. все угловые миноры должны быть положительными).

Вывод: форма знакопеременна.

Разминочные примеры для самостоятельного решения:

Исследовать квадратичные формы на знакоопределенность

а)

б)

В этих примерах всё гладко (см. конец урока), но на самом деле для выполнения такого задания критерия Сильвестра может оказаться не достаточно.

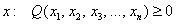
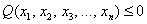
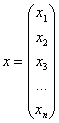
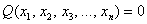
Дело в том, что существуют «краевые» случаи, а именно: если для любого ненулевого вектора , то форма определена неотрицательно, если – то неположительно. У этих форм существуют ненулевые векторы , при которых .

Здесь можно привести такой «баян»:

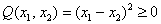
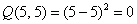
Выделяя полный квадрат, сразу видим неотрицательность формы: , причём, она равна нулю и при любом векторе с равными координатами, например: .

«Зеркальный» пример неположительно определённой формы: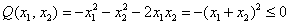

и ещё более тривиальный пример:
– здесь форма равна нулю при любом векторе , где – произвольное число.

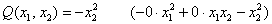
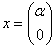
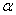
Как выявить неотрицательность или неположительнось формы?

Для этого нам потребуется понятие главных миноров матрицы. Главный минор – это минор, составленный из элементов, которые стоят на пересечении строк и столбцов с одинаковыми номерами. Так, у матрицы существуют два главных минора 1-го порядка:
(элемент находится на пересечении 1-й строки и 1-го столбца);
(элемент находится на пересечении 2-й строки и 2-го столбца),

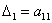
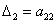
и один главный минор 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца.

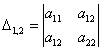
У матрицы «три на три» главных миноров семь, и тут уже придётся помахать бицепсами:
– три минора 1-го порядка,
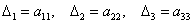
три минора 2-го порядка:
– составлен из элементов 1-й, 2-й строки и 1-го, 2-го столбца;
– составлен из элементов 1-й, 3-й строки и 1-го, 3-го столбца;
– составлен из элементов 2-й, 3-й строки и 2-го, 3-го столбца,
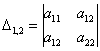
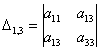
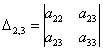
и один минор 3-го порядка:
– составлен из элементов 1-й, 2-й, 3-й строки и 1-го, 2-го и 3-го столбца.
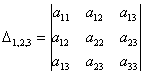
Задание на понимание: записать все главные миноры матрицы .
Сверяемся в конце урока и продолжаем.

Критерий Шварценеггера:

1) Ненулевая* квадратичная форма определена неотрицательно тогда и только тогда, когда ВСЕ её главные миноры неотрицательны (больше либо равны нулю).

* У нулевой (вырожденной) квадратичной формы все коэффициенты равны нулю.

2) Ненулевая квадратичная форма с матрицей 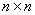определена неположительно тогда и только тогда, когда её:
– главные миноры 1-го порядка неположительны (меньше либо равны нулю);
– главные миноры 2-го порядка неотрицательны;
– главные миноры 3-го порядка неположительны (пошлО чередование);
…
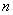
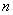
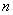
– главный минор -го порядка неположителен, если – нечётное либо неотрицателен, если – чётное.

Если хотя бы один минор противоположного знака, то форма знакопеременна.

Посмотрим, как работает критерий в вышеприведённых примерах:

Составим матрицу 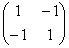формы, и в первую очередь вычислим угловые миноры – а вдруг она определена положительно или отрицательно?

Полученные значения не удовлетворяют критерию Сильвестра, однако второй минор не отрицателен, и это вызывает надобность проверить 2-й критерий (в случае 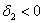2-й критерий будет не выполнен автоматически, т.е. сразу делается вывод о знакопеременности формы).

Главные миноры 1-го порядка:
– положительны,
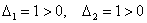
главный минор 2-го порядка:
– не отрицателен.

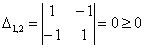
Таким образом, ВСЕ главные миноры не отрицательны, значит, форма неотрицательна.

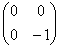
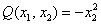
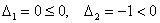
Запишем матрицу формы , для которой, очевидно, не выполнен критерий Сильвестра. Но и противоположных знаков мы тоже не получили (т.к. оба угловых минора равны нулю). Поэтому проверяем выполнение критерия неотрицательности / неположительности. Главные миноры 1-го порядка:
– не положительны,
главный минор 2-го порядка:
– не отрицателен.

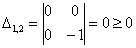
Таким образом, по критерию Шварценеггера (пункт 2), форма определена неположительно.

Теперь во всеоружии разберём более занятную задачку:

Исследовать квадратичную форму на знакоопределенность

Данную форму украшает орден «альфа», который может равняться любому действительному числу. Но это ж только веселее будет, решаем.

Сначала запишем матрицу формы, наверное, многие уже приноровились это делать устно: на главную диагональ ставим коэффициенты при квадратах, а на симметричные места – споловиненные коэффициенты соответствующих «смешанных» произведений:

Вычислим угловые миноры: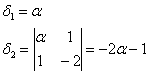

третий определитель я раскрою по 3-й строке:

Кстати, в силу симметрии, по 3-му столбцу он раскрывается точно так же.

Дальнейшее решение удобно разбить на 2 пункта:

1) Выясним, существуют ли значения «альфа», при которых форма определена положительно или неотрицательно. Согласно критерию Сильвестра, условию положительности формы соответствует следующая система линейных неравенств:

В соответствии с поставленной задачей, сначала разберёмся со 2-м неравенством: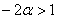

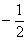
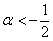
умножим обе его части на , сменив у неравенства знак:
, что противоречит первому неравенству системы.

Таким образом, система несовместна, а значит, форма не может быть положительно определённой ни при каких «альфа», из чего логически и автоматически следует, что она не может быть и неотрицательной.

2) Проведём исследование на отрицательность / неположительнось. По Сильвестру, условию отрицательности формы соответствует следующая система линейных неравенств:

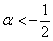
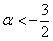
Второе неравенство уже решено: , и оно не противоречит первому. И третье неравенство тоже «вписалось в рамки»: .
Таким образом, имеем совместную систему: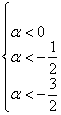

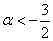
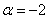
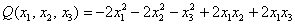
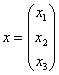
из которой следует, что форма определена отрицательно при . Например, если :
– то при любом ненулевом векторе данная форма будет строго отрицательна.

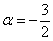
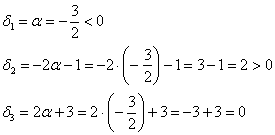
Осталось исследовать «пограничный» случай. Если , то:

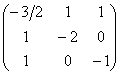
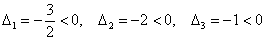
Последнее значение не удовлетворяет 2-му пункту критерия Сильвестра, однако оно равно нулю, что позволяет предположить неположительнось формы. Запишем матрицу формы и проверим критерий Шварценеггера. Главные миноры первого порядка:
– отлично, все миноры неположительны, поэтому проверка продолжается.

Рассчитываем миноры 2-го порядка. Если хотя бы один из них окажется отрицательным, то форма будет знакопеременной:

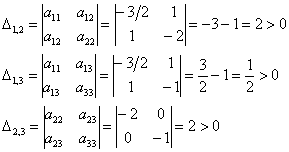
Нет, все миноры неотрицательны, и минор 3-го порядка уже рассчитан:

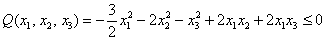
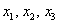
Таким образом, по критерию Шварценеггера (пункт 2), имеет место неположительнось формы, иными словами, , причём, нулю она равна и при некоторых ненулевых значениях .

Ответ: при 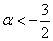форма определена отрицательно, при неположительно, в остальных случаях форма знакопеременна.

И творческое задание для самостоятельного решения:

Исследовать квадратичную форму на знакоопределенность

И в заключение статьи хочу выразить благодарность Сергею Хохлову, некогда ст. преподавателю МПГУ – за важные замечания и интересные дополнительные примеры, а также Арнольду Шварценеггеру, который сыграл в непривычном для себя амплуа и помог мне ярче объяснить материал 🙂

Как сказал актёр, I’ll be back, и я жду вас на следующем уроке – о каноническом виде квадратичной формы.

Пример 1. Решение: сначала приведём подобные слагаемые: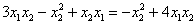

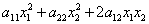
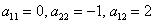
Квадратичная форма двух переменных имеет вид , в данном случае: . Запишем форму в матричном виде:

Проверка:

что и требовалось проверить.

Вычислим дискриминант формы: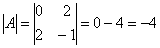

Поскольку 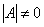, то ранг формы равен двум.

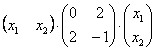
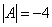
Ответ: , , ранг формы равен двум.

Пример 3. Решение: симметрическая матрица 4*4 определяет квадратичную форму 4 переменных. Коэффициенты главной диагонали 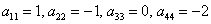, следовательно:

Симметричные коэффициенты 1-й строки: 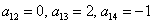, таким образом:

Оставшиеся симметричные элементы 2-й строки: 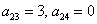, и:

И, наконец,

Ответ:

Пример 4. Решение:

а) запишем матрицу формы: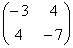

и вычислим её угловые миноры:

Таким образом, по критерию Сильвестра, форма определена отрицательно.

б) запишем матрицу формы: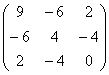

и вычислим её угловые миноры:

Вывод: форма знакопеременна.

Задание на понимание: у данной матрицы четыре главных минора 1-го порядка: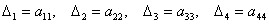
,
шесть главных миноров 2-го порядка: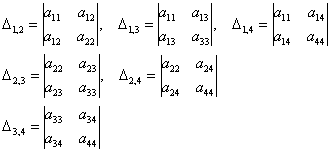

четыре главных минора 3-го порядка: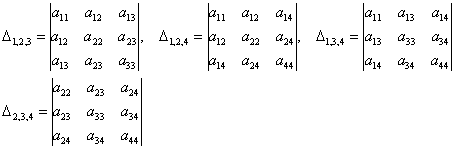

и один главный минор 4-го порядка, равный определителю матрицы.

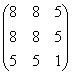
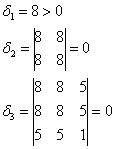
Пример 5*. Решение: запишем матрицу формы и вычислим её угловые миноры:

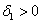
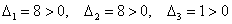
Таким образом, форма не удовлетворяет критерию Сильвестра, однако, может оказаться неотрицательной (т.к. и остальные миноры нулевые). Для этого все главные миноры должны быть неотрицательны. Главные миноры 1-го порядка:
.
Вычислим главные миноры 2-го порядка:

– среди главных миноров встретился отрицательный, следовательно, форма не удовлетворяет критерию неотрицательности.

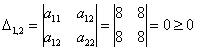
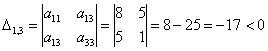
Ответ: форма знакопеременна.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник