кардинальное число отношения это
Кардинальное число отношения это
В конце 60-х годов появились работы, в которых обсуждались возможности применения различных табличных даталогических моделей данных, т.е. возможности использования привычных и естественных способов представления данных. Наиболее значительной из них была статья сотрудника фирмы IBM д-ра Э.Кодда (Codd E.F., A Relational Model of Data for Large Shared Data Banks. CACM 13: 6, June 1970), где, вероятно, впервые был применен термин «реляционная модель данных».
Будучи математиком по образованию Э.Кодд предложил использовать для обработки данных аппарат теории множеств (объединение, пересечение, разность, декартово произведение). Он показал, что любое представление данных сводится к совокупности двумерных таблиц особого вида, известного в математике как отношение – relation (англ.) [3, 7, 9].
Наименьшая единица данных реляционной модели – это отдельное атомарное (неразложимое) для данной модели значение данных. Так, в одной предметной области фамилия, имя и отчество могут рассматриваться как единое значение, а в другой – как три различных значения.
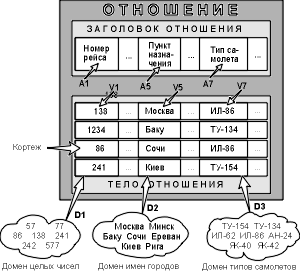
Доменом называется множество атомарных значений одного и того же типа. Так, на рис. 1.1 домен пунктов отправления (назначения) – множество названий населенных пунктов, а домен номеров рейса – множество целых положительных чисел.
Смысл доменов состоит в следующем. Если значения двух атрибутов берутся из одного и того же домена, то, вероятно, имеют смысл сравнения, использующие эти два атрибута (например, для организации транзитного рейса можно дать запрос «Выдать рейсы, в которых время вылета из Москвы в Сочи больше времени прибытия из Архангельска в Москву»). Если же значения двух атрибутов берутся из различных доменов, то их сравнение, вероятно, лишено смысла: стоит ли сравнивать номер рейса со стоимостью билета?
Тело состоит из меняющегося во времени множества кортежей, где каждый кортеж состоит в свою очередь из множества пар атрибут-значение (Ai:Vi), (i=1,2. n), по одной такой паре для каждого атрибута Ai в заголовке. Для любой заданной пары атрибут-значение (Ai:Vi) Vi является значением из единственного домена Di, который связан с атрибутом Ai.
Кардинальное число или мощность отношения – это число его кортежей. Мощность отношения «Рейс» равна 10. Кардинальное число отношения изменяется во времени в отличие от его степени.
Каждое отношение обладает хотя бы одним возможным ключом, поскольку по меньшей мере комбинация всех его атрибутов удовлетворяет условию уникальности. Один из возможных ключей (выбранный произвольным образом) принимается за его первичный ключ. Остальные возможные ключи, если они есть, называются альтернативными ключами.
Вышеупомянутые и некоторые другие математические понятия явились теоретической базой для создания реляционных СУБД, разработки соответствующих языковых средств и программных систем, обеспечивающих их высокую производительность, и создания основ теории проектирования баз данных. Однако для массового пользователя реляционных СУБД можно с успехом использовать неформальные эквиваленты этих понятий:
Отношение – Таблица (иногда Файл),
Кортеж – Строка (иногда Запись),
Атрибут – Столбец, Поле.
При этом принимается, что «запись» означает «экземпляр записи», а «поле» означает «имя и тип поля».
Фундаментальные свойства отношений.
Дата добавления: 2013-12-23 ; просмотров: 3310 ; Нарушение авторских прав
Основные определения реляционных БД.
Глава
Тема 2.3 Электропусковые системы.
Й семестр
Организация реляционных баз данных.
Работы над построением реляционных моделей данных ведутся с конца 60-х годов. Термин Реляционная СУБД впервые был использован Коддом (Codd E.F) в 1970 году. Кодд предложил использовать для обработки данных аппарат теории множеств (объединение, пересечение, разность, декартово произведение). Он показал, что любое представление данных сводится к совокупности двумерных таблиц особого вида, известного в математике как отношение – relation (англ.). в настоящее время благодаря своей простоте реляционные СУБД доминируют на рынке СУБД.
В соответствии с реляционной моделью данных база данных представляется в виде совокупности таблиц данных, над которыми могут выполняться операции реляционной алгебры или реляционного исчисления.
Различают бинарные реляционные модели и реляционные модели с произвольным числом арности отношения.
Наименьшая единица данных в реляционной модели – это атомарное (неразложимое) для данной модели значение данных. Так, в одной предметной области фамилия, имя и отчество могут рассматриваться как единое значение, а в другой – как три различных значения.
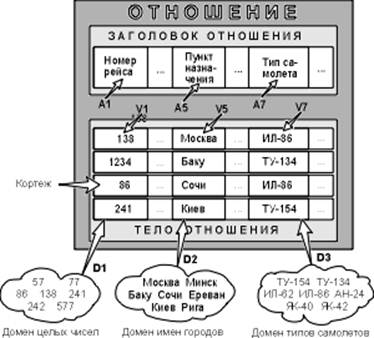
Доменом называется множество атомарных значений одного и того же типа, из которого извлекаются значения для атрибутов. Например, домен пунктов отправления (назначения) – множество названий населенных пунктов, а домен номеров рейса – множество целых положительных чисел.
Смысл доменов состоит в следующем. Если значения двух атрибутов берутся из одного и того же домена, то имеют смысл операции сравнения, использующие эти два атрибута. Например, можно задать запрос «Выдать рейсы, в которых время вылета из Москвы в Сочи больше времени прибытия из Архангельска в Москву«.
Если же значения двух атрибутов берутся из различных доменов, то их сравнение лишено смысла. Например, нельзя сравнить номер рейса со стоимостью билета, даже несмотря на то, что эти атрибуты имеют числовой тип. Обозначаются домены так :
Тело состоит из меняющегося во времени множества кортежей, где каждый кортеж состоит в свою очередь из множества пар атрибут-значение (Ai:Vi), (i=1,2. n), по одной такой паре для каждого атрибута Ai в заголовке. Для любой заданной пары атрибут-значение (Ai:Vi) Vi является значением из единственного домена Di, который связан с атрибутом Ai.
Кардинальное число или мощность отношения – это число его кортежей. Кардинальное число отношения изменяется во времени в отличие от его степени.
Поскольку отношение – это множество, а множества по определению не содержат совпадающих элементов, то никакие два кортежа отношения не могут быть дубликатами друг друга в любой произвольно-заданный момент времени.
Каждое отношение обладает хотя бы одним возможным ключом, поскольку по меньшей мере комбинация всех его атрибутов удовлетворяет условию уникальности. Один из возможных ключей (выбранный произвольным образом) принимается за его первичный ключ. Остальные возможные ключи, если они есть, называются альтернативными (вторичными) ключами.
Для пользователя реляционных СУБД можно использовать неформальные эквиваленты этих понятий:
Отношение – это таблица либо файл данных
Кортеж – это Строка (иногда Запись),
Атрибут – это Столбец либо Поле.
При этом принимается, что «запись» означает «экземпляр записи», а «поле» означает «имя и тип поля».
Рисунок – отношение с математической точки зрения
 |
Реляционная база данных – это совокупность отношений, содержащих всю информацию, которая должна храниться в БД.
Для каждого отношения реляционной БД должны выполняться следующие свойства :
2. Строки имеют фиксированное число полей (столбцов) и значений. Множественные поля и повторяющиеся группы полей недопустимы. Поэтому каждой позиции таблицы на пересечении строки и столбца всегда имеется в точности одно значение.
3. Строки таблицы обязательно отличаются друг от друга хотя бы единственным значением. Это позволяет однозначно идентифицировать любую строку такой таблицы.
4. Столбцам таблицы однозначно присваиваются имена, и в каждом из них размещаются однородные значения данных (даты, фамилии, целые числа или денежные суммы).
5. Полное информационное содержание базы данных представляется в виде явных значений данных, и такой метод представления является единственным.
6. При выполнении операций с таблицей ее строки и столбцы можно обрабатывать в любом порядке безотносительно к их информационному содержанию. Этому способствует наличие имен таблиц и их столбцов, а также возможность выделения любой их строки или любого набора строк с указанными признаками.
8. Отсутствие упорядоченности кортежей. Это является следствием определения отношения как множества кортежей. В случае упорядоченности кортежей получается не отношение, а некоторый упорядоченный список кортежей. Отсутствие требования упорядоченности дает дополнительную гибкость СУБД при хранении баз данных и выполнении запросов.
9. Атрибуты отношений не упорядочены. Для ссылки на значение атрибута в кортеже отношения всегда используется имя атрибута. Это свойство теоретически позволяет модифицировать схемы существующих отношений путем добавления новых атрибутов и путем удаления существующих атрибутов. Однако в большинстве существующих систем такая возможность не допускается
BestProg
Базовые понятия реляционной модели данных
Содержание
Поиск на других ресурсах:
1. Какие есть базовые понятия реляционной модели данных?
Как известно, реляционная модель данных основывается на сохранении данных в виде взаимосвязанных таблиц. Связь между таблицами может быть реализована по некоторому полю и называется отношением (relation).
Реляционная модель данных использует следующие основные понятия:
2. Что такое тип данных в реляционной модели данных?
Тип данных есть характеристикой объекта в языке программирования. Таким объектом может выступать переменная, константа и т.п. Тип данных определяет допустимое множество значений, которые может принимать переменная величина или объект.
В системах управления базами данных тип данных имеет такое самое значение как и языках программирования.
Пример. Пусть задана таблица Worker, описывающая данные о работнике предприятия.
В вышеприведенной таблице целесообразно установить следующий тип данных для каждого поля:
3. Какие типы данных поддерживаются системами управления базами данных?
Современные СУБД поддерживают следующие основные типы данных:
4. Домены в реляционной модели данных
Домен – это множество отдельных допустимых значений данных, которые:
Пример. Пусть дана таблица Worker, описывающая данные о работнике.
В домене «Идентификационный код» допустимыми являются строки из цифр, которые имеют строго 10 разрядов. В домене «Пол» возможны только 2 значения. В домене «Разряд» могут быть целочисленные значения от 1 до 6.
5. Атрибуты в реляционной модели данных
Атрибуты – это столбцы таблицы (поля таблицы). Атрибуты имеют имена. По имени атрибута осуществляется обращение к таблице.
Пример. В таблице Worker (см. п. 4) названия атрибутов следующие:
6. Что такое схема отношения? Что такое схема базы данных?
Схема отношения – это список имен атрибутов отношения с указанием имен типов.
Пример. Для таблицы Worker схема отношения будет приблизительно следующей:
Множество именованных схем отношения, называется схемой базы данных.
7. Что такое степень отношения?
Количество атрибутов в таблице называется степенью отношения. Для примера (см. п. 4) таблицы Worker степень отношения равна 6 (таблица имеет 6 полей).
Унарное отношение – это отношение степени один. Бинарное отношение – это отношение степени два. Тернарное отношение – это отношение степени три. n-арное отношение – это отношение степени n.
8. Что такое кортеж в базах данных?
Кортеж рассматривается для конкретной (данной) схемы отношения. В такой схеме кортеж есть множество пар, которые представлены следующим образом:
где имя_атрибута – имя конкретного атрибута.
Например. Пусть задана таблица Worker с такими данными
Схема отношения для данной таблицы будет следующая:
Тогда кортеж, который отвечает первой строке таблицы Worker будет иметь вид:
Таким самым образом можно определить кортеж, который соответствует второй строке таблицы Worker а также и следующим строкам таблицы.
9. Что называется кардинальным числом или мощностью отношения?
Кардинальное число – это количество кортежей. В таблице Worker (см. п. 8) кардинальное число равно 7. Кардинальное число еще называют мощностью отношения.
10. Что собою представляет пустое значение (NULL) в базе данных?
Существуют случаи, когда в таблице базы данных некоторые значения еще неизвестны на данный момент времени. Такие значения называются пустыми значениями и могут быть заполнены со временем (позже). Для задавания пустых значений, в базе данных используется слово NULL. Системы управления базами данных допускают использования значения NULL для задавания данных, которые могут быть заполнены позже.
Следует заметить, что значение NULL не является нулем и не является пустой строкой.
Например. В таблице Worker (п. 8) возможна ситуация, когда работник еще не имеет разряда. В этом случае в соответствующей ячейке нужно ввести значение NULL. Как только работнику будет присвоен некоторый разряд, значение NULL будет заменено этим новым значением.
11. Что такое ключи отношения? Что такое первичный ключ?
Важным условием любой базы данных есть то, что в ней не должно быть двух одинаковых записей. Или другими словами, в таблице базы данных не должно быть двух кортежей, которые содержат одинаковые значения. Во избежание этой проблемы, используются первичные ключи.
Первичный ключ – это специальное дополнительное поле (атрибут) таблицы, которое создается для обеспечения уникальности идентификации записей таблицы. Основная цель создания первичного ключа – предотвратить дублирование (повторение) записей таблицы.
Например. Пусть дана таблица Worker (см. п.8). Чтобы не повторялись записи, в этой таблице может быть создано дополнительное поле (атрибут) с именем, например, ID_Worker. Тип этого поля может быть выбран как счетчик (counter), который автоматически увеличивается при добавлении новой записи в таблицу.
12. Что такое простой и составной (сложный) ключи?
Простой ключ – это ключ, который содержит только один атрибут (поле). Сложный или составной ключ– это ключ, который содержит несколько атрибутов, то есть состоит из нескольких полей, значения в которых не могут повторяться.
Пример. Пусть дана таблица Student, содержащая данные о студенте. Таблица содержит следующие поля:
| Название поля | Тип | Описание |
| ID_Student | Целое число, int | Уникальный идентификатор поля, счетчик, первичный ключ, простой ключ |
| Num_book | Целое число, int | Номер зачетной книжки |
| Name | Строка с 100 символов, char(100) | Фамилия и имя студента |
| Course | Целое число, int | Курс, на котором учится студент |
В этой таблице поле ID_Student есть первичным ключом, которое обеспечивает уникальность. Это поле есть счетчиком. При добавлении нового студента в таблицу, значение счетчика увеличивается на некоторое число, как правило на 1. Если удалить студента из таблицы, максимальное значение счетчика уже не уменьшается. Таким образом обеспечивается уникальное число, которое соответствует данному студенту.
В таблице Student составным ключом может быть комбинация полей (атрибутов) ID_Student и Num_book (номер зачетной книжки). Однако, в данной таблице такая комбинация не имеет смысла, поскольку поле ID_Student и без того обеспечивает уникальность.
13. Что такое искусственный (суррогатный) ключ?
Искусственный ключ создается самой СУБД или пользователем. Этот ключ не содержит никакой информации. Искусственный ключ используется для создания уникальных идентификаторов строк. Создание идентификатора строки осуществляется таким образом, что сущность строки описывается полностью. Такой метод позволяет однозначно идентифицировать конкретный элемент (значение).
Система управления базами данных поддерживает искусственный ключ так, что он невидим для пользователя.
14. Что такое естественной ключ?
Естественной ключ базируется на атрибутах (полях), которые имеют смысл. Значение в таких атрибутах (полях) не могут повторяться по своей сущности.
Использование естественных ключей позволяет получить более компактную форму таблиц для представления данных.
Пример 1. В таблице Worker (см. п.8) поле «Идентификационный код» есть уникальным, так как не может быть двух людей с одинаковым идентификационным кодом. Это поле и есть естественном ключом.
Пример 2. В таблице Student поле Num_book (№ зачетной книжки) есть уникальным по своей природе. Не может быть двух студентов с одинаковым номером зачетной книжки.
15. Какие преимущества и недостатки использования естественных ключей?
Преимуществом использования естественных ключей есть то, что они несут информацию, и потому не нужно добавлять в таблицу дополнительных полей. Естественные ключи позволяют избегнуть избыточной (неинформативной) информации, которая используется только для связи между таблицами базы данных.
Основные недостатки естественных ключей:
Про Бурали-Форти, Пуанкаре и то самое определение единицы
Если вы, уважаемый мой читатель, имеете обыкновение проводить много времени в интернете, вы наверняка уже видели эту картинку с цитатой:
Наверняка также вы задавались вопросом: что, чёрт подери, здесь написано? Формула из этой цитаты интересна тем, что у человека, имеющего высшее математическое образование, этот вопрос возникает столь же неумолимо, как и у любознательного семиклассника. У нелюбознательных семиклассников несколько иной круг интересов, выходящий за рамки данной статьи; однако даже они не откажут себе в удовольствии похихикать над «этими чокнутыми ботаниками», или как оно там формулируется на современном молодёжном сленге.
В нижеследующем тексте я раскрою перед вами тайну этого загадочного сочетания символов. Пожалуйте под кат, однако помните поучительную историю о любопытной Варваре, которой на базаре рассказали про парадокс Банаха-Тарского, отчего она сошла с ума, разрезала себе нос на конечное количество частей и склеила из них рогатую сферу Александера.
Кто все эти люди?
Если вас не интересует историческая справка, смело переходите к следующему разделу.
Итак, перед нами цитата из текста безымянного автора, который цитирует Пуанкаре, цитирующего, в свою очередь, некоего Бурали-Форти. Чтобы разобраться во всём этом постмодернизме, начнём, пожалуй, с автора цитаты верхнего уровня. Зовут его Виктор Филиппович Журавлёв, он доктор физико-математических наук, профессор, академик РАН, а также автор книги под неизбитым названием «Основы теоретической механики». Именно в ней, на странице номер восемь (если смотреть по изданию 2008 года) и встречается вышеупомянутая формула. Приведу здесь немного контекста, чтобы стало понятно, к чему он это.
Заметим, что изложение любой формальной аксиоматизации классической механики в курсе механики неуместно, поскольку составляет фактически главу математической логики, а не собственно механики.
Точно так же аксиоматизация арифметики не является предметом самой арифметики.
Так и в механике, имеет смысл предполагать наличие у читателей достаточной физической интуиции, чтобы не перегружать изложение основ избыточным формализмом.
Кто такой Пуанкаре, я полагаю, объяснять не нужно. В свете недавних событий даже махровые гуманитарии должны помнить эту фамилию в сочетании со словом «гипотеза» и ещё одной фамилией «Перельман». Если совсем кратенько (для тех, кто с середины девятнадцатого века до текущего момента просидел в каменном мешке), Жюль Анри Пуанкаре — один из величайших математиков всех времён, учёный-энциклопедист, создатель топологии, математических основ теории относительности и ещё всяких забавных и полезных штук. Приведённая цитата-в-цитате позаимствована из его труда «Наука и метод» 1910 года издания. Данный труд представляет собой сборник эссе на различные математические, научные, философские и дидактические темы. Очень любопытная, лёгкая для прочтения и до сих пор актуальная вещь, которую можно растащить на цитаты чуть менее чем полностью.
Чем объяснить, что многие умы отказываются понимать математику? Не парадоксально ли это? В самом деле, вот наука, которая апеллирует только к основным принципам логики, например к принципу противоречия, апеллирует к тому, что составляет, так сказать, скелет нашего разумения, к тому, от чего нельзя отказаться, не отказываясь вместе с тем от самого мышления, и все же встречаются люди, которые находят эту науку темной! И этих людей большинство! Пусть бы они оказались неспособными изобретать — это еще допустимо. Но они не понимают доказательств, которые им предлагают, они остаются слепыми, когда им подносят свет, который для нас горит чистым и ярким пламенем, — вот что чрезвычайно странно.
Вот в четвертом классе. Преподаватель диктует: «окружность — это геометрическое место точек на плоскости, находящихся на одном и том же расстоянии от одной внутренней точки, именуемой центром». Хороший ученик вписывает эту фразу в свою тетрадь; плохой ученик рисует в ней «человечков», но ни тот, ни другой ничего не поняли. Тогда преподаватель берет мел и рисует круг на доске. «Ага, — думают ученики, — почему он не сказал сразу: окружность — это кружок, и мы бы сразу поняли».
Однако нас интересует одна конкретная цитата. Она расположена в главе «Математика и логика», которая начинается так:
Можно ли математику свести к логике, не обращаясь предварительно к тем принципам, которые ей, математике, свойственны? Существует школа математиков, которая со всей страстью и верой в дело стремится доказать это. Она выработала специальный язык, в котором нет больше слов, а имеются одни только знаки. Этот язык понятен только немногим посвященным, так что профаны склонны преклоняться перед категорическими утверждениями горячих адептов.
Я полагаю, читатель уже понял, о чём пойдёт речь дальше. Пуанкаре с некоторой горячностью нападает на математиков «новой школы» с их непонятными обозначениями и пересмотром основ. Как показали дальнейшие события, в этом вопросе он оказался ретроградом — впрочем, у него были для этого веские причины. То, что происходило в математике в суровые 1890-е, способно было ошеломить и более безразличного человека, чем этот восторженный француз.
Вот мы и добрались до конца цепочки, до цитаты, не содержащей внутренних цитат. Её автор — Чезаре Бурали-Форти, математик не то чтобы великий, но сумевший вписать своё имя в историю благодаря некоему парадоксу, к которому мы вернёмся позднее. Информация о нём довольно скудна, я не смог даже найти, как стоят ударения в его фамилии. Формула, сподвигнувшая меня на написание этой статьи, содержалась в его статье «Вопрос о трансфинитных числах». Я нашёл эту статью в книге Жана ван Хейенорта — кстати, известного троцкиста, — под названием «From Frege To Gödel: A Source Book in Mathematical Logic» (здесь и далее я не рискую переводить названия, поскольку май инглиш из нот вери велл). Это была большая удача, поскольку вместе с ней в книге содержалась статья Пеано «The principles of arithmetic, presented by a new method». Именно в этой статье были введены те самые «обозначения, понятные только немногим посвящённым», без которых статья Бурали-Форте была бы для меня всё равно что на китайском.
Лирическое отступление
Если вы не хотите посмотреть на забавные крякозябры, можете сразу переходить к следующему разделу
Перед статьями Пеано и Бурали-Форти в книге-сборнике ван Хейенорта шла статья Фреге «Исчисление понятий, или подражающий арифметике формальный язык чистого мышления». Фридрих Людвиг Готлоб Фреге, математик и философ, может, в принципе, считаться создателем исчисления предикатов. К теме данного хабрапоста он имеет отношение довольно опосредованное (Пуанкаре даже не упомянул его в своей книге, хотя именно Фреге, по сути, заварил всю эту кашу со сведением математики к логике). Однако я просто не мог не поделиться его моднейшими обозначениями. К счастью (или к сожалению), они не прижились в современной матлогике из-за своей сложности. Фреге заявлял, конечно, что «удобство наборщика в типографии определённо не есть высшее благо», однако, как мы можем видеть, определённую роль сыграл и этот фактор. Впрочем, довольно предисловий.

«Из А следует В»

«Из А следует В, и из этого следует Г»

«Неверно, что из того, что из отрицания А следует В, следует Г»

«Мгла ада, делённая на хтонический ужас»

«Пх’нглуи мглв’нафх Ктулху Р’лайх вгах’нагл фхтагн! Айя Ктулху, айя Дагон!»
Конечно, нужно признать, что для человека, далёкого от «вот этого всего», современная запись формул логики предикатов выглядит немногим более понятно.
Теоретические сведения
Если вы знаете, что такое порядковые числа и в чём состоит парадокс Бурали-Форти, можете немедленно перейти к заключительному разделу.
Немецкий математик Георг Кантор — один из первых, кто стал разбираться в сортах бесконечностей. До него этих сортов было только два — потенциальная бесконечность и актуальная бесконечность. Можно пояснить эти понятия следующим образом:
Натуральные числа применяются для обозначения конечных количеств, но что делать с бесконечными количествами? Для этого натуральный ряд расширили до множества так называемых кардинальных чисел. Кардинальное число — это количество (в широком смысле этого слова) элементов некоторого множества. Единица — количество элементов во множестве из одного элемента. Двойка — количество элементов во множестве из двух элементов. Дальше, за натуральными числами, маячит число N0, равное количеству натуральных чисел. Вообще, вместо буквы N должна быть еврейская буква «алеф», но при попытке вставить соответствующий символ юникода у меня из ушей полезла маца направление текста изменилось на «справа налево», и я, не разобравшись, как вернуть его в исходное состояние, плюнул.
Так вот, за N0 следует некое N1, однако вопрос о том, какое ему соответствует множество, оказался нетривиальным (см. Континуум-гипотеза). С понятием «следующего числа» при переходе от конечного к бесконечному возникла заминка.
Существуют, однако, и другие «бесконечные числа» — так называемые порядковые числа, они же ординалы, также придуманные Кантором. Их определение довольно сложно, но я постараюсь в двух словах его обрисовать. Если кардинальные числа соответствуют простым множествам, то ординалы — множествам упорядоченным, т.е. таким, что для любых их двух элементов указано. какой из них больше, а какой меньше. Отношение порядка должно соответствовать некоторым очевидным критериям, о которых мы скромно умолчим. Кроме того, для построения ординалов на упорядоченное множество накладываются дополнительные условия, при которых оно называется вполне упорядоченным. Если между двумя вполне упорядоченными множествами можно установить однозначное соответствие, сохраняющее отношение порядка, то эти множества обладают одним и тем же ординалом.
Как видите, Кантор был большой затейник. По иронии, именно порядковые числа стали началом конца его теории, которую впоследствии назовут «наивной теорией множеств». Используя порядковые числа, Бурали-Форти пришёл к парадоксу. Ход его рассуждений были примерно таким: возьмём множество ординалов и докажем, что оно является вполне упорядоченным. Значит, ему самому соответствует некоторый ординал. Докажем, что этот ординал больше или равен любому другому ординалу. Теперь прибавим к нему единицу. Сделаем удивлённые глаза.
Теперь, вооружённые знаниями и энтузиазмом, мы готовы перейти к сути и разобраться, что же всё-таки означает та формула в самом начале хабрапоста, далеко-далеко вверху.
Разобраться в обозначениях Бурали-Форти было нелегко. К нотации, введённой Пеано, он добавил некоторое количество собственных обозначений. В отличие от Пеано, он не стал в начале статьи подробно описывать свои нововведения. Возможно, эти описания содержатся где-то ещё, но, к сожалению (или к счастью), я не смог найти в интернете полное собрание сочинений Бурали-Форти. Поэтому в паре мест мне пришлось додумывать смысл исходя из контекста. Этот процесс напоминал решение известной головоломки от АНБ.
Начнём с того, что у Пуанкаре (и следом у Журавлёва) приведена не вполне верная формула. В оригинале она выглядит так: 
Обратите внимания на два надчёркивания, их наличие принципиально.
Надчёркиванием Бурали-Форти заменяет квадратные скобки, введённые Пеано как «знак инверсии». Пеано использовал его в довольно широком спектре случаев. Например, b[+a] у него означало b-a, выражение [sin](x) символизировало arcsin(x). Запись же [x ε](некое условие) означала множество иксов, удовлетворяющих этому условию. Таким образом, запись [(u, v) ε] (u ε Un) означает «множество таких пар (u, v), что u — множество из одного элемента». Я, пожалуй, буду использовать обозначения Пеано, поскольку не вижу удобного способа сделать надчёркивание в хабраредакторе.
Ko — это множество упорядоченных множеств. Упорядоченные множества у Бурали-Форти определяются как пары (множество, отношение порядка). Следовательно, запись
С помощью сочетания символов «T’» Бурали-Форте обозначает операцию взятия ординала. Более строго: выражение T'(u, v) означает ординал множества u, на котором задано отношение порядка v. Тут, однако, есть некоторая нестыковка: в рассматриваемой формуле функция T’ применяется не к паре (множество, отношение порядка), а к множеству таких пар. Исходя из контекста, могу лишь предположить, что существует некое соглашение, по которому в таких случаях функция применяется к каждому элементу, а на выходе получается множество, состоящее из её значений для всех элементов. При таком прочтении T’
Что касается закорючечки с чёрточкой, с её пониманием у меня возникло больше всего проблем. Пришлось поискать другие работы Бурали-Форти. В одной из них, «Logica Matematica» (судя по всему, некий учебник, но я до конца не уверен, поскольку написан он был на итальянском) я нашёл функцию L (там была строчная «l», но она слишком похожа на палочку, потому для ясности я буду использовать заглавную). Работает она следующим образом: берёт свой аргумент и преобразует его во множество, единственный элемент которого — этот самый аргумент. В современной нотации: L(x) =
Если идентифицировать закорючечку как L, а чёрточку — как инверсию, то получается, что [L] — обратное преобразование, извлекающее из множества его единственный элемент. В таком случае [L]T’
В следующий раз, когда кто-нибудь покажет вам картинку с этой формулой (а это случится обязательно, таков интернет), вы сможете рассказать ему, что эта формула означает. Точнее, сможете начать рассказывать. Вряд ли он дослушает до конца. И будет, в принципе, прав: это совершенно обыкновенная, ничем не примечательная формула. В рассуждениях Бурали-Форти она не занимала какого-то центрального места, а была лишь проходным моментом в формулировке парадокса. Вся её вина заключается в том, что она попалась на глаза Пуанкаре, который увидел в ней некий нежелательный философский смысл, «разгибание скреп». Что касается её инфернального вида — тут обозначения Фреге дадут сто очков форы.
Список литературы
Здесь я хотел бы разместить ссылки на упомянутые книги, однако благодаря стараниям правообглодателей качать мне их пришлось из всяких непонятных мест, с подозрительных файлообменников, из сети ed2k… Если вам интересно, найдите аналогичным образом и почитайте «Науку и метод» Пуанкаре, это действительно лёгкое и интересное чтиво. «От Фреге до Гёделя» ван Хейенорта также весьма любопытна, но тяжела для восприятия и на русском языке, кажется, не существует.