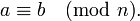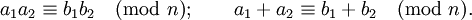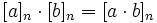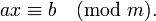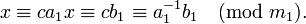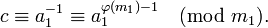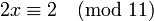кольцо классов вычетов по модулю m
Кольцо вычетов
Сравнение по модулю натурального числа — отношение эквивалентности на множестве целых чисел, связанное с делимостью. Оно даёт возможность работать с системой чисел, более простой чем целые числа, в которой значения «зацикливаются» (повторяются) после достижения определенного значения.
В дискретной математике, для сравнений по модулю используется также термин модульная (или модулярная) арифметика.
Содержание
Определения
Утверждение « a и b сравнимы по модулю n » записывается в виде:
Свойства
Отношение сравнения является отношением эквивалентности и обладает многими свойствами обычных равенств. Например, их можно складывать и перемножать: если
Сравнения, однако, нельзя, вообще говоря, делить друг на друга или на другие числа. Пример: 
, однако, сократив на 2, мы получаем ошибочное сравнение: 
. Правила сокращения для сравнений следующие.
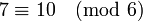
Нельзя также выполнять операции со сравнениями, если их модули не совпадают.
Классы вычетов
Поскольку сравнение по модулю n является отношением эквивалентности на множестве целых чисел 
, то классы вычетов по модулю n представляют собой классы эквивалентности; их количество равно n. Множество всех классов вычетов по модулю n обозначается 
или 
.
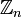
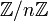
Операции сложения и умножения на индуцируют соответствующие операции на множестве :
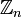
[a]n + [b]n = [a + b]n 
Относительно этих операций множество 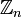является конечным кольцом, а если n простое — конечным полем.
Решение сравнений
Сравнения первой степени
В теории чисел, криптографии и других областях науки часто возникает задача отыскания решений сравнения первой степени вида:
Решение такого сравнения начинается с вычисления НОД(a, m)=d. При этом возможны 2 случая:
Практическое вычисление значения c можно осуществить разными способами: с помощью теоремы Эйлера, алгоритма Евклида, теории цепных дробей (см. алгоритм) и др. В частности, теорема Эйлера позволяет записать значение c в виде:
Поскольку 2 взаимно просто с модулем 11, можно сократить левую и правую части на 2. В итоге получаем одно решение по модулю 11: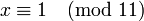 
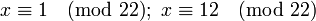
, эквивалентное двум решениям по модулю 22: 
.
Сравнения второй степени
Решение сравнений второй степени сводится к выяснению, является ли данное число квадратичным вычетом (с помощью квадратичного закона взаимности) и последующему вычислению квадратного корня по данному модулю.
История
В значительной степени теория делимости и вычетов была создана Эйлером. Сравнения по модулю впервые использовались Гауссом в его книге «Арифметические исследования», 1801 год. Он же предложил утвердившуюся в математике символику для сравнений.
Ссылки
Полезное
Смотреть что такое «Кольцо вычетов» в других словарях:
Кольцо (алгебра) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия
Кольцо (множество) — Кольцо это множество, на котором заданы две операции, «сложение» и «умножение», со свойствами, напоминающими сложение и умножение целых чисел. Содержание 1 Определения 2 Связанные определения 3 Простейшие свойства … Википедия
Кольцо (математика) — У этого термина существуют и другие значения, см. Кольцо. В абстрактной алгебре кольцо это один из наиболее часто встречающихся видов алгебраической структуры. Простейшими примерами колец являются алгебры чисел (целых, вещественных,… … Википедия
Кольцо алгебраическое — Кольцо алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия
Кольцо — алгебраическое, одно из основных понятий современной алгебры. Простейшими примерами К. могут служить указанные ниже системы (множества) чисел, рассматриваемые вместе с операциями сложения и умножения: 1) множество всех целых положительных … Большая советская энциклопедия
Кольцо когомологий — Гомология одно из основных понятий алгебраической топологии. Замкнутая линия гомологична нулю, если она ограничивает кусок поверхности, который отделяется от неё, если мы произведём разрез по этой линии. Например, на сфере любая замкнутая линия… … Википедия
Мультипликативная группа кольца вычетов — Приведённая система вычетов по модулю m множество всех чисел полной системы вычетов по модулю m, взаимно простых с m. Приведённая система вычетов по модулю m состоит из φ(m) чисел, где φ(·) функция Эйлера. В качестве приведённой системы вычетов… … Википедия
АНАЛИТИЧЕСКОЕ КОЛЬЦО — кольцо ростков аналитич. функций в точке аналитического пространства. Более точно: пусть kесть поле с нетривиальным абсолютным значением (обычно предполагаемое полным) и есть fc алгебра степенных рядов от с коэффициентами в k, сходящихся в нек… … Математическая энциклопедия
ЛОКАЛЬНОЕ КОЛЬЦО — коммутативное кольцо с единицей, имеющее единственный максимальный идеал. Если А Л. к. с максимальным идеалом то факторкольцо является полем и наз. полем вычетов Л. к. А. Примеры Л. к. Любое поле или кольцо нормирования является локальным.… … Математическая энциклопедия
ДИСКРЕТНОГО НОРМИРОВАНИЯ КОЛЬЦО — дискретно нормированное кольцо, кольцо с дискретным нормированием, т. е. область целостности с единицей, в к рой существует такой элемент я, что любой ненулевой идеал порождается нек рой степенью элемента я; такой элемент наз. униформизирующим и… … Математическая энциклопедия
Сравнения, система вычетов, решение линейных систем по модулю
Содержание
Сравнения по модулю [ править ]
Будем рассматривать целые числа в связи с остатками от деления их на данное целое число m, которое назовем модулем. Каждому целому числу отвечает определенный остаток от деления его на m. Если двум целым a и b отвечает один и тот же остаток r, то они называются сравнимыми по модулю m.
Сравнимость для a и b записывается так :
[math]a \equiv b(mod \text < >m)[/math]
Сравнимость чисел a и b по модулю m равносильна:
Арифметика сравнений [ править ]
Свойства сравнений [ править ]
Полная и приведенная система вычетов [ править ]
Числа равноостаточные(сравнимые по модулю m) образуют класс чисел по модулю m. Из такого определения следует, что всем числам класса отвечает один остаток r, и мы получим все числа класса, если в форме [math]mt + r [/math] заставим t пробегать все целые числа. Таким образом для каждого значения остатка имеется свой класс чисел.
Любые m чисел, попарно несравнимые по модулю m, образуют полную систему вычетов по этому модулю.
Согласно 10 свойству сравнений, числа одного класса по модулю m имеют одинаковый НОД. Особенно важны классы, содержащие числа, взаимно простые с модулем. Взяв вычет от каждого такого класса, получим приведенную систему вычетов по модулю m.
Решение линейных систем по модулю [ править ]
Примеры решения [ править ]
Кольцо вычетов
Целые числа a,b сравнимы по модулю n, если при делении на число n эти числа дают один остаток (a mod n = b mod n).
При делении на n возможные значения остатка 0,1,…,n-1.
Обозначим [k] – класс сравнимых между собой чисел, дающих при делении на n остаток k. Например, для n=4 образуется четыре класса:
Таким образом, при делении на n образуется n классов [0],[1],…,[n-1]. Эти классы называются классами вычетов по модулю n. Множество Zn=<[0],[1],…, [n-1]> называется полной системой вычетов. В дальнейшем квадратные скобки будем опускать Zn=<0,1,…,n-1>.
Число из класса [a] имеет вид in+a. Выясним, в какой класс попадет сумма чисел из классов [a],[b]:
Это число при делении на n дает остаток ((i+j)n+(a+b)) mod n = (a+b) mod n. Таким образом, сумма любых двух чисел из классов [a],[b] принадлежит классу [(a+b) mod n]. В соответствии с этим на множестве Zn введем операцию сложения:
В этом соотношении слева используется алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции сложения:
· операция коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция сложения в правой части соотношения a+b=(a+b) mod n.
· элемент, противоположный элементу a, определяется следующим образом —a=n—a, т.к. a+(—a)=(—a)+a=(a+n—a) mod n =0.
Таким образом, алгебра A= образует абелевую группу относительно операции сложения.
Теперь выясним, в какой класс попадет произведение чисел из классов [a],[b]:
Это число при делении на n дает остаток (ab) mod n.
Поэтому операция умножения на множестве Zn определяется как:
В этом соотношении слева – алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции умножения:
· операция умножения коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция умножения в правой части соотношения a*b=(ab) mod n.
Такую алгебру называют кольцом вычетов.
Кроме того, в кольце вычетов выполняется условие коммутативности умножения, следовательно, данная алгебра является коммутативным кольцом.
Если n – составное, то кольцо вычетов содержит делители нуля. Действительно, если n=kl, тогда по определению умножения k*l=(kl) mod n =0.
Результаты операций сложения умножения и вычитания в A= представлены в табл.1.2-1.4 соответственно. Делителями нуля является пара элементов a=2,b=2.
9.Сравнения. Кольцо классов вычетов. Делители нуля.
Решаем четыре системы сравнений 7 страница
3. (для кольца с единицей);
Определение 2. Два ненулевых элемента кольца, произведение которых равно нулю, называются делителями нуля кольца.
Если кольцо не имеет делителей нуля, то в нем справедливы т.н. законы сокращения:
Определение 3. Коммутативное кольцо с единицей и без делителей нуля называется областью целостности, или целостным кольцом.
Определение 17. Целостное кольцо, в котором каждый ненулевой элемент обратим, называется
Пример 10. – поле рациональных чисел.
Пример 11. – вещественное «квадратичное» поле.
Пример 13. – поле гауссовых чисел.
Конечно, полями являются и множества вещественных и комплексных чисел относительно стандартных операций сложения и умножения, заданных в них.
Лемма 1.Если кольцо с единицей и без делителей нуля имеет положительную
характеристику, то эта характеристика есть простое число.
Следствие. Положительная характеристика поля есть простое число. В частности, характеристика конечного поля есть простое число
Пример 14. Поле из примера 12 имеет характеристику, равную р.
Теорема1. Пусть – коммутативное кольцо простой характеристики р. Тогда
Пример 15. Четные числа образуют подкольцо в кольце всех целых чисел.
Пример 16. Диагональные матрицы образуют подкольцо в кольце квадратных матриц.
Теорема2. Непустое подмножество кольца является подкольцом в нем тогда и только тогда, когда выполнены условия:
Заметим, что подкольцо наследует не все свойства родительского кольца. Это хорошо видно на примерах 1 и 6.
Пример 17. Подкольцо четных чисел есть идеал в кольце всех целых чисел. По аналогии, числа кратные некоторому также образуют идеал в этом кольце.
Учитывая эти свойства нетрудно непосредственно показать, что следующие операции над классами корректны:
Дадим еще несколько определений. Пусть – коммутативное кольцо с единицей.
Определение 9. Делители единицы называются обратимыми элементами кольца.
Определение 12. Идеал кольца называется простым идеалом, если для
Определение 14. Целостное кольцо называется кольцом главных идеалов, если каждый идеал кольца является главным, т.е. существует элемент такой, что
Теорема 4. Пусть – коммутативное кольцо с единицей. Тогда
(i) Идеал M кольца R является максимальным тогда и только тогда, когда факторкольцо
(ii) Идеал P кольца R является простым тогда и только тогда, когда факторкольцо
является целостным кольцом.
(iii) Каждый максимальный идеал кольца R является простым.
Пример 22. – кольцо главных идеалов. Это легко показать, используя теорему о делении с остатком. В этом кольце роль простых элементов играют простые числа, правда, «со знаком». Отсюда получается еще одно доказательство, что кольцо классов вычетов по простому модулю есть поле.
Пример 24. Покажите, что – кольцо целых гауссовых чисел есть кольцо главных идеалов. Укажите простые элементы в этом кольце.
Определение 16. Поле называется простым, если не имеет собственных (т.е. отличных от него самого) подполей.
Пример 27. Поле рациональных чисел есть простое поле. Оно является подполем любого числового поля.
Пример 29. Поле является простым. Проверьте это.
Раздел девятнадцатый
Расширения полей. Простое расширение. Конечное расширение. Алгебраичность.
Надо отметить, что понятия алгебраичности и трансцендентности относительны, т.е. прямо связаны с полем, над которым рассматриваются.
Этим свойством и условием нормированности многочлен определен однозначно.
Определение 20. Пусть есть алгебраический над полем элемент. Тогда степень его
Следствие. Пересечение всех подполей данного поля является простым полем. Это поле называют простым подполем этого поля.
Кольцо вычетов
Целые числа a,b сравнимы по модулю n, если при делении на число n эти числа дают один остаток (a mod n = b mod n).
При делении на n возможные значения остатка 0,1,…,n-1.
Обозначим [k] – класс сравнимых между собой чисел, дающих при делении на n остаток k. Например, для n=4 образуется четыре класса:
Таким образом, при делении на n образуется n классов [0],[1],…,[n-1]. Эти классы называются классами вычетов по модулю n. Множество Zn=<[0],[1],…, [n-1]> называется полной системой вычетов. В дальнейшем квадратные скобки будем опускать Zn=<0,1,…,n-1>.
Число из класса [a] имеет вид in+a. Выясним, в какой класс попадет сумма чисел из классов [a],[b]:
Это число при делении на n дает остаток ((i+j)n+(a+b)) mod n = (a+b) mod n. Таким образом, сумма любых двух чисел из классов [a],[b] принадлежит классу [(a+b) mod n]. В соответствии с этим на множестве Zn введем операцию сложения:
В этом соотношении слева используется алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции сложения:
· операция коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция сложения в правой части соотношения a+b=(a+b) mod n.
· элемент, противоположный элементу a, определяется следующим образом —a=n—a, т.к. a+(—a)=(—a)+a=(a+n—a) mod n =0.
Таким образом, алгебра A= образует абелевую группу относительно операции сложения.
Теперь выясним, в какой класс попадет произведение чисел из классов [a],[b]:
Это число при делении на n дает остаток (ab) mod n.
Поэтому операция умножения на множестве Zn определяется как:
В этом соотношении слева – алгебраическая операция над элементами a,bÎZn. Справа – арифметические операции над числами a,b,n.
Свойства введенной операции умножения:
· операция умножения коммутативна и ассоциативна, поскольку коммутативна и ассоциативна арифметическая операция умножения в правой части соотношения a*b=(ab) mod n.
Итак, алгебра A= образует абелевую группу относительно операции сложения, является полугруппой относительно умножения (умножение ассоциативно), и умножение дистрибутивно относительно сложения, следовательно, алгебра A — кольцо.
Такую алгебру называют кольцом вычетов.
Кроме того, в кольце вычетов выполняется условие коммутативности умножения, следовательно, данная алгебра является коммутативным кольцом.
Если n – составное, то кольцо вычетов содержит делители нуля. Действительно, если n=kl, тогда по определению умножения k*l=(kl) mod n =0.
Результаты операций сложения умножения и вычитания в A= представлены в табл.1.2-1.4 соответственно. Делителями нуля является пара элементов a=2,b=2.
Не нашли то, что искали? Воспользуйтесь поиском:
Выписать все делители нуля в кольце классов вычетов по модулю 6
Вариант №1.
1082x1983+632x411+197x292+1410(mod11). Вариант №2.
368x663+1354x732+104x671+3430(mod11). Вариант №3.
а) Выписать все делители нуля в кольце классов вычетов по модулю 9.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №4.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №5.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №8.
304x622+359x433+191x81+264x231+1380(mod7). Вариант №9.
1082x1983+632x411+430x1832+197x292+1410(mod11). Вариант №10.
368x663+1354x732+890x1342+104x671+3430(mod11). Вариант №11.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №12.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №13.
63x708+35x319+426x602+947x394+37x2325+680(mod5). Вариант №14.
213x183+162x535+98x718+126x97+3380(mod7). Вариант №15.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №16.
304x622+359x433+191x81+264x231+1380(mod7). Вариант №17.
1082x1983+632x411+197x292+1410(mod11). Вариант №18.
368x663+1354x732+104x671+3430(mod11). Вариант №19.
5753x333+596x82+427x902+1006x61+5970(mod11). Вариант №20.
758x480+12x503+923x231+62x626+34x181+2090(mod5) Вариант №21.
63x708+35x319+426x602+947x394+37x2325+680(mod5). Вариант №22.
213x183+162x535+98x718+126x97+3380(mod7). Вариант №23.
214x145+124x95+340x167+58x101+4750(mod7). Вариант №24.
Многочлены над кольцом классов вычетов
p> 24x3 + 16x — 8 2x+3
6. Вычисление наибольшего общего делителя.
Наибольший общий делитель двух многочленов f и g из кольца R[x] многочленов над полем R может быть найден при помощи алгоритма Евклида. Алгоритм Евклида нахождения наибольшего общего делителя состоит в следующем.
Сначала делят с остатком многочлен f на многочлен g, затем многочлен g — на остаток от первого деления, затем остаток от первого деления — на остаток от второго деления и т.д., пока не получится нулевой остаток.
Это дает следующую цепочку равенств:
rk) и есть наибольший общий делитель многочленовf иg.
Полученный остаток разделим на 9 и выполним третье деление:
Наибольший общий делитель нескольких многочленов f1, f2, …, fm может быть найден индуктивным способом на основании следующей формулы:
Для нахождения линейного выражения наибольшего общего делителя d можно воспользоваться алгоритмом Евклида.
Пример. Найдем линейное выражение наибольшего общего делителя d многочленов f и g из примера 14.
На практике линейное выражение многочлена h удобнее искать не с помощью алгоритма Евклида, а методом неопределенных коэффициентов.
Запишем искомые многочлены u и v в общем виде с неопределенными (неизвестными) коэффициентами.
7. Наименьшее общее кратное.
Теорема Для двух многочленовfиgнаименьшее общее кратное [f, g] связано снаибольшим общим делителем (f, g) соотношением
Из формулы (12) вытекает
Следствие. Наименьшее общее кратное двух взаимно простых многочленов равно их произведению.
8. Сравнения многочленов по многочлену.
Теорема 7. Для любых многочленов и :
Доказательство. Разделим многочлены и с остатком на :
Где — любая из операций (т.е. сравнения можно почленно складывать, вычитать и перемножать).
Доказательство. Из условия, согласно теореме 7, имеем
Складывая, вычитая и перемножая последние равенства, получим:
т.е. обе части сравнения и многочлен можно делить и умножать на один и тот же многочлен.
И теперь эта теорема следует непосредственно из теоремы 7.
Определим на множестве операции сложения и умножения.
Это бы означало, что операции определены некорректно.
Докажем, что определение корректно.
Следовательно, результаты операций над
6.4. Кольцо классов вычетов
Утверждение.— отношение эквивалентности на Z.
Так как — отношение эквивалентности на Z,то Zразбивается на непересекающиесяклассы эквивалентных элементов.
Из утверждениямы получаем, что различных классов помодулю mровно столько, сколько существуетразличных остатков от деления на m,то есть существует mразличных классов, и Zm= <. …,>.
Определим операции сложения и умножения так:
Докажемкорректность нашего определения, тоесть независимость его от выборапредставителей в классах.
Проверим свойства операций.
=+(+)– это свойство ассоциативности сложенияв Zm следует изассоциативности сложения в Z.
элемент по сложению.
Свойства4, 5, 8, 9 из определения кольца следуют изсоответствующих свойств кольца целыхчисел и доказываются так же, как исвойство 1.
Упражнение.Доказать свойства 4, 5, 8, 9.
Такимобразом, мы доказали, что Zm — АКУ-кольцо.
Пример. Выпишем таблицы сложения и умножениядля Z6.
Таккак =,то и в Z6 являются делителями нуля. В то же время=,то есть — обратимый элемент в Z6.