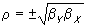Корреляция что это простыми словами
Корреляция что это простыми словами
Что означает понятие корреляции простыми словами?
Все в мире взаимосвязано. Каждый человек на уровне интуиции пытается найти взаимосвязи между явлениями, чтобы иметь возможность влиять на них и управлять ними. Понятие, которое отражает эту взаимосвязь, называется корреляцией. Что она означает простыми словами?
Понятие корреляции
Корреляция (от латинского «correlatio» – соотношение, взаимосвязь) – математический термин, который означает меру статистической вероятностной зависимости между случайными величинами (переменными).
Пример: возьмем два вида взаимосвязи:
Примерами взаимосвязи между природными явлениями являются: цепочка питания в природе, организм человека, который состоит из систем органов, взаимосвязанных между собой и функционирующих как единое целое.
Каждый день мы сталкиваемся с корреляционной зависимостью в повседневной жизни: между погодой и хорошим настроением, правильной формулировкой целей и их достижением, положительным настроем и везением, ощущением счастья и финансовым благополучием. Но мы ищем связи, опираясь не на математические расчеты, а на мифы, интуицию, суеверия, досужие домыслы. Эти явления очень сложно перевести на математический язык, выразить в цифрах, измерить. Другое дело, когда мы анализируем явления, которые можно просчитать, представить в виде цифр. В таком случае мы можем определить корреляцию с помощью коэффициента корреляции (r), отражающего силу, степень, тесноту и направление корреляционной связи между случайными переменными.
Сильная корреляция между случайными величинами – свидетельство наличия некоторой статистической связи конкретно между этими явлениями, но эта связь не может переноситься на эти же явления, но для другой ситуации. Часто исследователи, получив в расчетах значительную корреляцию между двумя переменными, основываясь на простоте корреляционного анализа, делают ложные интуитивные предположения о существовании причинно-следственных взаимосвязей между признаками, забывая о том, что коэффициент корреляции носит вероятностный характер.
Пример: количество травмированных во время гололеда и число ДТП среди автотранспорта. Эти величины будут коррелировать между собой, хотя они абсолютно не взаимосвязаны между собой, а имеют только связь с общей причиной этих случайных событий – гололедицей. Если же анализ не выявил корреляционной взаимосвязи между явлениями, это еще не является свидетельством отсутствия зависимости между ними, которая может быть сложной нелинейной, не выявляющейся с помощью корреляционных расчетов.
Первым, кто ввел в научный оборот понятие корреляции, был французский палеонтолог Жорж Кювье. Он в XVIII веке вывел закон корреляции частей и органов живых организмов, благодаря которому появилась возможность восстанавливать по найденным частям тела (останкам) облик всего ископаемого существа, животного. В статистике термин корреляции впервые применил в 1886 году английский ученый Френсис Гальтон. Но он не смог вывести точную формулу для расчета коэффициента корреляции, но это сделал его студент – известнейший математик и биолог Карл Пирсон.
Виды корреляции
По значимости – высокозначимая, значимая и незначимая.
Что такое Корреляция и её применение в трейдинге на примерах
Как начать торговать на бирже: Инструкции и Примеры, Обучение
Что такое корреляция на финансовом рынке, чем обусловлено её появление, как она определяется и используется в трейдинге. Примеры использования и особенности.
На финансовых рынках существует множество внутренних взаимосвязей. Например, изменение цены нефти влияет на курс рубля и прочих сырьевых валют, а динамика индекса S&P 500 определяет поведение акций американских компаний.
Эта связь называется корреляцией и широко используется не только в трейдинге, но и в инвестиционной деятельности. Этот прием помогает снизить риски и повысить доходность инвестиционного портфеля.
Что такое Корреляция (простыми словами)
Корреляция – это статистическая связь между 2 и более величинами.
Понятие корреляции часто встречается и используется в статистике, изучающей те или иные явления, процессы, закономерности.
Если говорить простыми словами, то корреляция показывает, в какой мере изменение одной величины приводит к изменению других величин. Знание этой закономерности позволяет прогнозировать поведение соответствующих переменных в тех или иных ситуациях.
Например, падение стоимости нефти всегда совпадает с падением канадского доллара. Национальная валюта Канады зависит в том числе и от цены на черное золото так как страна входит в число крупнейших экспортеров нефти. В этом примере есть прямая зависимость курса USDCAD от цены нефти.
Другой пример – в зимнее время при гололеде возрастает травматизм людей и аварийность на дорогах, между ними наблюдается прямая корреляция. Эти явления не зависят друг от друга, но есть общая причина, влияющая на обе величины.
Корреляция – это то, что позволяет прогнозировать изменение одной величины, опираясь в том числе и на поведение связанной с ней величины.
Она может наблюдаться между 3, 4 и большим числом явлений. Например, поведение американского индекса S&P 500 коррелирует с динамикой изменения курса акций большинства акций американских компаний.
Положительная и отрицательная корреляция
Взаимодействие между рыночными ценами финансовых активов может проявляться по-разному:
Также выделяют линейный и нелинейный тип связи. Линейная корреляция – такой тип связи, который может быть описан линейным уравнением регрессии (уравнение вида Y = a + b∙X, где a и b – коэффициенты, Y и X – связанные величины).
Нелинейная связь означает невозможность описать корреляцию между 2 и более величинами линейным уравнением регрессии. Зависимость может описываться, например, уравнение параболы или иной, более сложной кривой.
В трейдинге и инвестиционной деятельности тип связи не особо важен. Первостепенное значение имеет коэффициент корреляции (% совпадения динамики).
Корреляция ценовых движений: причины возникновения на разных рынках
Взаимосвязь активов финансового рынка предопределяется фундаментальными экономическими факторами. При этом важная роль принадлежит развитию торговых отношений между разными странами, интегрированными в систему мирового хозяйства. Таким образом, динамика рыночных котировок валюты, товаров, ценных бумаг находится под сильным влиянием процессов, происходящих как в международной экономике, так и в экономических системах отдельных стран.
Взаимозависимость валютных пар рынка Форекс
Движения курсов на Форекс часто взаимодействуют, отражая тесное экономическое сотрудничество стран – эмитентов соответствующих денежных единиц. Примером такой корреляции может считаться вышеупомянутая взаимосвязь валютных инструментов EURUSD (евро/доллар) и GBPUSD (фунт/доллар). Несмотря на некоторые противоречия, Великобритания является близким торговым партнером стран Европейского Союза (ЕС). Это значит, что знаковые события и ключевые процессы, происходящие в ЕС, неизбежно отражаются на курсовых позициях GBPUSD.
Межгрупповая корреляция на глобальном финансовом рынке
Взаимосвязь между активами, принадлежащими к разным сегментам финансового рынка, также предопределяется экономическими предпосылками. Актуальный пример – валютные котировки денежных единиц нефтедобывающих стран падают, если нефть на мировом рынке дешевеет. Сила такой корреляции напрямую определяется тем, в какой степени экономика конкретной страны зависит от экспорта углеводородного сырья.
Типичная ситуация – зависимость курсовых позиций российского рубля от динамики мировых нефтяных котировок. Как известно, экономика РФ характеризуется большим удельным весом поступлений от экспорта углеводородов. Это значит, что удешевление нефти приводит к адекватному падению курса отечественного рубля (RUB) относительно американского доллара (USD). Важный нюанс – углеводородное сырье на мировом рынке котируется именно в USD. Таким образом, падение нефтяных цен способствует росту котировок USD.
Взаимозависимость инструментов фондового рынка
Если деловая активность повышается или снижается для всей экономики, а также в её отдельных секторах, можно наблюдать корреляцию целых индексов фондового рынка. Однако решающее значение в этом случае имеет порядок вычисления индекса. При этом ценные бумаги и фондовые индексы могут пребывать в корреляции с Форекс.
Например, в США нередко реализуется программа «количественного смягчения». Она предусматривает выкуп ФРС ценных бумаг с одновременным наполнением американской экономики денежной ликвидностью. Такая программа часто сопровождается корреляцией пары EURUSD с большинством индексов американского рынка ценных бумаг. В данном случае можно констатировать обратную корреляцию инструмента EURUSD c индексом американского доллара и котировками казначейских облигаций США, поскольку такие облигации номинируются в USD.
Как определить корреляцию
Количественная оценка взаимосвязи определенных величин (например, изменений рыночных курсов конкретных акций) выражается значением коэффициента корреляции.
Чтобы определить данный показатель вручную, нужно выполнить пошаговый алгоритм математических вычислений, используя сложную формулу.
Трейдеры финансового рынка могут избежать подобных трудностей, воспользовавшись для расчета корреляции такими доступными опциями:
Еще один метод – построить график спреда (разницы), вычтя один график из другого. При наличии корреляции график спреда должен находиться примерно у одной величины, ненадолго отклоняясь от нее. Можно использовать и другие арифметические действия, например, разделить график одного актива на другой. Численные значения не важны, нужно лишь понять колеблется результат вокруг одного значения или наблюдаются значимые расхождения и зависимости между величинами нет.
Производить математические действия с котировками и строить синтетические графики можно прямо на живом графике цен, который обладает соответствующим функционалом.
Результаты вычисления корреляции можно применять как своеобразный фильтр, который позволяет выявить пары взаимосвязанных инструментов (активов) с наилучшим потенциалом извлечения прибыли. Однако случайные корреляции также нельзя исключать.
Влияние ГЭПов на корреляцию
В случае, если на обоих графиках наблюдается большой ГЭП или просто солидный импульсный рывок, коэффициент корреляции будет искусственно завышен. После импульса движение график может быть вообще не связано друг с другом, но расчетное значение корреляции будет оставаться высоким. Лишь с течением времени он понизится.
Можно обойти эту проблему, если в расчетной формуле использовать не непосредственно цены, а их приращения. Значение корреляции в этом случае будет меньше зависеть от случайных сильных импульсных движений.
Как использовать корреляцию в трейдинге
Как метод технического анализа, корреляция нередко используется в трейдинге. Однако инвесторы, предпочитающие диверсифицировать свои вложения, также руководствуются данными расчета корреляции при выборе подходящих активов. Учет взаимосвязи между различными финансовыми инструментами благоприятствует принятию верных торговых решений.
В торговле явление корреляции используется:
Важно то, что корреляцию можно интегрировать в любую торговую стратегию. Эффективность этого приема не зависит от использования индикаторов или инструментов графического анализа.
Что означает значение коэффициента корреляции
Расчет дает число в долях единицы, которое и является численным выражением связи между 2 величинами. В зависимости от значений принята следующая классификация:
Например, значение корреляции 0,90 для пар EURUSD и GBPUSD означает, что в 90% случаев восходящее движение на EURUSD совпадает с восходящим движением на GBPUSD.
Также корреляция может выражаться в процентах. Например, в характеристиках ETF фондов используется такой показатель как R-squared, он показывает уровень корреляции между бенчмарком и акциями фонда. R-squared выражается в процентах.
При этом корреляция может быть как случайной, так и экономически обоснованной. Случайные корреляции могут возникать на произвольных участках истории между несвязанными с собой активами. Например, на отдельных участках истории может возникать корреляция между акциями Apple и валютной парой AUDNZD. Но такая связь неустойчива и не носит систематический характер.
Устойчивая корреляция формируется между связанными экономически инструментами. Например, индекс RTS является барометром для российского фондового рынка. Между ним и акциями «голубых фишек» России есть устойчивая связь. Растет индекс – растет и стоимость бумаг крупных российских компаний.
Как использовать корреляцию в краткосрочной торговле (Биржа и Форекс)
В краткосрочном трейдинге (и на Форекс, и на фондовой бирже) связь между 2 инструментами используется и как основа торговой системы, и как фильтр. Один из самых популярных приемов – выявление ведомого и ведущего активов.
Выявляется устойчивая зависимость между 2 и более инструментами. Если есть небольшое запаздывание между движениями, это можно использовать, заключая сделки на более «медленном» инструменте. Например, фьючерсы на RTS резко упали в цене, а фьючерсы на акции Газпрома еще стоят на месте – можно открыть короткую позицию по Газпрому.
Диверсификация рисков. Здесь есть 2 варианта:
Парный трейдинг – эта методика предусматривает работу во время расширения спреда между 2 активами с высокой корреляцией.
Как применять корреляцию при портфельном инвестировании
Портфельное инвестирование, как известно, также не обходится без учета ценовой корреляции финансовых активов. Взаимосвязь между ценами доходных инструментов часто принимается во внимание портфельными инвесторами, проявляющими интерес к ценным бумагам.
На всех уровнях проводится диверсификация (отраслевая, страновая, по классам активов, по уровню риска). Коэффициент корреляции между разными классами инструментов или инструментами одно группы используется при ребалансировке портфеля.
Это не непосредственно торговля по корреляции, а скорее методика подбора «весов» компонентов инвестпортфеля. За счет этого снижается отклонение от средней доходности, иногда удается получить дополнительную прибыль.
Включим в тестовый портфель 2 инструмента – ETF фонды, копирующие американский S&P 500. Примерно половина инвестируемой суммы направлена в SPY, а остаток – в фонд с тикером SH (Proshares Trust Short S&P 500), он растет при падении индекса и наоборот, то есть движется зеркально. Между SPY и SH почти все время наблюдается высокая обратная корреляция.
Для наглядности взят сложный кризисный период 2007-2010 гг., результат следующий:
Если бы деньги на этом временном промежутке вкладывались только в один ETF фонд, то было бы зафиксировано снижение стоимости инвестпортфеля. Пример выбран упрощенный, в реальности все сложнее – корреляция меняется со временем, к тому же в портфеле находится сразу несколько инструментов. В итоге задача ребалансировки сводится к тому, что нужно решить систему из N уравнений с N неизвестными.
Основные стратегии торговли с использованием корреляции
Есть несколько полноценных торговых тактик, полностью построенных на связи между 2 или группой активов. К ним относятся:
По сути, все сводится к 2 подходам – созданию рыночно-нейтральной стратегии либо страховке части стоимости портфеля (или всей его стоимости). Парные корреляции используются во всех перечисленных случаях.
Статистический арбитраж
Статистический арбитраж – это методика онлайн-трейдинга, подразумевающая открытие позиции BUY (покупка) по одному активу с одновременным открытием позиции SELL (продажа) по второму активу. Чтобы реализовать данную стратегию, трейдер выбирает исключительно те финансовые инструменты, которые статистически связаны друг с другом. Иными словами, между торгуемыми активами должна быть определенная корреляция.
В пользу статистического арбитража говорят 2 фактора:
Стратегии статистического арбитража отличаются только методикой подбора инструментов для портфеля. Крупные хедж-фонды могут разрабатывать собственные алгоритмы отбора акций и прочих инструментов для инвестпортфеля, эти методики могут патентоваться.
Что касается торговой тактики, то торгуется спред. То есть между инструментами с высокой корреляцией измеряется разница и затем при ее увеличении более дорогой актив продается, а дешевый покупается в расчете на то, что спред должен уменьшиться. При сужении спреда до минимальных значений заключаются зеркальные сделки.
Это касается и валютных пар, и акций, и сырьевого рынка, и драгоценных металлов. Описанная тактика не имеет ограничений по классу актива. Заработок растет независимо от направления движения цены, важно только, чтобы было хоть какое-то движение.
Парный трейдинг
Эта стратегия – частный случай статистического арбитража. Используется пара инструментов с прямой либо обратной связью, это могут быть и валюты, и биржевой индекс + валютная пара. Используется та же логика, что и в статистическом арбитраже, но за счет того, что не нужно анализировать десятки инструментов работать можно и вручную.
Простейший пример – валютные пары EURUSD и USDCHF, между ними существует устойчивая обратная корреляция. Когда EURUSD растет пара USDCHF падает и наоборот.
Для определения моментов максимального расхождения EURUSD и USDCHF понадобится график спреда. Можно построить график EURUSD/USDCHF или EURUSD/USDCHF.
Далее с графиком спреда работа ведется по обычной схеме. Можно строить уровни поддержки и сопротивления, и открывать сделки по обеим валютным парам при развороте графика спреда от уровня. Можно использовать индикаторы, например, полосы Боллинджера, торговать при приближении синтетического графика к его границе и формировании разворота.
График EURUSD-USDCHF подошел к нижней границе ВВ. Это значит, что франк ослаб в паре с американским долларом, а евро укрепилось. Сделки заключаются в расчете на то, что спред между парами начнет снижаться:
После подхода графика спреда к противоположной границе полос Боллинджера обе сделки закрываются. В примере прогноз оправдался, сделки принесли профит в 195 и 118 пунктов.
Этот же принцип можно перенести на фондовый рынок, коррелирующими валютами дело не ограничивается. Например, следить за индексом, отражающим состояние рынка какой-либо страны и следить за акциями отстающих от него компаний.
Методика работает. Показателен пример трейдера с никнеймом CIS. Не имея профильного образования стартовые 1 млн. японских иен он смог превратить в 20+ млрд иен. При этом анализу рынка он практически не уделял время, точки входа определялись исключительно по методике парного трейдинга.
Частичное хеджирование
Методика немного напоминает парный трейдинг, но цели ставятся иные. Если трейдер пытается заработать за счет статистического арбитража, то инвестор хочет минимизировать риски. Значимость корреляции велика, на ее основе подбираются инструменты, с помощью которых будет выполняться хеджирование. Частичным оно называется из-за того, что страхуется не вся стоимость инвестпортфеля.
Пример – собран простейший портфель из акций IT гигантов (Apple + Google + Amazon + Microsoft). Стоимость портфеля составляет $1 млн. Инвестор хочет подстраховаться на случай кризиса и падения стоимости ценных бумаг.
Нужно подобрать актив, хорошо коррелирующий со всеми 4 инструментами или подбирать отдельный хеджирующий актив под каждый пункт инвестпортфеля. В примере бумаги всех перечисленных компаний в целом коррелируют с поведением индекса S&P 500, он подходит для хеджирования.
Так как инвестпортфель ориентирован на рост, открыты длинные позиции, то при хеджировании нужно продавать S&P 500. Можно делать это с помощью фьючерсов. При полном хеджировании размер короткой позиции должен быть равен стоимости инвестпортфеля, при частичном – нет.
В заключении
Если разобраться в вопросе, что такое корреляция глубже, то окажется, что это не просто любопытная закономерность, а основа для прибыльной торговой стратегии. Основная проблема в том, что нужно понять является закономерность случайной или устойчивой, обусловленной фундаментальными зависимостями между двумя величинами. Решение этой задачи облегчается различными онлайн-сервисами, рассчитывающими корреляцию в режиме реального времени.
Еще одно преимущество корреляции в том, что пользу из нее можно извлечь независимо от используемой торговой стратегии. Используя фактор устойчивой связи между двумя инструментами можно и снизить торговые риски, и повысить прибыль.
Что касается методики использования корреляции, то по сути все сводится к разным подвидам статистического арбитража. Существуют десятки стратегий, но базовая логика одна и та же.
Трейдер, инвестор, частный предприниматель. «Финансовые рынки объединяют разные интересы, бизнес, континенты. Это то место, где всегда можно найти, чем заняться, что и как сделать или создать.»
Что такое корреляция простыми словами
Корреляция – что это такое?
Слово «корреляция» – математический термин, название которого пришло в нашу речь из языка древних римлян – латыни. «Relatio» означало отношение, «correlatio» – взаимное отношение, или взаимосвязь.
Раздел математики, изучающий случайные явления и вероятность их возникновения, называется статистика. Любые события в природе и в обществе, подчиняющиеся статистическим закономерностям, могут быть связаны друг с другом. Исследования корреляции направлены на выявление таких зависимостей одних явлений от других.
Какие бывают типы взаимосвязи событий?
Каждый день на бытовом уровне мы переживаем череду событий. Одни из них влияют на другие, хотя не всегда такое влияние очевидно. По степени логической обусловленности можно выделить два главных класса последовательностей событий:
Подтвердить или опровергнуть стохастические утверждения можно только с помощью статистики, которая занимается подсчетом количества совпадений между независимыми явлениями. В результате можно сделать прогноз о том, насколько вероятно наступление того или иного события.
К числу подобных предсказаний можно отнести, например, народные приметы. Например, если человек утром встал с левой ноги, принято считать, что день сложится неудачно. Физиология не выявляет взаимной связи между этими событиями. Однако прямой подсчет может показать, что такое утверждение справедливо в трех случаях из четырех. Значит, можно предсказывать наступление события с соответствующей вероятностью в 75%.
Взаимосвязь явлений в природе и обществе
Впервые термин «корреляция» был использован в палеонтологии – изучении ископаемых животных. Находя похожие части скелетов динозавров, ученые могли обосновать принадлежность их к одному виду. Схожие биологические останки в горных породах в Азии и Африке позволили сделать вывод о формировании этих слоев в один геологический период.
Как правило, необходимость в статистических методах возникает при изучении сложных систем. Организм человека или отношения в социуме представляют собой тонкое переплетение взаимосвязей, которые бывает необычайно трудно проследить. Здесь и приходит на помощь статистика.
Например, есть убеждение, что полные люди добры и великодушны. Современная психология не может найти прямой логической связи темперамента и физиологии. Можно сделать два предположения:
Статистик не ставит себе задачу: выяснить, какое из предположений правильное? Он лишь постарается проверить, верное ли утверждение в принципе. Позднее, возможно, физиолог изучит функции печени и сделает вывод о ее влиянии на гормональный фон и образование жиров в организме. Гормоны ответят за хорошее настроение, а отложение жиров – за внешний облик. Причина же будет лежать в области генетики.
Измерение корреляции
Статистика предлагает измерять корреляционную взаимосвязь с помощью числового коэффициента, в который будет входить ее величина и направление. Чем больше это число, тем сильнее взаимная связь параметров. Направление взаимодействия будет определяться знаком коэффициента корреляции.
Отрицательный знак будет означать, что уменьшение одной величины ведет к росту другой. Например, уменьшение количества бензина, выдаваемого полицейским патрульным машинам, приведет к повышенным показателям хулиганских действий на улицах.
Положительный знак коэффициента, соответствует случаю, когда увеличение одной величины приводит к повышению уровня другой. Так, частота проведения родительских собраний в школе может быть связана с ростом успеваемости.
При отсутствии корреляции говорят, что она равна нулю. Уровень воды в реке во время паводка может быть никак не связан с количеством заболеваний гриппом.
Корреляция и вероятность
Величина коэффициента корреляции говорит о частоте совпадений, но не доказывает причинно-следственной связи между событиями. Например, снижение успеваемости в университете и частота обращений в медпункт общежития могут иметь одну и ту же причину – плохое качество пищи, приготовленной в студенческой столовой. В целом сильная корреляция соответствует 70% совпадений и более, а слабая – менее 20%.
Корреляция
Смотреть что такое «Корреляция» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
корреляция
Полезное
Смотреть что такое «корреляция» в других словарях:
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Корреляция
Полезное
Смотреть что такое «Корреляция» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Корреляции в дипломных работах по психологии
Термин «корреляция» активно используется в гуманитарных науках, медицине; часто мелькает в СМИ. Ключевую роль корреляции играют в психологии. В частности, расчет корреляций выступает важным этапом реализации эмпирического исследования при написании ВКР по психологии.
В этой статье мы простым языком объясним суть корреляционной связи, виды корреляций, способы расчета, особенности использования корреляции в психологических исследованиях, а также при написании дипломных работ по психологии.
Что такое корреляция
Корреляция – это связь. Но не любая. В чем же ее особенность? Рассмотрим на примере.
Представьте, что вы едете на автомобиле. Вы нажимаете педаль газа – машина едет быстрее. Вы сбавляете газ – авто замедляет ход. Даже не знакомый с устройством автомобиля человек скажет: «Между педалью газа и скоростью машины есть прямая связь: чем сильнее нажата педаль, тем скорость выше».
Это зависимость функциональная – скорость выступает прямой функцией педали газа. Специалист объяснит, что педаль управляет подачей топлива в цилиндры, где происходит сжигание смеси, что ведет к повышению мощности на вал и т.д. Это связь жесткая, детерминированная, не допускающая исключений (при условии, что машина исправна).
Теперь представьте, что вы директор фирмы, сотрудники которой продают товары. Вы решаете повысить продажи за счет повышения окладов работников. Вы повышаете зарплату на 10%, и продажи в среднем по фирме растут. Через время повышаете еще на 10%, и опять рост. Затем еще на 5%, и опять есть эффект. Напрашивается вывод – между продажами фирмы и окладом сотрудников есть прямая зависимость – чем выше оклады, тем выше продажи организации. Такая же это связь, как между педалью газа и скоростью авто? В чем ключевое отличие?
Правильно, между окладом и продажами заисимость не жесткая. Это значит, что у кого-то из сотрудников продажи могли даже снизиться, невзирая на рост оклада. У кого-то остаться неизменными. Но в среднем по фирме продажи выросли, и мы говорим – связь продаж и оклада сотрудников есть, и она корреляционная.
В основе функциональной связи (педаль газа – скорость) лежит физический закон. В основе корреляционной связи (продажи – оклад) находится простая согласованность изменения двух показателей. Никакого закона (в физическом понимании этого слова) за корреляцией нет. Есть лишь вероятностная (стохастическая) закономерность.
Численное выражение корреляционной зависимости
Итак, корреляционная связь отражает зависимость между явлениями. Если эти явления можно измерить, то она получает численное выражение.
Полученное число называется коэффициентом корреляции. Для его правильной интерпретации важно учитывать следующее:
Прямая и обратная
Сильная и слабая
Чем ниже численное значение коэффициента, тем взаимосвязь между явлениями и показателями меньше.
Рассмотрим пример. Взяли 10 студентов и измерили у них уровень интеллекта (IQ) и успеваемость за семестр. Расположили эти данные в виде двух столбцов.
Испытуемый
IQ
Успеваемость (баллы)
Посмотрите внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. Но также растет и уровень успеваемости. Из любых двух студентов успеваемость будет выше у того, у кого выше IQ. И никаких исключений из этого правила не будет.
Перед нами пример полного, 100%-но согласованного изменения двух показателей в группе. И это пример максимально возможной положительной взаимосвязи. То есть, корреляционная зависимость между интеллектом и успеваемостью равна 1.
Рассмотрим другой пример. У этих же 10-ти студентов с помощью опроса оценили, в какой мере они ощущают себя успешными в общении с противоположным полом (по шкале от 1 до 10).
Испытуемый
IQ
Успех в общении с противоположным полом (баллы)
Смотрим внимательно на данные в таблице. От 1 до 10 испытуемого растет уровень IQ. При этом в последнем столбце последовательно снижается уровень успешности общения с противоположным полом. Из любых двух студентов успех общения с противоположным полом будет выше у того, у кого IQ ниже. И никаких исключений из этого правила не будет.
А как понять смысл корреляции равной нулю (0)? Это значит, связи между показателями нет. Еще раз вернемся к нашим студентам и рассмотрим еще один измеренный у них показатель – длину прыжка с места.
Испытуемый
IQ
Длина прыжка с места (м)
Не наблюдается никакой согласованности между изменением IQ от человека к человеку и длинной прыжка. Это и свидетельствует об отсутствии корреляции. Коэффициент корреляции IQ и длины прыжка с места у студентов равен 0.
Мы рассмотрели крайние случаи. В реальных измерениях коэффициенты редко бывают равны точно 1 или 0. При этом принята следующая шкала:
Приведенная градация дает очень приблизительные оценки и в таком виде редко используются в исследованиях.
Чаще используются градации коэффициентов по уровням значимости. В этом случае реально полученный коэффициент может быть значимым или не значимым. Определить это можно, сравнив его значение с критическим значением коэффициента корреляции, взятым из специальной таблицы. Причем эти критические значения зависят от численности выборки (чем больше объем, тем ниже критическое значение).
Корреляционный анализ в психологии
Корреляционный метод выступает одним из основных в психологических исследованиях. И это не случайно, ведь психология стремится быть точной наукой. Получается ли?
В чем особенность законов в точных науках. Например, закон тяготения в физике действует без исключений: чем больше масса тела, тем сильнее оно притягивает другие тела. Этот физический закон отражает связь массы тела и силы притяжения.
Пример исследования на студентах из предыдущего раздела хорошо иллюстрирует использование корреляций в психологии:
Вот как могли выглядеть краткие выводы по результатам придуманного исследования на студентах:
Таким образом, уровень интеллекта студентов выступает позитивным фактором их академической успеваемости, в то же время негативно сказываясь на отношениях с противоположным полом и не оказывая значимого влияния на спортивные успехи, в частности, способность к прыгать с места.
Как видим, интеллект помогает студентам учиться, но мешает строить отношения с противоположным полом. При этом не влияет на их спортивные успехи.
Неоднозначное влияние интеллекта на личность и деятельность студентов отражает сложность этого феномена в структуре личностных особенностей и важность продолжения исследований в этом направлении. В частности, представляется важным провести анализ взаимосвязей интеллекта с психологическими особенностями и деятельностью студентов с учетом их пола.
Коэффициенты Пирсона и Спирмена
Рассмотрим два метода расчета.
Коэффициент Пирсона – это особый метод расчета взаимосвязи показателей между выраженностью численных значений в одной группе. Очень упрощенно он сводится к следующему:
Коэффициент ранговой корреляции Спирмена рассчитывается похожим образом:
В случае Пирсона расчет шел с использованием среднего значения. Следовательно, случайные выбросы данных (существенное отличие от среднего), например, из-за ошибки обработки или недостоверных ответов могут существенно исказить результат.
В случае Спирмена абсолютные значения данных не играют роли, так как учитывается только их взаимное расположение по отношению друг к другу (ранги). То есть, выбросы данных или другие неточности не окажут серьезного влияния на конечный результат.
Если результаты тестирования корректны, то различия коэффициентов Пирсона и Спирмена незначительны, при этом коэффициент Пирсона показывает более точное значение взаимосвязи данных.
Как рассчитать коэффициент корреляции
Коэффициенты Пирсона и Спирмена можно рассчитать вручную. Это может понадобиться при углубленном изучении статистических методов.
Однако в большинстве случаев при решении прикладных задач, в том числе и в психологии, можно проводить расчеты с помощью специальных программ.
Расчет с помощью электронных таблиц Microsoft Excel
Вернемся опять к примеру со студентами и рассмотрим данные об уровне их интеллекта и длине прыжка с места. Занесем эти данные (два столбца) в таблицу Excel.
Переместив курсор в пустую ячейку, нажмем опцию «Вставить функцию» и выберем «КОРРЕЛ» из раздела «Статистические».
Формат этой функции предполагает выделение двух массивов данных: КОРРЕЛ (массив 1; массив»). Выделяем соответственно столбик с IQ и длиной прыжков.
В таблицах Excel реализована формула расчета только коэффициента Пирсона.
Расчет с помощью программы STATISTICA
Заносим данные по интеллекту и длине прыжка в поле исходных данных. Далее выбираем опцию «Непараметрические критерии», «Спирмена». Выделяем параметры для расчета и получаем следующий результат.
Как видно, расчет дал результат 0,024, что отличается от результата по Пирсону – 0,038, полученной выше с помощью Excel. Однако различия незначительны.
Использование корреляционного анализа в дипломных работах по психологии (пример)
Большинство тем выпускных квалификационных работ по психологии (дипломов, курсовых, магистерских) предполагают проведение корреляционного исследования (остальные связаны с выявлением различий психологических показателей в разных группах).
Сам термин «корреляция» в названиях тем звучит редко – он скрывается за следующими формулировками:
Рассмотрим кратко этапы его проведения при написании дипломной работы по психологии на тему: «Взаимосвязь личностной тревожности и агрессивности у подростков».
1. Для расчета необходимы сырые данные, в качестве которых обычно выступают результаты тестирования испытуемых. Они заносятся в сводную таблицу и помещаются в приложение. Эта таблица устроена следующим образом:
Что такое Корреляция
Корреляция — это сходство или взаимосвязь между двумя вещами, людьми или идеями. Означает сходство или эквивалентность, существующие между двумя гипотезами, ситуациями или вещами.
В области статистики и математики корреляция относится к мере между переменными (двумя или более), связанными между собой.
Слово корреляция является существительным женского рода, произошло от латинского correlatiōne («cum» (одновременно) + «relatio» (отношение)), читается как «коррелатионе» и означает «соотношение» или «взаимосвязь».
Слово «корреляция» может быть заменено синонимами, такими как: связь, зависимость, соотношение, взаимосвязь, взаимозависимость и взаимосоответствие.
Корреляционный анализ
Цель коэффициента корреляции заключается в том, чтобы определить интенсивность соотношения, которое существует между известными наборами данных или другой известной информации.
Коэффициент корреляции Пирсона (Pearson)
В статистике коэффициент корреляции Пирсона (r-Пирсона), который также называется коэффициентом корреляции момента продукта Пирсона (или PPMCC, или PCC), измеряет взаимосвязь между двумя переменными в одной и той же метрической шкале.
Расчет коэффициента корреляции Пирсона
Метод 1) Расчет коэффициента корреляции Пирсона с использованием ковариации и стандартного отклонения



В этом случае расчет включает в себя сначала поиск ковариации между переменными и стандартное отклонение каждой из них.
Затем нужно разделить ковариацию на умножение из двух стандартных отклонений — сделайте дробь и поставьте ковариацию сверху, а умножение из двух стандартных отклонений — снизу.
Часто в данных задач уже есть либо стандартные отклонения переменных, либо ковариация между ними, остаётся только применить формулу.
Метод 2) Расчет коэффициента корреляции Пирсона с исходными данными (без ковариации или стандартного отклонения)
При таком методе наиболее лёгкая формула выглядит следующим образом:
Например, если предположить, что у нас есть данные с n = 6 наблюдениями двух переменных: уровня глюкозы (y) и возраста (x). Например, это статистические данные шести человек, от которых мы знаем их возраст и уровень глюкозы. На следующей таблице вы увидите эти данные: у первого человека, которому 43 года, уровень глюкозы 99, у второго, которому 21 год, уровень глюкозы 65, у третьего, которому 25 лет, глюкоза 79 и так далее. Вычисление следует производить по следующим шагам.
Шаг 1: Заполнить таблицу следующим образом: внести существующие данные i, x, y и добавить пустые столбцы для xy, x², y².
Шаг 2: Умножить x и y, чтобы заполнить столбец “xy”. Например, в первой строке будет x1y1 = 43 × 99 = 4257.
Шаг 3: Взять значение столбца x и возвести его в квадрат, записать результат в столбце x². Например, в первой строке в нашей таблице будет x12 = 43 × 43 = 1849.
Шаг 4: Сделать то же самое, что и в шаге 3, но теперь используйте столбец y и запишите ваши вычисления в столбце y². Например, в первой строке в нашей таблице будет y12 = 99 × 99 = 9801.
Шаг 5: Сделать сумму каждого из столбцов и поместить результат внизу, к каждой колонке. Например, сумма столбца возраст x равна 43 + 21 + 25 + 42 + 57 + 59 = 247.
Шаг 6: Использовать формулу коэффициента корреляции.
Т.е. возраст и уровень глюкозы зависят друг от друга (т. к. коэффициент 0,5298 далёк от 0), но не очень сильно (т. к. коэффициент всё же очень далёк и от 1). А положительная, так как коэффициент больше чем 0, это означает, что глюкоза и возраст поднимаются вместе, а не наоборот (т. е. чем выше возраст, тем выше уровень глюкозы).
Коэффициент корреляции Спирмена
В статистике также существует коэффициент корреляции Спирмена, который назван в честь статистика Чарльза Эдварда Спирмена (Spearman).
Цель этого коэффициента заключается в измерении интенсивности соотношения между двумя переменными, независимо от того, являются ли они линейными или нет.
Корреляция Спирмена служит для оценки того, может ли интенсивность взаимосвязи между двумя анализируемыми переменными быть измерена монотонной функцией (математическая функция, которая сохраняет или инвертирует соотношение начальной последовательности).
Как считать коэффициент корреляции Спирмена
Расчет коэффициента корреляции Спирмена уже немного отличается от предыдущей. Для этого необходимо организовать имеющиеся данные в следующую таблицу.
1. У вас должны быть две пары данных, соответствующих друг другу. Вы должны внести их в эту таблицу. Например, дирекция ресторана хочет узнать, есть ли связь между количеством заказов бутылок воды и количеством заказов десертов. Директор взял наугад данные 4-х столиков. Таким образом, у него получились две пары данных: где “Data А” — это заказы десертов, а “Data B” — заказы воды (т. е. первый столик заказал 7 десертов и 8 бутылок воды, второй — 6 десертов и 3 бутылки с водой и т. д.):
2. В столбце «Ranking А» мы будем классифицировать наблюдения, которые находятся в «Data А», нарастающим образом: «1» является самым низким значением в столбце и n (общее количество наблюдений) — самым высоким значением в столбце «Data А». В нашем примере это:
3. Сделайте то же самое позиционирование (классификацию наблюдений) для второго столбца “Data B”, записав это в столбце “Ranking B”.
5. Возведите во вторую степень каждое из значений, полученное в столбце «d».
6. Сделайте сумму всех данных, которые у вас получились в столбце «d2». Это будет Σd². В нашем примере Σd² = 0+1+0+1 = 2.
7. Теперь используем формулу Спирмена.
В нашем случае n = 4, мы это видим по количеству пар данных (соответствует числу наблюдений).
8. И наконец, замените данные в формуле.
Наш результат равен 0,8 или 80 %. Это означает, что переменные имеют положительную корреляцию.
Т. е. заказы бутылок воды и заказы десертов клиентами этого ресторана зависят друг от друга (т. к. коэффициент 0,8 далёк от 0), но не полностью (т. к. коэффициент очень близок к 1, но не равен 1). А положительная, так как коэффициент больше чем 0, это означает, что количество воды и количество десертов увеличиваются вместе, а не наоборот (т. е. чем выше количество потребляемой воды, тем выше количество потребляемых десертов).
Линейная регрессия
Это формула, используемая для оценки возможного значения переменной (y), когда известны значения других переменных (x).
Значение «x» является независимой переменной или предиктором, а «y» зависимая переменная (также переменная отклика) или ответ на заданный вопрос.
Линейная регрессия используется для проверки того, как значение «y» может меняться в зависимости от переменной «x». Прямая, содержащая значения проверки этой вариации, называется линией линейной регрессии.
Если отношение будет между зависимой переменной (“y”) и независимой переменной (“x”), регрессия будет называться простой линейной регрессией.
Простая линейная регрессия
Yi = β0 + β1Xi + εi
β0 — сдвиг (длина отрезка, отсекаемого на координатной оси прямой Y)
β1 — наклон прямой Y,
εi— случайная ошибка переменной Y в i-м наблюдении.
Что такое корреляция и что означает коррелировать — простыми словами о сложном
Блог ленивого инвестора > Forex
Валюты и биржевые активы не могут существовать в вакууме. Они связаны между собой многочисленными причинно-следственными связями. Поэтому изменение цены одного инструмента неизбежно влечёт за собой цепочку других изменений. Но если, например, фьючерсы на какао не вызовут паники на рынке нефти, то резкое укрепление доллара отразится на всех рынках (например, приведет к девальвации рубля). Зависимость между изменениями двух и более величин принято называть корреляцией. Сегодня я рассмотрю это явление с точки зрения инвестиций.
Определение корелляции — что это
Простыми словами корреляция – это взаимосвязь двух или нескольких случайных параметров. Когда одна величина растет или уменьшается, другая тоже изменяется.
Объясним на примере: существует корреляция между температурой воздуха и потреблением мороженого. Чем жарче погода, тем больше холодного лакомства покупают люди. И наоборот.
Такие закономерности устанавливаются путем исследования больших объемов статистических данных. Собираем информацию о потреблении мороженого за несколько лет и сведения о колебаниях температуры за тот же период. А дальше сопоставляем и ищем зависимость.
Коррелировать – это значит быть взаимосвязанным с чем-то. Существует положительная и отрицательная корреляции.
При положительной чем больше один параметр, тем больше и другой. Например, чем масштабнее траты фермера на удобрения, тем обильнее урожай. При обратной корреляции рост одной величины сопровождается уменьшением другой. Чем выше здание, тем хуже оно противостоит землетрясениям.
Корреляция — это взаимосвязь без гарантий
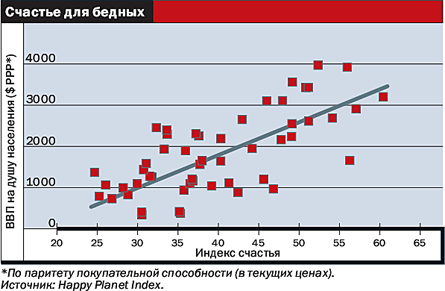
Рассмотрим пример прямой корреляции: чем выше уровень благосостояния человека, тем больше его продолжительность жизни. Обеспеченные люди питаются качественной пищей и своевременно получают врачебную помощь. В отличие от бедняков.
Однако нельзя с уверенностью сказать, что определенный олигарх проживет дольше вот этого нищего.
Это лишь статистическая вероятность, которая может не сработать для одного конкретного случая. Этим корреляция отличается от линейной зависимости, где исход известен со 100-процентной вероятностью.
Но если мы возьмем выборку из сотни тысяч богачей и такого же числа малоимущих, сравним их продолжительность жизни, то общая тенденция будет верна.
Математическая ловушка
Как я уже упоминал выше, формула расчёта коэффициента корреляции очень чувствительна к знакам отклонений значений величин от их средних значений. Если эти отклонения чаще имеют одинаковые знаки, получается высокое значение коэффициента корреляции. Но будет ли это значение иметь смысл? Ответ вовсе не очевиден. Рассмотрим практический пример. Предположим, на графиках двух величин одновременно имеется большой скачок или ГЭП:
Тогда новые значения этих величин будут систематически оказываться по одну сторону от их средних значений. Это приведёт к высокой положительной корреляции. К сожалению, никакой пользы от этой информации не будет, т.к. кроме наличия гэпа, ничего общего между графиками нет. Это лишь наглядный пример того, что при расчёте корреляции допускается использовать исключительно стационарные ряды значений, т.е. ряды, в которых нет трендовой составляющей. Это означает, что расчёт корреляций в мире финансовых активов неизбежно приводит к переоценке значимости факторов, в действительности имеющих случайный характер. Поймите правильно: важно не выискивать эти факторы и вводить на них специальные поправки, а показать саму суть явления и не искать очередной Грааль там, где его нет.
Впрочем, не всё так плохо. Есть способ обойти влияние трендов путём расчёта корреляции не самих цен, а их приращений. Тогда упомянутый выше ГЭП окажется статистическим выбросом, практически не влияющим на результат. Осталось лишь дождаться, когда такой подход возобладает. Не всегда можно найти свежие данные по корреляции активов. В таких случаях их можно рассчитать при помощи Microsoft Excel. Для этого котировки записываются в виде двух диапазонов ячеек, а затем в одной из свободных ячеек записывается функция следующего вида: =КОРРЕЛ (массив 1; массив 2). Массив может выглядеть, например, так: A1:A100. Для расчёта корреляции по приращениям цен, эта программа полезна вдвойне, ведь на основе цен закрытия нужно вначале рассчитать сами приращения.
Коэффициент корреляции
| Значение коэффициента | Какая корреляция? | О чем это говорит? |
| r=1 | Сильная положительная корреляция | Люди, которые едят чернику, обладают острым зрением. Ешьте чернику! |
| r | Слабая положительная корреляция | Некоторые люди, которые любят чернику, обладают острым зрением. Но это не точно. Короче, ничего не пока понятно. Но лучше есть чернику на всякий случай. |
| r=0 | Корреляция отсутствует | Черника и зрение никак не связаны. |
| r | Слабая отрицательная корреляция | Бывают случаи ухудшения зрения из-за черники. Не стоит рисковать. |
| r=-1 | Сильная отрицательная корреляция | Практически все, кто ел чернику, ослепли. Берегитесь черники! |
Величина коэффициента корреляции рассчитывается по формуле:
Если внезапно потемнело в глазах и возникло непреодолимое желание закрыть статью (синдром гуманитария), то есть вариант попроще. Microsoft Exel все выполнит сам при помощи функции «КОРРЕЛ». Делается это так:
Судя по расчетам, рост человека практически никак не влияет на уровень зарплаты.


Знание корреляции активов снижает риски портфеля
Рекомендую прочитать также:
Сервис копирования сделок RAMM от AMarkets
Что такое сервис RAMM и как в нём копировать сделки
Процесс, называемый ребалансировкой портфеля, позволяет получать доход, попеременно меняя долю активов в портфеле. Наиболее просто это достигается при ярко выраженной отрицательной корреляции. Предположим, что изначально в портфеле были активы А и В с обратной корреляцией и соотношением 1:1, на общую сумму 1 млн рублей. В течение полугода актив А упал в цене на 20% и его стоимость из первоначальных 500 тыс. рублей стала 400 тыс. рублей. Актив В, наоборот, вырос на 20% и его стоимость поднялась до 600 тыс. рублей. Общая стоимость портфеля не изменилась и по-прежнему составляет 1 млн рублей. Теперь 50% актива В (300 тыс.) перекладываем в А и его стоимость теперь составляет 700 тыс., а актива В – 300 тыс.
Как видно, чем ниже значение коэффициента корреляции инструментов, тем больше возможная доходность портфеля при одном и том же значении риска, либо тем меньше риск при одном и том же значении доходности.
Реальные причины корреляции и возможные гипотезы
Курс доллара и стоимость нефти отрицательно коррелируют. Можем выдвинуть гипотезу: повышение цен на черное золото вызывает падение стоимости американской валюты. Но почему так происходит? Откуда взялась связь между этими явлениями?
Определение причины корреляции – это очень сложная задача. Переплетаются тысячи различных факторов, часть из которых скрыта.
Возможно, дело в том, что США – крупнейший потребитель нефти в мире. Каждый день они импортируют около 7,2 миллиона баррелей. Снижение цены на черное золото – хорошо для американской экономики, ведь позволяет тратить меньше денег. Следовательно, доллар растет.
Корреляция предоставляет возможность сделать вывод из статистических данных.
Например, мы выяснили, что существует отрицательная взаимосвязь между доходом персонала и его эффективностью в работе. Наша гипотеза: «Лентяи и бездельники получают больше, чем ответственные сотрудники». Тогда мы пересмотрим систему мотивации и избавимся от бесполезных людей.
Гипотеза – это лишь статистический вывод, предположение. Она вполне может оказаться ошибочной.
Согласно статистике, чем больше пожарных участвует в тушении огня, тем существенней размер ущерба. Какую гипотезу можем сделать отсюда? Пожарные приносят вред, давайте сократим их! Но если разобраться, то настоящая причина повреждения – это огонь. А увеличение числа лиц, задействованных в его тушении, – следствие масштаба пожара.
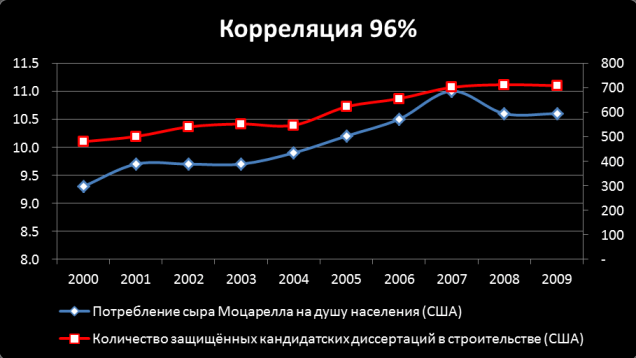
Наша вселенная бесконечна, а значит всегда можно найти несколько переменных, которые будут коррелировать между собой, несмотря на полное отсутствие причинно-следственных связей. Даже самое буйное воображение не сможет объяснить, что объединяет сыр и одеяло-убийцу:
Более подробно на эту тему смотрите в видео:
Не бывает следствий без причины
Корреляция цен активов в чём-то подобна трендам: чем больше временной интервал для её расчёта, тем медленнее она изменяется. Но есть и то, что выгодно отличает корреляцию от многих других методов. Её можно рассчитать для таких пар активов, которые не торгуются ни на одной бирже (нефть-газ, нефть-золото), что позволяет дополнить арсенал аналитика ценной информацией, позволяющей «читать рынок между графиками».
Любая корреляция двух и более величин всегда имеет причинно-следственную связь. Одна из величин является определяющей, от которой зависит другая (или другие). Корреляция на фондовом рынке – не исключение. Например, в паре нефть-газ длительное время определяющими были котировки нефти. На графике ниже можно заметить, что расширение спреда между нефтью и газом за счёт резкого относительного роста газа сменялось столь же резким возвратом к относительному равновесию:
В то же самое время, в другой паре активов, золото-нефть, определяющим является уже золото. При значительном расширении спреда между ними (резкий рост или падение нефти при более стабильном золоте) именно нефть восстанавливает нарушенное равновесие:
Отслеживая подобное поведение «ведомых» активов, можно открывать сделки в сторону восстановления баланса. Кстати, корреляция на рынке форекс часто имеет в основе привязку некоторых валют к сырьевым активам. Их так и называют: «сырьевые валюты». Например, сильно зависят от нефти канадский доллар и рубль. В обоих случаях, корреляция прямая: чем дороже нефть, тем выше курс этих валют по отношению к доллару США.
В случае рубля корреляция графиков настолько чёткая, что может быть использована в торговой стратегии. Рассмотрим начало 2014 года. Нефть торгуется около 110$ за баррель, после чего на некоторое время поднимается чуть выше. Рубль же в это время, напротив, с 33 за доллар США кратковременно снижается до 36. На какой-то момент корреляция становится практически обратной, но равновесие быстро восстанавливается и рубль возвращается к курсу 33 за доллар, послушно следуя за нефтью. Ещё более яркий пример мы видим в конце 2014 года, когда произошло резкое ослабление рубля на фоне гораздо более плавно снижающейся нефти. И в этот раз нарушенное равновесие вскоре восстановилось благодаря укреплению рубля. С течением времени корреляция может претерпевать сильные изменения и даже из прямой переходить в обратную. Особенно ярко это проявилось в случае корреляции индексов Dow Jones Industrial Average и РТС.
В конце 2007 года, когда начали проявляться первые признаки ипотечного кризиса в США, индекс DJ развернулся вниз, но индекс РТС, благодаря активному росту нефтяных котировок, ещё только подбирался к историческому максимуму. Однако, в дальнейшем резкий обвал всех фондовых индексов мира сказался и на нефти. Это привело к тому, что индекс РТС по темпам падения практически в 2 раза превысил DJ. Кроме нефти, на темпах падения индекса РТС сказался и общий отток капиталов из развивающихся рынков.
Однако, кризис был недолгим и уже в начале 2009 года сменился экономическим ростом. Высокая корреляция между DJ и РТС наблюдалась вплоть до апреля 2012 года, который ознаменовался исчерпанием возможностей сырьевой модели развития российской экономики. Начиная с этого года, даже дорогая нефть уже не обеспечивала экономический рост. В дальнейшем в России экономический спад лишь усугубился на фоне дешевеющей нефти, тогда как американская экономика получила дополнительный стимул для роста. Корреляция между индексами DJ и РТС стала обратной.
Рекомендую прочитать также:
Сервис копирования сделок RAMM от AMarkets
Что такое сервис RAMM и как в нём копировать сделки
Само по себе наличие корреляции между активами ещё не означает, что на этом можно строить стратегию торговли или инвестирования. Предположим, нас интересует корреляция акций компании IBM за последние 12 месяцев (см. impactopia.com/correlation). Итак, на 4 месте по величине корреляции находится Banco Santander (около 0,43). Скорее всего, это просто случайное совпадение или системный недостаток самого метода расчёта корреляций.
Как при помощи корреляции люди становятся богаче
Главное правило любого инвестора: не класть все яйца в одну корзину. Вложения рекомендуется диверсифицировать (что это?) – распределять. Поэтому люди покупают акции не одной компании, а десятка разных, формируя инвестиционные портфели. Если котировки какой-то фирмы упадут, то оставшиеся девять смогут отыграть падение или хотя бы уменьшить убытки.
Но это в теории, а на практике все портит корреляция. Проблема в том, что стоимости акций разных компаний внутри отрасли или даже всей страны могут сильно коррелировать. Проблемы огромной корпорации провоцируют панику на рынке, снижают стоимость иных активов, на первый взгляд не связанных между собой. В 2008 году случился крах Lehman Brothers, который вызвал цепную реакцию и обвал на мировых рынках.
Поэтому при инвестировании нужно стараться выбирать направления, которые не связаны между собой (r стремится к 0).
Территориальное приближение активов друг к другу усиливает корреляцию. Значит, нужно рассматривать варианты в разных точках мира, максимально удаленных друг от друга.
В жизни этот принцип тоже действует. Если ваши навыки и знания позволяют трудиться программистом, таксистом, сантехником и журналистом – вы хорошо защищены от риска безработицы.
Значение слова корреляция
Словарь Ушакова
коррел я ция, корреляции, жен. (лат. correlatio) (научн.).
1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.).
2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
Современный экономический словарь. 1999
в экономической статистике: понятие, отражающее наличие связи между явлениями, процессами и характеризующими их величинами.
Словарь лингвистических терминов
(средневековолат. correlatio — соотношение). Взаимная зависимость, соотносительность двух или более языковых единиц.
Начала Современного Естествознания. Тезаурус
(от лат. correlatio — соотношение)
1) взаимное соотношение предметов, понятий, взаимозависимость;
2) (в математике) понятие, которым отмечают связь между явлениями, если одно из них входит в число причин, определяющих другие, или если имеются общие причины, воздействующие на эти явления;
3) (в биологии) взаимная приспособленность, согласованность, соотнесенность всех органов, всех частей тела друг с другом, так что вообще изменение одного органа или одной части тела влечет за собой изменение остальных. Подобная корреляция имеет место в области психологии и социологии. В биологию термин «корреляция» ввел французский биолог Жорж Кювье.
Антропологический толковый словарь
взаимосвяз (взаимовлияние) двух данных единиц друг на друга (например, корреляция между признаками).
Толковый переводоведческий словарь
1. Взаимная обусловленность, семиологическая зависимость двух или более единиц языка.
Вестминстерский словарь теологических терминов
♦ ( ENG correlation)
соотношение одного к одному.
Тезаурус русской деловой лексики
Syn: соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность
Энциклопедический словарь
Словарь Ожегова
КОРРЕЛЯЦИЯ, и, ж. (книжн.). Взаимная связь, соотношение.
| прил. корреляционный, ая, ое.
Словарь Ефремовой
ж.
Взаимная связь, соотношение предметов, явлений или понятий.
Энциклопедия Брокгауза и Ефрона
(лат. correlatio) — термин, предложенный покойным профессором казанского университета Н. В. Крушевским (см.) для обозначения таких звуковых чередований (в области одного и того же языка), которые не обусловливаются более, в данный момент жизни языка, никакими реальными причинами и представляют собой просто остаток или след некогда действовавшего звукового процесса. Члены такого чередования (коррелятивы) уже утратили известную необходимую связь, соединявшую их между собой, и находятся в отношении простого «сосуществования» или «соотношения». Так, напр., гласные о и у в словах муха и мошка в настоящее время суть коррелятивы, так как их чередование теперь ничем не обусловлено. Таково же взаимное отношение звуков е, о, е в формах: реку, про-рок, речь и т. д. См. также Дивергенция (см.). Ср. Крушевский, «К вопросу о гуне» («Р. Филол. Вест.», 1887, кн. I, и отдельно: Введение); его же, «Ueber die Lautabwechslung» (Казань, 1881); его же, «Очерк науки о языке» (Казань, 1883); Бодуэн де-Куртенэ, «Некоторые отделы сравн. грамматики слав. яз.» («Р. Филол. Вест.», 1881, кн. 2); его же, «Pr ó ba teorji alternacyj fonetyczuych» (Краков, 1894, ч. I).
КОРРЕЛЯЦИЯ
Смотреть что такое «КОРРЕЛЯЦИЯ» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Корреляция
Смотреть что такое «Корреляция» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — [лат. correlatio] взаимная связь, соотношение предметов или понятий. Словарь иностранных слов. Комлев Н.Г., 2006. КОРРЕЛЯЦИЯ новолатинск. от relata. Взаимное отношение, например, существующее между опекуном и опекаемым. Объяснение 25000… … Словарь иностранных слов русского языка
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
КОРРЕЛЯЦИЯ
Полезное
Смотреть что такое «КОРРЕЛЯЦИЯ» в других словарях:
корреляция — КОРРЕЛЯЦИЯ (с. 325) (от позднелат. correlatio соотношение) термин, применяемый в различных областях знания, в том числе и в психологии, для обозначения взаимного соотношения, соответствия понятий и явлений. Большинство психологических… … Большая психологическая энциклопедия
КОРРЕЛЯЦИЯ — (correlation) Степень зависимости между двумя переменными. Линейная корреляция между двумя переменными х и у определяется знаком и величиной Σi (xi μx )(yi μy), где μx и μy среднее значение х и у. Между двумя переменными существует положительная… … Экономический словарь
корреляция — соотношение, соотнесение, взаимосвязь, взаимозависимость, взаимообусловленность, взаимосоответствие Словарь русских синонимов. корреляция сущ., кол во синонимов: 8 • автокорреляция (1) … Словарь синонимов
КОРРЕЛЯЦИЯ — (от франц. correlation соотношение) в статистике понимается как взаимоотношение между изучаемыми статистическими величинами, рядами и группами; для определения наличия или отсутствия К. статистика пользуется особым методом. Метод К. применяется… … Большая медицинская энциклопедия
корреляция — — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23] корреляция Величина, характеризующая взаимную зависимость двух случайных величин X и Y — безразлично, определяется ли она некоторой причинной связью или просто случайным… … Справочник технического переводчика
КОРРЕЛЯЦИЯ — в математической статистике вероятностная или статистическая зависимость. В отличие от функциональной зависимости корреляция возникает тогда, когда зависимость одного из признаков от другого осложняется наличием ряда случайных факторов … Большой Энциклопедический словарь
КОРРЕЛЯЦИЯ — (от лат. correlatio соотношение) 1) в логике – отношение между двумя одинаковыми по форме связями. Если благодаря закономерному изменению структуры одна связь становится изоморфной (равной по форме) другой, тогда это отношение обеих связей… … Философская энциклопедия
корреляция — и, ж. corrélation f., нем. Korrelation <лат. correlatio соотношение. Впервые отмечается в словаре Гавкина 1894 г. ЭС. Взаимная связь, соотношение предметов или понятий. Закон корреляции. Функциональная корреляция. БАС 1. Рост безработицы и… … Исторический словарь галлицизмов русского языка
Корреляция — [correlation] величина, характеризующая взаимную зависимость двух случайных величин X и Y безразлично, определяется ли она некоторой причинной связью или просто случайным совпадением (ложной корреляцией). Для того, чтобы определить эту… … Экономико-математический словарь
Значение слова корреляция
Корреляция в словаре кроссвордиста
корреляция
Корреляция Корреля́ция (от «соотношение, взаимосвязь»), или корреляционная зависимость, — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми).
1.Взаимосвязь, соотношение предметов, явлений или понятий.
Большой современный толковый словарь русского языка
Новый словарь иностранных слов
ж. Взаимная связь, соотношение предметов, явлений или понятий.
Новый толково-словообразовательный словарь русского языка Ефремовой
1. соотношение, соответствие, взаимосвязь, взаимозависимость предметов, явлений или понятий;
3. биол. взаимная приспособленность, согласованность строения и функций различных частей (клеток, тканей, органов) животного или растения, обеспечивающая поддержание постоянства его внутренней среды и приспособление организма к условиям обитания.
Словарь иностранных выражений
(средневеково лат. correlatio — соотношение). Взаимная зависимость, соотносительность двух или более языковых единиц.
Словарь лингвистических терминов
Словарь русского языка Лопатина
взаимная связь, соотношение
Словарь русского языка Ожегова
Современный толковый словарь, БСЭ
корреляция ж. Взаимная связь, соотношение предметов, явлений или понятий.
Толковый словарь Ефремовой
корреляции, ж. (латин. correlatio) (науч.).
1. Соотношение, взаимная зависимость сопоставляемых понятий (филос.).
2. Взаимная связь явлений, находящихся в известной зависимости друг от друга. Рост безработицы и количество уголовных преступлений находятся в прямой корреляции друг к другу.
Толковый словарь русского языка Ушакова
(лат. correlatio соотношение, корреляция)
1) в статистике – вероятностная или статистическая зависимость, возникающая, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или когда имеются общие условия, от которых зависят оба признака: анализ К. проводится при построении математических моделей, в т. ч. в биологии и медицине;
2) в биологии – взаимозависимость строения и (или) функции отдельных клеток, тканей, органов и систем организма, проявляющаяся в процессе его развития и жизнедеятельности.
Словарь экономических терминов
Полный орфографический словарь русского языка
Можно найти исследования, где корреляция показателей интеллекта и профессиональной успешности составляет r = 0,3, но можно указать и те, где такая корреляция r = 0,8 (по поводу последних см., например: Gottfredson, 1986).
Согласно исследованию Ассоциации Greatplacetowork, составителя рейтинга 100 лучших работодателей журнала Fortune, компании с сильным HR-брендом получают семь важных конкурентных преимуществ.1. Более высокая производительность труда и рентабельность.2. Устойчивость во время экономических спадов.3. Больше откликов от квалифицированных кандидатов.4. Снижение текучести персонала.5. Сокращение негативного воздействия стресса на сотрудников.6. Повышение уровня удовлетворенности и лояльности клиентов.7. Больше инициативы, творчества и инноваций со стороны сотрудников.Целый ряд исследований указывает на корреляцию показателей удовлетворенности сотрудников от работы в компании с потребительской удовлетворенностью (Sears, корреляция от 0,6 до 0,8), уровня лояльности сотрудников с ростом операционной прибыли (ISR), уровня вовлеченности сотрудников с размером чистой прибыли (Towers Perrin).
Лично для меня корреляция между талантом писателя-фантаста и его научной грамотностью, владением навыками научного мышления несомненна.
Но в действительности такое соотношение не представляется убедительным, поскольку указанная корреляция могла быть получена на основе данных о явлениях, которые, по существу, лишь вызывают ассоциации с одиночеством, например сосредоточенности человека на своем внутреннем мире или стремлении проводить время одному.
Имеется положительная корреляция между холерическим (безудержным) темпераментом и наличием у ведьм склонности к спонтанным злонамеренным чудесам («флуктуациям» по Раудерсону) и между меланхолическим темпераментом и наличием у ведьмы влечения к добрым чудесам.
А сейчас… «Математическое ожидание», « корреляция », «функции Гаусса», какие-то перфокарты, о, господи’ Не полицейская служба, а семинар по математике.
Далеко не для всех подсознательных процессов обнаруживается корреляция со специфической активностью синапсов головного мозга; нашлись теоретики, предположившие, что они протекают вне времени.
Корреляция
Корреляция — это показатель, отражающий взаимосвязь между объектами или событиями.
Это понятие активно используется в экономике, в статистическом анализе, математике, а также в биологии и психологии. Простой пример корреляции — это оценка вероятности событий. Например, увидев темные тучи на небе в летний сезон, мы можем предположить, что пойдет дождь, а в зимний — снег. Однако мы можем быть уверенными в этом на 100%. Вот эта вероятность альтернативного развития событий и заставляет нас коррелировать оценку своих предположений.
Таким образом, корреляция это вероятность, допущение альтернативного сценария, в отличие от линейной зависимости, когда то, что прогнозируется гарантированно произойдет.
Корреляция — это то, как взаимосвязаны случайные факторы. Она отражает их примерную взаимосвязь и вероятность там, где нет точного ответа, гарантий. Например, если в стране вырос показатель преступности и безработица, мы можем предположить, что эти два фактора могут быть взаимосвязанными, однако точных гарантий тут нет, потому что на уровень преступности может влиять еще большое количество факторов: менталитет, образованность, воспитание.
Там, где мы не можем составить точный прогноз из-за того, что существуют дополнительные факторы, появляется корреляция. И вот эта вероятность, связь между событиями, отражается в виде коэффициента корреляции.
Например, существует факт: радиация отрицательно влияет на здоровье. Чем выше уровень радиации, тем больше негативных последствий — обратная пропорциональная зависимость. В таком случае коэффициент корреляции отрицательный. Если между событиями нет связи, то коэффициент корреляции равен нулю. Например, утром вас разбудил телефонный звонок, а в обед вы съели борщ. Прямую взаимосвязь между событиями показывает положительный коэффициент корреляции. Например, чем выше уровень образования, тем больше шансов занять желаемую должность. Таким образом, понятие корреляции исходит из сферы причинно-следственных связей.
Понятие корреляции активно используется инвесторами при составлении инвестиционных портфелей. Они постоянно мониторят корреляцию цены нефти и курса доллара, оценивают коэффициент корреляции акций различных крупных компаний. Такие наблюдения помогают инвесторам составлять максимально эффективный портфель и диверсифицировать свои риски.
Настроить интеграцию без программистов ApiX-Drive
Статьи о маркетинге, автоматизации и интеграциях в нашем Блоге
Что такое корреляция
Корреляция – что означает слово
Корреляция (от лат. correlatio «соотношение») — взаимная зависимость значений нескольких величин друг от друга. В случае, когда между значениями существует корреляция, изменение одного из них всегда будет провоцировать изменение другого. Степень зависимости величин между собой определяет коэффициент корреляции.
История термина
Понятие корреляции впервые сформировал Жорж Кювье, занимавшийся палеонтологией в XVIII веке во Франции. Взаимная зависимость значений в его случае помогала в точности восстанавливать конечный облик древнего существа, располагая лишь отдельными его остатками.
Само значение слова интуитивно понятно даже для людей, далеких от точных наук. Relatio — общий корень множества европейских языков, всегда означающий «отношение». Префикс co- позволяет понять, что речь идет о двустороннем отношении двух и более значений.
Уже вскоре употребление слова вышло за рамки палеонтологии и благодаря работам Ф. Гальтона стало употребляться в статистике. Сперва лишь применимой к биологии, но затем применяемой во всех областях науки. Значительный вклад в развитие математической модели корреляционных связей сделал К. Пирсон.
Корреляция К. Пирсона
Английский математик, философ и биолог Карл Пирсон, сотрудничая с Р. Уэлдоном и Ф. Эджуортом, стал первым, кому удалось вывести точную формулу корреляционной связи. Она численно показывает степень зависимости между параметрами. Получаемое значение называется линейным коэффициентом корреляции. Его значение колеблется между значениями от «минус единицы» до «единицы».
Предложенная Пирсоном формула актуальна и до сегодня, и имеет широкую область применения:
Ковариация
Значимым элементом взаимной зависимости величин является ковариация — среднее значение случайной величины (при стремлении выборки к бесконечности) произведения отклонения.
Характеристики ковариации:
Эти недостатки ковариации делали невозможной её полноценное использование в качестве инструмента корреляционного анализа. Выходом из ситуации стало введение линейного коэффициента корреляции.
Особенности корреляционного анализа
Под корреляционным анализом подразумевает методика обработки данных статистики. Для этого определяется теснота связи между несколькими переменными, которые необходимо исследовать.
Нередко корреляционный анализ проводят совместно с регрессионным. В таком случае удается получить более развернутые данные, уменьшив при этом влияние на конечный результат тех или иных посторонних факторов.
Основные ограничения корреляционного анализа заключаются в следующем:
Несмотря на вышеперечисленные ограничения, свойственные корреляционному анализу, он пользуется значительной популярностью.
Сфера использования понятия
Корреляция широко распространена в разных видах деятельности с целью обработки массивов статистических данных. Это касается, прежде всего, таких наук, как:
Отдельно стоит выделить возможность применения корреляции в некоторых важных для человечества сферах деятельности. Это касается металловедения, агрохимии, биометрического анализа и биологии. В разных типах прикладных отраслей принято использовать предельные границы интервалов для оценки тесноты или же значимости связи.
Распространение использования метода корреляции обусловлено такими факторами, как:
Интерпретация корреляции тоже под силы практически любому человеку. Именно поэтому данный метод так широко используется в различных сферах, где требуется анализ тех или иных статистических данных.
Корреляция: как незаметно выстрелить себе в ногу
Если вы где-то читаете фразу вида «оказалось, что у данных событий корреляция вот такая вот», то примерно в 99,99% случаев, если прямо не оговорено иного, речь идёт о коэффициенте корреляции Пирсона. «Дефолт-корреляция» — это он.
Причём пользуются им далеко не только безграмотные журналисты, но и в целом довольно грамотные учёные. Что, на мой взгляд, весьма странно, ибо область его осмысленного применения сильно уже, чем область его фактического использования.
По этой причине мне хотелось бы рассказать, какими способами при помощи «дефолт-корреляции» можно сделать множество совершенно неправильных, однако весьма наукообразных и кажущихся весьма правдоподобными выводов.
Но для начала о том…
Что такое «коэффициент корреляции Пирсона»?
Вполне понятно, что для несведущих это — особая научная магия, однако довольно обидно, что для многих сведущих дела обстоят аналогично. «Я же биолог, а не математик — зачем мне лезть в эти тонкости?» — обычное дело.
Положим, у нас есть некие два предполагаемых процесса, для каждого из которых мы замеряем какой-то параметр, обычно называемый в данном случае «величиной». В результате у нас появляется набор пар чисел.
Предполагая заодно, что эти процессы не только существуют, но и как-то связаны, мы предполагаем же, что эта связь должна численно проявиться в сделанных нами измерениях. То есть из полученных пар чисел мы каким-то образом можем получить сведения о наличии или отсутствии связи.
Однако связи бывают разной степени жёсткости, поэтому желательно получать не бинарное «да» или «нет», а что-то типа непрерывной по пространству состояний оценки «силы связи».
И вот, встречайте, коэффициент корреляции Пирсона.
Я понимаю, что на этом месте очень многие испугались, что и дальше всё будет столь же непонятным. Какие-то страшные буковки в страшных комбинациях, всё такое.
Признаться, я тоже не особо-то люблю математический вариант записи. Мне «программистский» кажется гораздо более понятным. Поэтому я попытаюсь следовать именно ему.
Есть такое понятие «математическое ожидание величины», для краткости называемое «матожиданием». В простейшем случае его смысл крайне прост: это среднее арифметическое от всех полученных значений.
Получили мы какой-то набор измерений, представленный тут в виде списка
Потом мы просуммировали их все, поделили на количество чисел в этом списке — и вот оно, среднее арифметическое.
Далее мы найдём для каждого числа из списка его отклонение от матожидания.
…и получим, таким образом, список отклонений. Список отклонений каждого из значений от среднего арифметического по всему этому списку.
То же самое можно проделать и с другим списком, в котором находятся измерения второго параметра, измеренного одновременно с первым.
Например, мы у каждого пациента в палате померили температуру. И, кроме того, зафиксировали, сколько таблеток аспирина он сегодня принял. И теперь по вышеуказанной процедуре построим список отклонений температуры каждого пациента от средней температуры пациентов и соответствующий ему список отклонений количества принятых пациентом таблеток аспирина от среднего принятого их количества.
Да, тут уже и так есть суровые подозрения о множестве натяжек, но мы всё-таки не остановимся и предположим, что если температура как-то связана с приёмом аспирина, то должны быть связаны между собой и эти самые отклонения.
Например, если приём аспирина приводит к росту температуры, то мы будем видеть следующее.
Если пациент выпил больше таблеток, чем другие, то его температура отклоняется от средней в бо́льшую сторону.
Если пациент выпил меньше таблеток, чем другие, то его температура отклоняется от средней в меньшую сторону.
То есть оба отклонения — в одну и ту же сторону.
Если мы перемножим попарно все отклонения, то все произведения будут положительными.
И наоборот: если приём аспирина понижает температуру, то все произведения отклонений будут отрицательными.
Иными словами, у нас получилась некая величина, которая обладает чудесным свойством: для прямой связи явлений она положительная, а для обратной — отрицательная.
Однако что с ней будет, если явления не связаны?
Навскидку, с ней будет — «когда как».
Но ведь если явления действительно не связаны, то на большом количестве измерений приблизительно в равной мере должны быть распределены оба варианта: положительное произведение отклонений и отрицательное. Если их просуммировать, то, видимо, получится что-то около нуля. Причём, тем ближе к нулю, чем больше было измерений.
Собственно, вышевведённая функция «матожидание» именно это и делает: суммирует. Потом, правда, ещё делит на количество измерений, но для обнаруженного свойства это не так важно: ведь деление на положительное число не меняет знак результата и не может превратить ноль в не ноль или наоборот.
Поэтому вот он, критерий: ковариация.
Или, если расположить все формулы рядом…
Да, так несколько длиннее, чем в оригинальном определении, но зато и лучше понятно, что происходит.
Теперь, в общем, остался последний момент. Ковариация, увы, может иметь произвольную величину, а потому, для того, чтобы сделать по ней вывод о связи между списками, надо ещё знать максимальное её значение именно для этих величин.
Однако, по счастью, оное можно вычислить в общем виде.
Для этого введём ещё одну интересную величину — выведенную из списка квадратов отклонений от среднего.
Это, как можно видеть, корень из матожидания квадратов отклонений от среднего. Оно так и называется «среднеквадратическое отклонение».
Так вот, можно показать, что ковариация по своей абсолютной величине не превышает произведения среднеквадратических отклонений по этим двум спискам.
Ну а так как среднеквадратическое отклонение по построению всегда положительно, то можно заключить, что
В общем, если за меру взаимосвязи взять такую «нормированную величину», то она получится очень удобной и очень универсальной: будет показывать, связаны ли величины между собой, давая для прямой связи единицу, для обратной — минус единицу, а для несвязанных величин — ноль…
Всё очень удобно и универсально, однако в вышеприведённых рассуждениях есть изрядное количество изъянов, которые — ввиду очевидного удобства и универсальности полученной «меры взаимосвязей» — очень удобно игнорировать, и от этого иметь универсальный способ для поточной генерации совершенно неверных, но зато наукообразных выводов.
Впрочем, надо отметить, что процесса «нормировки» это не касается — со знаменателем всё зашибись, а способ стрельбы себе в ногу кроется в числителе. Да и в самом подходе в целом.
Поэтому, хотя для проформы я тут и привёл полное рассуждение, вскрываемые далее явления вызваны ковариацией и именно на способ её вычисления следует обратить особое внимание.
Выстрел номер один: Ньютон всё наврал
Предположим, некий физик усомнился в законе всемирного тяготения. И решил — в полном соответствии с научным методом — проверить, что тела и правда притягиваются по определённому закону.
Для этого он заказал себе очень точные приборы и сделал экспериментальную установку, в центре которой размещено массивное тело, на любом расстоянии от которого можно размещать другие тела и замерять воздействующую на них силу.
Со всей тщательностью физик измерил силу, действующее на тело, отнесённое от центра на самые разные расстояния. Запротоколировал данные. А потом посчитал корреляцию между координатой изображённого тут зелёным тела и действующей на него силой.
Хм. Ньютон вроде бы утверждал, что сила тяготения однозначно связана с расстоянием между центрами объектов. Почему же мы тут получаем не единицу, а что-то меньшее? Ну ладно, это, быть может, погрешность измерений. Всё равно ведь понятно, что определённо между расстоянием по оси икс и действующей силой есть заметная обратная связь.
На беду, у этого физика были свои личные подозрения об устройстве мира. «Вдруг», — думал он — «миру не всё равно, с какой стороны расположено тело?». Надо попробовать размещать тела не только справа, но и слева.
Правда, прибор для измерения силы умел измерять только её абсолютную величину, но ничего страшного: ведь если есть взаимосвязь между двумя величинами, то между величиной и модулем второй тоже должна быть взаимосвязь.
Поэтому физик провёл второй эксперимент: помещая теперь тело не только справа, но иногда и слева от центра.
В результате, его подозрения оправдались: теперь корреляция координаты с абсолютной величиной силы уже не просто отличалась от единицы или минус единицы…
Она стала нулевой.
Что же тут произошло?
Сейчас, подождите, сначала мы посмотрим на ещё один способ стрельбы в собственные конечности.
Выстрел номер два: хаос энергоснабжения
Однажды физик обнаружил у себя дома удивительный артефакт: электрическую розетку.
Ну ладно, пусть это будет другой физик, чтобы над одним и тем же не издеваться.
Про розетки он слышал, что в них есть электрический ток, которым как раз и питаются электроприборы. А у тока есть напряжение. Которое, вроде бы, в розетках переменное. Так вот, интересно, связано ли это переменное напряжение со временем? Или же, напротив, оно там совершенно хаотичное и меняется как попало?
Для ответа на этот вопрос физик собрал хитрую схему из компьютера и вольтметра, которая через равные промежутки времени измеряет напряжение в сети.
Если связь есть, — рассуждал физик, — то я её таким образом обнаружу. И он был прав: таким образом её действительно можно обнаружить. Причём для этого даже не обязательно быть физиком.
Но на беду и этот физик тоже решил не доверяться интуиции, а вычислить связь автоматически. Для этого он посчитал корреляцию измеренных напряжений с теми моментами времени, когда они были измерены.
Как вы думаете, что в результате получил физик?
Не спешите с ответом…
Физик получил случайную величину от минус до плюс единицы.
В зависимости от того, как встали звёзды, физик мог «выяснить», что напряжение связано со временем прямой или обратной связью, или же, что оно со временем вообще не связано.
Но как?! Как совершенно логичный математический коэффициент может привести к столь абсурдному результату?
Сбитый прицел номер один
Чтобы понять, откуда в мире берётся такая фигня, мы временно, для простоты забудем про знаменатель.
Расположенная в числителе ковариация — это среднее арифметическое произведений отклонений.
Отклонений от чего?
Когда первый физик меряет силу, в зависимости от координаты, слева и справа в симметричных точках у него получаются одинаковые силы. Они отклонены от средней силы совершенно идентично, какой бы эта сила ни была.
Средняя же координата — 0. Отклонения от неё в симметричных точках равны по абсолютной величине, но противоположны по знаку.
Пусть в точке 1 отклонение силы от среднего равно dF1. Тогда в точке −1 будет такое же отклонение dF1. Но вот отклонения в координатах будут уже 1 и −1. Если мы перемножим отклонения, то получим…
| Координата | dx | dF | dx*dF |
|---|---|---|---|
| 1 | 1 | dF1 | dF1 |
| −1 | −1 | dF1 | −dF1 |
С точки зрения ковариации, эти симметричные значения просто взаимно уничтожаются.
Поскольку же физик приблизительно равномерно измерял силы слева и справа, то в среднем все измерения взаимно уничтожились.
Вот как выглядит график произведений отклонений, в зависимости от координаты.
Если случайным образом набрать с него точек, то сумма значений в них будет приблизительно равна нулю. И, следовательно, будет равна нулю ковариация.
И чем больше точек мы возьмём, тем она ближе к нулю. Что наверняка будет убеждать физика, что тут нет никакой ошибки или случайности: чем больше измерений он производит, тем более очевидно, что корреляция — нулевая.
И это при том, что наличие связи между координатой и действующей силой видно невооружённым глазом.
Быть может, ошибка была в том, что физик измерял абсолютную величину силы? Быть может, стоило ему измерить силу с учётом направления, всё получилось бы правильно?
О да, в этом случае корреляция была бы не нулевой, а ранее упомянутыми −0,68. Ведь в этом случае произведения симметричных отклонений не уничтожали бы друг друга.
Только это всё равно был бы ошибочный результат. Просто вывод, сделанный по нему, случайно совпал бы с правильным.
Ведь предположим, что Ньютон действительно наврал, и тела, расположенные справа, притягиваются, но вот расположенные слева — отталкиваются. В этом случае, напротив, игнорирование направления силы дало бы ненулевую корреляцию, а вот его учёт — нулевую.
И в одном из двух вариантов по-прежнему можно было бы сделать вывод об отсутствии взаимосвязи при реальном её наличии.
Причём с правильным совпадал бы вывод, сделанный по тому методу, по которому в другом случае получался бы вывод, не совпадающий с правильным.
Таким образом, в рамках данного метода в обязательном порядке надо сделать выбор между вариантами, заранее зная правильный ответ, — иначе можно выбрать тот вариант, который приводит к ошибке.
То есть это сам метод ошибочен. С его помощью невозможно сделать правильный вывод, не зная его заранее.
Сбитый прицел номер два
Аналогичная история происходит и со вторым физиком: он измеряет процесс, в котором взаимно уничтожаются произведения отклонений от среднего, хотя сам процесс при этом вполне закономерен.
Я для примера взял колебания вокруг нуля, однако это только для наглядности: коэффициент корреляции зависит не от величины, а от её отклонения от среднего, поэтому «без разницы», где расположено это среднее.
Здесь мы тоже наблюдаем симметрию. И эта симметрия с неизбежностью приводит к тому, что на некотором отрезке — кратном двойному периоду колебаний — сумма произведений отклонений взаимно уничтожается. И фактически на корреляцию будет оказывать влияние только тот «хвостик», который останется после последнего обнуления.
Вот как для данного фрагмента будет вести себя корреляция — в зависимости от того момента, когда физик остановил измерения.
Поскольку момент начала и конца измерений зависит только от стечения обстоятельств, физик в реальности высчитывает случайное число, а вовсе не «надёжный показатель связи между явлениями».
Правда, тут выручает то, что одна из величин — время — неограниченно растёт с ростом количества измерений, а вторая величина — напряжение — ограничена определённым диапазоном. В результате, расположенное в знаменателе среднеквадратическое отклонение времени увеличивается до сколь угодно большой величины быстрее, а потому корреляция стремится к нулю с увеличением отрезка времени, на котором проводятся измерения.
Это позволяет уверенно «доказывать» независимость абсолютно любой ограниченной диапазоном величины от времени, а не просто диагностировать наличие или отсутствие связи, в зависимости от того, как звёзды встали.
Хотя, конечно, и тут есть шанс выбрать периодичность замеров, слегка некратную периодичности колебаний, и снова тщательно вычислить случайное число. Например, напряжение в сети колеблется со слегка плавающей частотой: 50 раз в секунду. Поэтому проведение измерений с интуитивно напрашивающейся частотой раз в секунду — серьёзная заявка на успех.
В общем, если физику повезёт, и он замерит много периодов колебаний, не попав при этом в нужную «слегка некратность», он обнаружит на них близкую к нулю корреляцию. После чего сделает ошибочный вывод, что связи между временем и напряжением нет.
Если не повезёт, то результат вообще будет случайным числом, и тут уже, разумеется, никакой ошибки не будет.
В любом случае, вывод ошибочен. Даже если он случайно совпадёт с правильным — ведь ошибочен сам метод его получения.
Но иллюзия о научном обнаружении наличия или отсутствия связи в обоих случаях вполне может сохраниться.
Hold your fire №1 and №2
Первые два примера демонстрируют штуку, которую надо помнить в обязательном порядке: введённая нами «мера взаимосвязи» не универсальна. Сделанные при её построении рассуждения относились только к линейным зависимостям одной величины от другой.
Грубо говоря, это работает только тогда, когда предполагается зависимость…
Если же зависимость иная, то, вообще говоря, коэффициент корреляции может оказаться произвольным.
Да-да, не нулевым, а произвольным.
Ведь даже при очень хорошем случае — при убывании одной величины при возрастании другой — первый физик уже получил странный результат. Ещё до того, как он начал пробовать помещать тело не только справа, но и слева, при наличии совершенно однозначной и непериодической зависимости, полученный им коэффициент корреляции уже заметно отличался от −1.
И дело тут не в погрешности измерений. Дело в том, что даже зависимость
достаточно нелинейна для коэффициента корреляции. Уже на ней результат опасно близок к «хм, возможно, на силу влияет что-то ещё». Да, это, конечно, не −0,1, но всё-таки −0,68 — это и не чистая минус единица. Всё выглядит так, будто бы тут не совсем детерминированная связь.
Так какие же заключения можно сделать, вычислив коэффициент корреляции?
Если она нулевая, значит ли это, что величины не связаны?
Два примера показывают, что нет, нельзя.
А если она ненулевая, значит ли это, что зависимость есть?
Второй пример показывает, что и это тоже совершенно не обязательно: ведь вполне возможно и даже весьма вероятно на, например, периодическом процессе получить случайное число, довольно существенно отличающееся от нуля.
Иными словами, исследователь откуда-то должен знать заранее, что тут либо линейная зависимость, либо вообще никакой, чтобы сделать более-менее правильный вывод.
Но откуда он может это знать до исследований? Только из других исследований. Где анализ делался другими методами. Например, основывался на вдумчивом разглядывании графиков или распределений, формированием на их основе гипотезы о функции, связывающей две величины, и последующей экспериментальной проверке того, что эта функция и правда именно такая, поскольку с её помощью удаётся предсказать значение второй величины, зная первую.
Но если это всё уже проделано, то зачем ему вообще считать корреляцию? У него же уже есть более надёжные результаты.
Может быть, коэффициент корреляции можно использовать как первое приближение? Как оценку связи навскидку?
Хороша же такая оценка, которая при весьма вероятных закономерностях даёт случайное число, и приводит, таким образом, к совершенно разным выводам — в зависимости от расположения звёзд.
То есть в сухом остатке оказывается, что единственное, что можно сделать при помощи корреляции — это вывод об отсутствии одной и той же линейной на всём отрезке взаимосвязи между величинами.
Именно об отсутствии — ведь даже о наличии такой взаимосвязи вывод сделать нельзя (см. «случайное число»).
И именно что линейной на всём отрезке, поскольку при фрагментарно линейной вполне возможно взаимное уничтожение произведений отклонений.
Причём натолкнуться на такое может совсем даже не только усомнившийся в законе всемирного тяготения физик. Ровно так же хлебнуть полную чашу горя может медик, решивший выяснить связь температуры тела пациента с самочувствием пациента. При нормальной температуре — 36,6 °C — самочувствие, видимо, наилучшее. При повышении температуры оно ухудшается. Однако и при понижении температуры оно тоже ухудшается…
Чувствуете схожесть ситуации с экспериментами первого физика? О да, и с корреляцией будет тоже: при симметричности оценок слева и справа от нормальной температуры корреляция окажется близкой к нулю. Из чего медик сможет заключить, что связи между температурой и самочувствием нет.
И ровно то же самое будет с лекарством, у которого есть оптимальная доза приёма: при этой дозе результаты будут наилучшими, но вот при меньшей и при большей они будут хуже, что тоже приведёт к чисто техническому занулению коэффициента корреляции.
И вы думаете, на этом проблемы с коэффициентом кончились?
Выстрел номер три: неубедительный экстрасенс
Однажды к группе заинтересованных в изучении паранормальных явлений пришёл человек, обладающий удивительной способностью — он абсолютно безошибочно умел угадывать выпавшее на кубиках.
Правда, по воле паранормальных сил эта способность у него была выражена в весьма странной форме: если кто-то собирался бросить четыре кубика, то Космос тут же шептал экстрасенсу сумму выпавшего на них в тридцатой степени. Увы, экстрасенс был безграмотен (он просто слушал голос Космоса), а потому извлекать корень тридцатой степени не умел.
Впрочем, паранормологи этого делать тоже не умели: ни извлекать корень тридцатой степени, ни возводить в тридцатую степень. Однако они предположили, что его предсказания всё равно должны коррелировать с суммой выпавшего на кубиках (которую они считать всё-таки умели) — ведь между числом и его тридцатой степенью имеется однозначная математическая связь.
Не поленившись, паранормологи провели 10 000 испытаний. Не было никаких сомнений в том, что такого вполне достаточно для исключения любых случайностей.
Но результат их разочаровал: предсказания экстрасенса имели корреляцию с суммой выпавшего на кубиках всего 0,2. Такой вшивой корреляции явно недостаточно, чтобы подтвердить экстрасенсорные способности. 0,5 ещё куда ни шло, но вот 0,2…
В результате экстрасенс был изгнан и высмеян.
Сбитый прицел номер три
Я специально придумал этот пример, чтобы развеять сомнения, будто бы «дефолт-корреляция» может не срабатывать только при попытках измерять связь времени и состояния, но вот для неких случайных событий она всегда подходит.
О нет. И данные паранормологи тому примером.
На самом деле они прогнали экстрасенса, который совершенно правильно угадал в 100% случаев. Да-да, он ни разу не ошибся.
Однако проведи они даже миллион испытаний, всё равно корреляция была бы всё столь же низкой. Ибо я не зря сказал о том, что корреляция более-менее корректно отображает только линейную связь между величинами.
Здесь же наблюдался аналог того, что произошло с первым физиком, только в гипертрофированной форме: корреляция была не просто несколько подозрительной, а существенно ниже порогового уровня достоверности.
Но это ещё не предел. Кидай они шесть кубиков, корреляция стала бы 0,15.
Случайно угадать все сто тысяч раз тридцатую степень суммы выпавшего на четырёх кубиках столь нереально, что такое вряд ли можно рассматривать всерьёз, но корреляция при этом утверждает, что экстрасенс как бы не угадывал.
Как бы утверждает.
Hold your fire №3
На самом же деле, совершенно не зря в справочниках пишут, что всё это осмыслено только при гауссовом распределении случайных величин. И зря так многие это либо не читают, либо игнорируют в своей практической деятельности.
«Гауссово» распределение подразумевает концентрацию основной массы результатов измерений вокруг некоторой величины (того самого «матожидания» или «среднего»). Причём чем дальше от неё случай, тем меньше раз мы его должны встречать.
Имеющаяся же в формуле корреляции σ — среднеквадратическое отклонение — характеризует в этом случае «ширину» данного колокола.
Негауссовость одного или обоих распределений — залог получения очень низкой корреляции даже при очевидной прямой взаимосвязи величин.
В данном случае сумма выпавшего на четырёх кубиках имела распределение, близкое к гауссову, но вот возведение результата в тридцатую степень убило даже намёк на гауссовость, что не замедлило сказаться на результате.
И не помогли даже 10 000 испытаний.
В реальных же исследованиях испытаний вполне может быть штук 100, например. И негауссовость распределения там может быть существенно менее экстремальной, но всё равно пагубно сказаться на результатах.
Выстрел номер четыре: убедительный экстрасенс
К тем же самым паранормологам через некоторое время пришёл ещё один посетитель. Он тоже имел паранормальную связь с кубиками, но его метод был проще: он бросал один кубик, а потом предлагал экспериментатору бросить второй. Благодаря тому, что в его руках была заключена особая магия, первый бросок кубика мистическим образом влиял на всю ситуацию в целом.
О нет, выпавшее на втором кубике он не брался предсказать, однако утверждал, что первый бросок окажет очень сильное влияние на второй бросок, суть коего влияния он, впрочем, не брался объяснить. Но предлагал просто взять и посчитать корреляцию выпавшего на первом кубике с суммой выпавшего на двух кубиках.
Первые сто испытаний повергли паранормологов в шок и трепет: корреляция действительно оказывалась весьма нехилой: 0,75.
Правда, они всё-таки усомнились, не было ли тут простого везения. Однако, проделав привычные для них 10 000 испытаний, они с удивлением отметили, что корреляция упала, но не так, чтобы очень сильно. Всё-таки 0,7 — это весьма неплохо. Согласно всем справочникам, это уже тянет на термин «высокая корреляция».
Определённо у этого экстрасенса был талант — оставалось только понять, каким способом из его предсказаний можно извлекать сведения о том, что выпадет на втором кубике…
Сбитый прицел номер четыре
…и правильный ответ: никаким. Нет никакого способа предсказать, что именно там выпадет. И даже, внезапно, нет никакого способа предсказать сумму.
Да-да, корреляция — высокая, однако всё, что можно сказать про сумму, это то, что она будет лежать на отрезке от выпавшего на первом кубике плюс один до выпавшего на первом кубике плюс шесть. Что было вполне понятно и безо всяких экстрасенсов.
Но никаких случайных совпадений — корреляция, правда, получится примерно вот такая.
Hold your fire №4
Разумеется, выпавшее на первом кубике влияет на сумму, поскольку оно входит туда как слагаемое. Однако корреляция показала всего лишь линейную связь первого со вторым. Выпавшего на первом кубике и случайной величины, полученной прибавлением к уже выпавшему второй случайной величины.
Но сколь же легко очароваться большим значением коэффициента и сделать вывод, который вовсе из него не следует: первый кубик как-то влияет на второй. Или даже, наоборот: ещё не брошенный второй кубик как-то влияет на первый.
Или хотя бы, что из результата броска первого кубика можно узнать что-то ещё, кроме и так очевидного.
Ах, сколько же раз такого рода эксперименты приводят к восторженным публикациям — причём не только в обычной прессе, но даже и во вполне научной.
Временами ничто не отделяет добросовестного биолога от того, чтобы путём сотен замеров открыть удивительный факт: все муравьи планеты строят муравейники, длина окружности основания которых примерно втрое больше диаметра этого основания.
Кажется, будто бы выполнение некого «научного» ритуала обязательно должно давать правильные результаты, даже если при этом не понимать сути этого ритуала, оправдывая фразами вида «я же паранормолог, а не математик».
Математика как бы работает сама. Ведь она же математика. Математика не обманывает.
И да, математика не обманывает — обманывают её трактовки.
Выстрел номер пять: хороший способ вызвать дождь
Как-то раз антрополог наблюдал за обычным городским жителем (конечно же, с его, этого жителя, согласия). И через некоторое время он заметил удивительную закономерность: если этот житель брал с собой зонт, то в этот день шёл дождь.
Конечно, так случалось не каждый раз: иногда объект наблюдения брал зонт, но дождь не шёл, иногда не брал, но дождь всё равно шёл, — однако слишком часто наличие зонта с наличием дождя и отсутствие зонта с отсутствием дождя случались одновременно.
Антрополог, как настоящий учёный, конечно, не доверился таким «навскидочным» оценкам, а вместо этого стал каждый день тщательно протоколировать свои наблюдения.
Через год он приписал событиям «взят зонт» и «был дождь» число 1, событиям «не взял зонт» и «не было дождя» число 0, и посчитал корреляцию по своим протоколам.
Корреляция была очень высокой: 0,95. Эти два события однозначно были связаны.
Гордый собой антрополог написал статью «Как вызывать дождь», в которой убедительно — по трём с половиной сотням наблюдений — доказывал, что именно вот этот житель управляет дождями по месту своего проживания. При помощи ношения зонта.
К сожалению, эту статью отказались печатать, ссылаясь на то, что как-то это всё неубедительно звучит.
Подумав некоторое время, антрополог пришёл к мысли, что наверно всё наоборот: это дождь управляет взятием зонта этим жителем. Просто данный гражданин способен видеть будущий дождь своим внутренним зрением. И, увидев будущий дождь, берёт с собой зонт — даже если на улице сейчас пока ещё нет никакого дождя. Если, конечно, не забыл с утра внутренним зрением посмотреть в будущее.
Ведь однозначно, столь высокая корреляция не может быть результатом случайности.
К сожалению, эту статью в журнал тоже не взяли, поскольку тамошние скептики не поверили в реальности внутреннего футуристического зрения, несмотря на столь яркие доказательства существования оного.
Однако антрополог не отчаялся. Подумав ещё, он сделал финальный вывод: существует мистическая незримая сила, которая вызывает дожди и одновременно с тем побуждает отдельных граждан брать с собой зонт. Поиском этой силы срочно следует заняться, поскольку она перевернёт все представления о мироздании.
В этот раз Фортуна улыбнулась антропологу: под это дело был создан специальный институт и много лет всевозможные учёные мужи пытались найти эту силу, под чутким руководством данного антрополога, которого хоть и не сделали директором, но всё-таки сделали замом. Вот так добро победило зло.
Сбитый прицел номер пять
Если коэффициент корреляции показал реальную связь одной величины с другой (а не случайное число, как это было со вторым физиком), это всё равно никак не доказывает, что одно явление вызывается другим. Даже если этим способом с самого начала хотели доказать наличие таковой связи, что многим почему-то кажется гарантией верности выводов.
Вполне может быть так, что первое явление не вызывается вторым, и при этом даже второе явление не вызывается первым.
В этих случаях говорят: «может быть, что есть некое третье явление, вызывающее оба два», — но и это в ряде случаев скорее вводит в заблуждение, нежели помогает. Ведь правда может быть такое явление, но на этом всё равно возможные варианты не кончаются.
И уж, тем более, никто не гарантирует, что именно то «третье явление», которое предположил кто-то там, и есть то самое искомое.
Улыбнувшаяся антропологу Фортуна, в это время со спины показывала человечеству средний палец, ибо не было никакой внешней мистической силы. Гражданин просто утром смотрел прогноз погоды, и, если там обещался дождь, брал с собой зонт.
Может показаться, что, ну ладно, пусть не мистическая сила, но всё-таки третье явление, вызывающее первые два, тут есть.
Предположим, есть. Но какое?
Прогноз погоды вызывает дождь?
Или ещё не случившийся дождь вызывает прогноз?
Ну Ok, не сам дождь, а атмосферное давление, скорость и направление ветра, наличие водоёмов и т. п. вызывают и дождь, и прогноз?
Однако мы могли бы убедиться, что, вообще говоря, данного жителя побуждают взять зонт сами опубликованные прогнозы, а вовсе не физические явления. Для этого надо было бы просто попросить тот источник, в котором он эти прогнозы читает, некоторое время публиковать неправильные прогнозы. И тем самым воочию узреть, что зонт берётся, если в прогнозе написано, что будет дождь, а вовсе не если какие-то физические параметры указывают на его высокую вероятность.
То есть некого одного «третьего явления», вызывающие первые два, не существует. Вместо этого есть целый набор явлений, состоящих друг с другом в весьма непростых отношениях.
Долгое время некая служба делала прогнозы, ориентируясь на ряд параметров. Их метод правда работал, поэтому их прогнозам начали доверять. Настолько, что некоторые даже стали игнорировать положение вещей, опираясь только на сказанное этой службой. И теперь слова этой службы побуждают этих людей брать зонт. И они достаточно долгое время брали бы его, даже если бы данные метеорологи поголовно сошли бы с ума и начали бы строить прогнозы на основе рисунка кофейной гущи.
Хотя в прошлом связь между явлениями через общую «третью силу» была, сейчас её уже нет. Но по инерции всё продолжает работать.
Выстрел номер шесть — прибытие автобуса
Один психолог наблюдал за ещё одним гражданином. И выяснил, что каждый раз, когда тот гражданин приходит на остановку, не позже, чем через пять минут, к ней приезжает автобус. Причём всё время один и тот же.
Естественно, предположение о том, что приход на остановку именно этого человека вызывает приезд этого автобуса, психолог сразу же отверг, как слишком абсурдное.
Но его заинтересовало, может ли быть верно обратное: что приезд этого автобуса вызывает приход этого человека на остановку? Это выглядело очень правдоподобным.
С согласия этого человека психолог начал за ним наблюдать. Оказалось, что этот человек каждый будний день встаёт в одно и то же время, за полчаса собирается и завтракает, а потом идёт на остановку.
Все введённые психологом способы измерить корреляцию данных событий указывали на одно и то же: связь тут очень жёсткая. Совершенно точно приезд этого автобуса вызывает приход человека на остановку. Точнее, не сам приезд, а знание о приезде.
Именно под приезд данного автобуса (время прибытия которого этот человек, видимо, вычислил на стихийной серии экспериментов) данный человек подстроил свой распорядок дня, учтя, разумеется, время на «успеть собраться».
Это вам не дождь, вызывающий зонт, тут всё тип-топ. Вон, даже читатели этой статьи сейчас думают: «А здесь-то что не так с выводами?!»
Сбитый прицел номер шесть
А с выводами здесь тоже не так всё.
Все способы подсчёта корреляции действительно могут показать однозначную линейную взаимосвязь. Совершенно честно. Без ошибок. И даже другие, не дефолтные, коэффициенты корреляции её покажут. И всё может казаться вообще очевидным. Но и в этом случае вполне возможны неверные выводы.
Дело в том, что описанный гражданин не вычислял время прибытия автобуса. И никогда не видел расписания. И не подстраивал под него свой график.
Он по городскому навигатору узнал время поездки от дома до работы, а потом поставил будильник на красивое круглое число, позволяющее ему успевать на работу. Ну, на девять утра, например.
Полчаса ему хватало на сборы, после этого он выходил на улицу, и — ну надо же — именно в это время приходил данный автобус. Да, вот так вот удачно совпало расписание.
Впрочем, там, в этом расписании, автобусы вообще ходили раз в пять минут, поэтому не совпасть оно просто не могло: округления времени будильника до красивого числа с запасом хватало на покрытие даже максимального ожидания — пяти минут. Приходи этот автобус на две минуты раньше, ну так этот человек ездил бы на следующем. И точно так же каждый раз успевал бы вовремя.
Да, можно понатягивать сову на глобус и выстроить какую-то отмазку про «третье явление». Ну, там, «третьим явлением в данном случае оказывается всё человеческое общество, где людей на работу развозит общественный транспорт, а потому какие-то работники автобусного парка составили правильное расписание с достаточно частым движением автобусов и так далее». Однако всё это совершенно не помогает понять то самое, что хотел понять психолог: почему этот человек так делает? Что его побуждает поступать именно так? Какая сила?
И в данном случае реальной «силой» оказалось «я попробовал почти наугад, оно сработало, поэтому я и дальше так делал».
Сравните это с нарисованной психологом картиной, согласно которой этот человек, как стихийный, но добросовестный исследователь, вычислял расписание автобуса, рассчитывал свои действия, составлял план… в общем, явно был кем-то не тем, кем оказался на самом деле.
И вся эта стройная теория отлично подтверждалась всеми возможными корреляциями и даже, вроде бы, правдоподобными рассуждениями.
Возможно даже, услышав о реальном положении вещей непосредственно от самого наблюдаемого, психолог всё равно решил бы сохранить свой вариант описания, добавив модификацию «он всё равно планирует, только подсознательно». И даже, не исключено, построил бы целую теорию подсознательного планирования, столь же хорошо подкреплённую высокими корреляциями, как и его первоначальный вывод.
Hold your fire №5 and №6
Мораль последних двух историй в том, что никакой статистический показатель сам по себе не может подтвердить нравящуюся вам теорию. Теории подтверждаются только совокупностью показателей в рамках правильно построенной серии экспериментов.
Серии, а не одного эксперимента — пусть даже с большим числом данных.
Какими бы ни оказались все подсчитанные вами статистические показатели, они лишь дают вам некоторую почву для размышлений и предположений. Для гипотез, а не для «теорий», о которых многие любят на первом же этапе заявлять.
Причём, что обидно, «теориями» результаты своих первых экспериментов называют и даже иногда считают не только какие-то безграмотные обыватели, но и некоторые учёные тоже.
Первый эксперимент — первый. По его результатам вам надо сформулировать гипотезу и в следующих экспериментах проверять, правда ли она даёт сбывающиеся прогнозы.
Намеренное в первом эксперименте — это ведь данные, на которых строится гипотеза. На этих данных нельзя проверить, правда ли гипотеза работает: ведь именно на них вы её построили — ясен пень, на них она будет работать. Так будет с любой гипотезой — даже с неверной.
При сбывшихся же прогнозах на новых экспериментах уже правда появится «статистическое доказательство»: ведь предположенная вами зависимость одной величины от другой правда позволяет делать прогнозы на тех данных, которые мы на момент её введения в качестве гипотезы ещё не получили. Вот это доказывает реальность связи, а не просто высокая корреляция.
Более того, мало повторить тот же эксперимент и убедиться, что и второй раз сработало. Сработало или нет, но надо всё это проверить и в других условиях тоже. Ведь реальная теория не может описывать один частный случай — она должна распространяться на довольно обширную область возможных вариантов.
Но и на этом всё не кончается: даже если эта гипотеза правда даёт сбывающиеся прогнозы на широкой области, всё равно на следующих экспериментах надо ещё проверить, что все альтернативные гипотезы на них не срабатывают. В ином случае окажется, что вы доказали не верность именно вашей гипотезы, а лишь верность довольно обширного множества гипотез, включая вашу.
Заметьте, в пунктах пять и шесть исследователи имели дело именно с таким случаем: полученные ими данные укладывались в несколько совершенно разных гипотез. И для окончательного вывода исследователям следовало экспериментально доказать, что в других случаях одна из гипотез срабатывает, а все остальные — нет. И именно по этой причине она стала бы наиболее вероятным объяснением наблюдаемого и заслужила бы звания «теории». А без этого она не «теория», но «одна из возможных гипотез».
Hold your fire now
Собственно, можно догадаться, какие эмоции я испытываю, читая очередную статью, где исследователи замерили две величины, посчитали корреляцию между ними и уже называют это «открытием» и «построением новой теории». О нет, на данном этапе вы ещё не сделали открытие. Вы получили какой-то намёк и первую порцию данных, которые потом, если вы не бросите это занятие и будете ставить корректные серии экспериментов с корректным же анализом результатов, возможно, приведут к открытию.
Увы, сейчас вся мировая наука медленно, но верно, движется в направлении безудержной генерации «теорий» на ровном месте, что в основном провоцируется специфическим подходом к оценке работы учёного.
Считается, что учёный отчитывается за свою работу строго публикациями в журналах. И что эти публикации должны следовать с определённой плотностью, иначе а-я-яй, плохо работал. При этом журналы имеют тенденцию публиковать те работы, где заявлено о «прорывах», «успехах» и «новых теориях», а вовсе не о «проверили — не работает»
Хотя это, повторюсь, ключевой момент доказательства верности гипотез: на большинстве экспериментов как раз и должно не работать — только тогда единственное оставшееся объяснение получит право называться «теорией».
И даже статьи, где измерено что-то полезное, зачастую получают низкий приоритет, если в них не содержится заявлений или хотя бы намёков на тему «мы с первой попытки поняли, как всё устроено».
Естественно, в данном эволюционном процессе преимущество получает стратегия высасывания «открытий» из пальца. Что фактически приводит к отсеву добросовестных учёных в пользу недобросовестных, а также склоняет всех учёных к подтасовке результатов исследований и фабрикации недостоверных выводов.
Метод незатейлив: взяли как можно больше данных, посчитали попарные корреляции всего со всем, нашли ту, которая — пусть даже случайно — «высокая», приписали к ней тот вариант объяснения, который первым пришёл в голову или просто понравился, и вот уже публикация об «открытии».
Даже странно, что всё ещё так мало статей, создаваемых на основании данных с сайта «Ложные корреляции». Давно уже пора построить стройную теорию о том, почему количество выпущенных за год фильмов с Николасом Кейджем так тесно связано с количеством утонувших в этом году в бассейне.
Тут, вон, не только корреляция 66%, но и даже сходство в графиках видно невооружённым глазом.
Кто-то обязательно должен объяснить всё это.
И тем более, объяснить, почему количество потребляемого на душу населения маргарина на 99,26% коррелирует с интенсивностью разводов в Майне.