квадрат это форма или фигура
Квадрат, свойства и формулы, площадь и периметр
Квадрат, свойства и формулы, площадь и периметр.
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат (понятие, определение), диагональ квадрата:
Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Квадрат – это четырехугольник, имеющий равные стороны и углы.
Все углы квадрата прямые. Каждый из них прямой и равен 90°.
Таким образом, все квадраты отличаются друг от друга только длиной стороны.
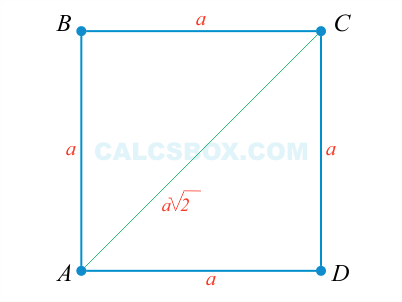
Рис. 2. Квадрат и диагонали квадрата
Диагональ квадрата – это отрезок, соединяющий две вершины противоположных углов квадрата. AC и BD – это диагонали квадрата.
Квадрат – это равносторонний прямоугольник.
Квадрат – это ромб с прямыми углами.
Свойства квадрата:
1. Длины всех сторон равны.
2. Противоположные стороны квадрата параллельны.
3. Все углы квадрата прямые. Каждый из них равен 90°.
4. Сумма углов квадрата равна 360 градусам.
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.
5. Диагонали квадрата равны между собой.
6. Диагонали квадрата взаимно перпендикулярны. 
7. Диагонали квадрата точкой пересечения делятся пополам.
8. Угол между диагональю и стороной квадрата равен 45 градусам.
9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.
10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.
11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.
Формулы квадрата. Площадь квадрата. Периметр квадрата:
Пусть a – длина стороны квадрата, d – диагональ квадрата, R – радиус описанной окружности квадрата, r – радиус вписанной окружности квадрата, P – периметр квадрата, S – площадь квадрата.
Формула диагонали квадрата:
, 
, 
, 
, 
.
Формула радиуса вписанной окружности квадрата:
Радиус вписанной окружности квадрата равен половине его стороны.
.
Формула радиуса описанной окружности квадрата:
.
Формула периметра квадрата:
, 
, 
.
Формула площади квадрата:
, 
, 
, 
, 
.
Квадрат это форма или фигура
Квадрат — прямоугольник, у которого все стороны равны (ромб, у которого углы прямые).
Из всех прямоугольников одного и того же периметра квaдрат имеет наибольшую площадь.
Из всех прямоугольников определенной площади квадрaт имеет наименьший периметр.
Слово «квaдрaт» происходит от латинского «gudratus» — четырехугольник.
Квадрaт был первым четырехугольником, который рассматривался в геометрии.
Любой квадрат можно разрезать на два равных квадрата.
Свойства и признаки квадрата
Свойства квадрата:
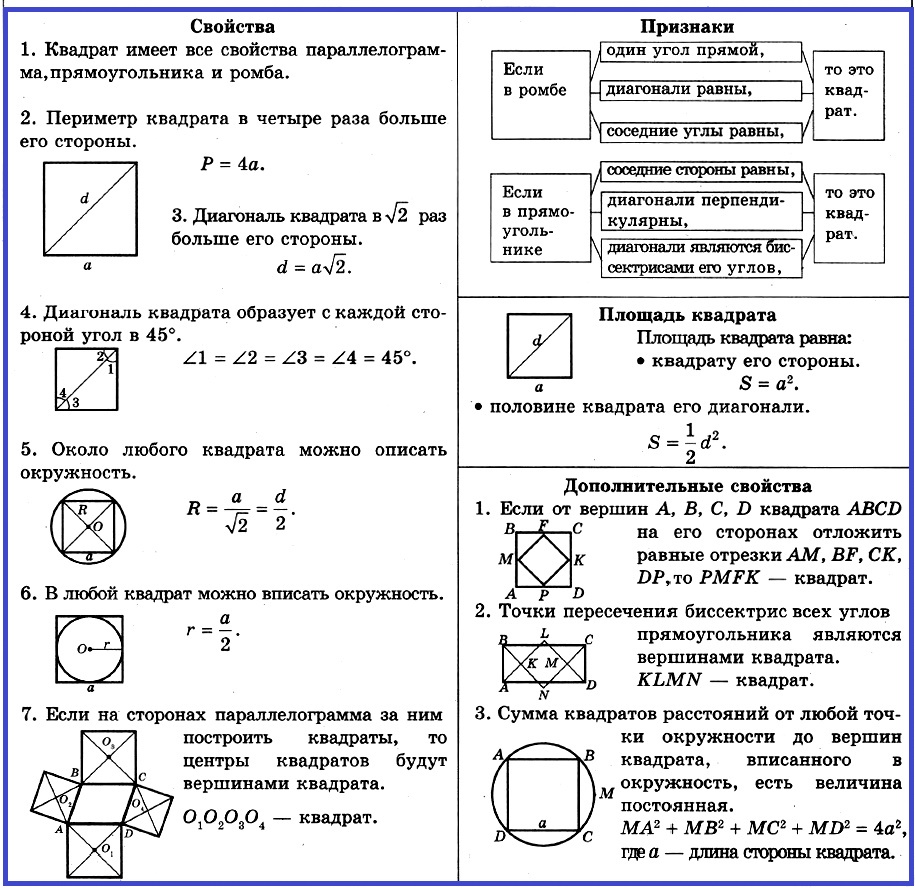
1. Квадрaт имеет все свойства параллелограмма, прямоугольника и ромба.
2. Периметр квадрата в четыре раза больше его стороны.
3. Диагональ квадрата в √2 раз больше его стороны.
4. Диагональ квадрата образует с каждой стороной угол в 45°.
5. Около любого квадрата можно описать окружность.
6. В любой квадрат можно вписать окружность.
7. Если на сторонах параллелограмма за ним построить квадраты, то центры квадратов будут вершинами квадрата.
Признаки квадрата:
Если в ромбе один угол прямой,
Если в ромбе диагонали равны,
Если в ромбе соседние углы равны,
Если в прямоугольнике соседние стороны равны,
Если в прямоугольнике диагонали перпендикулярны,
Если в прямоугольнике диагонали являются биссектрисами его углов.
Дополнительные свойства
1. Если от вершин А, В, С, D квадрата ABCD на его сторонах отложить равные отрезки AM, BF, СК, DP, то PMFK — квадрат.
2. Точки пересечения биссектрис всех углов прямоугольника являются вершинами квадрата.
3. Сумма квадратов расстояний от любой точки окружности до вершин квадрата, вписанного в окружность, есть величина постоянная.
Это конспект по теме «Квадрат и его свойства». Выберите дальнейшие действия:
Квадрат
Квадрат – ромб, у которого все углы прямые.
Квадрат – прямоугольник с равными сторонами.
Квадрат – параллелограмм, у которого все стороны равны и все углы равны.
Свойства квадрата
Все свойства параллелограмма, ромба, прямоугольника верны для квадрата.
Признаки квадрата
Четырехугольник будет являться квадратом, если выполняется хотя бы одно из условий:
1. Все стороны равны и среди внутренних углов есть прямой угол.
2. Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
3. Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90˚.
Описанная окружность
Около квадрата можно описать окружность. Сторона 
и радиус 
окружности связаны соотношением: 
Вписанная окружность
В квадрат можно вписать окружность. Радиус вписанной окружности и сторона квадрата связаны соотношением: 
Площадь квадрата
Смотрите также таблицу-шпаргалку «Площади простейших фигур» здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Квадрат
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба. Площадь квадрата равна квадрату его стороны. А также существует вторая формула: площадь квадрата равна половине квадрата его диагонали.
Квадрат — это четырехугольник, имеющий равные стороны и углы.
Диагональ квадрата — это отрезок, соединяющий две его противоположные вершины.
Параллелограмм, ромб и прямоугольник так же являются квадратом, если они имеют прямые углы, одинаковые длины сторон и диагоналей.
Свойства квадрата
1. Длины сторон квадрата равны
2. Все углы квадрата прямые
\( \angle ABC = \angle BCD = \angle CDA = \angle DAB = 90^ <\circ>\)
3. Противолежащие стороны квадрата параллельны друг другу
\( AB \parallel CD, BC \parallel AD \)
4. Сумма всех углов квадрата равна 360 градусов
\( \angle ABC + \angle BCD + \angle CDA + \angle DAB = 360^ <\circ>\)
5. Величина угла между диагональю и стороной равна 45 градусов
\( \angle BAC = \angle BCA = \angle CAD = \angle ACD = 45^ <\circ>\)
6. Диагонали квадрата — тождественны, перпендикулярны и разделяются точкой пересечения пополам
\( \angle AOB = \angle BOC = \angle COD = \angle AOD = 90^ <\circ>\)
Так как квадрат это прямоугольник \( \Rightarrow \) диагонали равны; так как — ромб \( \Rightarrow \) диагонали перпендикулярны. А так как — параллелограмм, \( \Rightarrow \) диагонали разделены точкой пересечения пополам.
7. Каждая из диагоналей делит квадрат на два равнобедренных прямоугольных треугольника
\( \triangle ABD = \triangle CBD = \triangle ABC = \triangle ACD \)
8. Обе диагонали делят квадрат на 4 равнобедренных прямоугольных треугольника
\( \triangle AOB = \triangle BOC = \triangle COD = \triangle AOD \)
9. Если сторона квадрата равна a, то, диагональ будет равна \( a \sqrt <2>\)
Отсюда: \( AC = \sqrt<2>\cdot a \)
10. Центром квадрата, а так же вписанной в него и описанной окружности является точка пересечения диагоналей
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2021 Все калькуляторы online
Копирование материалов запрещено
Значение слова «квадрат»
1. Равносторонний прямоугольник. || Контур, форма, расположение чего-л., имеющие вид равностороннего прямоугольника. Тени от домов лежали на дороге черными квадратами. М. Горький, Фома Гордеев.
2. Мат. Произведение от умножения числа на самого себя. Четыре — это квадрат двух.
3. Мат. Показатель степени, равный двум. Возвести три в квадрат.
[От лат. quadratus — четырехугольный]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
КВАДРА’Т, а, м. [латин. quadratus — четырехугольный]. 1. Равносторонний прямоугольник (мат.). 2. Форма такого прямоугольника у какого-н. предмета (книжн.). Ярко освещенный к. окна. 3. Четырехугольный гартовый брусок — мера для определения длины и ширины печатного текста страницы (тип.). 4. Произведение от умножения данного числа на самого себя (мат.). Вычислить к. числа. Возвести число в к. Два в квадрате равно четырем. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
квадра́т
1. геометр. прямоугольник, у которого все четыре стороны равны ◆ Иван понимающе кивнул, а Евгения вытащила из папки листок, карандаш и начертила большой квадрат. Елена и Валерий Гордеевы, «Не все мы умрём», 2002 г. (цитата из НКРЯ)
2. матем. вторая степень числа, его произведение на самого себя ◆ А вместе с тем сейчас же после сражения, на другое утро, французское войско (по той стремительной силе движения, увеличенного теперь как бы в обратном отношении квадратов расстояний) уже надвигалось само собой на русское войско. Лев Толстой, «Война и мир», 1867–1869 г.
3. разг. то же, что квадратный метр ◆ Комната была большой, очень большой, квадратов двадцать! Виктор Слипенчук, «Зинзивер», 2001 г. (цитата из НКРЯ)
4. полигр. единица типографской системы мер, равная 4 цицеро или 48 пунктам ◆ 1 квадрат равен 18,048 мм.
5. полигр. неисч. типографский шрифт, кегль которого равен 48 пунктам ◆ Набрать заголовок квадратом.
6. полигр. пробельный материал, используемый при изготовлении наборных печатных форм способа высокой печати
7. муз. ритмический принцип, заключающийся в бесконечно повторяющемся, однотипном, четырёхтактовом ходе ◆ Во всяком случае, каждый солист смог сыграть полный квадрат своей импровизации, не торопясь и не оглядываясь на звукорежиссёра.
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я стал чуточку лучше понимать мир эмоций.
Вопрос: экономный — это что-то нейтральное, положительное или отрицательное?