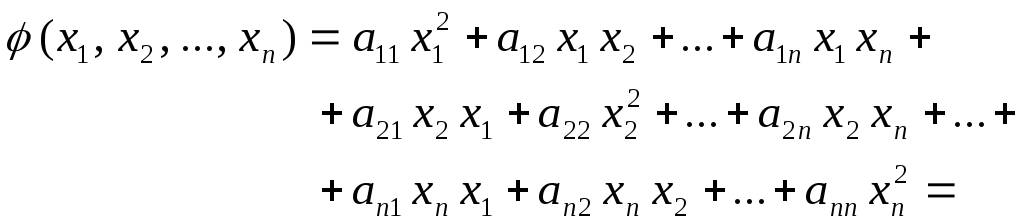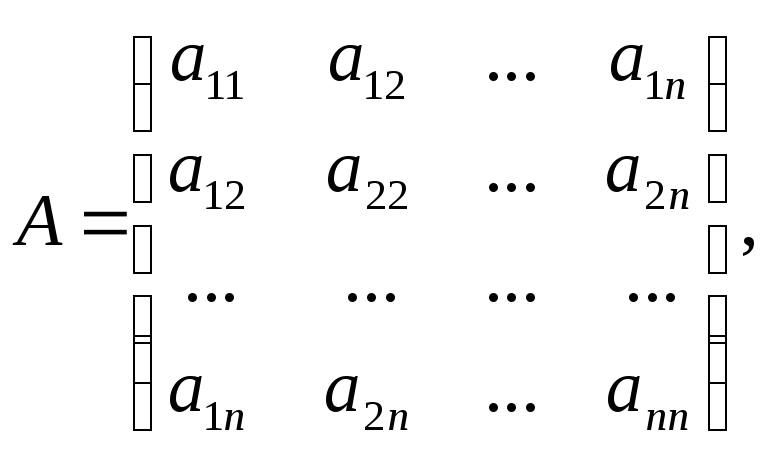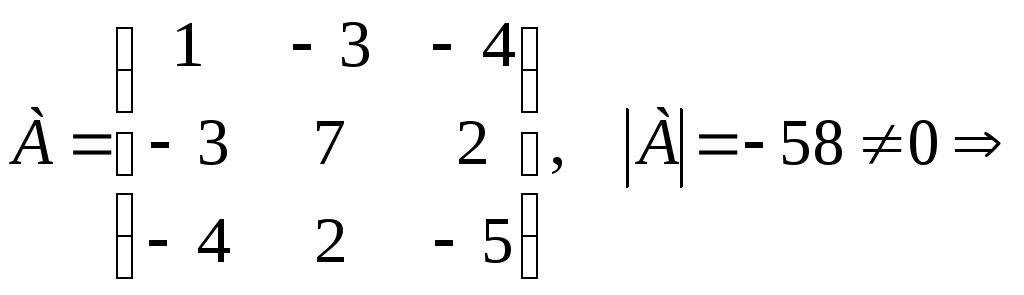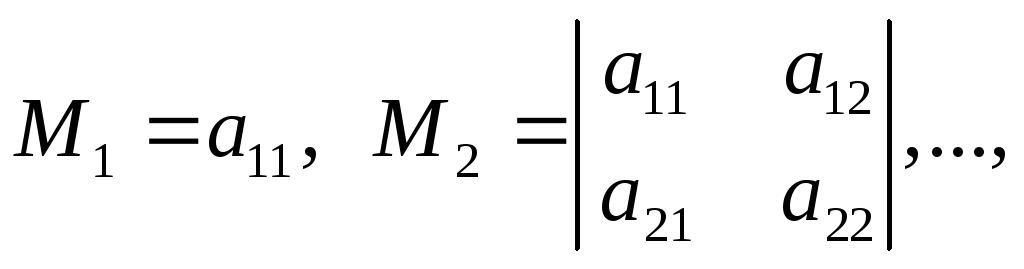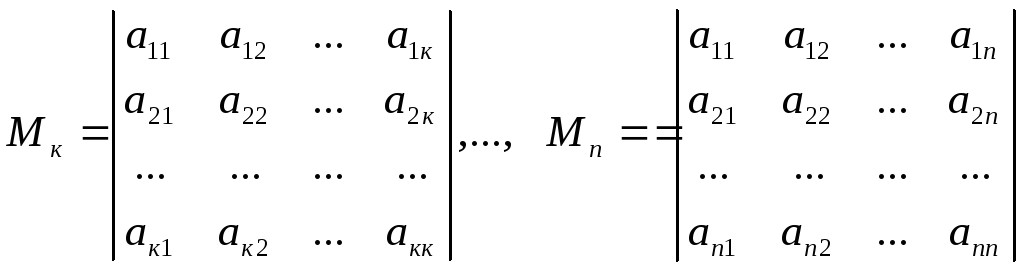квадратичная форма u соответствующая матрице a положительно определена называется
Положительно определенные квадратичные формы
Определение. Квадратичная форма называется положительно определенной, если все ее значения при вещественных значениях переменных, не равных одновременно нулю, положительны. Очевидно, что квадратичная форма 
Определение. Квадратичная форма называется отрицательно определенной, если все ее значения отрицательны, за исключением ненулевого значения при ненулевых значениях переменных.
Определение. Квадратичная форма называется положительно (отрицательно) полуопределенной, если она не принимает отрицательных (положительных) значений.
Квадратичные формы, принимающие как положительные, так и отрицательные значения, называются неопределенными.
При n=1 квадратичная форма 



Теорема (критерий Сильвестра положительной определенности квадратичной формы). Для того, чтобы квадратичная форма
была положительно определена, необходимо и достаточно выполнение условий:

Доказательство. Используем индукцию по числу переменных, входящих в 




1. Доказательство необходимости. Пусть
положительно определена. Тогда квадратичная форма
будет положительно определенной, так как если 

По предположению индукции все главные миноры формы 

Остается доказать, что 
Положительно определенная квадратичная форма 

Квадратичной форме 
с определителем 
Линейное преобразование, заданное невырожденной матрицей В, преобразует матрицу С квадратичной формы в матрицу 


2. Доказательство достаточности. Предположим, что все главные миноры квадратичной формы положительны: 
Докажем, что квадратичная форма 






где 
Осуществляя замену переменных 

Определитель матрицы этой квадратичной формы равен 



Для того чтобы квадратичная форма 
была положительно определенной, а значит, чтобы все главные миноры матрицы
были положительны. Но это означает, что
т.е. что знаки главных миноров матрицы C чередуются, начиная со знака минус.
Пример. Вычислить, является ли квадратичная форма положительно (отрицательно) определенной или неопределенной.
а) 
Решение. Матрица квадратичной формы 

Вычислим главные миноры матрицы С:
Квадратичная форма положительно определена.
б) 
Решение. Вычислим главные миноры матрицы
Квадратичная форма является неопределенной.
В заключение сформулируем следующую теорему.
Теорема (закон инерции квадратичных форм). Число положительных и число отрицательных квадратов в нормальном виде, к которому приводится квадратичная форма невырожденными линейными преобразованиями, не зависит от выбора этих преобразований.
7.5. Задания для самостоятельной работы по главе 7
7.1. Доказать, что если квадратичная форма с матрицей А положительно определена, то и квадратичная форма с обратной матрицей 
7.2. Найти нормальный вид в области вещественных чисел

7.3. Найти нормальный вид в области вещественных чисел

7.4. Найти нормальный вид в области вещественных чисел

7.5. Найти нормальный вид в области вещественных чисел

7.6. Найти нормальный вид в области вещественных чисел
7.7. Привести квадратичную форму к каноническому виду с целыми коэффициентами

7.8. Привести квадратичную форму к каноническому виду с целыми коэффициентами

7.9. Привести квадратичную форму к каноническому виду с целыми коэффициентами

7.10. Доказать, что в положительно определенной форме все коэффициенты при квадратах неизвестных положительны и что это условие не является достаточным для положительной определенности формы.
7.11. Выяснить, какие из форм эквивалентны между собой в области вещественных чисел
7.12. Выяснить, какие из форм эквивалентны между собой в области вещественных чисел
7.13. Найти все значения параметра 
7.14. Найти все значения параметра 
7.15. Найти все значения параметра 
Математический портал
Nav view search
Navigation
Search
Квадратичные формы. Матрица квадратичной формы. Положительно определенные квадратичные формы, критерий Сильвестра.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Примеры.
Решение.
Ответ: положительно определенная.
Решение.
Ответ: отрицательно определенная.
4.223.$2x_4^2+x_1x_2+x_1x_3-2x_2x_3+2x_2x_4.$
Решение.
Следовательно, квадратичная форма не является ни положительно, ни отрицательно определенной.
Ответ: общего вида.
Домашнее задание.
4.220.$x_1^2-15x_2^2+4x_1x_2-2x_1x_3+6x_2x_3.$
4.221.$12x_1x_2-12x_1x_3+6x_2x_3-11x_1^2-6x_2^2-6x_3^2.$
Ответ: отрицательно определенная.
4.222.$9x_1^2+6x_2^2+6x_3^2+12x_1x_2-10x_1x_3-2x_2x_3.$
Ответ: положительно определенная.
4.224.$x_1^2+4x_2^2+4x_3^2+8x_4^2+8x^2x_4.$
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Квадратичная форма
Определение
Пример. Функции
Оказывается, что в любой квадратичной форме можно так сгруппировать входящие в нее одночлены, что в результате получится ее (эквивалентное) представление в виде суммы квадратов.
Пример.
Метод Лагранжа приведения квадратичной формы к каноническому виду
Существует универсальный алгоритм, приводящий произвольную квадратичную форму к каноническому виду.
Пример. Привести форму
Пример. Привести форму
Пример. Привести форму
Матричная форма записи квадратичной формы
Задача. Установить правило формирования коэффициентов канонического вида квадратичной формы, получающегося применением метода Лагранжа.
Пример. Для приведенной выше квадратичной формы
| $ x_ <1>$ | $ x_ <2>$ | $ x_ <3>$ | |
|---|---|---|---|
| $ x_ <1>$ | $ f_ <11>$ | $ \frac<1><2>f_ <12>$ | $ \frac<1><2>f_ <13>$ |
| $ x_ <2>$ | $ \frac<1><2>f_ <12>$ | $ f_ <22>$ | $ \frac<1><2>f_ <23>$ |
| $ x_ <3>$ | $ \frac<1><2>f_ <13>$ | $ \frac<1><2>f_ <23>$ | $ f_ <33>$ |
Пример. Для
Вернемся к примерам предыдущего пункта, перепишем их на матричном языке.
Пример. Для формы
Поставленную в начале пункта задачу об установлении структуры канонического вида квадратичной формы попытаемся решить сначала для случая когда замену переменных можно подобрать именно в треугольном виде.
Метод Лагранжа и метод Гаусса
Пример. Рассмотрим матрицу квадратичной формы
Формула Якоби
Закон инерции для квадратичных форм
Для заданной квадратичной формы канонические виды, т.е. представления в виде сумм квадратов, можно построить разными способами. Выясним, какие характеристики являются общими (инвариантными) для этих представлений.
Ранг квадратичной формы
Ранг квадратичной формы равен числу ненулевых коэффициентов в ее каноническом виде.
Закон инерции
Теорема [закон инерции]. Индексы инерции не зависят от способа приведения квадратичной формы к каноническому виду.
Доказательство ☞ ЗДЕСЬ.
Доказательство следует из формулы Якоби.
Пример. Найти ранг и сигнатуру квадратичной формы
Рассмотренный только что пример относится к общей задаче оценки влияния параметров на характеристики квадратичной формы:
Как меняются ранг и сигнатура при непрерывном изменении параметров?
Справедливо и более общее утверждение.
Конгруэнтность квадратичных форм
Множество всех квадратичных форм с вещественными коэффициентами можно разбить на классы эквивалентности, в каждом из которых будут находиться только конгруэнтные между собой формы. Каждый из классов полностью описывается каким-то из своих представителей. Таким представителем можно взять нормальный вид.
Какое преобразование квадратичной формы оставляет ее инвариантной?
Знакоопределенность
Задача. Найти условия неотрицательности и положительной определенности квадратичной формы в терминах ее коэффициентов.
Теорема. Ненулевая квадратичная форма, представленная в правильном виде
Доказательство ☞ ЗДЕСЬ.
К счастью, явное представление канонического вида квадратичной формы уже имеется — как правило, он задается формулой Якоби. Индексы инерции вычисляются через знаки главных миноров матрицы квадратичной формы.
Теорема [Сильвестр]. Квадратичная форма
Доказательство ☞ ЗДЕСЬ.
Квадратичная форма будет отрицательно определенной тогда и только тогда, когда знаки главных миноров ее матрицы будут чередоваться следующим образом:
Пример. Квадратичная форма
Имеются ли конструктивные необходимые и достаточные условия неотрицательности квадратичной формы?
Теорема. Пусть линейное подпространство задано системой линейных однородных уравнений
Пример. Найти ортогональную замену переменных, приводящую квадратичную форму
Доказательство основано на правиле знаков Декарта.
Геометрия замен переменных
Оба преобразования координат не изменяют типа кривой: эллипс остается эллипсом. Но второе преобразование дает нечто большее: оно сохраняет размеры. Фактически, оно сводится к повороту исходного эллипса.
СОДЕРЖАНИЕ
Вступление
История
Действительные квадратичные формы
Любой п × п реальная симметричная матрица определяет квадратичную форму Q А в п переменных по формуле
Ниже эти результаты переформулированы иначе.
Любую симметричную матрицу A можно преобразовать в диагональную матрицу
Определения
Соответствующая билинейная форма квадратичной формы q определяется формулой
и эти два процесса противоположны друг другу. Как следствие, над полем характеристики, отличной от 2, теории симметричных билинейных форм и квадратичных форм от n переменных по существу одинаковы.
Квадратичные пространства
Отображение Q является однородной функцией степени 2, что означает, что оно обладает тем свойством, что для всех a в K и v в V :
Когда характеристика K не равна 2, определяется билинейное отображение B : V × V → K над K :
Обобщение
Квадратичная форма q : M → R может быть охарактеризована следующими эквивалентными способами:
Связанные понятия
Эквивалентность форм
Геометрический смысл
Целочисленные квадратичные формы
Это текущее использование термина; в прошлом он иногда использовался иначе, как подробно описано ниже.
Историческое использование
Исторически возникла некоторая путаница и разногласия по поводу того, должно ли понятие интегральной квадратичной формы означать:
двое в квадратичная форма, связанная с симметричной матрицей с целыми коэффициентами двое из многочлен с целыми коэффициентами (так что соответствующая симметричная матрица может иметь полуцелые коэффициенты вне диагонали)
Несколько точек зрения означают, что два выхода были приняты в качестве стандартного соглашения. К ним относятся:
Универсальные квадратичные формы
Есть также формы, изображение которых состоит из всех положительных целых чисел, кроме одного. Например, для <1,2,5,5>исключение составляет 15. Недавно теоремы 15 и 290 полностью охарактеризовали универсальные целочисленные квадратичные формы: если все коэффициенты являются целыми числами, тогда они представляют все положительные целые числа тогда и только тогда, когда они представляют все целые числа до 290; если он имеет целочисленную матрицу, он представляет все положительные целые числа тогда и только тогда, когда он представляет все целые числа до 15.
1. Понятие квадратичной формы и способы ее записи.
2. Знакоопределенность квадратичных форм. Критерии положительной и отрицательной определенностей.
Ключевые понятия
Квадратичная форма. Симметричная матрица. Невырожденность квадратичной формы. Положительная определенность. Отрицательная определенность. Критерий Сильвестра.
1. Понятие квадратичной формы и способы ее записи
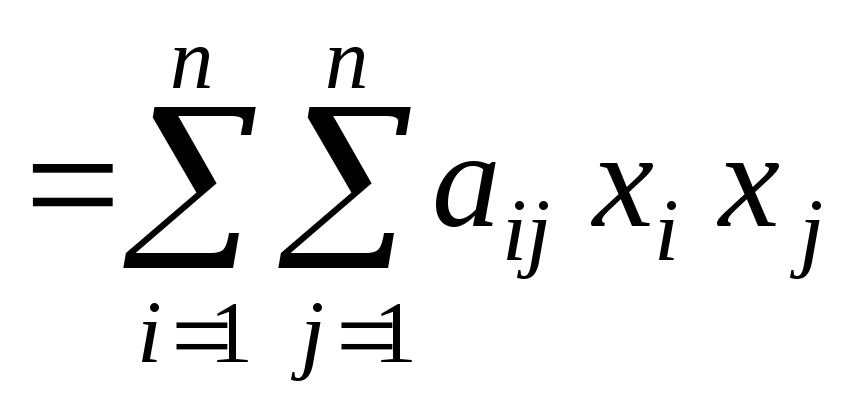
где aij – некоторые числа, называемые коэффициентами. Не ограничивая общности, можно считать, что aij = aji.
Квадратичная форма называется действительной, если aij ГR. Матрицей квадратичной формы называется матрица, составленная из ее коэффициентов. Квадратичной форме (1) соответствует единственная симметричная матрица
то есть А Т = А. Следовательно, квадратичная форма (1) может быть записана в матричном виде (х) = х Т Ах, где
И, наоборот, всякой симметричной матрице (2) соответствует единственная квадратичная форма с точностью до обозначения переменных.
Рангом квадратичной формы называют ранг ее матрицы. Квадратичная форма называется невырожденной, если невырожденной является ее матрица А. (напомним, что матрица А называется невырожденной, если ее определитель не равен нулю). В противном случае квадратичная форма является вырожденной.
Записать матрицу квадратичной формы (х1, х2, x3) = 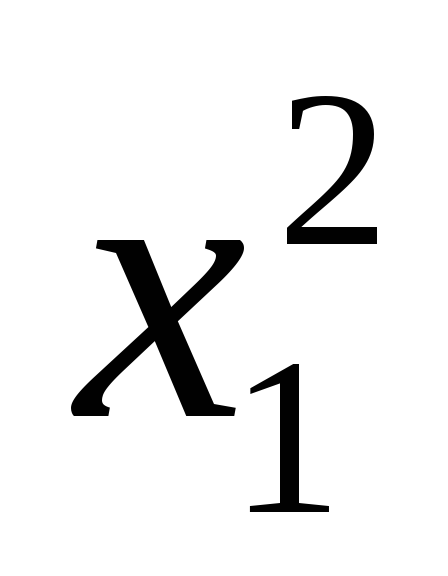
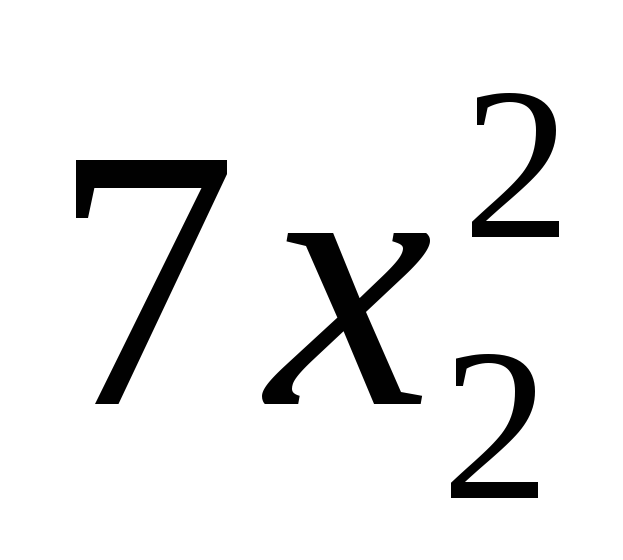
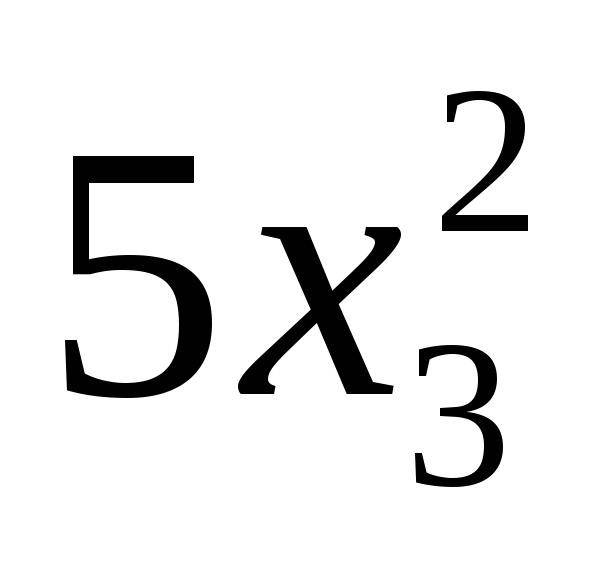
r(A) = 3 квадратичная форма невырождена.
2. Знакоопределенность квадратичных форм. Критерии положительной и отрицательной определенностей
Квадратичная форма (1) называется положительно определенной (или строго положительной), если
Матрица А положительно определенной квадратичной формы (х) также называется положительно определенной. Следовательно, положительно определенной квадратичной форме соответствует единственная положительно определенная матрица и наоборот.
Квадратичная форма (1) называется отрицательно определенной (или строго отрицательной), если
(х) 2 требуются специальные критерии для проверки знакоопределенности квадратичной формы. Рассмотрим их.
Главными минорами квадратичной формы называются миноры:
то есть это миноры порядка 1, 2, …, n матрицы А, расположенные в левом верхнем углу, последний из них совпадает с определителем матрицы А.
Критерий положительной определенности (критерий Сильвестра)
Для того чтобы квадратичная форма (х) = х Т Ах была положительно определенной, необходимо и достаточно, что все главные миноры матрицы А были положительны, то есть: