Натуральные числа это какие числа
Натуральные числа это какие числа
Что такое Натуральное число
Определение натурального числа
Натуральные числа — это те числа, которые появились натуральным способом, когда считали сколько у человека есть предметов. Например: 1, 2, 3, 4, 5 и т. д.
Наибольшее натуральное число: не существует. Наименьшее натуральное число: 1.
Например, люди считали, сколько у них было фруктов: 1 яблоко, 3 апельсина, 2 дыни.
Нуль (0) не является натуральным числом, хотя некоторые области математики всё-таки считают 0 натуральным числом.
Отрицательные числа (–1, –3, –5. ) не являются натуральными числами («–3» яблок сложно посчитать физически).
Дроби (например, ⅓ или ⅖) тоже не являются натуральными числами.
Такие понятия, как отрицательные («–3»), дроби («⅓») и нуль («0») появились много позже.
Множество натуральных чисел
Множество натуральных чисел бесконечно и обозначается буквой N, т. е.:
Натуральные числа:
Натуральные числа с нулём:
Ряд натуральных чисел
Если записать все натуральные числа в порядке возрастания (каждое натуральное число отличается от предыдущего на 1), это будет ряд натуральных чисел. Но если какие-то числа будут отсутствовать, это уже не будет считаться рядом натуральных чисел. Например:
Наибольшего натурального числа не существует — натуральный ряд бесконечен.
Ненатуральные числа
Ненатуральные числа — это отрицательные и нецелые числа (обычно 0 тоже считается ненатуральным, но не всегда).
Отрицательные числа — это все те, которые ниже нуля, например: –1, –2, –3, –4, –5 и др.;
Свойства натуральных чисел
Натуральные числа обладают следующими свойствами:
Натуральные числа
Натуральные числа — одно из старейших математических понятий.
В далёком прошлом люди не знали чисел и, когда им требовалось пересчитать предметы (животных, рыбу и т.д.), они делали это не так, как мы сейчас.
Количество предметов сравнивали с частями тела, например, с пальцами на руке и говорили: «У меня столько же орехов, сколько пальцев на руке».
Со временем люди поняли, что пять орехов, пять коз и пять зайцев обладают общим свойством — их количество равно пяти.
Наибольшего натурального числа не существует.
При счёте число ноль не используется. Поэтому ноль не считается натуральным числом.
Затем появились и особые знаки для обозначения чисел — предшественники современных цифр. Цифры, которыми мы пользуемся для записи чисел, родились в Индии примерно 1 500 лет назад. В Европу их привезли арабы, поэтому их называют арабскими цифрами.
Натуральный ряд — это последовательность всех натуральных чисел:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 …
Натуральный ряд бесконечен, наибольшего натурального числа в нём не существует.
Десятичной потому, что 10 единиц каждого разряда образуют 1 единицу старшего разряда. Позиционной потому, что значение цифры зависит от её места в записи числа, то есть от разряда, в котором она записана.
Разряды и классы (включая класс миллионов) подробно разобраны на нашем сайте в материалах для начальной школы.
Класс миллиардов
Если взять десять сотен миллионов, то получим новую разрядную единицу — один миллиард или в записи цифрами.
1 000 миллионов = 1 000 000 000 = 1 млрд
Десять таких единиц — десять миллиардов, десять десятков миллиардов образуют следующую единицу — сто миллиардов.
Миллиарды, десятки миллиардов и сотни миллиардов образуют четвёртый класс — класс миллиардов.
Разряды и классы натурального числа
Рассмотрим натуральное число 783 502 197 048
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
| Название класса | Миллиарды | Миллионы | Тысячи | Единицы | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Название разряда | Сотни миллиардов | Десятки миллиардов | Миллиарды | Сотни миллионов | Десятки миллионов | Миллионы | Сотни тысяч | Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
| Цифра (символ) | 7 | 8 | 3 | 5 | 0 | 2 | 1 | 9 | 7 | 0 | 4 | 8 |
C помощью таблицы разрядов прочитаем это число. Для этого надо слева направо по очереди называть количество единиц каждого класса и добавлять название класса.
Название класса единиц не произносят, также не произносят название класса, если все три цифры в его разрядах — нули.
Любое натуральное число можно записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000 … называются разрядными единицами. С их помощью натуральное число записывается в виде разрядных слагаемых. Так, например, число 307 898 будет выглядеть в виде разрядных слагаемых.
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Проверить свои вычисления вы можете с помощью нашего калькулятора разложения числа на разряды онлайн.
Следующие за миллиардом классы названы в соответствии с латинскими наименованиями чисел. Каждая следующая единица содержит тысячу предыдущих.
Все числа пересчитать невозможно, поскольку за каждым числом следует число на единицу большее, но очень большие числа в повседневной жизни не нужны.
Однако, физики нашли число, которое превосходит количество всех атомов (мельчайших частиц вещества) во всей Вселенной.
Это число получило специальное название — гугол. Гугол — число, у которого 100 нулей.
Основные определения. Натуральные числа и действия с ними
Содержание
Математика — самая древняя наука. Произошла она в Древней Греции. А натуральные числа — одно из старейших понятий в математике. На этом уроке мы расскажем, какие числа называются натуральными, что такое натуральное число и натуральный ряд, какие действия возможны с натуральными числами.
Натуральные числа
Сначала люди записывали цифры чёрточками и точками ($1 — I, 2 — II, 3 — III$ и т.д.). Позднее изобрели римские цифры, а чуть позже и десятичную систему счисления. Сейчас мы считаем с помощью арабских цифр.
Натуральные числа — это числа, которые используют при счёте или указывают порядковый номер предмета.
Рисунок 1.
Ноль — натуральное число?
Что такое «натуральный ряд»?
Множество всех натуральных чисел принято обозначают буквой N.
Действия с натуральными числами
Натуральные числа можно складывать, вычитать, умножать и делить.
Сложение
Важно! Сложение натуральных чисел всегда даёт натуральное число.
Примеры:
$5+5=10$ — натуральное
$48+50=98$ — натуральное
Вычитание
Вычитание из одного числа другого, равного или большего первому, не даёт натуральное число.
Умножение
Умножение натуральных чисел можно представить как их сложение.
Пример:
$2 \cdot 3=2+2+2=6$ — натуральное число
Таким образом, так как при сложении получается натуральное число, то и при умножении тоже получается натуральное число.
Деление
Натуральные числа. Ряд натуральных чисел.
История натуральных чисел началась ещё в первобытные времена. Издревле люди считали предметы. Например, в торговле нужен был счет товара или в строительстве счет материала. Да даже в быту тоже приходилось считать вещи, продукты, скот. Сначала числа использовались только для подсчета в жизни, на практике, но в дальнейшем при развитии математики стали частью науки.
Натуральные числа – это числа которые мы используем при счете предметов.
Например: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ….
Нуль не относится к натуральным числам.
Все натуральные числа или назовем множество натуральных чисел обозначается символом N.
Таблица натуральных чисел.
Натуральный ряд.
Натуральные числа, записанные подряд в порядке возрастания, образуют натуральный ряд или ряд натуральных чисел.
Свойства натурального ряда:
Пример №1:
Напишите первых 5 натуральных числа.
Решение:
Натуральные числа начинаются с единицы.
1, 2, 3, 4, 5
Пример №2:
Нуль является натуральным числом?
Ответ: нет.
Пример №3:
Какое первое число в натуральном ряду?
Ответ: натуральный ряд начинается с единицы.
Пример №4:
Какое последнее число в натуральном ряде? Назовите самое большое натуральное число?
Ответ: Натуральный ряд начинается с единицы. Каждое следующее число больше предыдущего на единицу, поэтому последнего числа не существует. Самого большого числа нет.
Пример №5:
У единицы в натуральном ряду есть предыдущее число?
Ответ: нет, потому что единица является первым числом в натуральном ряду.
Пример №6:
Назовите следующее число в натуральном ряду за числами: а)5, б)67, в)9998.
Ответ: а)6, б)68, в)9999.
Пример №7:
Сколько чисел находится в натуральном ряду между числами: а)1 и 5, б)14 и 19.
Решение:
а) 1, 2, 3, 4, 5 – три числа находятся между числами 1 и 5.
б) 14, 15, 16, 17, 18, 19 – четыре числа находятся между числами 14 и 19.
Пример №8:
Назовите предыдущее число за числом 11.
Ответ: 10.
Пример №9:
Какие числа применяются при счете предметов?
Ответ: натуральные числа.
Числа. Натуральные числа.
Простейшее число — это натуральное число. Их используют в повседневной жизни для подсчета предметов, т.е. для вычисления их количества и порядка.
Что такое натуральное число: натуральными числами называют числа, которые используются для подсчета предметов либо для указывания порядкового номера любого предмета из всех однородных предметов.
В натуральном ряду каждое число больше предыдущего на единицу.
Сколько чисел в натуральном ряду? Натуральный ряд бесконечен, самого большого натурального числа не существует.
Десятичной так как 10 единиц всякого разряда образуют 1 единицу старшего разряда. Позиционной так как значение цифры зависит от её места в числе, т.е. от разряда, где она записана.
Для подсчета времени в градусной мере углов существует шестидесятеричная система счисления (основа число 60). В 1 часе — 60 минут, в 1 минуте — 60 секунд; в 1 угловом градусе — 60 минут, в 1 угловой минуте — 60 секунд.
Всякое натуральное число легко записать в виде разрядных слагаемых.
Числа 1, 10, 100, 1000. – это разрядные единицы. При их помощи натуральные числа записывают как разрядные слагаемые. Таким образом, число 307 898 в виде разрядных слагаемых записывается так:
307 898 = 300 000 + 7 000 + 800 + 90 + 8
Обозначение натуральных чисел: Множество натуральных чисел обозначают символом N.
Классы натуральных чисел.
Всякое натуральное число возможно написать при помощи 10-ти арабских цифр:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Сравнение натуральных чисел.
Таблица разрядов и классов чисел.
1-й класс единицы
1-й разряд единицы
2-й разряд десятки
3-й разряд сотни
2-й класс тысячи
1-й разряд единицы тысяч
2-й разряд десятки тысяч
3-й разряд сотни тысяч
3-й класс миллионы
1-й разряд единицы миллионов
2-й разряд десятки миллионов
3-й разряд сотни миллионов
4-й класс миллиарды
1-й разряд единицы миллиардов
2-й разряд десятки миллиардов
3-й разряд сотни миллиардов
Числа от 5-го класса и выше относятся к большим числам. Единицы 5-го класса — триллионы, 6-го класса — квадриллионы, 7-го класса — квинтиллионы, 8-го класса — секстиллионы, 9-го класса — ептиллионы.
Основные свойства натуральных чисел.
Действия над натуральными числами.
1. Сложение натуральных чисел результат: сумма натуральных чисел.
Формулы для сложения:
(а + b) + с = а + (b + с)
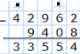
В основном, сложение натуральных чисел выполняется « столбиком ».
2. Вычитание натуральных чисел – операция, обратная сложению: разница натуральных чисел.
Если в + с = а, то
Формулы для вычитания:
а + (b – с) = (а + b) – с
Вычитание натуральных чисел удобно производить « столбиком ».
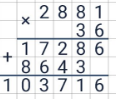
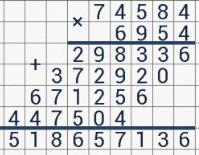
3. Умножение натуральных чисел : произведение натуральных чисел.
Формулы для умножения:
а ∙ b ∙ с = а ∙ (b ∙ с)
(а + b) ∙ с= а ∙ с + b ∙ с
(а – b) ∙ с = а ∙ с – b ∙ с
4. Деление натуральных чисел – операция, обратная операции умножения.
Если b ∙ с = а, то
Формулы для деления:
(a ∙ b) : c = a : (b ∙ c)
Числовые выражения и числовые равенства.
Запись, где числа соединяются знаками действий, является числовым выражением.
Записи, где знаком равенства объединены 2 числовых выражения, является числовыми равенствами. У равенства есть левая и правая части.
Порядок выполнения арифметических действий.
Когда числовое выражение состоит из действий только одной степени, то их выполняют последовательно слева направо.
Когда в выражении есть скобки – сначала выполняют действия в скобках.
Например, 36:(10-4)+3∙5= 36:6+15 = 6+15 = 21.
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
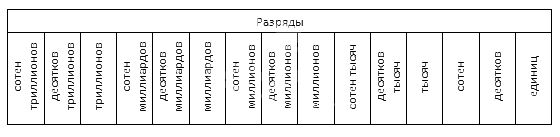
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами:
Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.
Общее представление о натуральных числах
На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.
Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.
Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.
Десятичная запись натурального числа
Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.
Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.
Количественный смысл натуральных чисел
Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.
Далее, по аналогии: Ψ Ψ Ψ – 3 предмета («три»), Ψ Ψ Ψ Ψ – 4 («четыре»), Ψ Ψ Ψ Ψ Ψ – 5 («пять»), Ψ Ψ Ψ Ψ Ψ Ψ – 6 («шесть»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 7 («семь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 8 («восемь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 9 («девять»).
С указанной позиции функция натурального числа заключается в указании количества предметов.
Однозначные натуральные числа
Однозначное натуральное число – натуральное число, при записи которого используется один знак – одна цифра.
Двузначные и трехзначные натуральные числа
Двузначные натуральные числа – натуральные числа, при записи которых используются два знака – две цифры. При этом используемые цифры могут быть как одинаковые, так и различные.
Рассмотрим, какой смысл заключен в двузначных числах. Опираться будем на уже известный нам количественный смысл однозначных натуральных чисел.
Введем такое понятие как «десяток».
Представим множество предметов, которое состоит из девяти и еще одного. В таком случае можно говорить об 1 десятке («один десяток») предметов. Если представить один десяток и еще один, то речь пойдёт о 2 десятках («два десятка»). Прибавив к двум десяткам еще один, получим три десятка. И так далее: продолжая добавлять по одному десятку, мы будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков и, наконец, девять десятков.
Трехзначные натуральные числа – натуральные числа, при записи которых используются три знака – три цифры. Цифры могут быть различными или повторяющимися в любом сочетании.
Чтобы понять количественный смысл трехзначных натуральных чисел, введем понятие «сотня».
Одна сотня ( 1 сотня) – это множество, состоящее из десяти десятков. Сотня и еще одна сотня составят 2 сотни. Прибавим еще одну сотню и получим 3 сотни. Добавляя постепенно по одной сотне, получим: четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен.
Так, трехзначное натуральное число 402 обозначает: 2 единицы, 0 десятков (отсутствуют десятки, не объединенные в сотни) и 4 сотни.
По аналогии дается определение четырёхзначных, пятизначных и так далее натуральных чисел.
Многозначные натуральные числа
От всего вышесказанного теперь возможно перейти к определению многозначных натуральных чисел.
Многозначные натуральные числа – натуральные числа, при записи которых используются два и более знаков. Многозначные натуральные числа – это двухзначные, трехзначные и так далее числа.
Одна тысяча – множество, включающее в себя десять сотен; один миллион состоит из тысячи тысяч; один миллиард – тысяча миллионов; один триллион – тысяча миллиардов. Еще более крупные множества также имеют названия, но использование их редко.
Аналогично принципу выше, мы можем рассмотреть любое многозначное натуральное число, как набор однозначных натуральных чисел, каждое из которых, находясь на определенном месте, свидетельствует о наличии и количестве единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов и так далее (справа налево соответственно).
Например, многозначное число 4 912 305 содержит в себе: 5 единиц, 0 десятков, три сотни, 2 тысячи, 1 десяток тысяч, 9 сотен тысяч и 4 миллиона.
Резюмируя, мы рассмотрели навык группировки единиц в различные множества (десятки, сотни и т.д.) и увидели, что цифры в записи многозначного натурального числа являются обозначением количества единиц в каждом из таких множеств.
Чтение натуральных чисел, классы
В теории выше мы обозначили названия натуральных чисел. В таблице 1 укажем, как верно использовать названия однозначных натуральных чисел в речи и при буквенной записи:
Один
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одна
Две
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одно
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 1 2 3 4 5 6 7 8 9 | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одного Двух Трех Четырех Пяти Шести Семи Восьми Девяти | Одному Двум Трем Четырем Пяти Шести Семи Восьми Девяти | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одним Двумя Тремя Четырьмя Пятью Шестью Семью Восьмью Девятью | Об одном О двух О трех О четырех О пять О шести О семи О восьми О девяти |
Для грамотного прочтения и написания двузначных чисел, необходимо выучить данные таблицы 2 :
Мужской, женский и средний род
11
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90
Одиннадцать
Двенадцать
Тринадцать
Четырнадцать
Пятнадцать
Шестнадцать
Семнадцать
Восемнадцать
Девятнадцать
Двадцать
Тридцать
Сорок
Пятьдесят
Шестьдесят
Семьдесят
Восемьдесят
Девяносто
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десяти Одиннадцати Двенадцати Тринадцати Четырнадцати Пятнадцати Шестнадцати Семнадцати Восемнадцати Девятнадцати Двадцати Тридцати Сорока Пятидесяти Шестидесяти Семидесяти Восьмидесяти Девяноста | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десятью Одиннадцатью Двенадцатью Тринадцатью Четырнадцатью Пятнадцатью Шестнадцатью Семнадцатью Восемнадцатью Девятнадцатью Двадцатью Тридцатью Сорока Пятидесятью Шестидесятью Семидесятью Восьмидесятью Девяностью | О десяти Об одиннадцати О двенадцати О тринадцати О четырнадцати О пятнадцати О шестнадцати О семнадцати О восемнадцати О девятнадцати О двадцати О тридцати О сорока О пятидесяти О шестидесяти О семидесяти О восьмидесяти О девяноста |
Для того, чтобы читать трёхзначные числа, изучим данные таблицы 3 :
Двести
Триста
Четыреста
Пятьсот
Шестьсот
Семьсот
Восемьсот
Девятьсот
| Число | Именительный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 100 200 300 400 500 600 700 800 900 | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двухсот Трехсот Четырехсот Пятисот Шестисот Семисот Восьмисот Девятисот | Ста Двумстам Тремстам Четыремстам Пятистам Шестистам Семистам Восьмистам Девятистам | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двумстами Тремстами Четыремстами Пятистами Шестистами Семистами Восьмистами Девятистами | О ста О двухстах О трехстах О четырехстах О пятистах О шестистах О семистах О восьмистах О девятистах |
Чтобы легко прочитать указанные натуральные числа, занесем их в таблицу:
| Класс триллионов | Класс миллиардов | Класс миллионов | Класс тысяч | Класс единиц |
| 134 | 678 | |||
| 31 | 013 | 736 | ||
| 23 | 476 | 009 | 434 | |
| 2 | 533 | 467 | 001 | 222 |
Разберем подробно чтение числа 2 533 467 001 222 :
— добавив название класса, получим: «два триллиона»;
— читаем следующее число, добавив название соответствующего класса: «пятьсот тридцать три миллиарда»;
— продолжаем по аналогии, зачитывая следующий класс правее: «четыреста шестьдесят семь миллионов»;
— читаем последний класс единиц, не добавляя его название – «двести двадцать два».
Таким образом, число 2 533 467 001 222 будет звучать так: два триллиона пятьсот тридцать три миллиарда четыреста шестьдесят семь миллионов одна тысяча двести двадцать два. Используя указанный принцип, прочтем и прочие заданные числа:
— 31 013 736 – тридцать один миллион тринадцать тысяч семьсот тридцать шесть;
— 134 678 – сто тридцать четыре тысячи шестьсот семьдесят восемь;
— 23 476 009 434 – двадцать три миллиарда четыреста семьдесят шесть миллионов девять тысяч четыреста тридцать четыре.
Таким образом, основой правильного прочтения многозначных чисел является навык разбивать многозначное число на классы, знание соответствующих названий и понимание принципа прочтения двух- и трехзначных чисел.
Разряды натурального числа, значение разряда
Как уже становится понятно из всего вышесказанного, от позиции, на которой стоит цифра в записи числа, зависит ее значение. Т.е., например, цифра 3 в составе натурального числа 314 обозначает количество сотен, а именно – 3 сотни. Цифра 2 – количество десятков ( 1 десяток), а цифра 4 – количество единиц ( 4 единицы). При этом мы будем говорить, что цифра 4 находится в разряде единиц и является значением разряда единиц в заданном числе. Цифра 1 стоит в разряде десятков и служит значением разряда десятков. Цифра 3 располагается в разряде сотен и является значением разряда сотен.
Разряд – это позиция цифры в записи натурального числа, а также и значение этой цифры, которое определяется ее позицией в заданном числе.
Разряды имеют свои названия, мы уже использовали их выше. Справа налево следуют разряды: единиц, десятков, сотен, тысяч, десятков тысяч и т.д.
Для удобства запоминания можно использовать следующую таблицу (укажем 15 разрядов):
Уточним такую деталь: количество разрядов в заданном многозначном числе такое же, как количество знаков в составе записи числа. К примеру, данная таблица содержит названия всех разрядов для числа, в котором 15 знаков. Последующие разряды также имеют названия, но используются крайне редко и очень неудобны для восприятия на слух.
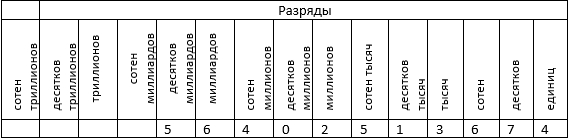
При помощи такой таблицы возможно наработать навык определения разряда, записывая заданное натуральное число в таблицу так, чтобы крайняя правая цифра была записана в разряде единиц и далее – в каждый разряд по цифре. К примеру, запишем многозначное натуральное число 56 402 513 674 так:
Введем также еще понятия низшего и высшего разрядов многозначного числа.
Низший (младший) разряд любого многозначного натурального числа – разряд единиц.
Высший (старший) разряд любого многозначного натурального числа – разряд, соответствующий крайней левой цифре в записи заданного числа.
Так, например, в числе 41 781 : низший разряд – разряд единиц; высший разряд – разряд десятков тысяч.
Логически следует, что возможно говорить о старшинстве разрядов относительно друг друга. Каждый последующий разряд при движении слева направо ниже (младше) предыдущего. И наоборот: при движении справа налево каждый следующий разряд выше (старше) предыдущего. К примеру, разряд тысяч старше разряда сотен, но младше разряда миллионов.
Уточним, что при решении некоторых практических примеров используется не само натуральное число, а сумма разрядных слагаемых заданного числа.
Кратко о десятичной системе счисления
Система счисления – метод записи чисел при помощи знаков.
Позиционные системы счисления – такие, в которых значение цифры в составе числа зависит от ее позиции в записи числа.
Помимо нее, существуют и прочие системы счисления. Например, информатика использует двоичную систему. Когда же мы ведем счет времени, то задействуем шестидесятеричную систему счисления.
Натуральные числа
Натура́льные чи́сла — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые числа — натуральными числами не являются.
Множество всех натуральных чисел принято обозначать знаком 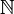
Существует бесконечное множество натуральных чисел — для любого натурального числа найдется другое натуральное число, большее его.
Содержание
Определение
Аксиомы Пеано
Теоретико-множественное определение
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Классы эквивалентности этих множеств относительно биекций также обозначают 0, 1, 2, ….
Замечание
В русской литературе обычно ноль исключен из числа натуральных чисел 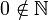
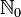
Если в определение натуральных чисел включен ноль, то множество натуральных чисел записывается как 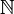
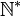
Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Теоретико-множественные определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:
где 
Основные свойства
Алгебраическая структура
Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел 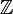
Натуральные числа
Определение
Натуральные числа — это числа, которые используются для счета: 1, 2, 3, …, n, …
Множество натуральных чисел принято обозначать символом N (от лат. naturalis — естественный).
Существуют два исторических подхода к определению натуральных чисел:
Натуральные числа в десятичной системе счисления записываются с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Множество натуральных чисел бесконечно, так как для любого числа n всегда найдется число m, которое больше n.
Операции над натуральными числами
К замкнутым операциям над натуральными числами (операциям в результате, которых получается натуральных чисел) относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как их результат не всегда будет натуральным числом.
Классы и разряды
Разряд — это положение (позиция) цифры в записи числа.
Низший разряд — самый правый. Старший разряд — самый левый.
Низший разряд — единицы, далее — десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллионы, десятки миллионов и т.д.
9 — единиц, 0 — десятков, 1 — сотя, 5 — тысяч, 3 — десятка тысяч, 4 — сотен тысяч, 2 — миллиона, 8 — десятков миллионов, 7 — сотен миллионов
Для удобства чтения, натуральных числа разбивают, на группы по три цифры в каждой начиная справа.
Класс — группа из трех цифр, на который разбито число, начиная справа. Последний класс может состоять из трех, двух или одной цифры.
Сравнение натуральных чисел
Сравнение натуральных чисел с разным количеством цифр
Среди натуральных чисел больше то, у которого больше цифр.
Сравнение натуральных чисел с равным количеством цифр
Сравнить числа поразрядно, начиная со старшего разряда. Больше то, у которого больше единиц в наивысшем одноименном разряде.
346 667 670 5 2 6 986
346 667 670 5 6 9 429
Что такое натуральные числа
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы расскажем, что такое НАТУРАЛЬНЫЕ ЧИСЛА.
С ними человек встречается с самого рождения. Например, когда считает пальцы на руке – 1, 2, 3, 4, 5. Или отмечает праздники – 8 марта, 23 февраля, 9 мая, 31 декабря.
Натуральные числа — это.
Натуральные числа – это те числа, которые возникают при подсчете чего-либо. Например, одно яблоко, два яблока, пять яблок десять яблок и так далее.
Лучше даже представить, что вы подсчитываете людей, ибо их нельзя поделить на части, как большинство предметов (например, разрезов яблоко пополам).
Само слово «naturalis» в переводе с латинского означает «естественный».
Если число не является ни дробным, ни отрицательным, то его можно назвать натуральным.
Натуральными числами люди пользуются уже много тысячелетий. Просто у разных народов были разные системы исчисления. Например, римляне для счета использовали палочки. Так и появились знаменитые римские цифры – I, V, X, L, C, D и M.
А вот в Древнем Вавилоне использовали шестеричную систему. И до наших дней она дошла в виде часов, в которых 1 час равен 60 минутам, а 1 минута равна 60 секундам.
И наконец, современное обозначение цифр (0, 1, 2, 3, 4, 5 и так далее) принадлежит арабам, хотя за основу они взяли индийскую десятеричную систему и добавили к ней «ноль».
Натуральный ряд
Если расположить натуральные числа в порядке возрастания, то полученная цепочка будет называться натуральным рядом.
Он всегда появляется, когда нам нужно что-то посчитать поштучно. Например, в магазине мы обычно так делаем с овощами или фруктами, берем 5 морковок или 3 яблока. А уже только потом взвешиваем их, так как цены указаны за килограмм.
И конечно, именно так учатся считать школьники в первом классе. Например, если в задачке нарисовано пять флажков и вопрос звучит «сколько?», то любой ребенок будет считать «пальцем», отмечая каждый флажок и озвучивая натуральный ряд «один, два, три, четыре, пять».
Ну и тут же будет важным упомянуть, что количество натуральных чисел бесконечно. А значит, и натуральный ряд является бесконечным.
Это записано в основном законе натуральных чисел:
Каким бы большим не было натуральное число N, всегда найдется натуральное число N+1, которое будет больше.
Ноль — это натуральное число или нет
Натуральный ряд можно построить двумя способами:
Вы спросите, в чем разница? Во втором случае возможен вариант, когда нужного предмета может и не быть вовсе. И тогда его количество равно нулю.
То есть натуральный ряд начинается не с единицы, а с ноля. И выглядит вот так: 0, 1, 2, 3, 4, 5 и так далее.
Соответственно, в первом случае ноль нельзя считать натуральным числом. А во втором – можно. Интересно, что споры, какой подход более правильный, у математиков идут до сих пор. И сторонников обеих теорий примерно поровну.
Но у российских школьников проблем с выбором нет. В нашей стране придерживаются той версии, что ноль – это натуральное число.
Операции с натуральными числами
Школьники в младших классах на уроках математики имеют дело только с натуральными числами. Помимо самих цифр учатся и самым простым действиям:
Вот и все, что мы хотели рассказать о натуральных числах.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
А стоит ли себе забивать голову, какое число натуральное, а какое нет? Мир от этого не станет, ни проще, ни сложнее. Да и что неестественного в отрицательных числах? Если человеку не хватает денег, чтобы рассчитаться с долгами, то его имущество как раз уйдет в минус, отдал за долги всё, что было, но остался должен, значит необходимо ещё заработать, чтоб из минуса выйти в ноль.
а нельзя сказать проще все недробные — натуральные?
Натуральное число
Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления).
Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые (рациональные, вещественные, …) числа натуральными не являются.
Множество всех натуральных чисел принято обозначать знаком 
Содержание
Определение
Аксиомы Пеано
Множество 


Перечисленные аксиомы отражают наше интуитивное представление о «натуральном ряде».
Поэтому, достаточно зафиксировать в качестве 
Теоретико-множественное определение (Определение Фреге-Рассела)
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Ноль как натуральное число
Иногда, в иностранной и переводной литературе, в первой и третьей аксиомах Пеано заменяют 


В русской литературе обычно ноль исключён из числа натуральных чисел 



В международной математической литературе, с учётом сказанного выше и во избежание неоднозначностей, множество 



Операции над натуральными числами
К замкнутым операциям (операциям, не выводящим результат из множества натуральных чисел) над натуральными числами относятся следующие арифметические операции:
Дополнительно рассматривают ещё две операции. С формальной точки зрения они не являются операциями над натуральными числами, так как не определены для всех пар чисел (иногда существуют, иногда нет).
Следует заметить, что именно операции сложения и умножения являются основополагающими. В частности, кольцо целых чисел определяется именно через бинарные операции сложения и умножения.
Теоретико-множественные определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Будем обозначать класс эквивалентности множества A относительно биекций как [A]. Тогда основные арифметические операции определяются следующим образом:
где 


Основные свойства
Алгебраическая структура
Сложение превращает множество натуральных чисел в полугруппу с единицей, роль единицы выполняет 0. Умножение также превращает множество натуральных чисел в полугруппу с единицей, при этом единичным элементом является 1. С помощью замыкания относительно операций сложения-вычитания и умножения-деления получаются группы целых чисел 

Натуральные числа
Содержание
Определение натуральных чисел [ править ]
Неформальное определение [ править ]
| Определение: |
| Натура́льные чи́сла (англ. natural numbers, естественные числа) — числа, возникающие естественным образом при счёте (как в смысле перечисления, так и в смысле исчисления). |
Существуют два подхода к определению натуральных чисел — числа, используемые при:
Отрицательные и нецелые числа натуральными числами не являются.
Формальное определение [ править ]
Определить множество натуральных чисел позволяют аксиомы Пеано (англ. Peano axioms):
Теоретико-множественное определение [ править ]
Согласно теории множеств, единственным объектом конструирования любых математических систем является множество.
Таким образом, и натуральные числа вводятся, исходя из понятия множества, по двум правилам:
Числа, заданные таким образом, называются ординальными.
Первые несколько ординальных чисел и соответствующие им натуральные числа:
Классы эквивалентности этих множеств относительно биекций также обозначают [math]0, 1, 2, \dots.[/math]
Перечисленные аксиомы отражают наше интуитивные представления о «натуральном ряде».
Операции над натуральными числами [ править ]
Сложение [ править ]
Умножение [ править ]
Вычитание [ править ]
Деление чисел с остатком [ править ]
Формула деления с остатком: [math]n = m \cdot k + r,[/math] где [math]n\,[/math] — делимое, [math]m\,[/math] — делитель, [math]k\,[/math] — частное, [math]r\,[/math] — остаток, причем [math]0\leqslant r \lt b [/math]
Основная теорема арифметики [ править ]
Лемма Евклида [ править ]
Основная теорема арифметики [ править ]
Существование. Пусть [math]n[/math] — наименьшее натуральное число, неразложимое в произведение простых чисел. Оно не может быть единицей по формулировке теоремы. Оно не может быть и простым, потому что любое простое число является произведением одного простого числа — себя. Если [math]n[/math] составное, то оно — произведение двух меньших натуральных чисел. Каждое из них можно разложить в произведение простых чисел, значит, [math]n[/math] тоже является произведением простых чисел. Противоречие.
Принцип индукции, существование наименьшего числа в любом множестве натуральных чисел [ править ]
Индукция [ править ]
Формулировка принципа математической индукции:
Верность этого метода доказательства вытекает из так называемой аксиомы индукции, пятой из аксиом Пеано, которые определяют натуральные числа. Рассмотрение аксиом Пеано выходит за рамки этой статьи.
Также существует принцип полной математической индукции. Вот его строгая формулировка:
Существование наименьшего элемента [ править ]
Аксиому индукции можно заменить на аксиому существования минимума, и доказать аксиому индукции как теорему.
















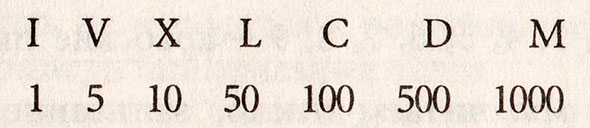





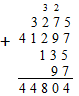
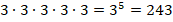
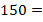
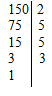
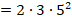
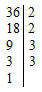
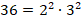
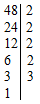
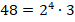
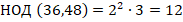
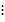 ».
».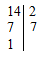
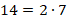
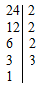
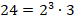
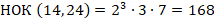
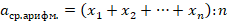



 В большинстве математических школ наименьшим значением N считается единица, так как отсутствие предметов считается пустотой.
В большинстве математических школ наименьшим значением N считается единица, так как отсутствие предметов считается пустотой. В разных математических школах можно встретить два интервала, которым принадлежит последовательность N:
В разных математических школах можно встретить два интервала, которым принадлежит последовательность N: Во многих простых и даже сложных задачах нахождение ответа зависит от умения школьников умножать. Fizzslots
Во многих простых и даже сложных задачах нахождение ответа зависит от умения школьников умножать. Fizzslots








 Известно, что большие числа часто используются в астрономии. Приведем примеры. Среднее расстояние Луны от Земли равно 384 тыс. км. Расстояние Земли от Солнца (среднее) составляет 149504 тыс. км, Земли от Марса 55 млн. км. На компьютере с помощью текстового редактора Word создайте таблицы так, чтобы каждая цифра в записи указанных чисел была в отдельной клеточке (ячейке). Для этого выполните команды на панели инструментов: таблица → добавить таблицу → число строк (с помощью курсора ставим «1») → число столбцов (посчитайте сами). Создайте таблицы и для других чисел (блока «Самоподготовка»).
Известно, что большие числа часто используются в астрономии. Приведем примеры. Среднее расстояние Луны от Земли равно 384 тыс. км. Расстояние Земли от Солнца (среднее) составляет 149504 тыс. км, Земли от Марса 55 млн. км. На компьютере с помощью текстового редактора Word создайте таблицы так, чтобы каждая цифра в записи указанных чисел была в отдельной клеточке (ячейке). Для этого выполните команды на панели инструментов: таблица → добавить таблицу → число строк (с помощью курсора ставим «1») → число столбцов (посчитайте сами). Создайте таблицы и для других чисел (блока «Самоподготовка»).