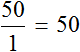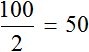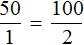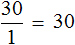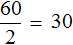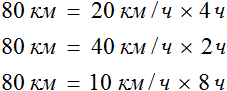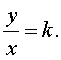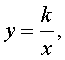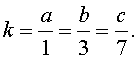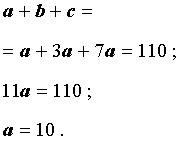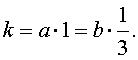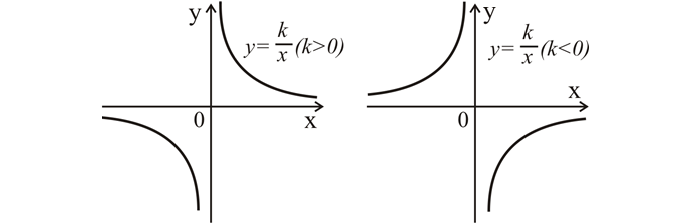Прямо пропорционально это как
Прямо пропорционально это как
Прямая пропорциональность
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина весят 1,6 кг, 5 л весят 4 кг, 7 л весят 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
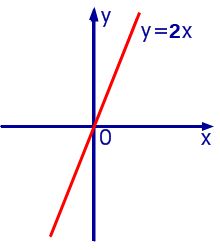
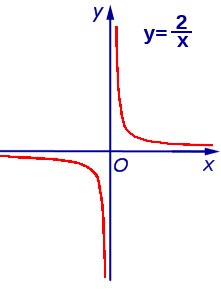
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
Математически обратная пропорциональность записывается в виде формулы:
См. также
Источники
Полезное
Смотреть что такое «Прямая пропорциональность» в других словарях:
прямая пропорциональность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN direct ratio … Справочник технического переводчика
прямая пропорциональность — tiesioginis proporcingumas statusas T sritis fizika atitikmenys: angl. direct proportionality vok. direkte Proportionalität, f rus. прямая пропорциональность, f pranc. proportionnalité directe, f … Fizikos terminų žodynas
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
пропорциональность — и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь
пропорциональность — и; ж. 1) к пропорциональный 1); соразмерность. Пропорциона/льность частей. Пропорциона/льность телосложения. Пропорциона/льность представительства в парламенте. 2) матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент… … Словарь многих выражений
Обратная пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия
линейная зависимость — прямая пропорциональность. множитель. см. константа … Идеографический словарь русского языка
Прямая и обратная пропорциональность
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
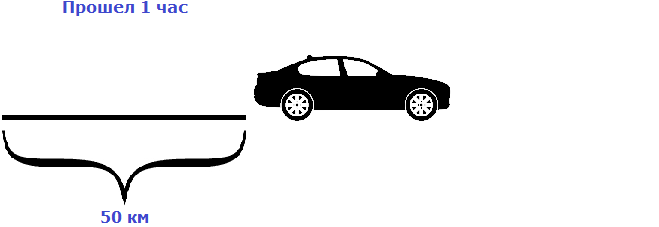
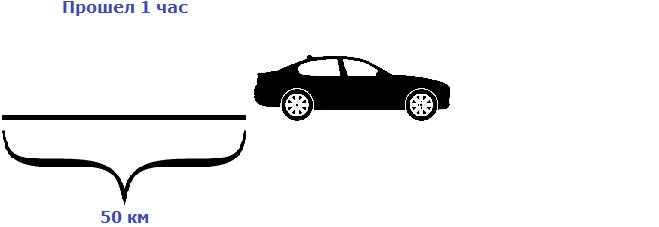
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
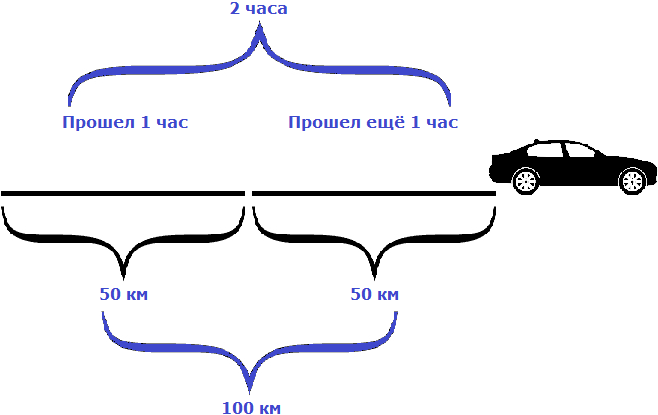
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения 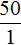
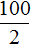
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
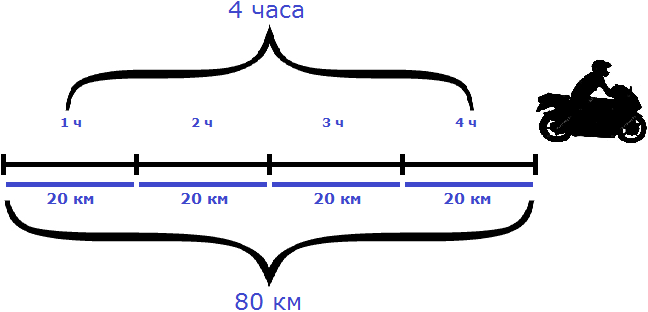
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
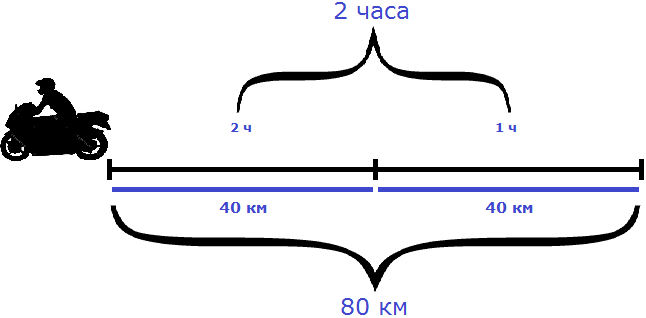
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
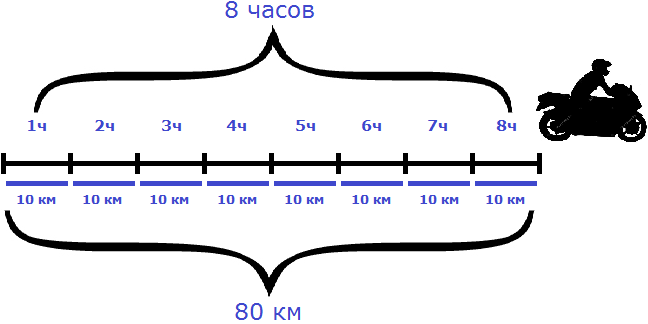
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
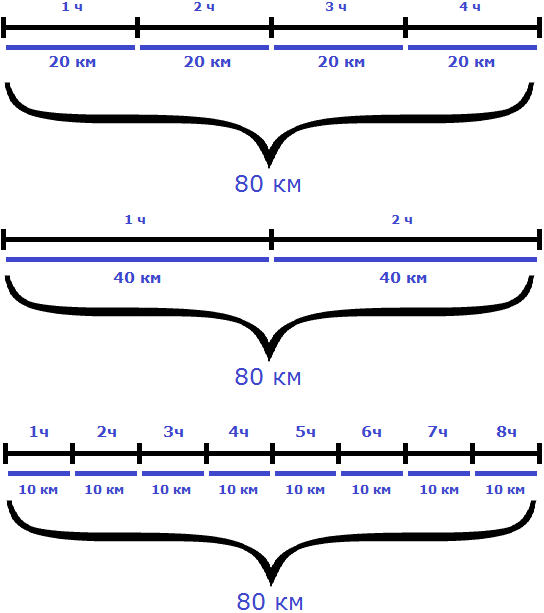
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
11 thoughts on “Прямая и обратная пропорциональность”
что ценно теория методически верно преподается. очень добрый сайт.
мне теперь всё понятно, большое спасибо сайту
Прямая и обратная пропорциональность
Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.
Пропорциональность величин может быть прямой и обратной.
Прямая пропорциональность
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Рассмотрим пример прямой пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При равномерном движении путь пропорционален времени движения. Если взять скорость v равной 5 км/ч, то пройденный путь s будет зависеть только от времени движения t:
| Скорость v = 5 км/ч | |||||
|---|---|---|---|---|---|
| Время t (ч) | 1 | 2 | 4 | 8 | 16 |
| Путь s (км) | 5 | 10 | 20 | 40 | 80 |
Из примера видно, что во сколько раз увеличивается время движения t, во столько же раз увеличивается пройденное расстояние s. В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.
В данном случае скорость (v = 5 км/ч) является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:
| 5 | = | 10 | = | 20 | = | 40 | = | 80 | = 5. |
| 1 | 2 | 4 | 8 | 16 |
Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:
| Время t = 2 ч | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 5 | 15 | 45 | 90 |
| Расстояние s (км) | 10 | 30 | 90 | 180 |
В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время (t = 2 ч):
| 10 | = | 30 | = | 90 | = | 180 | = 2. |
| 5 | 15 | 45 | 90 |
Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.
Формула прямой пропорциональности
Формула прямой пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Обратная пропорциональность
Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.
Рассмотрим пример обратной пропорциональности на формуле пути:
где s — это путь, v — скорость, а t — время.
При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь s равным 120 км, то потраченное на преодоление этого пути время t будет зависеть только от скорости движения v:
| Путь s = 120 км | ||||
|---|---|---|---|---|
| Скорость v (км/ч) | 10 | 20 | 40 | 80 |
| Время t (ч) | 12 | 6 | 3 | 1,5 |
Из примера видно, что во сколько раз увеличивается скорость движения v, во столько же раз уменьшается время t. В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.
В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:
10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.
Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Формула обратной пропорциональности
Формула обратной пропорциональности:
где y и x — это переменные величины, а k — это постоянная величина, называемая коэффициентом обратной пропорциональности.
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости
На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.
Прямая и обратная пропорциональность
Давайте сначала разберемся, что такое пропорциональность.
Зависимость величин друг от друга может быть прямой и обратной.
Отношение между величинами описываются прямой или обратной пропорциональностью.
Прямая пропорциональность выражается так: \(\mathbf
Обратная пропорциональность выражается так: \(\mathbf
x и y величины, зависящие друг от друга.
Пример
Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.
По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.
Какова эта зависимость, сейчас и рассмотрим.
Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.
Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.
Пусть одна клетка равна 1 см. Рассмотрим рисунок:
Ширина прямоугольника b постоянная величина
b = 4 см
a1 = 6 см
a2 = 7 см
Найдем площади прямоугольников S1 и S2
\(\mathbf
\(\mathbf
Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.
Рассмотрим другой вариант зависимости
Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см
Площадь прямоугольника S постоянная величина
S = 24 см 2
b1 = 4 см
Увеличим высоту прямоугольника- сторону прямоугольника b1 на 2 см, получим
b2 = 6 см
Найдем ширину прямоугольника- сторону a2
Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.
Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:
1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.
2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.
Примеров прямой и обратной пропорциональности множество.
Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.
Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.
Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается
Пройти тест и получить оценку можно после входа или регистрации
Алгоритм решение задач с прямой и обратной пропорциональной зависимостью
Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:
— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин
— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.
5. Записать пропорцию, учитывая характер пропорциональности величин
6. Составить уравнение
7. Найти неизвестный член уравнения (искомую величину)
8. Записать ответ задачи
Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.
Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.
Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.
Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.
При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.
Пройти тест и получить оценку можно после входа или регистрации
Математика. 6 класс
Конспект урока
Прямая и обратная пропорциональность. Решение задач
Перечень рассматриваемых вопросов:
Равенство двух отношений называют пропорцией.
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Теоретический материал для самостоятельного изучения
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз.
Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Для решения задач на пропорциональную зависимость, удобно составить таблицу или сделать краткую запись условия.
Столбцы таблицы соответствуют наименованиям зависимых величин.
Строки таблицы соответствуют значениям величин при первом и втором измерении.
Одинаково направленные стрелки показывают прямо пропорциональную зависимость, противоположно направленные – обратно пропорциональную.
Поезд, скорость которого 55 км/ч, был в пути 5 часов. За сколько часов пройдёт этот же участок пути товарный поезд, скорость которого 45 км/ч?
При постоянном пути скорость и время движения обратно пропорциональны.
Допустим, товарный поезд пройдёт этот же путь со скоростью 45 км/ч за x ч.
Сделаем краткую запись условия.
Двигаясь с постоянной скоростью, велогонщик проезжает 40 метров за 3 с. Какой путь проедет велогонщик за 45 с?
При постоянной скорости путь прямо пропорционален времени движения.
Пусть х м проедет велогонщик за 45 с.
Сделаем краткую запись условия.
Усилие при восхождении на высоту 600 м равно усилию, требуемому для перехода 25 км по равнине. Турист поднялся в горы на 792 м. Какому расстоянию на равнине соответствует этот подъём?
Четыре программиста могут написать игру за 12 месяцев. За сколько месяцев эту работу могут выполнить три программиста?
Количество программистов и скорость написания игры – это обратно пропорциональная зависимость.
Разбор заданий тренировочного модуля
№ 1. Подстановка элементов в пропуски в тексте.
Подставьте нужные элементы в пропуски.
Пешеход шёл 3 часа со скоростью 8 км/ч. За сколько часов он пройдёт то же расстояние со скоростью 6 км/ч?
При фиксированном расстоянии время в пути и скорость – ______ пропорциональны.
Пусть _____ часов – пешеход идёт со скоростью 6 км/ч.
При фиксированном расстоянии время в пути и скорость – обратно пропорциональны.
Пусть х часов – пешеход идёт со скоростью 6 км/ч.
№ 2. Подстановка элементов в пропуски в таблице.
Поезд движется со скоростью 45 км/ч. Какое расстояние он пройдёт, если будет в пути 3 ч; 4 ч; 5 ч; 6 ч.
При постоянной скорости пройденный путь и время прямо пропорциональны. Скорость движения поезда 45 км/ч означает, что за 1 час поезд преодолевает расстояние в 45 км. Обозначим за x км – расстояние, которое поезд пройдёт за 3, 4, 5 и 6 часов.
Таким же способом находим расстояние, которое пройдёт поезд за 4, 5 и 6 часов, и подставляем соответствующие варианты в таблицу.
Прямо пропорциональные величины, обратно пропорциональные величины
где k – некоторое число, называются прямо пропорциональными. Число k называется коэффициентом прямой пропорциональности.
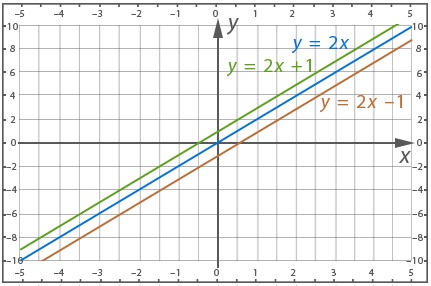
Графиком прямо пропорциональной зависимости величин является прямая линия. Например, при k = 2 график прямо пропорциональной зависимости имеет следующий вид
Отношение прямо пропорциональных величин является постоянным числом и равно k :
где k – некоторое число, называются обратно пропорциональными. Число k называется коэффициентом обратной пропорциональности.
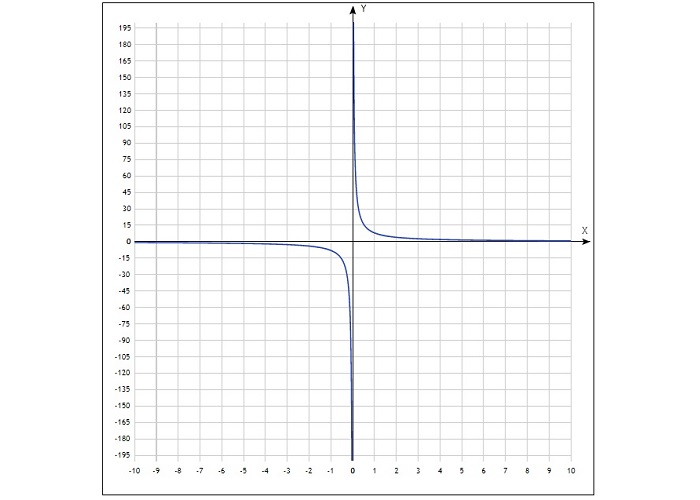
Графиком обратно пропорциональной зависимости величин является гипербола. Например, при k = 2 график обратно пропорциональной зависимости имеет следующий вид
Произведение обратно пропорциональных величин является постоянным числом и равно k :
Свойства прямой пропорциональности, область определения и значения
Прямая пропорциональность — базовые понятия
Пропорциональностью в алгебре называют зависимость между парой величин, при которой изменение одной из них приводит к изменению другой во столько же раз.
Пропорциональность бывает двух видов:
Предположим, что скорость движения автомобиля составляет 50 км/ч. По определению, скоростью является расстояние, преодолеваемое за единицу времени. В данном случае транспортное средство проезжает 50 километров в течение 1 часа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если автомобиль движется в течение еще одного часа с такой же скоростью 50 км/ч, то он преодолеет расстояние в 100 км.
Согласно примеру, увеличение времени в 2 раза сопровождается увеличением пройденного расстояния во столько же раз, то есть в 2 раза. Величины времени и расстояния будут прямо пропорциональными. Они обладают взаимосвязью, которую называют прямой пропорциональностью.
Прямая пропорциональность – это взаимосвязь между двумя величинами, при которой увеличение одной из них приводит к увеличению другой во столько же раз и, наоборот, при уменьшении одной величины в какое-то число раз, другая величина уменьшается во столько же раз.
Предположим, что вначале водитель планировал проехать 100 км за 2 часа, но после того, как он преодолел 50 км, произошла остановка. В таком случае, уменьшая расстояние в 2 раза, получим, что время уменьшится тоже в 2 раза.
Особенностью прямо пропорциональных величин является стабильность их отношений. Таким образом, во время изменения значений прямо пропорциональных величин, их отношение остается постоянным. Рассмотренная ситуация характеризуется изменением расстояния с 50 км при значении времени в 1 час. Отношение расстояния ко времени равно 50 и определяется формулой:
После увеличения времени движения автомобиля в 2 раза, оно составит 2 часа. Таким образом, расстояние также увеличилось в 2 раза до 100 км. Отношение 100 км к 2 часам равно числу 50:
Число 50 представляет собой коэффициент прямой пропорциональности. Эта величина демонстрирует, какое расстояние соответствует одному часу движения. В условиях рассматриваемого примера данный коэффициент является скоростью движения автомобиля, исходя из ее определения.
С помощью прямо пропорциональных характеристик можно составлять пропорции. Например, записанные ранее отношения составляют пропорционально:
Представленное выражение читают таким образом: 50 км так относятся к 1 часу, как 100 км относятся к 2 часам.
Линейное уравнение относительно двух переменных x и y имеет такой вид:
Известно, что график записанного равенства является прямая линия, любая точка на которой имеет два числа в виде координат x и y, то есть абсциссы и ординаты. Каждая точка этой прямой соответствует заданному уравнению. Если выразить y через x, получим:
Сделать уравнение более удобным можно с помощью следующих обозначений:
Данным способом была выведена линейная функция y от x в общем виде. В этом случае были применены новые обозначения:
В том случае, когда m = 0, уравнение примет вид:
Данная функция представляет собой прямую пропорциональность. Она определяется с помощью единственного параметра k.
Исследование функции прямой пропорциональности и ее график
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
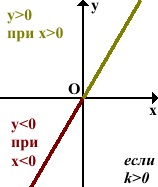
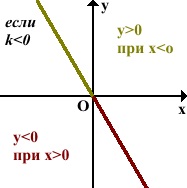
Прямая пропорциональность характеризуется следующими свойствами:
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
Если k 0 при x 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
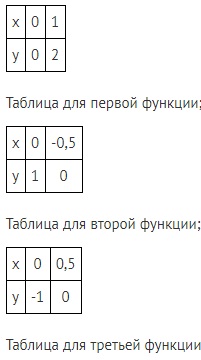
В качестве примера можно рассмотреть такие функции:
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Примеры задач на прямую пропорциональность
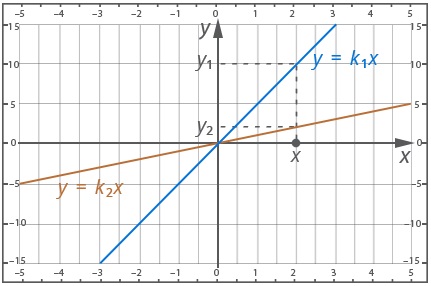
Требуется определить соотношение между угловыми коэффициентами, согласно графику:
Требуется построить график прямой пропорциональности при том, что на данном графике есть точка с координатами (2;8).
Построить прямую можно через пару точек. Первая будет обладать координатами (0;0), исходя из того, что любой график прямой пропорциональности пересекает точку (0;0). Вторая точка дана в условии задачи (2;8).
Задачу можно решить другим способом. Согласно координатам точки (2;8), получим:
Данные выражения подходят для уравнения вида:
Можно подставить известные значения и определить k:
Таким образом, уравнение примет вид:
С помощью данного уравнения можно построить график:
Прямая и обратная пропорциональности
Вы будете перенаправлены на Автор24
Типы зависимостей
Рассмотрим зарядку батареи. В качестве первой величины возьмем время, которое она заряжается. Вторая величина – время, которое она будет работать после зарядки. Чем дольше будет заряжаться батарея, тем дольше она будет работать. Процесс будет длиться до тех пор, пока батарея не полностью зарядится.
Зависимость времени работы батареи от времени, которое она заряжается
Такая зависимость называется прямой:
С увеличением одной величины увеличивается и вторая. С уменьшением одной величины уменьшается и вторая величина.
Рассмотрим другой пример.
Чем больше книг прочитает ученик, тем меньше ошибок сделает в диктанте. Или чем выше подняться в горы, тем ниже будет атмосферное давление.
Такая зависимость называется обратной:
С увеличением одной величины уменьшается вторая. С уменьшением одной величины увеличивается вторая величина.
Таким образом, в случае прямой зависимости обе величины изменяются одинаково (обе либо увеличиваются, либо уменьшаются), а в случае обратной зависимости – противоположно (одна увеличивается, а другая уменьшается либо наоборот).
Определение зависимостей между величинами
Готовые работы на аналогичную тему
Такую зависимость называют пропорциональной:
Во сколько раз изменится одна величина, во столько раз изменится и вторая.
В обоих примерах были рассмотрены пропорциональные зависимости. Но в примере с булками хлеба величины изменяются в одну сторону, следовательно, зависимость является прямой. А в примере с походом к другу зависимость между скоростью и временем – обратная. Таким образом, существует прямо пропорциональная зависимость и обратно пропорциональная зависимость.
Прямая пропорциональность
Как видно, эти отношения равны между собой:
Равенство двух отношений называется пропорцией.
При прямо пропорциональной зависимости получается отношение, когда изменение первой и второй величины совпадает:
Две величины называются прямо пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменяется (увеличивается или уменьшается соответственно) и другая величина.
Время прямо пропорционально расстоянию:
Во сколько раз увеличится расстояние, при постоянной скорости, во столько же раз увеличится время:
Запишем условие задачи в виде таблицы:
Чем больше расстояние проедет автомобиль, тем большее время ему понадобится. Следовательно, зависимость между величинами прямо пропорциональная.
Обратная пропорциональность
При обратно пропорциональной зависимости получается отношение, первая часть которого показывает, во сколько раз увеличилась первая величина, а вторая часть – во сколько раз уменьшилась вторая:
Две величины называются обратно пропорциональными, если при изменении (увеличении или уменьшении) одной из них во столько же раз изменится (уменьшится или увеличится соответственно) другая величина.
Время обратно пропорционально скорости:
Во сколько раз увеличивается скорость, при том же пути, во столько же раз уменьшается время:
Запишем условие задачи в виде таблицы:
Чем больше скорость автомобиля, тем меньше времени ему понадобится. Следовательно, зависимость между величинами обратно пропорциональная.
Т.к. пропорциональность обратная, второе отношение в пропорции переворачиваем:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 20.06.2022
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k 0;
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Пропорциональность
Содержание
Пример
Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:
1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.
Коэффициент пропорциональности
Символ
Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.
В юникоде для отображения используется символ U+221D.
Прямая пропорциональность
Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.
Математически прямая пропорциональность записывается в виде формулы:
Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.
Обратная пропорциональность
Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).
См. также
Источники
Полезное
Смотреть что такое «Пропорциональность» в других словарях:
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова
ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка
Пропорциональность — 1) соразмерность элементов и их связей в одной системе; 2) принцип организации политических систем и процессов, динамическая сбалансированность политической системы. В политологическом ракурсе «пропорциональность» подразумевает выяснение целого… … Политология. Словарь.
пропорциональность — соразмерность, соизмеримость; соответствие, стройность, гармоничность, рациональность, нормальность. Ant. непропорциональность, асимметрия Словарь русских синонимов. пропорциональность соразмерность Словарь синонимов русского языка. Практический… … Словарь синонимов
ПРОПОРЦИОНАЛЬНОСТЬ — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Современная энциклопедия
ПРОПОРЦИОНАЛЬНОСТЬ — простейший вид функциональной зависимости (см. Функция). Различают прямую пропорциональность. (y =kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S =vt… … Большой Энциклопедический словарь
Пропорциональность — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Иллюстрированный энциклопедический словарь
пропорциональность — ПРОПОРЦИОНАЛЬНОСТЬ, соразмерность ПРОПОРЦИОНАЛЬНЫЙ, соразмерный ПРОПОРЦИОНАЛЬНО, соразмерно, соответственно … Словарь-тезаурус синонимов русской речи
ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова
ПРОПОРЦИОНАЛЬНОСТЬ — англ. proportionality; нем. Proportionalitat. Простейший вид функциональной зависимости, фиксирующей соотношение между двумя величинами; показатель отношения исследуемой функции ко всему числу изучаемых случайностей. Antinazi. Энциклопедия… … Энциклопедия социологии
ПРОПОРЦИОНАЛЬНОСТЬ — (лат. proportionalis) соблюдение пропорций, рациональных структурных соотношений в экономике, согласованное развитие отраслей, сфер, регионов. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М … Экономический словарь
Прямая и обратная пропорциональность

Средняя оценка: 4.1
Всего получено оценок: 469.
Средняя оценка: 4.1
Всего получено оценок: 469.
Прямая и обратная пропорциональность – это одна из основ математики и геометрии 6 класса. Причем, это та основа, знания которой пригодятся не только при решении задач, но и в реальной жизни: пропорциональны друг другу бывают физические величины, заработные платы и конфеты, купленные в магазине.
Что такое пропорция?
Пропорция – это взаимосвязь двух величин. То есть, если меняется одна величина, меняется и другая. Если одна величина пропорциональна другой, а друга пропорциональна третьей, то все эти величины связаны между собой. Разделяют прямую и обратную пропорцию. Дадим им определения и приведем наглядные примеры.
Прямая пропорция
Прямая пропорция – это взаимоотношение величин, при котором, увеличивая одну величину, мы автоматически увеличим другую. Самый простой пример это булочки в магазине и цена на них. Булочка в любом случае стоит 30 руб. Покупая одну штуку мы платим 30 руб.
Если увеличим размер покупки, то соразмерно возрастет и цена. Она не может не возрасти, ведь булочник не будет отдавать свой товар просто так. За 2 булочки мы заплатим 60 рублей, за 3 – 90 и так далее.
Если устанавливать зависимость между количеством булочек и ценой на них, то получится следующее отношение:
Цена булочек/количество=30/1=60/2 и так далее. Заметим, что всегда это отношение равно одному и тому же числу. В данном примере это число 30. Оно будет постоянным для любого варианта данной пропорции. Конкретно в данном примере это число является одновременно и ценой одной булочки.
Иными словами, для приведенного примера пропорциональность можно объяснить так: сколько бы булочек мы ни купили, все равно цена одной будет 30 рублей. Вот и все. В рамках математики говорят, что если коэффициент пропорциональности не меняется, то числа пропорциональны.
Для того, чтобы понять, изменяется коэффициент или нет, нужно просто поделить друг на друга числа этой пропорции и сравнить результат. То есть, взять сначала отношение цены одной булочки к ее количеству, а затем цены 30 булочек к их количеству. Коэффициент сохранит свое значение, значит эти числа прямопропорциональны.
Обратная пропорция
Существует также понятие обратной пропорции. Часто бывает так, что одна величина зависит от другой, но не прямопропорционально. Сравним две взаимосвязанные между собой величины. Например, мотоциклист залил в бак бензин. Чем меньше бензина остается в баке мотоциклиста, тем больше проехал водитель. Здесь на лицо обратная зависимость количества бензина и пройденного расстояния.
Как просто запомнить?
Есть 4 простые схемы запоминания темы, по две для каждого вида пропорциональности.
Для прямой пропорции всегда работает схема: «больше-больше» или «меньше-меньше». То есть при увеличении одной величины, увеличится и другая, или при уменьшении одной величины уменьшится другая.
Соответственно, для обратной пропорциональности наоборот: «больше-меньше» или «меньше-больше». То есть, чем больше одна величина, тем меньше другая и наоборот.
Что мы узнали?
Мы привели объяснение прямой и обратной пропорциональности. Вывели простые схемы для запоминания темы и обговорили понятные примеры.
Прямая пропорциональность

Средняя оценка: 4.8
Всего получено оценок: 165.
Средняя оценка: 4.8
Всего получено оценок: 165.
Прямая и обратная пропорциональность – это базовые понятия математики. Чаще всего разного рода зависимости встречаются при решении задач. Разберемся вместе в том, что такое прямая пропорциональность.
Пропорциональность
Собственно любая пропорциональность это зависимость одного числа от другого. Выделяют прямую пропорциональность, при которой зависимое число при увеличении аргумента также увеличивается, и обратную пропорциональность. При обратной пропорциональности, уменьшении аргумента приводит к уменьшению зависимого числа.
Аргументом зовется число, которое меняется в процессе решения. Зависимым числом называют число, которое меняется в зависимости от изменений аргументов. В пропорциональных зависимостях аргумент и зависимое число могут меняться местами. Все зависит от конкретных задач при решении.
Прямая пропорциональность
Рассмотрим пример прямой пропорциональности на классической задаче на движение. Если автомобиль движется с постоянной скоростью 120 км/ч, то можно выделить три величины, которые описывают движение автомобиля:
Рассмотрим зависимость пройденного пути от времени. Если прошел один час, то всего автомобиль проехал 120 км, если два часа 240 км. То есть при увеличении времени в два раза, в два раза увеличивается и путь, такая зависимость и зовется прямой пропорциональной.
Обратите внимание, что всегда зависимое число возрастает во столько же раз, во сколько возрастает аргумент.
При этом, всегда аргумент может быть уменьшен, при этом уменьшится и зависимое число во столько же раз. Отношение двух чисел, находящихся в прямо пропорциональной зависимости называется коэффициентом пропорциональности и остается неизменным вне зависимости от изменения этих чисел.
Формула прямой пропорциональности выглядит так: у=кх и одновременно является функцией графика прямой линии. Причем число к и есть тот самый коэффициент пропорциональности.
Свойства пропорции
Вне зависимости от вида пропорциональности, соблюдаются свойства пропорции, которые говорят о том, что произведение крайних членов пропорции равняется произведению средних членов пропорции. То есть:
а*р=в*с – если использование этого свойства кажется ученику оправданным – его право использовать свои знания при решении задач.
Прямая пропорциональность чаще встречается в геометрии, чем в алгебре. Например, при изучении подобных треугольников, можно заметить, что соответствующие стороны треугольников относятся друг к другу с одинаковым коэффициентом подобия.
Поэтому для того, чтобы построить подобный треугольник нам придется использовать коэффициент прямой пропорциональности. Также нельзя забывать, что при прямой пропорциональности коэффициент всегда больше единицы.
Что мы узнали?
Мы сказали о том, что такое пропорциональность. Выделили основные виды пропорциональности и рассмотрели на примере прямо прямую пропорциональность пройденного пути от времени.
Прямая и обратная пропорциональность — формулы, свойства и графики функций
Одно из основных понятий курса математики в 6 классе – это прямая и обратная пропорциональность. Если некоторая величина (время, масса, цена) изменяется, и одновременно другая величина (расстояние, объем, затраты) тоже меняется, то величины находятся в зависимости между собой, то есть пропорциональны друг другу.
Взаимосвязь между величинами не всегда означает наличие пропорциональности. Так, высота дерева растет с его возрастом, но не во столько же раз. Составление пропорций помогает решить многие задачи как в математике, так и на практике.
Прямая пропорциональность
Если при изменении одного параметра другой изменяется таким же образом, то эти величины прямо пропорциональны друг другу. В этой пропорции увеличение расстояния вдвое означает увеличение времени также двукратно.
Например, при движении автомобиля с постоянной скоростью, время, затраченное на преодоление расстояния, будет прямо пропорционально этому расстоянию. То есть, если 50 км автомобиль проедет за 1 час, то 100 км с той же скоростью он преодолеет за 2 часа.
Функция прямой пропорциональности и ее график
Эта зависимость описывается следующей формулой:
Здесь k и называется коэффициентом пропорциональности.
Графически функция изображается прямой, которая пройдет через начальную точку координат. Строят график следующим образом: находят одну точку, затем чертят прямую через эту точку и начало координат.
Пример построения
Нужно построить график у = 3х. Подставляем вместо х единицу, вычисляем y = 3, то есть находим координаты (1; 3). Отмечаем эту точку на координатной плоскости, проводим прямую линию через нее и точку (0; 0).
Вот так будет выглядеть график y = k * x при k > 0 (слева) и при k Свойства функции прямой пропорциональности
Основные свойства следующие:
область определения, значений составляют все действительные числа;
возрастает при всех значениях x, если k > 0;
если коэффициент со знаком «-», т. е. если k 0, то прямая располагается в 1 — 3 координатных четвертях и образует острый угол с осью Х, если k Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Свойства функции обратной пропорциональности
области определения, значений функции D(y) – это все действительные числа, кроме 0, т. е. D(y):= x ≠ 0;
если коэффициент больше 0, функция является убывающей для всех x; если меньше 0, то y увеличивается для любых значений x;
оси координат 0х и 0у — это асимптоты по отношению к ветвям гиперболы, которые приближаются к ним, но не достигают их.
К составлению математических пропорций во многих случаях сводится решение самых разнообразных задач. Например, покупая 1 булочку по определенной цене, подсчитывают затраты на 4 булочки – получается в 4 раза больше.
Ускоряют шаг при ходьбе в 2 раза – достигнут цели вдвое быстрее. Вводят второго кассира в магазине – убывает очередь вдвое. Во всех этих случаях и им подобным применима теория о прямой и обратной пропорциональности.
Линейная функция. Прямая пропорциональность
Содержание
Из прошлого урока вы узнали многое о функциях, но далеко не все. Вспомним основные знания, которые нам будут нужны для понимания линейной функции:
Вот о функциях, график которых выглядит как прямая линия, и пойдет речь в данном уроке.
Примеры линейных функций
| $x$ | $4$ | $5$ | $6$ | $7$ |
| $y$ | $700$ | $750$ | $800$ | $850$ |
Что такое линейная функция
Прямая пропорциональность и другие особые случаи
Давайте посмотрим, какие функции также будут линейными:
Вспомнить, что такое прямая зависимость
Если при увеличении одной величины, увеличивается другая, то величины называют прямо пропорциональными, у них прямая зависимость.
Чем больше денег — тем больше можно купить мороженого
Прямая и обратная пропорциональность. Формулы, обозначение, примеры
Функция и ее свойства
Функцией прямой пропорциональности является частный случай линейной функции. Если линейная функция это y = k*x + b, то для прямой пропорциональности это выглядит так: y = k*x, гдеk называется коэффициентом пропорциональности, и это всегда не равно нулю число. Вычислитьk легко – он находится как частное функции и аргумента: k = у/х.
А теперь от прикладного применения знаний о прямой пропорциональности вернемся обратно к ее функции. К свойствам которой относится:
областью ее определения является множество всех действительных чисел (а также его подмножества);
изменение переменных прямо пропорционально осуществляется по всей длине числовой прямой.
Видео
Исследование функции прямой пропорциональности и ее график
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
Прямая пропорциональность характеризуется следующими свойствами:
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
Если k 0 при x 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
В качестве примера можно рассмотреть такие функции:
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
a и d называются крайними членами, b и c — средними.
Основное свойство пропорции
Произведение крайних членов равно произведению средних членов.
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
Формула прямой пропорциональности
y = kx,
где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
Пример 1.
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратная пропорциональность
Рост одного параметра ведет к уменьшению другого в такое же количество раз, и наоборот, при уменьшении одной величины другая увеличивается во столько же. Это значит, что они обратно пропорциональны друг другу.
Пример: трое рабочих выполнят порученную им работу за 2 часа, а 6 человек такое же задание осилят за 1 час. То есть двукратное увеличение числа работников привело к уменьшению затраченного времени вдвое. Конечно, если прочие факторы неизменны (производительность труда, условия работы).
Функция обратной пропорциональности и ее график
Функция задается формулой:
где k – любое действительное число, кроме 0.
График данной зависимости — это гипербола, ее ветви находятся в 1 и 3 четвертях системы координат при k > 0, или во 2 и 4, если коэффициент меньше 0. Ветви гиперболы симметричны относительно точки (0; 0).
Строят график так: нужно задать значения х, затем вычислить значения у, результаты оформить в виде таблицы. Верхняя строка таблицы заполняется значениями х, нижняя — y.
Пример построения
Нужно построить график функции y = 8/x.
Вот так выглядит таблица для данной функции:
Полученные точки отмечают на координатной плоскости, затем соединяют плавной линией. График будет выглядеть так:
Прямая и обратная пропорциональности
Лекция 19. Прямая и обратная пропорциональность
1. Прямая и обратная пропорциональность, линейная и квадратичная функции, их свойства и графики.
2. Построение графиков функций.
3. Основные выводы
Название функции у = kх связано с тем, что в формуле у = kх есть переменные х и у, которые могут быть значениями величин. А если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае y/x = k (k ≠ 0). Это число называют коэффициентом пропорциональности.
Функция у = kх является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана выше. Другой пример: если в одном пакете муки 2 кг, а куплено х таких пакетов, то всю массу купленной муки (обозначим ее через у) можно представить в виде формулы у = 2х, т.е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k = 2.
Напомним некоторые свойства прямой пропорциональности, которые изучаются в школьном курсе математики.
1. Областью определения функции у = kх и областью ее значений является множество действительных чисел.
2. 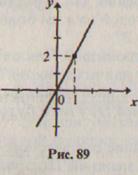
Например, чтобы построить график функции у = 2х, достаточно иметь точку с координатами (1, 2), а затем через нее и начало координат провести прямую (рис. 89).
3. При k > 0 функция у = kх возрастает на всей области определения; при k
Перейдем теперь к рассмотрению функции, называемой обратной пропорциональностью.
Определение. Обратной пропорциональностью называется функция, которая может быть задана при помощи формулы у = k/x, где k – не равное нулю действительное число.
Название данной функции связано с тем, что в у = k/x есть переменные x и у, которые могут быть значениями величин. А если произведение двух величин равно некоторому числу, отличному от нуля, то их называют обратно пропорциональными. В нашем случае xy = k (к ≠ 0). Это число k называют коэффициентом пропорциональности.
Функция у = k/x является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана перед определением обратной пропорциональности. Другой пример: если купили 12 кг муки и разложили ее в x банок по у кг в каждую, то зависимость между данными величинами можно представить в виде х · у = 12, т.е. она является обратной пропорциональностью с коэффициентом k = 12.
Напомним некоторые свойства обратной пропорциональности, известные из школьного курса математики.
1. Областью определения функции у = k/x и областью ее значений x является множество действительных чисел, отличных от нуля.
2. Графиком обратной пропорциональности является гипербола.
3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция у = k/x является убывающей на всей области определения x (рис. 90). При k
Дата добавления: 2014-01-06 ; Просмотров: 2515 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Значение слова пропорциональность
Пропорциональность в словаре кроссвордиста
пропорциональность
Пропорциональность Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным. Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.
ж.отвлеч. сущ. по прил. пропорциональный
Большой современный толковый словарь русского языка
Новый словарь иностранных слов
ж. Отвлеч. сущ. по знач. прил.: пропорциональный.
Новый толково-словообразовательный словарь русского языка Ефремовой
Словарь иностранных выражений
Словарь русского языка Лопатина
Словарь русского языка Ожегова
простейший вид функциональной зависимости (см. Функция). Различают прямую пропорциональность. (y =kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S =vt ; величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y =a/x.
Современный толковый словарь, БСЭ
пропорциональность ж. Отвлеч. сущ. по знач. прил.: пропорциональный.
Толковый словарь Ефремовой
пропорциональности, мн. нет, ж. (книжн.).
1. Отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения.
2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный во 2 знач.) изменяются (мат.). Обратная пропорциональность. Прямая пропорциональность.
Толковый словарь русского языка Ушакова
— соблюдение пропорций, рациональных структурных соотношений в экономике, согласованное развитие отраслей, сфер, регионов.
Словарь экономических терминов
Большая советская энциклопедия, БСЭ
Полный орфографический словарь русского языка
; соразмерность правильное соотношение между чем-либо пропорциональная зависимость каких-либо величин, количеств
пропорциональность силы массам и обратная пропорциональность квадрату расстояния) проверена с гораздо большей точностью, чем точность определения коэффициента G.
Маслов высказались в печати по этому «щекотливому вопросу», указавши на обратную пропорциональность (евреев и не-евреев) в правящем классе России, создающую предпосылки для юдофобии во всем населении страны.
Поэтому поддерживай пропорциональность занятий и естественным образом продлевай непоколебимую ясность, свободную от деятельности мышления.
Знали они, в частности, геометрическую пропорциональность и притом подвинулись в этом отношении так далеко, что умели, где требуется, применять увеличенный или уменьшенный масштаб.
Что такое прямо пропорционально и обратно пропорционально?
Что такое прямо пропорционально и обратно пропорционально?
Две величины называются прямо пропорциональными, если при увеличении одной из них в несколько раз другая увеличивается во столько же раз. Обратная пропорциональность. Две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.
Как рассчитать прямо пропорционально?
Прямую пропорциональность можно задать формулой. Формулу y=kx, где y и x — переменные величины, а k — постоянная величина, называют формулой прямой пропорциональности.
Как это обратно пропорционально?
Это значит, что скорость обратно пропорциональна времени. Если при увеличении (уменьшении) одной величины в несколько раз другая величина уменьшается (увеличивается) во столько же раз, то эти величины называют обратно пропорциональными. Обрати внимание! Произведение обратно пропорциональных величин не изменяется.
Что такое прямая пропорциональность?
Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.
Что такое пропорциональные величины?
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным. Равенство между отношениями двух или нескольких пар чисел или величин в математике называется пропорцией.
Как выглядит прямая пропорциональность?
Прямой пропорциональностью называется функция, которую можно задать формулой y = kx, где х – независимая переменная, k – не равное нулю число. Число k называют коэффициентом прямой пропорциональности. График прямой пропорциональности представляет собой прямую, проходящую через начало координат (см. рисунок).
Что такое прямая пропорциональность в алгебре?
Мы знаем, что графиком данного уравнения является прямая линия, каждая точка которой характеризуется двумя числами – координатами х и у – абсциссой и ординатой, и каждая точка удовлетворяет заданному уравнению. Данная функция называется прямой пропорциональностью.
Как выглядит линейная функция?
Понятие линейной функции Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент. Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Как определить линейная функция возрастает или убывает?
линейная функция или возрастает, или убывает. Если k>0, то линейная функция y = kx + m возрастает; если k Как определить функция линейная или нет?
Как проверить, проходит ли график через точку Достаточно подставить координаты точки в формулу функции (координату по оси «Ox» вместо «x», а координату по оси «Oy» вместо «y») и выполнить арифметические расчеты. Если получится верное равенство, значит, точка принадлежит графику функции.
Что такое К и Б в графике?
Линейной функцией называется функция вида y = kx + b, заданная на множестве всех действительных чисел. Здесь k – угловой коэффициент (действительное число), b – свободный член (действительное число), x – независимая переменная.
Что такое к в графике?
Как найти коэффициент k в графике функции?
Что такое угловой коэффициент k?
Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох. Он лежит в пределах от 0 до 180 градусов. То есть, если мы приведём уравнение прямой к виду y = kx + b, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Что значит угловой коэффициент?
Угловой коэффициент— коэффициент k в уравнении прямой на плоскости y = kx + b. Он численно равняется тангенсу угла между выбранной прямой и осью 0х. Этот угол отсчитывается от положительного направления оси 0х до прямой против хода часовой стрелки и располагается и пределах от 0 до 180 градусов.
Что означают коэффициенты в уравнении прямой?
Уравнение прямой в отрезках Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения с осью Оу.
В чем измеряется угловой коэффициент?
Угловой коэффициент равен отношению количества делений на оси Y к количеству делений на оси Х; в нашем примере угловой коэффициент равен 5/7.
Как составить уравнение с угловым коэффициентом?
Как найти угловой коэффициент производной?
Как связаны угловой коэффициент прямой и угол между прямой и положительным направлением оси абсцисс?
прямой на координатной плоскости, численно равен тангенсу угла (составляющего наименьший поворот от оси Ox к оси Оу) между положительным направлением оси абсцисс и данной прямой. При этом большим значениям углового коэффициента k будет соответствовать более крутая прямая, а меньшим — более пологая.
Что называют углом между прямой и положительным направлением оси абсцисс?
Угол наклона прямой к оси Ox в фиксированной прямоугольной декартовой системе координат Oxy на плоскости — это угол, отсчитываемый от положительного направления оси Ох до прямой против хода часовой стрелки. Угловым коэффициентом прямой называется тангенс угла наклона этой прямой.
Что называется угловым коэффициентом функции в данной точке?
Число k= tgα называется угловым коэффициентом прямой, а угол α – углом между этой прямой и осью Ох. Геометрический смысл производной. производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке. В этом и состоит геометрический смысл производной.
Что такое угловой коэффициент прямой и каков его геометрический смысл?
Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Таким образом, чтобы найти угловой коэффициент прямой, если известен ее угол наклона, нужно найти тангенс этого угла.
Что такое угловой коэффициент линейной функции?
Как найти угловой коэффициент прямой онлайн?
Разделив разницу y-координат на разницу x-координат, можно получить угловой коэффициент прямой:
Что такое угловые коэффициенты линейных функций?
Угловой коэффициент характеризует угол наклона прямой к оси абсцисс (угловой коэффициент численно равен тангенсу этого угла). Угловой коэффициент присутствует в уравнении прямой и используется в математическом анализе кривых, где всегда равен производной функции.
Прямая и обратная пропорциональности



Если t — время движения пешехода (в часах), s — пройденный путь ( километрах), и он движется равномерно со скоростью 4 км/ч, то зависимость между этими величинами можно выразить формулой s = 4t Так как каждому значению t соответствует единственное значение, то можно говорить о том, что с помощью формулы s = 4t задан функция. Ее называют прямой пропорциональностью и определяю следующим образом.
Определение. Прямой пропорциональностью называется функции которая может быть задана при помощи формулы у =kx, где k не равное нулю действительное число.
Название функции у = kх связано с тем, что в формуле у = kх есть переменные х и у, которые могут быть значениями величин. А если отношение двух величин равно некоторому числу, отличному от нуля, их называют прямо пропорциональными. В нашем случае 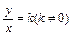
Это число называют коэффициентом пропорциональности.
Функция у = kх является математической моделью многих реальных ситуаций, рассматриваемых уже в начальном курсе математики. Одна из них описана выше.
Другой пример: если в одном пакете муки 2 кг, а куплено х таких пакетов, то всю массу купленной муки (обозначим ее через у) можно представить в виде формулы у = 2х, т. е. зависимость между количеством пакетов и всей массой купленной муки является прямой пропорциональностью с коэффициентом k = 2.
Напомним некоторые свойства прямой пропорциональности, которые изучаются в школьном курсе математики.
1. Областью определения функции у = kх и областью ее значений является множество действительных чисел.
2. Графиком прямой пропорциональности является прямая, проходящая через начало координат. Поэтому для построения графика прямой пропорциональности достаточно найти лишь одну точку, принадлежащую ему и не совпадающую с началом координат, а затем через эту точку и начало координат провести прямую.
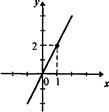 |
Например, чтобы построить график функции у = kх, достаточно иметь точку с координатами (1, 2), а затем через нее и начало координат провести прямую (рис. 7).
3. При k > 0 функция у = kх возрастает на всей области определения, при k
Замечание. Если значениями переменных х и у служат положительные действительные целые числа, то доказанное свойство прямой пропорциональности можно сформулировать так: с увеличением (уменьшением) значения переменной х в несколько раз соответствующее значение переменной у увеличивается (уменьшается) во столько же раз.
Это свойство присуще только прямой пропорциональности, и им можно пользоваться при решении текстовых задач, в которых рассматриваются прямо пропорциональные величины.
Задача 1. За 8 ч токарь изготовил 16 деталей. Сколько часов потребуется токарю на изготовление 48 деталей, если он будет работать с той же производительностью?
Решить задачу можно двумя арифметическими способами:
1 способ: 2 способ:
1) 16:8 =2 (дет.) 1) 48:16 = 3 (раза)
2) 48:2=24(ч) 2) 8×3=24(ч)
Решая задачу первым способом, мы сначала нашли коэффициент пропорциональности k, он равен 2, а затем, зная, что у = 2х, нашли значение х при условии, что у = 48.
При решении задачи вторым способом мы воспользовались свойством прямой пропорциональности: во сколько раз увеличивается количество деталей, сделанных токарем, во столько же раз увеличивается и количество времени на их изготовление.
Перейдем теперь к рассмотрению функции, называемой обратной пропорциональностью.
Если t — время движения пешехода (в часах), v— его скорость (в км/ч) и он прошел 12 км, то зависимость между этими величинами можно выразить формулой v × t = 20 или v = 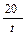
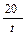
Название данной функции связано с тем, что в 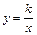
Функция 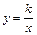
Одна из них описана перед определением обратной пропорциональности.
Другой пример: если купили 12 кг муки и разложили ее в х пакетов по у кг в каждую, то зависимость между данными величинами можно представить в виде х×у = 12, т.е. она является обратной пропорциональностью с коэффициентом k = 12. Напомним некоторые свойства обратной пропорциональности, известные из школьного курса математики.
1. Областью определения функции 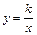
2. Графиком обратной пропорциональности является гипербола.
3. При k > 0 ветви гиперболы расположены в 1-й и 3-й четвертях и функция 
Значение слова «пропорциональный»
1. Обладающий пропорцией, находящийся в соразмерном соотношении частей. Пропорциональное сложение. □ [У Пушкина] было небольшое лицо и прекрасная, пропорциональная лицу, голова, с негустыми, кудрявыми волосами. И. Гончаров, Воспоминания. || Осуществляющийся с соблюдением пропорции, соразмерного соотношения частей. Пропорциональное развитие народного хозяйства. Пропорциональное распределение.
2. Находящийся в соответствующей зависимости от чего-л. Генерал жил во втором этаже и занимал помещение по возможности скромное, хотя и пропорциональное своему значению. Достоевский, Идиот.
3. Мат. Такой, который с увеличением или уменьшением одной из величин изменяется во столько же раз, находящийся в соотносительной количественной зависимости. Прямо пропорциональные величины. Обратно пропорциональные величины. □ Вычисления показали, что эта энергия [ветра] прямо пропорциональна высоте волн. Шулейкин, Дни прожитые.
[От лат. proportionalis — соразмерный]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Пропорциональные (между собой) величины. Прямо пропорциональные (см. прямой в 9 знач.), обратно пропорциональные (см. обратный в 4 знач.) величины. Пропорциональное деление (деление данной величины на части, пропорциональные заданным числам). Пропорционально (нареч.) чему-н. увеличиваться, уменьшаться. Длина окружности пропорциональна ее радиусу. || Находящийся в определенных соотношениях, в определенном количественном соответствии с чем-н. Пропорциональное обложение, п. налог (обложение всех доходов в одинаковом проценте, независимо от их величины, в противоп. прогрессивному; экон.). Пропорциональное представительство, пропорциональные выборы, пропорциональная избирательная система (система, при к-рой голосуют за списки, и количество избранных из списка соответствует количеству поданных за список голосов; полит.). П. циркуль (циркуль, употр. при увеличении или уменьшении чертежей в определенном масштабе; спец.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
пропорциона́льный
1. обладающий правильными пропорциями; соразмерный ◆ Старичок был весь чистота и благообразие: на лице его не было ни желтых пятен, ни морщин, обыкновенно портящих лица карликов; у него была очень пропорциональная фигурка, круглая как шар головка, покрытая совершенно белыми, коротко остриженными волосами, и небольшие коричневые медвежьи глазки. Н. С. Лесков, «Старые годы в селе Плодомасове», 1862 г. ◆ У него были большие загорелые руки, пропорциональные росту, с широкими ногтями. И. А. Гончаров, «Обрыв», 1869 г. ◆ Очевидно, что затрата сил должна быть пропорциональна трудности задачи〈…〉 Н. Я. Данилевский, «Россия и Европа», 1869 г. (цитата из НКРЯ)
2. осуществляющийся с соблюдением пропорции, соразмерного соотношения частей ◆ Всё, что было свежего, делилось пропорциональными частями, и опять ни одной жалобы и ни одного упрёка. Г. И. Невельской, «Подвиги русских морских офицеров на крайнем Востоке России», 1878 г. (цитата из НКРЯ) ◆ Горизонтальное бюджетное уравнивание подразумевает пропорциональное распределение налогов между субъектами федерации для нивелирования неравенства налоговых возможностей разных территорий. Т. Маглакелидзе, «Необходимость регулирования межбюджетных отношений в переходной экономике» (2003) // «Финансы и кредит», 15 мая 2003 г. (цитата из НКРЯ)
3. находящийся в определённом количественном соотношении с чем-либо ◆ Становясь на эту обобщающую точку зрения, мы не можем поэтому согласиться с коллективистами и не можем признать, чтобы вознаграждение, пропорциональное числу часов, употребленных каждым на производство этих богатств, представляло собою идеал или хотя бы шаг вперед по направлению к идеалу. П. А. Кропоткин, «Хлеб и воля», 1892 г. (цитата из НКРЯ) ◆ Применение пропорциональной системы, господствовавшей до 1993 года, при распределении депутатских мандатов на парламентских выборах вело к широкому представительству многих партий в обеих палатах парламента. Ж. М. Елубаева, «Система распределения доходных источников в Итальянской республике» (2003) // «Финансы и кредит», 19 мая 2003 г. (цитата из НКРЯ)
4. матем. такой, который с увеличением или уменьшением одной из величин изменяется во столько же раз, находящийся в соотносительной количественной зависимости ◆ Вообще, многоугольники называются подобные, когда в них все бока пропорциональны, все углы равны, притом бока следуют в том же порядке, в каком равные углы. Н. И. Лобачевский, «Новые начала Геометрии с полной теорией параллельных», 1835–1838 г. (цитата из НКРЯ) ◆ Лодж полагает, что количество пара, образующегося в каждый данный промежуток времени, не имеет надобности быть прямо пропорциональным количеству поглощаемого тепла и что, следовательно, вещество может перегреваться. А. М. Бутлеров, «Теоретические и экспериментальные работы по химии», 1851–1886 г. (цитата из НКРЯ)
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова грызенный (прилагательное):
6.1.3. Прямо пропорциональные величины
I. Прямо пропорциональные величины.
Пусть величина y зависит от величины х. Если при увеличении х в несколько раз величина у увеличивается во столько же раз, то такие величины х и у называются прямо пропорциональными.
Примеры.
1. Количество купленного товара и стоимость покупки (при фиксированной цене одной единицы товара — 1 штуки или 1 кг и т. д.) Во сколько раз больше товара купили, во столько раз больше и заплатили.
2. Пройденный путь и затраченное на него время (при постоянной скорости). Во сколько раз длиннее путь, во столько раз больше потратим времени на то, чтобы его пройти.
3. Объем какого-либо тела и его масса. (Если один арбуз в 2 раза больше другого, то и масса его будет в 2 раза больше)
II. Свойство прямой пропорциональности величин.
Если две величины прямо пропорциональны, то отношение двух произвольно взятых значений первой величины равно отношению двух соответствующих значений второй величины.
Задача 1. Для малинового варенья взяли 12 кг малины и 8 кг сахара. Сколько сахара потребуется, если взяли 9 кг малины?
Решение.
Рассуждаем так: пусть потребуется х кг сахара на 9 кг малины. Масса малины и масса сахара — прямо пропорциональные величины: во сколько раз меньше малины, во столько же раз нужно меньше сахара. Следовательно, отношение взятой (по массе) малины (12:9) будет равно отношению взятого сахара (8:х). Получаем пропорцию:
12:9=8:х;
х=9·8:12;
х=6. Ответ: на 9 кг малины нужно взять 6 кг сахара.
Решение задачи можно было оформить и так:
Пусть на 9 кг малины нужно взять х кг сахара.
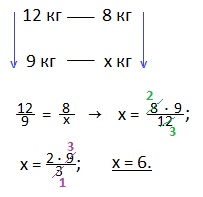
Ответ: на 9 кг малины надо взять 6 кг сахара.
Задача 2. Автомобиль за 3 часа проехал расстояние 264 км. За какое время он проедет 440 км, если будет ехать с той же скоростью?
Решение.
Пусть за х часов автомобиль пройдет расстояние 440 км.

Задача 3. Из трубы поступает вода в бассейн. За 2 часа она заполняет 1/5 бассейна. Какая часть бассейна заполняется водой за 5 часов?
Решение.
Отвечаем на вопрос задачи: за 5 часов наполнится 1/х часть бассейна. (Весь бассейн принимается за одну целую).