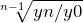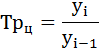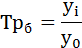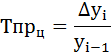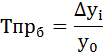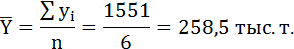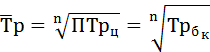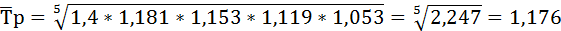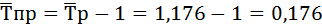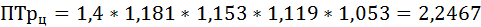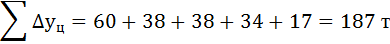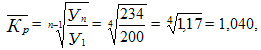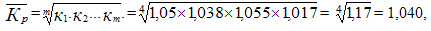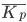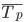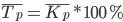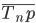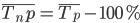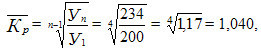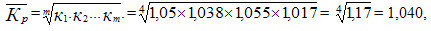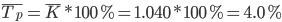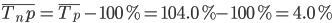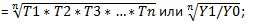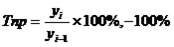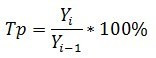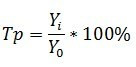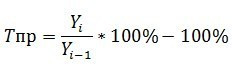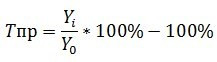Темп роста исчисляется как
Темп роста исчисляется как
Формула среднегодового темпа роста
Понятие темпа роста
Математическая статистика часто использует формулу темпа роста. Темп роста определяет интенсивность изменения (динамики) определенного явления.
Для того, что бы определить темп роста требуются следующие показатели:
Для расчета среднегодового темпа роста применяется временной интервал, который равен месяцу.
Понятие темп роста применяется во многих сферах (экономика, финансы, статистика, промышленность и др.). Темп роста является статистической величиной, позволяющей провести анализ:
Для вычисления темпа роста происходит сравнение значений, которые получены через выбранные промежутки времени.
Формула темпа роста
В общем виде, при наличии базисного и текущего показателя, формула темпа роста выглядит следующим образом:
Тр=Птек/Пбаз
Здесь Тр – темп роста,
Птек – показатель текущего периода,
Пкп – показатель базисного периода.
Что бы получить более наглядный результат, полученный ответ умножают на 100%, что позволяет выразить темп роста в процентах.
Порядок расчета среднегодового темпа роста
Для расчета среднего темпа роста требуется определить период, за который он будет рассчитан. В большинстве случаев таким периодом является календарный год или показатель, кратный ему.
Темп роста является относительным понятием, поскольку определяет изменение определенных величин по отношению к какому-либо начальному значению. Для расчета среднегодового темпа роста определяется начальное значение на 1 января исследуемого года. Расчет среднегодового темпа роста может проводиться в соответствии с величинами:
Общая формула расчета среднегодового темпа роста выглядит следующим образом:
Тр ср = 
Здесь n– количество месяцев (лет),
y0 – базисный показатель (например, на 1 января)
Особенности формулы среднегодового темпа роста
Формула среднегодового темпа роста использует в качестве базисного показателя численную величину, которая характеризует изучаемое явление и определяется по концу предыдущего года. Таким образом, базисная величина – это величина показателя на 1 января того года, для которого требуется определить темп роста.
При расчете формулы среднегодового темпа роста коэффициентом, базовый показатель принимают за единицу или 100 (если расчет осуществляется в процентах). В процессе вычисления базовых темпов роста на каждый месяц в году все показатели по окончанию каждого месяца должны соотноситься с базовым показателем (на 1 января).
При определении цепных показателей, за базовый показатель принимается показатель предыдущего периода, поэтому при расчете формула среднегодового темпа роста удобнее рассчитывается с помощью цепных показателей.
Значение среднегодового темпа прироста
За анализируемый период формула среднегодового темпа роста принимает календарный год, то есть промежуток с 1 января по 31 декабря. Для этого необходимы данные в абсолютном значении на конец каждого месяца. Всего должно быть 13 значение (базовый показатель и 12 показателей за каждый месяц).
Формула среднегодового темпа роста имеет значение, поскольку при ее расчете по нескольким годам можно получить результат для дальнейшего анализа и учета сезонных колебаний. Сам среднегодовой темп роста свободен от влияния фактора сезонности.
Примеры решения задач
| Задание | Рассчитайте среднегодовой темп роста по показателям, представленным за год: |
Январь – 240, февраль – 256, март – 258, апрель – 259, май – 262, июнь – 275, июль – 278, август – 279, сентябрь – 282, октябрь – 284, Ноябрь – 288, декабрь – 291.
Пср = (240+256+258+259+262+275+278+279+282+284+288+291) / 12 = 271 – среднее значение с 1 по 12 месяц.
Формула среднегодового темпа роста для решения данной задачи:
Тр ср =
Тр ср = 
| Задание | Рассчитать среднегодовой темп роста и прироста, по условным данным объема импорта государства: |
2011 год – 250 усл. ед.,
2012 год – 258усл. ед.,
2013 год – 262усл. ед.,
2014 год – 248усл. ед.,
2015 год – 259усл. ед.,
2016 год – 268усл. ед.,
Тр ср =
Тр ср = 
Вывод:За период с 2011 по 2016 год ежегодно объем импорта государства в среднем возрастал на 1,014 единиц.
Задача №56. Расчёт аналитических показателей динамики
Добыча нефти характеризуется следующими данными:
| Годы | Добыча нефти, тыс. т |
|---|---|
| 1-ый | 150 |
| 2-ой | 210 |
| 3-ий | 248 |
| 4-ый | 286 |
| 5-ый | 320 |
| 6-ой | 337 |
Произвести анализ ряда динамики по:
1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;
2) средний уровень и среднегодовой темп ряда динамики;
3) показать взаимосвязь между цепными и базисными показателями.
Решение:
Абсолютный прирост цепной (Δyц) – это разность между текущим уровнем ряда и предыдущим:
Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:
= 210 – 150 = 60 тыс. т.
В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:
Δyц 3-й год = 248 – 210 = 38 тыс. т.
Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.
Абсолютный прирост базисный (Δyб) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:
Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.
Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:
Δyб = 210 – 150 = 60 тыс. т
в 3-ем году базисный абсолютный прирост равен:
Δyб = y3 – y2 = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).
Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.
Цепной темп роста исчисляют отношением текущего уровня к предыдущему:
(гр. 5 расчётной таблицы);
базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:
(гр. 4 расчётной таблицы).
Темп прироста (Тпр) так же может быть цепной или базисный.
Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:
Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:
Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:
или как разность между темпами роста и 100%, если темпы роста выражены в процентах:
Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).
| Годы | Добыча нефти, тыс. т | Абсолютный прирост базисный, тыс. т | Абсолютный прирост цепной, тыс. т | Темп роста базисный, % | Темп роста цепной, % | Темп прироста базисный, % | Темп прироста цепной, % |
|---|---|---|---|---|---|---|---|
| А | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1-ый | 150 | 0 | — | 100,00 | — | — | — |
| 2-ой | 210 | 60 | 60 | 140,00 | 140,0 | 40,00 | 40,0 |
| 3-ий | 248 | 98 | 38 | 165,33 | 118,1 | 65,33 | 18,1 |
| 4-ый | 286 | 136 | 38 | 190,67 | 115,3 | 90,67 | 15,3 |
| 5-ый | 320 | 170 | 34 | 213,33 | 111,9 | 113,33 | 11,9 |
| 6-ой | 337 | 187 | 17 | 224,67 | 105,3 | 124,67 | 5,3 |
Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.
2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:
Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической
где ПТр – произведение цепных темпов роста (в коэффициентах),
– конечный базисный темп роста (в коэффициентах),
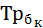
n – число темпов.
Среднегодовой темп прироста ряда динамики:
Добыча нефти ежегодно возрастала в среднем на 17,6%.
3) Между цепными и базисными темпами роста имеется взаимосвязь:
произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.
Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:
Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.
13 Ряды динамики
Статистическое изучение динамики социально-экономических явлений
Процессы и явления социально-экономической жизни общества, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении. Для того, чтобы выявить тенденции и закономерности социально-экономического развития явлений, статистика строит особые ряды статистических показателей, которые называются рядами динамики (иногда их называют временными рядами), то есть ‑ это ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В англоязычной литературе для временных рядов используется термин «time series». Ряды динамики получаются в результате сводки и обработки материалов периодического статистического наблюдения. Повторяющиеся во времени (по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности. Значения показателя, составляющие ряд динамики, называются уровнями ряда.
Каждый ряд динамики характеризуется двумя параметрами: значениями времени и соответствующими им значениями уровней ряда. Уровни ряда обычно обозначаются «yt»: y1, y2 и т.д. В качестве показателя времени в рядах динамики могут указываться отдельные периоды (сутки, месяцы, кварталы, годы и т.д.) времени или определенные моменты (даты). Время в рядах динамики обозначается через «t».
Ряд динамики состоит из двух элементов:
1) уровня ряда (значения изучаемого показателя);
2) моментов (периодов) времени, когда фиксируется этот показатель.
Основные способы обработки рядов динамики:
1) укрупнение интервалов и расчет для них средних показателей;
2) сглаживание уровней способом скользящей средней;
3) выравнивание по аналитическим формулам.
Суть последнего способа заключается в том, что по эмпирическим данным находят теоретические (вероятностные) уровни, которые рассматриваются как некая функция времени.
Ряды динамики, как правило, представляют в виде таблицы или графически.
Ряды динамики могут быть классифицированы по следующим признакам:
В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютных, относительных и средних величин. При этом ряды динамики абсолютных величин рассматриваются как исходные, а ряды относительных и средних величин ‑ как производные.
Ряды динамики абсолютных величин наиболее полно характеризуют развитие процесса или явления, например, грузооборота транспорта, инвестиций в основной капитал, добычи топлива, уставного капитала коммерческих банков и т.д.
Ряды относительных величин могут характеризовать во времени темпы роста (или снижения) определенного показателя; изменение удельного веса того или иного показателя в совокупности или изменение показателей интенсивности отдельных явлений, например, удельного веса приватизированных предприятий в той или иной отрасли; производства продукции на душу населения; структуры инвестиций в основной капитал по отраслям экономики, индекса потребительских цен и т.д.
Ряды динамики средних величин служат для характеристики изменения уровня явления, отнесенного к единице совокупности, например: данные о среднегодовой численности занятых в экономике; о средней урожайности отдельных сельскохозяйственных культур, о средней заработной плате в отдельных отраслях и т.д.
В зависимости от характера временного параметра ряды динамики делятся на моментные и интервальные.
Уровни моментных рядов динамики характеризуют явление по состоянию на определенный момент времени.
Пример. Моментный ряд динамики, характеризующий численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г., представлен в таблице 13.1.
Таблица 13.1 ‑ Численность персонала строительной фирмы на 1-е число каждого месяца за первое полугодие 2009 г
| Дата | 1.01 | 1.02 | 1.03 | 1.04 | 1.05 | 1.06 |
| Численность персонала, чел. | 780 | 810 | 880 | 930 | 940 | 970 |
Следует помнить, что моментные ряды абсолютных величин нельзя суммировать. Бессмысленно, например, складывать численность персонала по состоянию на 1 января, 1 февраля и т.д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же единицы совокупности.
Ряд, в котором уровни характеризуют результат, накопленный или вновь произведенный за определенный интервал времени, называется интервальным.
Пример. Интервальный ряд динамики, представлен в таблице 13.2.
Таблица 13.2. ‑ Характеристика динамики объема розничного товарооборота
| Дата | 2004 | 2005 | 2006 | 2007 | 2008 |
| Товарооборот, млн. руб. | 28,3 | 31,9 | 38,3 | 42,3 | 45,2 |
Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда вполне реальный показатель, например, общий объем розничного товарооборота за 2004-2008 г.г.
В зависимости от расстояния между уровнями, ряды динамики подразделяются на ряды с равноотстоящими уровнями и не равноотстоящими уровнями во времени.
Ряды динамики следующих друг за другом периодов или следующих через определенные промежутки дат называются равноотстоящими, пример (табл. 13.1 и табл. 13.2).
Если же в рядах даются прерывающиеся периоды или неравномерные промежутки между датами, то ряды называются не равноотстоящими, пример(табл. 13.3).
Пример. Рядом динамики с не равноотстоящими уровнями во времени может служить объем экспорта продукции предприятия, представленный в таблице 13.3.
Таблица 13.3. – Динамика объема экспорта продукции предприятия
| Годы | 1993 | 1996 | 1998 | 2000 | 2004 |
| Объем экспорта, млн. долл. | 1110 | 1220 | 1320 | 1450 | 1640 |
По числу показателей можно выделить изолированные (одномерные) и комплексные (многомерные) ряды динамики.
Если ведется анализ во времени одного показателя ряда, то ряд динамики изолированный (например, данные о производстве газа по годам). В многомерном ряду представлена динамика нескольких показателей, характеризующих одно явление.
Сопоставимость уровней и смыкание рядов динамики
Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней. Данное условие решается либо в процессе сбора и обработки данных, либо путем их пересчета.
Рассмотрим основные причины несопоставимости уровней ряда динамики.
Несопоставимость уровней ряда может возникнуть вследствие изменения единиц измерения и единиц счета.
Пример. Нельзя сравнивать и анализировать цифры о производстве тканей, если за одни годы оно дано в погонных метрах, а за другие ‑ в квадратных метрах.
На сопоставимость уровней ряда динамики непосредственно влияет методология учета или расчета показателей.
Например, если в одни годы среднюю урожайность считали с засеянной площади, а в другие ‑ с убранной, то такие уровни будут несопоставимы.
В процессе развития во времени, прежде всего, происходят количественные измерения явлений, а затем на определенных ступенях совершаются качественные скачки, приводящие к изменению закономерностей явления. Поэтому научный подход к изучению рядов динамики заключается в том, чтобы ряды, охватывающие большие периоды времени, разделять на такие, которые бы объединяли лишь однокачественные периоды развития совокупности, характеризующейся одной закономерностью развития.
Важно также, чтобы в ряду динамики интервалы или моменты, по которым определены уровни, имели одинаковый экономический смысл.
Например, при изучении роста поголовья скота бессмысленно сравнивать цифры поголовья по состоянию на 1 октября с данными 1 января, так как первая цифра включает не только скот, оставшийся на зимовку, но и предназначенный к убою, а вторая цифра включает только скот, оставленный на зимовку. Уровни ряда динамики могут оказаться несопоставимыми по кругу охватываемых объектов вследствие перехода ряда объектов из одного подчинения в другое.
Несопоставимость уровней ряда может возникнуть вследствие изменений территориальных границ областей, районов и так далее.
Для того, чтобы привести уровни ряда динамики к сопоставимому виду, иногда приходится прибегать к приему, который носит название смыкание рядов динамики. Под смыканием понимают объединение в один ряд (более длинный) двух или нескольких рядов динамики, уровни которых являются несопоставимыми. Для осуществления смыкания необходимо, чтобы для одного из периодов (переходного) имелись данные, исчисленные по разной методологии (или в разных границах).
Пример. Предположим, что в N-ом регионе имеются данные об общем объеме оборота розничной торговли за 2013-2015 гг. в фактически действующих ценах, и за 2015-2018 гг. ‑ в сопоставимых ценах (табл. 13.4.).
Таблица 13.4 ‑ Динамика общего объема оборота розничной торговли (млрд. руб.) цифры условные
Темпы роста и прироста, абсолютный прирост.
Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения.
Абсолютный прирост (базисный)
Абсолютный прирост с переменной базой (цепной), который называют скоростью роста,
Средний абсолютный прирост (средняя скорость роста) определяется как средняя арифметическая из показателей скорости роста за отдельные периоды времени:
Темп роста 
Темп прироста ТП определяется как отношение абсолютного прироста данного уровня к предыдущему или базисному.
Темп прироста базисный 
Темп прироста цепной 
Средний темп роста, %. Это средний коэффициент роста, который выражается в процентах:
Средний темп прироста 
, %. Для расчета данного показателя первоначально определяется средний темп роста, который затем уменьшается на 100%. Его также можно определить, если уменьшить средний коэффициент роста на единицу: 
Абсолютное значение одного процента прироста Ai. Этот показатель служит косвенной мерой базисного уровня. Представляет собой одну сотую часть базисного уровня, но одновременно представляет собой и отношение абсолютного прироста к соответствующему темпу роста.
Среднее абсолютное значение 1% прироста 
31.Среднегодовые темпы роста и прироста. Средний уровень динамического ряда, абсолютное значение 1% прироста.
Среднегодовой темп роста исчисляется в следующей последовательности:
1. сначала по формуле средней геометрической исчисляют среднегодовой коэффициент роста (снижения) — 
2. на базе среднегодового коэффициента определяют среднегодовой темп роста ( 
) путем умножения коэффиицента на 100%:
Среднегодовой темп прироста ( 
определяется путем вычитания из темпа роста 100%.
Среднегодовой коэффициент роста ( снижения ) по формулам средней геометрической может быть исчислен двумя способами:
1) на базе абсолютных показателей ряда динамики по формуле:
§ n — число уровней;
§ n — 1 — число лет в период;
2) на базе ежегодных коэффициентов роста по формуле
§ m — число коэффициентов.
Результаты расчета по формулам равны, так как в обеих формулах показатель степени — число лет в периоде, в течение которого происходило изменение. А подкоренное выражение — это коэффициент роста показателя за весь период времени (см. табл. 11.5, гр.6, по строке за 1998 г.).
Среднегодовой темп роста равен
Среднегодовой темп прироста определяется путем вычитания из среднегодового темпа роста 100%. В нашем примере среднегодовой темп прироста равен
Следовательно, за период 1995 — 1998 гг. объем производства продукта «А» в среднем за год возрастал на 4,0%. Ежегодные темпы прироста колебались от 1,7% в 1998 г. до 5,5% в 1997 г. (за каждый год темпы прироста см. в табл. 11.5, гр. 9).
Среднегодовой темп роста (прироста) позволяет сравнивать динамику развития взаимосвязанных явлений за длительный период времени (например, среднегодовые темпы роста численности работающих по отраслям экономики, объема производства продукции и др.), сравнивать динамику какого-либо явления по разным странам, исследовать динамику какого-либо явления по периодам исторического развития страны.
Абсолютное значение 1% прироста(гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 г. надо было произвести 2,0 тыс. т., а в 1998 г. — 2,3 тыс. т., т.е. значительно больше.
Определить величину абсолютного значения 1% прироста можно двумя способами:
§ уровень предшествующего периода разделить на 100;
§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.
Абсолютное значение 1% прироста = 
В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.
Заметим, что рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя заработная плата и т.п.).
Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики необходимо исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.
Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:
Среднегодовой объем производства продукта за 1994- 1998 гг. составил 218,4 тыс. т.
Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой:
Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см.гр.3), а среднегодовой прирост производства за период 1995 — 1998 гг. составил 8,5 тыс. т.
Методы расчета среднего темпа роста и среднего темпа прироста требуют более подробного рассмотрения. Рассмотрим их на примере приведенных в таблице годовых показателей уровня ряда.
Анализ рядов динамики
Для обоснованной оценки развития явлений во времени необходимо исчислить аналитические показатели: абсолютный прирост, коэффициент роста, темп роста, темп прироста, абсолютное значение одного процента прироста.
В таблице приведен цифровой пример, а ниже даны формулы расчета и экономическая интерпретация показателей ( таблица )
Абсолютные приросты ( Δy) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. — цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. — базисные абсолютные приросты). Формулы расчета можно записать следующим образом:
При уменьшении абсолютных значений ряда будет соответственно «уменьшение», «снижение».
Показатели абсолютного прироста свидетельствуют о том, что, например, в 1998 г. производство продукта «А» увеличилось по сравнению с 1997 г. на 4 тыс. т, а по сравнению с 1994 г. — на 34 тыс. т.; по остальным годам см. табл. 11.5 гр. 3 и 4.
Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 — цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 — базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:
Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 — цепные темпы роста) или по сравнению с начальным уровнем (гр.8 — базисные темпы роста). Формулы расчета можно записать следующим образом:
Так, например, в 1997 г. объем производства продукта «А» по сравнению с 1996 г. составил 105,5 % (
Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста ). Формулы расчета можно записать следующим образом:
Так, например, в 1996 г. по сравнению с 1995 г. продукта «А» произведено больше на 3,8 % (103,8 %- 100%) или (8:210)х100%, а по сравнению с 1994 г. — на 9% (109% — 100%).
Если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).
Абсолютное значение 1% прироста (гр. 11) показывает, сколько единиц надо произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 г. надо было произвести 2,0 тыс. т., а в 1998 г. — 2,3 тыс. т., т.е. значительно больше.
Определить величину абсолютного значения 1% прироста можно двумя способами:
Абсолютное значение 1% прироста =
В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.
Заметим, что рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя заработная плата и т.п.).
Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики необходимо исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.
Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:
Среднегодовой объем производства продукта за 1994- 1998 гг. составил 218,4 тыс. т.
Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической простой:
Ежегодные абсолютные приросты изменялись по годам от 4 до 12 тыс.т (см.гр.3), а среднегодовой прирост производства за период 1995 — 1998 гг. составил 8,5 тыс. т.
Методы расчета среднего темпа роста и среднего темпа прироста требуют более подробного рассмотрения. Рассмотрим их на примере приведенных в таблице годовых показателей уровня ряда.
Средний годовой темп роста и средний годовой темп прироста
Среднегодовой темп роста исчисляется в следующей последовательности:
Среднегодовой темп прироста ( определяется путем вычитания из темпа роста 100%.
Среднегодовой коэффициент роста ( снижения ) по формулам средней геометрической может быть исчислен двумя способами:
1) на базе абсолютных показателей ряда динамики по формуле:
2) на базе ежегодных коэффициентов роста по формуле
Результаты расчета по формулам равны, так как в обеих формулах показатель степени — число лет в периоде, в течение которого происходило изменение. А подкоренное выражение — это коэффициент роста показателя за весь период времени (см. табл. 11.5, гр.6, по строке за 1998 г.).
Среднегодовой темп роста равен
Среднегодовой темп прироста определяется путем вычитания из среднегодового темпа роста 100%. В нашем примере среднегодовой темп прироста равен
Следовательно, за период 1995 — 1998 гг. объем производства продукта «А» в среднем за год возрастал на 4,0%. Ежегодные темпы прироста колебались от 1,7% в 1998 г. до 5,5% в 1997 г. (за каждый год темпы прироста см. в табл. 11.5, гр. 9).
Среднегодовой темп роста (прироста) позволяет сравнивать динамику развития взаимосвязанных явлений за длительный период времени (например, среднегодовые темпы роста численности работающих по отраслям экономики, объема производства продукции и др.), сравнивать динамику какого-либо явления по разным странам, исследовать динамику какого-либо явления по периодам исторического развития страны.
Аналитические показатели динамики
Расчет аналитических производных показателей динамических рядов.
У нашего движка для создания калькуляторов онлайн появилась новая функциональность — возможность вводить для расчета произвольное число значений, иными словами, появилась входная таблица. Пользователь добавляет/редактирует/удаляет значения, калькулятор их подсчитывает.
Воспользовавшись этим, я немедленно создал калькулятор для расчета аналитических показателей статистических рядов динамики.
Тем более, что пользователь с ником Светлана очень давно просил калькулятор вычисляющий средний темп роста. Наконец-то это стало возможным. Но обо всем по порядку.
Начнем с теории.
Ряды динамики делятся на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемой величины на определенные момент времени. Интервальные ряды отображают состояние изучаемой величины за отдельные интервалы времени.
Приведу пример. Допустим, 1 января хлеб стоит 13 рублей, 1 февраля — 14 рублей, 1 марта — 15 рублей, это моментный ряд. Если за январь мы купили 10 буханок хлеба, за февраль — 12 буханок, за март — 14 буханок, это интервальный ряд. Заметим, что интервальный ряд обладает свойством суммарности, т. е. показатели можно складывать, и получится что-то осмысленное, например, потребление хлеба за три месяца.
Имея ряд показателей, можно просчитать всевозможные аналитические производные показатели. Производные показатели могут рассчитываться двумя основными способами — цепным и базисным.
При цепном методе каждый последующий показатель сопоставляется с предыдущим, при базисном — с одним и тем же показателем, принятым за базу сравнения. Обычно это первый показатель ряда.
Рассмотрим некоторые аналитические производные показатели:
Аналитические производные показатели
1. Абсолютный прирост
Разность значений двух показателей ряда динамики.
Базисный абсолютный прирост — разность текущего значения и значения принятого за постоянную базу сравнения
Цепной абсолютный прирост — разность текущего и предыдущего значений
2. Темп роста
Отношение двух уровней ряда (может выражаться в процентах).
Базисный темп роста — отношение текущего значения и значения принятого за постоянную базу сравнения
Цепной темп роста — отношение текущего и предыдущего значений
3. Темп прироста
Отношение абсолютного прироста к сравниваемому показателю.
Базисный темп прироста — отношение абсолютного базисного прироста и значения принятого за постоянную базу сравнения
Цепной темп прироста — отношение абсолютного цепного прироста и предыдущего значения показателя
4. Ускорение
Абсолютное ускорение — разница между абсолютным приростом за данный период и абсолютным приростом за предыдущий период равной длительности. Измеряется только цепным способом
Относительное ускорение — отношение цепного темпа прироста за данный период и цепного темпа прироста за предыдущий период
5. Темп наращивания
Отношение цепных абсолютных приростов к уровню, принятому за постоянную базу сравнения
6. Абсолютное значение одного процента прироста
Отношение абсолютного прироста к темпу прироста, выраженное в процентах.
После раскрытия формула упрощается до
Для получения обобщающих характеристик динамики изучаемого ряда рассчитываются средние показатели динамики.
Средние показатели динамики
1. Средний уровень
Характеризует типичную величину показателей
В интервальном динамическом ряду рассчитывается как простое арифметическое среднее
В моментном динамическом ряду с равными промежутками времени между отсчетами как хронологическое среднее
2. Средний абсолютный прирост
Обобщающий показатель скорости абсолютного изменения значений динамического ряда
3. Средний темп роста
Обобщающий характеристика темпов роста ряда динамики
4. Средний темп прироста
Отношение тоже что и между темпом роста и темпом прироста
Все производные и средние показатели, приведенные здесь, рассчитываются в калькуляторе (см. ниже) по мере того, как пользователь вводит значения ряда в таблицу.
На своей личной странице зарегистрированные пользователи могут сохранить калькулятор и запомнить введенные в него значения для повторного использования.
Относительные показатели динамики: темп роста (снижения), темп
Лекция No 8: «СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ
СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ»
Вступительная часть
1. Понятие рядов динамики
2. Показатели рядов динамики
3. Методы анализа рядов динамики
4. Методы изучения сезонных колебаний
ПОНЯТИЕ РЯДОВ ДИНАМИКИ
Одной из важнейших задач статистики является изучение изменений
анализируемых показателей во времени, т.е. их динамика. Эти изменения
можно изучать, если иметь данные по определенному кругу показателей на
ряд моментов времени или за ряд промежутков времени, следующих друг за
другом, при помощи анализа рядов динамики (временных рядов).
Рядами динамики называются статистические данные,
характеризующие изменение общественных явлений во времени.
Ряд динамики состоит из 2-х основных элементов:
1) показателя времени, t;
2) соответствующих им уровней развития изучаемого явления, у.
В качестве показателей времени в рядах динамики выступают либо
определенные даты (моменты) времени, либо отдельные периоды (годы,
кварталы, месяцы, сутки).
Уровнем ряда называется каждое отдельное числовое значение
показателя, характеризующего величину явления, его размер на определенную
дату или за определенный период времени. Уровни рядов динамики
отображают количественную оценку (меру) развития во времени изучаемого
4 явления. Они могут выражаться абсолютными, относительными или средними
Классификация рядов динамики осуществляется по следующим
1. По времени отражения в рядах динамики выделяют моментные
динамические ряды и интервальные.
Моментный ряд характеризует изменение изучаемого явления на
определенную дату. Так, посредством моментных рядов динамики изучают
товарные запасы, состояние кадров, количество оборудования и других
показателей, отображающих состояние изучаемых явлений на отдельные
даты (моменты) времени.
Интервальный ряд характеризует изменение изучаемого явления за
определенный период времени. Посредством интервальных рядов динамики
изучается изменение во времени поступления и реализации товаров, суммы
издержек обращения и других показателей, отображающих итоги
функционирования изучаемых явлений за отдельные периоды.
2. По полноте времени отражения в рядах динамики выделяют полные
динамические ряды, в которых даты следуют друг за другом с равным
интервалом, и неполные динамические ряды, в которых равные интервалы
между датами не соблюдаются.
3. В зависимости от показателей, представленных в рядах динамики
Различают: ряд динамики абсолютных величин, ряд динамики
Относительных величин, ряд динамики средних величин.
Средний уровень в моментном динамическом ряду определяется по
формуле средней хронологической, а в интервальном – по формуле средней
арифметической, причем, если ряд с равными интервалами применяется
средняя арифметическая простая, если ряд с неравными интервалами –
средняя арифметическая взвешенная.
5 При построении динамического ряда необходимо соблюдать правила их
построения и, в первую очередь, условия сопоставимости уровней:
1. Уровни динамического ряда должны охватывать одинаковый круг
объектов: все категории хозяйств, личные подсобные хозяйства, фермерские
хозяйства, сельскохозяйственные предприятия всех форм собственности.
2. Уровни ряда должны отражать изучаемое явление в одинаковых
3. Методика расчета показателей должна быть одинаковой за период
4. При построении динамических рядов необходимо учитывать единицы
измерения и размерность показателя.
5. Сопоставимость показателей по периоду или моменту наблюдений.
6. Необходимо учитывать периодическое изменение сопоставимых цен и
ПОКАЗАТЕЛИ РЯДОВ ДИНАМИКИ
Задача статистики заключается в том, чтобы выделить путем анализа
однородные этапы изучаемого явления, установить свойственные им
закономерности, охарактеризовать их при помощи статистических показателей.
Для этой цели рассчитываются следующие показатели динамики:
1. абсолютные показатели динамики: абсолютный прирост (снижение) и
среднегодовой абсолютный прирост (снижение);
относительные показатели динамики: темп роста (снижения), темп
прироста (снижения), среднегодовой темп роста (снижения);
3. абсолютное значение 1% прироста.
Для объективной оценки динамического ряда необходимо изучать
явления за длительный период времени (минимум 8–10 лет).
Расчет показателей динамики основан на сравнении уровней. Существует
два способа расчета показателей динамики: цепной и базисный. Принято
называть сравниваемый уровень отчетным, а уровень, с которым производят
При цепном способе расчета каждый последующий уровень
сравнивается с предыдущим.
При базисном способе каждый последующий уровень сравнивается с
уровнем года, принятым за базу сравнения.
Абсолютный прирост характеризует размер увеличения (или
уменьшения) уровня ряда за определенный промежуток времени. Он равен
разности двух сравниваемых уровней и выражает абсолютную скорость роста.
Цепной абсолютный прирост исчисляется как разность между
сравниваемым уровнем Y
и уровнем, который ему предшествует Y
− уровень предыдущего периода.
Базисный абсолютный прирост определяют как разность между
сравниваемым уровнем Y
и уровнем, принятым за базу сравнения, Y
б i Y базисный уровень.
Между базисным и цепным абсолютными приростами имеется связь:
сумма цепных абсолютных приростов равна базисному абсолютному приросту
последнего периода ряда динамики.
Средний абсолютный прирост показывает, на сколько единиц
увеличился или уменьшился уровень показателя по сравнению с базисным
уровнем в среднем за единицу времени. Он характеризует абсолютную
скорость роста уровня и определяется по формуле:
Y – конечный уровень ряда;
– начальный уровень ряда;
n – число уровней ряда.
Интенсивность изменения уровня оценивается темпом или
коэффициентом роста. Если показатель выражен в долях единицы, то он
называется коэффициентом роста, а если в процентах – темпом роста.
Темп роста (снижения) показывает, во сколько раз данный уровень
ряда больше базисного уровня (если темп роста больше 100%) или какую
часть базисного уровня составляет уровень текущего периода за некоторый
промежуток времени (если темп роста меньше 100%). Темп роста всегда
представляет собой положительное число.
8 Цепные темпы роста исчисляются делением сравниваемого уровня Y
предыдущий уровень Y
Базисные темпы роста определяют делением сравниваемого уровня Y
уровень, принятый за базу сравнения, Y
Между цепными и базисными коэффициентами роста существует
взаимосвязь: произведение последовательных цепных коэффициентов роста
равно базисному за соответствующий период:
Среднегодовой темп роста показывает, во сколько раз увеличился
уровень по сравнению с предыдущим в среднем за единицу времени. Его
определяют по формуле:
где k – цепные коэффициенты роста;
t – число цепных коэффициентов роста.
Относительную оценку скорости измерения уровня ряда в единицу
времени дают показатели темпа прироста (сокращения). Темп прироста
(сокращения) показывает, на сколько процентов сравниваемый уровень больше
(или меньше) базисного уровня.
Цепной темп прироста – это отношение сравниваемого цепного
абсолютного прироста А
к предыдущему уровню Y
9 Базисный темп прироста вычисляется делением сравниваемого
базисного абсолютного прироста А
на уровень, принятый за постоянную
базу сравнения Y
Темп прироста может быть положительным, отрицательным или равным
нулю, выражается он в процентах и долях единицы (коэффициент прироста).
Темп прироста (сокращения) можно получить и из темпа роста:
(%) – 100% (при выражении темпа роста в процентах),
– 1 (при выражении темпа роста в коэффициентах).
Аналогичным образом можно вычислить и среднегодовой темп
(%) – 100% (при выражении темпа роста в процентах),
– 1 (при выражении темпа роста в коэффициентах).
Абсолютное значение 1% прироста определяется отношением
абсолютного прироста к темпу прироста. Рассчитывается этот показатель
только цепным способом и выражается в натуральных единицах измерения:
п р Абсолютное значение 1% прироста равно сотой части предыдущего
уровня. Оно показывает, какое абсолютное значение скрывается за
относительным показателем – одним процентом прироста.
Абсолютное значение 1% прироста вычисляется в том случае, если
абсолютный прирост, принятый за базу сравнения, число положительное. Если
абсолютные приросты отрицательны, тогда данный показатель не рассчитывают.
Пример, Рассчитанные показатели оформлены в таблице.
10 Таблица 1 – Динамика посевной площади зерновых культур в Орловском
районе за 2001 – 2006 годы
Годы Посевная площадь зерна, тыс. га
Абсолютный прирост (снижение), тыс. га
Темп роста (снижения), %
Темп прироста, % Абсолютное
значение 1% при- роста, тыс. цепной базисный цепной базисный цепной базисный
Анализируя данные таблицы 1, можно сделать вывод о том, что цепные
показатели динамики имеют положительную тенденцию роста только в 2008
на 117,5 тыс. га или 18,7% и в 2009 гг. на 49,3 тыс. га или на 6,6%. Тогда как в
2007 г., 2009 – 2011 гг. наблюдается отрицательная тенденция роста
абсолютных и относительных снижений. Базисные показатели динамики
свидетельствуют о росте посевной площади зерновых культур в 2008 – 2011
гг. по сравнению с 2006 г. (так как рассчитанные показатели темпа роста выше
100%). Исключение составляет 2007 г., когда посевная площадь на10,8 тыс. га
или на 1,7% ниже, чем в 2006 г. Анализируя абсолютное значение 1%, мы
видим, что замедление темпа прироста сопровождается уменьшением
абсолютных приростов. Абсолютное значение 1% прирост наблюдается
только в 2008 и 2009 гг.Поскольку размер посевной площади колеблется из
года в год, общий вывод по абсолютным и относительным показателям
динамики мы сделать не можем.
Поэтому определим среднегодовые показатели динамики:
Темп роста и темп прироста — особенности расчета, формулы и примеры
Экономический рост и его факторы
Экономический рост – это изменение объема производимых в стране товаров и услуг.
Рост факторов производства может осуществляться двумя способами:
— увеличения количества работников, занятых на производстве/в сфере услуг.
— увеличения количества инвестиций (при условии, что техника и технологии производства не меняются);
— увеличение объемов потребляемого сырья, топлива, энергии и других ресурсов.
Например, чтобы печь больше хлеба, владелец хлебозавода может нанять новых работников и закупить больше муки для выпечки хлеба, то есть его затраты на производство увеличатся. Так, с помощью увеличения количественных характеристик производства, предприятие будет расти.
— использования в производстве новых технологий, более современной и качественной техники;
— повышение квалификации или уровня образования работников;
— увеличение качества и организации труда;
— улучшение использования ресурсов (устранение потери времени, безотходное производство) или улучшение качества ресурсов.
Для примера возьмем тот же хлебозавод. Если предприниматель решит пойти интенсивным путем, то он заменит старое оборудование на более современное, обучит работников обслуживать новую технику (то есть повысит их квалификацию), составит новый график работы, при котором новая аппаратура не будет простаивать, закупит муку высшего сорта для производства более качественного продукта.
В реальности интенсивный и экстенсивный пути развития не существуют в чистом виде. Как правило, они комбинируются в разных соотношениях. Примером такой комбинации может стать фермер, который решил расширить масштабы своего хозяйства. Он может одновременно использовать как экстенсивные (купить больше животных и земли под с/х культуры) и интенсивные (приобрести новую, более современною технику, более качественные корма для животных или культуры для посева).
Критика
После того, как термин ВВП стал активно использоваться в экономике, многие экономисты заявили, это понятие – отнюдь не показатель благосостояния общества. Даже сам Саймон Кузнец, основоположник этой теории и терминологии, говорил, что рост ВВП еще не означает рост экономического или социального благосостояния.
Такой скептицизм имеет под собой почву. Так как ВВП учитывает лишь операции по производству и продаже товаров и услуг, то этот показатель не может стать отображением социальной и природной системы, где существует человек. Наибольшее опасение у ученых вызывало то, что все методы подсчета ВВП является своего рода поощрением истощения природных богатств. Ведь доход страны растет именно за счет уменьшения природных ресурсов. Даже, невзирая на все эти выпады, практически во всем мире пытаются всеми силами увеличить ВВП.
Экономический рост в развитых странах
На современном этапе развития экономики, когда на хозяйственную жизнь огромное влияние оказывает научно-техническая революция (НТР), экономический рост приобретает новые характеристики:
Во-первых, от частично-интенсивного совершается переход к полностью интенсивному развитию. При этом производители могут экономить все виды ресурсов, в том числе и труд, то есть экономическое развитие становится ресурсосберегающим.
Во-вторых, развивается практика выпуска специализированных, созданных под конкретного человека, продуктов, и снижаются затраты на их производство (например, возможность печатать футболки, кружки и тетради с индивидуальным дизайном сейчас есть в любом городе, при этом стоимость таких индивидуализированных товаров не сильно превышает стоимость товаров массовых).
В-третьих, прирост производства происходить только за счет технического прогресса.
В-четвертых, переоценивается роль человеческого фактора в производстве. В современном мире труд человека становится более комфортным и безопасным, используются разные способы стимулирования труда (надбавки к заработной плате, премии).
В-пятых, появляется возможность выделять больше средств на охрану окружающей среды, например, предприятия выделяют деньги на очистительные установки, отходы человеческой жизнедеятельности перерабатываются. Появляется тенденция к сохранению невосполнимых природных ресурсов (угля, нефти, газа). В большинстве современных стран охрана окружающей среды и развитие экономики находятся под контролем государства.
О чем говорит изменение ВВП
Разобравшись с тем, что такое ВВП, давайте рассмотрим, чем важен этот показатель. Так, любое государство занимается производством товаров и услуг как для внутреннего потребления, так и для экспорта. Если их количество растет, значит, экономика развивается. Если же по какой-то причине рост товаров и услуг идет на спад, говорят о замедлении экономики.
Обычно экономисты измеряют темпы его роста, то есть процент, на который вырос показатель за определенный период (месяц, квартал, год). На графике ниже вы можете увидеть темпы роста ВВП США.
Когда темпы роста на протяжении нескольких лет растут менее чем на 2-3 %, это сигнализирует о состоянии, называемой рецессией. Если же наблюдается резкое сокращение ВВП — это один из сигналов наступления экономического кризиса.
На основании динамики роста ВВП выделяют еще два состояния экономики: стагнацию и депрессию. Стагнация имеет место тогда, когда ВВП почти не растет, но и не наблюдается резкого падения. Когда же несколько лет наблюдается сильное падение, это уже называется экономической депрессией и является затяжным кризисом.
Темпы экономического роста. Понятие ВВП
Экономический рост измеряется динамикой реального валового внутреннего продукта (ВВП), то есть объемом всех товаров и услуг, произведенных в стране за определенный отрезок времени (чаще всего за год) или на душу населения.
Формулы расчета темпа роста и темпа прироста (в процентах)
Темп роста – это показатель изменения объема ВВП. Он отражает, во сколько раз ВВП одного конкретного года (например, 2019) больше или меньше ВВП другого года (например, 2020).
В случае положительного экономического роста объем ВВП из года в год увеличивается, вследствие этого повышается уровень жизни населения, полнее удовлетворяются разные категории человеческих потребностей, у государства появляется возможность решить социально-экономические проблемы.
В случае отрицательного экономического роста объем ВВП из года в год падает, это происходит из-за экономических проблем или кризиса в стране, приводит к ухудшению уровня жизни людей, возникновению социально-экономических конфликтов.
История
С аббревиатурой ВВП знаком каждый. Это – валовой внутренний продукт, исчисляемый по ценам года выпуска. Эти оба показателя являются отражением результатов экономики за прошедший год.
Сам термин ВВП пришел из Америки, его праотцом стал экономист Саймон Кузнец, он еще в начале двадцатого века делал расчеты по определению национального дохода США. За эти разработки он даже удостоился Нобелевской премии, так как они были выделены, как значимый вклад в развитие экономики.
Однако, наиболее широко этот термин и все, что с ним связано, стало применяться после 1991 года.
Многие экономисты были и остаются против самого понятия и методов расчета ВВП. Это связано с тем, что ВВП базируется только на основе денежных операций, поэтому вся картина проявляется не в полной мере. Несмотря на это, во всех странах широко используется этот термин и, более того, вся мировая экономика строится на этом показателе.
В чем разница между реальным и номинальным ВВП
Реальный рассчитывается с учетом множества макроэкономических показателей и дефлятор, что позволяет узнать фактический объем произведенных товаров и услуг и сделать анализ изменений в экономике. Разница в том, что номинальный вычисляется без корректировок на какие-либо показатели.
Еще одно отличие реального ВВП от номинального – зависимость номинального показателя от индексации и роста цен. Во время инфляции номинальный ВВП растет, так как имеет прямую зависимость от уровня цен. Если цены падают, то и номинальный показатель состояния экономики тоже стремится вниз.
Реальный показатель учитывает, в какой степени за определенный промежуток времени выросло производство, а не на сколько изменились цены.
Разница между номинальным и реальным ВВП
| Реальный | Номинальный |
| Оценивает динамику роста экономики. | Показывает состояние экономики лишь поверхностно. Как правило, он близок к действительным показателям ситуации только в том случае, если инфляция близка к нулю. |
| В большей степени взаимосвязан с паритетом покупательской способности населения. | Существенно отличается от ППС. |
| Рассчитывается с учетом множества параметров, показывающих изменение цен. | Вычисляется без коэффициента-дефлятора. |
Порядок и особенности расчета
Показатель ВВП используется для оценки благосостояния общества, но не дает возможности прямо сказать, чем обусловлен рост. Повышение процента валового продукта может быть вызвано увеличением производственных объемов и низким уровнем инфляции, стабильными показателями объемов производства и только инфляцией или другими сочетаниями ключевых параметров.
Формула ∑ptqt демонстрирует, как правильно найти номинальный ВВП.
Расчет реального ВВП выглядит как отношение номинального к индексу цен или корректировка первого пункта на второй. Формула, чтобы рассчитать реальный (фактический) ВВП выглядит следующим образом: Реальный ВВП = номинальный ВВП / индекс цен = ∑p0qt
Такие расчеты позволяют определить рыночную стоимость ежегодного объема выпуска, измеренную в постоянных ценах. Индекс цен может быть:
Отношение номинального объема ВВП к реальному имеет обозначение – дефлятор. Дефлятор измеряется как Д ВНП = НВНП/РВНП. Дефлятор демонстрирует общее изменение цен в стране. Его принято считать общим уровнем инфляции.
Реальный и номинальный валовой внутренний продукт измеряются в ценах. Подсчет ведется исключительно в денежном эквиваленте. Для определения показателя используется индекс потребительских цен. ИПЦ демонстрирует соотношение рыночной корзины для конкретного периода времени и цены сходной группы позиций в базовом периоде. Под корзиной подразумевается цена определенного набора платных услуг, продовольственных и непродовольственных товаров.
Дефлятор ВВП отличается от ИПЦ тем, что рассчитанный валовой продукт основан на меняющихся ценах потребительской корзины, а индекс цен является базовым неизменным показателем. ИПЦ – это условный показатель, измерения которого не учитывают качество товара и соотношение позиций в потребительской корзине.
Наличие данных о процентном изменении двух видов ВВП и общего уровня цен дает следующее соотношение показателей: Изменение РВВП в % = изменение НВВП в % — изменение уровня цены в %.
Например, рост номинального ВВП на 30% при темпе инфляции в 20% означает, что реальный ВВП равен 10%. Такой подход актуален при невысоком уровне инфляции и незначительных темпах изменений. Это важно учитывать в трейдерской деятельности. Да решения задач корректней применять формулу в общем виде.
Важность и актуальность показателя валового внутреннего продукта
Страны стремятся повысить свой показатель ВВП. Этим достигается экономический рост и как может показаться на первый взгляд, экономическое «процветание» государства. Но на самом деле это лишь гонка за деньгами, поскольку показатель не является отражением благосостояния населения или какого-то человеческого прогресса.
Из-за гонки за лидерство истощаются ресурсы планеты. Это негативно влияет на экологию и климат. Нашим будущим поколениям придётся искать методы для сохранения текущего уровня жизни, расходуя природные ресурсы более разумно.
Также «Валовой внутренний продукт» не отражает затрат на загрязнение окружающей среды. Например, Китаю за десяти процентный рост в год пришлось отдавать 3% на восстановление природы. Поэтому реальный рост оказался 7%.
Что не отражает ВВП:
Несмотря на это, ВВП можно назвать самым главным экономическим параметром. Он оказывает сильное влияние на фондовые рынки, курс национальной валюты, приток инвестиций в страну. Опыт предыдущих лет говорит о том, что стабильный рост экономики достигается уровнем 2-4% — так растут страны с развитой экономикой.
Подводя итоги, можно сказать: ВВП является косвенным признаком развития в стране, но не является панацеей.
EREPORT.RU
Автор — Матвеева Татьяна Юрьевна, преподаватель НИУ-ВШЭ «Макроэкономика: Курс лекций для экономистов», 2001 год
Все основные показатели в системе национальных счетов отражают результаты экономической деятельности за год, т.е. выражены в ценах данного года (в текущих ценах) и поэтому являются номинальными. Номинальные показатели не позволяют проводить как межстрановые сравнения, так и сравнения уровня экономического развития одной и той же страны в различные периоды времени. Такие сравнения можно делать только с помощью реальных показателей (показателей реального объема производства и реального уровня дохода), которые выражены в неизменных (сопоставимых) ценах. Поэтому важно различать номинальные и реальные (очищенные от влияния изменения уровня цен) показатели.
Номинальный ВВП – это ВВП, рассчитанный в текущих ценах, в ценах данного года. На величину номинального ВВП оказывают влияние два фактора:
Чтобы измерить реальный ВВП, необходимо «очистить» номинальный ВНП от воздействия на него изменения уровня цен. Реальный ВВП – это ВВП, измеренный в сопоставимых (неизменных) ценах, в ценах базового года. При этом, базовым годом может быть выбран любой год, хронологически как раньше, так и позже текущего. Последнее используется для исторических сравнений (например, для расчета реального ВВП 1980 года в ценах 1999 года. В этом случае 1999 год будет базовым, а 1980 год – текущим).
Реальный ВВП = Номинальный ВВП / Общий уровень цен
Общий уровень цен рассчитывается с помощью индекса цен. Очевидно, что в базовом году номинальный ВВП равен реальному ВВП, а индекс цен равен 100% или 1.
Номинальный ВВП любого года, поскольку он рассчитывается в текущих ценах, равен ∑ptqt, а реальный ВВП, подсчитываемый в ценах базового года, равен ∑p0qt. И номинальный, и реальный ВВП подсчитываются в денежных единицах (в рублях, долларах и т.п.).
Если известны процентные изменения номинального ВВП, реального ВВП и общего уровня цен (а это есть темп инфляции), то соотношение между этими показателями следующее:
изменение реального ВВП (в %) = изменение номинального ВВП (в %) — изменение общего уровня цен (в %)
Например, если номинальный ВВП вырос на 15%, а темп инфляции составил 10%, то реальный ВВП вырос на 5%. (Однако следует иметь в виду, что эта формула применима лишь при низких темпах изменений и, в первую очередь при очень небольших изменениях общего уровня цен, т.е. при низкой инфляции. При решении задач корректнее использовать формулу соотношения номинального и реального ВВП в общем виде.)
Различают несколько видов индексов цен: 1) индекс потребительских цен; 2) индекс цен производителей; 3) дефлятор ВНП и др.
Реальный ВВП России, млрд. долларов США
Источник — CIA World Factbook
Посмотреть данные в виде таблицы за 1991-2011 годы
Посмотреть данные о реальном ВВП других стран мира
Индекс потребительских цен (ИПЦ) рассчитывается на основе стоимости рыночной потребительской корзины, которая включает набор товаров и услуг, потребляемых типичной городской семьей в течение года. (В развитых странах потребительская корзина включает 300-400 видов потребительских товаров и услуг).
Индекс цен производителей (ИЦП) рассчитывается как стоимость корзины товаров производственного назначения (промежуточной продукции) и включает, например, в США 3200 наименований. И ИПЦ, и ИЦП статистически подсчитываются как индексы с весами (объемами) базового года, т.е. как индекс Ласпейреса:
ИПЦ = IL = (∑p0iqti/∑ptiqti) * 100%
где pi — цены на отдельные товары; qi — количества товаров каждого вида; надстрочные знаки t и 0 означают, что данные относятся соответственно к изучаемому и базисному периодам.
Дефлятор ВВП, рассчитываемый на основе стоимости корзины конечных товаров и услуг, произведенных в экономике в течение года. Статистически дефлятор ВВП выступает как индекс Пааше, т.е. индекс с весами (объемами) текущего года:
def ВВП = (∑ptiqti/∑p0iqti) * 100%
где pti, poi — цены товаров соответственно для изучаемого (t) и базисного (0) периода; qi1 — количество товаров, проданных в изучаемый период.
Как правило, для определения общего уровня цен и темпа инфляции используются ИПЦ (если набор товаров, включаемых в потребительскую рыночную корзину, достаточно велик) и дефлятор ВВП.
Отличия ИПЦ от дефлятора ВВП, помимо того, что при их подсчете используются разные веса (базового года для ИПЦ и текущего года для дефлятора ВВП), заключаются в следующем:
Темп инфляции (равен отношению разницы уровня цен (например, дефлятора ВВП) текущего (t) и предыдущего года (t — 1) к уровню цен предыдущего года, выраженному в процентах:
Темп инфляции = дефлятор ВВП текущего года – дефлятор ВВП предыд. года * 100%;
Темп изменения стоимости жизни подсчитывается аналогично, но через ИПЦ и равен:
Темп ИСЖ = ИПЦ текущего года – ИПЦ предыдущего года * 100%
а) ИПЦ недооценивает структурные сдвиги в потреблении (эффект замещения относительно более дорогих товаров относительно более дешевыми), поскольку рассчитывается на основе структуры потребительской корзины базового года, т.е. приписывает структуру потребления базового года текущему году (например, если к данному году относительно подорожали апельсины, то потребители увеличат спрос на мандарины, и структура потребительской корзины изменится – доля (вес) апельсинов в ней сократится, а доля (вес) мандаринов увеличится. Между тем, это изменение не будет учтено при подсчете ИПЦ, и текущему году будет приписан вес (количество килограммов относительно подорожавших апельсинов и относительно подешевевших мандаринов, потребляемых за год) базового года, и стоимость потребительской корзины будет искусственно завышена. Дефлятор же ВНП переоценивает структурные сдвиги в потреблении (эффект замещения), приписывая веса текущего года базовому году;
б) ИПЦ игнорирует изменение цен товаров в связи с изменением их качества (рост цен на товары рассматривается как бы сам по себе, и не учитывается, что более высокая цена на товар может быть связана с изменением его качества. Очевидно, что цена утюга с вертикальной глажкой выше, чем цена обычного утюга, однако в составе потребительской корзины этот товар фигурирует как просто «утюг»). Между тем, дефлятор ВВП переоценивает этот факт и занижает уровень инфляции.
В связи с тем, что оба индекса имеют недостатки и не могут точно отразить изменение общего уровня цен, может использоваться так называемый «идеальный» индекс Фишера, который снимает эти недостатки и представляет собой среднее геометрическое из индекса Пааше и индекса Ласпейреса:
Индекс Фишера используется для более точного расчета темпа роста общего уровня цен, т.е. темпа инфляции. В зависимости от того, повысился или понизился общий уровень цен (Р – price level) (как правило, определяемый с помощью дефлятора) за период времени, прошедший от базового до текущего года, номинальный ВВП может быть как больше, так и меньше реального ВВП. Если за этот период общий уровень цен повысился, т.е. дефлятор ВВП > 1, то реальный ВНП будет меньше номинального. Если же за период от базового года до текущего уровень цен снизился, т.е. дефлятор ВВП
Другие статьи раздела «Макроэкономика»
Что не отражается в ВВП
ВВП играет ключевую роль в прогнозировании и аналитике. Однако данный инструмент отражает не все факторы. Перечислим тем аспекты, которые не затрагиваются в ВВП:
Реальный и номинальный ВВП – это ключевые показатели финансового климата и роста экономики. Изменение данных абсолютных показателей характеризует качественное улучшение и увеличение общественных проектов в рассматриваемом периоде.
Требуется консультация по учебной работе? Задай вопрос преподавателю и получи ответ через 15 минут! Задать вопрос
Рассчитать прирост в процентах
Расчет темпа роста начинается с определения ряда чисел, между которыми нужно найти процентное соотношение. Контрольное число обычно сравнивают с предыдущим показателем или с базой, стоящей в начале числового ряда. Оценка выражается в процентах.
Формула скорости роста выглядит следующим образом:
Скорость роста = скорость потока / базовая скорость * 100%. Если результат больше 100%, наблюдается рост. Следовательно, меньше 100 — это уменьшение.
Вы можете использовать вариант увеличения и уменьшения заработной платы в качестве образца. Сотрудник получил ежемесячную заработную плату: в январе — 30 000, в феврале — 35 000. Темп роста составил:
35 000 / 30 000 * 100 = 116,66. В феврале по сравнению с январем зарплата составила 116%.
Общая характеристика
Часто сравнивают 2 показателя, но каждый из них имеет свои характеристики и цель для анализа. Вы можете рассчитать темпы роста и прироста с помощью формул.
Понятие и предназначение
Расчет темпа роста (ТР) осуществляется путем поиска чисел, между которыми найдена процентная связь. Это означает, что контрольное число сравнивается с прошлым, базовым уровнем. Окончательная сумма должна быть выражена в процентах, что позволяет анализировать динамику показателей.
TP = Текущее значение/Базовое значение*100%.
При сумме больше 100% коэффициенты увеличиваются, а при числах меньше 100 – уменьшаются. Формула расчета темпа роста в процентах показывает, во сколько раз новое значение отличается от предыдущего базового или постоянного значения. Показатель ТП можно определить как увеличение, рост, снижение уровня.
Данные о темпах роста (GT) отражают то, насколько ценная бумага выросла или упала за определенное время. Отображается конкретный показатель, позволяющий судить о результатах деятельности в динамике по разным отраслям. При расчете коэффициента заработной платы или других параметров по формуле величины ТП определяют, на сколько процентов изменилась эта сумма.
Темп роста = (Текущее значение — базовое значение) / базовое значение * 100%.
Два варианта расчета идентичны. Отрицательный результат свидетельствует о снижении стоимости за анализируемый период. Всегда измеряется в процентах. ТП рассчитывается через коэффициент роста, ТП или через значения, которые являются исходными данными и участвуют в расчетах.
Чтобы определить средний или среднегодовой темп роста (CAGR), сложите числа всех периодов и разделите полученную сумму на количество периодов. Также рассчитывается средний темп роста.
Среднемесячные TR и TP используются для определения средней величины изменения показателей за год или другой период.
Можно определить экспортно-импортные общественные отношения объема производства, производства, населения или других показателей. Можно рассчитать среднегодовую средневзвешенную цену – соотношение между оборотом текущего периода и показателями года. Расчетным путем можно установить TR заболеваемости в стране. В большинстве случаев его можно применять к периоду времени – одному году.
Основные вычисления
В статистических и аналитических отчетах часто используются проценты. Они также характеризуют, насколько изменилось значение величины за определенный период времени.
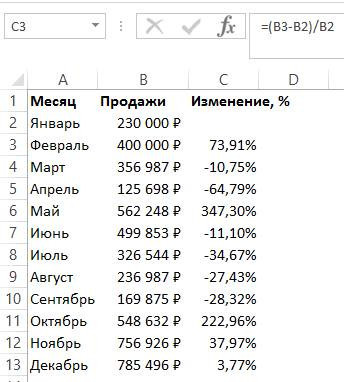
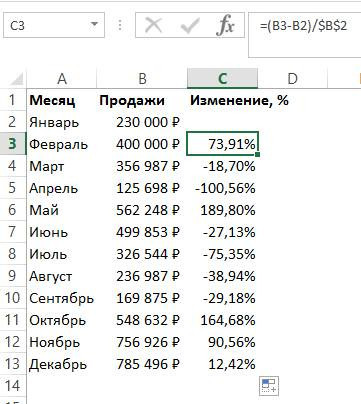
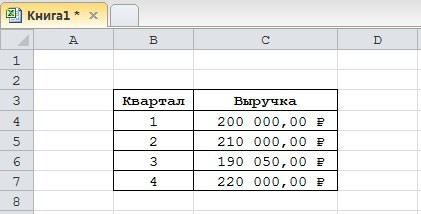
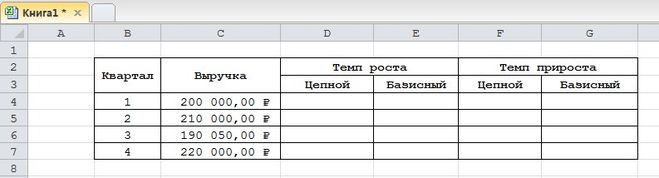
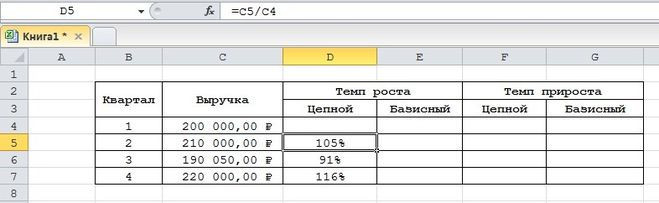
В программе Excel на примере наглядно показан метод расчета с использованием ТР, базовой и цепной ТП.
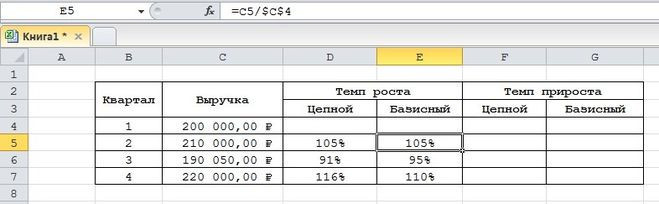
Для расчета базового ФР необходимо рассчитать темпы роста всех показателей. TR и TP первого индикатора учитывать не следует. Показатель 1 принимается за базовое значение, поэтому базовые ТР и ТП необходимо рассчитывать исходя из этого положения. При расчете Показатель (П) 2 делится на Показатель 1 и умножается на 100, затем П3 делится на П1 и умножается на 100.
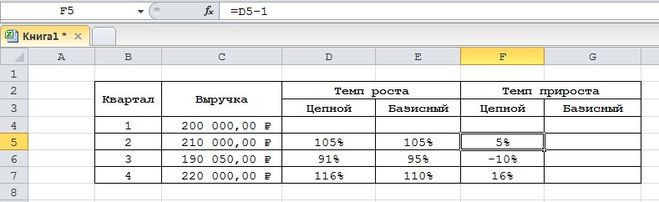
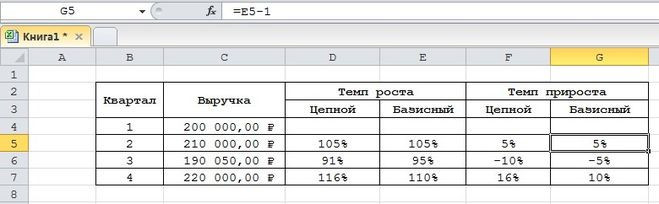
При расчете скорости роста цепи (СТГ) используются все показатели, кроме первого. Метод расчета отличается тем, что Показатель 2 делится на Р1, умножается на 100. Затем Р3 делится на Р2 и умножается на 100. Основой расчета является основной показатель. Р4 делится на Р3 и умножается на 100, при расчете ЦП из каждого показателя ЦГ вычитается 100.
При расчете базового и цепного показателей значения ТР и прироста будут одинаковыми, так как при выборе в качестве показателя первого из рядов они рассчитываются одинаково.
Абсолютное приращение рассчитывается как разница между двумя значениями. Цепочка и базовый ТР взаимосвязаны: произведение ОСАГО равно базовому ТР за весь период.
Между этими двумя значениями существует прямая связь. Разница составляет 100% и отражается в формуле TP.
Практические навыки
TR показывает, на сколько процентов одно число составляет другое. С помощью ТП можно рассчитать, на сколько процентов увеличилось или уменьшилось одно число по отношению к другому.
Использование формул
TR никогда не бывает отрицательным, но TP может быть отрицательным. ТП определяется на основании ТП, обратный порядок не допускается. Для расчета значения используется PP, так как он наглядно отражает динамику изменений.
Эти параметры имеют большое значение для анализа и планирования показателей в науке, статистике, экономике и других областях. Он широко используется для оптимизации доходов от продаж, заработной платы, выставления счетов и денежных средств.
Вы можете использовать пример для расчета скорости роста в процентах. Заводской рабочий ежемесячно получал жалованье в зависимости от выработки. В январе работник получил 40 000 руб., в феврале 45 000 руб. ТР находится по формуле: 45 000/40 000 * 100 = 112,5. Таким образом, в феврале доход относительно предыдущего месяца можно рассчитать на уровне 112%.
Формулы широко используются в повседневной жизни населения. В Интернете есть онлайн-калькулятор, позволяющий получить реальный результат или проверить собственные решения. Его использование позволяет исключить расчетные ошибки.
Разные методы расчета
Наглядное использование формул на примере позволит проанализировать назначение ТР и ТП. В таблице представлен валовой внутренний продукт России с 2010 по 2017 год. Необходимо найти ТР (в процентах) основным и цепным методами.
Таблица данных ВВП в национальной валюте за 2011-2018 гг
| Период | ВВП России ТР | (%) | |
| в миллиардах рублей | Цепной метод | Основной метод | |
| 2011 | 48000 | – | – |
| 2012 | 57 698 | 120,2 | 120,2 |
| 2013 | 66 817 | 115,8 | 139,2 |
| 2014 | 71 117 | 106,4 | 148,2 |
| 2015 | 78 945 | 111,0 | 164,5 |
| 2016 | 80 826 | 102,4 | 168,4 |
| 2017 | 83 871 | 103,8 | 174,7 |
| 2018 | 88 177 | 105.1 | 183,7 |
На 2011 год значения не будет. С 2012 года: 57698/48000*100 = 120,2%. На 2013 год: 66817/57698*100 = 115,8%. Таким образом рассчитываются суммы за каждый период.
Базовый метод: TP = Yi/Ybasic*100. Это отношение с первым старшим коэффициентом. Например, за 2012 год рассчитаны суммы 57698/48000*100 = 120,2%, за 2013 год: 66817/48000*100 = 115,8%. Таким образом рассчитываются все остальные периоды.
Таким же образом рассчитывается процентное соотношение данных актива баланса, отчета о прибылях и убытках. Показатели, отражающие сумму чистой прибыли за 2 года, позволят выявить рост или снижение показателей.
| Данные | 2017 | 2018 | ТР % |
| Доход от продаж | 1500000 | 1600000 | 106,7 |
| Финансовые доходы | 400000 | 350000 | 87,5 |
В 2018 году TR составит 106,7% от выручки, а инвестиционный доход увеличится на 87,5%.
TR нужен, чтобы узнать, какой процент составляет одно значение от другого. Последнее число является предыдущим. Скорость роста позволяет узнать, насколько сильно изменился заданный параметр.
На основании одного из коэффициентов невозможно дать правильную оценку определяемому явлению (по международному, национальному рынку, компании, показателю эффективности компании). Необходимы комплексные измерения для изучения и расчета показателей в динамике. Для анализа финансовой деятельности можно брать разную информацию из отчетных форм.
Примеры решения задач
| Домашнее задание | Для ООО «Севермет» предусмотрены следующие показатели за 2015 и 2016 годы: |
2015 г. — 120 млн руб,
2016 г. — 110,4 млн руб
Известно, что в 2017 году сумма дохода увеличилась на 25 млн рублей по сравнению с 2016 годом.
На основании имеющихся данных рассчитайте скорость роста и прироста, при этом сделайте выводы.
Решение Определим темп роста в процентах за 2015 и 2016 годы, для чего нам понадобится формула темпа роста:
Где Tr – скорость роста,
P2015 — показатель за 2015 год,
P2016 — показатель за 2016 год.
Тр=110,4 млн руб./120 млн руб. * 100% = 92 %
Темп роста показывает процентное изменение стоимости в текущем периоде по сравнению с предыдущим. Для расчета формулы скорости роста нужно:
Или второй способ:
Рассчитаем показатели за 2017 год
Тр = (120 млн руб. + 25 млн руб.) / 120 млн руб. = 1,21 (или 121 %)
Производство. Мы видим, что темп роста при сравнении 2015 и 2016 годов составил 92%. Это означает, что прибыль компании в 2016 году уменьшилась на 92% по сравнению с 2015 годом. При расчете темпа роста получено отрицательное значение (-8%), что свидетельствует о том, что прибыль компании в 2016 году (по сравнению с 2015 годом) уменьшилась на 8%. В 2017 году прибыль составила 121% по сравнению с 2016 годом. При расчете темпа роста видим, что он составил 20,8%. Положительное значение указывает на увеличение прибыли на этот процент.
Ответ При сравнении 2015 и 2016 гг. Tr=92%, Tp=8%, при сравнении 2016 и 2017 гг. Tr=121%, Tp=20,8%.
| Домашнее задание | Рассчитайте прирост заработной платы в ООО «Севермет» за 2015 и 2016 годы. Приведены следующие показатели: |
Заработная плата 2015 г. — 31,5 тыс руб.,
заработная плата в 2016 г. — 33 тыс руб.,
Решение Темп роста показывает процентное изменение стоимости в текущем периоде по сравнению с предыдущим. Для расчета нужна формула:
Вывод: Таким образом, мы видим, что темп роста составил 4,8%, значит, заработная плата в 2016 году по сравнению с 2015 годом увеличилась на 4,8%.
Средний годовой темп роста и средний годовой темп прироста
Во-первых, отметим, что темпы роста в таблице (столбцы 7 и 8) представляют собой динамические ряды относительных величин, полученные из динамических интервальных рядов (столбец 2). Годовые темпы роста (столбец 7) варьируются от года к году (105%; 103,8%; 105,5%; 101,7%). Как рассчитать среднее значение годового прироста? Эта величина называется среднегодовым темпом роста.
Среднегодовой темп роста рассчитывается в следующей последовательности:
сначала по формуле среднего геометрического рассчитывается среднегодовой темп прироста (убыли) —
2 на основе среднегодового коэффициента среднегодовой темп прироста (
) умножая коэффициент на 100%:
Среднегодовой темп роста (
определяется путем вычитания 100% из скорости роста%.
Среднегодовой темп прироста (убыли) по формулам среднего геометрического можно рассчитать двумя способами:
на основе абсолютных показателей ряда динамики по формуле:
§ n — количество уровней;
§ n — 1 — количество лет периода;
исходя из годовых темпов роста по формуле
§ m — количество коэффициентов.
Результаты расчета по формулам одинаковы, так как в обеих формулах показатель степени — количество лет в периоде, в течение которого произошло изменение. А корневым выражением является коэффициент роста показателя за весь период времени (см табл. 11.5, столбец 6, для строки 1998 г.).
Среднегодовой темп роста составляет
CAGR определяется путем вычитания 100% из CAGR. В нашем примере среднегодовой темп роста равен
Таким образом, за период 1995 — 1998 гг объем производства продукции «А» увеличивался в среднем на 4,0% в год. Годовые темпы роста колебались от 1,7% в 1998 г до 5,5% в 1997 г. (для каждого года см таблицу 11.5, столбец 9).
Среднегодовые темпы роста (прироста) позволяют сравнивать динамику развития взаимосвязанных явлений за длительный период времени (например, среднегодовые темпы роста численности занятых по отраслям экономики, объема производства и др.), сравнить динамику явления в разных странах, исследовать динамику одного или явлений по периодам исторического развития страны.
Формулы роста и прироста: базисный, цепной и посредственный
Темп роста и прибыль можно найти различными способами, в зависимости от цели расчета. Существуют формулы получения базовых, цепных и посредственных темпов роста и роста.
База роста и темп роста показывают связь показателя, выбранного из ряда, с показателем, аккредитованным доверителем (расчетной базой). Обычно он стоит в начале очереди. Формулы для расчета следующие:
Рост и скорость роста цепочки демонстрируют изменение показателя в динамике по цепочке. То есть разница каждого последующего показателя во времени по отношению к предыдущему. Формулы выглядят следующим образом:
Существует взаимосвязь между цепными и базовыми темпами роста. Отношение между результатом деления текущего показателя на основание и результатом деления предыдущего показателя на основание равно скорости роста цепочки.
Средний рост и темп роста используются для определения средней величины изменения показателей за год или другой отчетный период. Для определения этого значения необходимо определить среднее геометрическое всех показателей на этапе или найти его, определив отношение конечного значения к начальному:
Как рассчитать темп прироста
Он рассчитывается несколькими способами, самый простой способ – вычислить показатель на основе темпа роста путем вычитания 100. Разберем его на тех же примерах, что и выше.
Темп роста = 33 000/31 500 * 100 — 100 = 104,76-100 = 4,76%. Таким образом, средняя заработная плата увеличивается на 4,76% (+4,76%).
Как еще можно посчитать темп прироста?
Если в задании вы рассчитали абсолютное отклонение, то можно использовать это значение и разделить его на значение базисного года, рассмотрим пример №1.1
Абсолютное отклонение = 33 000 — 31 500 = 1 500 руб.
Темп роста = 1500/31500*100%=4,76%. Мы видим, что после изменения метода расчета результат не изменился, поэтому выбирайте тот, который вам больше нравится.
Вернемся к теме статьи и подытожим, в чем разница между темпом роста и прибылью. Разница между показателями следующая:
Если после прочтения материала вам непонятно, как рассчитать показатель или у вас остались вопросы по теме, задавайте их в комментариях, не стесняйтесь.
Подсчет процентов в табличном редакторе
Табличный редактор хорош тем, что большую часть расчетов он делает самостоятельно, а пользователю нужно только ввести начальные значения и указать принцип расчета. Расчет выполняется следующим образом: Часть/Все = Процент. Подробная инструкция выглядит так:
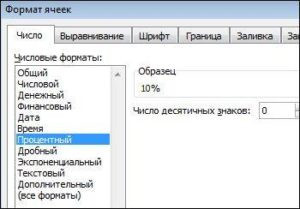
При работе с процентной информацией ячейка должна быть отформатирована соответствующим образом.
Здесь нужно щелкнуть левой кнопкой мыши по пункту «Формат», а затем пунктом «ОК» сохранить внесенные изменения.
Давайте рассмотрим небольшой пример, чтобы понять, как работать с процентной информацией в редакторе электронных таблиц. Подробная инструкция выглядит так:
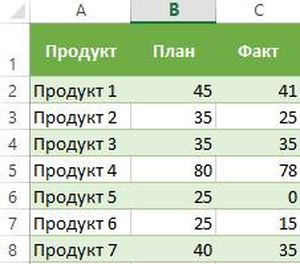
У нас есть три столбца в таблице. На первом отображается наименование товара, на втором — плановые показатели, на третьем — фактические.
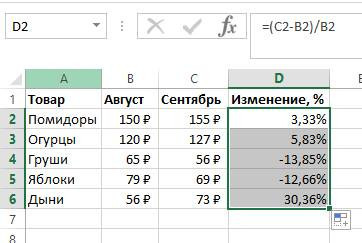
В строку D2 вводим следующую формулу: = C2/B2.
По инструкции выше переводим поле D2 в процентную форму.
С помощью специального маркера заполнения мы растягиваем введенную формулу на весь столбец.
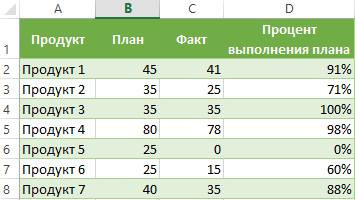
Готовый! Табличный редактор сам рассчитывал процент выполнения плана по каждому продукту.
Нюансы вычислений
Представленные формулы очень похожи и могут вызвать затруднения и путаницу. Для этого объясним следующее:
В экономической практике чаще используется показатель роста, так как он более четко отражает динамику изменений.
Вычисление изменения в процентах при помощи формулы прироста
С помощью табличного редактора можно реализовать процедуру сравнения 2-х акций. Для осуществления этого действия отлично подходит формула роста. Если пользователю необходимо сравнить числовые значения А и В, формула будет выглядеть так: = (ВА) / А = разность. Давайте рассмотрим все более подробно. Подробная инструкция выглядит так:
Расчет темпа прироста в табличном редакторе
Разберемся подробно, как рассчитать темп роста в табличном редакторе. Рост/скорость роста означает изменение определенного значения. Делится на два вида: базовый и цепной.
Темп роста цепочки обозначает процентное отношение к предыдущему показателю. Формула скорости роста цепи выглядит следующим образом:
Базовая ставка роста относится к отношению процента к базовой ставке. Основная формула скорости роста выглядит следующим образом:
Индикатор выше — это показатель за последний квартал, месяц и т д. Базовая линия является отправной точкой. Тема роста цепочки — это расчетная разница между двумя показателями (настоящим и прошлым). Формула скорости роста цепи выглядит следующим образом:
Базовый темп роста – это рассчитанная разница между 2-мя показателями (настоящим и базовым). Основная формула скорости роста выглядит следующим образом:
Рассмотрим все подробно на конкретном примере. Подробная инструкция выглядит так:
Например, у нас есть табличка, в которой отражен доход за квартал. Задание: Рассчитать скорость роста и прироста.
Изначально мы реализуем добавление четырех столбцов, в которых будут находиться приведенные выше формулы.
Мы уже обнаружили, что такие значения рассчитываются в процентах. Нам нужно установить процентный формат для таких ячеек. Щелкаем по нужному диапазону правой кнопкой мыши. В появившемся специальном маленьком контекстном меню выберите кнопку «Формат ячеек». Здесь нужно щелкнуть левой кнопкой мыши по пункту «Формат», а затем с помощью кнопки «ОК» сохранить внесенные изменения.
Мы вводим эту формулу для расчета скорости роста цепи и копируем ее в ячейки ниже.
Вводим такую формулу скорости роста основной цепи и копируем в ячейки ниже.
Мы вводим эту формулу для расчета скорости роста цепи и копируем ее в ячейки ниже.
Вводим такую формулу скорости роста основной цепи и копируем в ячейки ниже.
Готовый! Мы реализовали расчет всех необходимых показателей. Вывод на нашем конкретном примере: в 3 квартале динамика плохая, так как темп роста стопроцентный, и рост положительный.