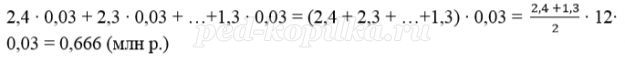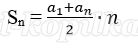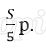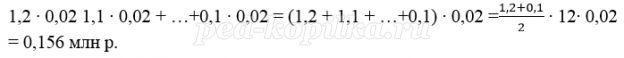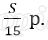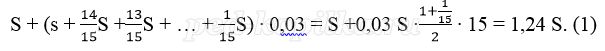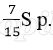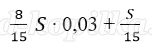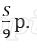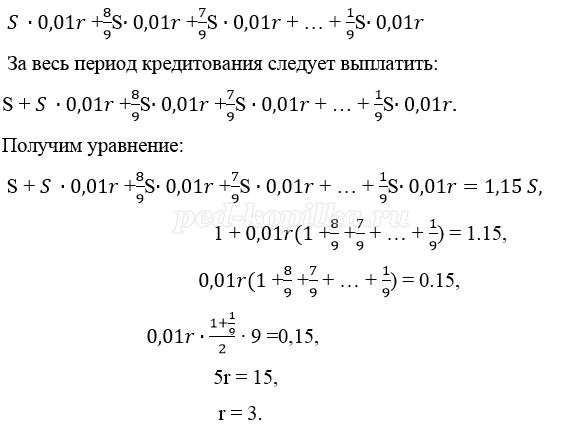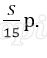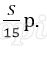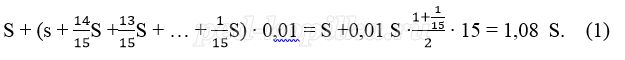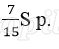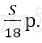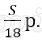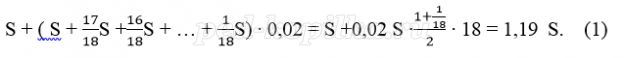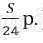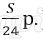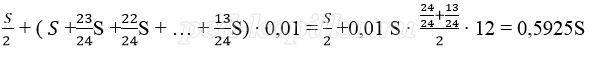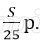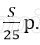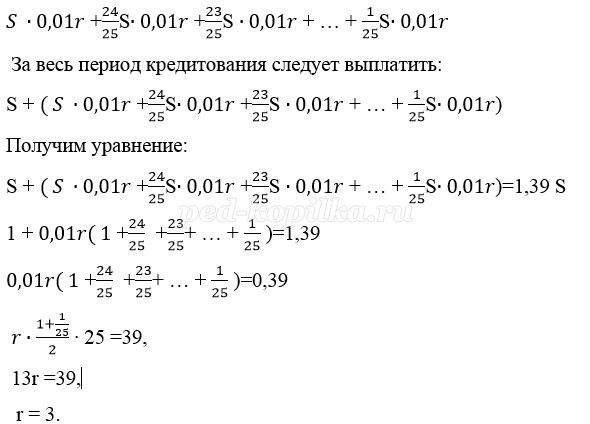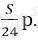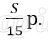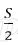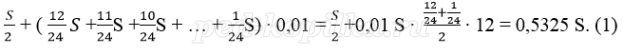задачи на простые и сложные проценты по кредиту с решением
Задачи на простые и сложные проценты по кредиту с решением
1. Задача по банковскому делу
Клиент банка положил 5 тысяч под 9 процентов на 2 года. Найдите полученную сумму процентов при простой и сложной процентной ставке.
При простых процентах I=P*i*n/100%.
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
I – сумма процентов.
При сложных процентах
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
S – наращенный капитал.
I=5000*(1+0,09) 2 – 5000 =5940-5000=940 рублей.
2. Задача по банковскому делу
52500 руб. в кредит под 20% годовых на 1 год как рассчитать сумму дохода?
При сложной процентной ставке:
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
S – наращенный капитал.
3. Задача по банковскому делу
64 процента от 20000 тысяч рублей
4. Задача по банковскому делу
900 000 вложены в банк под 12% годовых, это сколько процентов в год?
При простых процентах I=P*i*n/100%.
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
I – сумма процентов.
I= 90 0000*0, 12 = 108000 рублей.
5. Задача по банковскому делу с решением
Дали карту на 15000 тысяч под 19 процентов, если купить продуктов на 20000 рублей и вовремя не заплатить, сколько процентов (в рублях) придется уплатить через 1 месяц просрочки (не считая льготного периода).
Поскольку просрочка лишь 1 месяц, то простая учетная ставка будет равна сложной процентной ставке. И сумма процентов за просрочку будет 20000*0,19 / 12=317 рублей. Т.е. придется вернуть 20317 рублей.
6. Задача по банковскому делу с решением
Определить сумму накопленных % на 1 августа, если клиент положил в банк 3 апреля 20 000 рублей под 15% годовых, а 2 июня ставка увеличилась на 2% срок вклада до 31 сентября.
С 3 апреля по 1 июня ставка 15% годовых. При английской методике (используемой в России) это 27+31+1=59 дней.
20000* 0,15*59 /365=485 рублей процентов.
Со 2 июня по 1 августа ставка 15% годовых. При английской методике (используемой в России) это 29+31+1=61 дней.
20000* 0,17*61 /365= 568 рублей процентов.
На 1 августа накоплено 485+568=1053 рублей.
Однако вклад до 31 сентября.
С 2 августа до 31 сентября ставка 17% годовых. При английской методике (используемой в России) это 30+30=60 дней (первый и последний день вклада не учитываем).
20000* 0,17*60 /365= 558 рублей процентов.
На 31 сентября накоплено 1053+558=1611 рублей процентов.
7. Задача по банковскому делу с решением
определить сумму вклада в банке (на базе простого и сложного процента) через 3 года при условии, что первоначальное значение вклада составляет 5000 рублей при процентной ставке 10%.
При простых процентах I=P*i*n/100%.
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
I – сумма процентов. S=P+I.
S – наращенный капитал.
Расчет: S=5000+5000*0,1*3=6500 рублей.
При сложных процентах
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
S – наращенный капитал.
S=5000*(1+0,1) 3 =6655 рублей.
8. Задача по банковскому делу
рассчитать 12% годовых с 150000.
0,12*150 000=18000 рублей.
9. Задача по банковскому делу
Рассчитать сумму процентов на кредит в 1 миллион под 17 процентов на 5 лет.
При сложной процентной ставке
P – первоначальная сумма. i – процентная ставка. n – срок в годах.
S – наращенный капитал.
S= 1 000 000 *(1+0,1 7 ) 5 = 2 192 448 рублей.
Сумму процентов 1 192 448 рублей, а всего придется заплатить 2 192 448 рублей.
Решение экономических задач на кредиты
Задача 2.
31 декабря 2014 года Дмитрий взял в банке 4 290 000 рублей в кредит под 14,5 годовых. Схема выплаты кредита следующая – 31 декабря следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк х рублей. Какой должна быть сумма х, чтобы Дмитрий выплатил долг двумя равными платежами (то есть за два года)?
Решение:
Дмитрий взял в банке кредит 4 290 000 рублей.
При решении задач на кредиты с дифференцированным платежом начисляемые проценты за весь период кредитования можно вычислить с помощью формулы суммы n-первых членов арифметической прогрессии. И потом найти сумму общего платежа. Считаю, что этот метод будет прост и понятен для учащихся.
Задача 3
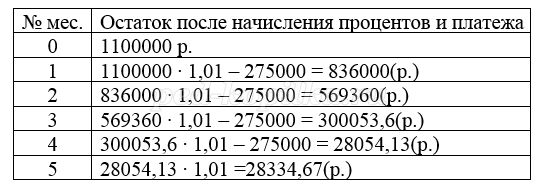
15 января планируется взять кредит в банке на сумму 2,4 млн. рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму надо выплатить банку за первые 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных «процентов» за 12 месяцев (в млн. р.):
За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за первые 12 месяцев банку нужно выплатить 1 200 000 + 666 000 = 1 866 000 р.
Ответ: 1 866 000 рублей.
Задача 4
15 января планируется взять кредит в банке на 5 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь срок кредитования?
Решение:
Пусть в банке взяли кредит S рублей. Платёж за месяц состоит из величины ежемесячного долга (он равен
Всего банку будет выплачено S + 0,03S = 1,03S. Значит общая сумма выплаченных денег от суммы кредита составляет 103%.
Ответ: 103%.
Задача 5
15 января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку за последние 12 месяцев?
Решение:
Платёж за месяц состоит из величины ежемесячного долга (он равен 2400000:24=100000(р.)) и начисленных к остатку процентов. В каждый месяц долг уменьшается 100000р.
Сумма начисленных процентов за 12 последних месяцев (в млн):
За 12 месяцев буде выплачена половина долга, то есть 1,2 млн р.
Значит за последние 12 месяцев банку нужно выплатить 1 200 000 + 156 000 = 1 356 000 р.
Ответ: 1 356 000 рублей.
Задача 6
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 3 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 99,2 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит за весь срок кредитования будет выплачено 1 488 000 рублей.
Ответ: 1 488 000 рублей.
Задача 7
15 января планируется взять кредит в банке на 9 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма денег, которую нужно выплатить банку за весь срок кредитования, на 15% больше, чем сумма взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит кредит взят под 3% в месяц.
Ответ: 3%.
Задача 8
15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что восьмая выплата составила 108 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
В (1) подставим (2), получим: 1,08 ∙1 500 000 = 1620000
Значит за весь срок кредитования будет выплачено 1 620 000 рублей.
Ответ: 1 620 000 рублей.
Задача 9
15 января планируется взять кредит в банке на 18 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Сколько процентов от суммы кредита составляет общая сумма денег, которую нужно выплатить банку за весь период кредитования?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит сумма выплаченных банку денег составляет 119% от суммы долга.
Ответ: 119%.
Задача 10
15 января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за первые 12 месяцев нужно выплатить банку 177,75 тыс. рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Получим уравнение: 0,5925 S = 177750,
S = 300000
Значит в кредит взяли 300 000 рублей.
Ответ: 300 000 рублей.
Задача 11
15 января планируется взять кредит в банке на 25 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на r % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что я сумма денег, которую нужно выплатить банку за весь срок кредитования, на 39% больше, чем сумма, взятая в кредит. Найдите r.
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Значит кредит взят под 3% в месяц.
Ответ: 3%.
Задача 12
15 января планируется взять кредит в банке на 24 месяцев. Условия его возврата таковы:
– 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
– со 2-го по 14 число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен быть на одну величину меньше долга на 15-е число предыдущего месяца.
Известно, что за последние 12 месяцев нужно выплатить банку 1597,5 тысяч рублей. Какую сумму планируется взять в кредит?
Решение:
Пусть взяли кредит S рублей.
Платёж за месяц состоит из величины ежемесячного долга (он равен
Получим уравнение: 0,5325 S = 1597500; S = 3 00 000.
Значит планируется взять 3 000 000 рублей.
Ответ: 3 000 000 рублей.
Литература
И.В.Ященко. Математика. Профильный уровень. Типовые тестовые задания. Издательство «Экзамен», М. 2017.
Задачи по простым и сложным процентам с решением
Задача 1. Под какой процент была вложена 4000 рублей, если через 8 лет сумма наращенного капитала составила 7000 рублей.
i = 100*I/(P*n) = 100*3000/(4000*8) = 9,4%
Сумма была положена под i = 9,4%
Задача 2. Определить сумму наращенного капитала на 1 ноября, если клиент положил на депозитный счет 3 мая 15000 рублей под 15% годовых, а 2 августа ставка увеличилась на 4%. Расчеты ведутся по французской методике расчета процентов.
d 1 = с 3 мая по 2 августа = 91 день
d 2 = со 2 августа по 1 ноября = 91 день
k = 360 дней (французская методика)
I 1 = P 1* i 1* d 1/( k *100) = 15000*15*91/(100*360) = 568,75 руб.
S 2 = P 2+ I 2 = 15568,75 + 747,735 = 16316,485 руб.
Сумма наращенного капитала на 1 ноября составляет 16316,485 руб.
Задачи на расчет простых и сложных %
Задача 3
1. На какой срок необходимо вложить 5000 рублей при 30% годовых, чтобы сумма дохода составила 560 рублей?
560 = (5000*30* d )/100*365;
150000* d = 20440000
Ответ: 5000 руб. надо положить на 136 дней, чтобы получить доход в 560 руб. при 30% годовых
Клиент положил в банк депозит в размере 25 000 руб. 15 апреля. 19 июня клиент снял со счета 8 000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 января по депозиту клиента составил 1000 руб. Расчеты ведутся по английской методике расчета процентов.
Р = 25000- 8000=17000 руб.
1000 = (17000* i *261)/100*365;
4437000* i = 36500000
Ответ: ставка банка по вкладу равна 8,2%
Для решения задачи воспользуемся формулой
Из формулы получаем, что n = I *100% / P * i
n = 2 000 * 100 % / 15 000 * 9 % = 1,481 лет
Ответ: нужно вложить на 1, 481 лет.
Для решения задачи воспользуемся формулой
d – срок в днях, на который положили деньги;
Английская практика (в России) – 365 дней.
Из формулы получаем, что i = I * 100% * K / P * d
P = 45 000 – 7 000 = 38 000 рублей
d = (31-15) +30+31+31+30+31+30+31+1 = 231
i = 6 000 * 100 % * 365 / 38 000 * 231 = 24,95 %
Ответ: ставка банка по вкладу 24,95 %.
Под какой процент была вложена 1000 рублей, если через 7 лет сумма наращенного капитала составила 5600 рублей.
1) Процентный платеж или доход кредитора:
S – сумма наращенного капитала
2) Процентную ставку:
i =100* I /( P * n )=100*4600/(1000*7)=66%
Ответ: процентная ставка равна 66% годовых.
Определить сумму наращенного капитала на 12 октября, если клиент положил на депозитный счет 3 апреля 20 000 рублей под 15% годовых, а 12 августа ставка увеличилась на 2%. Расчеты ведутся по немецкой методике расчета процентов.
Согласно немецкой методике год условно принимается за 360 дней, а месяц – 30 дней.
1) Количество дней, в течении которых вклад лежал под 15 % годовых:
d = 128 дней – время пользованию ссудой
2) Количество дней, в течении вклад лежал под 17 % годовых:
d = 61 день – время пользованию ссудой
3) Доход, получаемый кредитором от заемщика за пользование денежной ссудой:
Р – первоначальный капитал
i – процентная ставка
d – количество дней
4) Сумма наращенного капитала:
S = P + I = 20000 + 1642,78 = 21642,78 руб.
Ответ: наращенный капитал равен 21642,78 руб.
2.Индекс номинальной и реальной заработной платы.
Имеются следующие данные о составе и использовании денежных доходов населения РФ в текущих ценах, млрд руб.:*
* Россия в цифрах. 2008: Стат. сб. — М.: Росстат, 2008. С. 120.
-доходы от предпринимательской деятельности 1915,1 2118,3
-оплата труда 11237,0 14940,0
-социальные выплаты 2080,4 2317,8
-доходы от собственности 1720,6 1423,1
-другие доходы 336,8 424,3
Денежные расходы и сбережения:
-покупка товаров и оплата услуг 11927,5 14792,4
-обязательные платежи и разнообразные взносы 1813,0 2661,0
-приобретение недвижимости 572,3 690,5
-прирост финансовых активов
Определить за каждый год:
1. Номинальные и располагаемые денежные доходы населения в текущих ценах.
2. Прирост финансовых активов.
3. Структуру денежных доходов и расходов населения.
4. Изменение структуры денежных доходов населения с помощью обобщающих показателей
Больший капитал вложен на 6 месяцев при ставке 5%, а меньший на 3 месяца при ставке 6%. Разница между двумя капиталами 1000 рублей. Найти величину капиталов, если известно, что процентный платеж по первому капиталу равен двойному процентному платежу за второй капитал.
Задача на простые проценты.
Сравнить доход по различным вкладам:
1 – 5000 рублей с 1 мая по 10 ноября по 15 % годовых (английская практика расчета процентов)
2 – 4000 рублей с 5 апреля по 28 августа под 20% годовых (немецкая практика расчета процентов).
Задача на простые проценты.
По английской практике расчета процентов в году 365 дней и в месяце число дней соответствует календарю. Значит, доход по первому вкладу нужно рассчитывать на следующее количество дней: 30+30+31+31+30+31+10=193;
I 1=( P 1* i 1* d 1) / ( K 1*100)=5000*15*193/(365*100)=396,58 руб.
По немецкой практике расчета процентов в году 360 дней и 30 дней в каждом месяце. Значит, доход по первому вкладу нужно рассчитывать на следующее количество дней: 25+30+30+30+28=143
I 2=( P 2* i 2* d 2) / ( K 2 *100)=4000*20*143/(360*100)=317,78 руб.
Следовательно, доход по первому вкладу больше, чем по второму на 78,8 рублей.
Капитал величиной 15 000 рублей вложен в банк на 3 месяца под 6% годовых. Найти сумму наращенного капитала.
Решение задачи на простые проценты:
Будем решать данную задачу с использованием методики простых процентов.
Определим доход от вклада 15 000руб, положенных в банк на 3 месяца:
I = P * i * m / (12*100) = 15000*6*3/ (12*100)=225 руб.
Сумма наращенного капитала
Клиент положил в банк депозит в размере 20 000 руб. 15 мая. 10 августа клиент снял со счета 15 000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 февраля по депозиту клиента составил 11 000 руб. Расчеты ведутся по немецкой методике расчета процентов.
При определении числа дней ссуды по немецкой методике расчета процентов год условно принимается за 360 дней, а месяц – 30 дней. Учитывая это, посчитаем сколько дней составит время депозита в размере 20 000 рублей:
Определим доход от депозитного вклада суммы 20 000 рублей на срок 85 дней:
I=(P*i*d) / (K*100)=20000*85*i/(360*100)=47,22 i.
После того, как клиент 10 августа снял со счета 15 000 рублей, сумма депозита составила 5 000 рублей. Посчитаем сколько дней составит время депозита в размере 5 000 рублей
Тогда, I2=(P2*i*d2) / (K*100)=5000*170*i/(365*100)=23,288 i.
Определим суммарный доход от депозитного вклада:
I=I1+I2=47,22 i.+23,288 I = 70,51* i = 11000;
При заданных условиях ставка банка по вкладу составила 156%.
Под какой процент была вложена 5000 рублей, если через пять лет сумма наращенного капитала составила 3600 рублей.
По условию, была вложена сумма P =5000 рублей.
Сумма наращенного капитала I =3600 рублей.
i =3600/(5000*5)=0,144, т.е. 14,4%
Определить сумму наращенного капитала на 1 октября, если клиент положил на депозитный счёт 3 апреля 20000 рублей под 15 % годовых, а 2 августа ставка увеличилась на 2 процента. Расчеты ведутся по немецкой методике расчета процентов.
По условию, была вложена сумма P =20000 рублей.
Разобьём это время на два периода:
d 1=27+30+30+30+2=119-первый период по немецкой системе
d 2=28+30+1=59-второй период по немецкой системе
I = I 1+ I 2-наращеный капитал за два периода.
k – база дней по немецкой системе.
I=P*i*d/K=I1+I2= 20000*0,15*119/360+ 20000*0,17*59/360= 1548,99 рублей.
Ответ: сумма наращенного капитала I =1548,99 рублей.
Капитал величиной 40000 рублей вложен в банк на 3 месяца под 6% годовых. Найти сумму наращенного капитала.
Клиент положил в банк депозит в размере 50000 руб. 15 мая. 10 августа клиент снял со счета 25000 руб. Определить ставку банка по вкладу, если суммарный доход на 1 февраля по депозиту клиента составил 5000 руб. Ресчеты ведутся по немецкой методике расчета процентов.
I = I 1+ I 2; Составим уравнение, решив которое получим: i = 31.5121%
Под какой процент была вложена 1000 рублей, если через 7 лет сумма наращенного капитала составила 5600 рублей.
Теперь определим процентную ставку:
Ответ: процентная ставка равна 15,71% годовых.
Определить сумму наращенного капитала на 12 октября, если клиент положил на депозитный счет 3 апреля 20 000 рублей под 15% годовых, а 12 августа ставка увеличилась на 2%. Расчеты ведутся по немецкой методике расчета процентов.
Немецкая методика: год условно принимается за 360 дней, а месяц – 30 дней. При определении числа дней ссуды по календарю в России первый и последний дни не учитываются.
Сосчитаем количество дней, при которых вклад лежал под 15 % годовых:
И количество дней, при которых вклад лежал под 17 % годовых:
I = P * i * d /(100*360)=[20000*15*128/36000 ]+ [20000*17*60/36000 ] = 1633,33.
I = 1633,33 рубля, где
i – процентная ставка
d – количество дней
S = P + I = 20000 + 1633,33 = 2163,33 рубля.
Ответ: наращенный капитал равен 2163,33 рубля.