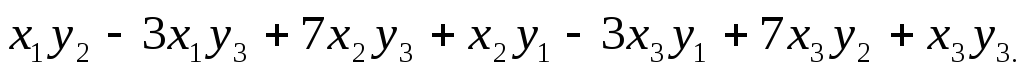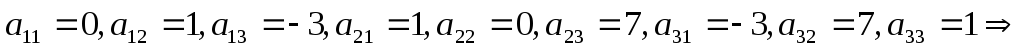задание билинейной формы матрицей

Задание билинейной формы матрицей

Индивидуальные онлайн уроки: Отправьте запрос сейчас: ut2018@protonmail.com
Математика (ЕГЭ, ОГЭ), Английский язык (разговорный, грамматика, TOEFL)
Решение задач: по математике, IT, экономике, психологии Билинейные формы Учебные дисциплины на сайте Bodrenko.org
Портабельные Windows-приложения на сайте Bodrenko.com

Глава 7
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

В этой главе изучаются билинейные формы, определенные в вещественном линейном пространстве, т. е. числовые функции двух векторных аргументов, линейные по каждому из этих аргументов. Подробно исследуются так называемые квадратичные формы, представляющие собой билинейные формы, определенные для совпадающих значений их аргументов. Рассматриваются также некоторые приложения теории билинейных и квадратичных форм.

§ 1. Билинейные формы

1. Понятие билинейной формы. Понятие билинейной формы в произвольном линейном пространстве было введено нами ранее в гл.5. Однако для удобства изложения в этом пункте мы напомним некоторые определения и простейшие утверждения.

Определение 1. Числовая функция А(х, у), аргументами которой являются всевозможные векторы х и у вещественного линейного пространства L, называется билинейной формой, если для любых векторов х, у и z из L и любого вещественного числа λ выполняются следующие соотношения:

Иными словами, билинейная форма представляет собой числовую функцию А(х, у) двух векторных аргументов х и у, определенную на всевозможных векторах х и у вещественного линейного пространства L и линейную по каждому из этих аргументов (при этом часто говорят, что билинейная форма А(х, у) задана на линейном пространстве L).
Простейшим примером билинейной формы может служить произведение двух линейных форм f (х) и g(y), определенных на векторах х и у линейного пространства L.
Определение 2. Билинейная форма А(х, у) называется симметричной (кососимметричной), если для любых векторов х и у линейного пространства L выполняются соотношения:

a ξ _i и η _i — координаты в базисе е векторов х и у соответственно.
Доказательство. Пусть — разложение векторов х и у по базису е. Так как форма В(х, у) линейна по каждому из аргументов х и у (см. 7.1)), то

Таким образом, для формы В(х, у) справедливо представление G.3) с выражениями G.4) для коэффициентов b_ij .
Чтобы доказать однозначность этого представления, предположим, что для В(х, у) справедливо представление (7.3) с некоторыми коэффициентами b_ij . Беря в (7.3) х = е_i, у = е_j, мы сразу же получим выражения (7.4) для коэффициентов b_ij. Теорема доказана.
Определение. Матрица

элементы b_ij которой определены с помощью соотношений (7.4), называется матрицей билинейной формы В(х, у) в данном базисе е.
Замечание 1. Обратимся к вопросу о построении всех билинейных форм в данном конечномерном вещественном пространстве L. Ответ на этот вопрос следующий: любая квадратная матрица (b_ij) является в данном базисе е = (е₁, е₂. е _n ) матрицей некоторой билинейной формы.
Убедимся в справедливости этого утверждения.
Определим в линейном пространстве L с данным базисом е = (е₁, е₂. е _n ) с помощью матрицы (b_ij) числовую функцию В(х, у) двух векторных аргументов вида

где С = (c_pq) — матрица перехода от базиса е к базису f, а С ‘ — транспонированная матрица С.
Доказательство. Элементы f_q нового базиса f выражаются через элементы е_р старого базиса е с помощью матрицы С = (c_pq) по формулам

Сумма (по определению произведения матриц) представляет собой элемент матрицы А(е) С. Отсюда следует, что выражение в правой части (7.10) является элементом матрицы С’ А(е) С. Но в левой части (7.10) стоит элемент матрицы A(f). Поэтому A(f) = С ‘ А(е) С. Теорема доказана.
Следствие. Ранг матрицы A(f) равен рангу матрицы А(е).
Это сразу вытекает из соотношения (7.7), из того, что матрица С и, стало быть, матрица С ‘ являются невырожденными, и из теоремы о том, что ранг матрицы не изменяется при умножении ее на невырожденную матрицу.
Это следствие позволяет ввести важный числовой инвариант билинейной формы — так называемый ранг билинейной формы.
Определение 1. Рангом билинейной формы, заданной в конечномерном линейном пространстве L, называется ранг матрицы этой формы в произвольном базисе пространства L.
Определение 2. Билинейная форма А(х, у), заданная в конечномерном линейном пространстве L, называется невырожденной (вырожденной), если ее ранг равен (меньше) размерности пространства L.

Источник

§4.2.6. Билинейная форма

Функция f(x, y):V × V K называетсябилинейной формой, если для любыхx, y, z из линейного пространства V/ K и любоговыполняются соотношения

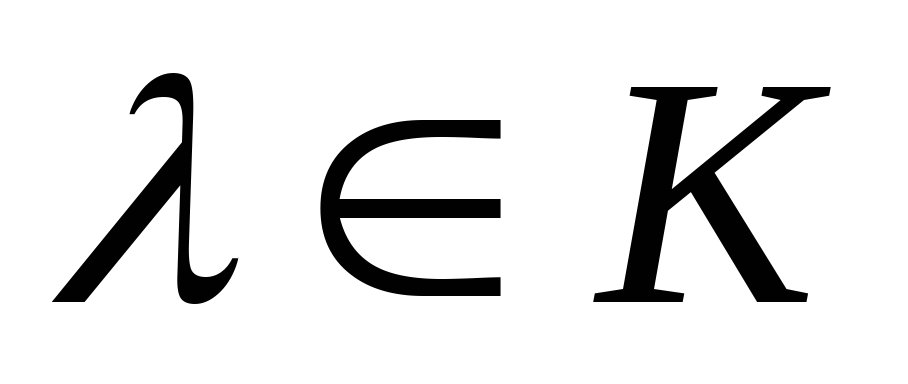
f(x, y + z) = f(x, y) + f(x, z),

f(x, y) =f(x, y),

f(x, y) =f(x, y).

Иными словами, билинейная форма – это функция двух векторных аргументов, линейная по каждому аргументу.

Свойства билинейной формы

f(,y) = 0,

f(х,) = 0.

Билинейная форма называется симметричной, если для любых векторов линейного пространства

Билинейная форма называется кососимметричной, если для любых векторов линейного пространства

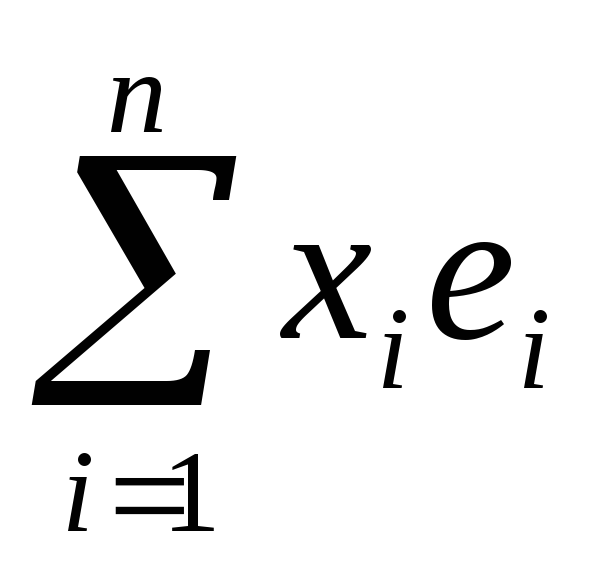
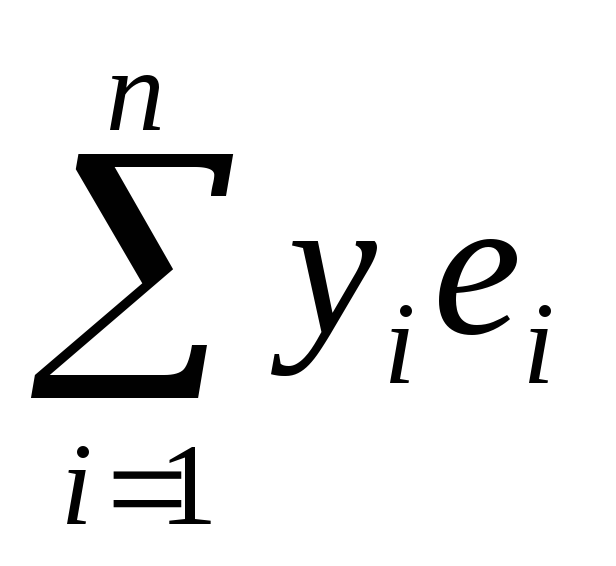
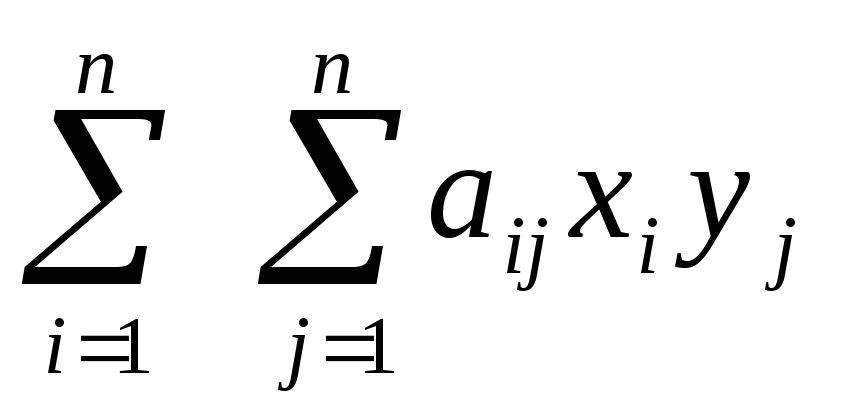
Пример. Пусть А – квадратная матрица порядкаn,а e_1, e₂, …, e_n – базис линейного пространства V/K, x = , y = . Тогдаf(x, y) = – билинейная форма, где– элементы матрицыА.

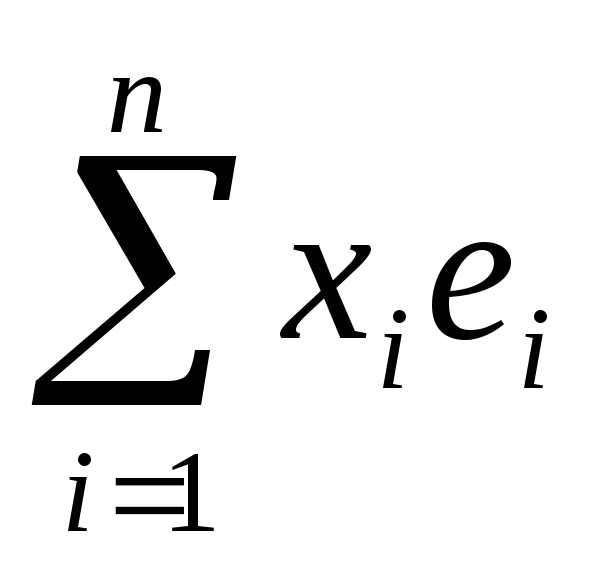
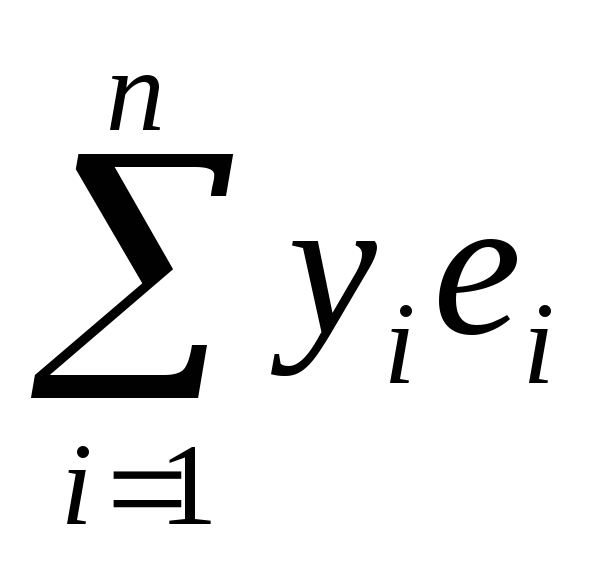
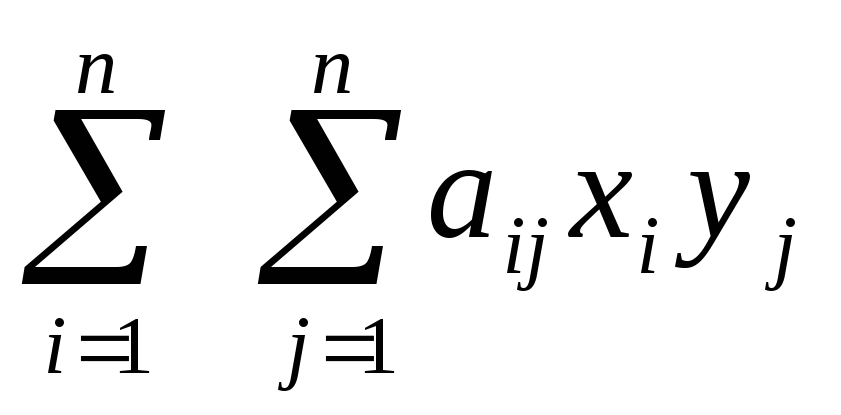
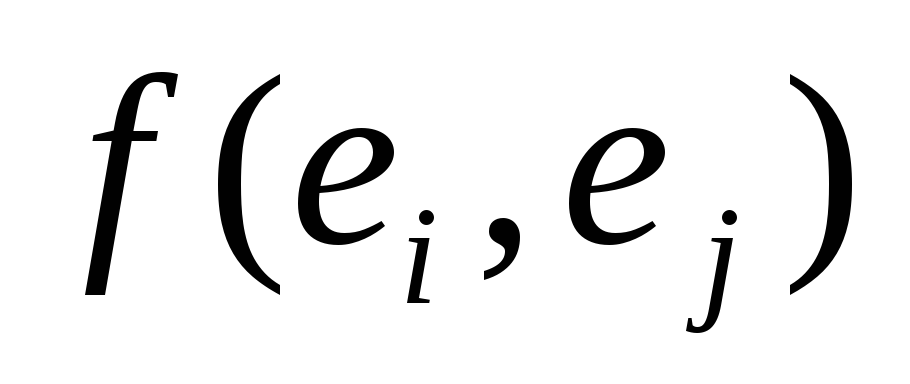
Если f(x, y) – билинейная форма,e_1, e₂, …, e_n – базис линейного пространства V/K, x = , y = , тоf(x, y) = , где=. Обозначим черезХ столбец из координат векторах, а черезY – столбец из координат векторауи пусть

А = .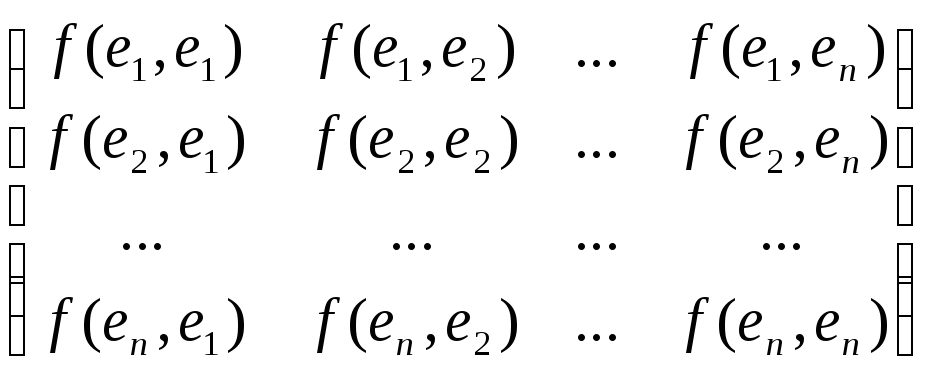

Квадратная матрица А называетсяматрицей билинейной формыf(x, y).Билинейную форму можно записать в матричном виде:

Билинейная форма называется симметричной, если для любых векторов линейного пространства

Билинейная форма называется кососимметричной, если для любых векторов линейного пространства

Теорема.Билинейная форма симметрична тогда и только тогда, когда ее матрица в любом базисе симметрична.

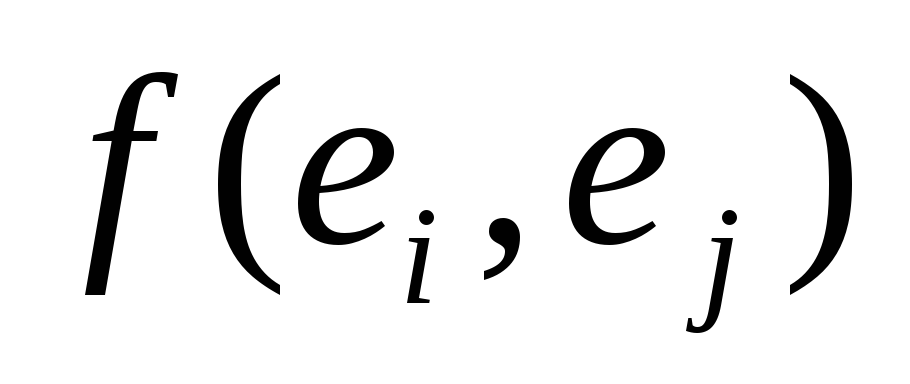
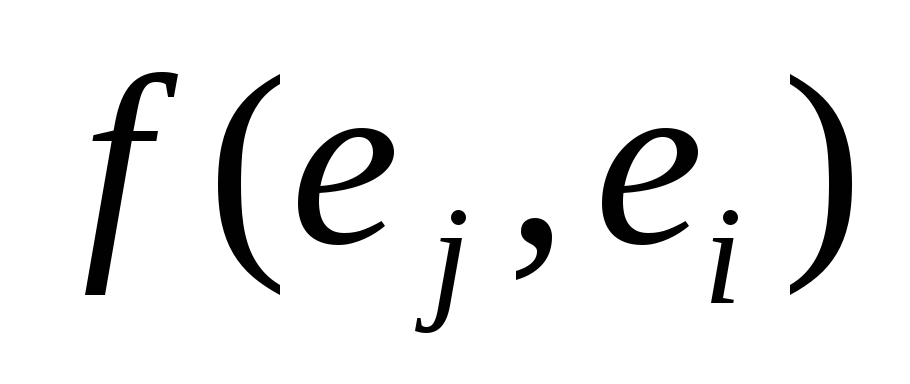
Доказательство. Если билинейная формаf(x, y) симметрична, то=для элементов любого базиса, а это и означает, что матрицаА симметрична.

Теорема. Любую билинейную форму можно представить в виде суммы симметричной и кососимметричной.

Доказательство. Для билинейной формыf(x, y) рассмотрим билинейные формы

, .

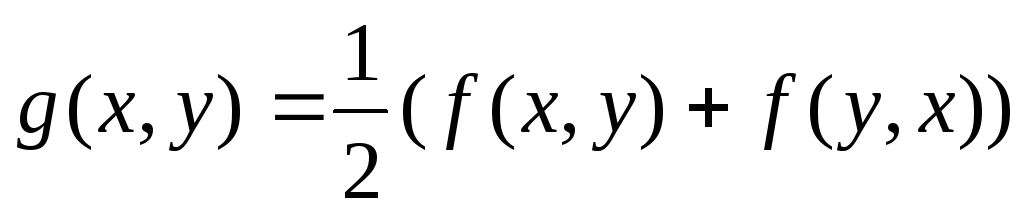
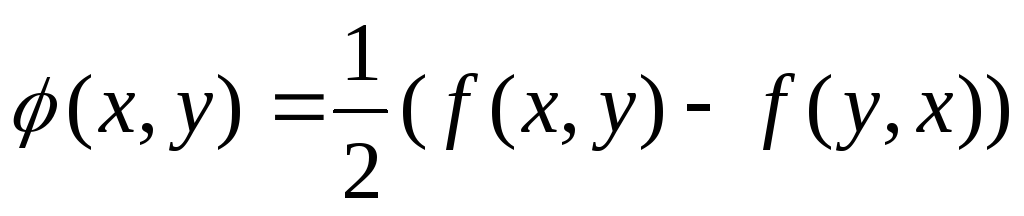
Очевидно, что первая из них симметричная, вторая – кососимметричная, а в сумме они дают форму f(x, y).■

Г(u_1, u₂, …, u_n ) =.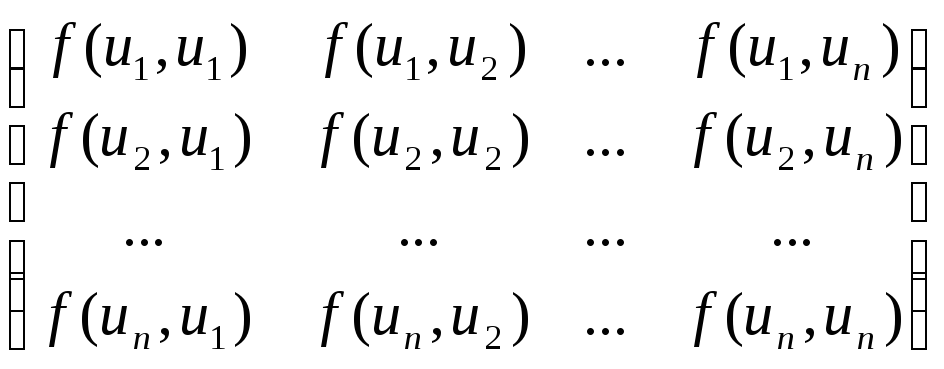

Теорема. Если векторы u_1, u₂, …, u_n линейно зависимы, то матрица Грамма вырожденная.

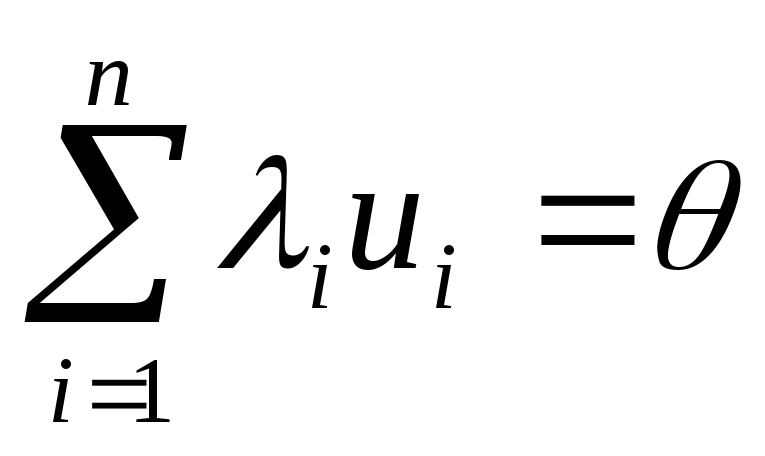
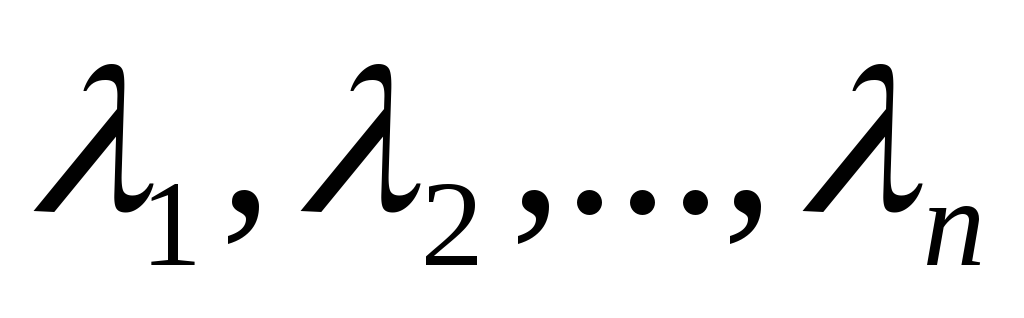
Доказательство. Пусть – нетривиальная линейная зависимость векторов u_1, u₂, …, u_n. Тогда линейная комбинация строк матрицы Грамма с коэффициентами– нулевая стока, а так как среди коэффициентов есть отличные от нуля, то строки линейно зависимы. ■

Квадратичной формой называется функцияf(x, х) одного векторного аргументах, которая получается из симметричной билинейной формыf(x, y) прих = у. Легко видеть, что это определение вполне согласуется с тем, которым мы пользовались в предыдущих параграфах.

Задача. Найдите матрицу билинейной формы и запишите соответствующую ей квадратичную форму

f(x, y) =

Решение.

Матрица билинейной формы:

.

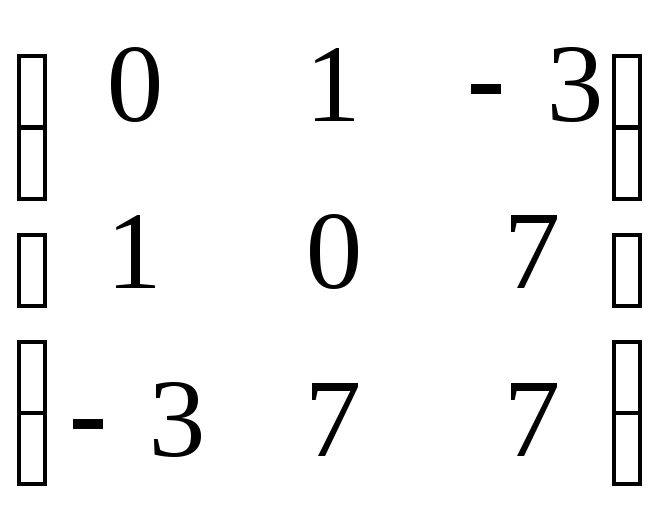
Квадратичная форма: f(x, х) =.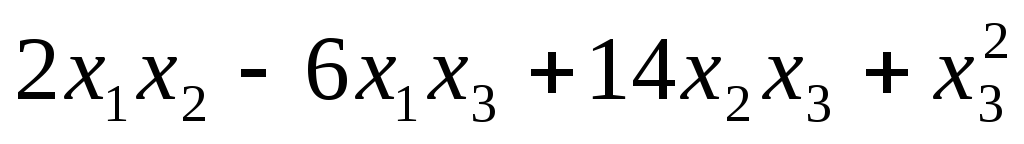

Источник

2.15.Билинейные формы

Остыловский А.Н. Лекция 2.15. Билинейные формы Определение и примеры. Матрица билинейной формы. Преобразование матрицы билинейной формы при замене базиса. Ранг билинейной формы. Псевдоевклидовы пространства.

1. Определение. Примеры

Пусть L линейное пространство над полем R.

B(x + y; z) = B(x; z) + B(y; z);

B(x; y + z) = B(x; y) + B(x; z);

для любых векторов x; y; z 2 L и для любого числа 2 R.

Пример 1. Скалярное произведение в евклидовом пространстве E является билинейной формой.

B(x; y) = x T By = x i y j b ij :

(При B = E получаем предыдущий пример.)

Пример 4. Билинейная форма в пространстве C([a; b]; R) непрерывных функций на отрезке [a; b] задает равенство

B(f 1 ; f 2 ) = G(t)f 1 (t)f 2 (t)dt:

Здесь G(t) фиксированная функция, называемая весом формы B. Пример 9.5. В пространстве C([a; b]; R) билинейную форму можно

B(f 1 ; f 2 ) = G(s; t)f 1 (s)f 2 (t)dsdt;

где G(s; t) функция непрерывная в [a; b] [a; b]. При G(s; t) = 1

B(f 1 ; f 2 ) = f 1 (s)ds f 2 (t)dt:

Билинейная форма B на L называется симметричной, если

для любых векторов x; y 2 L.

Если же B(x; y) = B(y; x), то билинейная форма B называется

2. Матрица билинейной формы

Выберем в L базис e. Числа b ij = B(e i ; e j ) называют компонентами билинейной формы B в базисе e.

B(x; y) = B( i e i ; j e j ) = i j B(e i ; e j ) = i j b ij :

Мы получили тензорную форму записи значения билинейной формы на паре векторов x, y:

Введем в рассмотрение матрицу билинейной формы B в базисе e

Таким образом, при фиксированном базисе каждой билинейной форме соответствует единственная матрица.

Теперь значение билинейной формы на паре векторов x, y можно записать в матричной форме

B(x; y) = x 1 y 1 2x 1 y 3 + 3x 2 y 2 :

Возьмем в качестве базиса L три вектора

e 1 = (1; 1; 1); e 2 = (0; 1; 1); e 3 = (0; 1; 1):

Построим матрицу B билинейной формы B(x; y) в этом базисе. В соответствии с (3) имеем

= B(e 1 ; e 1 ) = 1 1 2 1 1 + 3 1 1 = 2

B(e 1 ; e 2 ) = 1 0 2 1 1 + 3 1 1 = 1

B(e 1 ; e 3 ) = 1 1 2 1 1 + 3 1 ( 1) = 5

Таким образом при фиксированном базисе e имеется взаимно однозначное соответствие между квадратными n n-матрицами над и билинейными формами на L (n = dimL).

Предложение 1. Билинейная форма B(x; y) симметричн а тогда и только тогда, когда в любом (некотором) базисе ее матрица B симметрична.

Доказательство. Пусть B(x; y) симметрична. Тогда ввиду (4) в произвольном базисе имеем:

Будучи числом T B не меняется при транспонировании

Обратно, пусть в некотором базисе матрица B симметрична. Тогда

B(y; x) = T B = ( T B ) T = T B T = T B = B(x; y):

3. Преобразование матрицы билинейной формы при замене базиса

Одной и той же билинейной формы в различных базисах отвечают, конечно же, различные матрицы. Установим связь этих матриц.

b 0 ij = B(e 0 i ; e 0 j ) = B( i k e k ; j l e l ) = i k j l B(e k ; e l ) = i k j l b kl ;

b ij 0 = i k j l b kl :

Как легко проверить (проверьте), равенства (5) равносильны матрич-

Теорема 1. Матрицы B и B 0 билинейной формы B в базисах e и e 0 связаны соотношением

Следствие 1. Знак определителя матрицы билинейной формы не зависит от выбора базиса.

4. Ранг билинейной формы

Рангом rank(B) билинейной формы называется ранг rank(B) ее матрицы в каком-либо базисе.

rank A = rank (AE) = rank (fAe 1 ; : : : ; Ae n g) = dim A(R n ):

В частности, rank B = dim L, где L = B(R n ). Далее,

rank (S T BS) = dim S T BS(R n ) = dim S T B(S(R n )):

rank (S T BS) = dim S T B(R n ) = dim S T (L) = dim L;

Таким образом, доказана

Теорема 2. Ранг билинейной формы является ее инвариантом, не зависящим от выбора базиса.

5. Псевдоевклидовы пространства

Евклидово пространство было определено как линейное пространство L, снабженное симметричной билинейной формой B(x; y) с условием положительности: B(x; x) > 0 для всех x 2 L. Если отбросить это условие, то получатся, так называемые, псевдоевклидовы пространства.

Следуя аналогии с евклидовым случаем, векторы x, y называют B-ортогональными, если B(x; y) = 0. Однако, нормировать в псевдоевклидовых пространствах можно те и только те векторы x для которых B(x; x) 6= 0.

Теорема 3. (Алгоритм Лагранжа) Для любой симметричной билинейной формы B существует B-ортогональный базис.

т.е. вектор e 0 1 нового базиса B-ортогонален ко всем его остальным векторам.

вектора которого B-ортогональны друг другу и остальным векторам и т.д.

Если описанное преобразование применимо вплоть до n-го шага, то искомый базис будет построен. Кроме того, его можно легко перестроить в ортонормированный, т.е. добиться выполнения условия

Пусть b kk = b k+1;k+1 = = b nn = 0 для некоторого k. Если при этом еще b ij = 0 для i; j k, i 6= j, то имеющийся базис уже B- ортогонален. Если же b ij 6= 0 для некоторых i; j k, i 6= j, например,

e 0 k = e k + e k+1 ; e 0 i = e i ; i k + 1:

b 0 kk = B(e 0 k ; e 0 k ) = 2b k;k+1 6= 0

и мы вновь можем применить самое первое преобразование. 2

В B-ортогональном базисе матрица билинейной формы B, очевидно, диагональна.

6. Группа линейных операторов, сохраняющая билинейную форму

Для произвольной билинейной формы B рассмотрим множество G обратимых линейных операторов P, её сохраняющих, т.е. удовлетворяющих условию

Скалярное произведение является билинейной формой. Поэтому условие (7) является обобщением понятия ортогонального оператора. Множество G образует группу, т.е. удовлетворяет следующим трём условиям:

1) B((PQ)x; (PQ)y) = B(P(Qx); P(Qy)) = B(Qx; Qy) = B(x; y):

2) Обозначим P 1 (x) = u, P 1 (y) = v. Тогда

B(P 1 x; P 1 y) = B(u; v) = B(Pu; Pv) = = B(PP 1 x; PP 1 y) = B(x; y):

1. Билинейная форма кососимметрична тогда и только тогда, когда

в любом (некотором) базисе ее матрица кососимметрична.

2. В некотором базисе билинейная форма B задана матрицей

Источник

СОДЕРЖАНИЕ

Формальное определение

Последние две аксиомы устанавливают линейность только по первому аргументу, но первая аксиома (симметрия) сразу же подразумевает линейность и по второму аргументу.

Примеры

Матричное представление

Ортогональность и сингулярность

А Икс знак равно 0 ⟺ Икс Т А знак равно 0. <\ displaystyle Ax = 0 \ Longleftrightarrow x ^ <\ mathsf> A = 0.>

Матрица A сингулярна тогда и только тогда, когда радикал нетривиален.

Ортогональный базис

Подпись и закон инерции Сильвестра

В более общей форме закон инерции Сильвестра гласит, что при работе с упорядоченным полем числа диагональных элементов в диагонализованной форме матрицы, которые являются положительными, отрицательными и нулевыми соответственно, не зависят от выбранного ортогонального базиса. Эти три числа образуют сигнатуру билинейной формы.

Реальный случай

Теперь новое матричное представление A будет диагональной матрицей только с 0, 1 и −1 на диагонали. Нули появятся тогда и только тогда, когда радикал нетривиален.

Сложный случай

Теперь новое матричное представление A будет диагональной матрицей только с 0 и 1 на диагонали. Нули появятся тогда и только тогда, когда радикал нетривиален.

Ортогональные полярности

Это отображение является ортогональной полярностью на проективном пространстве PG ( W ). Наоборот, можно доказать, что все ортогональные полярности индуцированы таким образом, и что две симметричные билинейные формы с тривиальным радикалом индуцируют одну и ту же полярность тогда и только тогда, когда они равны с точностью до скалярного умножения.

Источник

11. Билинейные и квадратичные формы

11.1. Билинейные формы

Определение 11.1. Билинейной формой называется функция (отображение) f: V  V  R (или C), где V – произвольное векторное пространство, и для любых векторов x, y  V и любого числа λ  R (или C) выполняются соотношения

Определение 11.2. Билинейная форма A(x, y) называется симметрической, если для любых x, y  V выполняется: A(x, y) = A(y, x).

Определение 11.3. Билинейная форма A(x, y) называется кососимметрической, если для любых x, y  V выполняется: A(x, y) = –A(y, x).

Свойства билинейных форм

Любую билинейную форму можно представить в виде суммы симметричной кососимметричной форм.

При выбранном базисе e₁, e₂, …, e_n в векторном пространстве V любая билинейная форма A однозначно определяется матрицей

A(е) = ,

A(x, y) = (x₁ x₂ … x_n), то есть

A(x, y) = ,где А_ij = A(e_i, e_j). (1)

Вид (1) назовем общим видом билинейной формы в n-мерном векторном пространстве.

Замечание. Если билинейная форма A(x, y) симметрическая, то и матрица (A_ij) будет симметрической, то есть A_ij = A_ji для i, j = 1, 2, …, n. Если билинейная форма A(x, y) кососимметрическая, то и матрица (A_ij) будет кососимметрической, то есть A_ij = –A_ji для i, j = 1, 2, …, n.

Преобразование матрицы билинейной формы при переходе к новому базису. Ранг билинейной формы

Теорема 11.1. Матрицы A(e) и A(f) билинейной формы A(x, y) в базисах <e> и <f> связаны соотношением

где C – матрица перехода от базиса <e> к базису <f>, а C t –транспонированная матрица C.

Следствие. Ранг матрицы A(f) равен рангу матрицы A(e).

Это утверждение следует из равенства (): так как С – матрица перехода от одного базиса к другому, то матрица С и матрица C t – невырожденные, поэтому умножение на них матрицы A(e) не меняет ее ранга.

Определение 11.5. Билинейная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

11.2. Квадратичные формы

Пусть A(x, y) – симметрическая билинейная форма, заданная на векторном пространстве V.

Определение 11.6. Квадратичной формой называется числовая функция одного векторного аргумента x, которая получается из билинейной формы A(x, y) при x = y.

Определение 11.7. Симметрическая билинейная форма A(x, y) называется полярной квадратичной форме A(x, x).

Пусть дана билинейная форма A(x, y) = , положим в ней x_i = y_j, тогда мы получим представление квадратичной формы A(x, x) в конечномерном векторном пространстве V с заданным базисом <e>:

A(x, x) = . (2)

Определение 11.8. Матрица (a_ij) называется матрицей квадратичной формы A(x, x) в заданном базисе <e>.

При переходе к новому базису матрица квадратичной формы преобразуется по формуле A(f) = C t A(e)C и ранг этой матрицы не меняется при переходе к новому базису.

Определение 11.9. Ранг матрицы квадратичной формы A(x, x) называется рангом квадратичной формы.

Определение 11.10. Квадратичная форма называется невырожденной, если ее ранг равен размерности пространства V и вырожденной, если ее ранг меньше размерности пространства V.

Определение 11.11. Квадратичная форма A(x, x) называется

Положительно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) > 0.

Отрицательно определенной, если для любого ненулевого вектора x выполняется неравенство A(x, x) 0 и A(y, y) 0 при х ≠ 0, т. к. A(x, x) положительно определена.

Вывод. Скалярное произведение в векторных пространствах может быть задано с помощью билинейной формы:

(x, y) = = A(x, y).

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник