задания для счета в уме
Тренажер : Арифметика
Категории тренажеров:
Популярные тренажеры:
Порекомендовать друзьям:
- Увеличивает скорость мышления Концентрирует внимание Логическое мышление
Тренироваться
1709 KS: 48
Самый разнообразный из математических тренажеров для ума, тем самым и более сложный, так как включает в каждом примере минимум две операции в уме, порядок которых также важен и определяется игроком.
Подобные игры для мозга не редкость среди многих культур, однако, выход и в онлайн-платформу Мозготрен, позволил сделать нагрузку более гибкой и разнообразить задания. Также дополнительного азарта тренировкам придает возможность состязаний в режиме реального времени, пригласив друзей померяться силами.
Что тренирует
Арифметический тренажер не является узкоспециализированным, та как он одновременно включает в работу несколько систем нашего мозга. Примеры включают несколько операций и отличаются необходимостью хорошо напрячь мозг. В данном тренажере вы будете тренировать счет в уме: сложение, вычитание, умножение и деление.
Оперативная и кратковременная память – увеличение количества знаков в числах, а также необходимость выполнить несколько расчетов в уме даже на минимальных настройках сложности, требуют хорошего развития оперативной и кратковременной памяти, тем самым данные действия стимулируют этот процесс. Благо, такое место в нашем мозгу не имеет постоянного ограничения и расширяется упражнениями.
Логическое мышление – важное отличие данного тренажера от подобных в разделе заданий на мышление в том, что среди нескольких операций с числами в каждом примере, нужно определять их приоритет, соответственно законам математики. К тому же, выбор правильного алгоритма действий может повлиять на скорость поиска правильного ответа и на результат в целом.
Скорость мышления – посредством многократных выполнений операций с числами, центральная нервная система «приучается» к быстрому повторению подобных действий. Чем больше игрок считает в уме, тем скорее он будет это делать в дальнейшем.
Внимание – это задание требует концентрации не только при поиске нужной ячейки с ответом, но и в ряде случаев с усложнениями, такими как переворот или отрицательные числа. Не менее важно быть внимательным при выполнении нескольких математических операций подряд, учитывая тот факт, что отрицательные ответы могут встречаться даже на самом легком уровне.
Правила
Для настройки сложности, установите разрядность чисел, это может быть число от 3 до 5. Данный параметр указывает сколько чисел будет участвовать в каждом примере для вычисления. Размер каждого числа не зависит от этого условия, они будут увеличиваться с ростом уровня сложности (после каждого правильного ответа). Разрядность чисел значительно влияет на коэффициент сложности – число, отображенное в верхнем левом углу рабочего поля.
Переворот – усложнение, которое меняет пространственное положение примеров. Перевернутые примеры воспринимаются тяжелее для нашего мозга, и это требует больше драгоценного времени, поэтому и коэффициент сложности при включении данного параметра вырастет.
Отрицательные – как очевидно из названия, в примерах будут появляться отрицательные числа, что сделает процесс подсчета интереснее и сложнее. Заметьте, в ответах отрицательные числа могут присутствовать даже на самых легких настройках.
Кнопка рестарт позволяет быстро начать тренировку заново, при этом сохраняться все выбранные ранее настройки сложности.
Начисление очков
Для удобного отслеживания результатов каждой тренировки, по ее окончании вам начисляется соответствующее число баллов, основанных на нескольких важных показателях.
Формула начисления баллов за правильный ответ выглядит так:
Ваша сумма очков + КС*Уровень
КС – коэффициент сложности, он зависит от настроек сложности выбранных до начала теста, эту цифру вы сможете увидеть в верхнем левом углу рабочего поля. При усложнении настроек повышается коэффициент сложности.
Уровень – это не постоянная величина, в начале тренировки он имеет минимальное значение и растет на одну позицию с каждым правильным ответом. При неправильном ответе, уровень стает ниже на позицию.
Формула вычитания баллов за неправильный ответ выглядит так:
Ваша сумма очков – (КС*Уровень)/2
При этом в минусовые значения сумма очков не заходит.
Мульти-игра
Для более интересного прохождения тренировки, всегда есть возможность пригласить друзей и устроить состязание. Для этого, после выбора настроек сложности, в разделе мульти-игра нужно поделиться ссылкой с друзьями, скопировав ее или нажав иконку необходимой соцсети.
Соревнование можно начинать после того, как все игроки подтвердят свою готовность (кнопка «Готов к игре»).
Примеры для всех играющих будут появляться одновременно, для получения баллов, необходимо дать правильный ответ первым. При этом задание обновится, и остальные участники вынуждены будут считать уже новый пример.
Если первый игрок нажал неверный ответ, задание останется на экранах пока соперник не ответит правильно или не правильно.
В верхнем левом углу рабочего поля вы сможете отслеживать текущее количество баллов у вас и у соперника. Зеленый цвет вашего счета подсказывает, что вы лидируете, а красный говорит об отставании.
Результаты соревнований будут занесены в таблицу личных достижений на mozgotren.ru, и отобразятся в графике тренировок на ряду с остальными занятиями.
Игры, задания и упражнения, с которыми вы быстро научите ребёнка считать в уме
Когда обучение счёту начинается с классических примеров, ребёнок решает, что считать и заниматься математикой скучно. Попробуйте лучше занимательные игры и задания от ЛогикЛайк. Полезные идеи для детей 3-5 и 6-8 лет.
На LogicLike.com дети развивают логику и способности к математике. Решайте ребусы, закономерности, логические задачи и головоломки. У нас более 3500 занимательных заданий.
Попробуйте наш курс в игровой форме!
Первое знакомство с цифрами и игры с ними
Наверняка вы уже перешагнули эту ступеньку и успели использовать самые разные способы, чтобы запомнить цифры: рисовали, вырезали, лепили и т.д. В возрасте 3-5 лет дети на лету схватывают всё, что интересно, поэтому их несложно вовлекать в обучающие игры.
Давайте рассмотрим пару необычных приёмов для обучения счёту, которые одинаково полезны не только младшим и средним, но и старшим дошкольникам.
«Язык чисел» и математические задачки из воздуха
Мы, взрослые, каждый день думаем числами, но не всегда называем их вслух. А ведь детей может заинтересовать именно «язык чисел»: «Во сколько мы сегодня проснулись? В 7 утра. А какой автобус ждали на остановке? 12-й. Сколько минут ехали? 10».
Постепенно просто называть числа станет скучно. Покажите ребёнку, как интересно считать всё, что его окружает: подъезды в доме, машины на парковке, деревья возле детской площадки, номера домов. Если вы находчивый родитель, то сможете на ходу придумать небольшие математические задачки на сложение и вычитание.
Замечено: с бо́льшим энтузиазмом ребёнок пересчитает то, что ему нравится. Поэтому всем известные задачи с конфетами действуют, как магнит.
Дома ребёнку всегда есть, что посчитать. Можно следить за стрелками часов, превратить в игру измерение веса и роста. Надолго занимает детей отрывной календарь или календарь-игрушка, в котором нужно каждый день переворачивать кубики с цифрами.
А вот этот Lego-календарь и вовсе нужно каждый месяц разбирать и собирать заново.
Для детей старшего дошкольного возраста все перечисленные выше упражнения можно усложнить. Попробуйте вместе составлять текстовые задачи, опираясь на увиденное за день. Пусть ребёнок больше считает в уме, решая прикладные задачи.
А вообще, чтобы придумать интересные задачи самостоятельно или найти качественный материал в интернете, потребуется время. Команда ЛогикЛайк уже провела всю методическую и другую подготовительную работу за вас!
2500+ заданий на развитие логики и математических способностей. Озвучка заданий, ответы и пояснения в вашем онлайн-кабинете.
Простые игры с числами помогут познакомить ребёнка с арифметическими действиями
Кубики, магниты, карточки, счётные палочки — самые что ни на есть стандартные материалы для обучения счёту. Но они быстро наскучат ребёнку. Гораздо интереснее ему будет играть с тем, что он сделает своими руками. Можно пофантазировать вместе с ребёнком и смастерить собственные игры для изучения чисел и отработки простейших математических действий.
Интересное применение найдётся ракушкам, привезенным с моря. Такая игра поможет младшим дошкольникам быстрее научиться складывать и вычитать. Теперь абстрактные арифметические действия можно видеть на наглядном примере.
Лоток из-под яиц и капсулы от киндеров тоже не спешите выбрасывать, их можно превратить в нескучную игру. На фото вариант со сложением, но его можно заменить на вычитание, умножение или деление. Игра хороша тем, что ребёнок может руками «разбирать» и «собирать» новые примеры.
Конструкторы типа Lego тоже подходят для изучения счёта. Подобные игры помогают развивать мелкую моторику, логику и пространственное мышление.
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
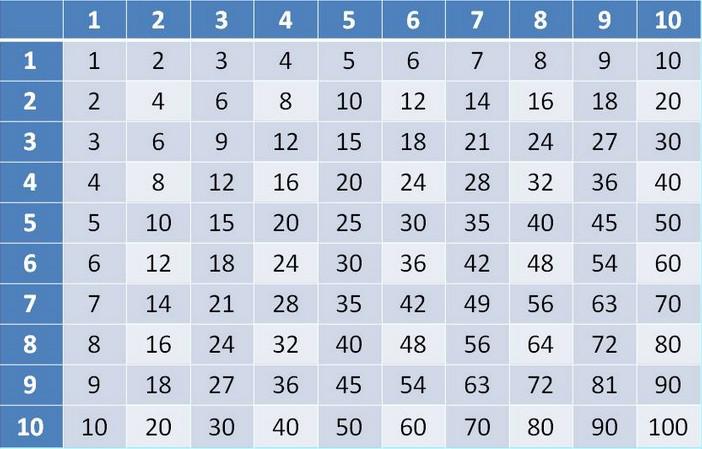
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Устный счет: техника быстрого счета в уме
Секреты устного счёта
Существуют приемы устного счета — простые алгоритмы, которые желательно довести до автоматизма. После овладения простыми приёмами можно переходить к освоению более сложных.
Прибавляем числа 7,8,9
Для упрощения вычислений числа 7,8,9 сначала надо округлять до 10, а затем вычитать прибавку. К примеру, чтобы прибавить 9 к двузначному числу, надо сначала прибавить 10, а затем вычесть 1 и т.д.
Быстро складываем двузначные числа
Если последняя цифра двузначного числа больше пяти, округляем его в сторону увеличения. Выполняем сложение, из полученной суммы отнимаем «добавку».
Если слагаемые поменять местами, то сначала можно округлить число 57 до 60, а потом вычесть из общей суммы 3:
Складываем в уме трехзначные числа
Особенности вычитания: приведение к круглым числам
Вычитаемые округляем до 10, до 100. Если надо вычесть двузначное число, надо округлить его до 100, вычесть, а затем к остатку прибавить поправку. Это актуально если поправка невелика.
Вычитаем в уме трехзначные числа
Если в свое время был хорошо усвоен состав чисел от 1 до 10, то вычитание можно производить по частям и в указанном порядке: сотни, десятки, единицы.
Умножить и разделить
Хотя на мой взгляд достаточно знать таблицу от 1 до 10, чтобы мочь перемножать бо´льшие числа. Например:
Умножаем и делим на 4, 6, 8, 9
Овладев таблицей умножения на 2 и на 3 до автоматизма, сделать остальные расчеты будет проще простого.
Для умножения и деления двух- и трехзначных чисел применяем простые приёмы:
Как умножать и делить на 5
Еще проще правило деления на 5. Сначала умножаем на 2, а затем полученное делим на 10.
Умножение на 9
Чтобы умножить число на 9, необязательно его дважды умножать на 3. Достаточно его умножить на 10 и вычесть из полученного умножаемое число. Сравним, что быстрее:
Счет на пальцах
Например, в защиту «пальчиковой» методики приводится приём умножения на 9. Хитрость приёма такова:
Также существует еще множество подобных приемов с применением пальцев для каких-то единичных математических операций, но это актуально пока вы этим пользуетесь и тут же забывается при прекращении применения. Поэтому лучше выучить стандартные алгоритмы, которые останутся на всю жизнь.
Устный счёт на автомате
Во-первых, необходимо хорошо знать состав числа и таблицу умножения.
Во-вторых, надо запомнить приемы упрощения расчётов. Как выяснилось, таких математических алгоритмов не так уж много.
Как научиться считать в уме
Считать в уме, по мнению многих, в наше время уже неактуально, ведь калькулятор есть в каждом смартфоне, компьютере и ноутбуке. Однако калькулятор не будет сопровождать вас при каждом вашем шаге, а считать необходимо постоянно и много. Способность сосчитать в уме – умение весьма нужное даже в 21 веке. А тем более это нужно школьникам для решения примеров по математике из нелёгкой школьной программы. И им весьма полезно будет уметь считать быстро, не пребегая к электронным устройствам.
Опыт и постоянные тренировки играют важную роль в развитии любых способностей, но навык устного счета не состоит только лишь из опыта. Это могут доказать люди, умеющие считать в уме гораздо более сложные примеры: например, умножать и делить трех- и четырехзначные числа, находить суммы и разности огромных примеров.
Что необходимо знать и делать человеку, дабы повторить такое?
• Во-первых, концентрация или же умение ненадолго удерживать в памяти несколько вещей одновременно.
• Во-вторых, алгоритмы, специальные методы вычислений и математические уловки, значительно облегчающие процесс устного счёта.
• В-третьих, практика. Постоянные тренировки и постепенное усложнение решаемых задач позволят улучшить скорость и качество устного счета.
Важно отметить, что именно практика имеет наибольшее значение. Не обладая достаточным опытом, вы не сможете быстро применять удобные алгоритмы, подходящие под определённые ситуации. И помните, что максимальный эффект будет достигнут при оптимальном использовании всех трёх составляющих. Тренировать сразу все аспекты этого навыка Вы можете в онлайн тренажере устного счёта.
Внимание и концентрация
Чтобы максимально быстро считать в уме, необходимо уметь концентрироваться на конкретном примере. Этот навык полезен не только для совершения математических операций, но и для решения любых жизненных задач. Существует несколько способов улучшить свою внимательность и способность к концентрации:
При счете в уме, важно ясно представлять себе решаемый пример – визуализировать его. Запоминать промежуточные результаты нужно не на слух, а так как они выглядят в записи, например, на бумаге. Тренировать подобное восприятие можно разными способами, и отчасти визуализация решения приходит с опытом.
Старайтесь всегда находить что-то интересное в рутине, превращая действие в игру. Так поступают и некоторые родители, желающие, чтобы их ребёнок выполнил какую-либо скучную работу.
Огромное количество людей всегда хотят «быть лучше» соперника. Именно поэтому состязательность является еще одним способом развить свою внимательность. В устном счете Вы можете найти себе соперника и пытаться его в этом превзойти.
Еще одним фактором, создающим азарт при счете, может стать борьба с самим собой при достижении определенного результата, то есть личные рекорды. Их можно ставить, например, в скорости счета, в количестве решенных примеров и своей точности ответов.
Наконец, максимальная концентрация может быть достигнута при спонтанном увлечении процессом счета. Как пример, во время чтения Вы перестаёте думать об окружающих вас предметах, людях, ситуациях, полностью погружаетесь в книгу. Именно неподдельный интерес к чему-либо способен заставить вас приобрести наибольшую внимательность в этом деле.
Безусловно, все эти способы надо отрабатывать, практиковать. В этом могут помочь различные тренажеры зрительной памяти и улучшения внимательности.
Простые арифметические закономерности
Решение любой по сложности задачи всегда сводится к применению базовых принципов, и именно эти принципы и закономерности позволят вам быстро выполнять различного рода операции. Существует определенный набор таких правил и закономерностей, которые необходимо довести до автоматизма с помощью разных онлайн тренажеров по математике.
Таблица умножения. Для быстрого устного счета хорошо бы безупречно знать таблицу умножения, которая является основой счета. Если у Вас с этим еще проблемы, можете воспользоваться онлайн Тренажером таблицы умножения.
Деление на 2. Несмотря на то, что многим умножение и деление на 2 дается достаточно просто, в сложных случаях так же пытайтесь округлять числа. Например, чтобы разделить 198 на 2, нужно сначала разделить 200 (это 198 + 2 ) на 2 и отнять 2 деленое на 2. Итого: 198 : 2 = 200 :2- 2 :2=100-1=99.
Деление и умножение на 4 и 8. Деление (или умножение) на 4 и на 8 являются двукратным или трехкратным делением (или умножением) на 2. Производить эти операции удобно последовательно. Например, 46 × 4 = 46 × 2×2 = 92 × 2 =184.
Умножение на 11. Чтобы умножить любое двузначное число на 11, нужно между первой и второй цифрой умножаемого числа вписать сумму первой и второй цифры. Например: 23×11= 2 (2+3) 3 = 2 5 3. Или если сумма чисел в центре дает результат больше 10: 29×11 = 2 (2+9) 9 = 2 (11) 9 = 3 1 9.
Более сложные методики
Эффективность умножения в уме некоторых двузначных чисел может быть выше за счет меньшего количества действий, если использовать специальные алгоритмов. Ниже представлены три специальные методики, в том числе введение и использование опорного числа.
Квадрат суммы и квадрат разности
23 2 = (20+3) 2 = 20 2 + 2×3×20 + 3 2 = 400+120+9 = 529
69 2 = (70-1) 2 = 70 2 – 70×2×1 + 1 2 = 4 900-140+1 = 4 761
Возведение в квадрат чисел, заканчивающихся на 5
25 2 = (2×(2+1)) 25 = 625
85 2 = (8×(8+1)) 25 = 7 225
155 2 = (15×(15+1)) 25 = (15×16)25 = 24 025
Опорное число
Наиболее популярной методикой умножения больших чисел в уме является прием использования, так называемого, опорного числа. Опорное число при умножении – это число, к которому близко находятся оба множителя и на которое удобно умножать. А методика использования этого числа зависит от того, являются ли множители больше или меньше него самого.
Оба множителя больше опорного. Действовать нужно точно так же, но не вычитать недостаток, а прибавлять избыток:
Один множитель меньше, другой больше опорного. Схема та же, но произведение недостатка и избытка нужно вычитать: