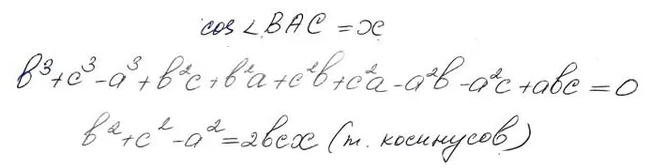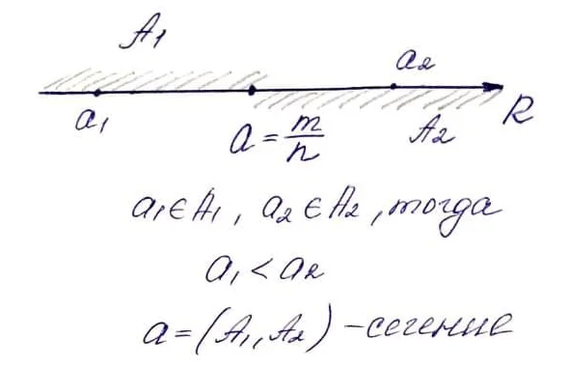задания на быстрый счет
5 ускорителей устного счета
В устном счете, как и везде, есть свои хитрости, и чтобы научиться быстрее считать нужно, знать эти хитрости и уметь применять на практике.
Сегодня мы этим и займемся!
1. Как быстро складывать и вычитать числа
Рассмотрим три случайных примера:
Если считать в уме обычным способом, то возникают затруднения, ведь вычитаемое число больше чем вторая цифра в первом числе и начинаются затруднения и торможения с запоминанием остатка.
Типа 25 – 7 = (20 + 5) – (5- 2) = 20 – 2 = (10 + 10) – 2 = 10 + 8 = 18
Согласитесь, что такие операции сложно проворачивать в голове.
Но есть более простой способ:
Намного проще вычесть из числа 10 и прибавить 3, чем городить сложные вычисления.
Вернемся к нашим примерам:
Оптимизируем вычитаемые числа:
Итого получим:
Вот теперь намного интересней и проще!
Посчитайте сейчас представленные ниже примеры этим способом:
2. Как быстро умножать на 4, 8 и 16
В случае умножения мы тоже разбиваем числа на более простые, например:
Если помните таблицу умножения, то все просто. А если нет?
Тогда нужно упростить операцию:
Наибольшее число ставим первым, а второе раскладываем на более простые:
Удваивать числа гораздо легче, нежели чем учетверять или увосьмирять их.
8 * 4 = 8 * 2 * 2 = 16 * 2 = 32
Примеры раскладывания чисел на более простые:
Отработайте этот способ на следующих примерах:
3. Деление числа на 5
Возьмем следующие примеры:
Деление и умножение с числом 5 всегда очень простые и приятные, ведь пять это половина от десяти.
И как их быстро решить?
Для того чтобы проработать этот способ решите следующие примеры:
4. Умножение на однозначные числа
С умножением немного сложнее, но не сильно, как бы Вы решили следующие примеры?
Без специальных фишек решать их не очень приятно, но благодаря методу «Разделяй и властвуй» мы можем сосчитать их гораздо быстрее:
Нам остается только перемножить однозначные числа, некоторые из которых с нулями и сложить полученные результаты.
Для проработки этой техники решите следующие примеры:
Делимость числа на 2, 3, 4, 5, 6 и 9
Проверьте числа: 523, 221, 232
Число делится на 3, если сумма его цифр делится на 3.
Например, возьмем число 732, представим его как 7 + 3 + 2 = 12. 12 делится на 3, а значит, число 372 делится на 3.
Проверьте, какие из следующих чисел делятся на 3:
12, 24, 71, 63, 234, 124, 123, 444, 2422, 4243, 53253, 4234, 657, 9754
Число делится на 4, если число, состоящее из последних двух его цифр, делится на 4.
Например, 1729. Последние две цифры образуют 20, которое делится на 4.
Проверьте, какие из следующих чисел делятся на 4:
20, 24, 16, 34, 54, 45, 64, 124, 2024, 3056, 5432, 6872, 9865, 1242, 2354
Число делится на 5, если его последняя цифра 0 или 5.
Проверьте, какие из следующих чисел делятся на 5 (самое легкое упражнение):
3, 5, 10, 15, 21, 23, 56, 25, 40, 655, 720, 4032, 14340, 42343, 2340, 243240
Число делится на 6, если оно делится и на 2 и на 3.
Проверьте, какие из следующих чисел делятся на 6:
22, 36, 72, 12, 34, 24, 16, 26, 122, 76, 86, 56, 46, 126, 124
Число делится на 9, если сумма его цифр, делится на 9.
Например, возьмем число 6732, представим его как 6 + 7 + 3 + 2 = 18. 18 делится на 9, а значит, число 6732 делится на 9.
Проверьте, какие из следующих чисел делятся на 9:
9, 16, 18, 21, 26, 29, 81, 63, 45, 27, 127, 99, 399, 699, 299, 49
Игра «Быстрое сложение»
Отличный тренажер для развития быстрого счета. На экране дана таблица 4х4, а над ней показаны числа. Самое большое число нужно собрать в таблице. Для этого нажмите мышкой на два числа, сумма которых равна этому числу. Например, 15+10 = 25.
Игра «Быстрый счет»
Игра «быстрый счет» поможет вам усовершенствовать свое мышление. Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.
Игра «Угадай операцию»
Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Игра «Упрощение»
Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.
Задание на сегодня
Решить все примеры и тренироваться минимум 10 минут в игре Быстрое сложение.
Урок взят из курса «Устный счет за 30 дней»
Научитесь быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. Научу использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Другие развивающие курсы
Деньги и мышление миллионера
Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.
Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.
Скорочтение за 30 дней
Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.
Развитие памяти и внимания у ребенка 5-10 лет
Цель курса: развить память и внимание у ребенка так, чтобы ему было легче учиться в школе, чтобы он мог лучше запоминать.
После прохождения курса ребенок сможет:
Супер-память за 30 дней
Запоминайте нужную информацию быстро и надолго. Задумываетесь, как открывать дверь или помыть голову? Уверен, что нет, ведь это часть нашей жизни. Легкие и простые упражнения для тренировки памяти можно сделать частью жизни и выполнять понемногу среди дня. Если съесть суточную норму еды за раз, а можно есть порциями в течение дня.
Как улучшить память и развить внимание
Бесплатное практическое занятие от advance.
Секреты фитнеса мозга, тренируем память, внимание, мышление, счет
Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.
Как быстро считать в уме: приемы устного счета больших чисел
Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.
Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а минимум двухзначными и трехзначными числами.
После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).
Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.
Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.
Гаусс и устный счет

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.
По его собственным словам, он научился считать раньше, чем говорить. Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.
В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.
Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.
Сложение чисел в уме
Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.
Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.
Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14
Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.
Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6. Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:
356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084
Вычитание чисел в уме
Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.
Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.
Теперь считаем: 528-300-20-1=228-20-1=208-1=207
Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.
Умножение чисел в уме
Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.
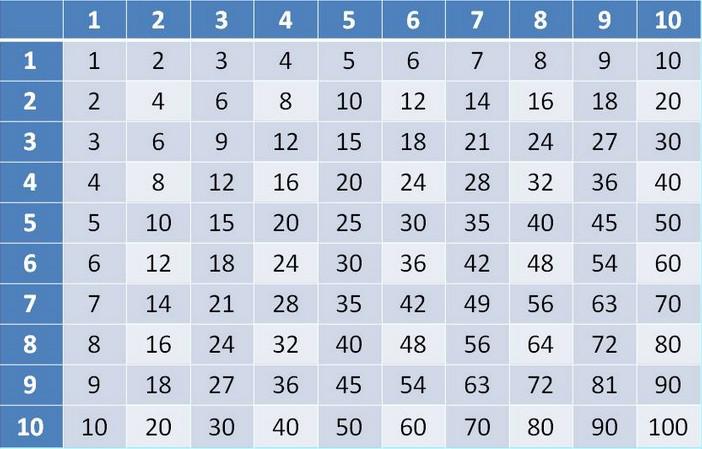
Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.
Умножение многозначных чисел на однозначные
Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.
528=500+20+8
528*6=500*6+20*6+8*6=3000+120+48=3168
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Умножение двузначных чисел
Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.
Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2
28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896
Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.
Умножение на 11
Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.
Проверим и умножим 54 на 11.
Возведение в квадрат
С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.
Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.
Проверим! Возведем в квадрат число 75.

Деление чисел в уме
Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.
Деление на однозначное число
При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.
Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:
6144:8=(5600+544):8=700+544:8
Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:
544:8=(480+64):8=60+64:8
Осталось разделить 64 на 8 и получить результат, сложив все результаты деления
6144:8=700+60+8=768
Деление на двузначное число
При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.
При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.
Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.
Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.
Сколько будет 4424:56?
Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.
56*80=4480
Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Проверяем:
79*56=4424
Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

Полезные советы
В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:
Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Конспект по математике «Приемы быстрого счета» на примерах с заданиями для самостоятельной работы (5-11 класс)
Ищем педагогов в команду «Инфоурок»
Приемы быстрого счета
Автор подборки: Корякина Елена Викторовна,учитель математики, МБОУ СОШ №32 г.Озерск Челябинской области
В наше время существует мнение, что человеку не надо знать приемы быстрых вычислений, что для этого существуют калькуляторы, компьютеры. Однако польза устных вычислений огромна, особенно для школьника:
1) Применяя законы арифметических действий к устным вычислениям, можно закрепить, усвоить их не механически, а осознано.
2) Устный счет тренирует память.
3) В устных вычислениях нет готового шаблона, приемы вычислений разнообразны, каждый раз надо думать, какой из них целесообразнее, а эта умственная деятельность способствует развитию очень полезных качеств человека, как внимание, логика, сосредоточенность, смекалка, самостоятельность, творческое мышление.
(1)Прием округления при сложении многозначных чисел
Имеем: 599 + 1 + 387 – 1 = 600 + 386 = 986
Вывод: если одно из слагаемых увеличить на несколько единиц, а другое уменьшить на столько же единиц, то величина суммы не изменится. Округлением слагаемых можно пользоваться также при сложении обыкновенных и десятичных дробей.
Примеры: 173 + 59 = 172+60=232
8127 + 893 = 8120+900=9020
Примеры для самостоятельной работы:
(2)Умножение на однозначное число
А)Чтобы устно умножить число на однозначный множитель ( например, 27 * 8 ) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20*8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Б) Полезно знать на память таблицу умножения до 19*9:
В)Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350
(3)Умножение на двузначное число
А) Умножение на двузначное число стараются облегчить, приводя это действие к более привычному умножению на однозначное число. Когда множимое однозначное, мысленно переставляют множители и выполняют умножение на однозначное число. Например: 6*28=28*6=120+48=168
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
41*16=41*10+41*6 = 410+246 =656
или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз. Например: 45*14 =90*7=630
Примеры для самостоятельной работы:
(4)Умножение на 4 и на 8. Деление на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например:
Чтобы устно умножить число на 8, его трижды удваивают. Например:
Можно и так: 217*8=200*8 +17*8= 1600+136=1736.
Чтобы устно разделить число на 4, его дважды делят пополам. Например:
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
Примеры для самостоятельной работы:
Система быстрого счета (может кому пригодится)
Тридцать простых приемов устного счета
Умножение на однозначное число
Чтобы устно умножить число на однозначный множитель (например, 27 X 8) выполняют действие, начиная с умножения не единиц, как при письменном умножении, а иначе: умножают сначала десятки множимого (20X8 = 160), затем единицы (7*8 =56) и оба результата складывают.
Полезно знать на память таблицу умножения до 19*9:
Зная эту таблицу, можно умножение например, 147*8 выполнить в уме так: 147*8-140*8+7*8= 1120 + 56= 1176
Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350
Умножение на двузначное число
Умножение на двузначное число стараются облегчить для устного выполнения, приводя это действие к более привычному умножению на однозначное число.
Когда множимое однозначное, мысленно переставляют множители и выполняют действие, как указано в § 1. Например:
Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
41*16=41*10+41*6 = 410+246 =656
(или 41*16=16*41 = 16*40+16*1=640+16=656
Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.
Если множимое или множитель легко разложить в уме на однозначные числа (напр., 14 = 2*7), то пользуются этим, чтобы уменьшить один из множителей, увеличив другой во столько же раз (ср. § 3). Например:
Умножение на 4 и на 8
Чтобы устно умножить число на 4, его дважды удваивают. Например:
Чтобы устно умножить число на 8, его трижды удваивают. Например:
(Eще удобнее: 217*8=200*8 +17*8= 1600*13=1736.
Деление на 4 и на 8
Чтобы устно разделить число на 4, его дважды делят пополам. Например:
Чтобы устно разделить число на 8, его трижды делят пополам. Например:
516:8=258:4=129:2= 64 1/2
Умножение на 5 и на 25
Чтобы устно умножить число на 5 умножают его на 10/2, т. е. приписывают к числу ноль и делят пополам. Например:
При умножении на 5 числа четного удобнее сначала делить пополам и к полученному приписать ноль. Например:
Если же число при делении на 4 дает остаток, то прибавляют
при остатке: к частному
Основание приема ясно из того, что
Чтобы устно умножить число на 1/ прибавляют к множимому его половину. Например:
23*1/=23 + 11/ = 34/ (или 34,5)
Чтобы устно умножить число на 1/Прибавляют к множимому его четверть. Например:
58*1/= 58+14 /=72/ или 72,5
Чтобы устно умножить число на 2/. к удвоенному числу прибавляют половину множимого.
Например: 18*2/.=36+9= 45;
39*2/.= 78 + 19/.= 97/ (или 97,5)
Другой способ состоит в умножении на 5 и делении пополам:
Чтобы устно умножить число на / (т. е. чтобы найти / этого числа), умножают число на 1 и делит пополам. Например:
30 * / = (30+15)/2= 22/ (или 22,5)
Видоизменение способа состоит в том, что от множимого отнимают его четверть или к половине множимого прибавляют половину этой половины.
Умножение на 15, на 125, на 75
Умножение на 15 заменяют умножением на 10 и на 1/, (потому что 10*1/=15) Например:
Умножение на 125 заменяют умножением на 100 и на 1 (потому что 100*1125). Например:
26*125 = 26*100*1= 2600 + 650 = 3250
47*125 = 47*100*1 = 4700+4700/4= 4700+1175 = 5875
Умножение на 75 заменяют умножением на 100 и на / (потому что 100*/=75). Например:
18*75= 18*100*/=1800* / =(1800 + 900)/2=1350
Примечание. Некоторые из приведенных примеров удобно выполняются также приемом § 6
26*125 = 130*25 = 3250
Умножение на 9 и на 11
Чтобы устно умножить число на 9, приписывают к нему ноль и отнимают множимое. Например:
Чтобы устно умножить число на 11, приписывают к нему ноль и прибавляют множимое. Например:
Деление на 5, на 1,на 15
Чтобы устно разделить число на 5, отделяют запятой в удвоенном числ-последнюю цифру. Например:
Чтобы устно разделить число на 1делят удвоенное число на 3. Например:
Чтобы устно разделить число на 15, делят удвоенное число на 30. Например
462:15=924:30=30/=30/=30,8 (или 924:30 =308:10=30,8)
Возвышение в квадрат
Чтобы возвысить в квадрат число, оканчивающееся цифрой 5 (например 85), умножают число десятков (8) на него же плюс единица (8*9=72) и приписывают 25 (в нашем примере получается 7225). Еще примеры:
145; 14*15 = 210; 21025
Прием этот вытекает из формулы (10х+5) = 100х+100х+25=100х(х+1)+25
Сейчас указанный прием приложим и к десятичным дробям, оканчивающимся цифрой 5:
Так как 0,5= ½, а 0,25 = ¼, то приемом § 25 можно пользоваться также и для возвышения в квадрат чисел, оканчивающихся дробью ½:
При устном возвышении в квадрат часто удобно бывает пользоваться формулой (a +-b) = a+b+- 2ab.
Например: 4140 +1+2*40= 1601+80= 1681
36 =(35+1)=1225+1+ 2*35=1296
Прием удобен для чисел, оканчивающихся на 1, 4, 6 и 9.
Вычисления по формуле
Пусть требуется выполнить устно умножение 52*48
Мысленно представляем эти множители в виде (50 + 2)*(50—2)
и применяем приведенную в заголовке формулу:
Подобным же образом поступают во всех вообще случаях, когда один множитель удобно представить в виде суммы двух чисел, другой — в виде разности тех же чисел:
Указанным сейчас приемом удобно пользоваться и для вычислений следующего рода:
Запомнив это, легко выполнять устно умножение числа 37 на 6, 9, 12 и т. п.
37*15=37*3*5 =555 и т. д,
Запомнив это, легко выполнять устно умножения следующего рода:
Не помешала бы ссылка на источник, ну или как минимум отсылка к господину Перельману
Прикалываешься что ли? Почему тебе показалось хорошей идеей скопипастить сюда памятку для первоклассника и даже не проверить, нормально ли она скопипастилась?
Немного криво скопировано, но, в целом, полезная информация
7 ½*6½=(7 + ½ )*(7 — ½)=48 что это?
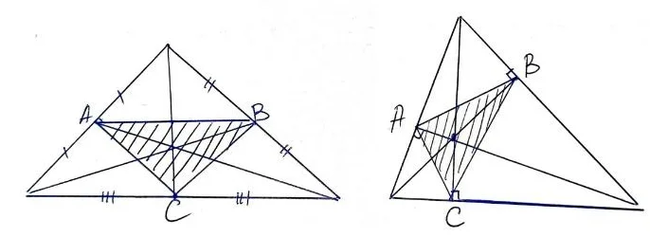
Единственный в своём роде треугольник Шарыгина, открытый лишь в 1982 году
Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать об удивительном геометрическом объекте, впервые рассмотренным советским математиком Игорем Федоровичем Шарыгиным.
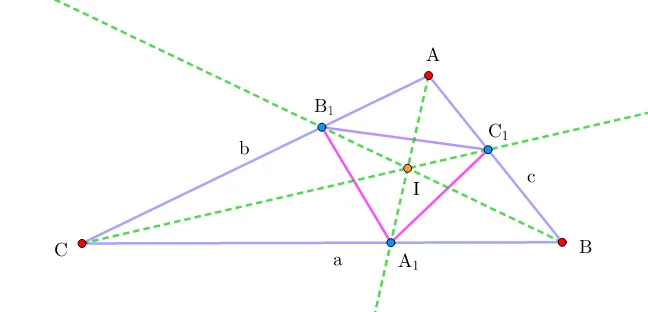
Для начала посмотрите на рисунок ниже. Что Вы на нём видите?
Но, погодите, есть же еще биссектрисы!
И тут становится интересно! Оказывается, и это показал Игорь Федорович, полученный из биссектрис треугольник может быть равнобедренным!
Заметка Шарыгина об этом объекте опубликована в книге «Задачи по геометрии. Планиметрия», 1982.
Впрочем, есть одно очень тонкое условие: угол такого треугольника должен попадать в диапазон от 102,663 до 104,478 градусов!
Основная суть доказательства сводится к рассмотрению подобных треугольников и применению теоремы косинусов, что позволяет получить вот такие выражения для сторон треугольника:
Самим доказательством (доступным каждому школьнику 9 класса!) можно проникнуться в телеграмм-канале «Математика не для всех».
Тогда еще, наверное, не знали, что квадратные уравнения будут уметь решать все.
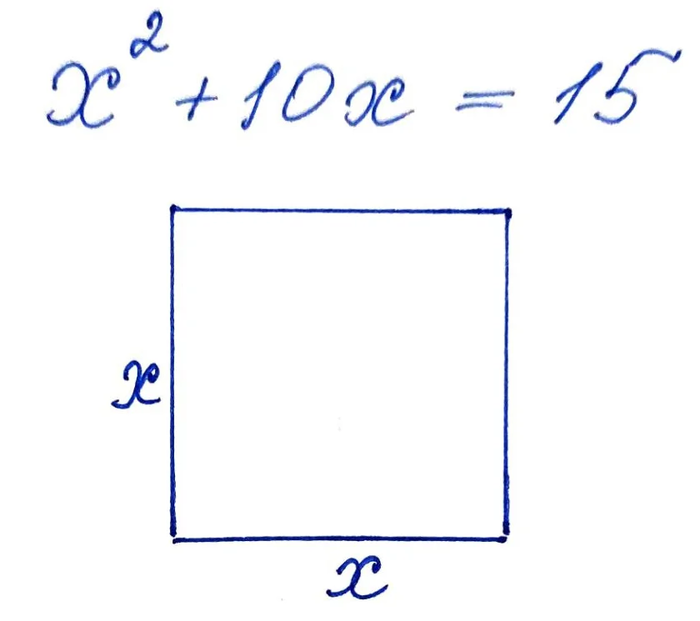
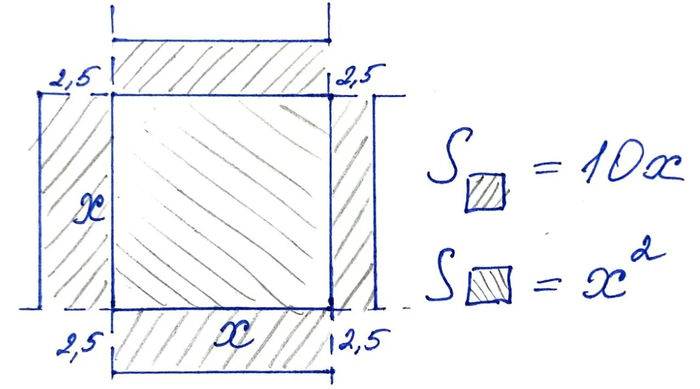
Сегодня я хочу рассказать Вам о методе дополнения до квадрата, который широко использовал арабский математик Аль-Хорезми, живший в 8 веке нашей эры. Пусть имеется такое квадратное уравнение:
Отдельно стоит сказать, что отрицательные числа во времена Аль=Хорезми еще были не в ходу. Отсюда и необычная запись условия.
Сразу же мы построили квадрат со стороной х. Теперь необходимо коэффициент при х разделить на 4 и отложить по сторонам квадрата соответствующие прямоугольники:
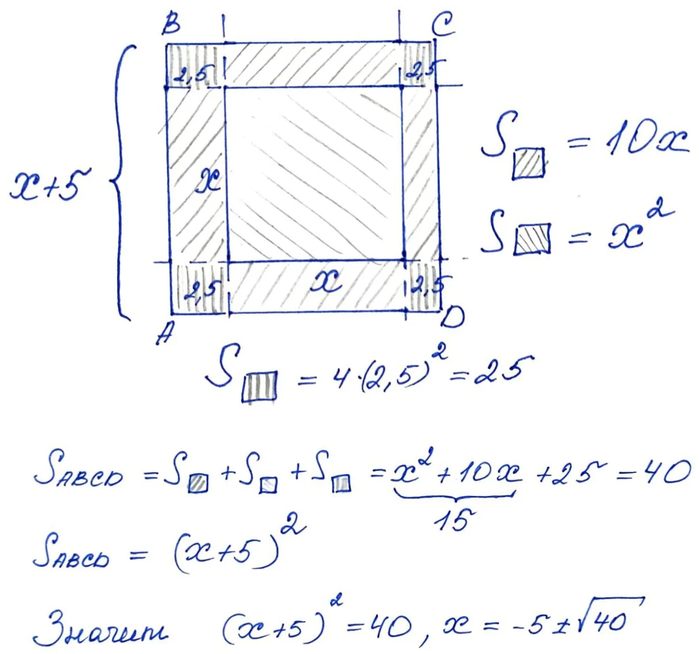
Теперь еще одно построение: дополним нашу фигуру до квадрата и посчитаем площади двумя способами:
Получается точь-в-точь как при решении через дискриминант. Можете проверить
Гениальная, но простая идея Рихарда Дедекинда, ставшая озарением для математики
Что мы знаем об этом поле? В нём существуют понятные каждому законы:
1. Если число a > b, b > c, то a > c. На числовой прямой, иначе говоря, это будет значить, что b лежит между a и c.
2. Если a и b различные числа, то между ними существует бесконечное количество других чисел.
Без потери общности можно рассматривать только положительные рациональные числа
3.
Важно добавить, что число a является наибольшим элементом в A1 либо в наименьшим в A2.
Само число а можно произвольно отнести к первому или второму классу, но самый важный вывод в том, что получено определение рационального числа а как сечения (A1, A2). С другой стороны понятно, что каждое заданное таким образом сечение определяет натуральное число.
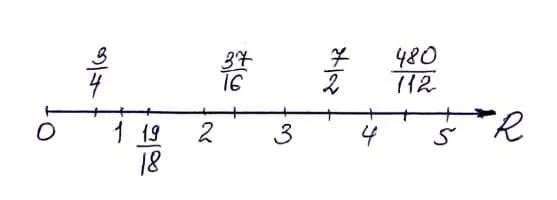
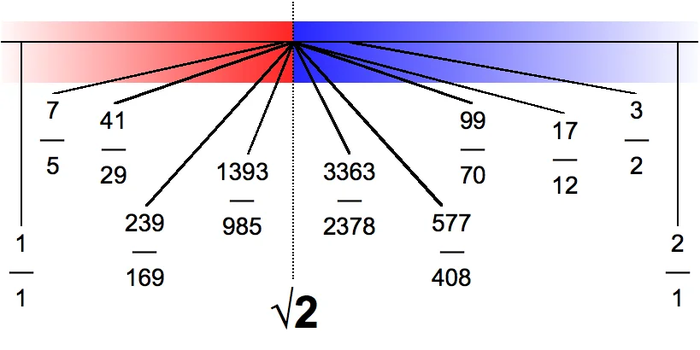
На самом деле, сечение, производимое √2 имеет значительные различия от сечений, которые производят рациональные числа. Например, в классе А1 (красный цвет) нет наибольшего числа: мы сколько угодно можем приближать к √2 слева, применяя всё более точные рациональные дроби, но никогда не найдем «того самого наибольшего». Такая же ситуация и справа: для класса А2 (синий цвет) никогда не найти «наименьшего» в мире рациональных чисел.
Таким образом, мы закрываем всю вещественную прямую плотным слоем рациональных и иррациональных чисел, а доопределив среди них отношение порядка и арифметические операции, порождаем совокупный класс вещественных чисел, каждое из которых может быть приближено рациональными числами с любой точностью.