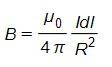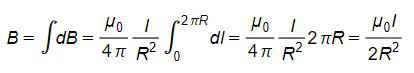закон био савара лапласа в скалярной форме

Закон Био Савара Лапласа

Закон Био Савара Лапласа — Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемая отдельными участками токов.

.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности:

.

Закон Био-Савара-Лапласа для некоторых токов:

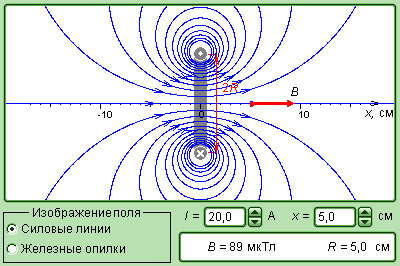
Магнитное поле прямого тока: .

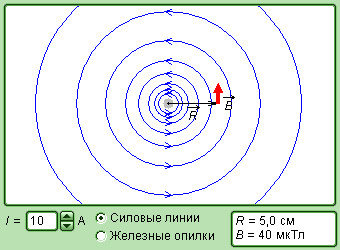
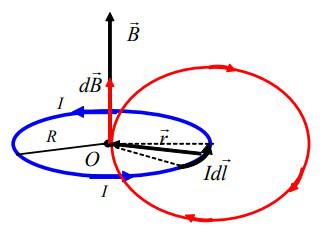
Магнитное поле кругового тока: .

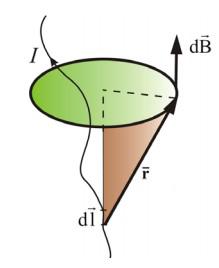
dB — магнитная индукция;

dl — вектор, по модулю равный длине dl элемента проводника и совпадающий по направлению с током;

— магнитная постоянная;

μ — относительная магнитная проницаемость (среды);

I — сила тока;

R — расстояние от провода до точки, где мы вычисляем магнитную индукцию;

α — угол между вектором dl и r.

В современной формулировке закон Био — Савара — Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля:

где квадратными скобками обозначено векторное произведение, r — положение точек контура γ, dr — вектор элемента контура (ток течет вдоль него); μ₀ — магнитная постоянная; r,r₀ — единичный вектор, направленный от элемента контура к точке наблюдения.

В принципе контур γ может иметь ветвления, представляя собой сколь угодно сложную сеть. В таком случае под выражением, приведенным выше, следует понимать сумму по всем ветвям, слагаемое же для каждой ветви является интегралом приведенного выше вида (контур интегрирования для каждой ветви может быть при этом незамкнутым).

В случае простого контура, ток I одинаков на всех участках контура и может быть вынесен за знак интеграла. (Это справедливо отдельно и для каждого неразветвленного участка разветвленной цепи).

Если же взять за точку отсчёта точку, в которой нужно найти вектор магнитной индукции, то формула немного упрощается:

где — вектор, описывающий кривую проводника с током I, r — модуль , — вектор магнитной индукции, создаваемый элементом проводника .

Пример решения задачи закона Био Савара Лапласа.

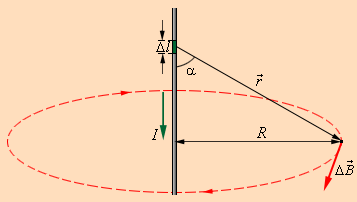
Применим закон Био — Савара — Лапласа для вычисления поля прямого тока, т. е. поля, создаваемого током, текущим по тонкому прямому проводу бесконечной длины (рис. 1). Все векторы dB в данной точке имеют одинаковое направление (в нашем случае «к нам»). Поэтому сложение векторов dB можно заменить сложением их модулей. Точка, для которой мы вычисляем магнитную индукцию, находится на расстоянии r₀ от провода. Из рис. 1 видно, что

r =R/sinα, dl =rdα/sinα = R dα/ sin 2 α.

Подставим эти значения в формулу магнитной индукции:

dB = (μ₀ μ/4π) I R sinα sin 2 α dα /R 2 sin 2 α = (μ₀ μ/4π) I sinα dα /R.

Угол α для всех элементов бесконечного прямого тока изменяется в пределах от 0 до π. Следовательно,

B = ∫ dB = (μ₀μ/4π) I/R∫ sinα dα = (μ₀ μ/4π) 2I/R.

Таким образом, магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током

B = (μ 0 μ/4π) 2I/R,

где R – кратчайшее расстояние от оси проводника.

Аналогичным образом можно найти магнитное поле в центре кругового проводника с током (рис. 2). Как следует из рисунка, все элементы кругового тока создают в центре магнитное поле одинакового направления — вдоль нормали витка. Поэтому сложение векторов dB можно заменить сложением их модулей. Так как все элементы проводника перпендикулярны радиусу-вектору (sin α=l) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то, согласно закону Био-Савара-Лапласа,

dB=(μ₀ μ/4π) I/R 2 dl. Тогда

Следовательно, магнитная индукция поля в центре кругового проводника с током равна B = μ 0 μI/2R.

Источник

Закон Био-Савара. Теорема о циркуляции

Принцип суперпозиции: если магнитное поле работает за счет нескольких проводников с током, тогда индукция результативного поля – это совокупность индукций полей, которые создаются каждым проводником по отдельности.

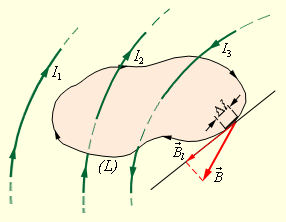
Индукция B → проводника с током представлена, как векторная сумма элементарных индукций ∆ B → вырабатываемых отдельными участками проводника. На практике нельзя отделить один участок проводника с током, поскольку постоянные токи всегда замкнутые. Возможно лишь измерить совокупную индукцию магнитного поля, которое создают все элементы тока. Как найти индукцию магнитного поля?

Закон Био–Савара

В формуле r – это расстояние от заданного участка Δ l до точки наблюдения, α – это угол между направлением на точку наблюдения и направлением тока на заданном участке, μ 0 – это магнитная постоянная.

С помощью этого закона можно определять магнитные поля токов с различными конфигурациями. Запросто рассчитать магнитное поле в центре кругового витка с током. Вычисления приводят к соотношению:

где R – это радиус кругового проводника.

Чтобы определить направление вектора B → тоже используется правило буравчика, только в этом случае рукоятка вращается по направлению кругового тока, а поступательное движение буравчика указывает, куда направлен вектор магнитной индукции.

Теорема о циркуляции вектора магнитной индукции

Вычисления магнитного поля зачастую упрощаются с учетом симметрии в конфигурации токов. В этом помогает теорема о циркуляции вектора магнитной индукции.

Некоторые токи, при которых магнитное поле создается, пропускают выбранный контур L тем временем, как остальные токи находятся в стороне от контура.

Согласно теореме о циркуляции, циркуляция вектора B → магнитного поля постоянных токов по любому из контуров L все время определяется, как произведение магнитной постоянной μ 0 на сумму всех токов:

∑ ( L ) B l ∆ l = μ 0 ∑ l i.

Теорема о циркуляции в этом примере математически выражается следующей формулой:

Общий вид теоремы о циркуляции можно вывести из принципа суперпозиции и закона Био-Савара.

отсюда можно вывести формулу для модуля магнитной индукции поля прямолинейного проводника с током, приведенную раньше.

Из данного примера видно, что теорема о циркуляции вектора магнитной индукции B → можно использовать для вычисления магнитных полей, которые создаются симметричным распределением токов, когда можно наугад определить общую структуру поля.

Существует много примеров определения магнитных полей при помощи теоремы о циркуляции.

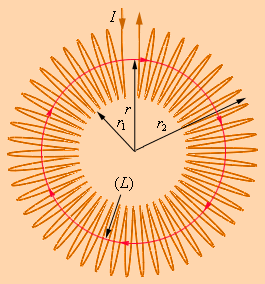
Предположим, что катушка намотана виток к витку на ненамагниченный тороидальный сердечник. В ней линии магнитной индукции сходятся внутри катушки и выступают концентрическими окружностями. Они имеет такое направление, что, смотря вдоль них, наблюдатель увидел бы ток в витках, циркулирующих по часовой стрелке.

Однако в пределе каждая часть тороидальной катушки при необходимости рассматривается в качестве длинной прямолинейной катушки, которая называется соленоид. Вдали торцов такой катушки модуль магнитной индукции определяется, как соотношение в случае с тороидальной катушкой.

Данное вычисление совпадает с формулой для магнитного поля тонкой тороидальной катушки.

Источник

Закон Био—Савара

Магнитное поле в точке пространства, создаваемое малым отрезком проводника, по которому течет электрический ток, пропорционально силе тока, обратно пропорционально квадрату расстояния от этой точки до проводника и направлено перпендикулярно по отношению и к току, и к направлению на проводник.

Одним из величайших прорывов в естествознании XIX века стала серия открытий, позволивших установить неразрывную связь между двумя, казалось бы, не связанными между собой природными феноменами — электричеством и магнетизмом, — которые на поверку оказались просто двумя сторонами одной медали. Одним из первых фрагментов пазла, который предстояло собрать ученым, стало осознание того, что движущиеся электрические заряды (то есть электрический ток) могут порождать магнитное поле. Это открытие сделал датский ученый Ханс Кристиан Эрстед (см. открытие Эрстеда), а представил его в количественной форме французский ученый Андре-Мари Ампер (см. Закон Ампера). Обобщением этой работы стал закон Био—Савара (его еще называют «закон Био—Савара—Лапласа». — Прим. переводчика), содержащий окончательную формулировку соотношения между электрическими токами и магнитными полями, которые они производят.

Жан Батист Био, яркий и смелый ученый, был профессором физики в Сорбонне и действительным членом французской Академии наук. Сразу после открытия Эрстеда вместе со своим коллегой Феликсом Саваром он принялся за изучение взаимосвязи между электрическим током и магнитными полями.

В отличие от Ампера, изучавшего магнитные поля опосредованно, путем измерения силы взаимодействия между парами проводников с током, Био и Савар предприняли прямые измерения магнитных полей, используя для этого множество легких магнитных стрелок компасов. Смысл их закона проще всего понять, если представить себе, что проводник с током разбит на крошечные отрезки — т. н. элементы тока (такой подход предложил ученым их старший коллега Пьер Симон Лаплас (Pierre-Simon Laplace, 1749–1827), стоявший у истоков дифференциального и интегрального исчисления, который затем и обобщил полученные результаты. — Прим. переводчика). На каждом из этих крошечных отрезков кривизной проводника можно пренебречь — их можно рассматривать как отрезки прямой. Так вот, согласно закону Био—Савара, магнитное поле В на расстоянии r от такого элемента тока пропорционально

где I — сила тока, а L — длина элемента тока.

Я уже упоминал, что закон Био—Савара является наиболее полным формальным обобщением взаимосвязи между электрическим током и магнитным полем. Это значит, что можно взять проводник с током сколь угодно сложной и асимметричной конфигурации и разбить его на элементы тока. Каждый элемент вносит свой вклад в магнитное поле в рассчитываемой точке. Сделав эти расчеты, мы можем затем просуммировать вклад от каждого элемента проводника и найти общее магнитное поле (этот процесс суммирования относится к области высшей математики и выглядит он достаточно сложно). Таким образом, закон Ампера является частным случаем закона Био—Савара для случая линейного проводника.

Я еще не сказал, что закон Био—Савара предсказывает также направление получающегося магнитного поля. Это направление можно определить с помощью так называемого правила правой руки, ставшего настоящим бичом целых поколений студентов физических и технических вузов. Правило гласит: если вытянутый указательный палец правой руки показывает направление электрического тока в элементе тока, а средний палец направлен на точку, в которой вы вычисляете магнитное поле, то выставленный под прямым углом к двум другим пальцам большой палец укажет направление магнитного поля.

Как я уже говорил, полное математическое выражение закона Био—Савара требует довольно сложных вычислений, поскольку оно представляет собой интегральное уравнение. Оно является, по сути, общим решением четвертого уравнения Максвелла.

Источник

Задачи на применение закона Био-Савара-Лапласа с решением

Закон Био-Савара-Лапласа в магнитостатике – примерно то же самое, что и закон Кулона в электростатике. С помощью этого закона определяется индукция магнитного поля, созданного постоянным электрическим током. В сегодняшней статье разберем несколько примеров решения задач по магнитостатике на применение закона Био-Савара-Лапласа.

Присоединяйтесь к нам в телеграме, чтобы вовремя получать полезную рассылку и актуальные новости. А еще, не пропустите приятные скидки и акции на нашем втором канале.

Закон Био-Савара-Лапласа: решение задач

В нашем блоге есть материалы, которые помогут справиться с задачами по разным темам:

Задача на закон Био-Савара-Лапласа №1

Условие

Прямой провод согнут в виде квадрата со стороной а=8 см. Какой силы ток надо пропустить по проводнику, чтобы напряженность магнитного поля в точке пересечения диагоналей была 20 А/м?

Решение

Согласно принципу суперпозиции напряженность магнитного поля в точке пересечения диагоналей квадрата будет равна сумме напряженностей, которые создают стороны. Поскольку стороны одинаковые, то:

H = 4 H 1 = 4 B 1 μ 0

Будем использовать формулу для магнитной индукции поля, создаваемого отрезком прямого провода с током (выводится из закона Био-Савара-Лапласа):

Тогда для напряженности в точке пересечения диагоналей получим:

Отсюда можем выразить ток:

Ответ: 1,78 А.

Задача на закон Био-Савара-Лапласа №2

Условие

Используя закон Био-Савара-Лапласа, определите магнитную индукцию в вакууме B поля в центре кругового проводника радиусом 10 см, если сила тока в проводнике равна 5 A.

Решение

Модуль магнитной индукции в центре кругового тока вычисляется по формуле:

Ответ: 0,31 мкТл.

Задача на закон Био-Савара-Лапласа №3

Условие

Используя закон Био-Савара-Лапласа выведите формулу для индукуии из предыдущей задачи.

Решение

Пусть ток идет по тонкому проводу в форме окружности, имеющей радиус R.

Разобъем провод на бесконечно малые элементы dl. Каждый такой элемент создает в центре окружности индукцию dB, направленную вдоль положительной нормали к контуру. По закону Био-Савара-Лапласа:

B = μ 0 4 π I d l sin α r 2

Угол альфа между векторами r и Idl равен 90 градусам, а r=R. Тогда, можно записать:

Интегрируя это выражение по контуру, получим:

Задача на закон Био-Савара-Лапласа №4

Условие

По квадратной рамке со стороной a=0,2 м течет ток 4 А. Определить напряженность и индукцию магнитного поля в центре рамки.

Решение

Будем рассматривать каждую из четырех сторон рамки, как отдельный проводник, создающий в ее центре магнитную индукцию. Направление векторно-магнитной индукции определяется по правилу правого винта: все векторы направлены в одну сторону, перпендикулярно рамке.

Найдем индукцию, создаваемую одной стороной рамки:

По принципу суперпозиции, запишем формулу для общей индукции в центре рамки и вычислим:

Ответ: 22,6 мкТл.

Задача на закон Био-Савара-Лапласа №5

Условие

Проводник согнут в виде правильного треугольника со стороной а=20 см. Какой ток протекает по периметру треугольника, если в его центре напряженность поля равна Н = 71,64 А/м?

Решение

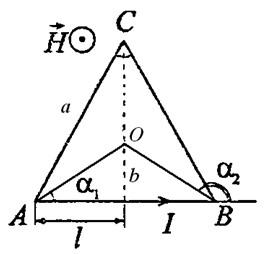
Условно разбиваем проводник на три проводника, каждый из которых создает магнитное поле. По закону Био – Савара – Лапласа элемент контура dl, по которому течет ток I, создает в некоторой точке А пространства магнитное поле напряженностью:

d H 0 = I sin α 4 π r 2 d l

r – расстояние от точки А до элемента тока dl, α – угол между радиус-вектором и элементом тока dl. Напряженность магнитного поля в точке О будет равна:

Теперь выражение для напряженности можно переписать в следующем виде:

Из рисунка видно, что угол α1 равен 30 градусам, а угол α2 = 150. Очевидно, что результирующая напряженность:

Ответ: 10 А.

Вопросы на закон Био-Савара-Лапласа

Вопрос 1. Сформулируйте закон Био-Савара-Лапласа

Ответ. Закон Био-Савара-Лапласа гласит:

Магнитное поле любого тока может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.

Элементарный участок dl с током I создает магнитную индукцию:

B = μ 0 4 π I d l sin α r 2

Здесь альфа — угол между радиусом-вектором и направлением тока в проводнике.

Вопрос 2. Что такое магнитная индукция?

Ответ. Магнитная индукция — векторная физическая величина, силовая характеристика магнитного поля. Определяет, с какой силой поле действует на заряд, движущийся в нем.

Вопрос 3. Сформулируйте теорему о циркуляции магнитной индукции.

Ответ. Циркуляция вектора магнитной индукции по произвольному замкнутому контуру, охватывающему токи, прямо пропорциональна алгебраической сумме токов, пронизывающих этот контур:

Вопрос 4. Как определяется направление вектора магнитной индукции?

Ответ. Направление вектора магнитной индукции определяется по правилу буравчика (правого винта):

Направление вращения головки винта дает направление вектора магнитной индукции, поступательное движение винта соответствует направлению тока в элементе.

Вопрос 5. Что такое напряженность магнитного поля?

Ответ. Напряженность — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M. Связана с индукцией формулой:

Нужна помощь в решении задач и выполнении других заданий? Профессиональный сервис для учащихся всегда к вашим услугам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Закон Био-Савара-Лапласа и его применение к расчету магнитного поля в центре кругового проводника с током

Закон Био-Савара-Лапласа в векторной и скалярной формах. Принцип суперпозиции магнитных полей.

Закон Био — Савара — Лапласа для проводника с током I, элемент dl которого создает в некоторой точке А индукцию поля dB, записывается в виде:

— это векторная форма закона

Навравление dB всегда перпендикулярно плоскости в которой лежат dl и r, и совпадает с касательной к линии магнитной индукции. Оно может быть найдено методом правого винта.

Скалярная выражение Закона Био-Савара-Лапласа.

Принцип суперпозиции МП:

Магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равно ВЕКТОРНОЙ сумме магнитных индукций всех полей, создаваемых каждым током.

Как следует из рисунка, все элементы кругового проводника с током создают в центре магнитные поля одинакового направления — вдоль нормали от вит- ка. Поэтому сложение векторов dB можно заменить сложением их мо- дулей. Так как все элементы проводни- ка перпендикулярны радиусу-вектору (sin a = 1) и расстояние всех элементов проводника до центра кругового тока одинаково и равно R, то:

Отсюда следует что:

Следовательно магнитная индукция поля в центре кругового проводника равна:

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник