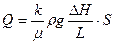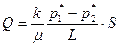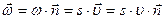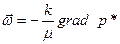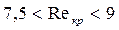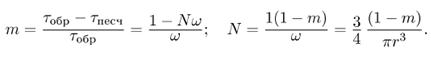закон дарси в дифференциальной форме

. (5)

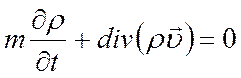
Для стационарной фильтрации сжимаемого флюида:

(6)

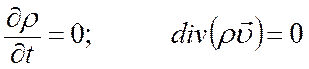
Если сжимаемостью флюида можно пренебречь:

, то уравнение (6) приводится к виду:

. (7)

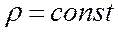
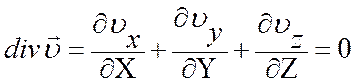
2. Дифференциальное уравнение движения.

Дифференциальное уравнение движения флюида в пористой среде является обобщением закона фильтрации Дарси:

. (8)

—- пространственная производная давления ( в направлении оси Х).

.

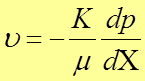
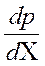
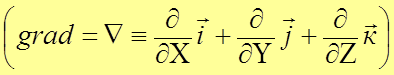
Т.о. в векторной форме закон фильтрации Дарси записывается в виде:

. (9)

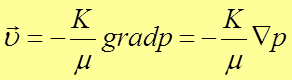
В подземной гидромеханике используется специальная функция:

. (10)

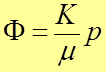
Функция 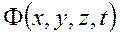называется потенциалом скорости фильтрации.

Если кроме давления действуют другие силы (например, сила тяжести), то потенциал скорости фильтрации):

(10а)

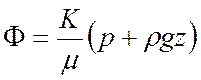
Таким образом закон фильтрации Дарси можно записать в обобщенной форме:

. (11)

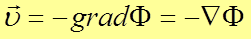
Из уравнения неразрывности (4) и закона фильтрации (11) можно получить уравнение движения флюида в пористой среде:

; (12)

. (13)

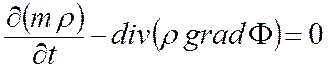
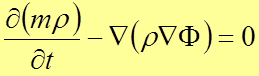
В подробной (координатной) записи уравнение (13) имеет вид:

. (14)

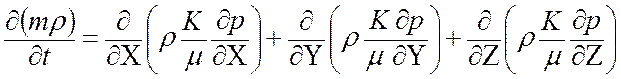
Для решения дифференциального уравнения движения (13) необходимо иметь начальные и граничные условия.

Начальные условия заключаются в задании искомой функции во всей области в некоторый начальный момент времени (например, значения давления в пласте до начала разработки).

Граничные условия задаются на границах пласта: на внешней границе и на внутренней границе (на забое скважины).

Закон Дарси (11) и соответствующее ему дифференциальное уравнение движения (13) пригодны для изотропной пористой среды, т.е. среды, проницаемость которой во всех направлениях одинакова.

На практике часто встречаются пористые среды, проницаемость которых различна в разных направлениях (например, осадочные пласты с отчетливой слоистой структурой). Пористые среды, в которых коэффициент проницаемости зависит от направления потока, называются анизотропными.

Для анизотропных пористых сред закон фильтрации (и соответственно, уравнение движения) имеют более сложный вид, чем выражения (9) или (14), т.к. векторы скорости фильтрации и градиента давления не совпадают по направлению.

Для анизотропных пористых сред закон Дарси и уравнение движения записываются в тензорной форме:

(15)

— тензор проницаемости пористой среды:

;

. (16)

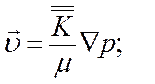
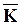
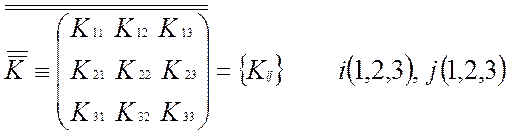
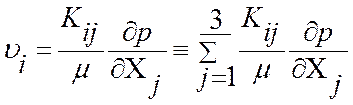
Анизотропия естественных осадочных пород – коллекторов обусловлена их отчетливой слоистой структурой. Фильтрационные свойства таких пород одинаковы в направлениях, лежащих в плоскости слоя, но изменяются в перпендикулярном направлении.

В данном случае систему координат выбирают таким образом, чтобы плоскость XY лежала в плоскости слоя, а ось Z была перпендикулярна слою. Выбранные таким образом оси координат называются главными осями пласта. Закон Дарси в этом случае можно записать в виде:

. (17)

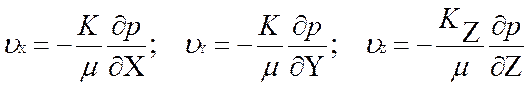
Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Закон Дарси

,

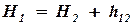(1.14)

где 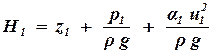— гидродинамический напор;

h₁₂ = h(u)— потери напора между сечениями, которые зависят от скорости фильтрации и не могут рассчитываться по формулам трубной гидравлики.

Скорости фильтрации жидкости в пористой среде малы, поэтому скоростным напором можно пренебречь. Разрешая уравнение (1.14) относительно скорости фильтрации, получим:

.

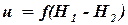(1.15)

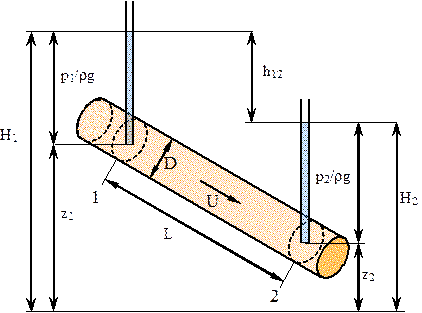Рис. 1.2. Схема опытной установки

Тогда формула (1.15) запишется:

.

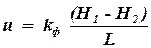(1.16)

Эта формула впервые была экспериментально полечена французским инженером Дарси и подтверждается для многих жидкостей и газов в широких пределах изменения скоростей. Но для некоторых жидкостей и значений скоростей фильтрации эта формула не подтверждается. Коэффициентом фильтрации k_ф используется в тех случаях, когда фильтруется вода. При фильтрации нефти, газа, воды и их смесей желательно учитывать свойства породы и жидкости отдельно. Свойства жидкости характеризуются коэффициентом динамической вязкости μ и плотностью r. Тогда коэффициент фильтрации можно записать в виде:

,

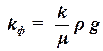(1.17)

С введение коэффициента проницаемости закон Дарси примет вид:

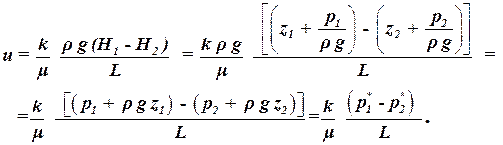(1.18)

Расстояния z от плоскости сравнения до данной точки считается положительным, если точка лежит выше плоскости сравнения, и отрицательной, если ниже. За плоскость сравнения можно принять любую горизонтальную плоскость. Обычно принимают границу газонефтяного (ГНК) или водонефтяного (ВНК) контакта. При движении жидкости в горизонтальных пластах (z = const), поэтому второе слагаемое в приведенном давлении постоянно и при подстановке в формулу обращается в нуль. Поэтому в горизонтальных пластах при движении однородной жидкости приведенное давление можно положить равным давлению в данной точке и знак (*) в законе Дарси можно опустить.

Рассмотрим трубку тока, вдоль которой происходит фильтрация жидкости. Обозначим расстояние вдоль вектора скорости у этой трубки через s. Выберем две точки на расстоянии Ds друг от друга и запишем для этих точек закон Дарси:

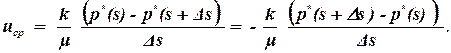(1.19)

Получим значение средней скорости на этом участке u_ср. Если устремить расстояние между точками к нулю, то получим закон Дарси в дифференциальной форме:

.

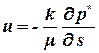(1.20)

В векторной форме закон Дарси запишется:

.

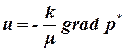(1.21)

или в проекциях на оси координат

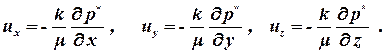(1.22)

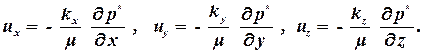(1.23)

Для плоскорадиального и радиально-сферического потока Закон Дарси можно записать в виде:

.

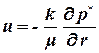(1.24)

В пластах часто встречаются непроницаемые границы (сбросы). Жидкость двигаться перпендикулярно непроницаемой границе не может, поэтому нормальная к границе скорость равна нуль u_n = 0. Тогда из закона Дарси следует:

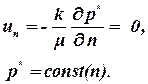(1.25)

Это означает, что перпендикулярно непроницаемой границе давление не меняется и линии равного давления (изобары) перпендикулярны этой границе.

Дата добавления: 2015-09-25 ; просмотров: 1722 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Закон Дарси в дифференциальной форме

Границы применимости закона Дарси:

Закон справедлив при следующих условиях :

Пористая среда мелкозерниста и поровые каналы достаточно узки

Скорость фильтрации и градиент давления малы

Изменение скорости фильтрации и градиента давления малы.

Закон Дарси нарушается:

При повышении скорости движения жидкости из-за увеличения потерь давления на эффекты связанные с инерционными силами – верхняя граница.

Дарси может нарушаться и при малых скоростях фильтрации в процессе начала движения жидкости из-за появления неньютоновских реологических свойств жидкости – нижняя граница.

Коэффициент фильтрации – характеризует среду и жидкость одновременно. Зависит от размера частиц их формы и степени шероховатости, пористости среды и вязкости жидкости, в гидротехнических расчетах при наличии различных жидкостей.

–коэффициент динамической вязкости.

Проницаемость песчаных коллекторов 100-1000мД

Имеется множество попыток теоретически установить зависимость проницаемости от этих характеристик исходя из закона Пуазеля для ламинарного движения в трубах, исходя из Стогса для обтекания частиц при той или иной модели пористой среды.

Поскольку реальные породы не укладываются в рамки геометрических моделей, то теоретические расчеты проницаемости ненадежны, поэтому обычно проницаемость определяют опытным путем.

Границы применимости закона Дарси:

Закон справедлив при следующих условиях :

Пористая среда мелкозерниста и поровые каналы достаточно узки

Скорость фильтрации и градиент давления малы

Изменение скорости фильтрации и градиента давления малы.

Закон Дарси нарушается:

При повышении скорости движения жидкости из-за увеличения потерь давления на эффекты связанные с инерционными силами – верхняя граница.

Дарси может нарушаться и при малых скоростях фильтрации в процессе начала движения жидкости из-за появления неньютоновских реологических свойств жидкости – нижняя граница.

Верхняя граница- ее критерием служит сопоставление числа R_e с его критическим значением.

А – зависит от вида фильтрации.

Закон Павловского

; ; Re_крП=7,5…9

; Re_кр=1…1,2

; Reкр=0,022…0,29

Число Рейнольдса определяется следующим соотношением:

ρ — плотность среды, кг/м 3 ;

v — характерная скорость, м/с;

L — характерный размер, м;

η — динамическая вязкость среды, Н·с/м 2 ;

ν — кинематическая вязкость среды, м 2 /с( ) ;

Q — объёмная скорость потока;

A — площадь сечения трубы.

Нижняя граница закона Дарси – при очень малых скоростях с ростом градиента давления увеличение с ростом фильтрации происходит более быстро, это объясняется тем, что становится существенным силовое взаимодействие между твердым скелетом и жидкостью за счет образования аномальных неньютоновских систем: устойчивые колойдные растворы в виде студнеобразных пленок, перекрывающих поры и разрывающихся при градиенте , называемым начальным, и зависящим от доли глинистого материла и величины остаточной водонасыщенности.

,

;

Источник

Границы применимости закона Дарси

Коэффициент фильтрации, имеет размерность скорости и характеризует скорость потока через единицу площади сечения, перпендикулярного потоку, под действием единичного градиента напора.

При исследовании фильтрации газа, нефти и их смесей необходимо разделить влияние свойств пористой среды и флюида. Поэтому для разделения свойств флюида и пористой среды равенство представляют в виде:

или

где μ – динамический коэффициент вязкости,

— приведенное давление,

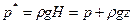
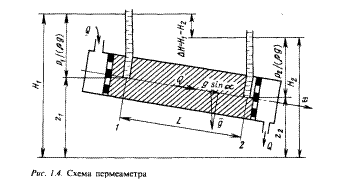
Коэффициент фильтрации и проницаемости определяются экспериментально (рис. 1.4) и могут быть связаны между собой соотношением:

(10)

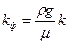
Равенства справедливы, если фильтрационные свойства недеформируемой пористой среды изотропные и однородные, т.е. проницаемость не зависит от направления и постоянна для всех точек.

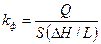
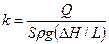
Из формул имеем или ,

где перепад напора, приходящийся на единицу длины (модуль градиента давления) можно представить в следующем виде

.

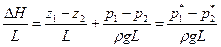
Пермеаметр содержит образец исследуемого грунта, общий расход Q фильтрационного потока поддерживается постоянным, напоры Н₁ и Н₂ измеряют двумя пьезометрами, соединенными с пористой средой в сечениях 1 и 2.

Обычно соотношения или называют следствием закона Дарси.

Этот закон является хронологически первым законом теории фильтрации. Закон Дарси можно записать в виде

,

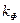
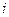
где — коэффициент фильтрации, имеющий размерность скорости;

— гидравлический уклон (или градиент давления).

Закон Дарси связывает меду собой вектор скорости и градиент фильтрационного давления.

Если обе части равенства разделить на площадь сечения, то получим

, (11)

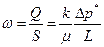
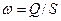
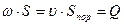
выражение имеет размерности скорости, и определяет модуль вектора скорости фильтрации. При определении расхода считается, что вектор скорости фильтрации направлен перпендикулярно плоскости (галерее), через которую фильтруется флюид. Скорость фильтрации – это фиктивная скорость, т.к. она определяется в любой точке сечения пористой среды – и в порах, и в твердом скелете, а на самом деле течение проходит только по поровым каналам с некоторой истинной скоростью υ. Между фиктивной и истинной скоростью существует взаимосвязь:

или

Таким образом, скорость фильтрации равна истинной средней скорости, умноженной на просветность. Заменять просветность на пористость теоретически неправомерно.

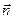
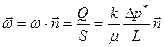
Равенство можно представить в векторной форме. В случае изотропных фильтрационных свойств векторы скорости фильтрации и градиент фильтрационного давления лежат на одной прямой. Поэтому, если умножить равенство на орт , задающий направление фильтрации, получим

(13)

В равенстве множитель 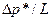представляет собой модуль приведенного давления при линейном законе распределения давления. Тогда можно записать

Векторное уравнение представляет собой закон Дарси для изотропной пористой среды.

Знак «минус» в правой части равенства появляется из-за того, что скорость фильтрации направлена в сторону уменьшения приведенного давления. Поэтому векторы скорости фильтрации и градиента фильтрационного давления направлены в разные стороны (градиент давления направлен в сторону роста давления, а скорость фильтрации в обратную сторону – от большего давления к меньшему).

Равенство задает закон Дарси в универсальной безындексной форме записи, справедливой для любой системы координат. В декартовой системе координат равенство записывается в виде

, (15)

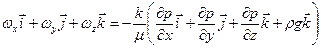
где 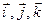— орты декартовой системы координат (ось z направлена вертикально вверх).

Это равенство можно спроектировать на оси координат

, , . (16)

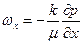
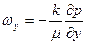
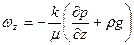
Таким образом, закон Дарси заключается в том, что скорость фильтрации пропорциональна градиенту давления.

Закон Дарси имеет силу, если соблюдаются следующие условия:

1) мелкозернистая пористая среда или достаточно узкие поровые каналы;

2) малая скорость фильтрации при небольшом градиенте давления;

3) незначительные изменения скорости фильтрации или градиента давления.

Закон Дарси справедлив для медленных фильтрационных движений, для которых силы инерции несущественны. Поэтому для таких движений несущественна плотность жидкости, определяющая свойство ее инерции.

Закон Дарси, в дифференциальной форме он имеет вид:

, (17)

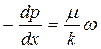
Знак (-) в левой части формулы означает, что течение газа происходит в направлении, противоположном росту давления.

Фундаментальный закон фильтрации устанавливает связь между скоростью фильтрации и градиентом давления.

Нелинейные законы фильтрации ввести нумерацию.

Проведенные в дальнейшем эксперименты показали, что закон Дарси не является универсальным и нарушаются области малых и больших скоростей. Нарушение в области малых скоростей связано с молекулярным эффектом. Причины, вызывающие отклонение от закона Дарси при больших скоростях, являются до настоящего времени предметом дискуссии среди исследователей.

В 1901 году австрийский ученый Форхгейме, ссылаясь на исследования Мазони, рекомендовал выражать зависимость градиента давления от скорости двучленным законом фильтрации:

, (18)

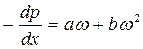
Двучленный закон фильтрации в дифференциальной форме при прямолинейной фильтрации газа в принятых сейчас обозначениях, без учета силы тяжести имеет два вида записи:

, (19)

(20)

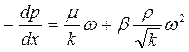
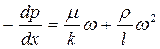
Первое слагаемое в правой части уравнения учитывает потери давления вследствие вязкости жидкости, второе слагаемое – инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов.

При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации (больших значений числа Рейнольдса). Она связана с проявлением неньютоновских свойств фильтрующихся флюидов, а также других физико-химических эффектов и больших поверхностных сил (сил взаимодействия между флюидом и твердым скелетом).

При очень малых скоростях фильтрации неньютоновскими свойствами в пористой среде могут обладать даже ньютоновские жидкости. Но с ростом скорости этот эффект в ньютоновских жидкостях исчезает. В нефтегазовом деле к жидкостям, проявляющим неньютоновские свойства, относят аномальные нефти и буровые растворы. Поэтому для качественного изучения вопроса и количественной оценки этих эффектов необходимо отказаться от модели вязкой однородной жидкости и заменить ее какой-либо другой реологической моделью пластового флюида.

Ограничимся формулировкой наиболее простого нелинейного закона фильтрации неньтоновских жидкостей, в основе которого лежит модель фильтрации с предельным градиентом. Для случая одномерного линейного потока его можно представить в виде

, при , (21)

, при ,

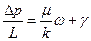
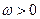
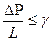
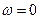
где 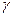— предельный (начальный) градиент давления, по достижении которого начинается движение жидкости: при меньших значениях градиента давления фильтрационное течение отсутствует, этот параметр измеряется в лабораторных условиях. зависит от начального сдвига жидкости и эффективного диаметра капилляра.

Закон фильтрации записывают также в виде одночленной степенной формулы:

(22)

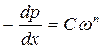
Л.С. Лейбензон предложил выразить коэффициент проницаемости в виде:

(23)

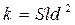
где d – линейный размер (диаметр) зерен пористой среды, Sl – безразмерный критерий (число Слихтера), зависящий от коэффициента пористости и структуры порового пространства, т. е.

(24)

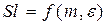
В связи с тем, что линейный закон фильтрации Дарси всё-таки является приближенным законом, при увеличении скорости фильтрации жидкости и соответствующем увеличении скоростного напора сделанное ранее при выводе линейного закона фильтрации допущение может оказаться несправедливым, тогда и возникнут погрешности в расчетах. В этих случаях говорят, что линейный закон фильтрации (закон Дарси) имеет верхнюю и нижнюю границы применения.

Верхняя граница определяется группой причин связанных с проявлением инерционных сил при высоких скоростях фильтрации. Верхнюю границу применимости закона Дарси связывают обычно с некоторым критическим (предельным) значением Re_кр числа Рейнольдса:

, , (25)

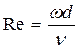
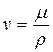
где d – линейный размер пористой среды,

v – кинематический коэффициент вязкости флюида.

В таких случаях принято говорить о так называемых нелинейных законах фильтрации, например выражения.

Первая количественная оценка верхней границы применимости закона Дарси была выполнена Павловским, который, опираясь на результаты Слихтера, полученные для модели идеального грунта, и полагая характерный размер dравный эффективному диаметру d_эф вывел следующую формулу для числа Рейнольдса:

,

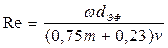
Использовав эту формулу и данные экспериментов, Н.Н. Павловский установи, что критическое значение числа Рейнольдса находится в пределах

Достаточно узкий диапазон изменения значений Re_кробъясняется тем, что в опытах использовались не слишком разнообразные образцы пористых сред.

Для удобства обработки результатов многочисленных экспериментов различных авторов В.Н. Щелкачев предложил использовать безразмерный параметр, названный им параметром Дарси

.

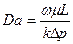
Отсюда видно, что параметр Дарси представляет собой отношение силы вязкого трения к силе давления. Из выражения следует, что если параметр Дарси равен единицы

,

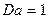
то закон Дарси справедлив.

6. Определить пористость, удельную поверхность и просветность для рыхлой кубической упаковки шаров.

7. Определить пористость для кубической и гексагональной упаковок шаров.

8. Определить коэффициент проницаемости пористой среды (в м 2 и Дарси), если известно, что коэффициент фильтрации k_ф = 0,3·10 – 4 см/с, кинематический коэффициент вязкости жидкости ν = 10 – 6 м 2 /с.

Решение. Из формулы (1.9) .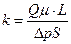

Переведем все размерности в СИ:

10. Определить коэффициент фильтрации для керна, помещенного под углом α к горизонту, если массовый расход жидкости равен Q_м, плотность жидкости ρ и вязкость μ, разница напоров в начале и конце керна составляет ΔН, площадь сечения S, длина керна L.

11. Образец пористой среды длиной 10 см и диаметром 5 см после насыщения под вакуумом керосином с плотностью 810 кг/м 3 стал тяжелее на 20 г. Определить коэффициент пористости образца.

Тогда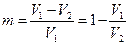, V₁ – весь объем шаров,V₂ – объем породы.

Суммарная поверхность Sпесчинок, заключенных в 1 м 3 песчаного пласта, равна:

Источник