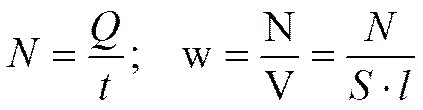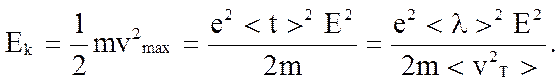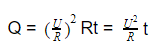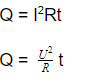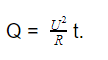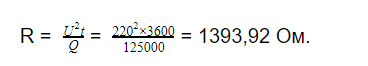закон джоуля ленца в дифференциальной форме вывод

Закон Джоуля-Ленца в дифференцированной и интегральной форме

Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предполо­жим, что на концах участка проводника имеется разность потен­циалов U = φ₁ – φ₂.

Тогда работа по переносу заряда Q на этом участке равна:

Если ток постоянный, то:

и

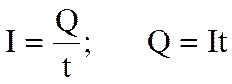
Эта работа равна количеству теплоты Q, и формула Q = I · U · t вы­ражает закон Джоуля-Ленца в интегральной форме.

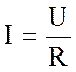
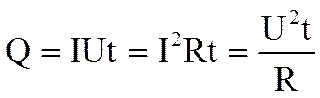
Используя выражение закона Ома получим:

.

Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

,

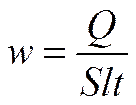
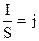
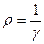
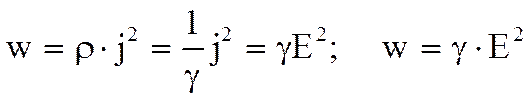
Здесь — плотность тока, , и учитывая, что j = γE, получим

.

Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удель­ная проводимость проводника.

Вывод законов Ома и Джоуля-Ленца из классических электрон­ных представлений

Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3,5 ·10 6 Кл. Взвешивание показало неизменный вес цилинд­ров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.

Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.

Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти час­тицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет пе­ренесен некоторый заряд.

Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с прово­дом вокруг ее оси. К концам катушки подключили телефон, в кото­ром был слышен звук, обусловленный импульсами тока. Был полу­чен качественный результат – зарегистрирован импульс тока.

Толмен и Стюарт в 1916 г. получили количественный ре­зультат. Катушка с проводом длиной 500 м приводилась во враще­ние со скоростью v=300 м/с. Катушка резко тормозилась и с по­мощью баллистического гальванометра измеряли заряд, протекав­ший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m полу­чалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны.

Исходя из представлений о свободных электронах была создана классическая теория электро­проводности металлов в предположении, что:

— электроны в металле ведут себя подобно молекулам иде­ального газа;

— движение электронов подчиняется законам классической механики;

— взаимодействие электронов сводится к соударениям с ио­нами кристаллической решетки;

— силами взаимодействия между электронами можно пре­небречь и они между собой не сталкиваются;

— электроны в отсутствие электрического поля движутся хаотически.

Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.

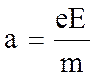
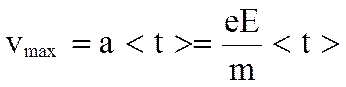
На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение: и к концу свободного про­бега он достигнет скорости:

, а средняя скорость

Подставляя в формулу для получим:

.

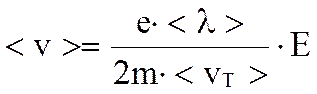
Подставляя в формулу для j, получим:

,

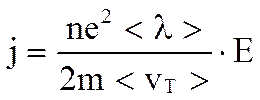
т.е. плотность тока прямо пропорциональна Е, а это и есть выраже­ние закона Ома в дифференциальной форме. Если положить, что:

то

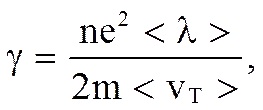
j= γ E.

Удельная проводимость γ

T, поэтому проводимость снижа­ется с ростом температуры, а удельное сопротивление 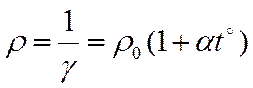по­вышается с ростом температуры. К концу свободного пробега электрон приоб­ретает кинетическую энергию

Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон ис­пытывает / cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в еди­нице объема за единицу времени выделится количество тепла

.

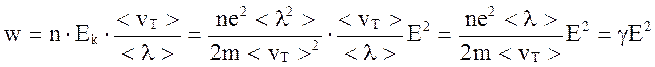
Таким образом, — выражение закона Джоуля-Ленца в дифференциальной форме.

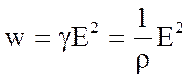
Закон Видемана-Франца. Затруднения классической электрон­ной теории

Известно, что металлы наряду с высокой электропроводностью обладают также большой теплопроводностью. Видеман и Франц в 1853 г. эмпирически установили закон: отношение коэффициента теплопроводности χ к коэффициенту электропроводности γ для всех металлов приблизительно одинаково и прямо пропорционально аб­солютной температуре

.

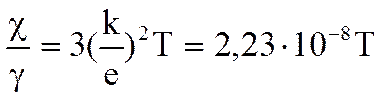
Таким образом, классическая электронная теория хорошо объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца, позволяет выразить удельную тепло­проводность через атомарные постоянные металла, объясняет зави­симость электропроводности от температуры и позволяет понять связь между теплопроводностью и электропроводностью металлов.

Однако в некоторых вопросах, классическая электронная теория приходит к выводам, находящимся в противоречии с опы­том.

1. Исходя из классической электронной теории удельная электропроводность равна:

,

, но ,

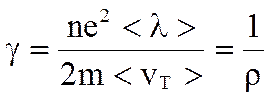
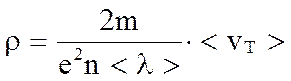
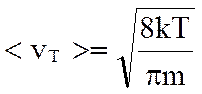
т.е. ∼ .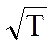

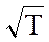
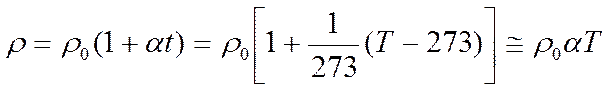
Следовательно, по теории ρ ∼ , тогда как на практике

,

т.е. удельное сопротивление пропорционально первой степени тем­пературы Т.

Кроме того, согласно классической электронной теории удельное сопротивление ρ должно монотонно уменьшаться при охлаждении, оставаясь при всех температурах по значению конечным. Это и наблюдается при сравнительно высоких температурах. Однако при достаточно низ­ких температурах удельное сопротивление перестает зависеть от температуры и достигает некоторого предельного значения, кото­рое называют остаточным сопротивлением (велико у сплавов, су­ществует у чистых металлов и тем меньше, чем чище металл и меньше структурных дефектов).

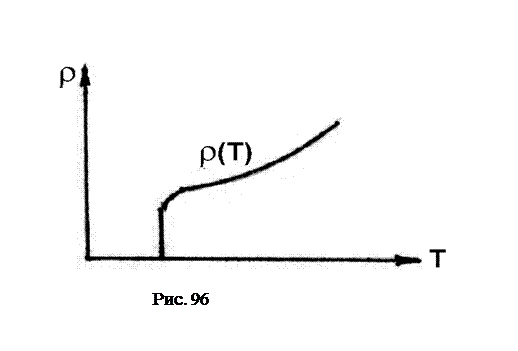
Если понижать температуру еще ниже, то в некоторых веществах наблюдается явление сверхпроводи­мости, т.е. удельное сопротивление внезапно скачком уменьшается прак­тически до нуля (рис. 96). В сверхпро­водниках однажды возбужденный электрический ток может длительно существовать без источника тока (в течение нескольких суток). В таком состоянии не выполняется за­кон Ома.

2. Другим затруднением классической электронной теории металлов может служить теория теплоемкости кристаллов. Со­гласно этой теории “электронный газ” металлов должен обладать молярной теплоемкостью 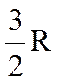. Добавляя эту теплоемкость к тепло­емкости кристаллической решетки, составляющей 3R, получим для молярной теплоемкости металла значение (9/2)R. Таким образом, согласно классической электронной теории молярная теплоемкость металла должна быть в 1,5 раза выше, чем у диэлектриков. Однако на практике их молярные теплоемкости практически не различа­ются. Объяснение этих различий и явлений дается в рамках кванто­вой теории металлов.

В классической теории неверным является предположение, что электроны проводимости подчиняются законам статистики Максвелла-Больцмана и что для них справедлив закон распределе­ния энергии Максвелла. На самом деле они подчиняются законам квантовой статистики и закону распределения энергий Ферми-Ди­рака.

Энергия электронов в металлах слабо зависит от темпера­туры и теплоемкость электронного газа оказывается близка к нулю, поэтому наличие электронного газа в металлах практически не ска­зывается на теплоемкости.

Далее, в классической электронной теории не учитывается взаимодействие электронов друг с другом, а их взаимодействие с решеткой металла описывается с помощью представления о соуда­рениях. При низких температурах взаимодействие между электро­нами начинает играть решающую роль. Кроме того, оказалось, что взаимодействие электронов с решеткой имеет иной характер – электроны движутся в периодическом поле электрического потен­циала решетки.

И, наконец, движение электронов в металлах подчиняется законам квантовой, а не классической механики.

Источник

Закон Джоуля-Ленца

Закон Джоуля-Ленца

На примере многих бытовых приборов понятно, что если через участок цепи проходит электроток и при этом не совершается какая-либо работа, то происходит нагревание проводника. Иногда оно идет на пользу — например, в лампе накаливания или в аппарате дуговой сварки. Но в других случаях тепловой эффект нежелателен — например, перегрев электрической проводки в здании может вызвать пожар. Поэтому в наших интересах управлять таким эффектом, и правило Джоуля-Ленца определяет, от чего зависит тепловое действие тока.

Правило было сформулировано в результате опытов двух ученых — англичанина Джеймса Прескотта Джоуля и российского физика Эмилия Христиановича Ленца. Поскольку ученые работали независимо друг от друга, новый закон назвали двойным именем.

Закон Джоуля-Ленца кратко: нагревание проводника или полупроводника прямо пропорционально его сопротивлению, времени действия тока и квадрату силы тока.

Поскольку сопротивление проводника определяют такие характеристики, как его длина, площадь и проводимость, верны следующие утверждения:

количество теплоты в проводнике снижается при увеличении площади его сечения;

тепловой эффект снижается при уменьшении длины проводника.

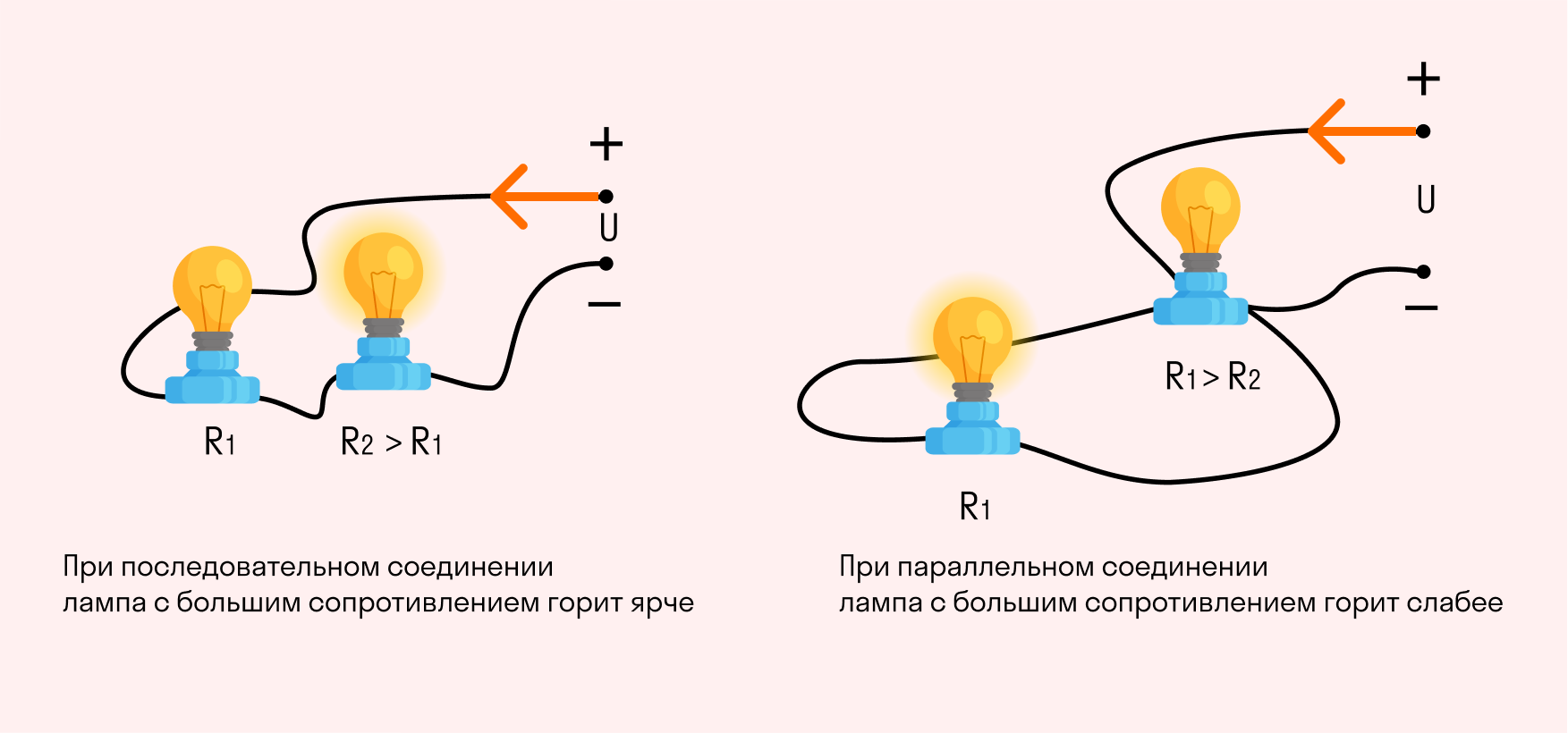
Это легко проиллюстрировать, подключив к источнику питания две лампы с разным сопротивлением вначале последовательно, а после — параллельно. При последовательном подключении лампа с большим сопротивлением будет светить ярче, а при параллельном — наоборот.

Природа тепла в проводниках

Разберемся, как происходит нагрев проводника и каким образом этот процесс отвечает формулировке законе Джоуля-Ленца. Как известно, электрический ток представляет собой направленный поток электронов, если речь идет о металлах, и направленный поток ионов — если о растворах электролитов. Проводником называют такой металл, в котором много свободных электронов.

При подключении проводника к сети электроны начинают двигаться в одном направлении под действием электрического поля. При движении они сталкиваются с атомами проводника и передают им свою кинетическую энергию. Чем выше скорость заряженных частиц, тем чаще происходят такие столкновения и больше выделяется кинетической энергии. Часть этой энергии трансформируется в тепло, поэтому проводник нагревается.

Высокая сила тока означает, что через сечение проводника проходит много свободных электронов и столкновения происходят часто. Соответственно, частицам проводника передается много энергии, и он греется сильнее. Именно поэтому в законе Ленца-Джоуля говорится о том, что количество выделяемой теплоты пропорционально квадрату силы тока.

Теперь представим, что сечение проводника увеличилось. Конечно, столкновений частиц будет меньше, а значит — выделится меньше тепла. Вспоминаем, что удельное сопротивление проводника обратно пропорционально его сечению. Чем меньше сечение материала, тем выше его сопротивление и тем сильнее он нагревается. Вот мы и описали тепловое действие тока в соответствии с законом Джоуля-Ленца.

Уравнение Джоуля-Ленца

Посмотрим, как данный закон выражается в математическом виде. Допустим, на некоем участке цепи проходит электрический ток и вызывает нагревание проводника. Если на этом участке нет каких-либо механических процессов или химических реакций, требующих энергозатрат, выделенная проводником теплота Q равна работе тока A.

Q = A

Поскольку А = IUt, где I — сила тока, U — напряжение, а t — время, Q = IUt.

Теперь вспомним, что напряжение можно выразить через сопротивление и силу тока U = IR. Подставим это в формулу:

Q = IUt = I(IR)t = I 2 Rt

Q = I 2 Rt

Мы выразили количество теплоты в проводнике через сопротивление — эта формула для закона Джоуля-Ленца называется интегральной.

Но бывает так, что сила электрического тока неизвестна, зато есть информация о напряжении на участке цепи. В таком случае нужно использовать закон Ома:

I = U/R

Исходя из этого, закон Джоуля-Ленца можно записать в виде дифференциальной формулы:

Напомним, что такое уравнение, как и предыдущее, верно только в том случае, когда вся работа электрического тока уходит на выделение тепла и нет других потребителей энергии.

Итак, у нас есть две формулы для определения количества теплоты, выделяемой проводником при прохождении через него электричества:

При расчетах используют следующие единицы измерения:

количество тепла Q— в джоулях (Дж);

силу тока I — в амперах (А);

сопротивление R — в омах (Ом);

время t — в секундах (с).

Практическое применение

Применение на практике закона Джоуля-Ленца заключается в том, что тепловым действием электрического тока можно управлять, подбирая проводники с нужным сопротивлением. К примеру, для электрических нагревательных приборов, которые должны выделять максимум тепла, выбирают проводники с высоким сопротивлением.

Низкое сопротивление, напротив, позволяет проводнику практически не нагреваться при прохождении тока. Поэтому на промышленных предприятиях с усиленными требованиями к пожаробезопасности для прокладки линий электропередач используется медный кабель. Удельное сопротивление меди сечением 1 мм 2 равно 0,0175 Ом, в то время как у алюминия оно составляет 0,0271 Ом. Медь практически не нагревается, чем снижает риск возгораний.

Примеры задач

Задача 1

Электроплита подключена к сети с напряжением 220 В. Какое количество тепла выделит ее нагревательный элемент за 50 минут, если известно, что сила тока в цепи составляет 10 А.

Решение:

Для того, чтобы рассчитать количество тепла, в данном случае подойдет интегральная формула Джоуля-Ленца Q = I 2 Rt, однако мы не знаем, чему равно сопротивление R. Однако согласно закону Ома R = U/I.

Вычислим сопротивление: R = U/I = 220/10 = 22 Ом.

Подставим имеющиеся данные в формулу:

Q = I 2 Rt = 10 2 × 22 × 3000 = 6 600 000 Дж = 6,6 МДж.

Ответ: плита выделит 6,6 мегаджоулей тепла.

Задача 2

Для обогрева дома требуется, чтобы отопительный прибор выделял 125 кДж тепла в час. Напряжение в электрической сети составляет 220 В. Каким должно быть электрическое сопротивление проводника, чтобы обеспечить данную теплоотдачу?

Решение:

Q = 125 Дж = 125 000 Дж;

В данном случае подойдет уравнение

Ответ: сопротивление проводника 1393,92 Ом.

Источник

Закон Джоуля-Ленца: определение, формулы

Мы ежедневно пользуемся электронагревательными приборами, не задумываясь, откуда берётся тепло. Разумеется, вы знаете, что тепловую энергию вырабатывает электричество. Но как это происходит, а тем более, как оценить количество выделяемого тепла, знают не все. На данный вопрос отвечает закон Джоуля-Ленца, обнародованный в позапрошлом столетии.

В 1841 году усилия английского физика Джоуля, а в 1842 г. исследования русского учёного Ленца увенчались открытием закона, применение которого позволяет количественно оценить результаты теплового действия электрического тока [ 1 ]. С тех пор изобретено множество приборов, в основе которых лежит тепловое действие тока. Некоторые из них, изображены на рис. 1.

Рис. 1. Тепловые приборы

Определение и формула

Тепловой закон можно сформулировать и записать в следующей редакции: «Количество тепла, выработанного током, прямо пропорционально квадрату приложенного к данному участку цепи тока, сопротивления проводника и промежутка времени, в течение которого электричество действовало на проводник».

Обозначим символом Q количество выделяемого тепла, а символами I, R и Δt – силу тока, сопротивление и промежуток времени, соответственно. Тогда формула закона Джоуля-Ленца будет иметь вид: Q = I 2 *R*Δt

Согласно законам Ома I=U/R, откуда R = U/I. Подставляя выражения в формулу Джоуля-Ленца получим: Q = U 2 /R * Δt ⇒ Q = U*I*Δt.

Выведенные нами формулы – различные формы записи закона Джоуля-Ленца. Зная такие параметры как напряжение или силу тока, можно легко рассчитать количество тепла, выделяемого на участке цепи, обладающем сопротивлением R.

Дифференциальная форма

Здесь u – скорость хаотического движение (векторная величина), а υ_max – максимальная скорость электрического заряда в данный момент времени.

Поскольку установлено, что скорость хаотического движения с одинаковой вероятностью совпадает с максимальной (по направлению и в противоположном направлении), то выражение 2*u*υ_max в среднем равно нулю. Тогда полная энергия, выделяющаяся при столкновениях электронов с атомами, образующими узлы кристаллической решётки, составляет:

Это и есть закон Джоуля-Ленца, записанный в дифференциальной форме. Здесь γ – согласующий коэффициент, E – напряжённость поля.

Интегральная форма

Предположим, что проводник имеет цилиндрическую форму с сечением S. Пусть длина этого проводника составляет l. Тогда мощность P, выделяемая в объёме V= lS составляет:

гдеR – полное сопротивление проводника.

Учитывая, чтоU = I×R, из последней формулы имеем:

Если величина тока со временем меняется, то количество теплоты вычисляется по формуле:

Данное выражение, а также вышеперечисленные формулы, которые можно переписать в таком же виде, принято называть интегральной формой закона Джоуля-Ленца.

Формулы очень удобны при вычислении мощности тока в нагревательных элементах. Если известно сопротивление такого элемента, то зная напряжение бытовой сети легко определить мощность прибора, например, электрочайника или паяльника.

Физический смысл

Вспомним, как электрический ток протекает по металлическому проводнику. Как только электрическая цепь замкнётся, то под действием ЭДС движение свободных электронов упорядочивается, и они устремляются к положительному полюсу источника питания. Однако на их пути встречаются стройные ряды кристаллических решёток, атомы которых создают препятствия упорядоченному движению, то есть оказывают сопротивление.

На преодоление сопротивления уходит часть энергии движущихся электронов. В соответствии с фундаментальным законом сохранения энергии, она не может бесследно исчезнуть. Она-то и превращается в тепло, вызывающее нагревание проводника. Накапливаемая тепловая энергия излучается в окружающее пространство или нагревает другие предметы, соприкасающиеся с проводником.

На рисунке 2 изображёна схема опыта, демонстрирующего закон теплового действия тока, разогревающего участок провода в электрической цепи.

Рис. 2. Тепловое действие тока

Явление нагревания проводников было известно практически с момента получения электротока, но исследователи не могли тогда объяснить его природу, и тем более, предложить способ оценки количества выделяемого тепла. Эту проблему решает закон Джоуля-Ленца, которым мы пользуемся по сегодняшний день.

Практическая польза закона Джоуля-Ленца

При сильном нагревании можно наблюдать излучение видимого спектра света, что происходит, например, в лампочке накаливания. Слабо нагретые тела тоже излучают тепловую энергию, но в диапазоне инфракрасного излучения, которого мы не видим, но можем ощутить своими тепловыми рецепторами.

Допускать сильное нагревание проводников нельзя, так как чрезмерная температура разрушает структуру металла, проще говоря – плавит его. Это может привести к выводу из строя электрооборудования, а также стать причиной пожара. Для того, чтобы не допустить критических параметров нагревания необходимо делать расчёты тепловых элементов, пользуясь формулами, описывающими закон Джоуля-Ленца.

Проанализировав выражение U 2 /R убеждаемся, что когда сопротивление стремится к нулю, то количество выделенного тепла стремится к бесконечности. Такая ситуация возникает при коротких замыканиях. В это основная опасность КЗ.

В борьбе с короткими замыканиями используют:

Применение и практический смысл

Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.

Перечислим некоторые из них:

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.

Рис. 3. Бытовые нагревательные приборы

Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.

Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.

Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.

Источник