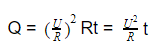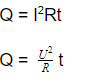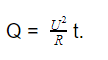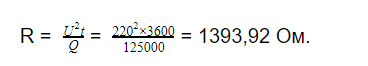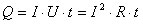закон джоуля ленца в локальной форме

Закон Джоуля-Ленца

Электричество — неотъемлемый признак нашей эпохи. Абсолютно всё вокруг завязано на нём. Любой современный человек, даже без технического образования, знает, что электрический ток, текущий по проводам, способен в некоторых случаях нагревать их, зачастую до очень высоких температур. Казалось бы, это заведомо всем известно и не стоит упоминания. Однако, как объяснить это явление? Почему и как происходит нагрев проводника?

Опыты Ленца

Перенесемся в 19 век-эпоху накопления знаний и подготовки к технологическому прыжку 20 века. Эпоха, когда по всему миру различные учёные и просто изобретатели-самоучки чуть ли не ежедневно открывают что-то новое, зачастую тратя огромное количество времени на исследования и, при этом, не представляя конечный результат.

Один из таких людей, русский учёный Эмилий Христианович Ленц, увлекался электричеством, на тогдашнем примитивном уровне, пытаясь рассчитывать электрические цепи. В 1832 году Эмилий Ленц «застрял» с расчётами, так как параметры его смоделированной цепи «источник энергии — проводник — потребитель энергии» сильно разнились от опыта к опыту. Зимой 1832-1833 года учёный обнаружил, что причиной нестабильности является кусочек платиновой проволоки, принесённый им с холода. Отогревая или охлаждая проводник, Ленц также заметил что существует некая зависимость между силой тока, электрическим сопротивлением и температурой проводника.

При определённых параметрах электрической цепи проводник быстро оттаивал и даже слегка нагревался. Измерительных приборов в те времена практически никаких не существовало — невозможно было точно измерить ни силу тока, ни сопротивление. Но это был русский физик, и он проявил смекалку. Если это зависимость, то почему бы ей не быть обратимой?

Для того чтобы измерить количество тепла, выделяемого проводником, учёный сконструировал простейший «нагреватель» — стеклянная ёмкость, в которой находился спиртосодержащий раствор и погружённый в него платиновый проводник-спираль. Подавая различные величины электрического тока на проволоку, Ленц замерял время, за которое раствор нагревался до определённой температуры. Источники электрического тока в те времена были слишком слабы, чтобы разогреть раствор до серьёзной температуры, потому визуально определить количество испарившегося раствора не представлялось возможным. Из-за этого процесс исследования очень затянулся — тысячи вариантов подбора параметров источника питания, проводника, долгие замеры и последующий анализ.

Закон Джоуля-Ленца

В итоге, спустя десятилетие, в 1843 году Эмилий Ленц выставил на всеобщее обозрение научного сообщества результат своих опытов в виде закона. Однако, оказалось, что его опередили! Пару лет назад английский физик Джеймс Прескотт Джоуль уже проводил аналогичные опыты и также представил общественности свои результаты. Но, тщательно проверив все работы Джеймса Джоуля, русский учёный выяснил что собственные опыты гораздо точнее, наработан больший объём исследований, потому, русской науке есть чем дополнить английское открытие.

Q — количество выделяемого тепла (Джоули)

I — сила тока, протекающего через проводник (Амперы)

R — сопротивление проводника (Омы)

t — время прохождения тока через проводник (Секунды)

Почему греется проводник

Применение закона Джоуля-Ленца в жизни

Открытие закона Джоуля-Ленца имело огромные последствия для практического применения электрического тока. Уже в 19 веке стало возможным создать более точные измерительные приборы, основанные на сокращении проволочной спирали при её нагреве протекающим током определённой величины — первые стрелочные вольтметры и амперметры. Появились первые прототипы электрических обогревателей, тостеров, плавильных печей – использовался проводник с высоким удельным сопротивлением, что позволяло получить довольно высокую температуру.

Проводник (угольная палочка, бамбуковая нить, платиновая проволока и т.д.) помещали в стеклянную колбу, откачивали воздух для замедления процесса окисления и получали незатухаемый, чистый и стабильный источник света – электрическую лампочку

Заключение

Таки образом, можно сказать что на законе Джоуля-Ленца держится чуть ли не вся электрика и электротехника. Открыв этот закон, появилась возможность уже заранее предсказать некоторые будущие проблемы в освоении электричества. Например, из-за нагрева проводника передача электрического тока на большое расстояние сопровождается потерями этого тока на тепло. Соответственно, чтобы компенсировать эти потери нужно занизить передаваемый ток, компенсируя это высоким напряжением. А уже на оконечном потребителе, понижать напряжение и получать более высокий ток.

Закон Джоуля-Ленца неотступно следует из одной эпохи технологического развития в другую. Даже сегодня мы постоянно наблюдаем его в быту – закон проявляется всюду, и не всегда люди ему рады. Сильно греющийся процессор персонального компьютера, пропадание света из-за обгоревшей скрутки «медь-алюминий»,выбитая вставка-предохранитель, выгоревшая из-за высокой нагрузки электропроводка – всё это тот самый закон Джоуля-Ленца.

Раз уж заговорили про ДжОУля )) Читайте статья про ОУ — Операционный усилитель.

Источник

Закон Джоуля-Ленца: определение, формулы

Мы ежедневно пользуемся электронагревательными приборами, не задумываясь, откуда берётся тепло. Разумеется, вы знаете, что тепловую энергию вырабатывает электричество. Но как это происходит, а тем более, как оценить количество выделяемого тепла, знают не все. На данный вопрос отвечает закон Джоуля-Ленца, обнародованный в позапрошлом столетии.

В 1841 году усилия английского физика Джоуля, а в 1842 г. исследования русского учёного Ленца увенчались открытием закона, применение которого позволяет количественно оценить результаты теплового действия электрического тока [ 1 ]. С тех пор изобретено множество приборов, в основе которых лежит тепловое действие тока. Некоторые из них, изображены на рис. 1.

Рис. 1. Тепловые приборы

Определение и формула

Тепловой закон можно сформулировать и записать в следующей редакции: «Количество тепла, выработанного током, прямо пропорционально квадрату приложенного к данному участку цепи тока, сопротивления проводника и промежутка времени, в течение которого электричество действовало на проводник».

Обозначим символом Q количество выделяемого тепла, а символами I, R и Δt – силу тока, сопротивление и промежуток времени, соответственно. Тогда формула закона Джоуля-Ленца будет иметь вид: Q = I 2 *R*Δt

Согласно законам Ома I=U/R, откуда R = U/I. Подставляя выражения в формулу Джоуля-Ленца получим: Q = U 2 /R * Δt ⇒ Q = U*I*Δt.

Выведенные нами формулы – различные формы записи закона Джоуля-Ленца. Зная такие параметры как напряжение или силу тока, можно легко рассчитать количество тепла, выделяемого на участке цепи, обладающем сопротивлением R.

Дифференциальная форма

Здесь u – скорость хаотического движение (векторная величина), а υ_max – максимальная скорость электрического заряда в данный момент времени.

Поскольку установлено, что скорость хаотического движения с одинаковой вероятностью совпадает с максимальной (по направлению и в противоположном направлении), то выражение 2*u*υ_max в среднем равно нулю. Тогда полная энергия, выделяющаяся при столкновениях электронов с атомами, образующими узлы кристаллической решётки, составляет:

Это и есть закон Джоуля-Ленца, записанный в дифференциальной форме. Здесь γ – согласующий коэффициент, E – напряжённость поля.

Интегральная форма

Предположим, что проводник имеет цилиндрическую форму с сечением S. Пусть длина этого проводника составляет l. Тогда мощность P, выделяемая в объёме V= lS составляет:

гдеR – полное сопротивление проводника.

Учитывая, чтоU = I×R, из последней формулы имеем:

Если величина тока со временем меняется, то количество теплоты вычисляется по формуле:

Данное выражение, а также вышеперечисленные формулы, которые можно переписать в таком же виде, принято называть интегральной формой закона Джоуля-Ленца.

Формулы очень удобны при вычислении мощности тока в нагревательных элементах. Если известно сопротивление такого элемента, то зная напряжение бытовой сети легко определить мощность прибора, например, электрочайника или паяльника.

Физический смысл

Вспомним, как электрический ток протекает по металлическому проводнику. Как только электрическая цепь замкнётся, то под действием ЭДС движение свободных электронов упорядочивается, и они устремляются к положительному полюсу источника питания. Однако на их пути встречаются стройные ряды кристаллических решёток, атомы которых создают препятствия упорядоченному движению, то есть оказывают сопротивление.

На преодоление сопротивления уходит часть энергии движущихся электронов. В соответствии с фундаментальным законом сохранения энергии, она не может бесследно исчезнуть. Она-то и превращается в тепло, вызывающее нагревание проводника. Накапливаемая тепловая энергия излучается в окружающее пространство или нагревает другие предметы, соприкасающиеся с проводником.

На рисунке 2 изображёна схема опыта, демонстрирующего закон теплового действия тока, разогревающего участок провода в электрической цепи.

Рис. 2. Тепловое действие тока

Явление нагревания проводников было известно практически с момента получения электротока, но исследователи не могли тогда объяснить его природу, и тем более, предложить способ оценки количества выделяемого тепла. Эту проблему решает закон Джоуля-Ленца, которым мы пользуемся по сегодняшний день.

Практическая польза закона Джоуля-Ленца

При сильном нагревании можно наблюдать излучение видимого спектра света, что происходит, например, в лампочке накаливания. Слабо нагретые тела тоже излучают тепловую энергию, но в диапазоне инфракрасного излучения, которого мы не видим, но можем ощутить своими тепловыми рецепторами.

Допускать сильное нагревание проводников нельзя, так как чрезмерная температура разрушает структуру металла, проще говоря – плавит его. Это может привести к выводу из строя электрооборудования, а также стать причиной пожара. Для того, чтобы не допустить критических параметров нагревания необходимо делать расчёты тепловых элементов, пользуясь формулами, описывающими закон Джоуля-Ленца.

Проанализировав выражение U 2 /R убеждаемся, что когда сопротивление стремится к нулю, то количество выделенного тепла стремится к бесконечности. Такая ситуация возникает при коротких замыканиях. В это основная опасность КЗ.

В борьбе с короткими замыканиями используют:

Применение и практический смысл

Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.

Перечислим некоторые из них:

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.

Рис. 3. Бытовые нагревательные приборы

Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.

Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.

Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.

Источник

Закон Джоуля-Ленца

Закон Джоуля-Ленца

На примере многих бытовых приборов понятно, что если через участок цепи проходит электроток и при этом не совершается какая-либо работа, то происходит нагревание проводника. Иногда оно идет на пользу — например, в лампе накаливания или в аппарате дуговой сварки. Но в других случаях тепловой эффект нежелателен — например, перегрев электрической проводки в здании может вызвать пожар. Поэтому в наших интересах управлять таким эффектом, и правило Джоуля-Ленца определяет, от чего зависит тепловое действие тока.

Правило было сформулировано в результате опытов двух ученых — англичанина Джеймса Прескотта Джоуля и российского физика Эмилия Христиановича Ленца. Поскольку ученые работали независимо друг от друга, новый закон назвали двойным именем.

Закон Джоуля-Ленца кратко: нагревание проводника или полупроводника прямо пропорционально его сопротивлению, времени действия тока и квадрату силы тока.

Поскольку сопротивление проводника определяют такие характеристики, как его длина, площадь и проводимость, верны следующие утверждения:

количество теплоты в проводнике снижается при увеличении площади его сечения;

тепловой эффект снижается при уменьшении длины проводника.

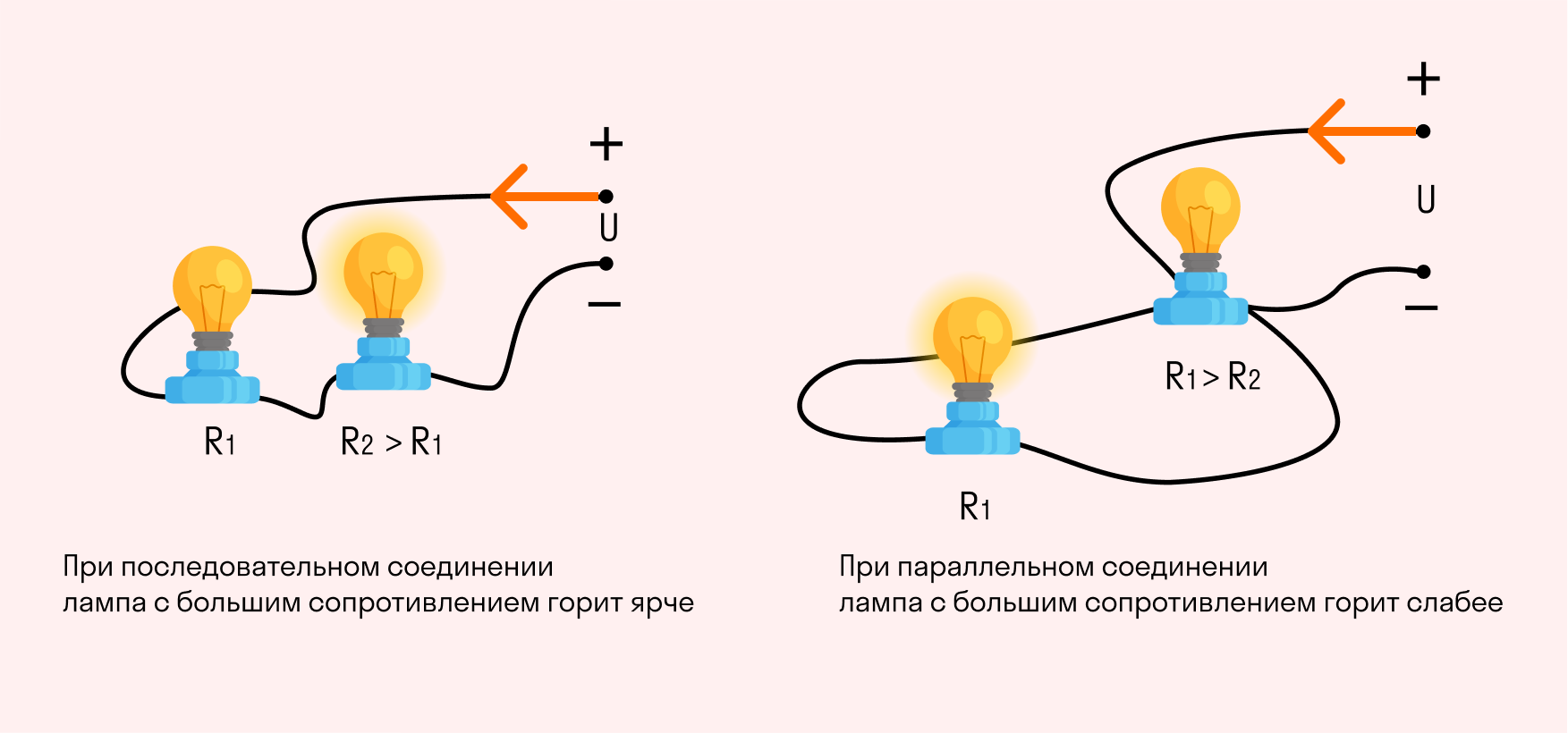
Это легко проиллюстрировать, подключив к источнику питания две лампы с разным сопротивлением вначале последовательно, а после — параллельно. При последовательном подключении лампа с большим сопротивлением будет светить ярче, а при параллельном — наоборот.

Природа тепла в проводниках

Разберемся, как происходит нагрев проводника и каким образом этот процесс отвечает формулировке законе Джоуля-Ленца. Как известно, электрический ток представляет собой направленный поток электронов, если речь идет о металлах, и направленный поток ионов — если о растворах электролитов. Проводником называют такой металл, в котором много свободных электронов.

При подключении проводника к сети электроны начинают двигаться в одном направлении под действием электрического поля. При движении они сталкиваются с атомами проводника и передают им свою кинетическую энергию. Чем выше скорость заряженных частиц, тем чаще происходят такие столкновения и больше выделяется кинетической энергии. Часть этой энергии трансформируется в тепло, поэтому проводник нагревается.

Высокая сила тока означает, что через сечение проводника проходит много свободных электронов и столкновения происходят часто. Соответственно, частицам проводника передается много энергии, и он греется сильнее. Именно поэтому в законе Ленца-Джоуля говорится о том, что количество выделяемой теплоты пропорционально квадрату силы тока.

Теперь представим, что сечение проводника увеличилось. Конечно, столкновений частиц будет меньше, а значит — выделится меньше тепла. Вспоминаем, что удельное сопротивление проводника обратно пропорционально его сечению. Чем меньше сечение материала, тем выше его сопротивление и тем сильнее он нагревается. Вот мы и описали тепловое действие тока в соответствии с законом Джоуля-Ленца.

Уравнение Джоуля-Ленца

Посмотрим, как данный закон выражается в математическом виде. Допустим, на некоем участке цепи проходит электрический ток и вызывает нагревание проводника. Если на этом участке нет каких-либо механических процессов или химических реакций, требующих энергозатрат, выделенная проводником теплота Q равна работе тока A.

Q = A

Поскольку А = IUt, где I — сила тока, U — напряжение, а t — время, Q = IUt.

Теперь вспомним, что напряжение можно выразить через сопротивление и силу тока U = IR. Подставим это в формулу:

Q = IUt = I(IR)t = I 2 Rt

Q = I 2 Rt

Мы выразили количество теплоты в проводнике через сопротивление — эта формула для закона Джоуля-Ленца называется интегральной.

Но бывает так, что сила электрического тока неизвестна, зато есть информация о напряжении на участке цепи. В таком случае нужно использовать закон Ома:

I = U/R

Исходя из этого, закон Джоуля-Ленца можно записать в виде дифференциальной формулы:

Напомним, что такое уравнение, как и предыдущее, верно только в том случае, когда вся работа электрического тока уходит на выделение тепла и нет других потребителей энергии.

Итак, у нас есть две формулы для определения количества теплоты, выделяемой проводником при прохождении через него электричества:

При расчетах используют следующие единицы измерения:

количество тепла Q— в джоулях (Дж);

силу тока I — в амперах (А);

сопротивление R — в омах (Ом);

время t — в секундах (с).

Практическое применение

Применение на практике закона Джоуля-Ленца заключается в том, что тепловым действием электрического тока можно управлять, подбирая проводники с нужным сопротивлением. К примеру, для электрических нагревательных приборов, которые должны выделять максимум тепла, выбирают проводники с высоким сопротивлением.

Низкое сопротивление, напротив, позволяет проводнику практически не нагреваться при прохождении тока. Поэтому на промышленных предприятиях с усиленными требованиями к пожаробезопасности для прокладки линий электропередач используется медный кабель. Удельное сопротивление меди сечением 1 мм 2 равно 0,0175 Ом, в то время как у алюминия оно составляет 0,0271 Ом. Медь практически не нагревается, чем снижает риск возгораний.

Примеры задач

Задача 1

Электроплита подключена к сети с напряжением 220 В. Какое количество тепла выделит ее нагревательный элемент за 50 минут, если известно, что сила тока в цепи составляет 10 А.

Решение:

Для того, чтобы рассчитать количество тепла, в данном случае подойдет интегральная формула Джоуля-Ленца Q = I 2 Rt, однако мы не знаем, чему равно сопротивление R. Однако согласно закону Ома R = U/I.

Вычислим сопротивление: R = U/I = 220/10 = 22 Ом.

Подставим имеющиеся данные в формулу:

Q = I 2 Rt = 10 2 × 22 × 3000 = 6 600 000 Дж = 6,6 МДж.

Ответ: плита выделит 6,6 мегаджоулей тепла.

Задача 2

Для обогрева дома требуется, чтобы отопительный прибор выделял 125 кДж тепла в час. Напряжение в электрической сети составляет 220 В. Каким должно быть электрическое сопротивление проводника, чтобы обеспечить данную теплоотдачу?

Решение:

Q = 125 Дж = 125 000 Дж;

В данном случае подойдет уравнение

Ответ: сопротивление проводника 1393,92 Ом.

Источник

Закон Джоуля Ленца — самая полная теория

Давним давно, жили два ученых, один из которых, кстати, был нашим соотечественником — Эмилий Христофорович Ленц. Так вот, примерно в одно и тоже время, наш герой, вместе со своим английским коллегой, Джеймсом Джоулем, провели опыт (независимо друг от друга). Результаты их исследований со временем назовут законом Джоуля Ленца. В тонкостях этой области физики мы и будем разбираться в нашей сегодняшней статье.

Эти два ученых ставили перед собой цель, выяснить, от чего зависит нагревание проводников, которые оказываются частью одной цепи и посчитать количество тепла, которое уходит на нагревание того или иного проводника. Логично предположить, что чем больше ток, который протекает через проводник, тем выше температура, до которой этот элемент нагревается. Также, тем выше скорость нагревания. Чтобы проверить свое предположения оба физика собрали цепи, в которой были последовательно соединены три проводника из разных материалов. Ученые последовательно пропускали ток разной силы, проводя замеры. Что они выяснили?

Немного истории

Многочисленные опыты, проведенные в конце XVIII – начале XIX века, позволили не только установить основные свойства и законы электричества, но и сформулировать эпохальный по своей значимости вывод об эквивалентности между теплотой и механической работой: работа, или, как впоследствии стали формулировать, «энергия», никогда не теряется, а лишь переходит из одного вида в другой. Этот вывод, получивший впоследствии название закона сохранения и превращения энергии (см. подраздел 1.2), и заключался в том, что теплоту можно обратить в механическую работу и наоборот и что из определенного количества теплоты можно получить только определенное количество механической работы. Можно привести тысячи примеров, когда с помощью этого закона нашли свое объективное толкование результаты опытов в различных областях естествознания.

Основными положениями закона сохранения энергии воспользовались и электротехники при определении, например, количества тепловой энергии, выделяющегося в гальванической батарее вследствие химической реакции и превращающегося впоследствии в электрическую энергию. Однако особенность электрической энергии состоит в том, что само по себе электричество неприменимо. Человечество не может использовать его непосредственно подобно тому, как оно согревается теплотой, видит благодаря свету и т.п. Можно пользоваться только действием электрического тока, при котором электричество переходит в другие формы энергии.

В своих работах В.В. Петров описывает опыты по электролизу растительных масел, в результате которых он обнаружил высокие электроизоляционные свойства этих масел. Позднее масла получили широкое применение в качестве электроизоляционного материала. Желая продемонстрировать явление электролиза одновременно в нескольких трубках с водой, Петров впервые применил параллельное соединение приемников электрического тока. Работы этого выдающегося ученого установили возможность практического использования электрического тока для нагревания проводников.

Эмилий Христианович Ленц (1804–1865) – известный российский физик и электротехник, академик Петербургской академии наук, ректор Петербургского университета – родился в Дерпте (ныне Тарту, Эстония) в семье чиновника. После второго курса Дерптского университета отправился в 1823 году в трехлетнее кругосветное плавание. С помощью сконструированных им приборов (глубометра и батометра) занимался физическими исследованиями в водах Берингова пролива, Тихого и Индийского океанов, установил происхождение теплых и холодных морских течений, открыл закон океанических циркуляций. В 1829 г. принял участие в экспедиции на Кавказ, где проводил магнитные, термометрические и барометрические измерения в горных районах Кавказа и на побережье Каспийского моря. В 1830 году был назначен экстраординарным профессором и директором физического кабинета при Петербургской АН, в 1836 г. возглавил кафедру физики в Петербургском университете, а в 1863 г. стал ректором этого университета. Основные его работы посвящены электромагнетизму, вопросам теории и практического применения электричества, исследования в области которого Ленц начал в 1831 году в лаборатории первого русского электротехника – академика В.В. Петрова. Ленц стоял у истоков первой в России школы физиков-электротехников, последователями которой стали А.С. Попов, Ф.Ф. Петрушевский, В.Ф. Миткевич и др.

Зависимость количества выделяемой теплоты от силы тока изучали английский физик Джеймс Джоуль и русский физик Эмилий Ленц. Они пропускали ток по спирали, помещенной в калориметр с водой. Через некоторое время вода нагревалась. По её температуре легко было вычислить количество выделившейся теплоты. Из проведенных опытов практически одновременно Джоуль и Ленц пришли к выводу, что при прохождении гальванического тока I по проводнику, обладающему определенным сопротивлением R, в течение времени t совершается работа А :

проявляющаяся в виде выделившейся теплоты.

Этот важнейший вывод обратимости электрической и тепловой энергии, теоретически обоснованный Уильямом Томсоном, получил название закона Джоуля–Ленца, а именем Джоуля названа единица механической работы в системе СИ.

Комбинируя проводники различного сопротивления, включенные последовательно в общую цепь, можно добиться концентрированного выделения большого количества теплоты на малом участке проводника с большим сопротивлением. На таком концентрировании выделения теплоты были основаны все первоначальные опыты превращения энергии электрического тока в тепловую и даже в световую энергию.

Всю свою жизнь В.В. Петров – член двух академий – прожил скромно и незаметно. 41 год он проработал в Медико-хирургической академии. За это время он провел много физических опытов, написал три книги и учебник по физике, которым пользовались в гимназиях всей России. Книги и научные статьи Петров писал на русском языке, чтобы их читало как можно больше людей, хотя в то время научные работы было принято писать на латыни. Он писал: «Я надеюсь, что просвещенные и беспристрастные физики по крайней мере некогда согласятся отдать трудам моим ту справедливость, которую важность сих последних опытов заслуживает».

О законе Джоуля Ленца

Эта мощность может расходоваться на совершение работы над внешними телами; на протекание химических реакций; на нагревание данного участка цепи и др.

В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Принято говорить, что при протекании тока в проводнике выделяется тепло

Это соотношение называется законом Джоуля – Ленца. Оно было экспериментально установлено английским физиком Д. П. Джоулем и подтверждено точными опытами Э. Х. Ленца.

Если сила тока изменяется со временем, то количество теплоты, выделяющееся в проводнике за время t, вычисляется по формуле

От формулы (4.1), можно перейти к выражению, характеризующему выделение тепла в различных точках проводника. Выделим в проводнике элементарный объем в виде цилиндра. Согласно закону Джоуля – Ленца, за время dt, в этом объеме выделится количество теплоты

где – dV элементарный объем. Разделив это выражение на dV и dt, найдем количество теплоты, выделяющееся в единице объема в единицу времени:

Величину называют удельной тепловой мощностью тока. Эта формула представляет собой дифференциальную форму закона Джоуля – Ленца.

Из курса лекций

При протекании тока через проводник, обладающий сопротивлением, проводник нагревается (если он неподвижен и в нём нет химических превращений, то работа тока расходуется на нагревание проводника). Определим количество теплоты, выделяющегося в единицу времени на участке цепи. Рассмотрим однородный и неоднородный участки цепи, будем использовать закон Ома и закон сохранения энергии.

Однородный участок цепи

Рассчитаем работу, которую совершают силы поля над носителями тока на участке 1–2 за время dt. Сила тока в проводнике I, разность потенциалов между точками 1 и 2 – (j₁ – j₂). Тогда: – такой заряд протечёт через поперечное сечение участка 1-2.

Согласно закону сохранения энергии, энергия, эквивалентная этой работе, выделяется в виде тепла, если проводник неподвижен и в нём не происходят химические превращения, т.е. проводник нагревается. Носители тока (в металлах электроны) в результате работы сил поля приобретают дополнительную кинетическую энергию, а затем расходуют её на возбуждение колебаний решётки при столкновении с её узлами-атомами. Тогда:

Эта формула выражает закон Джоуля-Ленца для однородного участка цепи в интегральной форме записи. Если сила тока изменяется со временем, то количество теплоты, выделяющееся за время t вычисляется по формуле:

Получим дифференциальную форму записи закона Джоуля-Ленца.

; ; – величина элементарного объема.

Формула(24.6) определяет тепло, выделяющееся во всём проводнике, можно перейти к выражению, характеризующему выделение тепла в различных местах проводника. Выделим в проводнике элементарный объём в виде цилиндра. Согласно закону Джоуля-Ленца за время dt в этом объеме выделяется тепло.

Разделив это выражение на dV и dt, найдём количество тепла, выделяющееся в единице объема в единицу времени, эту величину назвали удельной тепловой мощностью тока w.

Удельная тепловая мощность тока – это количество теплоты выделяющееся в единицу времени в единице объема проводящей среды.

Формула (24.9) – дифференциальная форма записи закона Джоуля-Ленца. Сформулируем его:

Уравнение применимо к любым проводникам вне зависимости от их формы, однородности и от природы сил, возбуждающих электрический ток. Если на носители тока действуют только электрические силы, то, согласно закону Ома:

Это уравнение имеет менее общий характер, чем уравнение

Неоднородный участок цепи

На неоднородном участке цепи на носители тока действуют не только электрические, но и сторонние силы, т.к. участок цепи содержит источник ЭДС. Тогда по закону сохранения энергии в неподвижном проводнике выделяемая теплота равна энергии, т.е. алгебраической сумме работ электрических и сторонних сил. Это же относится и к соответствующим мощностям: тепловая мощность должна быть равна алгебраической сумме мощностей электрических и сторонних сил:

– выделяющаяся на участке тепловая мощность. При наличии сторонних сил величина тепловой мощности определяется по той же формуле, что и для однородного участка цепи. Последнее слагаемое в правой части формулы: – представляет собой мощность, развиваемую сторонними силами на данном участке цепи, но величина – алгебраическая, в отличие от величины она изменяет знак при изменении направления тока I.

Таким образом, данная формула означает, что тепловая мощность, выделяемая на участке цепи между точками 1 и 2, равна алгебраической сумме мощностей электрических и сторонних сил. Сумму этих мощностей, называютмощностью токана рассматриваемом участке цепи. Тогда можно сказать, что в случае неподвижного участка цепи мощность выделяемой на этом участке теплоты равна мощности тока.

Для полной неразветвлённой цепи

– формула определяет общее количество выделяемой за единицу времени во всей цепи джоулевой теплоты (Q), оно равно мощности только сторонних сил.

Итак, теплота производится только сторонними силами, а электрическое поле только перераспределяет эту теплоту по различным участкам цепи.

Получим выражение закона Джоуля-Ленца в дифференциальной форме записи.

Магнитное поле в вакууме Магнитное поле. Магнитная индукция

Как в пространстве, окружающем электрический заряд возникает ЭП, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным (МП).

Опыт Эрстеда заключался в следующем: над магнитной стрелкой натягивалась проволока, по которой пропускали ток. Магнитная стрелка могла вращаться на игле. При включении тока магнитная стрелка поворачивалась и устанавливалась перпендикулярно к проволоке. При изменении направления тока, магнитная стрелка поворачивалась в противоположную сторону и опять устанавливалась перпендикулярно к проволоке.

Электрическое поле действует как на неподвижные, так и на движущиеся заряды, а МП – только на движущиеся в этом поле заряды.

Важнейшая особенность МП: оно действует только на движущиеся заряды.

Для обнаружения ЭП в него вносят пробный заряд. Для обнаружения МП в него вносят проводник с током (плоский замкнутый контур с током) или рамку с током, линейные размеры рамки с током малы по сравнению с расстоянием до токов, порождающих МП.

МП действует на рамку с током и рамка с током поворачивается. Ориентация контура с током в пространстве характеризуется направлением нормали ( ), т.е. за направление МП в данной точке принимают направление положительной нормали к рамке.

За направление индукции МП в данной точке принимается направление, вдоль которого располагается положительная нормаль к контуру с током.

Пусть ток течет по контуру против хода часовой стрелки, тогда ось магнитной стрелки, помещенной в МП, устанавливается вдоль направления поля (ось магнитной стрелки направлена так, что соединяет южный полюс S магнита с северным N).

На магнитную стрелку действует пара сил, поворачивающая ее до тех пор, пока ось стрелки не установится вдоль направления поля.

Вращающий момент, действующий на рамку с током равен:

Вращающий момент зависит от свойств поля в данной точке и свойств рамки, где – вектор магнитного момента рамки с током, – вектор магнитной индукции.

магнитный момент плоского контура с током, где I – сила тока в контуре, S – площадь поверхности контура (рамки), – единичный вектор нормали к поверхности рамки.

Индукция МП определяется так:

Вектор – силовая характеристика МП, но по историческим причинам ее назвали индукцией МП.

МП можно изображать с помощью линий магнитной индукции – силовых линий МП.

Направление силовых линий задается правилом правого винта: острие винта, движется по направлению тока, а направление вращения головки винта показывает направление обхода по силовым линиям.

Свойства силовых линий (линий магнитной индукции) МП:

(Силовые линии ЭСП разомкнуты. Они начинаются на (+q) и заканчиваются на (–q)).

Поле, силовые линии которого замкнуты, называется вихревым. МП – вихревое поле. Изобразим линии магнитной индукции полосового магнита. Силовые линии выходят из северного полюса и входят в южный. Разрезая магнит на части, нельзя разделить полюса магнита.

Внутри (установлено на опыте) полосовых магнитов имеется магнитное поле, силовые линии которого являются продолжением силовых линий вне магнита. Т.е. силовые линии МП постоянных магнитов тоже замкнуты. Свободных магнитных зарядов не существует.

В СИ единицей измерения магнитной индукции является тесла:

1 Тл = Дж/А·м² = Н·м/А·м² = Н/А·м

Магнитной проницаемостью среды является безразмерная величина, показывающая, во сколько раз МП в среде больше чем МП в вакууме:

где В – величина МИ в вакууме, а В_ср – величина магнитной индукции в среде.

Гн/м – магнитная постоянная.

В заключении предлагаем скачать интересный труд Натисова из Московского государственного института имени Баумана “Закон Джоуля Ленца”

Источник