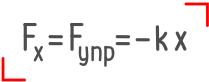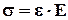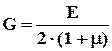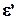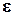закон гука в дифференциальной и интегральной форме
Закон гука в дифференциальной и интегральной форме
§ 5. Виды деформаций, закон Гука
Из наличия упругих свойств твёрдых тел можем заключить, что между молекулами и атомами существуют как силы притяжения, так и силы отталкивания. Исследования показали, что эти силы сильно зависят от расстояния между молекулами.
Если две молекулы разместить так, чтобы расстояние между их центрами составило примерно два радиуса, то сумма сил притяжения и отталкивания равна нулю.
 |
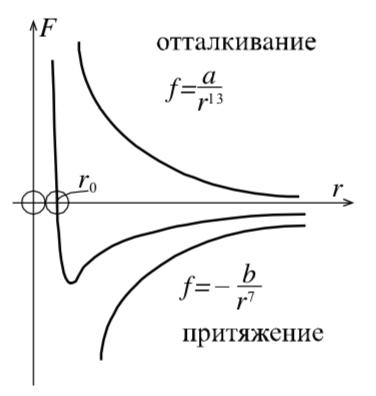| рис. 7 |
Теперь понятно, что даже если сила притяжения или отталкивания между парой молекул мала, то при деформации макроскопического тела таких пар сил возникнет колоссально много, и они дадут в сумме макроскопическую силу упругости, компенсирующую внешнюю силу.
называют изменение формы и размеров тела под действием внешних сил.
Все деформации можно разделить на четыре вида: сжатия – растяжения, изгиб, сдвиг и кручение.
Величина деформации так же характеризуется безразмерной величиной:
Примеров таких деформаций очень много: ножки стула, стола, стены зданий, некоторые кости скелета, мачта парусника во время штиля и др.
Робертом Гуком экспериментально было установлено, что:
 |
| Рис. 8 |
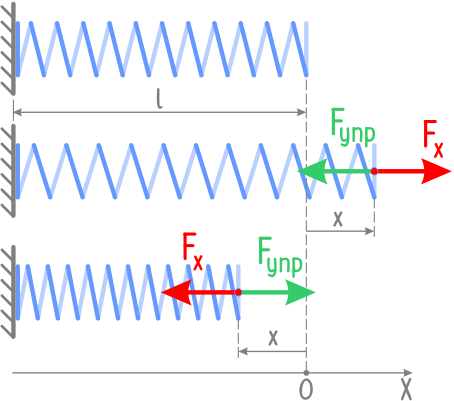
Сила упругости, возникающая при деформации, прямо пропорциональна смещению частиц и направлена в сторону, противоположную смещению частиц при деформации.
На практике пружину, подчиняющуюся закону Гука, градуируют на разные значения силы для измерения силы. Далее воздействуют ею на тело так, чтобы тело стало двигаться равномерно. В этом состоянии сила, ранее действовавшая на тело, стано вится равной силе, действующей со стороны пружины, определяемой по граду и рованной шкале. Прибор для измерения силы называется динамометром.
Во втором случае половинки шнура соединены между собой параллельно, следовательно, условие равновесия груза теперь выглядит так:
Сила упругости
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
Сила упругости: Закон Гука
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука
Fупр = kx
Fупр — сила упругости [Н]
k — коэффициент жесткости [Н/м]
х — изменение длины (деформация) [м]
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем. Это, конечно, сила тяжести. Не забываем массу представить в единицах СИ – килограммах.
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
Тогда из Закона Гука выразим модуль удлинения лески:
Выражаем модуль удлинения:
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
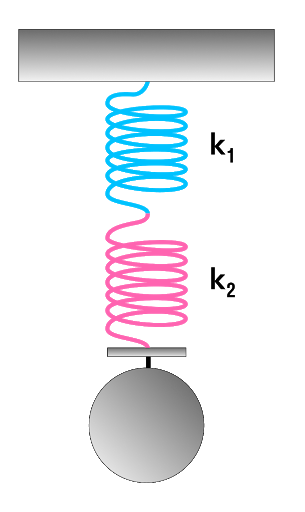
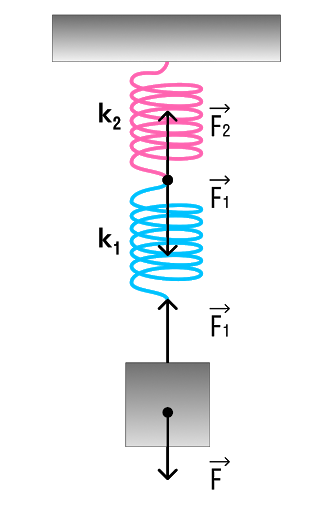
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k_i
k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
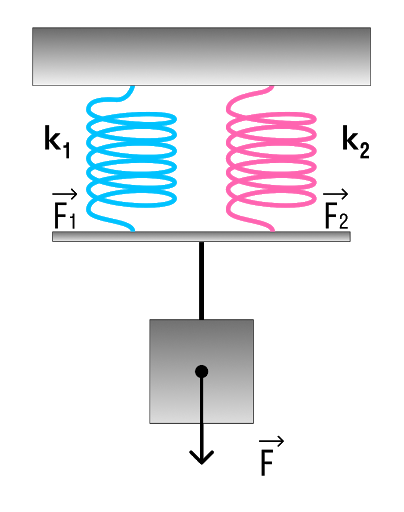
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин
k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-]
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
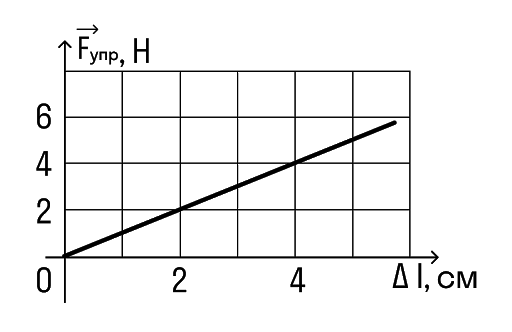
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
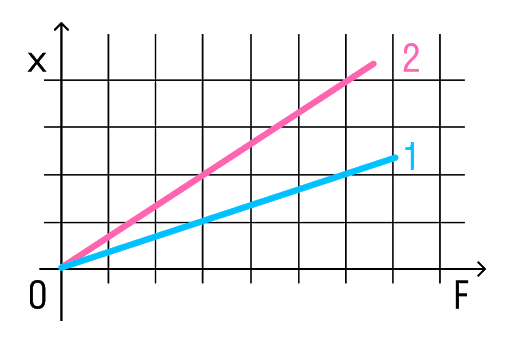
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
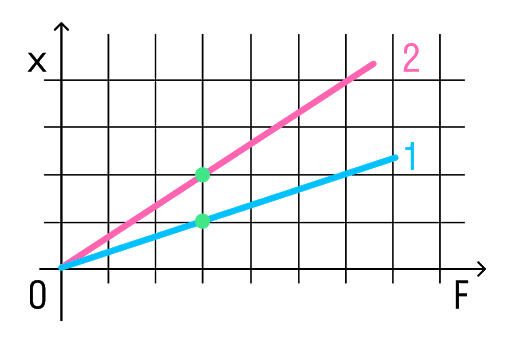
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Закон гука в дифференциальной и интегральной форме
1. Силы упругости. Виды деформации: растяжение, изгиб, сдвиг, кручение. Механическое напряжение. Закон Гука, модуль Юнга, коэффициент Пуассона
Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.
Сила упругости имеет электромагнитную природу, являясь макроскопическим проявлением межмолекулярного взаимодействия. В простейшем случае растяжения/сжатия тела сила упругости направлена противоположно смещению частиц тела, перпендикулярно поверхности.
Деформа́ция — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга.
Наиболее простые виды деформации тела в целом:
В большинстве практических случаев наблюдаемая деформация представляет собой совмещение нескольких одновременных простых деформаций. В конечном счёте, однако, любую деформацию можно свести к двум наиболее простым: растяжению (или сжатию) и сдвигу.
Растяжение-сжатие — вид продольной деформации стержня или бруса, возникающий в том случае, когда нагрузка прикладывается по продольной оси стержня и проходит через его центр масс.
Сдвиг — вид продольной деформации бруса, возникающий в том случае, если сила прикладывается касательно его поверхности (при этом нижняя часть бруска закреплена неподвижно).
Изгиб — вид деформации, при котором происходит искривление осей прямых брусьев или изменение кривизны осей кривых брусьев.
Кручение —вид деформации тела, возникающий в том случае, если нагрузка прикладывается к телу в виде пары сил (момента) в его поперечной плоскости. При этом в поперечных сечениях тела возникает только один внутренний силовой фактор —крутящий момент.
Упругая деформация — деформация, исчезающая после прекращения действий внешних сил. При этом тело принимает первоначальные размеры и форму.
Пластическая деформация — деформация, не исчезающая или исчезающая не полностью после прекращения действий внешних сил.
Механическое напряжение — это векторная физическая величина, мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов.
Зако́н Гу́ка — уравнение теории упругости, связывающее напряжение и деформацию упругой среды.
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Для тонкого растяжимого стержня закон Гука имеет вид:
Модуль Юнга (модуль упругости) — физическая величина, характеризующая свойства материала сопротивляться растяжению/сжатию при упругой деформации. Назван в честь английского физика XIX века Томаса Юнга. В динамических задачах механики модуль Юнга рассматривается в более общем смысле — как функционал среды и процесса. В Международной системе единиц (СИ) измеряется в ньютонах на метр в квадрате или в паскалях.
Модуль Юнга рассчитывается следующим образом:
Если ввести относительное удлинение
и нормальное напряжение в поперечном сечении
то закон Гука для относительных величин запишется как
В такой форме он справедлив для любых малых объёмов материала.
Также при расчёте прямых стержней применяют запись закона Гука в относительной форме
| текучесть |
| Область пропор- циональности |
| предел упругости |
Коэффициент Пуассона (обозначается как 
или 
) — абсолютная величина отношения поперечной и продольной относительной деформации образца материала. Этот коэффициент зависит не от размеров тела, а от природы материала, из которого изготовлен образец.
,
— коэффициент Пуассона;
— деформация в поперечном направлении (отрицательна при осевом растяжении, положительна при осевом сжатии);
— продольная деформация (положительна при осевом растяжении, отрицательна при осевом сжатии).
При приложении к телу растягивающего усилия оно начинает удлиняться (то есть продольная длина увеличивается), а поперечное сечение уменьшается. Коэффициент Пуассона показывает, во сколько раз поперечная деформация деформируемого тела больше продольной деформации, при его растяжении или сжатии. Для абсолютно хрупкого материала коэффициент Пуассона равен 0, для абсолютно несжимаемого — 0,5. Для большинства сталей этот коэффициент лежит в районе 0,3, для резины он примерно равен 0,5.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10581 – 
| 7334 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Теоретическая механика и сопромат
Свои наблюдения он оформил в виде закона: «Какова сила, таково и удлинение».
Современная формулировка закона существенно отличается от оригинала и зависит от дисциплины, в которой рассматривается зависимость от усилий.
Подробнее про закон Гука смотрите в нашем видео:
В современных учебниках физики Закон Гука имеет вид:
Дифференциальный закон гука
2.1 Внутренние усилия при растяжении и сжатии.
Закон Гука при растяжении и сжатии: абсолютная и относительная деформации, коэффициент Пуассона.
Обобщенный закон Гука: формулы обобщенного закона Гука, относительное изменение объема параллелепипеда.
9.8. Формулы обобщенного закона Гука
Гипотеза пластичности Хубера—Мизеса Согласно этой гипотезе переход тела из упругого состояния в пластическое происходит, когда
достигнет некоторого постоянного значения. Возникает вопрос: почему гипотеза Мизеса, приводящая к более сложному выражению для
, принимается наряду с гипотезой Сен—Венана.
Она достигает максимума при чистом сдвиге, когда
Закон Гука
Сила упругости, возникающая в теле при его деформации, прямо пропорциональна величине этой деформации.
Основные понятия механики сплошных сред
ОСНОВНЫЕ ПОНЯТИЯ МЕХАНИКИ СПЛОШНЫХ СРЕД Основные объекты теоретической механики • Материальная точка • Дискретные системы материальных точек • Абсолютно твердые тела Основные объекты механики сплошных сред • Газообразные среды • Жидкие среды • Твердые деформируемые тела Характеристики сплошных сред • Однородность (неоднородность) относительно некоторого свойства • Изотропность (анизотропность) относительно некоторого свойства Типы сил в механике сплошных сред • Массовые силы действуют на все элементы сплошной среды.
• Поверхностные силы действуют на элемент поверхности, ограничивающей тело, или ограничивающей внутренний элемент среды.
Закон Гука Деформация ε – относительное изменение размеров тела:
Закон гука определение и формула
Министерство образования АР Крым Таврический Национальный Университет им.
Вернадского Исследование физического закона ЗАКОН ГУКА Выполнил: студент 1 курса физического факультета гр.
Ф-111 Потапов Евгений Симферополь-2010 План:
Связь между какими явлениями или величинами выражает закон: Закон Гука связывает такие явления, как напряжение и деформацию твердого тела, модуль силы упругости и удлинение.
Закон Гука
был открыт в XVII веке англичанином Робертом Гуком.
Это открытие о растяжении пружины является одним из законов теории упругости и выполняет важную роль в науке и технике.
Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации. Математическая запись закона выглядит так: Рис. 1. Формула закона Гука где Fупр – соответственно сила упругости, x – удлинение тела (расстояние, на которое изменяется исходная длина тела), а k – коэффициент пропорциональности, называемый жесткостью тела.
Сила измеряется в Ньютонах, а удлинение тела – в метрах.
Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее получив выражение для k. Рис.
Закон Гука для линейных деформаций
, где Е – модуль Юнга или модуль упругости I-го рода, для стали Eст = 2×105 МПа Относительная угловая деформация g — относительный угол деформации, равен изменению прямого угла при приложении нагрузки.
Рис. 4.2 Относительная угловая деформация Закон Гука для угловых деформаций где G – модуль сдвига или модуль упругости II-го рода Упругие постоянные материала связаны зависимостью:
где m — коэффициент Пуассона.
Он равен отношению поперечной деформации
бруса к продольной деформации
, взятого по модулю. mстали = 0,25 –0,35 5. Основные гипотезы,
Обобщенный закон Гука
Законом Гука обычно называют линейные соотношения между компонентами деформаций и компонентами напряжений.
Возьмем элементарный прямоугольный параллелепипед с гранями, параллельными координатным осям, нагруженный нормальным напряжением σх, равномерно распределенным по двум противоположным граням (рис. 1). При этом σy = σz = τхy = τхz = τyz = 0.
Рис. 1 Вплоть до достижения предела пропорциональности относительное удлинение дается формулой где Е — модуль упругости при растяжении.
Для стали Е = 2*105 МПа, поэтому деформации очень малы и измеряются в процентах или в 1*105 (в тензометрических приборах, измеряющих деформации). Удлинение элемента в направлении оси х сопровождается его сужением в поперечном направлении, определяемом компонентами деформаций где μ – константа, называемая коэффициентом поперечного сжатия или коэффициентом Пуассона.
Определение и формула закона Гука
Формулировка этого закона выглядит следующим образом: сила упругости, которая появляется в момент деформации тела, пропорциональна удлинению тела и направлена противоположно движению частиц этого тела относительно других частиц при деформации.
Математическая запись закона выглядит так:
Рис. 1. Формула закона Гука
где Fупр – соответственно сила упругости, x – удлинение тела (расстояние, на которое изменяется исходная длина тела), а k – коэффициент пропорциональности, называемый жесткостью тела. Сила измеряется в Ньютонах, а удлинение тела – в метрах.
Для раскрытия физического смысла жесткости, нужно в формулу для закона Гука подставить единицу, в которой измеряется удлинение – 1 м, заранее получив выражение для k.
Рис. 2. Формула жесткости тела
Эта формула показывает, что жесткость тела численно равна силе упругости, которая возникает в теле (пружине), когда оно деформируется на 1 м. Известно, что жесткость пружины зависит от ее формы, размера и материала, из которого произведено данное тело.
Сила упругости
Теперь, когда известно, какая формула выражает закон Гука, необходимо разобраться в его основной величине. Основной величиной является сила упругости. Она появляется в определенный момент, когда тело начинает деформироваться, например, когда пружина сжимается или растягивается. Она направлена в обратную сторону от силы тяжести. Когда сила упругости и сила тяжести, действующие на тело, становятся равными, опора и тело останавливаются.
Деформация – это необратимые изменения, происходящие с размерами тела и его формой. Они связанны с перемещением частиц относительно друг друга. Если человек сядет в мягкое кресло, то с креслом произойдет деформация, то есть изменятся его характеристики. Она бывает разных типов: изгиб, растяжение, сжатие, сдвиг, кручение.
Так как сила упругости относится по своему происхождению к электромагнитным силам, следует знать, что возникает она из-за того, что молекулы и атомы – наименьшие частицы, из которых состоят все тела, притягиваются друг другу и отталкиваются друг от друга. Если расстояние между частицами очень мало, значит, на них влияет сила отталкивания. Если же это расстояние увеличить, то на них будет действовать сила притяжения. Таким образом, разность сил притяжения и сил отталкивания проявляется в силах упругости.
Сила упругости включает в себя силу реакции опоры и вес тела. Сила реакции представляет особый интерес. Это такая сила, которая действует на тело, когда его кладут на какую-либо поверхность. Если же тело подвешено, то силу, действующую на него, называют, силой натяжения нити.
Особенности сил упругости
Как мы уже выяснили, сила упругости возникает при деформации, и направлена она на восстановление первоначальных форм и размеров строго перпендикулярно к деформируемой поверхности. У сил упругости также есть ряд особенностей.
Применение закона на практике
Закон Гука применяется как в технических и высокотехнологичных устройствах, так и в самой природе. Например, силы упругости встречаются в часовых механизмах, в амортизаторах на транспорте, в канатах, резинках и даже в человеческих костях. Принцип закона Гука лежит в основе динамометра – прибора, с помощью которого измеряют силу.
Что мы узнали?
Статья подробно знакомит учащихся с материалом о том, как формулируется обобщенный закон Гука, который изучают в 7 классе, и его основной величине – силе упругости.