закон ома в комплексной форме для резистивного индуктивного и емкостного элементов
Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элементов
Резистивный элемент. Если ток в резистивном элементе синусоидальный
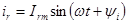
то по закону Ома напряжение, приложенное к элементу равно
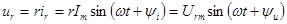
где амплитуды тока и напряжения связаны соотношением
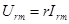
а их начальные фазы одинаковы:
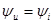
т.е. ток и напряжение в резистивном элементе изменяются синфазно.
Разделив правую и левую части выражения (2.12) на 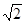
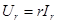
т.е. ток и напряжение в резистивном элементе изменяются синфазно.
Представим синусоидальные ток и напряжение в комплексной форме:
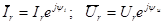
Учитывая (2.13) и (2.14), получим закон Ома в комплексной форме для резистивного элемента:
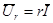
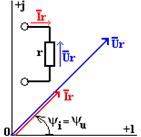
Соотношение между комплексными значениями тока и напряжения для резистивного элемента иллюстрируется векторной диаграммой, приведенной на рис. 2.3.
Индуктивный элемент. Если ток в индуктивном элементе синусоидальный
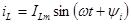
то по закону электромагнитной индукции напряжение на индуктивном элементе равно
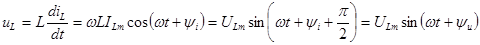
где амплитуды напряжения и тока связаны соотношением
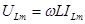
а начальные фазы соотношением
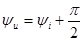
Разделив правую и левую части выражения (2.19) на 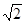
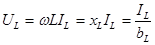
Представим синусоидальные ток iL и напряжение uL индуктивного элемента в комплексной форме:
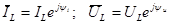
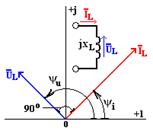
На рис. 2.4 приведена векторная диаграмма для индуктивного элемента. На векторной диаграмме показано, что вектор комплексного значения тока отстает от комплексного значения напряжения на угол π/2.
Пользуясь выражением (2.21) и частными случаями формулы Эйлера
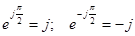
получим закон Ома в комплексной форме для индуктивного элемента:
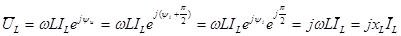
Входящая в полученное выражение величина 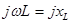
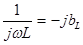
Емкостной элемент. Если напряжение между выводами емкостного элемента изменяется по синусоидальному закону
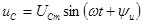
то синусоидальный ток
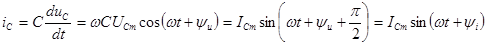
где амплитуды напряжения и тока связаны соотношением
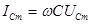
а их начальные фазы – соотношением
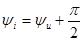
Разделив левую и правую части выражения (2.26) на 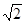
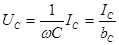
Представим синусоидальные ток и напряжение емкостного элемента соответствующими комплексными значениями:
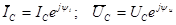
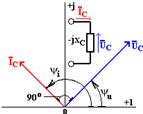
На рис. 2.5 приведена векторная диаграмма для емкостного элемента, из которой видно, что вектор комплексного значения напряжения отстает по фазе от векторного комплексного значения тока на угол π/2.
Учитывая выражения (2.26) и (2.27), получим закон Ома в комплексной форме для емкостного элемента:
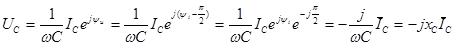
Величина 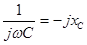
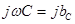
Дата добавления: 2016-02-16 ; просмотров: 6048 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
электрические и магнитные цепи. 1 электротехнические устройства постоянного тока
2.7 ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ ДЛЯ РЕЗИСТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО ЭЛЕМЕНТОВ
Зависимости между токами и напряжениями резистивных, индуктивных и емкостных элементов определяются происходящими в них физическими процессами. Математическое описание физических явлений для каждого из этих элементов зависит от выбранного способа аналитического представления синусоидальных величин. В дальнейшем при аналитическом представлении синусоидальных токов, напряжений и т. д. будем пользоваться как тригонометрическими функциями и для наглядности их графиками, так и комплексными значениями, для которых разработан эффективный математический аппарат анализа электрических цепей.
А. Резистивный элемент. Выберем положительное направление синусоидального тока
в резистивном элементе с постоянным сопротивлением г совпадающим с положительным направлением синусоидального напряжения, приложенного к элементу (рис. 2.13). В этом случае для мгновенных значений напряжения-и тока справедливо соотношение, определяемое аналогично (1.1) законом Ома:
или
где амплитуды тока и напряжения связаны соотношением
Urm=rIrm (2.27а) а их начальные фазы одинаковые:
т. е. ток и напряжение в резистивном элементе изменяются синфазно — совпадают по фазе, как показано на рис. 2.13 для начальной фазы ¥u= ¥i > 0.
Разделив правую и левую части выражения (2.27а) на , получим соотношение для действующих значений напряжения и тока резистивного элемента
Представим теперь синусоидальные ток и напряжение резистивного элемента соответствующими комплексными значениями (2.22):
Так как Ur,=rIr (2.28) и ¥u = ¥1(2.276), то для комплексных значений тока Ir, и напряжения Uг резистивного элемента получим закон Ома в комплексной форме:
Соотношение между комплексными значениями тока и напряжения для резистивного элемента наглядно иллюстрируется векторной диаграммой элемента (рис. 2.14). Из векторной диаграммы также видно, что векторы комплексных значений тока и напряжения резистивного элемента совпадают по фазе.
Б. Индуктивный элемент. Если в индуктивном элементе ток синусоидальный:
то по закону электромагнитной индукции (2.3) на индуктивном элементе появится напряжение
где амплитуды напряжения и тока связаны соотношением
а их начальные фазы — соотношением
Разделив правую и левую части выражения (2.30а) на , получим соотношение для действующих значений напряжения и тока индуктивного элемента:
На рис. 2.15 показан график мгновенных значений синусоидальных тока и напряжения индуктивного элемента (построен при ¥i > 0),
из которого видно, что синусоидальный ток отстает по фазе от синусоидального напряжения
Индуктивное сопротивление пропорционально угловой частоте синусоидального тока, при постоянном токе (w = 0) оно равно нулю. По этой причине многие аппараты и машины, предназначенные для работы в цепи переменного (синусоидального) тока, нельзя включать в цепь постоянного тока. Для постоянного тока их сопротивление относительно мало, и большой постоянный ток может быть для них разрушительным (например, для первичной обмотки трансформатора в радиоприемнике).
Представим синусоидальные ток il и напряжение ul индуктивного элемента соответствующими комплексными значениями:
На рис. 2.16 приведена векторная диаграмма для индуктивного элемента. На векторной диаграмме показано, что вектор комплексного значения тока /, отстает по фазе от вектора комплексного значения напряжения ULна угол п/2, что соответствует сдвигу фаз ф = я/2 на рис. 2.15. Пользуясь выражениями (2.31) и (2.26), получим закон Ома в комплексной форме для индуктивного элемента;
Входящая в это выражение величина iwL=ixL называется комплексным сопротивлением индуктивного элемента, а обратная ей величина I/iwL =-ibL — комплексной проводимостью индуктивного элемента.
Комплексное значение напряжения на индуктивном элементе можно выразить и через комплексное значение потокосцепления.
Из (2.1) следует, что ¥ = LiL, и по (2.32)
Это — математическая формулировка закона электромагнитной индукции (2.3) в комплексной форме.
В. Емкостный элемент. Если напряжение между выводами емкостного элемента изменяется по синусоидальному закону:
то по (2.11) синусоидальный ток
где амплитуды связаны соотношением
а начальные фазы соотношением
Разделив правую и левые части выражения (2.34а) на , получим соотношение для действующих значений напряжения и тока емкостного элемента:
На рис. 2.17 показан график мгновенных значений синусоидальных напряжения и тока для емкостного элемента (построен при ¥u > 0), из которого видно, что синусоидальное напряжение uсотстает по фазе от синусоидального тока iс на угол ¥u-¥n = п /2, т. е. сдвиг по фазе между напряжением и током ¥ = ¥u-¥i=- п /2.
Представим синусоидальные ток iс и напряжение uс емкостного элемента соответствующими комплексными значениями:
На рис. 2.18 приведена векторная диаграмма для емкостного элемента. На векторной диаграмме показано, что вектор комплексного значения напряжения uс отстает по фазе от вектора комплексного значения тока ic на угол п /2.
Учитывая (2.34) и (2.26), получим закон Ома в комплексной форме для емкостного элемента:
Величина 1/iwС =-ixс, входящая в это выражение, называется комплексным сопротивлением емкостного элемента, а обратная ей величина iwС = iЬС — комплексной проводимостью емкостного элемента.
2.8 ЗАКОНЫ КИРХГОФА ДЛЯ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
Математическая формулировка двух законов Кирхгофа для цепей синусоидального тока зависит от выбранного вида представления синусоидальных величин. Будем далее пользоваться для аналитического представления синусоидальных величин тригонометрическими функциями и соответствующими им комплексными значениями. При первом виде представления законы Кирхгофа определяют зависимость между мгновенными значениями соответствующих синусоидальных величин (для любого момента времени). При втором виде представления законы Кирхгофа определяют зависимость между комплексными значениями соответствующих синусоидальных величин.
∑ n R=1 ImRsin(wt+¥iR)=0 (2.38)
где п — число ветвей, сходящихся в узле. В дальнейшем все синусоидальные токи, положительные направления которых выбраны к узлу (от узла), будем записывать со знаком плюс (минус).
На рис. 2.19 в качестве примера для одного из узлов построены мгновенные. значения трех синусоидальных токов:
при выбранных положительных направлениях. По первому закону Кирхгофа
для любого момента времени.
Чтобы получить математическую формулировку первого закона Кирхгофа в комплексной форме, представим все синусоидальные токи в (2.38) соответствующими им комплексными значениями (2.21): iR=Ir¥iR

Рис. 2.19. Рис. 2.20.
Первый закон Кирхгофа в комплексной форме записывается следующим образом:
(2.39)
т. е. алгебраическая сумма комплексных значений токов всех ветвей, сходящихся в каком-либо узле электрической цепи синусоидального тока, равна нулю. Здесь комплексные значения токов, для которых положительные направления выбраны к узлу (от узла), записываются со знаком плюс (минус).
На рис. 2.20 построена векторная диаграмма трех токов: I1=i1¥ На векторной диаграмме должно выполняться равенство

Б. Второй закон Кирхгофа. По второму закону Кирхгофа алгебраическая сумма напряжений на резистивных, индуктивных и емкостных элементах, т. е- на пассивных элементах, в любом контуре электрической цепи в каждый момент времени равна алгебраической сумме ЭДС этого контура. В цепях синусоидального тока значения различных ЭДС и значения напряжений на пассивных элементах любого контура непрерывно изменяются. Но тем не менее алгебраические суммы мгновенных значений напряжений и ЭДС одинаковы:
где пи m — соответственно числа пассивных элементов и ЭДС в контуре. В выражении (2.40.) будем считать, что все синусоидальные напряжения иьи ЭДС е. для которых положительные направления совпадают с произвольно выбранным направлением обхода контура, записываются со знаком плюс и в противном случае — со знаком минус. Например, для контура на рис. 2.21 с направлением, обхода по направлению движения часовой стрелки по второму закону Кирхгофа
Чтобы получить математическую формулировку второго закона Кирхгофа в комплексной форме, представим все синусоидальные напряжения и,, и ЭДС ей в (2.40) соответствующими комплексными значениями (2.21):
Второй закон Кирхгофа в комплексной форме записывается следующим образом:

т. е. алгебраическая сумма комплексных значений напряжений на всех пассивных элементах (резистивных, индуктивных, емкостных) какого-либо контура электрической цепи синусоидального тока равна алгебраической сумме комплексных значений всех ЭДС этого контура. Здесь комплексные значения напряжений и ЭДС, положительные направления которых совпадают с произвольно выбранным направлением обхода контура, записываются со знаком плюс и в противном случае — со знаком минус.
Например, для контура рис. 2.21, показанного еще па рис. 2.22, а, по второму закону Кирхгофа в комплексной форме
На рис. 2.22, б построена векторная диаграмма ЭДС и напряжений для этого контура, которая наглядно иллюстрирует второй закон Кирхгофа в комплексной форме.
2.9 КОМПЛЕКСНЫЙ МЕТОД АНАЛИЗА ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА
В § 2.7 было показано, что между мгновенными значениями синусоидальных величин (2.20) и их комплексными значениями (2.21) существует взаимно однозначное соответствие. Поэтому для описания режима работы цепи синусоидального тока можно применять любой из этих видов представления синусоидальных величин. Однако в случае представления синусоидальных величин комплексными значениями законы Ома для резистивных (2.29), индуктивных (2.32) и емкостных (2.36) элементов, первый (2.39) и второй (2.41) законы Кирхгофа записываются в виде алгебраических, а не дифференциальных уравнений. Совместное решение алгебраических уравнений для определения комплексных значений токов и напряжений всех элементов электрической цепи, т. е. применение комплексного метода расчета, — достаточно простая задача. По найденным комплексным значениям можно сразу записать при необходимости и соответствующие им мгновенные значения синусоидальных величин.
При расчете режима работы электрической цепи синусоидального тока комплексным методом полезно выделить несколько логически самостоятельных этапов:
1) Представить исходные данные о параметрах всех элементов анализируемой цепи в комплексной форме. Это означает, что, во-первых, синусоидальные ЭДС или токи источников энергии, заданные мгновенными значениями (в тригонометрической форме), следует представить комплексными значениями (табл. 2.3) и, во-вторых, для индуктивных и емкостных элементов цепи определить соответствующие комплексные сопротивления или комплексные проводимости (табл. 2.4).
2) Выбрать положительные направления для токов во всех ветвях, указав их стрелками на схеме цепи.
3) Пользуясь законами Ома и Кирхгофа в комплексной форме и учитывая выбранные положительные направления токов в ветвях, составить систему уравнений, определяющую режим работы цепи.
Таблица 2.3. Представление мгновенных значений синусоидальных ЭДС и токов источников комплексными значениями
4) Решить полученную систему уравнений, т. е. определить комплексные значения токов в ветвях цепи и комплексные значения напряжений на ее элементах.
Найденные комплексные значения токов и напряжений однозначно определяют соответствующие им мгновенные значения синусоидальных токов и напряжений.
.В качестве примера рассмотрим анализ (расчет режима работы) комплексным методом электрической цепи синусоидального тока по рис. 2.23, а с источником ЭДС и источником тока положительные направления которых заданы, а также с резистивным г, индуктивным Ь и емкостным С элементами. Для этого выполним последовательно все этапы анализа.
Определим комплексные сопротивления индуктивного jwL=jxL и емкостного 1/jwC = — jхс. элементов электрической цепи (см. табл. 2.4)
На рис. 2.23, б изображена схема электрической цепи, соответствующая схеме электрической цепи рис. 2.23, а, но для которой исходные данные о параметрах всех элементов представлены в комплексной форме.
2. Выберем положительные направления неизвестных токов в ветвях (рис. 2.23, а) и положительные направления напряжений на пассивных элементах совпадающими с направлениями токов. Положительные направления соответствующих им комплексных значений такие же (рис. 2.23, б).
3. При выбранных положительных направлениях токов и напряжений составим полную систему уравнений для анализа цепи. Так как у цепи три узла (а, Ь, с), то по первому закону Кирхгофа в комплексной форме (2.39) составим уравнение для двух узлов, например а и Ь:
Цепь имеет три контура-ячейки, т. е. в общем случае по второму закону Кирхгофа следовало бы составить три независимых уравнения. Но так как в верхнем контуре действует источник тока, т. е. в этом контуре ток ^ известен, то составляем уравнения только для двух других контуров, обозначенных на рис. 2.23, б цифрами 1и 2:
По закону Ома в комплексной форме для резнстнвного (2.29), индуктивного (2.32) и емкостного (2.36) элементов электрической цепи
Следовательно, уравнения (2.42в) и (2.42г) можно записать в виде
Для найденных комплексных значений тока запишем соответствующие им мгновенные значения:
Комплексные значения напряжения определяются по 2.10 НЕРАЗВЕТВЛЕННАЯ ЦЕЛЬ СИНУСОИДАЛЬНОГО ТОКА
В неразветвленной цепи (рис. 2.24) при действии источника синусоидальной ЭДС
ток также синусоидален:
и напряжения на резистивном, индуктивном и емкостном элементах:
Для расчета режима неразветвленной цепи синусоидального тока применим комплексный метод. Представим все синусоидальные величины соответствующими комплексными значениями по (2.21):
Выберем направление обхода контура по направлению движения часовой стрелки и запишем уравнение по второму закону Кирхгофа (2.41):
здесь учтен закон Ома для резистивного (2.29), индуктивного (2.32) и емкостного (2.36) элементов.
Из (2.43). найдем комплексный ток в цепи:
напряжение между выводами неразветвленной цепи (рис. 2.24).
Величина, стоящая в знаменателе выражения для комплексного тока (2.44), называется комплексным сопротивлением(неразветвленной цепи):
Каждому значению комплексного сопротивления 2, т. е. комплексному числу, соответствует точка на комплексной плоскости. Ее положение однозначно определяется вектором на комплексной плоскости (рис. 2.25). Этот вектор является геометрической интерпретацией комплексного сопротивления и имеет такое же обозначение 7,.
Слагаемые комплексного сопротивления изображены на рис. 2.25 также в виде векторов для двух случаев: хLxс (рис. 2.25,о) и хLxс (рис. 2.25, б). В первом случае комплексное сопротивление имеет индуктивный характер, во втором — емкостный. Геометрическая интерпретация комплексного сопротивления позволяет легко перейти от алгебраической формы записи комплексного сопротивления (2.45 а) к тригонометрической и показательной формам:
ного сопротивления. В зависимости от знака величины аргумент комплексного сопротивления может быть либо положительным (индуктивный характер), либо отрицательным (емкостный характер),
Подставим значение комплексного сопротивления в показательной форме (2.45в) в (2.44). При этом ток в цепи будет определен по закону Ома для неразветвленной цепи:
Если значения параметров резистивного, индуктивного и емкостного элементов известны и задано напряжение между выводами неразветвленной цепи (рис. 2.24), то по закону Ома для неразветвленной цепи (2.46) однозначно определяется комплексный ток в цепи. При известном комплексном токе в цени комплексные напряжения на ре-зистивном, индуктивном и емкостном элементах рассчитываются соответственно по (2.29), (2.32), (2.36).
На рис. 2.26 приведены векторные диаграммы тока и напряжений неразветвленной цепи (рис. 2.24) для двух случаев: (рис. 2.26, а) (рис. 2.26, б) при одинаковом заданном напряжении. Если комплексное сопротивление цепи имеет индуктивный характер, то ток / отстает по фазе от напряжения U, так как ф > 0 (рис. 2.25, а) к по (2.47) ¥i 0, т. е. при индуктивном характере комплексного сопротивления, а на рис. 2.27, б — при х 2.14 ЭЛЕКТРИЧЕСКАЯ ЦЕПЬ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ВЕТВЕЙ
На рис. 2.33 представлена схема электрической цепи, состоящей из параллельного соединения резистивного, индуктивного и емкостного элементов. Будем считать заданными проводимость резистивного элемента комплексные проводимости ипдуктив и емкостного И элементов и одинаковое напряжение на каждом из элементов
о первому закону Кирхгофа определим комплексное значение общего тока, равного току источника ЭДС:
где учтено, что по [закону Ома Iг = qU; Iь =-jblU комплексы токов в резистивиом, индуктивном и емкостном элементах. Сумма комплексных проводимостей всех параллельных ветвей в выражении (2.61) равна комплексной проводимости данной цепи (в алгебраической форме):
Обратная величина комплексной проводимости 1/Y = Z = Rе-это комплексное сопротивление. Поэтому в показательной форме комплексная проводимость
и в тригонометрической форме
цепи или ‘полная проводимостьцепи;
На комплексной плоскости (рис. 2.34) слагаемые комплексной про-,Мост1 цепи изображены в виде векторов для двух случаев: Ь, >• Ьс (рис2 34 а) Ь, >• Ь (рис. 2.34, б). В первом случае комплексная проводимость цепи индуктивный характер, во втором емкостный.
Подставив значение комплексной проводимости цепи в показательной форме (2.63а) в (2.61), получим комплексное значение тока в виде
Из (2.64) следует, что действующее значение тока в неразветвленной части цепи
|Если электрическая цепь содержит несколько резистивных, индуктивных и емкостных элементов, включенных параллельно, то комплекс-
ЭДС Е источника, а тока в индуктивном элементе не было. Поэтому
Подставим эти значения в (5.32а) а учтем, что по формуле Эйлера (2.25>
В результате получим зависимость изменения напряжения на емкостном элементе от времени в виде
Сумму косинусоидальной и синусоидальной функций можно заменить одной синусоидальной функцией. Для этого положим, что отношение w0/ б =tqф т.е.- будем считать, что wи б — катеты прямоугольного треугольника (рис. 5.7), гипотенуза которого
Разделив и умножив (5.33) на 1/LC, получим:
и по (5.27) разрядный ток
Зависимости (5.34) и (5.35) показывают, что напряжение емкостного элемента И разрядный ток можно рассматривать как синусоидально изменяющиеся во времени величины, но с амплитудами, уменьшающимися по экспоненциальному закону при постоянной времени т= 1/6= 21./г.
Для построения соответствующих зависимостей можно сначала построить вспомогателыне экспоненты
Кривые изменения напряжения и тока (рис. 5.И) должны вписаться в пределы, ограниченные указанными вспомогательными экспонентами. Для нахождения характерных точек кривой изменения напряжения на емкостном элементе, таких как ис(0) = Е и «с (0 = 0, на рисунке показана точками вспомогательная кривая —
Рассмотрим теперь случай действительных отрицательных корней р1Лхарактеристического уравнения (5.29).
Если г 2 / 4L 2 > 1/LС, то действительные корни имеют различные значения, причем р2 2 / 4L 2 =1/LС, характеристическое уравнение имеет два одинаковых действительных корня р1=р2=р= —г/2L (кратные корни). При кратных корнях общее решение дифференциального уравнения (5.28) отличается от (5.30) и имеет вид:
где постоянные А1 и А2определяются на основании законов коммутации. Зависимости напряжения на емкостном элементе и тока для предельного апериодического процесса разрядки
5.6. ПОДКЛЮЧЕНИЕ НЕРАЗВЕТВЛЕННОИ ЦЕПИ С ИНДУКТИВНЫМ, РЕЗИСТИВНЫМ И ЕМКОСТНЫМ ЭЛЕМЕНТАМИ К ИСТОЧНИКУ ПОСТОЯННОЙ ЭДС
Для неразветвленной цени с индуктивным, резистнвным и емкостным элементами и источником постоянной ЭДС (рис. 5. 10, а) дифференциальное уравнение цепи неодно родное. Поэтому переходный процесс можно рассматривать как наложение у ста но вившегося и свободного процессов. Так, для напряжения на емкостном элементе
где составляющая свободного процесса совпадает с (5.30), а составляющая установившегося процесса ис = Е, т. е. общее решение для напряжения
а зарядный ток
До замыкания ключа напряженения на емкостном элементе и тока в цепи не было. Поэтому в соответствии с законами коммутации получим для момента включения ключа (t= 0) два уравнения для определения двух постоянных А <и Аа:
Ограничимся здесь анализом колеба- Рис. 5.10. тельного (5.31) процесса зарядки. Выпол-
нив преобразования, аналогичные переходу от (5.33) к (5.34), получим зависимости изменения во времени напряжения на емкостном элементе и зарядного тока (рис. 5.10,6):
Напряжение на емкостном элементе достигает наибольшего значения в момент времени Оно тем больше, чем постоянная времени т = 1/6 больше периода собственных колебаний Тй = 2л/и0, и в пределе может превышать почти в 2 раза установившееся напряжение. Такое перенапряжение может быть опасно для изоляции высоковольтных установок. Чтобы исключить перенапряжение, нужно осуществить апериодический режим зарядки, например включить последовательно в цепь добавочный резистор.
1.7. ПОДКЛЮЧЕНИЕ ПОСЛЕДОВАТЕЛЬНОГО СОЕДИНЕНИЯ ИНДУКТИВНОГО И РЕЗИСТИВНОГО ЭЛЕМЕНТОВ К ИСТОЧНИКУ СИНУСОИДАЛЬНОЙ ЭДС
В цепи, состоящей из последовательно соединенных индуктивного элемента I. и резистивного элемента с сопротивлением г (рис. 5.11, а) и подключенной к источнику синусоидальной ЭДС при установившемся режиме синусоидальной ток (см. § 2.11)
где амплитуда тока аргумент комплексного сопротивления цепи; — начальная фаза ЭДС источника.
Дифференциальное уравнение цепи первого порядка такое же, как (5.3):
Поэтому свободная составляющая тока 1СВ = АеР’ и общее решение!
На основании закона коммутации для индуктивного элемента (5.1) а момент коммутации (1= 0)
Подставив значение постоянной в общее решение, найдем зависимость тока от времени:
где т=L/r— постоянная времени цепи.
Таким образом, во время переходного процесса ток в цепи состоит из синусоидальной составляющей и свободной составляющей, убывающей экспоненциально
(рис. 5.11,6). Практически через интервал времени Зт после замыкания ключа свободной составляющей можно пренебречь.
Если момент коммутации (/= 0) выбран так, что начальная фаза напряжения источника >|>н = ф, то свободная составляющая тока равна нулю, т. е. переходного процесса нет и в цепи сразу устанавливается» синусоидальный ток.
Ток в цепи во время переходного процесса может достигнуть максимального значения, почти в 2 раза превышающего амплитуду 1т синусоидальной составляющей. Если постоянная времени велика по сравнению с периодом синусоидальной составляющей
тока и начальная фаза напряжения источника, то примерно наибольшее значение свободной составляющие тока равно /„, и в момент времени /=в Т/2 значение тока близко к 2/ш.
Аналогично рассчитывается переходный процесс при подключении источника синусоидального напряжения к цепи с последовательно соединенными резистивлым и емкостным элементами и в других случаях. И здесь переходный процесс зависит от начальной фазы напряжения источника: он отсутствует при, где, и выражен наиболее сильно при % = ф, когда максимальное напряжение на емкостном элементе может почти н 2 раза превысить амплитуду установившегося напряжения. Такое перенапряжение может привести к пробою изоляции в высоковольтных установках.
5.8. ГЕНЕРАТОР ПИЛООБРАЗНОГО НАПРЯЖЕНИЯ
Переходный процесс служит основным рабочим режимом электрической цепи во многих электротехнических устройствах, например в генераторах пилообразного напряжения. Такие генераторы применяются, например, в электронных осциллографах для развертки осциллограммы вдоль оси абсцисс— оси времени. На рис. 5. 12, а приведена простейшая схема генератора пилообразного напряжения. При замыкании ключа К в момент времени (0=0 к цепи, состоящей из последовашльно соединенных резистивного т и емкостного С
элементов. подключается источник постоянного напряжения Е. Ветвь с резистивным элементом К отключена, так как нет разряда между электродами газоразрядной лампы. В цепи возникает переходный процесс (см. рис. 5.4б), при котором напряжение на емкостном элементе нарастает по закону (5.22)
В момент времени t=t1, напряжение на емкостном элементе достигает значения Uзаж — напряжения зажигания газоразрядной лампы и емкостный элемент начинает разряжаться (рис. 5.12, б)
Если время зарядки емкостного элемента значительно меньше постоянной времени т = гС, то можно приближенно считать, что скорость изменения напряжения ыс постоянная и равна;
Изменяя значения параметров г и С зарядной цепи, можно регулировать параметры пилообразных импульсов, т. е. линейность нарастания напряжения нс и дли-