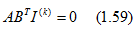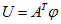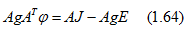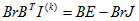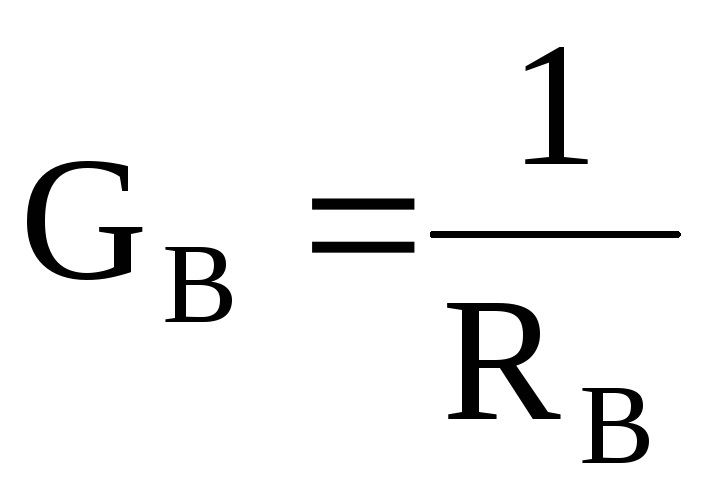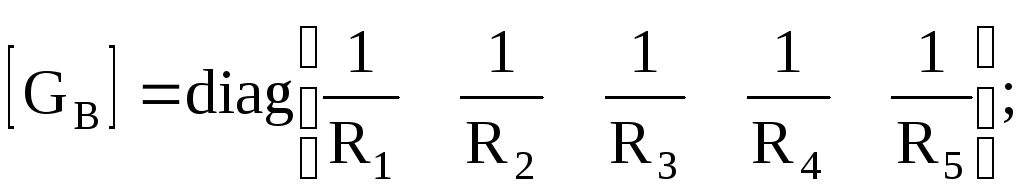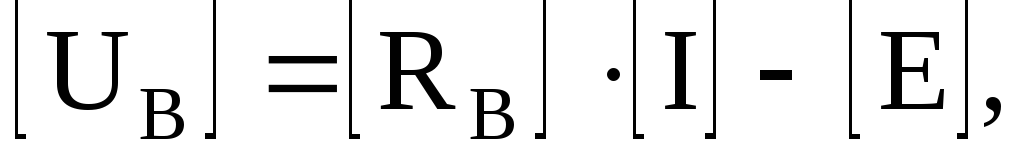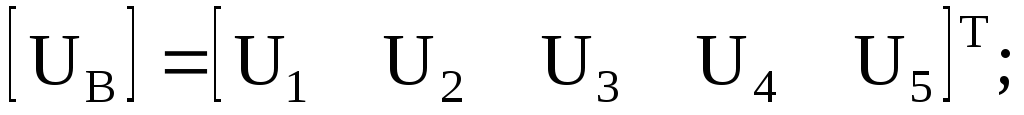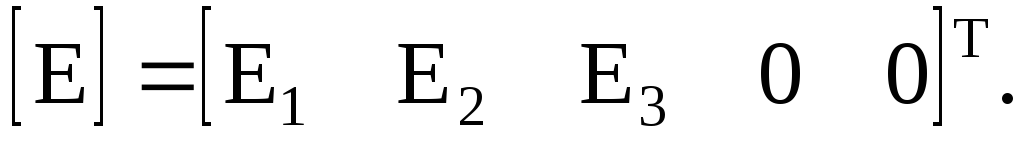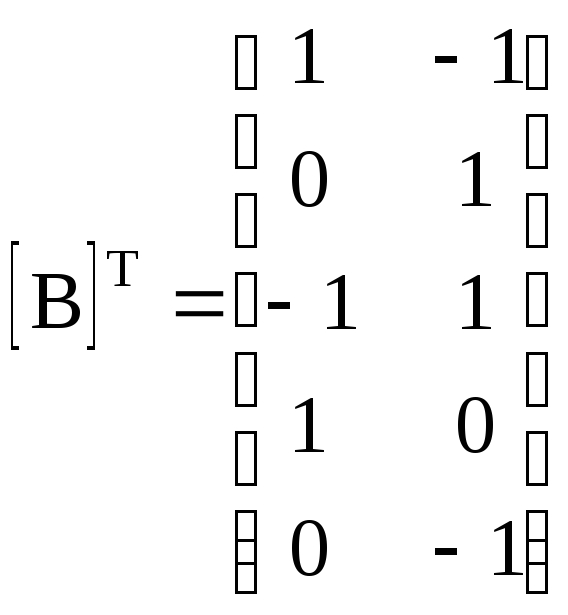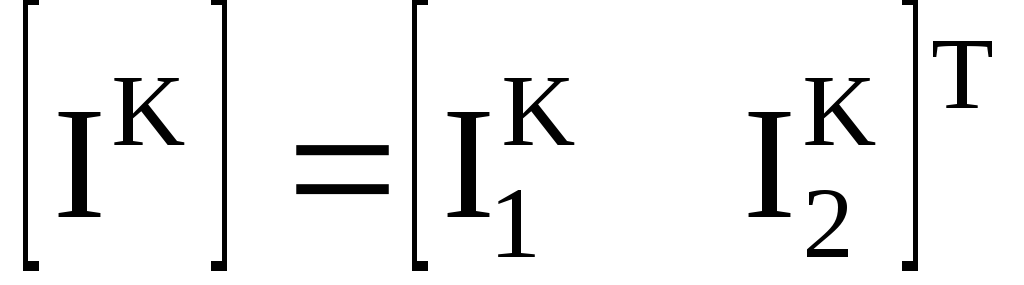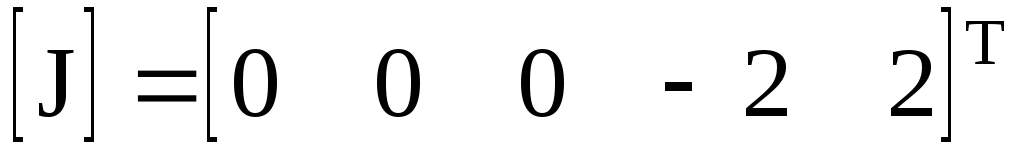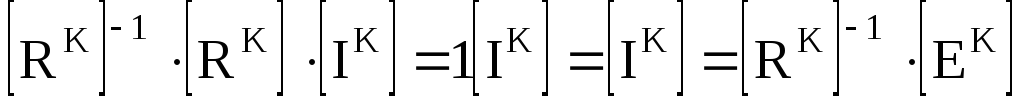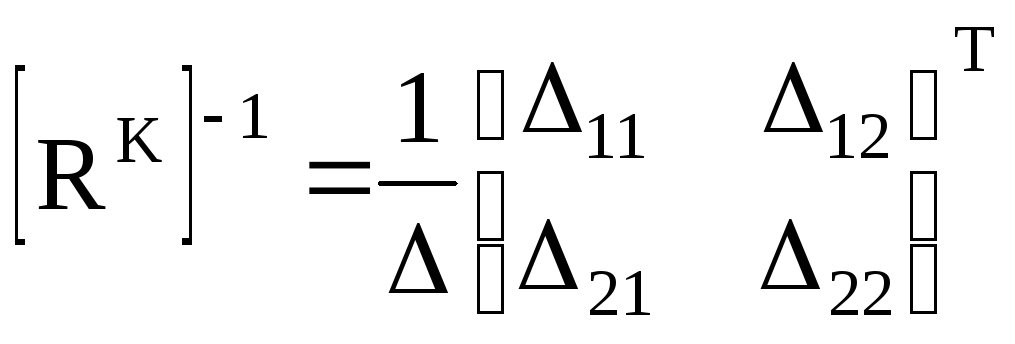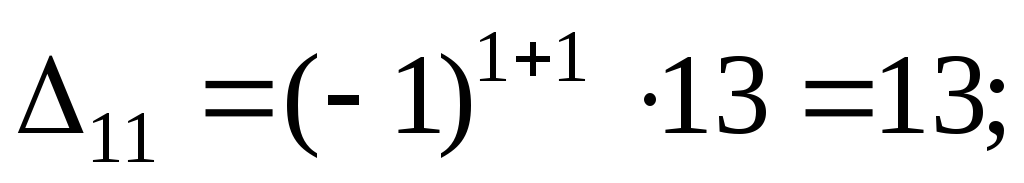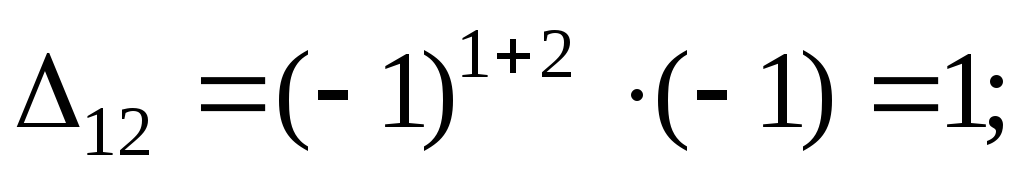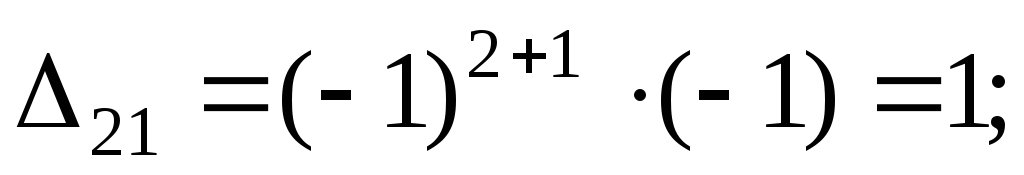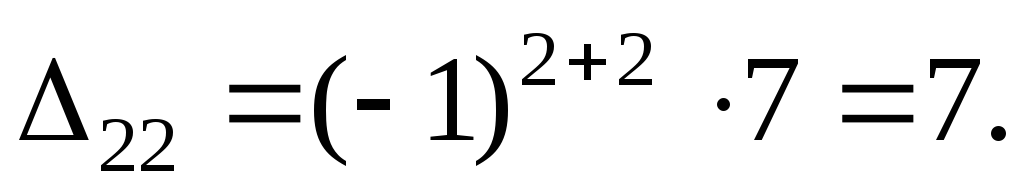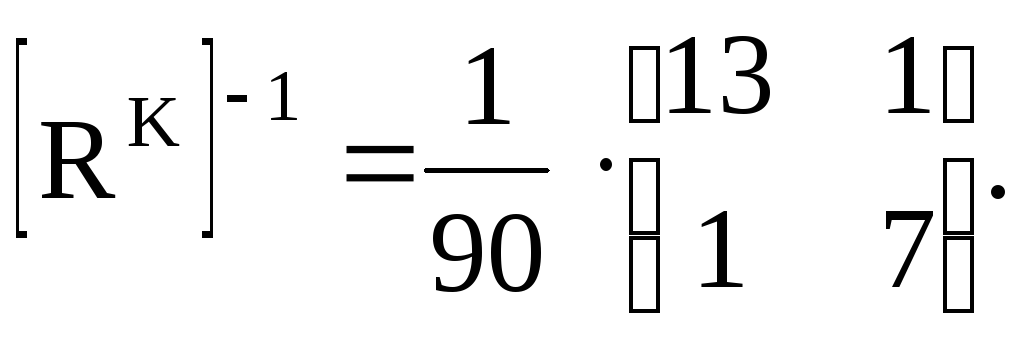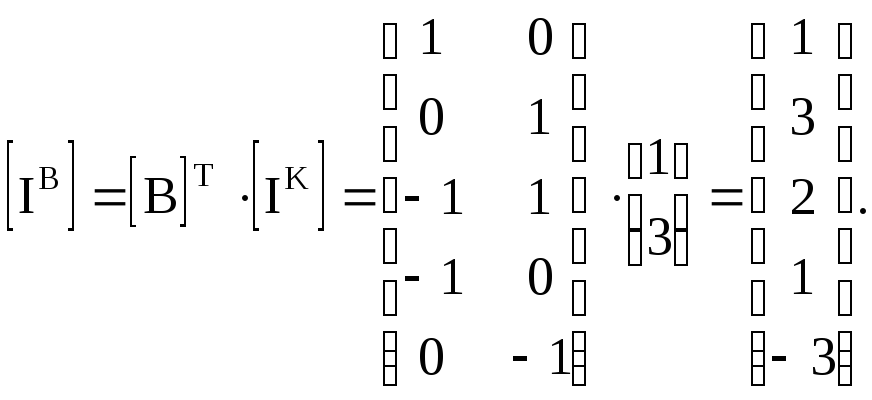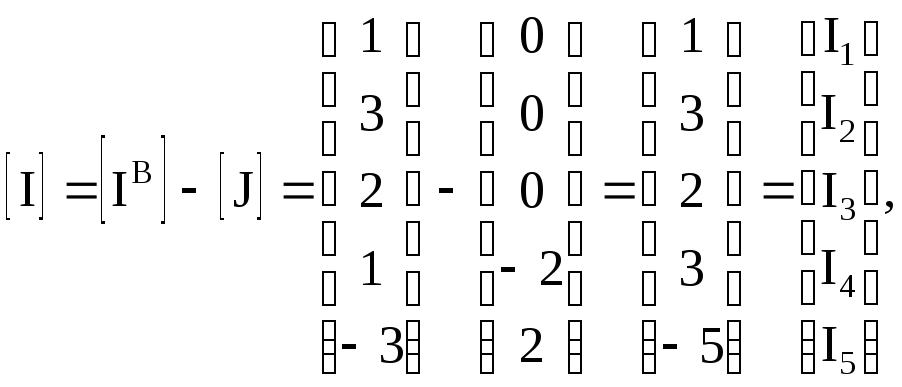закон ома в матричной форме
Закон ома в матричной форме
Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.
Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.
Подставив (2) в (1), получим:
 . . | (3) |
Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).
Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства
где Z – диагональная квадратная (размерностью матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.
Соотношение (4) представляет собой матричную запись закона Ома.
Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому
 , , | (5) |
 , , | (6) |
то есть получили новую запись в матричной форме второго закона Кирхгофа.
Метод контурных токов в матричной форме
В соответствии с методов контурных токов токи всех ветвей могут быть выражены как линейные комбинации контурных токов или в рассматриваемом случае токов ветвей связи. Если элементы j –го столбца матрицы В умножить соответствующим образом на контурные токи, то сумма таких произведений и будет выражением тока j –й ветви через контурные токи (через токи ветвей связи). Сказанное может быть записано в виде матричного соотношения
С учетом (8) соотношение (7) можно записать, как:
 | (9) |
Полученное уравнение представляет собой контурные уравнения в матричной форме. Если обозначить
то получим матричную форму записи уравнений, составленных по методу контурных токов:
В развернутой форме (12) можно записать, как:
 , , | (13) |
то есть получили известный из метода контурных токов результат.
Рассмотрим пример составления контурных уравнений.
Пусть имеем схему по рис. 2. Данная схема имеет четыре узла ( m =4) и шесть обобщенных ветвей ( n =6). Число независимых контуров, равное числу ветвей связи,
Граф схемы с выбранным деревом (ветви 1, 2, 3) имеет вид по рис. 3.
Запишем матрицу контуров, которая будет являться матрицей главных контуров, поскольку каждая ветвь связи входит только в один контур. Принимая за направление обхода контуров направления ветвей связи, получим:
B
Диагональная матрица сопротивлений ветвей
Z
Матрица контурных сопротивлений
Zk=BZB T
Матрицы ЭДС и токов источников
 |  |
 |  |
Тогда матрица контурных ЭДС
Матрица контурных токов
Таким образом, окончательно получаем:
Анализ результатов показывает, что полученные три уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу контурных токов.
Метод узловых потенциалов в матричной форме
На основании полученного выше соотношения (4), представляющего собой, как было указано, матричную запись закона Ома, запишем матричное выражение:
Умножив обе части равенства (14) на узловую матрицу А и учитывая первый закон Кирхгофа, согласно которому
Выражение (16) перепишем, как:
Тогда получаем матричное уравнение вида:
Данное уравнение представляет собой узловые уравнения в матричной форме. Если обозначить
то получим матричную форму записи уравнений, составленных по методу узловых потенциалов:
 | (22) |
В развернутом виде соотношение (22) можно записать, как:
 | (23) |
то есть получили известный из метода узловых потенциалов результат.
Рассмотрим составление узловых уравнений на примере схемы по рис. 4.
А
Диагональная матрица проводимостей ветвей:
Y
Матрица узловых проводимостей
Матрицы токов и ЭДС источников
 |  |
 |  |
Следовательно, матрица узловых токов будет иметь вид:
Таким образом, окончательно получаем:
Анализ результатов показывает, что полученные уравнения идентичны тем, которые можно записать непосредственно из рассмотрения схемы по известным правилам составления уравнений по методу узловых потенциалов.
Контрольные вопросы и задачи
Трансформаторные подстанции высочайшего качества
с нами приходит энергия
develop@websor.ru
Уравнения цепи в матричной форме
Пользуясь матрицей соединений А и матрицей контуров В, а также законами Кирхгофа, можно получить узловые и контурные уравнения, определяющие режим цепи, в матричной форме, при этом получаются и выражения для определения матрицы узловых проводимостей (1.39), и матрицы контурных сопротивлений (1.53).
Запишем еще раз в матричной форме первый и второй законы Кирхгофа (1.26) и (1.27):
AI = 0; BU = 0, (1.58)
где I — матрица-столбец токов ветвей; U — матрица-столбец напряжений между концами ветвей.
Подставив (1.57) в (1.58), получим
Это выражение справедливо при всех значениях 
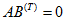
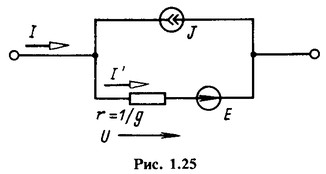
Уравнения цепи в матричной форме, в том числе с узловыми потенциалами и контурными токами, получаются наиболее коротким путем при введении понятия обобщенной ветви — двухполюсника общего вида (рис. 1.25). Для такой ветви I’ = I + J и U = rI’ — Е, откуда следует, что
Это так называемые компонентные уравнения (связывают напряжение и ток ветви).
В матричной форме для всех ветвей схемы вместо (1.60) и (1.61) получим обобщенный закон Ома
где g — диагональная матрица проводимостей ветвей; r — диагональная матрица сопротивлений ветвей.
Уравнения Кирхгофа (1.58) — топологические уравнения — вместе с компонентными уравнениями (1.62) или (1.63) составляют полную систему уравнений линейной электрической цепи в матричной форме.
Для получения узловых уравнений в матричной форме умножим (1.62) на матрицу А
AI = AgU + AgE — AJ = 0
и после замены по (1.40)
где 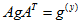
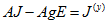
Для получения контурных уравнений в матричной форме умножим (1.63) на матрицу В
и так как BU = 0 (второй закон Кирхгофа) и 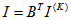
3.4. Матричная форма записи законов Ома и Кирхгофа
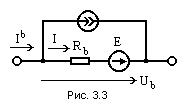
Сначала введем понятие обобщенной ветви (рис. 3.3).Для нее можно записать по первому закону Кирхгофа
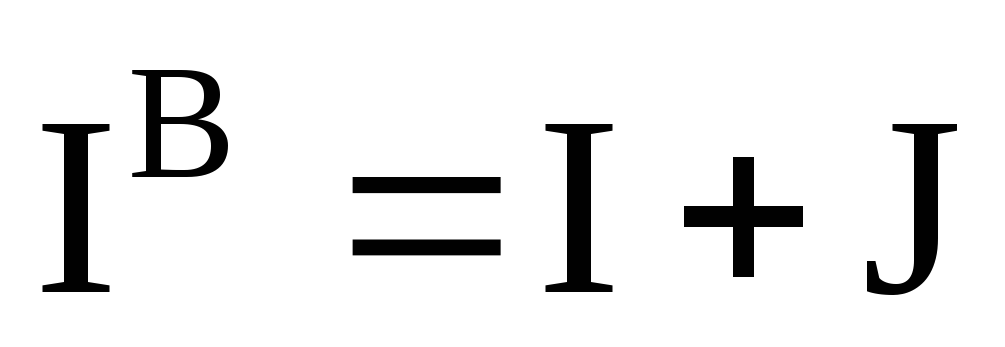
И по обобщенному закону Ома
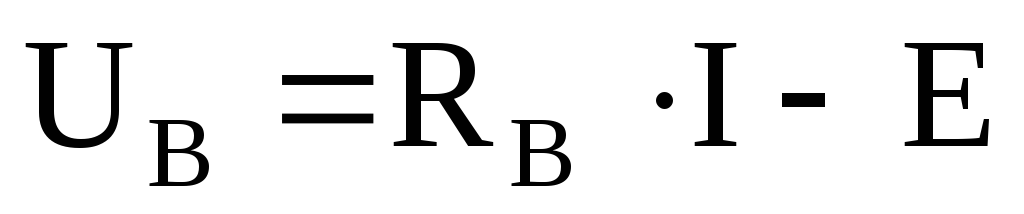
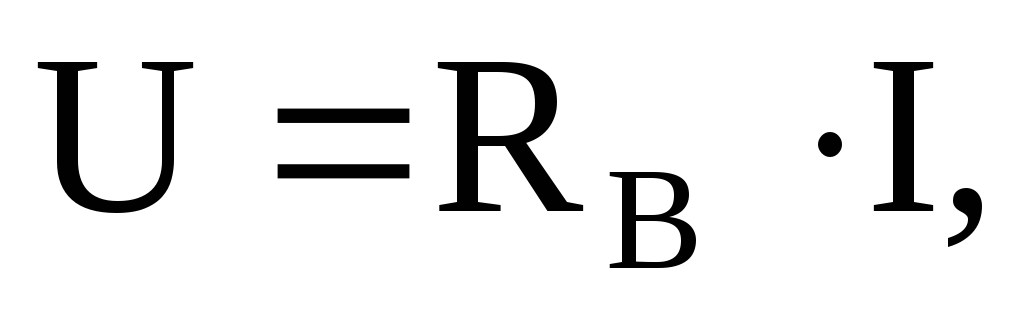
Или для тока через проводимость ветви
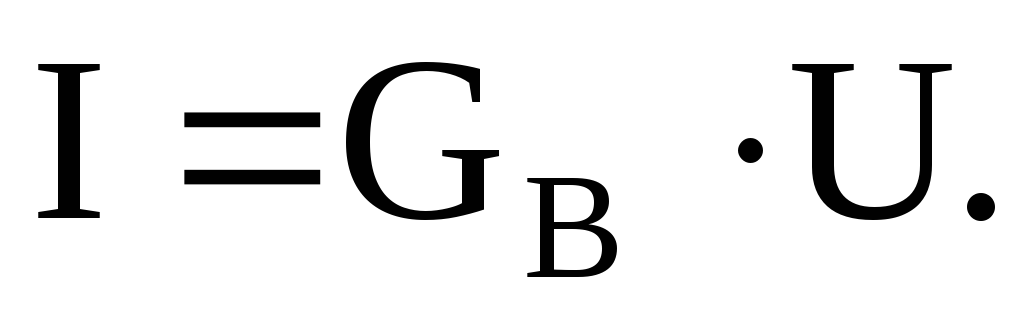
Закон Ома в матричной форме
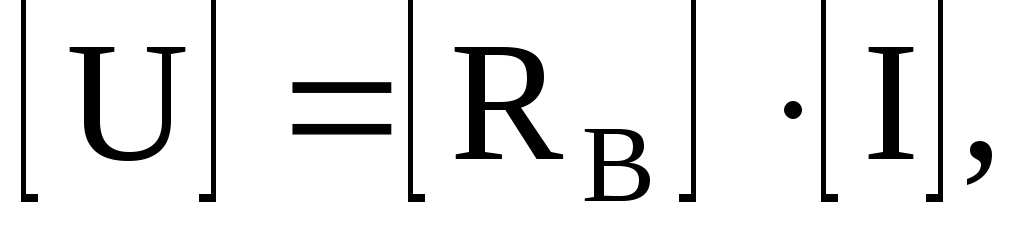

где U и I – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы, а
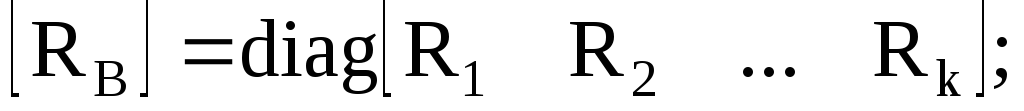
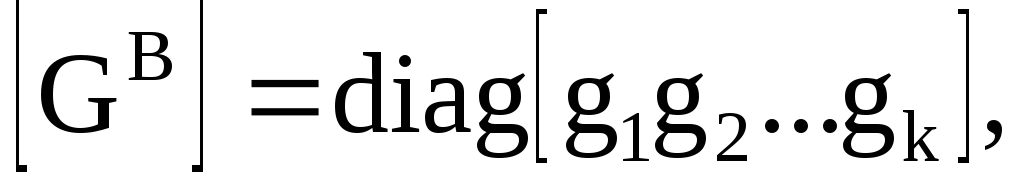
Например, для схемы рис. 3.1

Обобщенный закон Ома в матричной форме, исходя из (3.7), получим в виде
где U в и I в – столбцовые матрицы, число строк которых совпадает с числом ветвей схемы.
Вводится понятие узловой матрицы [А].
Узловая матрица – это прямоугольная матрица, строки которой соответствуют узлам, а столбцы – ветвям направленного графа схемы.
Число строк матрицы равно числу независимых узлов. Элементы матрицы а ij, где (i – номер строки, j – номер столбца, принимают значения 1, – 1 или 0.
Элементы а ij = 1, если ветвь j соединена с узлом i и направлена от него.
Например, в схеме рис. 3.1 и 3.2
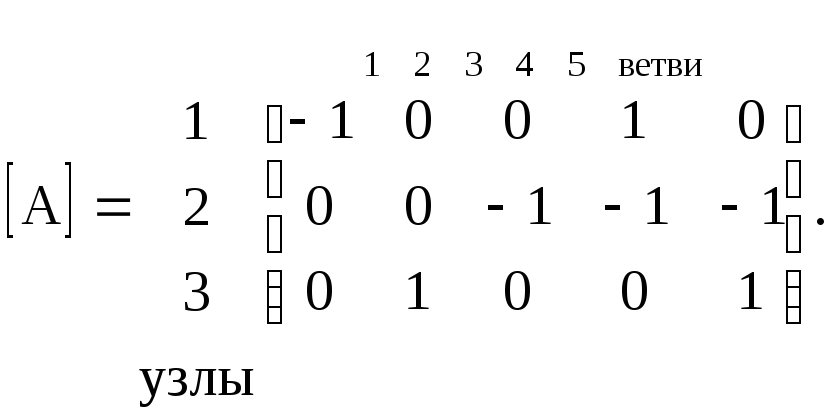
С помощью матрицы [А] запишем первый закон Кирхгофа с учетом (3.6)
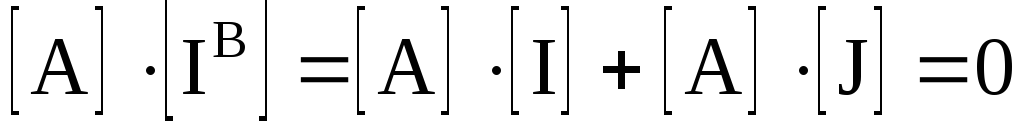
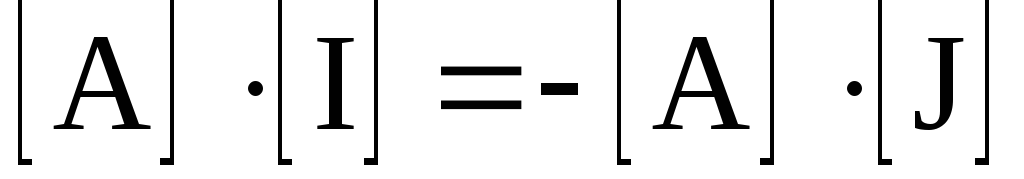
где [J] – столбцовая матрица источников тока, число строк которой совпадает с числом ветвей схемы.
Например, в схеме рис. 3.1 и 3.2
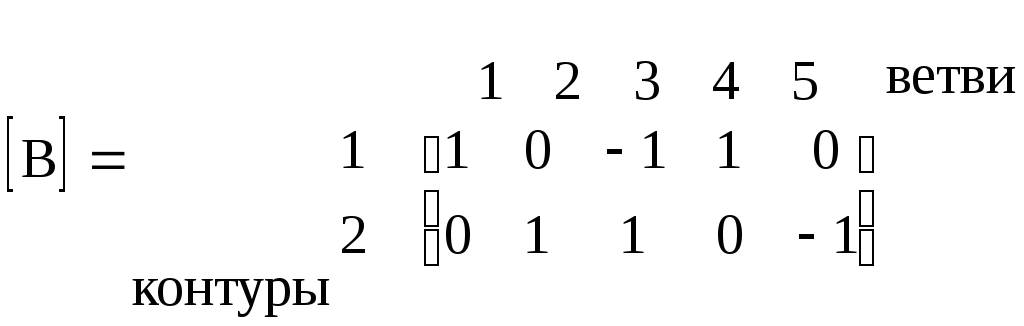
С помощью матрицы В запишем второй закон Кирхгофа с учетом (3.12)
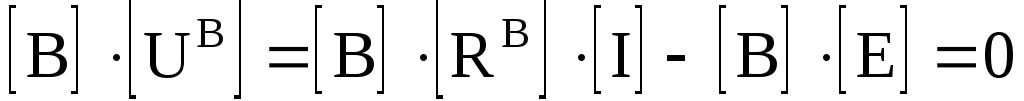
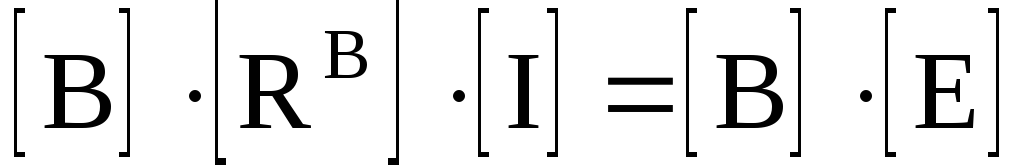
3.5. Матричная форма записи метода контурных токов
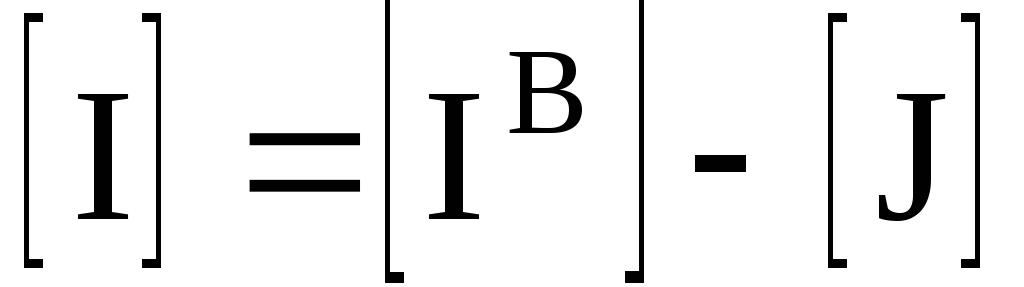
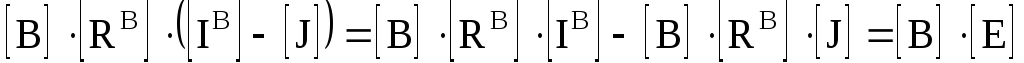
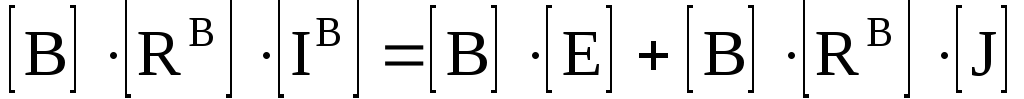
Можно показать, что с помощью транспонированной контурной матрицы [В] Т токи ветвей схемы [/ в ] могут быть выражены через матрицу контурных токов [/ к ]
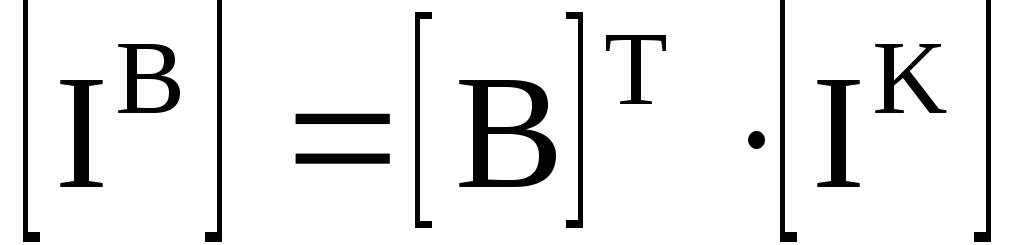
где [/ к ]–столбцовая матрица контурных токов. Тогда выражение (3.21) примет вид
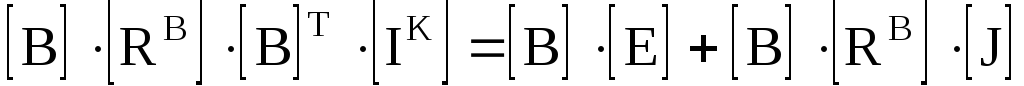
или в более компактной форме

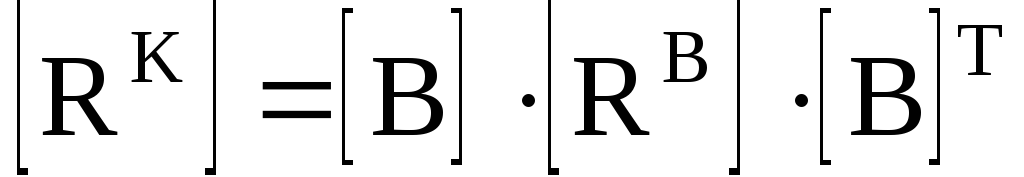
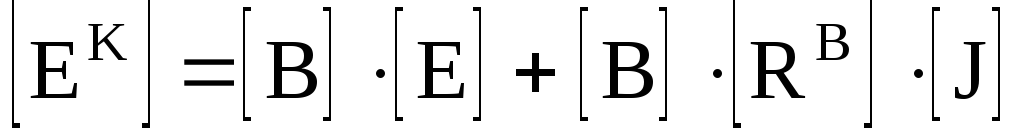
Матрицы уравнения (3.23) более просты для составления, поэтому уравнением (3.23) пользуются при решении на ЭВМ.
После решения уравнения (3.23) относительно контурных токов схемы решают последовательно уравнение (3.22) относительно токов ветвей и (3.19) относительно токов в резисторах.
Пример 3.1. В схеме рис. 3.1 определить токи в резисторах методом контурных токов, если
1. Запишем матрицы для решения уравнения (3.23), исходя из графа схемы (рис. 3.2). Римскими цифрами I и II обозначены контуры. Указаны направления обхода контуров.
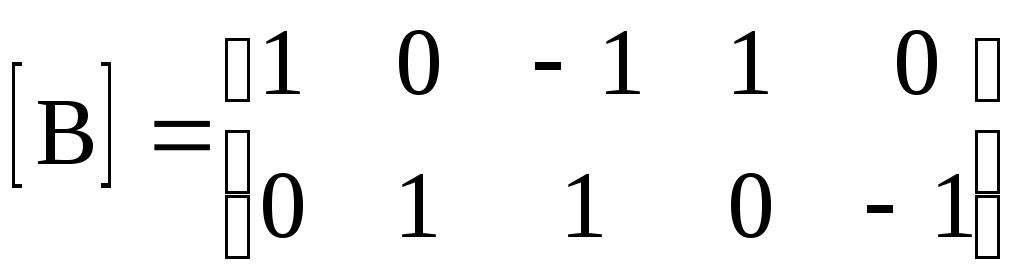
Контурная матрица
Диагональная матрица сопротивлений ветвей
Транспонированная контурная матрица
контурных токов
ЭДС ветвей
токов источников токов
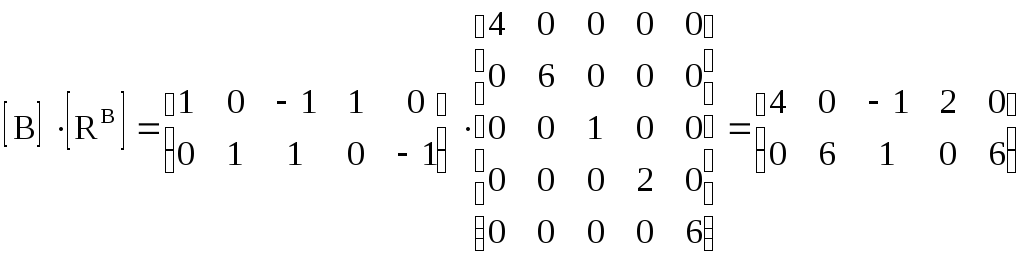
2. Перемножаем матрицы [В] и [R в ]
3. Получаем матрицу контурных сопротивлений
R ik – собственные и взаимные сопротивления контуров.
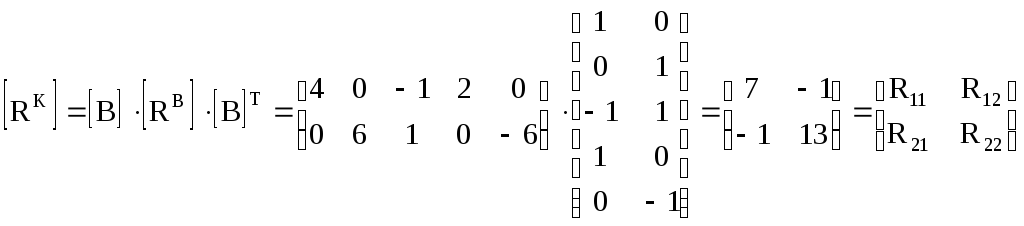
4. Запишем матрицу контурных ЭДС, воспользовавшись ранее найденным произведением матриц [В] на [R B ]
Обратная матрица
Отсюда
6. Определим контурные токи 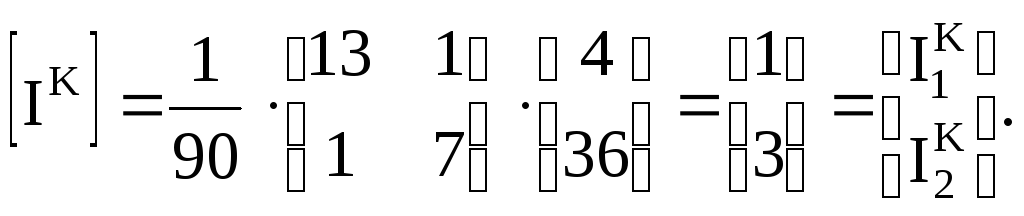
7. Определим токи в ветвях схемы. Решаем уравнение (3.22)
8. Определим токи в резисторах (3.19)
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Закон Ома в матричном виде



U в r=R в *I в
I в =G в U в r
Обобщенная ветвь электрической цепи (Закон Ома для обобщенной ветви)
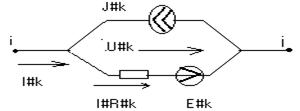
Найдем зависимость напряжения и тока
Напишем то же для напряжения:
Запишем в матричной форме:
E в =
Уравнение Кирхгофа в матричной форме: A*I в =0
B*U в =0 U в = Ur- E в
Соберем все эти уравнения в одно:
 |  |  |  |  |  |
B* R в 0 B E в
B* R в 0 B E в
î_____ ______þ