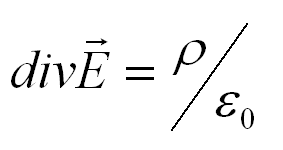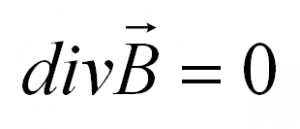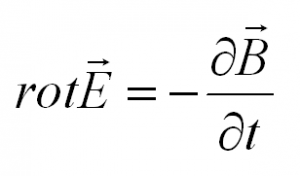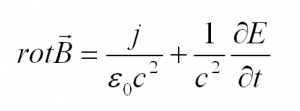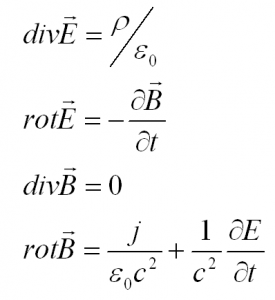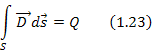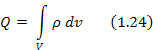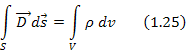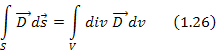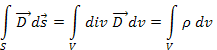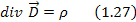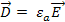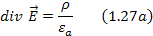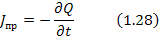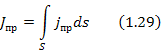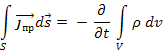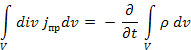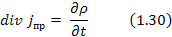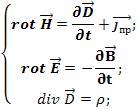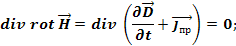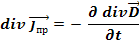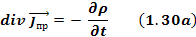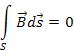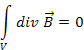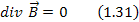закон отсутствия магнитных зарядов в дифференциальной форме уравнений максвелла

Система уравнений Максвелла для электромагнитного поля: смысл, способы решения

Уравнения Максвелла в электродинамике – это как законы Ньютона в классической механике или как постулаты Эйнштейна в теории относительности. Фундаментальные уравнения, в сущности которых мы сегодня будем разбираться, чтобы не впадать в ступор от одного их упоминания.

Полезная и интересная информация по другим темам – у нас в телеграм.

Уравнения Максвелла – это система уравнений в дифференциальной или интегральной форме, описывающая любые электромагнитные поля, связь между токами и электрическими зарядами в любых средах.

Уравнения Максвелла неохотно принимались и критически воспринимались учеными-современниками Максвелла. Все потому, что эти уравнения не были похожи ни на что из известного людям ранее.

Тем не менее, и по сей день нет никаких сомнений в правильности уравнений Максвелла, они «работают» не только в привычном нам макромире, но и в области квантовой механики.

Уравнения Максвелла совершили настоящий переворот в восприятии людьми научной картины мира. Так, они предвосхитили открытие радиоволн и показали, что свет имеет электромагнитную природу.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

По порядку запишем и поясним все 4 уравнения. Сразу уточним, что записывать их будем в системе СИ.

Первое уравнение Максвелла

Современный вид первого уравнения Максвелла таков:

Тут нужно пояснить, что такое дивергенция. Дивергенция – это дифференциальный оператор, определяющий поток какого-то поля через определенную поверхность. Уместным будет сравнение с краном или с трубой. Например, чем больше диаметр носика крана и напор в трубе, тем большим будет поток воды через поверхность, которую представляет собой носик.

В первом уравнении Максвелла E – это векторное электрическое поле, а греческая буква «ро» – суммарный заряд, заключенный внутри замкнутой поверхности.

Так вот, поток электрического поля E через любую замкнутую поверхность зависит от суммарного заряда внутри этой поверхности. Данное уравнение представляет собой закон (теорему) Гаусса.

Третье уравнение Максвелла

Сейчас мы пропустим второе уравнение, так как третье уравнение Максвелла – это тоже закон Гаусса, только уже не для электрического поля, но для магнитного.

Что это значит? Поток магнитного поля через замкнутую поверхность равен нулю. Если электрические заряды (положительные и отрицательные) вполне могут существовать по отдельности, порождая вокруг себя электрическое поле, то магнитных зарядов в природе просто не существует.

Второе уравнение Максвелла

Второе уравнение Максвелла представляет собой ни что иное, как закон Фарадея. Его вид:

Ротор электрического поля (интеграл через замкнутую поверхность) равен скорости изменения магнитного потока, пронизывающего эту поверхность. Чтобы лучше понять, возьмем воду в ванной, которая сливается через отверстие. Вокруг отверстия образуется воронка. Ротор – это сумма (интеграл) векторов скоростей частиц воды, которые вращаются вокруг отверстия.

Как Вы помните, на основе закона Фарадея работают электродвигатели: вращающийся магнит порождает ток в катушке.

Четвертое уравнение Максвелла

Это уравнение еще называется теоремой о циркуляции вектора магнитной индукции. Оно говорит нам о том, что электрический ток и изменение электрического поля порождают вихревое магнитное поле.

Приведем теперь всю систему уравнений и кратко обозначим суть каждого из них:

Первое уравнение: электрический заряд порождает электрическое поле

Второе уравнение: изменяющееся магнитное поле порождает вихревое электрическое поле

Третье уравнение: магнитных зарядов не существует

Четвертое уравнение: электрический ток и изменение электрической индукции порождают вихревое магнитное поле

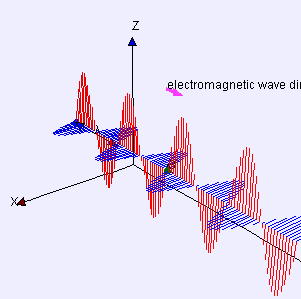
Решая уравнения Максвелла для свободной электромагнитной волны, мы получим следующую картину ее распространения в пространстве:

Надеемся, эта статья поможет систематизировать знания об уравнениях Максвелла. А если понадобиться решить задачу по электродинамике с применением этих уравнений, можете смело обратиться за помощью в студенческий сервис. Подробное объяснение любого задания и отличная оценка гарантированы.

Источник

Уравнения Максвелла

Уравнения Максвелла — основная идея и физическая суть

Закономерности, выведенные Максвеллом, в электродинамике имеют такое значение, как, к примеру, законы Ньютона для классической механики и постулаты Эйнштейна в теории относительности. Это фундаментальные уравнения, которые подтверждены экспериментальным путем.

Уравнения Максвелла являются системой уравнений в дифференциальном или интегральном виде, которые описывают любые электромагнитные поля, взаимосвязи токов и электрических зарядов в разных средах, включая вакуум.

Уравнения Максвелла подвергались критике со стороны современников ученого, так как не вписывались в установленные стандарты и представления того времени. Однако закономерности послужили началом активного развития науки и причиной переворота в восприятии картины мира. Постулаты предшествовали открытию радиоволн и продемонстрировали электромагнитную природу света. Формулы Максвелла справедливы для макромира и области квантовой механики.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Что описывают четыре уравнения

Смысл уравнений Максвелла:

Как записать в интегральной форме

Первое уравнение

Первое уравнение Максвелла представляет собой дифференциальную формулировку закона полного тока. Формула выглядит следующим образом:

S опирается на контур L.

Согласно теореме Стокса:

Уравнение справедливо для любых поверхностей, которые опираются на материальный контур L. Исходя из этого, подынтегральные функции равны.

Данная формула является дифференциальной формой закона Ома.

Первое уравнение Максвелла имеет вид:

Физический смысл данной расшифровки заключается в том, что в качестве источников вихревых магнитных полей выступают токи проводимости и токи смещения.

Второе уравнение

Второе уравнение Максвелла представляет собой дифференциальную формулировку закона электромагнитной индукции и ее свойств:

Второе уравнение Максвелла имеет следующий вид:

Физический смысл заключается в том, что переменное электрическое поле создается вихревым электрическим полем.

Третье уравнение

Третье уравнение Максвелла представляет собой дифференциальную формулировку теоремы Гаусса для электрических полей:

С помощью теоремы Островского-Гаусса можно выполнить переход от поверхностного интеграла \( \left(\vec \right)\) к объемному интегралу ( \(div D\) ):

Можно записать правую часть формулы для объемного заряда. После объединения двух уравнений получим:

Третье уравнение Максвелла:

Физический смысл закономерности заключается в том, что электрическое поле образовано источниками в виде зарядов с определенной плотностью.

Четвертое уравнение

Четвертым уравнением Максвелла является дифференциальная формулировка теоремы Гаусса, справедливая в условиях магнитного поля:

Четвертое уравнение Максвелла имеет вид:

Физический смысл четвертого уравнения Максвелла выражается в нулевом значении дивергенции вектора \(\vec\) для какой-либо точки в пространстве. Таким образом, сделан вывод об отсутствии источников или магнитных зарядов в природе.

Закон сохранения заряда в дифференциальной форме

Данная формула имеет следующий вид:

С помощью теоремы Островского-Гаусс можно вывести уравнение, которое будет являться результатов предыдущих закономерностей:

Источник

Уравнения Максвелла

Вы будете перенаправлены на Автор24

Значение уравнений Максвелла

Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.

Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.

Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.

Система уравнений Максвелла

Систему уравнений Максвелла составляют:

Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:

Готовые работы на аналогичную тему

В скалярном виде уравнение (2) запишем как:

Третье уравнение из системы Максвелла в скалярном виде:

Четвертое уравнение в скалярной форме примет следующий вид:

Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:

Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.

Физический смысл уравнений Максвелла

Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($\overrightarrow$) и токи смещения ($\frac<\partial \overrightarrow><\partial t>$).

Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.

Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.

Уравнения поля линейны и учитывают принцип суперпозиции.

Границы применимости уравнений Максвелла

Система уравнений Максвелла ограничена следующими условиями:

Материальные тела должны быть неподвижны в поле.

В поле не должно находиться постоянных магнитов и ферромагнитных тел.

Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.

Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.

Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.

Решение:

В качестве основания для решения задачи используем из системы Максвелла уравнение:

Проведем операцию дивергирования в обеих частях выражения (1.1):

Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:

Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:

В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:

Что позволяет нам записать уравнение (1.4) в виде:

Что дает нам закон сохранения заряда, который записан в виде:

Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:

тогда если области замкнуты и изолированы получаем:

Что требовалось доказать.

Решение:

За основу решения примем уравнение:

Возьмём дивергенцию от обеих частей уравнения:

В соответствии с теоремой равенстве нулю дивергенции ротора имеем:

Соответственно, получаем, что

Источник

Третье уравнение Максвелла. Закон сохранения заряда.

Третье уравнение Максвелла определяет источники электрического поля. Физический смысл этого уравнения состоит в том, что электрическое поле в некоторой области пространства связано с электрическим зарядом внутри этой поверхности.

Исходным для этого уравнения является уравнение Гаусса, которое говорит о том, что поток вектора 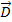через замкнутую поверхность S равен заряду Q, заключенному в данной поверхности:

где ρ – объемная плотность заряда.

Подставим 1.24 в 1.23, получим

Уравнение 1.25 есть третье уравнение Максвелла в интегральной форме.

Для того чтобы получить интегральную форму, воспользуемся теоремой Гаусса-Остроградского, которая устанавливает связь между объемным и поверхностным интегралом:

Применим 1.26 к левой части уравнения 1.25, получим

Данное равенство справедливо только в том случае, когда равны подынтегральные функции:

Уравнение 1.27 – третье уравнение Максвелла в интегральной форме.

и получим следующее уравнение

Для переменных полей заряды и токи связаны соотношением

j_пр – плотность тока проводимости;

В итоге, с учетом этих соотношений получим

Воспользуемся теоремой Гаусса – Остроградского

Уравнение 1.30 выражает закон сохранения заряда:

Источник тока проводимости – это изменение заряда во времени.

Уравнение 1.30 также является необходимым дополнением к системе уравнений Максвелла, так как в этой системе необходимо было связать ρ и 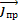. Это уравнение можно вывести, воспользовавшись уже имеющимися уравнениями Максвелла. Запишем систему уравнений Максвелла

Применим оператор div к первому уравнению Максвелла:

§1.5. Четвертое уравнение Максвелла.

Четвертое уравнение Максвелла устанавливает отсутствие магнитных зарядов и то, что магнитные силовые линии всегда замкнуты. В интегральном виде этот факт записывается в виде уравнения

Поток вектора магнитной индукции через замкнутую поверхность равен нулю, поскольку магнитных зарядов одного знака в природе не обнаружено.

Применяя теорему Гаусса – Остроградского

Уравнение 1.31 – это четвертое уравнение Максвелла в дифференциальной форме.

Дата добавления: 2016-01-29 ; просмотров: 2217 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

Уравнения максвелла в интегральной форме, с примерами

Сохрани ссылку в одной из сетей:

Ограниченность теории дальнодействия. Гипотеза Максвелла. Вихревое электрическое поле. Ток смещения. Система уравнений Максвелла для электромагнитных полей в интегральной форме. Закон неразрывности заряда.

Открытое Фарадеем явление электромагнитной индукции поставило вопрос о природе ЭДС в неподвижном контуре, находящемся в переменном магнитном поле.

Максвелл предложил гипотезу, в соответствии с которой всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое и является причиной возникновения индукционного тока в контуре.

Последовательная теория единого электромагнитного поля произвольной системы электрических зарядов и токов.

Решает основную задачу электродинамики – по заданному распределению зарядов и токов определяются характеристики их электрического и магнитного полей.

Является обобщением важнейших законов для электрических и электромагнитных явлений – теоремы Остроградского-Гаусса, закона полного тока, закона электромагнитной индукции.

Феноменологическая – в ней не рассматривается дискретное строение среды и механизм процессов, происходящих в среде в электромагнитном поле. Свойства среды – относительная диэлектрическая проницаемость, относительная магнитная проницаемость и удельная электрическая проводимость (известны из опыта).

Макроскопическая – в ней изучаются макроскопические электромагнитные поля таких систем зарядов и токов, пространственные размеры которых много больше размеров атомов и молекул.

Является теорией близкодействия – электрические и магнитные взаимодействия осуществляются посредством электромагнитного поля и распространяются со скоростью света

Макроскопические поля в теории Максвелла представляют собой усредненные непрерывно изменяющиеся микрополя, создаваемые микроскопическими зарядами и токами. Усреднение производится по интервалам времени, значительно превышающим периоды внутриатомных процессов, и по объемам, значительно превышающим размеры атомов и молекул.

Первое уравнение Максвелла является обобщением закона электромагнитной индукции, которое в интегральной форме имеет вид

Из выражения для магнитного потока следует

Интеграл в правой части является функцией только от времени.

Неравенство нулю циркуляции вектора напряженности электрического поля по замкнутому контуру означает, что возбуждаемое переменным магнитным полем электрическое поле является вихревым, как и само магнитное поле.

Из первого уравнения Максвелла следует, что всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле.

По теореме Стокса в векторном анализе

где ротор вектора Е выражается определителем

что позволяет записать первое уравнение Максвелла в дифференциальном виде

Второе уравнение Максвелла представляет собой обобщение закона полного тока.

Второе уравнение Максвелла основано на предположении, что всякое изменение электрического поля вызывает возникновение в окружающем пространстве вихревого магнитного поля.

Количественной мерой магнитного действия переменного электрического поля является ток смещения.

Током смещения сквозь произвольную замкнутую поверхность S называется физическая величина, равная потоку вектора плотности тока смещения сквозь эту поверхность

Токи смещения проходят по тем участкам цепи переменного тока, где отсутствуют проводники (например, между обкладок конденсатора).

В диэлектрике вектор электрического смещения равен

где – плотность тока смещения в вакууме, а – плотность тока поляризации (смещение зарядов в молекулах неполярных диэлектриков или поворот диполей полярных диэлектриков).

Токи смещения не сопровождаются выделением теплоты.

Второе уравнение Максвелла в интегральной форме имеет вид

вследствие чего в дифференциальном виде второе уравнение Максвелла имеет вид

Для областей поля, где нет макротоков

Третье и четвертое уравнения Максвелла представляют собой обобщения теоремы Остроградского-Гаусса для электрического и магнитного полей

В интегральной форме эти уравнения имеют вид

По теореме Гаусса из векторного анализа

В дифференциальной форме третье и четвертое уравнения Максвелла имеют вид

где – объемная плотность свободных зарядов в рассматриваемой точке поля.

Полная система уравнений Максвелла включает четыре уравнения

Из первых двух уравнений следует, что переменные электрическое и магнитное поля неразрывно связаны друг с другом, образуя единое электромагнитное поле. Разные знаки в правых частях первых двух уравнений обеспечивают устойчивость электромагнитного поля.

Уравнения Максвелла в дифференциальной форме предполагают, что все величины в пространстве и времени изменяются непрерывно. Если же существуют поверхности разрыва (где свойства среды меняются скачком), то более общей является система интегральных уравнений.

Для стационарных электрического и магнитного полей

Систему уравнений Максвелла необходимо дополнить «материальными уравнениями«, которые характеризуют электрические и магнитные свойства среды

Введение. Принято считать, что токи смещения входят в правую часть уравнений Максвелла [1] совершенно равноправно с токами переноса. Однако «до настоящего времени эти уравнения через токи смещения никто еще не решал, так как решения

В настоящее время в ЦНИИ проводятся разработки по изучению солитонных полей, солитонных каналов связи, а так же изучается воздействие на третий глаз человека излучений от соответствующих генераторов.

Специальная теория относительности (СТО) покоится на двух китах: оптике и механике, и прошла свое развитие от Галилея до Эйнштейна в механике и от Гюйгенса и Максвелла до Эйнштейна в теории света и электродинамике.

Джеймс Клерк Максвелл родился 13 июня 1831г. в Эдинбурге, в семье юриста — обладателя поместья в Шотландии. В мальчике рано проявились любовь к технике и стремление постичь окружающий мир.

В статье предлагается альтернативный подход к решению проблемы единого поля электромагнетизма и гравитации в рамках классической теории Максвелла, вместо общей теории относи– тельности Эйнштейна.

Уравнения Максвелла: дифференциальные формы закона Гаусса для электро и магнитных полей, закона Ампера и закона Фарадея

В статье мы, используя теорему Гаусса-Остроградского и теорему Стокса приведем четыре уравнения Максвелла к дифференциальной форме. В конце статьи вы сможете посмотреть видео-лекцию для закрепления информации.

Четыре фундаментальных уравнения электромагнетизма сформулированы Джеймсом Клерком Максвеллом. Они описывают свойства электрического и магнитного полей и отношения между этими полями. Из уравнений Максвелла можно вывести уравнение электромагнитной волны, распространяющейся в вакууме со скоростью света

Первое уравнение Максвелла, дифференциальной формы Фарадея

Закон Фарадея — интегральная форма:

На основании теоремы Стокса мы меняем линейный интеграл (циркуляцию) в левой части уравнения на поверхностный интеграл:

Мы можем оставить правую сторону в законе Фарадея в виде:

Теперь мы можем сравнить оба поверхностных интеграла:

Итак, мы получаем закон Фарадея — дифференциальную форму:

Второе уравнение Максвелла, дифференциальной формы обобщенного закона Ампера

Обобщенный закон Ампера — интегральная форма:

На основании теоремы Стокса мы меняем линейный интеграл (циркуляцию) с левой части уравнения на поверхностный интеграл:

Мы можем представить правую часть в обобщенном законе Ампера как поверхностный интеграл:

С учетом того, что прямой ток I можно выразить плотностью тока j :

записываем правую сторону как один поверхностный интеграл:

Теперь мы сравним оба поверхностных интеграла друг с другом:

Чтобы это уравнение было истинным для каждой поверхности A, независимо от ее размера и формы, подфункции с обеих сторон уравнения должны быть равны.

Таким образом, мы получаем обобщенный закон Ампера — дифференциальную форму :

Третье уравнение Максвелла, дифференциальной формы закона Гаусса для электрического поля

Закон Гаусса для электрического поля — интегральная форма:

Основываясь на теореме Гаусса — Остроградского, мы меняем поверхностный интеграл в левой части уравнения на интеграл объема:

Нагрузка Q также представлена ​​как интеграл объема от плотности заряда ρ :

Из равенства обоих интегралов объема:

получаем закон Гаусса для электрического поля — дифференциальную форму:

Четвертое уравнение Максвелла,дифференциальная форма закона Гаусса для магнитного поля

Закон Гаусса для магнитного поля — интегральная форма:

Основываясь на теореме Гаусса — Остроградского, мы меняем поверхностный интеграл в левой части уравнения на интеграл объема:

Поскольку на основе закона Гаусса для магнитного поля оба этих интеграла равны нулю, то подфункции также равны нулю, поэтому мы сразу получаем закон Гаусса для магнитного поля — дифференциальную форму:

Финальный вывод уравнений Максвелла

Видео-лекция

В данном видео подробно разберем уравнения Максвелла.

Граничные условия. Уравнения Максвелла в интегральной форме

4.
Граничные условия.Уравнения Максвелла в интегральной форме. Граничные
условия.

4.1.
Уравнения Максвелла для материальных сплошных сред в интегральной форме. Граничные
условия. Дифференциальные системы
уравнений Максвелла для материальных сплошных средв четырех,
приведенных выше формах, эквивалентны. Применимы они лишь для описания полей в
областях, где нет разрывов (скачков) соответствующих функций.

На поверхностях
разрыва функций происходит обращение в бесконечность производных. Необходимо
иметь граничные условия (соотношения на разрыве) для «сшивания» полей по разные
стороны от поверхности разрыва. Такая ситуация возникает, в частности на
фронтах ударных волн по причине проявления нелинейности.

В линейных задачах
разрывы полей возникают на поверхностях (контактные поверхности),
разделяющих среды с различными свойствами. Конечно, такая трудность возникает
из-за чрезмерной идеализации в постановке задачи. В линейной ситуации поля
будут изменяться непрерывно, если заменить границу раздела сред неоднородной
переходной областью.

Однако это приводит к большому усложнению решения задачи.
По этой причине часто используется более «грубая» идеализация резкой границы
раздела сред. Боле первичными по отношению к дифференциальным уравнениям
Максвелла являются уравнения Максвелла в интегральной форме. Переход от
дифференциальных уравнений к уравнениям в интегральной форме неоднозначен.

«Наиболее первичными», являются уравнения Максвелла в интегральной форме в виде
законов сохранения. По сути, это первичные постулаты электродинамики сплошных
сред (в рамках теории сплошной среды они ни откуда не выводятся). Из этих
уравнений и получаются граничные условия.

Отметим, что предельный переход от
неоднородной переходной области к резкой границе раздела сред, дает те же граничные
условия, что и уравнения в интегральной форме в виде законов сохранения. Это
является дополнительным аргументом правильности граничных условий, получаемых
из уравнений в интегральной форме.

Связь
уравнения (4.1) с известным нам дифференциальным уравнением

Это
условие непрерывности нормальной к границе раздела сред компоненте вектора
магнитной индукции.

Получим
теперь граничное условие для вектора электрической индукции

можно
прейти к первичной интегральной форме следующим способом: проинтегрируем (4.3)
по объему

С
учетом формулы Гаусса-Остроградского будем иметь первичную интегральную форму

Не
следует воспринимать приведенные рассуждения, как вывод уравнения (4.4) из
(4.3). На самом деле первичным является уравнение (4.4). Более того: уравнение
(4.4) это постулат.

получим
из (4.7), (4.8) два граничные условия

где- произвольное касательное к границе
раздела сред направление. Аналогичные рассуждения, позволяют представить
граничное условие (4.10) в векторной форме

где
— вектор плотности поверхностного тока
проводимости.

Уравнения Максвелла

Интегральная форма

При помощи формул Остроградского — Гаусса и Стокса дифференциальным уравнениям Максвелла можно придать форму интегральных уравнений:

где — относительная диэлектрическая проницаемость, — относительная магнитная проницаемость. Размерные величины (в единицах СИ — Ф/м) и (в единицах СИ — Гн/м), возникающие в системе СИ, называются абсолютная диэлектрическая проницаемость и абсолютная магнитная проницаемость соответственно.

где — удельная проводимость среды (в единицах СИ — Ом−1•м−1).

Аналогичные уравнения получаются в гауссовой системе СГС (если формально положить ).

Система уравнений Максвелла в интегральной форме

В основе теории Максвелла, позволившей с единых позиций объяснить не только электрические и магнитные явления, но и предсказать новые, лежат рассмотренные уже ранее четыре уравнения:

1. Электрическое поле может быть как потенциальным [его циркуляция определяется (77.3) и равна нулю], так и вихревым [его циркуляция

циркуляция вектора напряженности суммарного электрического поля

Это уравнение показывает, что источниками электрического поля могут быть не только электричеасие заряды, но и изменяющиеся во времени магнитные поля.

2. Обобщенная теорема о циркуляции вектора Н [см. (78.8)]:

Это уравнение показывает, что магнитные поля могут возбуждаться либо движущимися зарядами (электрическими токами), либо переменными электрическими полями.

3. Теорема Гаусса для поля D |см. (20.3)], которая, как предположил Максвелл, справедлива для любого электрического поля, как стационарного, так и переменного,

где Q — алгебраическая сумма заключенных внутри поверхности свободных электрических зарядов.

Если заряд распределен внутри замкнутой поверхности непрерывно с объемной плотностью р, то формула (79.3) запишется в виде

4. Теорема Гаусса для поля В [см. (60.5)], которая, как предположил Максвелл, справедлива для любого магнитного поля:

Таким образом, система уравнений Максвелла в интегральной форме включает четыре уравнения: (79.1), (79.2), (79.4) и (79.5):

Величины, входящие в уравнения Максвелла, не являются независимыми и между ними существует следующая связь (изотропные несегнето- электрические и неферромагнитные среды):

Физический смысл уравнений Максвелла: источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля, а магнитные поля могут возбуждаться либо движущимися электрическими зарядами (электрическими токами), либо переменными электрическими полями.

Уравнения Максвелла не симметричны относительно электрического и магнитного полей. Это связано с тем, что в природе существуют электрические заряды, но нет зарядов магнитных.

т. е. источниками электрического поля в данном случае являются только электрические заряды, а источниками магнитного — только токи проводимости. В данном случае электрические и магнитные ноля независимы друг от друга, что и позволяет изучать отдельно постоянные электрическое и магнитное поля.

Источник