закон распределения вейбулла имеет симметричную форму
Распределение Вейбулла
Закон Вейбулла-Гнеденко представляет собой двухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений.
Они названы по фамилиям инженера В. Вейбулла, введшего эти распределения в практику анализа результатов усталостных испытаний, при описании экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов ее упругости. и математика Б.В.Гнеденко (1912 – 1995), получившего такие распределения в качестве предельных при изучении максимального из результатов испытаний. Закон Вейбулла удовлетворительно описывает наработку до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оценки надежности машин в процессе их приработки.
Плотность распределения описывается зависимостью
где a — параметр формы кривой распределения; l — параметр масштаба; е = 2,71828 — основание натурального логарифма.
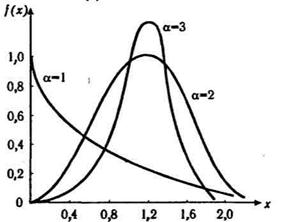
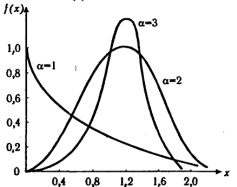
График плотности распределения дан на рис. 6.7.
Функция распределения Вейбулла
Функция надежности для этого закона:
Математическое ожидание случайной величины Х равно:
где Г(х) — гамма-функция. Для непрерывных значений х
. (6.33)
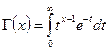
Для целочисленных значений х гамма-функцию вычисляют по формуле
Дисперсия случайной величины равна:
Рис. 6.7. Плотность распределения Вейбулла для l = 1
Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр a. Подбирая нужным образом параметры aи l,можно получить лучшее соответствие расчетных значений опытным данным по сравнению с экспоненциальным законом, который является однопараметрическим (параметр l).
Так, для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быстро падает. Функция надежности для такого изделия хорошо описывается законом Вейбулла с параметром a 1. При a = 3,3 распределение Вейбулла близко к нормальному.
Распределение Вейбулла и нормальный закон распределения
Распределение Вейбулла применяют для случая, когда поток отказов не стационарный, т.е. плотность потока изменяется с течением времени. Характеристики надежности в этом случае определяются по формулам.
Средняя наработка до первого отказа определится из следующего выражения:
Значения Г (гамма-функции) табулированы (табл. П.1). Нормальное распределение. Плотность вероятности (частота) отказов
Вероятность отказа за время t
Значение функции распределения (вероятность отказа) определяется формулой
Функция F(t) табулирована, значения функции приведены в табл. П.2. Вероятность отсутствия отказа за время t
Примеры решения задач
Значение гамма-функции Г(1,67) = 0,90330 определяем по табл. П.1
Задача 4.2. Вероятность безотказной работы гироскопа в течение t =150 час
равна 0,9. Время исправной работы подчинено закону Вейбулла с параметром α = 2,6. Необходимо определить интенсивность отказов, частоту отказов гироскопов для t =150 час и среднюю наработку до первого отказа.
Значение гамма-функции Г(1,38) = 0,88854 определяем по табл. П.1
Задача 4.4. Наработка до отказа вилки выключения сцепления имеет распределение Вейбулла с параметром α = 1,5. Вероятность безотказной работы вилки в течение наработки 200 часов равна 0,95. Определить интенсивность отказов и среднюю наработку до отказа.
Задача 4.5. Наработка до отказа партии подшипников имеет распределение Вейбулла с параметром α = 1,8. Вероятность безотказной работы партии подшипников в течение наработки t = 100 часов равна 0,95. Определить интенсивность отказов в период времени 100 часов и среднюю наработку до первого отказа.
Задача 4.6. Определить вероятность безотказной работы, частоту отказов и интенсивность отказов изделия за 200 часов работы, если его надежность подчиняется нормальному закону распределения с параметрами Тср = 1600 час, о = 1000 час.
По табл. П2 определяем F(t) = Q(t) = 0,08, P(t) = 0,92.
Тогда, частота отказов
Задача 4.7. Время безотказной работы гальванической батареи постоянного тока имеет нормальное распределение с математическим ожиданием Тср = 30 час и среднеквадратическим отклонением σ = 4 час. Определить какова веро-ятность безотказной работы батареи в течение 25 часов. Когда необходимо заменить батарею, чтобы гарантировать, что вероятность появления отказа до момента замены не превысит 5%.
По табл. П2 F(t) = Q(t) = 0,106, а P(t) = 0,894;
Тогда время работы батареи до ее замены с вероятностью отказа
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Распределение Вейбулла
Двухпараметрический закон Вейбулла характеризует распределение непрерывной СВ, которая принимает только положительные значения.
Функция плотности распределения случайной величины Вейбулла находится по формуле:
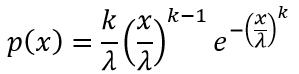
Интегральная функция распределения определяется выражением:
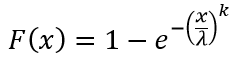
Переменная x часто рассматривается как наработка. 
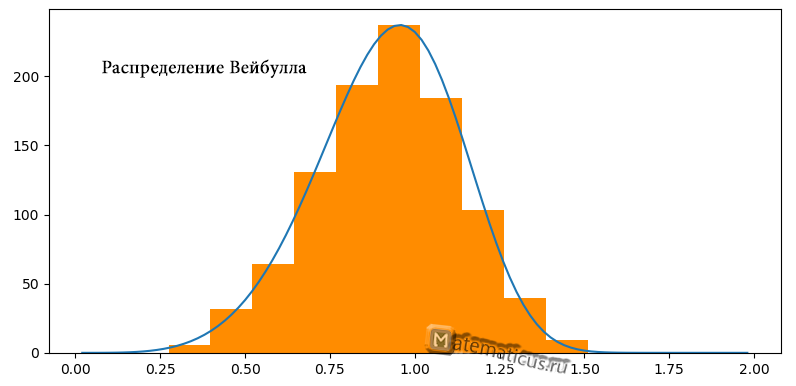
Распределение Вейбулла в виде гистограммы
Параметры распределения:
λ — масштаба распределения распределения случайной величины Вейбулла;
k — параметр формы распределения СВ Вейбулла.
Обратная функция распределения Вейбулла вычисляется по формуле:
При k=1 закон распределения Вейбулла переходит в показательный (экспоненциальный) закон распределения.
При k=2 закон распределения Вейбулла превращается в закон распределения Рэлея.
Распределение Вейбулла применяется в теории надежности (анализ отказов деталей:
— при k>1 — старение, то есть частота отказов увеличивается с течением времени;
— при k=1 — интенсивность отказов постоянна во времени.
Распределение Вейбулла применяют при прогнозировании времени до отказа технической системы, для непрерывных показателей, погоды (скорость ветра подчиняется этому закону) и т.д.
Закон распределения Вейбулла-Гнеденко
Закон распределения Вейбулла-Гнеденко.
, λ0, β – параметры распределения
λ0 – масштабный пар-р распределения
β – пар-р кривизны распределения
все функции зависят от времени. β изменяется в 3-х областях и определяет вид граф. зависимостей.
β=1: 
— распределительный закон переходит в экспоненциальный. – для аппаратной техники β 1 – используется для описания наработки до отказа мех-х и электр-х устройств, имеющих период приработки и старения. (рис.2)
Распределение Вейбулла-Гнеденко используется при проведении форсированных испытаний объекта на надежность.
Нормальное распределение (Гаусса).
Оно используется для описания работы устройств в периоде старения
где m и σ =√D[t] – распределительные параметры
σ =√D[t] – среднеквадратичное отклонение
Усеченное нормальное распределение:
f(t)= 
это распределение используется: в период старения, при определении показ-ей надежности, при постепенных отказах, а также для учета ухода параметров за допустимые пределы.
(рис.4)
Это распределение используется для описания периода старения. В области малых значений наработки до отказа (t Pэ(t), поэтому объекты, функционирующие малое непрерывное время целесообразно строить на рэлеевских элементах.
Потоки отказов восстан-х объектов.
Отказы происходят в случайные моменты времени, продолжительность восстановления – величина случайная, время восстановления
Распределение Вейбулла
Закон Вейбулла представляет собой деухпараметрическое распределение. Этот закон является универсальным, так как при соответствующих значениях параметров превращается в нормальное, экспоненциальное и другие виды распределений. Автор данного закона использовал его при описании экспериментально наблюдавшихся разбросов усталостной прочности стали, пределов ее упругости. Закон Вейбулла удовлетворительно описывает наработку до отказа подшипников, элементов радиоэлектронной аппаратуры, его используют для оценки надежности деталей и узлов машин, в частности автомобилей, а также для оценки надежности машин в процессе их приработки. Плотность распределения описывается зависимостью
(29)
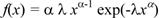
где α — параметр формы кривой распределения; λ — параметр масштаба; е =2,71828 — основание натурального логарифма.
График плотности распределения дан на рис. 4.
Функция распределения Вейбулла
(30)
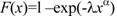
Функция надежности для этого закона:
(31)
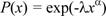
Математическое ожидание случайной величины X равно:
(32)
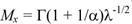
где Г(х) — гамма-функция. Для непрерывных значений х
(33)
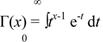
Для целочисленных значений х гамма-функцию вычисляют по формуле
(35)
(36)
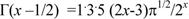
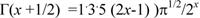
Дисперсия случайной величины равна:
(37)
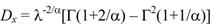
Рис. 4. Плотность распределения Вейбулла для λ=1
Широкое применение закона распределения Вейбулла объясняется тем, что этот закон, обобщая экспоненциальное распределение, содержит дополнительный параметр α. Подбирая нужным образом параметры α и λ, можно получить лучшее соответствие расчетных значений опытным данным по сравнению с экспоненциальным законом, который является однопараметрическим (параметр λ).
Так, для изделий, у которых имеются скрытые дефекты, но которые длительное время не стареют, опасность отказа имеет наибольшее значение в начальный период, а потом быстро падает. Функция надежности для такого изделия хорошо описывается законом Вейбулла с параметром α 1. При α =3.3 распределение Вейбулла близко к нормальному.