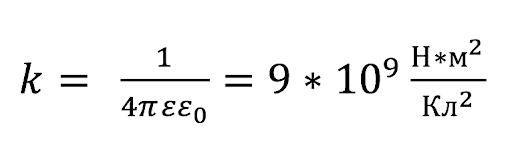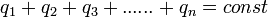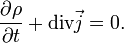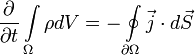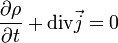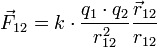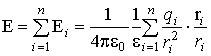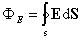закон сохранения заряда в дифференциальной форме выражает уравнение
Закон сохранения электрического заряда
Электрический заряд
Электрический заряд — это физическая величина, которая определяет способность тел создавать электромагнитное поле и принимать участие в электромагнитном взаимодействии.
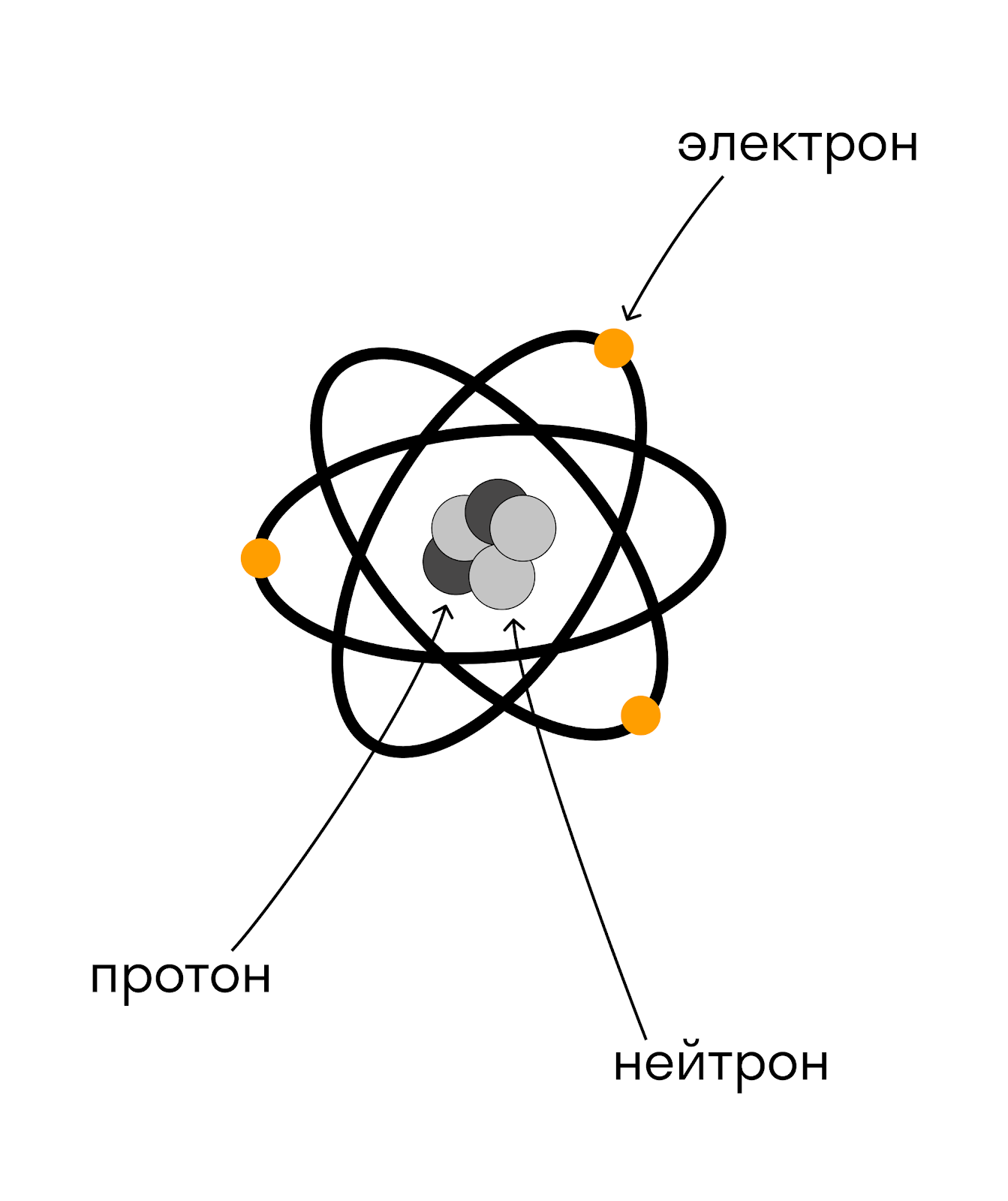
Мы состоим из клеток, клетки состоят из молекул, молекулы в свою очередь состоят из атомов, а атомы — из ядра и электронов. Ядро состоит из протонов и нейтронов.
Протон — это частица, которая заряжена положительно, нейтрон — нейтрально, а электрон — отрицательно. Электрон вращается по орбитам, которые во много раз больше, чем размер электрона.
Размер электрона с размером орбиты можно сравнить так: представьте футбольный мяч и футбольное поле. Во сколько раз поле больше мяча, во столько же раз орбита больше, чем электрон.
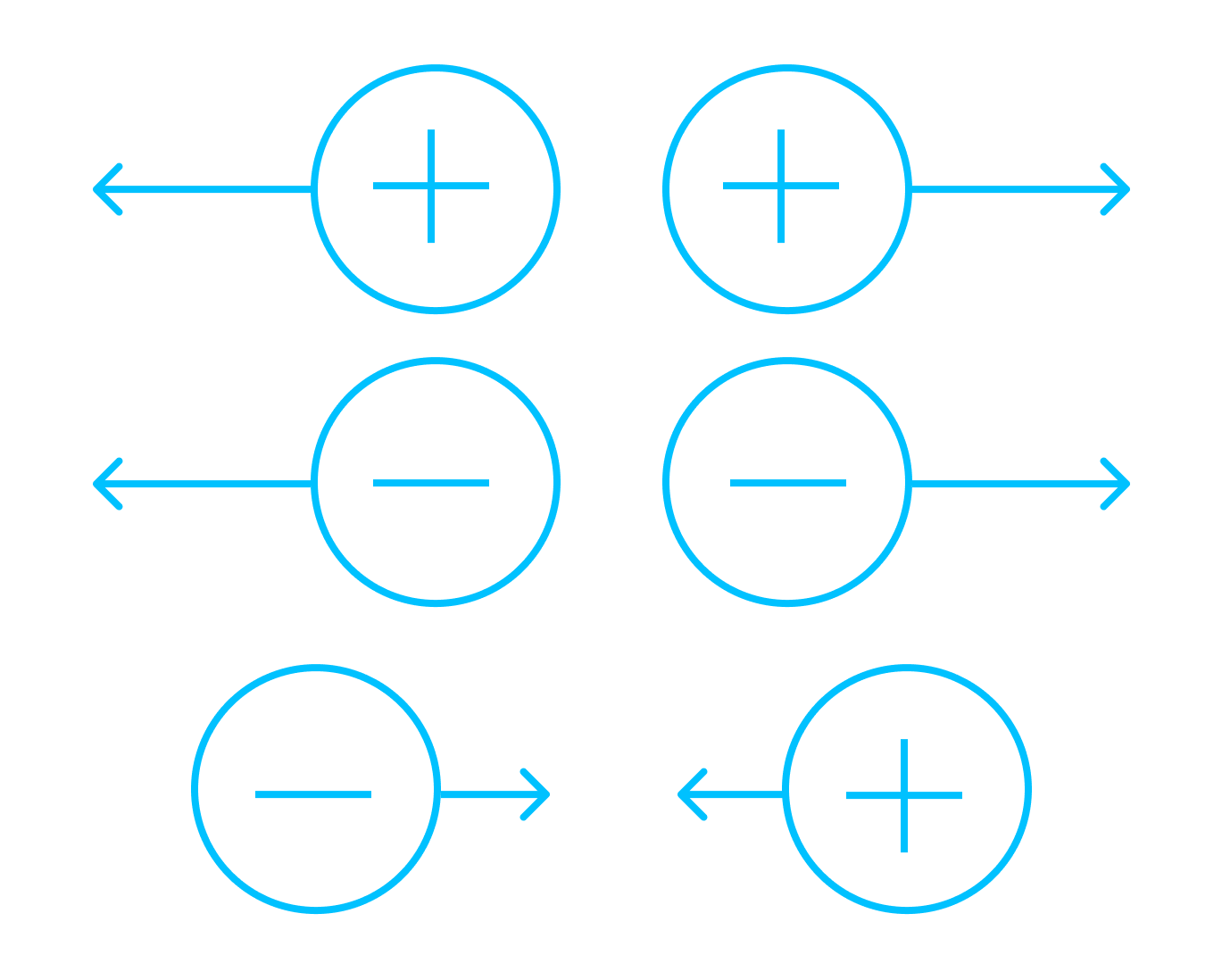
Как мы уже выяснили, электрические заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, разноименные притягиваются:
А вот измерять Электрический заряд мы будем в Кулонах [Кл]. Нет, не тех, что болтаются на цепочке. Шарль Кулон — это физик, который изучал электромагнитные явления.
Электризация
Чтобы разобраться с тем, как тело приобретает электрический заряд и сохраняет его, нам для начала нужно поближе познакомится с протоном и электроном. Протон — ленивый и неповоротливый — он точно не будет никуда перемещаться, если мы не переместим атом целиком.
А вот электрон — парень подвижный, и ему перебежать с одного атома на другой — ничего не стоит.
Мы поговорим о двух типах электризации: электризация соприкосновением и электризация трением.
Свободные электроны переходят с незаряженного тела на нейтральное. А если мы возьмем положительно заряженное тело вместо отрицательного, то свободные электроны перейдут с нейтрального тела, чтобы уравновесить заряды.
Электроны переходят от одного тела к другому и в отличии от электризации соприкосновением заряжаются противоположными по знаку и равными по модулю зарядами.
То есть при соприкосновении заряд раздают одного знака и поровну. Как если бы ты поделился с другом конфетами, которых у тебя с избытком.
При трении наоборот — заряды у тел будут разных знаков, но также в одинаковом количестве. Например, у вас есть равное количество денег в рублях и долларах, и у меня аналогичная ситуация с той же суммой. Вы решили лететь в США, а мне как раз доллары не нужны. Чтобы не ходить в банк, мы можем просто поменяться. Тогда у вас будут только доллары, а у меня — только рубли. Главное, договориться про курс 🙂
Давайте решим пару задач по этой теме.
Задачка один
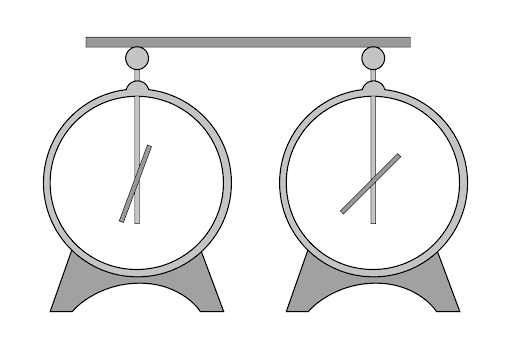
Из какого материала может быть сделан стержень, соединяющий электрометры, изображённые на рисунке?
Решение:
Он может быть сделан либо из проводника, либо из диэлектрика. Проводник пропускает через себя заряды, а диэлектрик — нет. Если мы посмотрим на показания электрометров, то увидим, что они отличаются.
Как мы помним, при соприкосновении заряды уравниваются по величине (один электрометр делится конфетами с другим). В данном случае никто ни с кем не делился, это значит, что стержень не пропускает — он диэлектрик. И стекло, и эбонит являются диэлектриками. Значит подходят оба варианта!
Задачка два
В процессе трения о шёлк стеклянная линейка приобрела положительный заряд. Как при этом изменилось количество заряженных частиц на линейке и шёлке при условии, что обмен при трении не происходил?
А) количество протонов на стеклянной линейке
Б) количество электронов на шёлке
Решение:
Вспомните, как мы охарактеризовали протон: он ленивый и неподвижный! Значит количество протонов ни на стеклянной линейке, ни на шелке измениться просто не может. Мы же не отламываем кусок линейки вместе с атомами, из которых она состоит. А вот электроны охотно перемещаются. Нам известно, что линейка приобрела положительный заряд. Получается, электроны сбежали от нее к шелку. Следовательно, количество электронов на шелке увеличилось.
Электростатическая индукция
Кажется, с электризацией разобрались. Теперь разберемся, что произойдет, если мы поднесем одно тело к другому, но не вплотную. Произойдет такое явление, как электростатическая индукция — явление перераспределения зарядов в нейтрально заряженных телах.
Давай разбираться на примере задачи:
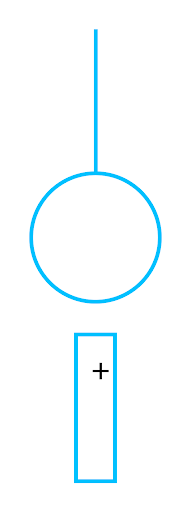
На нити подвешен незаряженный металлический шарик. К нему снизу поднесли положительно заряженную палочку. Как изменится при этом сила натяжения нити?
Решение:
Здесь важно подчеркнуть, что незаряженный — значит заряжен нейтрально. То есть в теле равное количество положительных и отрицательных зарядов.
Электроны металлического шарика будут притягиваться к поднесенной положительной палочке. В результате шарик притягивается к палочке, следовательно, сила натяжения нити увеличивается.
Ответ: сила натяжения нити увеличивается
Поляризация диэлектрика
Давайте возьмем два, на первый взгляд, одинаковых задания из ЕГЭ.
Задание 1
Если к незаряженному металлическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?
Мы только что это разобрали: то электростатическая индукция.
Задание 2
Если к незаряженному диэлектрическому шару поднести, не касаясь, точечный положительный заряд, то на стороне шара, ближайшей к заряду, появится отрицательный заряд. Как называется это явление?
Кажется, что очень похоже на электростатическую индукцию, но это явление будет называться поляризация. В чем разница:
В первом случае — это проводник, а во втором — диэлектрик. Если не вдаваться в подробности, то поляризация диэлектрика — процесс, очень похожий по природе своей на электростатическую индукцию, только происходит в непроводящих материалах.
Закон сохранения электрического заряда
И последнее, о чем мы сегодня поговорим — этот закон сохранения заряда
Алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда
q1 + q2 + q3 + … + qn = const
q1, q2, q3, …, qn — заряды электрически замкнутой системы [Кл]
Задачка раз
Решение:
Для решения этой задачи нам нужно найти алгебраическую сумму зарядов.
Это суммарный заряд шариков и до, и после и во время взаимодействия.
Так как суммарный заряд сохраняется, но шарики соприкоснулись, суммарный заряд разделится между всеми шариками поровну. То есть нам нужно суммарный заряд просто поделить на количество шариков — на 2.
И это ответ к нашей задаче.
Задачка два
Металлическая пластина, имевшая положительный заряд, по модулю равный 10е, при освещении потеряла шесть электронов. Каким стал заряд пластины?
Решение:
q = q₀ — 6(— e) = 10e + 6e = 16e
Красный знак «минус» образуется из-за того, что мы «отнимаем» электроны, а зеленый — из-за того, что электрон отрицательный. «Минус на минус» дает плюс, поэтому мы получаем 10e + 6e = 16е.
Ответ: 16е
Задачка три
Решение:
По закону сохранения заряда сумма зарядов в замкнутой системе остается постоянной.
Два шарика привели в соприкосновение и развели, значит их суммарный заряд разделится между шариками поровну.
Ответ: заряды шариков равны 2q.
Закон Кулона и связь с гравитацией
Мы уже упоминали Шарля Кулона. В честь него названа единица измерения заряда — Кулон. Он придумал закон о взаимодействии зарядом.
Закон Кулона
k — коэффициент пропорциональности
E₀= 8,85 * 10-12Н*м²/Кл² — электрическая постоянная
E — диэлектрическая проницаемость среды — показывает во сколько раз сила электростатического взаимодействия в вакууме больше силы в среде (в вакууме равна 1)
q1 — заряд первого тела [Кл]
q2 — заряд второго тела [Кл]
r — расстояние между телами [м]
F — сила электростатического взаимодействия (кулоновская) [Н]
Мы уже знаем, что заряды бывают положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные — притягиваются. Это значит, что сила направлена туда же, куда заряд будет стремиться двигаться.
Например, у положительного заряда сила будет направлена в сторону отрицательного, если он есть где-то поблизости, и от положительного, так как одноименные заряды отталкиваются.
Согласно третьему закону Ньютона, силы одной природы возникают попарно, равны по величине, противоположны по направлению. Если взаимодействуют два неодинаковых заряда, сила, с которой больший заряд действует на меньший (В на А) равна силе, с которой меньший действует на больший (А на В).
Интересно, что у различных законов физики есть некоторые общие черты. Вспомним закон тяготения. Сила гравитации также обратно пропорциональны квадрату расстояния, но уже между массами. И невольно возникает мысль, что в этой закономерности таится глубокий смысл. До сих пор никому не удалось представить тяготение и электричество, как два разных проявления одной и той же сущности.
Сила и тут изменяется обратно пропорционально квадрату расстояния, но разница в величине электрических сил и сил тяготения поразительна. Пытаясь установить общую природу тяготения и электричества, мы обнаруживаем такое превосходство электрических сил над силами тяготения, что трудно поверить, будто у тех и у других один и тот же источник. Нельзя говорить, что одно действует сильнее другого, ведь все зависит от того, какова масса и каков заряд.
Рассуждая о том, насколько сильно действует тяготение, мы не вправе говорить: «Возьмем массу такой-то величины», потому что мы выбираем ее сами. Но если мы возьмем то, что предлагает нам сама Природа: ее собственные числа и меры, которые не имеют ничего общего с нашими дюймами, годами — с любыми нашими мерами, вот тогда мы можем сравнивать.
Мы возьмем элементарную заряженную частицу, например, электрон. Две элементарные частицы, два электрона, за счет электрического заряда отталкивают друг друга с силой, обратно пропорциональной квадрату расстояния между ними, а за счет гравитации притягиваются друг к другу опять-таки с силой, обратно пропорциональной квадрату расстояния.
Закон Всемирного тяготения
G= 6,67 * 10⁻¹¹*11м³/кг*c² — гравитационная постоянная
m1 — масса первого тела [кг]
m2 — масса второго тела [кг]
r — расстояние между телами [м]
F — сила гравитационного притяжения [Н]
Тяготение относится к электрическому отталкиванию, как единица к числу с 42 нулями. Да, это огромное число! Исследователи перебирали все большие числа, чтобы понять — откуда это взялось. Одно из таких больших чисел — это отношение диаметра Вселенной к диаметру протона — как ни удивительно, это тоже число с 42 нулями. Нормально так перебрали.
Если вы смотрели Рика и Морти, то знаете о теории параллельных вселенных и о том, что эти вселенные расширяются. Из-за расширения вселенной постоянная сила тяготения меняется. Хотя эта гипотеза еще не опровергнута, у нас нет никаких свидетельств в ее пользу. Наоборот, некоторые данные говорят о том, что постоянная сила тяготения не менялась таким образом. Это громадное число по сей день остается загадкой.
От расширяющихся вселенных и мультиков перейдем к чему-то более приземленному — к задачам.
Задачка раз
Расстояние между двумя точечными электрическими зарядами уменьшили в 3 раза, каждый из зарядов увеличили в 3 раза. Во сколько раз увеличился модуль сил электростатического взаимодействия между ними?
Решение:
Возьмем закон Кулона.
Если расстояние уменьшилось в 3 раза, то знаменатель уменьшился в 9 раз. Каждый из зарядов увеличился в три раза, значит числитель увеличился в 9 раз. Уменьшаем знаменатель в 9 раз, тем самым увеличивая всю дробь в 9 раз, увеличиваем числитель в 9 раз, получаем, что вся дробь увеличилась в 81 раз. И это ответ.
Ответ: модуль сил электростатического взаимодействия увеличится в 81 раз.
Задачка два (последняя!)
Два одинаковых маленьких отрицательно заряженных металлических шарика находятся в вакууме на достаточно большом расстоянии друг от друга. Модуль силы их кулоновского взаимодействия равен F₁. Модули зарядов шариков отличаются в 5 раз.
Если эти шарики привести в соприкосновение, а затем расположить на прежнем расстоянии друг от друга, то модуль силы их кулоновского взаимодействия станет равным F₂. Определите отношение F₂ к F₁.
Решение:
Для начала найдем заряд шариков после соприкосновения.
Теперь по закону кулона найдем силу F2
И находим отношение сил
Ответ: отношение сил равно 1,8
Закон сохранения заряда
В современном мире электронная техника развивается семимильными шагами. Каждый день появляется что-то новое, и это не только небольшие улучшения уже существующих моделей, но и результаты применения инновационных технологий, позволяющих в разы улучшить характеристики.
Не отстает от электронной техники и приборостроительная отрасль – ведь чтобы разработать и выпустить на рынок новые устройства, их необходимо тщательно протестировать, как на этапе проектирования и разработки, так и на этапе производства. Появляются новая измерительная техника и новые методы измерения, а, следовательно – новые термины и понятия.
Для тех, кто часто сталкивается с непонятными сокращениями, аббревиатурами и терминами и хотел бы глубже понимать их значения, и предназначена эта рубрика.
Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.
Закон сохранения заряда выполняется абсолютно точно. На данный момент его происхождение объясняют следствием принципа калибровочной инвариантности. Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
Закон сохранения заряда и калибровочная инвариантность
| Симметрия в физике | ||
|---|---|---|
| Преобразование | Соответствующая инвариантность | Соответствующий закон сохранения |
| ↕ Трансляции времени | Однородность времени | …энергии |
| ⊠ C, P, CP и T-симметрии | Изотропность времени | …чётности |
| ↔ Трансляции пространства | Однородность пространства | …импульса |
| ↺ Вращения пространства | Изотропность пространства | …момента импульса |
| ⇆ Группа Лоренца | Относительность Лоренц-инвариантность | …4-импульса |
| Калибровочная инвариантность | …заряда | |
Физическая теория утверждает, что каждый закон сохранения основан на соответствующем фундаментальном принципе симметрии. Со свойствами симметрий пространства-времени связаны законы сохранения энергии, импульса и момента импульса. Законы сохранения электрического, барионного и лептонного зарядов связаны не со свойствами пространства-времени, а с симметрией физических законов относительно фазовых преобразований в абстрактном пространстве квантовомеханических операторов и векторов состояний. Заряженные поля в квантовой теории поля описываются комплексной волновой функцией




Закон сохранения заряда в интегральной форме
Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме:
Здесь 
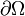


Закон сохранения заряда в дифференциальной форме
Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)
Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. В правилах Кирхгофа предполагается, что электронная система не может значительно изменять свой суммарный заряд.
Экспериментальная проверка
Наилучшей экспериментальной проверкой закона сохранения электрического заряда является поиск таких распадов элементарных частиц, которые были бы разрешены в случае нестрогого сохранения заряда. Такие распады никогда не наблюдались.Лучшее экспериментальное ограничение на вероятность нарушения закона сохранения электрического заряда получено из поиска фотона с энергией mec2/2 ≈ 255 кэВ, возникающего в гипотетическом распаде электрона на нейтрино и фотон:
| e → νγ | время жизни больше 4,6·1026 лет (90 % CL), |
однако существуют теоретические аргументы в пользу того, что такой однофотонный распад не может происходить даже в случае, если заряд не сохраняется. Другой необычный несохраняющий заряд процесс — спонтанное превращение электрона в позитрон и исчезновение заряда (переход в дополнительные измерения, туннелирование с браны и т. п.). Наилучшие экспериментальные ограничения на исчезновение электрона вместе с электрическим зарядом и на бета-распад нейтрона без эмиссии электрона:
Закон сохранения заряда в интегральной форме:
Закон сохранения заряда в дифференциальной форме
Закон сохранения заряда в электронике
Правила Кирхгофа для токов напрямую следуют из закона сохранения заряда. Объединение проводников и радиоэлектронных компонентов представляется в виде незамкнутой системы. Суммарный приток зарядов в данную систему равен суммарному выходу зарядов из системы. Вправилах Кирхгофа предполагается что электронная система не может значительно изменять свой суммарный заряд.
Зако́н Куло́на — это закон о взаимодействии точечных электрических зарядов.
Был открыт Шарлем Кулоном в 1785 г. Проведя большое количество опытов с металлическими шариками, Шарль Кулон дал такую формулировку закона:
Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме направлена вдоль прямой, соединяющей заряды, прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними. [1]
Важно отметить, что для того, чтобы закон был верен, необходимы:
точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;
их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поледвижущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;
взаимодействие в вакууме.
В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:
где 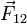
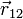
Закон Кулона применим для точечных зарядов и для среды, в которой отсутствуют свободные заряды. Если же заряд неточечный, но распределен по некоторой поверхности или объему, тогда обычно эти поверхность и объем разбивают на множество отдельных элементов и заряд каждого элемента рассматривают как точечный, а потом производят суммирование воздействий от всех зарядов. Если же во внешней среде будут присутствовать свободные заряды, они под действием электрического поля основного заряда так распределятся по объему, что создадут собственное электрическое поле, которое компенсирует поле основного заряда.
2.Электрическое поле — одна из составляющихэлектромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающихэлектрическим зарядом, а также в свободном виде при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может наблюдаться благодаря его силовому воздействию на заряженные тела.
Для количественного определения электрического поля вводится силовая характеристика — напряжённость электрического поля. Напряжённостью электрического поляназывают векторную физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещённый в данную точку пространства, к величине этого заряда. Направление вектора совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд.
В классической физике, применимой при рассмотрении крупномасштабных (больше размера атома) взаимодействий, электрическое поле рассматривается как одна из составляющих единого электромагнитного поля и проявление электромагнитного взаимодействия. В квантовой электродинамике — это компонент электрослабого взаимодействия.
Сила Лоренца описывает воздействие электромагнитного поля на частицу.
Эффект поля заключается в том, что при воздействии электрического поля на поверхность электропроводящей среды в её приповерхностном слое изменяется концентрация свободных носителей заряда. Этот эффект лежит в основе работы полевых транзисторов.
Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:
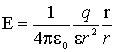
Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q1, q2, q3, ¼, qn, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
где ri – расстояние между зарядом qi и рассматриваемой точкой поля.
Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq.
Графическое изображение электрического поля. Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.
Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.
Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.
С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.
Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.
3.Поток вектора напряженности электрического поля. Пусть небольшую площадку DS (рис.1.2) пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол a. Полагая, что вектор напряженности Е не меняется в пределах площадки DS, определим поток вектора напряженности через площадку DS как
Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку DS, будет численно равно значению потока DFE через поверхность DS. Представим правую часть выражения (1.3) как скалярное произведение векторов E и DS = n DS, где n – единичный вектор нормали к поверхности DS. Для элементарной площадки dS выражение (1.3) принимает вид
Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности
Теорема Гаусса (закон Гаусса) — один из основных законовэлектродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.
Применяется отдельно для вычисления электростатических полей.
Также теорема Гаусса верна для любых полей, для которых верен закон Кулона или его аналог (например, для ньютоновской гравитации). При этом она является, как принято считать, более фундаментальной, так как позволяет в частности вывести степень расстояния [1] в законе Кулона «из первых принципов», а не постулировать ее (или не находить эмпирически).
В этом можно видеть фундаментальное значение теоремы Гаусса (закона Гаусса) в теоретической физике.
Существуют аналоги (обобщения) теоремы Гаусса и для более сложных полевых теорий, чем электродинамика.