закон сохранения импульса второй закон ньютона в импульсной форме
Закон cохранения импульса
9 класс, 10 класс, ЕГЭ/ОГЭ
Импульс: что это такое
Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.
Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.
Импульс тела
→ →
p = mv
p — импульс тела [кг*м/с]
Закон сохранения импульса
В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:
Закон сохранения импульса
Векторная сумма импульсов тел в замкнутой системе постоянна
А выглядит — вот так:
Закон сохранения импульса
→ → →
p1 + p2 + … + pn = const
p — импульс тела [кг*м/с]
Простая задачка
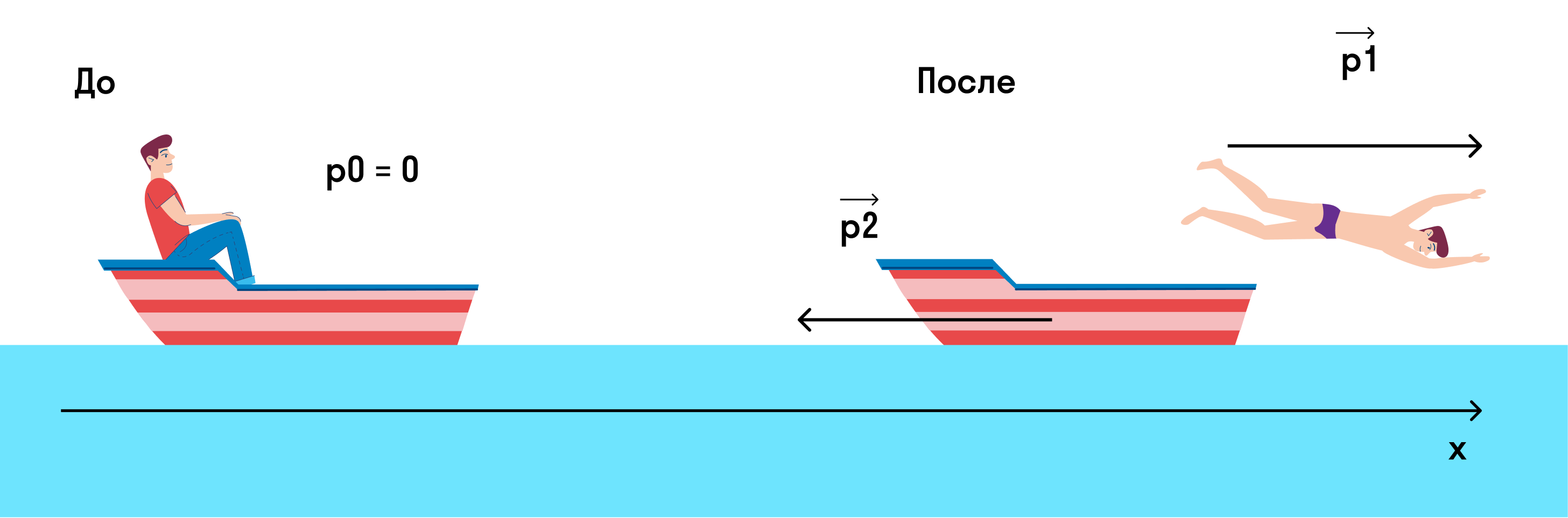
Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?
Решение:
Запишем закон сохранения импульса для данного процесса.
p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,
p1 — это импульс мальчика после прыжка,
p2 — это импульс лодки после прыжка.
Изобразим на рисунке, что происходило до и после прыжка.
Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2
Подставим формулу импульса.
mV1 = MV2
Выразим скорость лодки V2:
V2 = mV1/M
Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с
Ответ: скорость лодки после прыжка равна 0,5 м/с
Задачка посложнее
Решение: Для данной системы выполняется закон сохранения импульса:
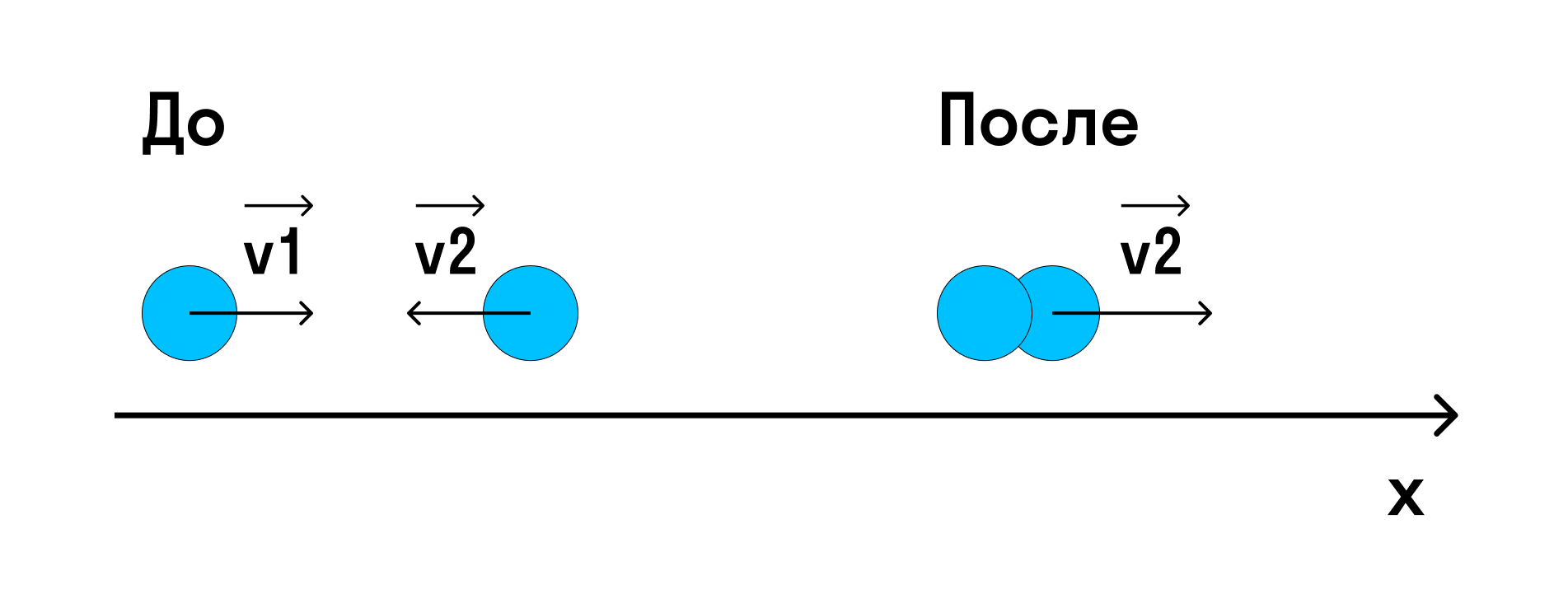
Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.
Спроецируем импульсы на ось х:
После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:
m1v1 — mv2 = (m1 + m2) v
Отсюда находим скорость тела, образовавшегося после удара:
v = (m1v1 — mv2)/(m1 + m2)
Переводим массу в килограммы и подставляем значения:
В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.
Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.
Ответ: скорость системы тел после соударения равна v = 0,2 м/с.
Второй закон Ньютона в импульсной форме
Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:
В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.
Преобразуем правую часть
Раскрыв скобки, получим
Заменим произведение массы и скорости на импульс:
То есть, вектор Δv⋅m – это вектор Δp.
Тогда второй закон Ньютона в импульсной форме запишем так
Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.
Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме
Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?
Решение:
Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).
Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.
Реактивное движение
В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.
Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.
Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:
Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.
Закон сохранения импульса позволяет оценить скорость ракеты.
mг vг = mр vр,
где mг — это масса горючего,
vг — скорость горючего,
vр — скорость ракеты.
Отсюда можно выразить скорость ракеты:
Скорость ракеты при реактивном движении
vр = mг vг / mр
mг — это масса горючего [кг]
vг — скорость горючего [м/с]
mр — масса ракеты [кг]
v р — скорость ракеты [м/с]
Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.
Закон сохранения импульса второй закон ньютона в импульсной форме
Два тела движутся по взаимно перпендикулярным пересекающимся прямым, как показано на рисунке. Модуль импульса первого тела равен а второго тела равен
Чему равен модуль импульса системы этих тел после их абсолютно неупругого удара? (Ответ дайте в килограммах на метр в секунду.)
В системе не действует никаких внешних сил, следовательно, выполняется закон сохранения импульса. Вектор полного импульса системы есть сумма векторов и
Так как эти вектора перпендикулярны, то модуль импульса системы равен по теореме Пифагора
Напомните, пожалуйста, определения центральных, неупругих и прочих ударов; посмотрел бы в интернете, только везде написано не по-русски. Объясните, пожалуйста, доходчиво для простого человека, а не физика.
В следующий раз постарайтесь все-таки найти 🙂 Я же не могу начать отвечать всем на такие вопросы. Но в качестве исключения, так и быть, поясню, по-простому:
Для чего в условии задачи приплетена неупругость удара? Ведь закон сохранения имьпульса справедлив для любого взаимодействия тел, если сумма внешних сил равна нулю.
Таково было желание автора задачи. Это условие излишне, но в этом нет ничего страшного, так часто случается в тестах, в связи с тем, одна задача с разными вопросами входит в несколько вариантах.
Добрый день.А разве абсолютно неупругий и абсолютно упругий удары не являются центральными ударами?заранее спасибо
Нет, это независимые способы классификации ударов: упругий/неупругий, центральный/нецентральный. Ведь, в бильярде, например, не все удары происходят центрально.
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? Ответ выразите в килограммах на метр в секунду и округлите до десятых.
Используя масштаб рисунка, определим модули импульсов тел a и b. Из рисунка видно, что и
Импульс всей системы равен
Так как вектора
и
перпендикулярны, то модуль импульса всей системы равен
Система состоит из двух тел a и b. На рисунке стрелками в заданном масштабе указаны импульсы этих тел. Чему по модулю равен импульс всей системы? (Ответ дайте в килограммах на метр в секунду.)
Сложим импульсы по правилу параллелограмма, суммарный импульс обозначен на рисунке красной стрелкой. Видно, что его длина равна 4 клеткам, следовательно, импульс системы по модулю равен
Второй способ (более длинный и менее удачный):
Используя масштаб рисунка, определим модули импульсов тел a и b. Из рисунка видно, что
Импульс всей системы равен Так как вектора
и
перпендикулярны, то модуль импульса всей системы равен
Система состоит из двух тел 1 и 2, массы которых равны 0,5 кг и 2 кг. На рисунке стрелками в заданном масштабе указаны скорости этих тел. Чему равен импульс всей системы по модулю? (Ответ дайте в килограммах на метр в секунду.)
Используя масштаб рисунка, определим величины скоростей тел: и
Вычислим модули импульсов тел:
и
Импульс всей системы равен Так как вектора
и
перпендикулярны, то модуль импульса всей системы равен
Второй закон Ньютона в импульсной форме
Любое тело, обладающее скоростью, обладает импульсом.
Скорость тела будет меняться, когда на него подействует сила и появится ускорение. Об этом сообщает второй закон Ньютона. А если изменяется скорость тела, то будет изменяться его импульс.
Второй закон Ньютона в импульсной форме описывает изменение импульса тела под действием силы.
Формула второго закона Ньютона в импульсной форме
Импульсная форма записи второго закона выглядит так:
Словами это выражение можно сформулировать так:
\(\overrightarrow <\Delta p>\left( \text <кг>\cdot \frac<\text<м>>
\( \overrightarrow < F \cdot \Delta t>\left( H \cdot \text <м>\right) \) – вектор импульса силы;
Слева и справа в формуле находятся два вектора. Так как между ними записан знак равенства, значит у векторов \(\overrightarrow <\Delta p>\) и \( \overrightarrow < F \cdot \Delta t>\) совпадают обе характеристики — направление и длина.
С помощью математики фразу «длины векторов равны» можно записать так:
\( \left| \overrightarrow <\Delta p>\right | = \left| \overrightarrow < F \cdot \Delta t>\right | \)
Как посчитать длину вектора, и как ее обозначать, читайте тут.
Пояснения и вывод формулы с помощью геометрии
Чтобы получить импульсный вид записи для второго закона, рассмотрим такую задачу.
Представим, что мы склонились над бильярдным столом и смотрим на него сверху. А в это время по столу катится бильярдный шар с какой-то постоянной скоростью.
Примечание: с постоянной скоростью, значит — с одной и той же скоростью. О такой скорости физики часто говорят «с неизменной скоростью», а математики применяют для нее запись \( \vec
Пусть для определенности масса шара равна двум килограммам.
\( m = 2 \left( \text <кг>\right) \)
Пусть до того, как мы подействовали на шар, он двигался по столу в направлении, указанном на рисунке 1а. Шар вначале движется по горизонтали (рис. 1а), вектор начальной скорости обозначен \( \vec
После удара шар будет катиться уже не по горизонтали на рисунке. Физики скажут: направление движения шара изменилось. Направление, в котором шар движется после удара, обозначено вектором \( \vec
Нам известны начальная и конечная скорости тела, а также, его масса. Мы можем вычислить импульс тела до удара (рис 2а), и после удара (рис 2б).
\( m \cdot \vec
\( m \cdot \vec
\) – импульс тела после удара (конечный).
Обратите внимание, что у векторов начального импульса \( \vec
\), так же, сонаправлен с вектором \( \vec
Для удобства совместим начала векторов \( \vec
\) (рис. 3). Зададимся вопросом, как из вектора начального импульса \( \vec
\) вектор?
Очевидно, нужно к вектору \( \vec
Подробнее о том, как складывать векторы, написано тут.
Сумму можно записать так:
Это уравнение записано в векторном виде. Стрелки над символами подчеркивают тот факт, что векторы складывают с помощью геометрии, то есть, учитывают их направления.
Выразим теперь вектор, обозначенный \( \overrightarrow <\Delta p>\). Для этого, из обеих частей уравнения вычтем вектор \( \vec
Видно, что вектор \( \overrightarrow <\Delta p>\) – это разница между конечным \( \vec
\) и начальным \( \vec
Физики для вектора \( \overrightarrow <\Delta p>\) используют такое название:
\( \overrightarrow <\Delta p>\left( \text <кг>\cdot \frac<\text<м>>
Рассмотрим теперь совместно векторы \( \overrightarrow <\Delta p>\) и \( \vec
Направления векторов совпадают, а длина – различается.
Примечание: Математики вместо выражения «длина вектора» употребляют термин «модуль вектора».
Предположим, у нас есть точный хронометр и мы измерили кусочек времени, в течение которого сила действовала на бильярдный шар.
Умножим теперь вектор \( \vec
Из рисунка 6 видно, что у векторов \(\overrightarrow <\Delta p>\) и \( \overrightarrow < F \cdot \Delta t>\) совпадают не только направления, но и длины.
Если у векторов совпадают обе характеристики, то их можно приравнять. Подробнее о том, какие у векторов есть характеристики, написано тут.
Это выражение называют вторым законом Ньютона, записанным в импульсной форме.
Примечания
1). Сумму векторов
можно теперь переписать в таком виде:
2). Складывать можно векторы, у которых размерность совпадает.
О сложении векторов простым языком написано тут.
Обратим внимание на размерность.
\( \overrightarrow < F \cdot \Delta t>\left( H \cdot c \right) \)
На первый взгляд, она отличается, но с помощью простых преобразований можно показать, что
\[ \large 1 \text <кг>\cdot \frac< 1\text<м>> <1 c>= 1 H \cdot 1 c \]
Вывод формулы с помощью алгебры
Второй закон Ньютона в импульсной форме можно получить из алгебраических соображений.
Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.
Применим выражение для ускорения
Полученное выражение является пропорцией. Применив одно из свойств пропорции, получим такое выражение:
В правой части находится вектор \(\overrightarrow <\Delta v>= \vec
Преобразуем правую часть
\(\overrightarrow<\Delta v>\cdot m = \left( \vec
Раскрыв скобки, получим
\(\overrightarrow<\Delta v>\cdot m = \vec
Подставляя их, получим
\(\overrightarrow<\Delta v>\cdot m = \overrightarrow<\Delta p>\)
То есть, вектор \(\overrightarrow <\Delta v\cdot m>\) – это вектор \(\overrightarrow <\Delta p>\).
Тогда второй закон Ньютона в импульсной форме запишем так
Импульс
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.
Импульс тела — это векторная величина, равная произведению массы тела на его скорость:
Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:
Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.
Второй закон Ньютона в импульсной форме
С учётом того, что ускорение тела равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:
Вносим константу под знак производной:
Как видим, в левой части получилась производная импульса:
Соотношение ( 1 ) и есть новая форма записи второго закона Ньютона.
Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.
Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.
Производную в формуле ( 1 ) можно заменить на отношение конечных приращений:
В задачах, как правило, интервал времени достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда — средняя сила, действующая на мяч со стороны стенки во время удара.
Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1 ):
 |
| Рис. 1. Изменение импульса |
Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен ) и отскакивает назад без потери скорости (импульс после удара равен ). Несмотря на то, что импульс по модулю не изменился ( ), изменение импульса имеется:
Геометрически эта ситуация показана на рис. 2 :
 |
| Рис. 2. Изменение импульса при отскоке назад |
Перепишем формулу ( 2 ) следующим образом:
или, расписывая изменение импульса, как и выше:
Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:
(Обратите внимание, что оказывается ещё одной возможной единицей измерения импульса тела.)
Словесная формулировка равенства ( 3 ) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.
Пример вычисления силы
В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.
Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом (рис. 3 ).
 |
| Рис. 3. К задаче (вид сверху) |
Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила — сила упругости, направленная перпендикулярно стене (рис. 4 ).
 |
| Рис. 4. К задаче |
 |
| Рис. 5. К задаче |
Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:
И тогда искомая средняя сила, действующая на шарик:
Импульс системы тел
Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами и соответственно. Импульс системы данных тел — это векторная сумма импульсов каждого тела:
Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1 ). Давайте выведем эту формулу.
Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть — результирующая внешняя сила, действующая на тело 1. Аналогично — результирующая внешняя сила, действующая на тело 2 (рис. 6 ).
 |
| Рис. 6. Система двух тел |
Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1 ):
Сложим равенства ( 4 ) и ( 5 ):
Но — это импульс системы тел 1 и 2. Обозначим также — это результирующая внешних сил, действующих на систему. Получаем:
Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6 ), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.
Формула ( 6 ) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.
Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:
Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4 ) и ( 5 ), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6 ) останется справедливым и в общем случае.
Закон сохранения импульса
Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.
Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:
Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.
Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.
 |
| Рис. 7. К задаче |
Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:
Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:
Импульс системы до удара — это сумма импульсов тел:
Из закона сохранения импульса ( 7 ) имеем:
Отсюда находим скорость тела, образовавшегося после удара:
Переходим к проекциям на ось :
По условию имеем: м/с, м/с, так что
Закон сохранения проекции импульса
Покажем это более строго. Спроектируем равенство ( 6 ) на ось :
Следовательно, проекция есть константа:
Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция импульса системы не меняется с течением времени.
Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.
 |
| Рис. 8. К задаче |
Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.