законы электрических цепей в операторной форме

20.03.202303.04.2023 admin 0 Комментариев

Законы электротехники в операторной форме

Мгновенные значения тока i(t) и напряжения u(t) на идеальных элементах электрических схем связаны между собой дифференциальной формой уравнений: u_R(t) = iR – для резистора; 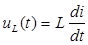— для катушки индуктивности; — для конденсатора.

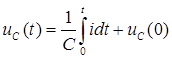
Применим к дифференциальным уравнениям преобразование Лапласа и получим соответствующее им операторные изображения: 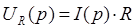— для резистора; — для катушки индуктивности; — для конденсатора.

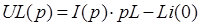
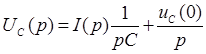
Операторным уравнениям будут соответствовать новые схемные представления элементов в операторной форме (см. табл.).

Здесь R, pL,1/pC – операторные сопротивления соответственно резистора R, катушки L и конденсатора C. Операторное сопротивление Z(p)любого участка схемыможно получить из его комплексного сопротивления Z(jw), заменив в выражении множитель jw на оператор p.

Li(0), u_C(0)/p – внутренние источники ЭДС, обусловленные запасами энергии в магнитном и электрическом полях в момент коммутации при t=0. Направления действия внутренних источников ЭДС принимаются по направлению тока i(0) для источника L i(0)и навстречу напряжению u_C(0) для источника u_C(0)/p.

Электричес-кая схема	Дифференциаль-ные уравнения	Операторные уравнения	Операторная схема
u	I(p) U(p)
u	U(p)
u	U(p)

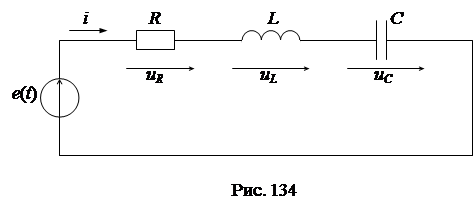
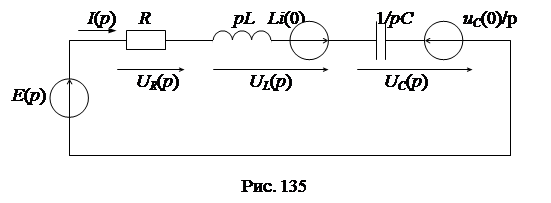
C учетом полученных соотношений любую электрическую схему для оригиналов функций i(t), u(t) можно заменить соответствующей ей операторной схемой для изображений функций I(p) ,U(p). Например, электрической схеме рис. 134 соответствует операторная схема, представленная на рис. 135.

законы электрических цепей в операторной форме

Для электрической схемы рис. 134 справедливо дифференциальное уравнение, составленное по 2-му закону Кирхгофа:

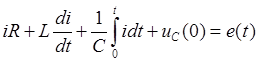
Для операторной схемы рис. 135 справедливо аналогичное уравнение, но в операторной форме:

, откуда следует:

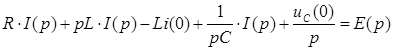
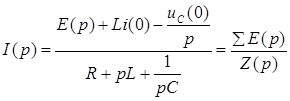
где 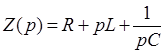– операторное сопротивление всей схемы, — сумма всех источников ЭДС контура, в том числе и внутренних.

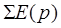
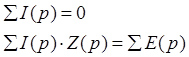Для сложных операторных схем справедливы 1-й и 2-й законы Кирхгофа в операторной форме:

Для расчета таких схем можно применять любые методы расчета линейных цепей: метод законов Кирхгофа, метод контурных токов, метод узловых потенциалов и другие. Порядок составления операторных уравнений для сложных схем аналогичен методу, тому порядку, который применяется по этому методу для электрических схем.

Источник

Законы электрических цепей в операторной форме

Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной , которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим моментом при этом в практическом плане является необходимость определения только независимых начальных условий, что существенно облегчает расчет переходных процессов в цепях высокого порядка по сравнению с классическим методом.

Изображение заданной функции определяется в соответствии с прямым преобразованием Лапласа:

(1)

В сокращенной записи соответствие между изображением и оригиналом обозначается, как:

или

Следует отметить, что если оригинал увеличивается с ростом t, то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются на практике при расчете переходных процессов, этому условию удовлетворяют.

В качестве примера в табл. 1 приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.

Таблица 1. Изображения типовых функций

Оригинал	Изображение
A

Некоторые свойства изображений

С использованием этих свойств и данных табл. 1, можно показать, например, что

Изображения производной и интеграла

В курсе математики доказывается, что если , то , где — начальное значение функции .

Таким образом, для напряжения на индуктивном элементе можно записать

или при нулевых начальных условиях

Отсюда операторное сопротивление катушки индуктивности

Аналогично для интеграла: если , то .

С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:

или при нулевых начальных условиях

откуда операторное сопротивление конденсатора

Закон Ома в операторной форме

Пусть имеем некоторую ветвь (см. рис. 1), выделенную из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу, при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем случае ненулевые.

Для мгновенных значений переменных можно записать:

Тогда на основании приведенных выше соотношений получим:

(2)

где — операторное сопротивление рассматриваемого участка цепи.

Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению ветви в цепи синусоидального тока при замене оператора р на .

Уравнение (2) есть математическая запись закона Ома для участка цепи с источником ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать операторную схему замещения, представленную на рис. 2.

Законы Кирхгофа в операторной форме

Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна нулю

Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости учета ненулевых начальных условий (если они имеют место). С их учетом последнее соотношение может быть переписано в развернутом виде

В первом случае в соответствии с законом Ома .

Во втором случае, т.е. при , для цепи на рис. 3 следует составить операторную схему замещения, которая приведена на рис. 4. Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных токов:

откуда ; и .

Переход от изображений к оригиналам

Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:

1. Посредством обратного преобразования Лапласа

которое представляет собой решение интегрального уравнения (1) и сокращенно записывается, как:

На практике этот способ применяется редко.

2. По таблицам соответствия между оригиналами и изображениями

В специальной литературе имеется достаточно большое число формул соответствия, охватывающих практически все задачи электротехники. Согласно данному способу необходимо получить изображение искомой величины в виде, соответствующем табличному, после чего выписать из таблицы выражение оригинала.

Например, для изображения тока в цепи на рис. 5 можно записать

Тогда в соответствии с данными табл. 1

что соответствует известному результату.

3. С использованием формулы разложения

Пусть изображение искомой переменной определяется отношением двух полиномов

где .

Это выражение может быть представлено в виде суммы простых дробей

(3)

где — к-й корень уравнения .

Для определения коэффициентов умножим левую и правую части соотношения (3) на ( ):

При

Рассматривая полученную неопределенность типа по правилу Лопиталя, запишем

Поскольку отношение есть постоянный коэффициент, то учитывая, что , окончательно получаем

(4)

Соотношение (4) представляет собой формулу разложения. Если один из корней уравнения равен нулю, т.е. , то уравнение (4) сводится к виду

В заключение раздела отметим, что для нахождения начального и конечного значений оригинала можно использовать предельные соотношения

которые также могут служить для оценки правильности полученного изображения.

С использованием теоремы об активном двухполюснике записать операторное изображение для тока через катушку индуктивности в цепи на рис. 6.

Ответ: .

Источник

№64 Законы электротехники в операторной форме.

Мгновенные значения тока i(t) и напряжения u(t) на идеальных элементах электрических схем связаны между собой дифференциальной формой уравнений:

для котушки индуктивности:

Применим к дифференциальным уравнениям преобразование Лапласа и получим соответствующее им операторные изображения:

для котушки индуктивности:

Таким образом, идеальным элементам R, L, C электрической схемы будут соответствовать новые схемные представления этих элементов в операторной схеме (см. табл.).

Здесь R, pL, 1/pC – операторные сопротивления соответственно резистора R, катушки L и конденсатора C. Операторное сопротивление Z(p) любого участка схемы можно получить из его комплексного сопротивления Z(jω), заменив в выражении множитель jω на оператор p.

Li(0), uC(0)/p – внутренние источники ЭДС, обусловленные запасами энергии в магнитном и электрическом полях в момент коммутации при t=0. Направления действия внутренних источников ЭДС принимаются по направлению тока i(0) для источника Li(0) и навстречу напряжению uC(0) для источника uC(0)/p.