жители древнего египта использовали при счете

Что такое египетская система счисления? История, описание, примеры

С непозиционной египетской системой счисления, которая употреблялась в Древнем Египте, нас наглядно знакомят немногие сохранившиеся папирусы. Примеры задач и их решения в них настолько интересны, что остается только сожалеть, что их так мало.

Из них видно, что математика и египетская система счисления были тесно связаны с хозяйственными нуждами и практическим применением. Каждый год после разлива Нила приходилось восстанавливать строения, заново межевать земельные наделы, рассчитывая площадь и границы, вести учет урожая, календарь.

Что такое позиционная и непозиционная системы счислений?

Ответ таится в самом названии. Если позиция цифры влияет на результат вычислений, перед нами позиционная система чисел, если нет – непозиционная.

Если мы пишем 12 – это двенадцать, а с теми же цифрами 21 – это двадцать один. По египетской системе счисления: чтобы написать 12, понадобится использовать два раза символ единицы и один раз символ десятки, а 21 будет выглядеть как один знак единицы и два знака десятки, то есть всего надо написать три знака.

К непозиционным относятся: знакомая нам римская система, в которой цифры обозначались римскими буквами, славянская система, где также каждая буква обозначала какую-то цифру или число. Римская система справлялась со своими функциями в Западной Европе до 16 века.

Непозиционные системы хорошо подходили для выполнения простых арифметических действий, так как сложные вычисления предполагали громоздкие записи, что не мешало в Древнем Египте успешному развитию алгебры и геометрии.

Как считали египтяне?

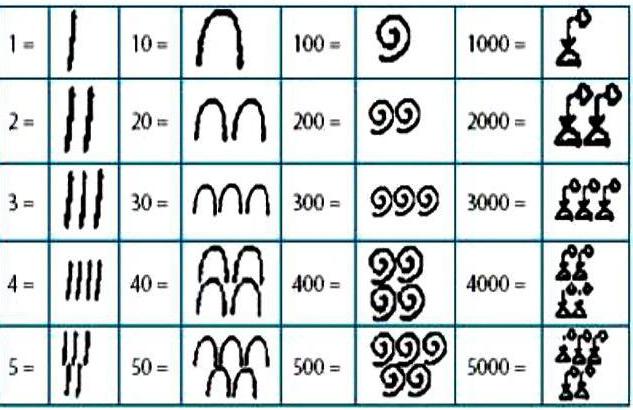
Что это такое – египетская система счисления? Чтобы написать какое-либо число, использовали иероглифы, обозначавшие определенные числа, сумма которых равнялась нужному значению.

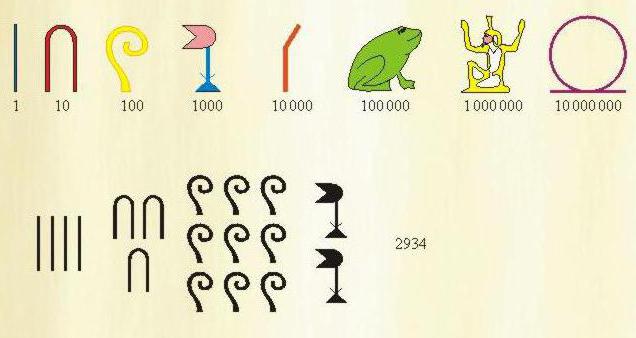
Специальные обозначения имелись для чисел 1, 10, 100, 1000, 10000, 100000, 1000000. При написании нужного числа каждое обозначение использовалось до 9 раз. Запись в египетской системе счисления шла по возрастанию: вначале единицы, потом десятки, сотни и так далее.

Причем писали, как правило, справа налево, но можно было и слева направо, сумма от этого не менялась. Использовалось и вертикальное написание, но тогда отсчет шел сверху вниз.

Использовалось два способа написания:

Экскурс в историю

История египетской системы счисления возникла в глубокой древности, первые рукописи с цифрами относятся ко второму тысячелетию до нашей эры. Денег тогда не было, поэтому система использовалась как для невероятных по сложности и величию математических задач, так и для решения ежедневных бытовых вопросов.

Ведь знание математики использовалось и при межевании земель, и при построении календарей, карт в астрономии, мореплавании, при строительстве дворцов, каналов и военных укреплений.

Египетская непозиционная система счисления применялась до 10 века нашей эры.

Она имела и мистическое значение, тайну которого унесли с собой жрецы, но частично приоткрыл миру Пифагор. У него есть труды, в которых он описывает символические значения, которые придаются цифровым иероглифам, написанные им после пребывания в Египте. Поэтому относят их описание к египетской системе счисления.

Сохранилось всего несколько папирусов тех времен, по которым можно понять, что уровень математики был высокий. Достоверно известно, что греки изучали древнеегипетскую математику. Одним из сокровенных знаний является египетская непозиционная система счисления.

Папирус Ахмеса

Папирус Ахмеса датируется 1650 г. до н.э., содержит 84 математические задачи. Он был найден в Фивах, хранится в Британском музее.

Все задачи в папирусе рассмотрены на конкретных примерах египетской системы счисления. В них показываются примеры расчетов с дробями, с целыми числами, делением и умножением.

Даны расчеты для нахождения площадей геометрических фигур: четырехугольника, круга, треугольника.

Сведения из папируса доказывают, что египетские математики умели извлекать корень, составлять арифметическую и геометрическую прогрессию, уравнения с неизвестными.

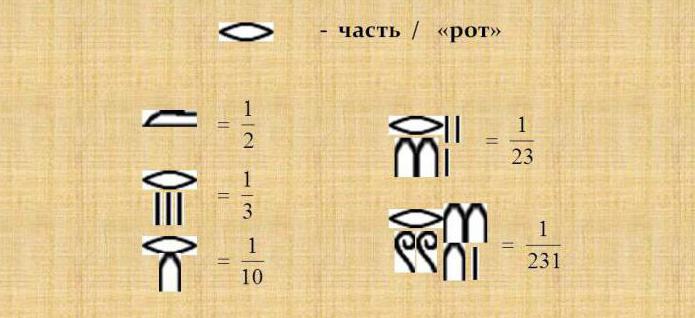
Аликвотные дроби

Интересно, что в расчетах использовались только аликвотные дроби, в которых числитель равнялся единице и обозначался таким знаком, а под ним писались значения знаменателя, а все другие дроби для расчетов вначале нужно было разложить до аликвотных. Но использовались и имели специальное обозначение дроби 2/3 и 3/4.

Для приведения обычных дробей в состояние аликвотных по египетской системе счисления нужно было потрудиться:

4/5 = 16/20 = 10/20 + 5/20 + 1/20 = 1/2+1/4 + 1/20

2/5 = 1/5 + 1/5, 2/7 = 1/4 + 1/28

3/7 = 12/28 = 24/56 = 14/56+7/56+3/56 = 1/4+1/8+1/18+1/56.

Складывались дроби современным способом: приведением к общему знаменателю, для многих значений имелись многочисленные готовые таблицы.

Умножение

Египтяне узнавали нужный результат, не зная таблицы умножения, но используя знание о том, что, если один множитель увеличить в два раза, а другой уменьшить, то результат не изменится:

Интересно, что этот способ умножения был известен на Руси, и считалось, что он пришел из Древнего Египта, а в Европе его называли русским.

Папирус Голенищева

Благодаря стараниям ученого-египтолога В. С. Голенищева, в Москве хранится папирус еще на 200 лет древнее папируса писца Ахмеса. Ученый купил его во время своей работы в Фивах.

Он был написан иератическим способом, курсивом, в нем рассматривается 25 задач, дано их описание по египетской системе счисления и решение. Его длина более 5 м при ширине 7 см. К этим задачам нет никаких комментариев, как и в предыдущем папирусе, есть только математические расчеты.

Он показывает, что египтяне умели вычислять площади треугольника, трапеции, прямоугольника, круга, а также объёмы пирамиды, призмы, параллелепипеда, цилиндра и усечённой пирамиды с большой точностью, а многие формулы полностью совпадают с современными.

При египетской системе счисления было вычислено число «пи» 3,16, которое почти соответствовало современному значению 3,14, хотя в те времена повсеместно на Востоке использовалось значение, равное 3.

Все вещи – суть числа

Считается, Пифагор прожил в Египте 22 года, глубоко изучая геометрию, философию, мистику цифр. Те открытия, которые позднее делала Пифагорейская школа, вполне могли быть совершены еще в Древнем Египте.

Поэтому считается, что труды Пифагора о мистике цифр, которые он написал позже, основаны на тайных знаниях, полученных им от египетских жрецов. Они не брали на обучение иностранцев, попал он к ним по высокой протекции, после собеседования с главным жрецом, который счел его достойным быть посвященным в тайны.

Числа были живыми сущностями, отражающими свойства пространства, музыки, энергии. Все можно выразить через математику, описав формулами видимые явления предсказать невидимые, опираясь на логику и математические закономерности.

Высота, ширина основания, угол наклона пирамиды Хеопса в Египте соответствуют математическому правилу построения пирамиды Пифагора, что также подтверждает взаимосвязь сделанных им открытий и знаний, полученных от древнеегипетских жрецов, использовавших египетскую систему счисления.

Работая с цифрами, древние мыслители не только понимали суть вещей, но и могли воздействовать на них.

Изучая математику Древнего Египта, использующую египетскую систему счисления, можно только восхищаться тем, как много было открыто людям за тысячи лет до нашей эры.

Источник

Жители древнего египта использовали при счете

Зарегистируйтесь или войдите с помощью соц.сетей, чтобы получить расширенные возможности

Математика в Древнем Египте

анная статья посвящена состоянию и развитию математики в Древнем Египте в период примерно с XXX по III век до н. э. Древнейшие древнеегипетские математические тексты относятся к началу II тысячелетия до н. э. Математика тогда использовалась в астрономии, мореплавании, землемерии, при строительстве зданий, плотин, каналов и военных укреплений. Денежных расчётов, как и самих денег, в Египте не было. Египтяне писали на папирусе, который сохраняется плохо, и поэтому наши знания о математике Египта существенно меньше, чем о математике Вавилона или Греции. Вероятно, она была развита лучше, чем можно представить, исходя из дошедших до нас документов — известно, что греческие математики учились у египтян.

Нам ничего не известно о развитии математических знаний в Египте как в более древние, так и в более поздние времена. После воцарения Птолемеев начинается чрезвычайно плодотворный синтез египетской и греческой культур.

1. Источники

Часть папируса Ахмеса. Задачи с 49 по 55.

Основные сохранившиеся источники относятся к периоду Среднего царства, времени расцвета древнеегипетской культуры:

От Нового царства до нас дошли несколько фрагментов вычислительного характера.

Авторы всех этих текстов нам неизвестны. Дошедшие до нас экземпляры — это в основном копии, переписанные в период гиксосов. Носители научных знаний тогда именовались писцами и фактически были государственными или храмовыми чиновниками.

Все задачи из папируса Ахмеса (записан ок. 1650 года до н. э.) имеют прикладной характер и связаны с практикой строительства, размежеванием земельных наделов и т. п. Задачи сгруппированы не по методам, а по тематике. По преимуществу это задачи на нахождение площадей треугольника, четырёхугольников и круга, разнообразные действия с целыми числами и аликвотными дробями, пропорциональное деление, нахождение отношений, возведение в разные степени, определение среднего арифметического, арифметические прогрессии, решение уравнений первой и второй степени с одним неизвестным.

Полностью отсутствуют какие бы то ни было объяснения или доказательства. Искомый результат либо даётся прямо, либо приводится краткий алгоритм его вычисления.

Такой способ изложения, типичный для науки стран древнего Востока, наводит на мысль о том, что математика там развивалась путём индуктивных обобщений и гениальных догадок, не образующих никакой общей теории. Тем не менее, в папирусе есть целый ряд свидетельств того, что математика в Древнем Египте тех лет имела или, по крайней мере, начинала приобретать теоретический характер. Так, египетские математики умели извлекать корни и возводить в степень, решать уравнения, были знакомы с арифметической и геометрической прогрессией и даже владели зачатками алгебры: при решении уравнений специальный иероглиф «куча» обозначал неизвестное.

2. Нумерация (запись чисел)

Иероглифическая запись числа 35736

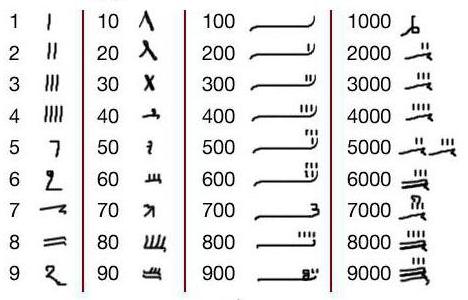
Древнеегипетская нумерация, то есть запись чисел, была похожа на римскую: поначалу были отдельные значки для 1, 10, 100, … 10 000 000, сочетавшиеся аддитивно (складываясь). Египтяне писали справа налево, и младшие разряды числа записывались первыми, так что в конечном счёте порядок цифр соответствовал нашему. В иератическом письме уже есть отдельные обозначения для цифр 1-9 и сокращённые значки для разных десятков, сотен и тысяч.

Любое число в Древнем Египте можно было записать двумя способами: словами и цифрами. Например, чтобы написать число 30, можно было использовать обычные иероглифы:

или то же самое написать цифрами (три символа десятки):

Иероглифы для изображения чисел

1	10	100	1,000	10,000	100,000	1,000,000

Умножение египтяне производили с помощью сочетания удвоений и сложений. Деление заключалось в подборе делителя, то есть как действие, обратное умножению.

Примеры изображения часто встречающихся дробей

1/2	1/3	2/3	1/4	1/5

Пример записи дробей из Папируса Ринда

Плита с гробницы принцессы Неферетиабет (2590—2565 до н. э., Гиза). Лувр

5 + 1⁄2 + 1⁄7 + 1⁄14 (= 5 5⁄7)

3. Арифметика

3.1. Знаки сложения и вычитания

Чтобы показать знаки сложения или вычитания использовался иероглиф

Если направление ног у этого иероглифа совпадало с направлением письма, тогда он означал «сложение», в других случаях он означал «вычитание».

3.2. Сложение

Если при сложении получается число большее десяти, тогда десяток записывается повышающим иероглифом.

Например: 2343 + 1671

Собираем все однотипные иероглифы вместе и получаем:

Окончательный результат выглядит вот так:

3.3. Умножение

Древнеегипетское умножение является последовательным методом умножения двух чисел. Чтобы умножать числа, им не нужно было знать таблицы умножения, а достаточно было только уметь раскладывать числа на кратные основания, умножать эти кратные числа и складывать.

Египетский метод предполагает раскладывание наименьшего из двух множителей на кратные числа и последующее их последовательное переумножение на второй множитель.

Этот метод можно и сегодня встретить в очень отдаленных регионах.

3.4. Разложение

Египтяне использовали систему разложения наименьшего множителя на кратные числа, сумма которых составляла бы исходное число.

Чтобы правильно подобрать кратное число, нужно было знать следующую таблицу значений:

1 x 2 = 2

2 x 2 = 4

4 x 2 = 8

8 x 2 = 16

16 x 2 = 32

Пример разложения числа 25:

Иероглифическая запись уравнения x(2/3 + 1/2 + 1/7 + 1) = 37

Таким образом «25» — это сумма трех слагаемых: 16, 8 и 1.

Пример: умножим «13» на «238»:

Итог: 13 х 238 = 3094

Известно, что 13 = 8 + 4 + 1. Каждое из этих слагаемых нужно умножить на 238. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094.

3.5. Уравнения

Пример задачи из папируса Ахмеса:

Найти число, если известно, что от прибавления к нему 2/3 его и вычитания из результата его трети получается 10.

4. Геометрия

В области геометрии египтяне знали точные формулы для площади прямоугольника, треугольника, трапеции и сферы, могли высчитывать объемы параллелепипеда, цилиндра, конуса и пирамид. Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как

S = ((a + c)/2) x ((b + d)/2) ;

эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику.

Египтяне предполагали, что площадь круга S диаметром d равна площади квадрата, сторона которого составляет 8/9 диаметра:

Ещё одна ошибка содержится в Акмимском папирусе: автор считает, что если радиус круга A есть среднее арифметическое радиусов двух других кругов B и C, то и площадь круга A есть среднее арифметическое площадей кругов B и C.

Вычисление объёма усечённой пирамиды: пусть мы имеем правильную усечённую пирамиду со стороной нижнего основания a, верхнего b и высотой h; тогда объём вычислялся по оригинальной, но точной формуле:

V = (a 2 + ab + b 2 ) x (h/3).

Реконструкция водяных часов по чертежам из Оксиринха

4.1. Египетский треугольник

Египетским треугольником называется прямоугольный треугольник с соотношением сторон 3:4:5.

4.2. Объём усечённого конуса

Древний свиток папируса, найденный в Оксиринхе, свидетельствует, что египтяне могли вычислять объём усечённого конуса. Эти знания ими использовались для сооружения водяных часов. Так, например, известно, что при Аменхотепе III были построены водяные часы в Карнаке.

Источник

Обозначение чисел и системы счисления в Древнем Египте и Вавилоне

Ищем педагогов в команду «Инфоурок»

Обозначение чисел и системы счисления в Древнем Египте и Вавилоне

МКОУ СОШ 3 с Кугульта

Обозначение чисел и система счисления в Древнем Египте…………….5

Обозначение чисел и система счисления в Вавилоне …………………. 9

Древние римляне говорили: «Слова улетают, написанное остается». И правда, сказанное сегодня может быть забыто завтра, а уж «что написано пером, того не вырубишь топором». Но еще долгое время после того, как появились названия чисел, люди их не записывали. Причина для этого была у них самая уважительная: они еще не умели писать. Поэтому, если кому-нибудь надо было переслать другому человеку сведения, где участвовали числа, прибегали к зарубкам на дереве или на кости, к узелкам на веревках и т. д.

Персидский царь Кир, начав войну со скифами, прика­ зал своим союзникам охранять переправу через Дунай. А так как они не умели считать, Кир оставил их вождям связку из 60 веревок с узлами и приказал каждый день развязывать один узел. «Когда все узлы будут развязаны,— сказал он,— можете разрушить переправу и уходить домой». Узлами на разноцветных шнурках «записывали» раньше числа жители Центральной Америки, но их система узелкового письма была весьма сложной.

Впрочем, глиняные шарики и другие фигурки, с помощью которых вели учет своих стад древние пастухи, тоже можно считать формой записи чисел. Но польза от такой записи была не слишком велика, а для изображения больших чисел она совсем не годилась. Шаг вперед был сделан, когда шарики и фигурки заменили их оттисками на мягкой глине. Эти оттиски имели форму больших и малых кругов, треугольников, квад­ратов, овалов и т. д. Такие знаки уже нельзя было переклады­ вать руками с места на место, убирать одни и добавлять дру­ гие. Вместо этого приходилось думать, мысленно выполняя операции над знаками.

Для управления государством понадобились специальные люди. Они вели учет поступавшим налогам, выдавали про­довольствие рабочим, строившим каналы и плотины, храмы и дворцы, ведали снабжением войска. А чтобы проверять этих людей, не допускать расхищения казны, нужна была строгая отчетность. Тут уж ни зарубками на бирках, ни узелками, ни глиняными фигурками нельзя было обойтись.

И вот примерно 5 тысяч лет тому назад было сделано заме­ чательное открытие. Ведавшие государственными доходами и расходами люди сообразили, что можно обозначать одним знаком не каждую голову скота, а сразу десять или сто голов, не один мешок зерна, а сразу шесть или шестьдесят мешков.

Русский поэт Николай Степанович Гумилев выразил зна­ чение этого открытия следующими словами:

«А для низкой жизни были числа.

Как домашний подъяремный скот,

Потому что все оттенки смысла

Умное число передает».

Целью данного проекта является: знакомство с обозначением чисел и системой счисления в древнейших рабовладельческих государствах – Египет и Вавилон.

— сравнение обозначений чисел и систем счислений Египта и Вавилона.

Обозначение чисел и система счисления в Древнем Египте

Больше чем на 6 тысяч километров протянулась по Африке могучая река Нил. Она надвое разрезает выжженную солнцем пустыню. Вдоль реки тянется узкая полоса очень плодородной земли. Каждый год в середине лета Нил разливается. Когда вода спадает, на полях остается слой ила, который служит отличным удобрением.

В долине Нила с незапамятных времен люди занимались земледелием. Примерно 5 с лишним тысяч лет назад там обра­ зовалось одно из первых на земле государств.

Древние египтяне были замечательными инженерами. Всем известно о пирамидах — огромных гробницах еги­петских царей (фараонов). В Египте насчитывается около 80 пирамид, расположенных неровной полосой на западном берегу Нила. Еще в древности говорили: «Все боится времени, но само время боится пирамид». И действительно, более четы­ рех с половиной тысячелетий стоят эти каменные горы, сло­ женные из сотен тысяч каменных блоков по 15 тонн каж­ дый (впрочем, некоторые ученые полагают, что пирамиды явля­ются скалами, обложенными со всех сторон такими каменными блоками). И если одни из этих блоков вырублены на месте, то другие приходилось везти за сотни километров. «Кубики», из которых сложены пирамиды, подогнаны друг к другу так, что между ними невозможно даже протиснуть почтовую от­ крытку. А ведь при строительстве пирамид египтяне приме­ няли лишь самые простые инструменты — у них не было в то время никаких подъемных приспособлений. Все делали рабы, которые использовали лишь рычаги и катки.

Строили египтяне и другие здания — дворцы, лабиринты и т. д. На кораблях из папируса они совершали далекие путе­шествия. Ясно, что они должны были и знать, и уметь очень много.

Кроме замечательных построек — пирамид, храмов и двор­ цов, до нас дошли многие записи, и даже большие рукописи, сделанные древними египтянами. Некоторые из них высечены на камне, а большая ч асть написана чернилами на папирусе — плотной бумаге, которую египтяне делали из тростника. Уче­ные-историки научились читать древнеегипетские рукописи. Поэтому мы представляем, как жили древние египтяне: чем они занимались, что знали, во что верили.

Некоторые из египетских рукописей специально посвящены математике. Это что-то вроде учебников, или, вернее, задач­ ников, где даны решения разных практических задач. Древ­ нейшая сохранившаяся математическая рукопись египтян написана около 4 тысяч лет назад. Она хранится в Москве — в Музее изобразительных искусств имени А. С. Пушкина — и называется Московским папирусом.

Другой математический папирус, написанный лет на двести- триста позднее Московского, хранится в Лондоне. Он называет­ ся «Наставление, как достигнуть знания всех темных вещей, всех тайн, которые скрывают в себе вещи. По старым памят­ никам писец Ахмес написал это». Рукопись так и называют папирусом Ахмеса или папирусом Райнда — по имени англи­ чанина, который разыскал и купил этот папирус в Египте.

В папирусе Ахмеса даются решения 84 задач на различные вычисления, которые могут понадобиться на практике.

Некоторые из этих задач показались бы довольно слож­ ными ученику-старшекласснику нашей школы. Представляете себе, как трудно было их решить 4 тысячи лет назад?! Ведь у древних египтян не было ни удобного способа записи чисел, ни наших правил арифметических действий, ни таблицы.

Большая часть задач папируса Ахмеса относится к арифме­тике: задачи на арифметические действия, на пропорциональ­ ное деление и т. д. При этом сгруппированы они не по математи­ ческому содержанию, а по тому, о чем идет в них речь.

Но некоторые из задач в папирусе Ахмеса имеют отвле­ ченный характер. Например, такая задача:

В доме 7 кошек, каждая кошка съедает 7 мышей, каждая мышь съедает 7 колосьев, каждый колос дает 7 растений, па каждом растении вырастает 7 мер зерна. Сколько всех вместе?

Тут интересно, что в задаче надо ответить на вопрос: сколь­ ко всех вместе? Автора задачи не интересует, о каких вещах или предметах идет речь, однородны они или разнородны,— важно только их общее количество. Значит, очень давно егип­ тяне уже представляли себе не число кошек, или колосьев, или мышей, а именно само по себе число. Но ведь это совсем не так просто.

Расшифровка системы счисления, созданной в Египте во времена первой династии (ок. 2850 до н.э. ), была существенно облегчена тем, что иероглифические надписи древних египтян были аккуратно вырезаны на каменных монументах.

— jj 1 проп — jj 5

Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.

В этих папирусах более древнее иероглифическое письмо уступило место скорописному иератическому письму, и это изменение сопровождалось использованием нового принципа обозначения чисел. Группа одинаковых символов заменялись более простой по начертанию пометой или знаком, например, девять записывалось как вместо , а семьсот как вместо

.

В этой записи число 6789 имело вид , причем знаки более высокого порядка располагались справа, а не слева.

Иероглифическая запись чисел использовалась преимущественно в официальных документах и текстах. Еще позднее иератическая система обозначения чисел уступила место демотическим системам записи.

Введение египтянами цифровых обозначений ознаменовало один из важных этапов в развитии систем счисления.

Обозначение чисел и система счисления в Вавилоне

Самым известным из государств Месопотамии был Вавилон (то же имя носил и главный город этого государства). Во время разливов Тигра и Евфрата землю Междуречья покрывал плодо­ родный ил. Вавилоняне, как и жители Египта, были земле­ дельцами. Только им приходилось труднее, чем египтянам. Текущие с Армянского нагорья Тигр и Евфрат разливаются очень бурно. Для защиты от наводнении приходилось строить дамбы, обносить поля и селения насыпями. А для строитель­ ства таких больших сооружений нужны знания. Не удиви­ тельно, что вавилоняне стали хорошими математиками.

Земля в Междуречье плодородная, но там не было ни метал­ лов, ни камня, ни леса, чтобы строить дома. Все это вавило­ нянам приходилось покупать у других народов. Поэтому Ва­ вилон раньше других стран стал вести большую торговлю. И как это всегда бывает, вместе с товарами вавилонские купцы привозили и знания других народов.

О вавилонской науке известно гораздо больше, чем о еги­петской. Дело в том, что папирус, на котором писали египтяне, был очень непрочным, да притом еще и горючим материалом. А вавилоняне писали, выдавливая острой палочкой клинья на табличке, сделанной из мягкой глины. Если писец делал ошибку, он мог стереть неверную запись и внести исправление. Но когда табличка была заполнена, ее обжигали в печи и она становилась твердой как кирпич. До нас дошли сотни тысяч таких табличек, сотни из которых посвящены математике, а десятки тысяч содержат хозяйственные расчеты. Поэтому мы и знаем много о вавилонской математике. Ученые установили даже, что в те времена происходили международные матема­тические съезды, на которые издалека приезжали математики других стран. Правда, что они там обсуждали, нам неиз­ вестно.

Многие знания вавилоняне получили от шумеров, которые до них населяли Междуречье. В частности, от них позаимст вовали они большую часть математических знаний. Эти знания были более обширными, чем у египтян. В Вавилоне умели ре­ шать более трудные задачи; у вавилонян была лучше разра­ ботана система записи чисел, в том числе и дробных. Хорошо разбирались вавилонские ученые и в движении звезд и планет.

Математика была нужна вавилонянам и при строитель­ стве дворцов и сооружений. До нас дошли сказания о висячих садах, построенных вавилонской царицей Семирамидой (что это такое, и сейчас не до конца ясно, быть может, сады с подзем­ ным орошением), о башне, которую хотели построить такой высокой, чтобы она достала до неба. И действительно, ученые, проводившие раскопки Вавилона, нашли остатки удивитель­ ных сооружений. Достаточно сказать, что этот город был окру­ жен двумя толстыми стенами, имевшими десятки метров в высоту. Нашли и остатки восьмиэтажной башни, высота кото­ рой достигала 82 м.

Применялась математика и в финансовых расчетах. Вави­лонские купцы давали деньги в долг под очень высокие про­ центы и разоряли крестьян и ремесленников, доводя их до рабства. Если долг не возвращался- вовремя, то на следующий год надо было платить проценты не только за занятую сумму, но и за набежавшие проценты на эту сумму. Все это требовало сложных математических расчетов.

Как и в Египте, самыми учеными людьми в Вавилоне были жрецы. Особенно прославились вавилонские жрецы своими знаниями по астрономии. И действительно, для своего времени они были замечательными астрономами. Вавилоняне пытались вычислять, предугадывать наперед пути движения планет на небе.

Особенно интересовались жрецы затмениями Солнца и Луны. Четыре с лишним тысячи лет назад по своим летописям они составили список всех затмений, которые были до этого. Оказалось, что солнечные затмения происходят через один и тот же промежуток времени. Значит, затмения можно пред­ сказывать? Жрецам это было очень важно. Жрец, который заранее знал и мог предсказать, что разгневанные боги по­ гасят Солнце, был в глазах темных людей великим волшеб­ ником. Разве можно в чем-нибудь ослушаться такого могучего колдуна?

Для того чтобы еще больше подчинить себе простой народ, вавилонские жрецы придумали специальную «науку» — астрологию. Они убеждали людей, что расположение звезд на небе влияет на судьбу человека, что по звездам можно пред­ сказывать будущее. Конечно, « предсказывать» по звездам могли только сами жрецы. Простой народ верил в эти «пред­ сказания» жрецов. Предсказания затмений подкрепляли веру в могущество жрецов. Для этого жрецам и нужно было знание астрономии.

Впрочем, и сейчас в Соединенных Штатах и Западной Европе в газетах печатают астрологические предсказания, и многие люди верят в них. Да и у нас есть еще люди, которые верят во влияние звезд на их жизнь. Так что с вавилонян спрос невелик: они жили, когда еще не было настоящей науки. Но они во многом и были зачинателями этой науки.

Казавшееся правдоподобным предположение относительно того, почему выбор пал на число 60 как на основу вавилонской системы счисления, и утверждавшее, будто это связано с тем, что продолжительность земного года считалась равной 360 дням, не получило подтверждения. Ныне принято считать, что шестидесятеричная система была выбрана из метрологических соображений: число 60 имеет много делителей.

Для малых чисел вавилонская система счисления в основных чертах напоминала египетскую. Одна вертикальная клинообразная черта (в раннешумерских табличках – небольшой полукруг) означала единицу; повторенный нужное число раз, этот знак служил для записи чисел меньше десяти; для обозначения числа 10 вавилоняне, как и египтяне, ввели новый коллективный символ – более широкий клиновидный знак с острием, направленным влево, напоминающий по форме угловую скобку, (в раннешумерских текстах – небольшой кружок).

— 1 ррр — 10

Но для записи чисел больше 59 древние вавилоняне впервые использовали новый принцип – одно из самых выдающихся достижений в развитии систем обозначений чисел – принцип позиционности, т.е. зависимости значения символа от его местоположения в записи числа.

Вавилоняне заметили, что в качестве коллективных символов более высокого порядка можно применять уже ранее использованные символы, если они будут занимать в записи числа новое положение левее предыдущих символов.

Так, например, число 302 будет иметь вид:

оло , то есть 302 = 5 х 60 + 2

р рр ррр , то есть 3725 = 1 х 60 х 60 + 2 х 60 + 5

При отсутствии разряда вставлялся значок , игравший роль нуля. Однако отсутствие низшего разряда не обозначалось, и

Шестидесятеричная запись целых чисел не получила широкого распространения за пределами Ассиро-вавилонского царства, но шестидесятеричные дроби проникли далеко за эти пределы: Ближний Восток, Средняя Азия, Северная Африка, Западная Европа пользовались ими. Они широко применялись, особенно в астрономии, вплоть до изобретения десятичных дробей, т. е. до начала XVII века.

В данной работе были рассмотрены системы счисления и обозначения чисел двух древнейших государств – Египта и Вавилона.

Вавилон и Египет, как государства возникли на самых плодородных местах. Собрать хороший урожай, конечно, не просто. Надо уметь обработать землю, выбрать и вовремя посеять семена, выпалывать сорняки, поливать. Земледельцам приходилось отводить воду из рек на поля, прорывать каналы, да так, чтобы вода текла туда, куда нужно. В тех местах, где поля были выше реки, надо было поднимать воду наверх. Приходилось ломать голову над тем, как облегчить эту тяжёлую работу.

Народам-земледельцам, для того чтобы прожить и прокормится, нужно было знать гораздо больше, чем кочевникам-скотоводам. Жизнь заставляла их учиться быстрее. Поэтому у земледельческих народов математика из набора отдельных простейших правил постепенно стала превращаться в науку.

Данная работа может использоваться как дополнительный материал на уроках математики и во внеклассной работе.

Источник