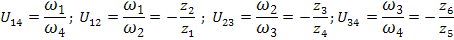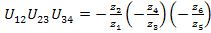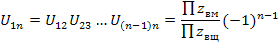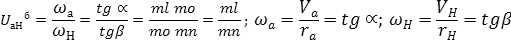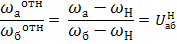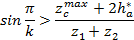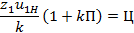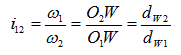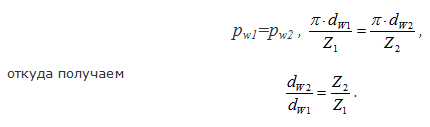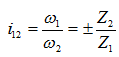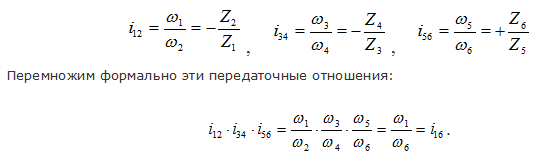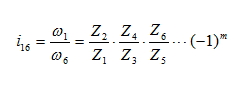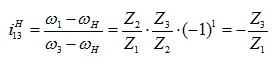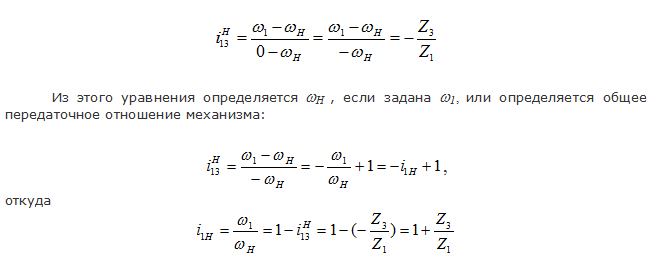зубчатые механизмы передаточные отношения сложных зубчатых механизмов ступени механизмов

Зубчатые механизмы передаточные отношения сложных зубчатых механизмов ступени механизмов

Сложными зубчатыми механизмами называются механизмы с зубчатыми передачами с числом зубчатых колес больше двух. Это могут быть механизмы с оригинальными структурными схемами или механизмы, образованные последовательным и (или) параллельным соединением простейших типовых зубчатых механизмов.
Механизмы, в которых кинематические цепи образуют один или несколько замкнутых контуров и в которых входной поток механической мощности в процессе передачи и преобразования делится на несколько потоков, а затем суммируется на выходном звене, называются многопоточными механизмами. Распределение передаваемых усилий по нескольким кинематическим парам уменьшает нагрузку на элементы пар и позволяет существенно уменьшать габаритные размеры и массу механизмов. Многозонный контакт звеньев механизма существенно увеличивает жесткость механизма, а за счет осреднения ошибок и зазоров, уменьшает мертвый ход и кинематическую погрешность механизма. Однако, за счет образования в структуре механизма внутренних контуров, число избыточных или пассивных связей в механизме увеличивается. Поэтому при изготовлении и сборке механизма необходимо либо повышать точность деталей, либо увеличивать зазоры в кинематических парах.
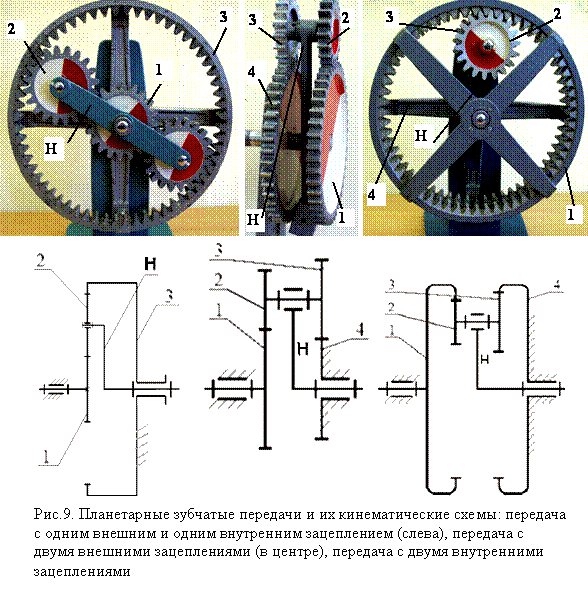
Сложные зубчатые механизмы, в которых ось хотя бы одного колеса подвижна, называются планетарными механизмами. К типовым планетарным механизмам относятся:

В таблице 15.1 приведены структурные схемы типовых планетарных механизмов, а также диапазоны рекомендуемых передаточных отношений и ориентировочные значения КПД при этих передаточных отношениях.

Источник

Передаточные отношения сложных зубчатых механизмов с неподвижными осями

Последовательный (ступенчатый) ряд зубчатых колес.

, т.о. для получения общего передаточное отношения следует перемножить передаточное отношения отдельных ступеней.

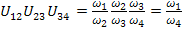
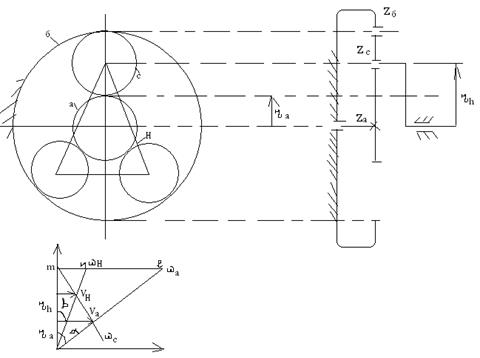
42. Структура и кинематика планетарной передачи

Планетарные передачи с внутренним и внешним зацеплением (Ряд Джеймса)

а – центральное зубчатое колесо, с – сателлит, б – неподвижное, Н – водило.

43. Основное уравнение кинематики планетарного ряда

Соотношение между угловыми скоростями и звеньями дифференциального механизма дает формула Виллиса. Для ее вывода используется метод инверсии, который заключается в том, что всем звеньям механизма сообщается дополнительное вращение , равное по абсолютной величине угловой скорости водилы, но противоположное по направлению. В результате суммарного движения получаем механизм с остановленным водилой и неподвижными осями зубчатых колес.

— основное уравнение кинематики дифференциального механизма.

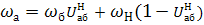
Планетарные зубчатые механизмы

Различают два типа планетарных механизмов:

1. Эпициклические механизмы, в которых наряду с зубчатыми колёсами с подвижными осями, имеются хотя бы одно колесо жёстко связанное со стойкой (степень подвижности меньше 1)

2. Дифференциальные механизмы, в которых все звенья подвижны (имеют степень подвижности больше 1). Дифференциальные механизмы служат для сложения или вычитания угловых скоростей звеньев.

Преимущества планетарных механизмов:

1)Большое передаточное отношение И=1-10 12 (пример: дорожный каток)

2)Малый вес и габарит

3)Высокий КПД

4)Лёгкость разветвлений передаваемых мощностей и силовых потоков

5)Возможность автоматизации управления.

Недостаток: трудность, сложность сборки

Примечание: дифференциалы главных передач автомобилей, колёсные передачи. Используется в тягачах, в дорожных машинах, в авиационной технике.

Источник

Зубчатые механизмы передаточные отношения сложных зубчатых механизмов ступени механизмов

Лабораторная работа №14

Определение передаточных отношений зубчатых передач

Цель работы – изучить различные виды зубчатых передач, научиться определять тип и вид зубчатых передач, их передаточные отношения и передаточные числа.

Зубчатая передача – трехзвенный механизм, в котором два подвижных звена являются зубчатыми колесами, образующими с неподвижным звеном вращательную или поступательную пару (рис.1).

Рис.1. Зубчатая передача с внешним зацеплением

Шестерня – зубчатое колесо передачи с меньшим числом зубьев.

Колесо – зубчатое колесо передачи с большим числом зубьев.

Ведущее зубчатое колесо – зубчатое колесо передачи, которое сообщает движение парному зубчатому колесу.

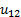
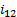
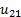
Передаточное отношение u 12 (иногда используется обозначение i 12 ) определяется при ведущем колесе 1, передаточное отношение u 21 определяется если ведущим является колесо 2:

Рис.2. Виды зубчатых зацеплений: внешнее (слева) и внутреннеее

Передаточное число зубчатой передачи – это отношение числа зубьев ведомого зубчатого колеса к числу зубьев ведущего колеса. Передаточное число зубчатой передачи определяется по формуле:

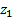
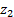
где z 1 и z 2 — числа зубьев колес 1 и 2, соответственно.

Знак «+» берется для внешнего зацепления (рис.1 и рис.2), знак «–» для внутреннего зацепления. Виды зацеплений приведены на рис.2. Знаки учитываются только для зубчатых передач с параллельными осями вращения колес.

Типы зубчатых передач

Аксоидная поверхность зубчатого колеса – каждая из поверхностей, описываемых мгновенной осью относительного движения зубчатых колес передачи, относящаяся к данному зубчатому колесу. В цилиндрической и конической передачах начальные поверхности совпадают с аксоидными.

Ортогональная зубчатая передача (показан на рис.3) – коническая зубчатая передача, угол между осями которой равен 90°.

Неортогональная зубчатая передача – коническая зубчатая передача, угол между осями которой отличен от 90°.

Рис.3. Типы зубчатых передач (слева), коническая (в центре), винтовая зубчатая передача

Для конических зубчатых передач и передач со скрещивающимися осями передаточное отношение определяется по тем же формулам, что и для цилиндрических передач, но без учета знаков.

Рис.4. Червячная (слева) и гиперболоидная зубчатая передача

Виды зубчатых колес

Рис.5. Виды зубчатых колес: цилиндрическое косозубое (слева), шевронное (в центре),

В зависимости от вида зубьев зубчатые колеса цилиндрических передач делятся на прямозубые (рис.3 слева), косозубые и шевронные (рис.5). Зубчатые колеса конических передач – на прямозубые (рис.5), тангенциальные, с круговым зубом (рис.3 в центре), с криволинейным зубом.

В зависимости от профиля зубьев зубчатые колеса и передачи делятся на эвольвентные (рис.2, рис.6), циклоидальные, зубчатые колеса цилиндрической передачи Новикова (рис.6), профили зубьев которой контактируют по дуге окружности.

Рис.6. Виды зубчатых колес: с эвольвентным профилем зубьев (слева),

зубчатые колеса передачи Новикова

МНОГОСТУПЕНЧАТЫЕ ЗУБЧАТЫЕ ПЕРЕДАЧИ

Зубчатые передачи с неподвижными осями вращения колес

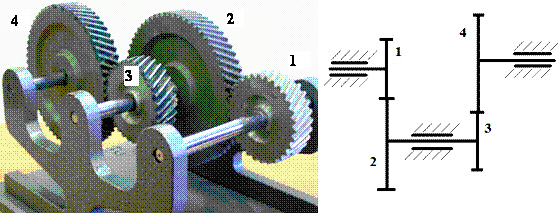
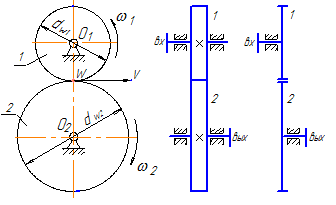
Рис.7. Двухступенчатая зубчатая передача и ее кинематическая схема

Простейший зубчатый механизм (рис.1) состоит из двух зубчатых колес ведущего и ведомого, которые одновременно являются входным и выходным, соответственно. Для получения необходимых передаточных отношений в машинах и приборах часто применяют сложные зубчатые механизмы, имеющие кроме входного и выходного колес несколько промежуточных колес, каждое из которых вращается вокруг своих осей. Применение сложных механизмов объясняется различными причинами. Например, оси входного и выходного колес расположены далеко друг от друга. В этом случае непосредственная передача вращения при помощи двух колес потребовала бы создания передачи с большими габаритами. В другом случае передаточное отношение может быть очень велико или очень мало, тогда удобно между входным и выходным колесами иметь промежуточные колеса со своими осями. Передавая вращение с входного колеса на промежуточные колеса и с них на выходное колесо, мы как бы последовательно отдельными ступенями изменяем скорость вращения звеньев, получая в результате требуемые передаточные отношения между входным и выходным колесами.

Таким образом, сложный механизм передачи можно разделить на отдельные части – ступени, каждая из которых представляет собой два колеса, образующих зубчатое зацепление. В соответствии с указанным бывают одно- и многоступенчатые передачи, по большей части двух- и трехступенчатые (рис.7). Количество ступеней равно числу зубчатых зацеплений, образованных зубчатыми колесами механизма. Одно колесо может входить в несколько ступеней (рис.8). Любая ступень может представлять собой цилиндрическую, коническую, червячную, глобоидную и т.д. передачу. На рис.8 показан многоступенчатый механизм, содержащий цилиндрические и конические ступени.

Рис.8. Многоступенчатая зубчатая передача

с паразитными колесами

Общее передаточное число (отношение) зубчатой передачи при последовательном соединении ступеней равно произведению передаточных чисел входящих в них ступеней. Для передачи на рис.7:

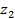
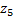
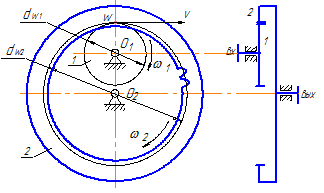
Знаки ступеней не учитываются так как передача включает кроме цилиндрических и конические ступени. Зубчатые колеса с числами зубьев z 2 и z 5 являются паразитными, каждое из них входит в два зубчатых зацепления.

Планетарные зубчатые передачи

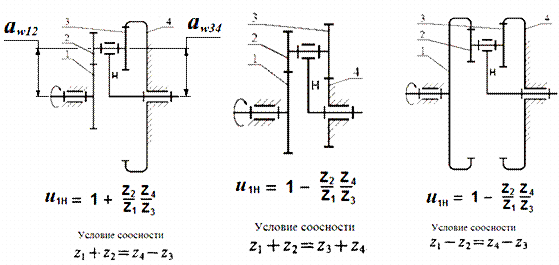
Передаточное число планетарного механизма определяется по формуле:

u 1 H (4) =1- u 14 H ; u 14 H = u 12 H u 34 H ;

На рис.10 приведены формулы для определения передаточных чисел планетарных механизмов. Передаточные числа между подвижным центральным колесом и водилом связаны соотношением:

Рис.10. Определение передаточных чисел планетарных механизмов

При выборе чисел зубьев колес планетарных зубчатых передач для них проверяются условия:

1. Условие соосности, обеспечивающее совпадение осей центральных зубчатых колес и водила: a w 12 = a w 34 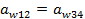(рис.10). Условия, приведенные на рис.10, получены для планетарных передач, зубчатые колеса которых имеют одинаковый модуль.

2. Условие соседства, обеспечивающее совместное размещение нескольких сателлитов по общей окружности в одной плоскости, без соприкосновения вершин зубьев соседних сателлитов:

sin π k > z c max +2 h a * z 1 + z 2

Условие соседства получено для планетарных передач, у которых сателлиты располагаются равномерно по окружности водила.

3. Условие сборки зубчатых колес передачи, определяющее возможность сборки передачи при использовании нескольких сателлитов:

z 1 u 1 H k 1+ k П =Ц

Макеты цилиндрических, конических, червячных, многоступенчатых и планетарных зубчатых механизмов.

Порядок выполнения работы

1. Получить задание и лабораторные макеты у преподавателя.

Каждый студент должен определить передаточное отношение и передаточное число пяти зубчатых передач:

1) цилиндрической зубчатой передачи;

2) конической зубчатой передачи;

3) зубчатой передачи со скрещивающимися осями;

4) многоступенчатой передачи с неподвижными осями колес;

5) планетарной зубчатой передачи.

2. Для каждой передачи:

2.1. Нарисовать кинематическую схему.

2.2. Дать полное название зубчатой передачи (определить ее тип и вид). Например, механизм, показанный на рис.7, называется цилиндрическая косозубая эвольвентная зубчатая передача.

2.3. Определить подвижность передачи по формуле Малышева для плоских механизмов.

2.4. Опытным путем определить передаточное отношение зубчатой передачи. Для этого посчитать число оборотов ведущего колеса соответствующее целому числу оборотов ведомого колеса.

2.5. Рассчитать передаточное число аналитически. Для чего посчитать числа зубьев колес передачи и по формулам найти передаточное число.

Для сложных зубчатых передач определить количество ступеней, указать паразитные колеса. Рассчитать передаточное число механизма, выразив его через числа зубьев колес.

2.6. Для планетарной передачи проверить выполнения условий соосности, соседства и сборки.

2.7. Составить сложную зубчатую передачу, соединив последовательно три из рассмотренных зубчатых передач. Нарисовать ее кинематическую схему и опредилить общее передаточное отношение.

2.8. Все результаты занести в отчет по лабораторной работе.

1. Перечислить звенья, входящие в простейшие зубчатые механизмы.

2. Перечислить звенья, входящие в сложные зубчатые механизмы.

3. Цель использования многоступенчатых передач.

4. Перечислить основные типы зубчатых передач.

5. Написать формулу для определения передаточного числа многоступенчатой зубчатой передачи.

6. Написать формулу для определения передаточного числа одноступенчатой зубчатой передачи.

7. В чем достоинства и недостатки прямозубых и косозубых зубчатых колес?

9. Зачем устанавливают несколько сателлитов в планетарном механизме?

10. Как определить передаточное число планетарной зубчатой передачи?

11. Какие условия проверяются для планетарной передачи? В чем их смысл?

12. Когда учитываются знаки передаточных чисел ступеней зубчатой передачи?

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21

Источник

iSopromat.ru

Рассмотрим кинематику основных видов зубчатых механизмов:

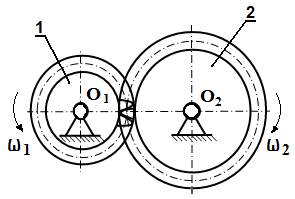
Одна пара зубчатых колес

При пересопряжении зубьев следующий зуб второго колеса должен попасть в следующую впадину первого, т.е. шаги на начальных окружностях находящихся в зацеплении колес должны быть одинаковыми:

Таким образом, для одной пары колес передаточное отношение прямо пропорционально отношению угловых скоростей и обратно пропорционально отношению чисел зубьев колес, составляющих пару:

Знак передаточного отношения показывает направление вращения колеса на выходе по отношению к направлению вращения на входе:

На рисунке 35 дана фронтальная проекция передач, а также их условное изображение на кинематических схемах при виде сбоку (или в разрезе).

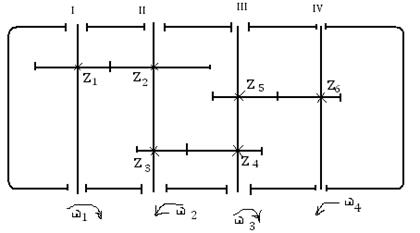
Многоступенчатая передача

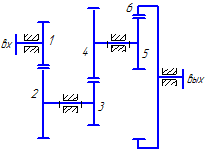
Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый механизм. Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей. Схема одного из таких механизмов приведена на рисунке 36.

Запишем передаточные отношения для каждой пары колес данного механизма:

Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:

В этой формуле “m” – число передач внешнего зацепления (если число передач внешнего зацепления четное, то знак «+», т.е. колеса на входе и на выходе вращаются в одну сторону; если нечетное, то знак «–». Количество передач внутреннего зацепления не учитывается, т.к. внутреннее зацепление не изменяет направление вращения).

В приведенном примере m=2 (пары Z_1* Z₂ и Z_3* Z₄; пара Z_5* Z₆ – пара внутреннего зацепления) и, таким образом, колеса «1» и «6» вращаются в одну сторону.

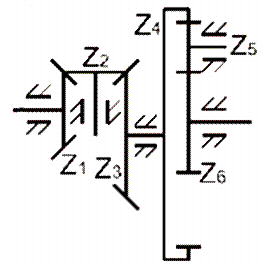
Планетарные и дифференциальные механизмы

В практике применяются зубчатые механизмы, имеющие колеса с подвижными геометрическими осями (сателлиты). Такие механизмы называются планетарными (если имеют одну степень свободы) или дифференциальными (если степень свободы равна двум).

Планетарные и дифференциальные механизмы позволяют получить более высокий кинематический эффект, более высокий кпд, более удобную компоновку. Дифференциальные механизмы позволяют также раскладывать одно движение на два или складывать два движения в одно.

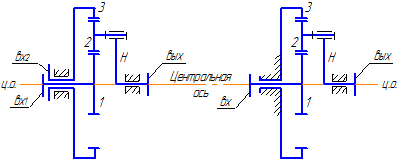
На рисунке 37 приведен пример дифференциального (рисунок 37 а) и планетарного механизмов (рисунок 37 б). В этих механизмах колесо «2» имеет подвижную геометрическую ось – это и есть сателлит.

Неподвижная геометрическая ось, вокруг которой движется ось сателлита, называется центральной осью. Колеса, геометрические оси которых совпадают с центральной, также называются центральными (на рисунке 37 колеса «1» и «3» – иногда такие колеса называют солнечными). Звено, соединяющее ось сателлитов с центральной осью, называется водилом (водило обычно обозначается «H»).

При кинематическом исследовании дифференциальных и планетарных механизмов применяется метод обращения движения (по-другому его называют методом остановки водила). Смысл этого метода заключается в том, что если всем звеньям системы добавить (с любым знаком) одну и ту же скорость, то характер относительного движения этих звеньев не изменится.

Добавим всем этим звеньям угловую скорость (– ω_H ). Тогда они будут иметь следующие скорости: ( ω₁– ω_H ), ( ω₂ – ω_H ), ( ω₃ – ω_H ), ( ω_H – ω_H ) = 0. Водило стало неподвижным, значит и ось сателлита 2 также стала неподвижной, т.е. механизм превратился в обычный многоступенчатый механизм с неподвижными осями всех зубчатых колес.

Записываем уравнение передаточного отношения между центральными колесами этого многоступенчатого механизма (для того, чтобы отличить передаточное отношение механизма с остановленным водилом от первоначально заданного, в верхнем индексе ставят обозначение водила H. Для данного примера читается – передаточное отношение от первого к третьему при остановленном водиле):

Формулу такого типа, полученную на основе метода обращения движения, называют формулой Виллиса. В данном конкретном механизме (рисунок 38) имеется еще одна особенность – колесо 2 входит последовательно в два зацепления (с первым и третьим колесами), являясь ведомым для первого колеса и ведущим – для второго.

В результате в уравнении его число зубьев сократилось, т.е. его число зубьев не влияет на общее передаточное отношения механизма. Такие колеса часто называют «паразитными», хотя правильно их называть ведомо-ведущими.

Полученная формула является универсальной для обоих механизмов, изображенных на рисунке 37. Дифференциальный механизм, изображенный на рисунке 37а, имеет две степени свободы, а поэтому для определенности движения надо задать законы движения двум звеньям. При этом возможны следующие варианты:

Таким образом, планетарный механизм это частный случай дифференциального, когда одно из центральных колес неподвижно (заторможено).

Поэтому решаются эти механизмы совершенно одинаково, по одним и тем же уравнениям, только в планетарном механизме для неподвижного колеса в уравнение подставляется значение угловой скорости, равное нулю. Для изображенного на рисунке 37б планетарного механизма:

Здесь приведен конкретный пример решения, но на самом деле на этом примере надо усвоить метод решения, подход к решению такого рода задач, т.к. метод один, но для каждой схемы механизма будут получаться свои уравнения.

Сложные механизмы

Существуют механизмы, включающие в свой состав различные части (обычные, планетарные, дифференциальные). В этом случае необходимо разделить механизм на части, записать уравнения передаточных отношений для каждой из них, используя соответствующий метод решения.

Совместным решением полученных алгебраических уравнений находят общее передаточное отношение механизма. (Пример см. в рекомендациях по выполнению расчетно-графического задания).

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник