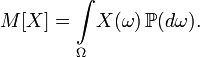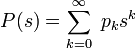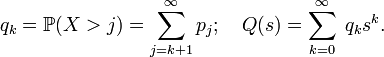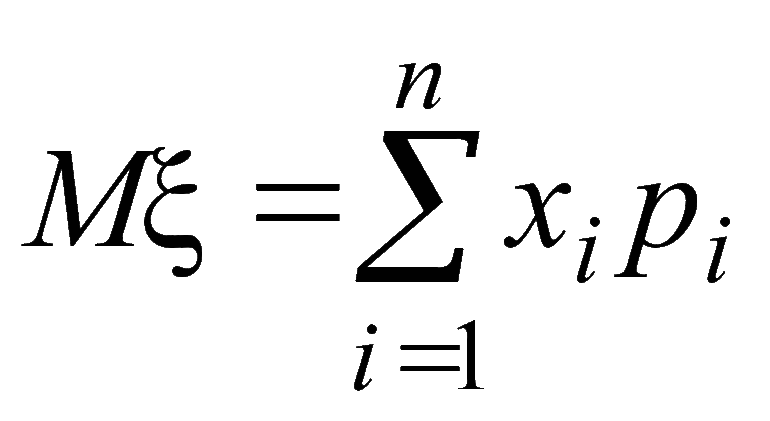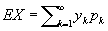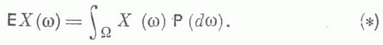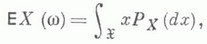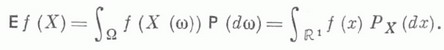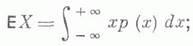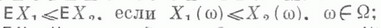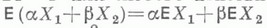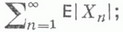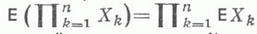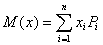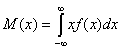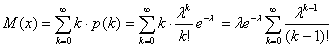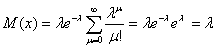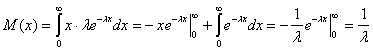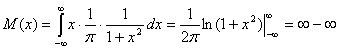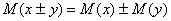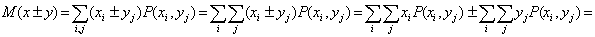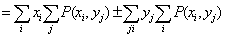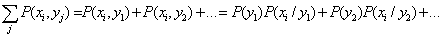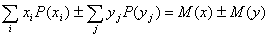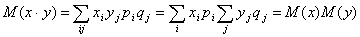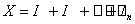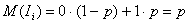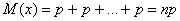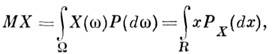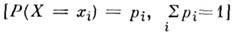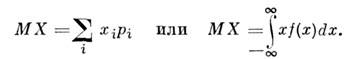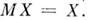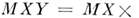Что такое математическое ожидание
Что такое математическое ожидание
Ожидание математическое
Содержание
Определение
Основные формулы для математического ожидания
Математическое ожидание дискретного распределения
то прямо из определения интеграла Лебега следует, что
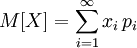
Математическое ожидание целочисленной величины
Теперь возьмём производящую функцию Q(s) последовательности «хвостов» распределения <qk>
Математическое ожидание абсолютно непрерывного распределения
Математическое ожидание случайного вектора
Пусть 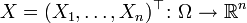
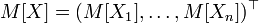
то есть математическое ожидание вектора определяется покомпонентно.
Математическое ожидание преобразования случайной величины
Пусть 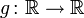
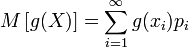
если X имеет дискретное распределение;
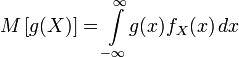
если X имеет абсолютно непрерывное распределение.
Если распределение 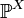
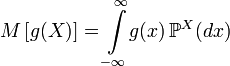
Простейшие свойства математического ожидания
Дополнительные свойства математического ожидания
Примеры
равно среднему арифметическому всех принимаемых значений.
то есть математическое ожидание X не определено.
См. также
Литература
Полезное
Смотреть что такое «Ожидание математическое» в других словарях:
Ожидание математическое — см. Математическое ожидание … Большая советская энциклопедия
Математическое — обеспечение автоматизированной системы МО Совокупность математических методов, моделей и алгоритмов, применяемых в АС Источник: ТЕРп Карачаево Черкесская Ре … Словарь-справочник терминов нормативно-технической документации
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Краткое описание
Чтобы понять смысл условного математического ожидания случайной величины, необходимо изучить ряд правил, а также ознакомится с примерами, дабы в будущем можно было избежать грубых ошибок. Одной из важнейших числовых характеристик дискретной величины является матожидание. Для изучения всех нюансов необходимо ввести понятие системы случайных процессов. Если представить значение в виде графика, то итоговое ожидание будет выступать в виде некоторого центра массы, изображённой на графике фигуры. Для решения классической задачи можно задействовать следующую формулу: Е (х) = Х1О1 + Х1О2 + … + Х n О n.
Расшифровка формулы выглядит следующим образом:
В теории вероятности специалистам удалось доказать, что среднее значение постоянной величины даже после многочисленных испытаний всё равно будет стремиться к матожиданию. В некоторых случаях результат может быть отрицательный. А это значит, что если количество итоговых испытаний слишком велико, то среднее значение обязательно будет равно матожиданию (прогноз среднего значения). Для более тщательного изучения темы специалисты рекомендуют использовать следствие (теорема с небольшим доказательством, которое следует из другой теоремы).
Гораздо проще разобраться в этой теме в том случае, если изучить наглядный пример. Если человек несколько раз бросит самый обычный шестигранный игральный кубик, и будет записывать все выпавшие значения, то при большом количестве испытаний можно получить число 3,5. Аналогичный результат будет достигнут и в том случае, если просчитать матожидание. Подсчёт выглядит следующим образом:
Правильный подход позволяет составить закон распределения случайных магнитуд выигрыша. Классическая формула математического ожидания часто используется для качественной оценки рентабельности какой-либо деятельности. Этот математический подход также используется на рынке ФОРЕКС при прогнозировании реальной суммы дохода какой-либо торговой стратегии опытных трейдеров.
Основы теории
Для случайной непрерывной величины незаменимая механическая интерпретация матожидания всегда сохраняет основное своё правило: центр массы соответствует единичной массе, которая непрерывным образом распределена на оси абсцисс g (a). В отличие от распространённой независимой величины, у которой итоговый аргумент функции х может меняться скачкообразно, у непрерывной величины аргумент таким колебаниям не подвержен.
Чтобы отыскать матожидание и дисперсию непрерывной случайной величины, обязательно нужно найти определённые интегралы. Если по условиям задачи была дана функция плотности величины непрерывного типа, то она обязательно входит в подынтегральное выражение. Когда дана функция распределения вероятностей, тогда обязательно нужно найти функцию плотности. Количество испытаний константы равно самой константе.
Арифметическое среднее всех задействованных значений непрерывной величины называется её матожиданием, что тоже нужно запомнить. Величина интеграла называется дисперсией непрерывной случайной величины.
Среднее квадратичное произведение непрерывной величины всегда определяется специалистами как арифметическое значение квадратного корня из дисперсии. Только тщательное изучение всех правил поможет решать все поставленные математические задачи без допущения ошибок.
Ключевые особенности дисперсии
За дисперсию принято понимать средний квадрат отклонений полученных значений признака от среднего арифметического числа. Для обозначения используется одна заглавная латинская буква D.
Для правильного расчёта дисперсии необходимо посчитать разность между имеющимся числом и средним арифметическим, чтобы в итоге возвести результат в квадрат. Значений получится столько, сколько может быть реальных исходов у рассматриваемого события. После этого остаётся только просуммировать все полученные данные и разделить на количество элементов в последовательности. Если максимальное количество исходов приравнивается к 5, тогда делить нужно именно на эту цифру.
У дисперсии также есть свойства, которые обязательно нужно знать, чтобы решать различные математические задачи. К примеру:
К примеру: нужно представить, что был проведён 21 эксперимент и в итоге 7 разных исходов. Первым делом нужно рассчитать среднее арифметическое: сумма элементов равняется 21. Эту цифру нужно разделить на 7. В результате получится цифра 3. После этого из каждого числа исходной последовательности нужно вычесть 3. Каждое значение возводят в квадрат, а результат слаживают вместе. Если всё сделать правильно, то в итоге можно получить 12. На финальном этапе остаётся разделить число на количество элементов.
Зависимость итога от количества экспериментов
Многочисленные свойства математического ожидания очень важны для правильного решения поставленных задач. Для изучения этой темы необходимо знать, что собой представляет квадратическое отклонение. Для обозначения этого термина используются буквы sd, либо греческая строчная «сигма». Квадратическое отклонение отображает то, насколько именно отклоняются значения от центрального признака. Если в основе лежит нахождение нужного значения, тогда следует постараться правильно рассчитать квадратный корень из дисперсии.
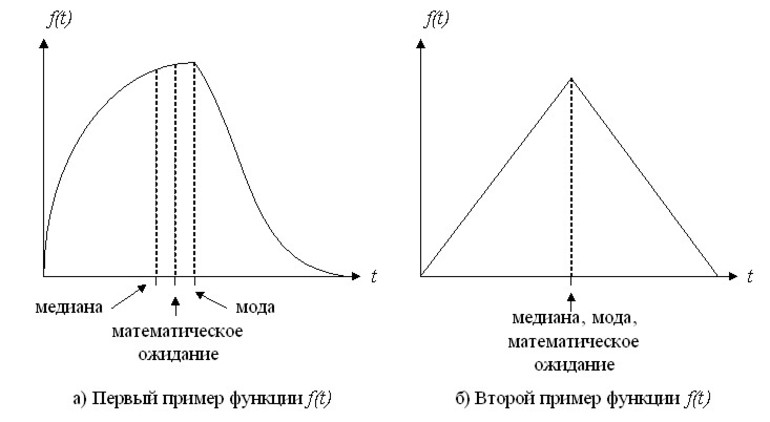
Можно построить график равномерного распределения, чтобы непосредственно на нём увидеть реальную величину среднего квадратного отклонения. Для этих целей необходимо выполнить несколько несложных заданий. Нужно взять половину изображения справа и слева от моды (центральное значение), дабы постараться провести перпендикуляр к горизонтальной оси так, чтобы площади получившихся фигур были абсолютно равными.
Размер отрезка между серединой распределения и получившейся проекцией на горизонтальную ось и будет самое обычное среднее квадратичное отклонение.
Актуальность применения медианы и моды
Математики склонны утверждать, что средние величины представляют собой своего рода отвлечённую величину. Отвлекаясь от определённых величин каждого варианта, эти числа отлично отображают общее положение, которое присуще всей совокупности единиц. В некоторых случаях можно наблюдать, что величина не имеет какого-либо равенства ни с одним из конкретных вариантов распространённых вариантов.
К примеру: среднее число членов одной семьи приравнивается к 4,85. Этот показатель был получен на основе исчисления соответствующей совокупности данных. Число не имеет ничего общего с определённым составом конкретной семьи, так как дробного числа членов семьи быть не может. В этом случае принято понимать за основу показатель средней величины состава семьи. Возле дробного числа группируются реальные варианты.
Когда стоит задача определить какую-либо абстрактную величину, тогда можно смело задействовать величины конкретных вариантов, содержащихся в рассматриваемой совокупности величин. Именно эти величины занимают определённое место в ранжированном ряду индивидуальных значений признака. Такими величинами чаще всего являются медиана, а также мода. Мода — это самая распространённая величина, которую принято обозначать символами Мо.
Мода как величина в прерывистом ряду всегда определяется на примере выявления самого большого процента мужчин, которые носят одинаковый размер обуви. После несложных математических действий можно понять, что большинство мужчин носят обувь 40 размера. А это значит, что Мо = 40, модой является сорок первый размер обуви.
А вот когда необходимо отыскать достоверную медиану, то первым делом нужно постараться найти один из центральных вариантов рассматриваемой совокупности. На примере изучаемого варианта за основу будет взят эксперимент, в котором участвовали 100 человек: 100:2 = 50. После этого по накопленным частотам выполняют определение достоверной величины пятидесятого ряда. Если следовать накопленной частотности, то полученная цифра будет находиться между 41 и 69 позициями. Это значит, что 50-й член ряда имеет величину 40 (Ме = 40-й размер обуви).
Доступное программное обеспечение
Из всех перечисленных правил и формул можно сделать вывод, что используемое математическое ожидание обозначается самым простым образом, но в этой теме нужно хорошо разбираться. Правильные расчёты дисперсии и математического ожидания — это не самая простая задача, с арифметической точки зрения.
Чтобы не тратить драгоценное время на поиски решения можно воспользоваться специальной онлайн-калькулятор, которая активно используется в высших учебных заведениях. Это программное обеспечение носит название R. В ней предусмотрено наличие специальных функций, которые позволяют рассчитать значения для многих понятий из статистики и теории вероятности.
Математическое ожидание
Полезное
Смотреть что такое «Математическое ожидание» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
математическое ожидание простыми словами, что это такое и что с его помощью мы распознаем
Математи́ческое ожида́ние — среднее значение случайной величины (распределение вероятностей случайной величины, рассматривается в теории вероятностей)
Случайная величина — это математическое понятие, служащее для математического представления состояния объектов и процессов, свойств объектов, процессов и событий, которые принципиально не могут быть однозначно определены до проведения опыта по их измерению, или для событий — до их осуществления. Примером объектов, для представления состояния которых требуется применение случайных величин являются микроскопические объекты, описываемые квантовой механикой. Случайными величинами описываются события передачи наследственных признаков от родительских организмов к их потомкам (см. Законы Менделя). К случайным относятся события радиоактивного распада ядер атомов.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их исхода.
Дима, это математический термин и «на пальцах » его не объяснить. Зубрить придётся.
Математическое ожидание
Абсолютно любому трейдеру и инвестору обязательно нужно хорошо понимать что такое математическое ожидание (часто пишут сокращённо «мат.ожидание» или «матожидание»). Дело в том что это матожидание это и есть главная цель для трейдера и инвестора. Не прибыль, а матожидание. Трейдер стремящийся к прибыли менее вероятно получит прибыль, чем трейдер стремящейся к положительному матожиданию. Местами нужно себя заставлять не поддаваться жадности, и желать матожидание вместо прибыли. Ниже Вы поймете почему так, и даже согласитесь, потому что будет понятно.
Что такое
Разумеется, в интернете есть огромное количество статей по теме «что такое математическое ожидание», в том числе и в контексте трейдинга/инвестирования, в том числе и на русском языке. Если Вам моя статья вдруг окажется непонятной, то Вы можете найти такие статьи в Интернете. Конечно, статья об этом есть и в русскоязычной Википедии, однако, если Вы не математик, то Вы эту страницу в Википедии быстро закроете после беглого взгляда. Проще говоря:
Математическое ожидание =
кол-во прибыльных сделок * средняя прибыль прибыльной сделки /
кол-во убыточных сделок * средний убыток убыточной сделки
Чем полезно
Чем трейдеру полезно это понимание? Например, многие новички ошибочно стремятся к большому % прибыльных сделок (то есть прибыльных сделок должно быть в разы больше чем убыточных — так он считает), но при этом ради повышения % прибыльных сделок такой трейдер сильно жертвует прибыльностью сделок. Либо жертвует другой переменной из формулы в невыгодную для него сторону. В итоге трейдеру ошибочно кажется что увеличив % прибыльных сделок он сделал свою торговлю лучше, а на самом деле он лишь снизил своё матожидание, и его торговля стала менее выгодной ему. А поймет он это не скоро.
Простой пример
Если Вы подумали и всё правильно поняли, то ответите: «Стоит».
Варианты действий
Убыток повлияет на Ваш конечный результат (прибыль по итогу года, например) точно так же как и прибыль. Посмотрите формулу матожидания. Поэтому для трейдера в принципе не важно что сделать: увеличить прибыль от прибыльных, или же уменьшить убыток от убыточных. Куда важнее насколько. То есть у трейдера аж 4 варианта как улучшить своё матожидание:
Проблема в том, что трейдер меняя один параметр, чаще всего будет менять и другие. Ну, например, увеличили Вы таймфрейм и убыточных сделок у Вас теперь меньше. Вот только прибыльных сделок у Вас тоже меньше. Выиграли ли Вы?
Вот поэтому так складывается, что вполне возможно иметь большой доход, имея лишь 30% прибыльных сделок (а 70% остальных сделок — убыточные). Верно и обратное, можно создать такую стратегию где 90% сделок прибыльные, а по итогу она окажется убыточной. Это вполне возможно. Непонимание матожидания приводит к появлению подобных стратегий.
Фактор случайности
Уменьшить его можно. Можно уменьшить во много раз. А вот уйти от него нельзя. Перейдем к понятным примерам.
Из этого примера должно быть понятно что «Чем больше игр — тем лучше». Чем больше раз мы сыграем, тем меньше Ваши шансы проиграть деньги. Потому что матожидание такой игры положительное — оно в Вашу пользу.
Но здесь не все понимают что вероятность проигрыша свести к нулю на самом деле… невозможно. Парадокс, но решка может выпасть не только 2 раза подряд, но и 10 раз подряд, и даже миллион раз подряд. Да, миллион решек подряд это крайнемеловероятно, но… не исключено. Не исключено, потому что каждый следующий бросок монеты не зависит от предыдущего броска — это независимые события. Поэтому после выпадения 10 решек подряд, шанс что в следующий раз монета снова будет решкой всё те же 50%. Так как каждый бросок не зависит от прошлых бросков. Монета как бы не знает кем она была в прошлый раз, орлом или решкой. Ей и знать нечем.
Это всё приводит нас к печальному выводу: снизить вероятность проигрыша до абсолютного нуля невозможно в принципе. И с орлянкой, и с трейдингом, и с инвестициями. Мы можем лишь уменьшать шансы проигрыша, мы даже можем их уменьшить в тысячи раз, но не можем свести шансы проигрыша до абсолютного нуля. Потому что монетка может выпасть решкой миллион раз подряд. Просто вряд ли.
Как же его уменьшить?
Диверсификация
Задача диверсификации, как для инвестора так и для трейдера, как раз в том и состоит — уменьшить фактор случайности. Как в орлянке в положительным матожиданием: Вам лучше сыграть 10 раз, а не 1 раз — тогда Вы более вероятно выиграете деньги. Так же и инвестору лучше купить 10 разных акций компаний, чем акции только одной компании (которая может обанкротится, от чего он всё потеряет). Здесь часто пишут принцип «Не держите все яйца в одной корзине».
Для трейдера диверсификация это количество сделок. Инвестор купил акцию и держит, а трейдер активом торгует. У трейдера есть 2 пути для увеличения количества сделок:
Если вдуматься, то и срок и диверсификация просто увеличивает количество сделок. К примеру, если трейдеру дать очень прибыльную стратегию, а он будет торговать по ней всего один день, то его вероятность проиграть деньги значительно больше, чем если бы он по ней торговал 365 дней. Так же и диверсификация — она лишь увеличит количество сделок. Так же как орлянка — лучше сыграть 10 раз, а не один.
То есть чем больше сделок у трейдера по системе — тем меньше влияние фактора случайности — тем меньше шансов получить убыток.
Не стремиться к прибыли?
Трейдер, который стремится к прибыли обязательно начнет совершать ошибки. Ведь он захочет увеличить прибыль от прибыльных сделок, при этом не обращая внимания насколько сильно он увеличит убыток от убыточных сделок. То есть трейдер, гонящийся за прибылью может просто испортить себе матожидание, сделать себе только хуже, но этого не понять.
В погоне за прибылью у трейдера образуются ложные оценки своих действий. Из-за высокого фактора случайности у него может быть очень прибыльный месяц, и он ошибочно полагает что он всё сделал правильно. А на самом деле он сделал полно ошибок и ему просто везло. Это ложные ориентиры. Трейдер, который гонится за прибылью отчасти гонится за удачей (случайным фактором). Ведь конечный его результат за месяц зависит не только от матожидания, но и от фактора случайности. Глупо ставить себе цель гоняться за случайной удачей. К хорошему не приведет.
Трейдеру нужно ставить себе цель добиваться положительного матожидания, а не прибыли. Даже если месяц был убыточный, а матожидание остается положительным в его пользу, трейдеру нужно понимать: «Мне в этом месяце просто не повезло, но вероятно повезёт в следующем месяце, и я всё сделал правильно». А вот чтобы уменьшить фактор случайности и не быть таким зависимым от везения и случайностей нужно увеличивать диверсификацию и срок. К счастью, увеличить можно и то и то.
Что обязательно нужно для успеха любому трейдеру инвестору?
Ботоводство
А теперь чуть более практично. Как можно применить это знание используя робота.
Про последний пункт: если Вы вручную вмешиваетесь в торговлю робота, закрывая позиции, например, то Вы образуете еще один новый фактор случайности. А задача трейдера в том чтобы фактор случайности уменьшать, а не увеличивать. Кроме того, если Вы часто меняете настройки робота, пытаясь найти идеальные, то это тоже не хорошо, так как это тоже фактор случайности. Постоянно вмешиваясь в торговлю без чёткой логики («мне вот кажется сейчас упадет еще» — это не логика, не система), постоянно меняете настройки, то Вы увеличиваете фактор случайности, то есть превращаете бизнес в рулетку.
Кстати, про рулетку в казину — у неё отрицательное матожидание. Выпало «зеро» — значит Вы теряете деньги в любом случае. А в американском варианте рулетки добавили еще и «двойное зеро» (ну чтобы клиент побыстрее проиграл и побольше). Подумайте. Выиграть в рулетку Вы можете если угадаете цвет, и при этом не выпадет «зеро». Однако, ячеек с не Вашим цветом плюс зеро БОЛЬШЕ чем ячеек с Вашим цветом. При этом суммы выигрыша и проигрыша равны. Так и образуется отрицательное матожидание. У некоторых трейдеров перед носом такая же рулетка с отрицательным матожиданием, но зато там 80% прибыльных сделок 🙂 Любители мартингейла поймут.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
М. о. может быть вычислено и как интеграл Лебега от хпо распределению вероятностей Р Х величины X:
при этом интегрируемость Xв смысле (*) равносильна конечности интеграла
если Xимеет абсолютно непрерывное распределение с плотностью вероятности р(х), то
при этом существование М. о. равносильно абсолютной сходимости соответствующего ряда или интеграла. Основные свойства М. о.:
а)
б) ЕС=С для любого действительного С:
в)
для любых действительных a и b;
г)
д) 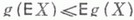
е) любая ограниченная случайная величина имеет конечное М. о. Кроме того,
ж)
Естественным образом можно определить понятие случайной величины с бесконечным М. о. Типичным примером служат времена возвращения в нек-рых случайных блужданиях (см., напр., Бернулли блуждание).
С помощью М. о. определяются многие числовые и функциональные характеристики распределения (как М. о. соответствующих функций от случайной величины), напр, производящая функция, характеристическая функция, моменты любого порядка, в частности дисперсия, ковариация.

Понятие М. о. как ожидаемого значения случайной величины впервые наметилось в 18 в. в связи с теорией азартных игр. Первоначально термин «М. о.» был введен как ожидаемый выигрыш игрока, равный 


Лит.:[1] Колмогоров А. Н., Основные понятия теории вероятностей, 2 изд., М., 1974; [2] Феллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., тт. 1-2, М., 1967; [3] Лоэв М., Теория вероятностей, пер. с англ., М., 1962; [4] Крамер Г., Математические методы статистики, пер. с англ., 2 изд., М., 1975. А. В. Прохоров.
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
Математическое ожидание и его свойства



Математическим ожиданием (или средним значением) дискретной случайной величины называется сумма произведений всех её возможных значение на соответствующие им вероятности.
| X | 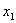 | 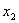 | … | 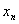 |
| P | 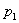 | 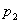 | … | 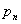 |
Т.е., если сл. величина имеет закон распределения, то
называется её математическим ожиданием. Если сл. величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда 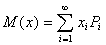
Для непрерывной сл. величины, заданной функцией плотности вероятности f(x), математическое ожидание определяется в виде интеграла
при условии, что этот интеграл существует (если интеграл расходится, то говорят, что математическое ожидание не существует).
Пример 1. Определим математическое ожидание случайной величины распределённой по закону Пуассона. По определению
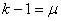
Значит, параметр 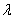
Пример 2. Для случайной величины, имеющей показательный закон распределения 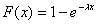
( 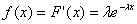
(в интеграле пределы взять, с учётов того. что f (x) отлична от нуля только при положительных x).
Пример 3. Случайнаявеличина, распределенная по закону распределения Коши, не имеет среднего значения. Действительно
Свойства математического ожидания.
Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.
Постоянная С принимает это значение с вероятностью единица и по определению М(С)=С×1=С
Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической суме их математических ожиданий.
Ограничимся доказательством этого свойства только для суммы двух дискретных случайных величин, т.е. докажем, что
Под суммой двух дискретных сл. Величин понимается сл. Величина, которая принимает значения 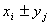
Но
где 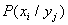
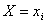
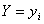
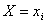
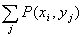
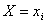
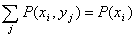
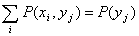
Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
| У | 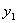 | 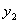 | … | 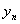 |
| Q | 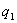 | 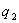 | … | 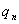 |
| Х | 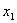 | 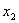 | … | 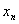 |
| Р | 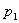 | 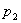 | … | 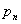 |
Приведем доказательства этого свойства только для дискретных величин. Для непрерывных случайных величин оно доказывается аналогично.
Пусть Х и У независимы и имеют законы распределения
Произведением этих случайных величин будет случайная величина, которая принимает значения 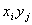
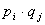
Следствие. Постоянныймножитель можно выносить за знак математического ожидания. Так век постоянная С не зависит от того какое значение примет сл. величина X, то по свойству 3. имеем
Пример. Если a и b постоянные, то М(ах+b)=аМ(х)+b.
Математическое ожидание числа появления события в схеме независимых испытаний.
Пусть производится n независимых опытов, вероятность появления события в каждом из которых равна Р. Число появлений события в этих n опытах является случайной величиною Х распределённой по биномиальному закону. Однако, непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно: Число появления события в n опытах состоит изчисла появлений события в отдельных опытах, т.е.
где 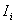
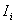 | ||
| Р | 1-р | р |
Поэтому
т.е. среднее число появлений события в n независимых опытах равно произведению числа опытов на вероятность появления события в одном опыте.
Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 20×0,1=2.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
где 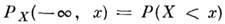
или имеет непрерывное распределение с плотностью вероятностей 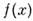
Аналогично определяют M. о. и для случайных величин со значениями в векторных пространствах.
Операция вычисления M. о. линейна и монотонна, для неслучайной величины X получим
Если величины 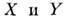
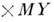
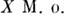
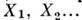
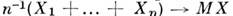
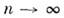
С помощью математического ожидания определяют многие важные характеристики случайной величины, напр, моменты (в т. ч. дисперсию), характеристическую функцию.
Лит.:Fеллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., [4 изд.], т. 1-2, M., 1984.
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
Математическое ожидание
Источник:
«АНАЛИЗ ПОВОЗРАСТНЫХ РИСКОВ СМЕРТНОСТИ НАСЕЛЕНИЯ. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ»
(утв. Минздравом РФ 22.01.2001 N 11-3/25-09)
Смотреть что такое «Математическое ожидание» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
где 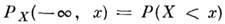
или имеет непрерывное распределение с плотностью вероятностей 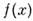
Аналогично определяют M. о. и для случайных величин со значениями в векторных пространствах.
Операция вычисления M. о. линейна и монотонна, для неслучайной величины X получим
Если величины 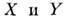
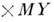
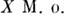
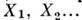
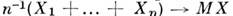
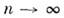
С помощью математического ожидания определяют многие важные характеристики случайной величины, напр, моменты (в т. ч. дисперсию), характеристическую функцию.
Лит.:Fеллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., [4 изд.], т. 1-2, M., 1984.
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
Теория вероятностей и антропогенный фактор
Введение
Общая информация
Я все же введу пару определений, чтобы хоть немного формализовать написанное.
1) Если имеется несколько возможных случайных исходов, «равновозможных» между собой, то классическая вероятность — это отношение количества «хороших» случайных (элементарных) событий к их общему количеству. Например, если у вас есть 5 шариков, 2 из которых белые, то вероятность взять именно белый шар будет равняться 2/5.
2) Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до ее измерения нельзя точно предсказать. Классический пример — игральная кость. Кидая ее, можно случайно получить одно из шести возможных значений.
3) Математическое ожидание случайной величины — это сумма всех возможных ее значений, помноженных на их вероятность. Говоря простым языком, это «среднее значение» принимаемой случайной величины. Для игральной кости оно равно (1+2+3+4+5+6)*1/6=3.5. Что нам это дает? То, что кидая кость много (например 100) раз, в среднем каждый раз будет выпадать 3.5, а в сумме выпадет примерно 100*3.5=350. При увеличении количества бросков, относительная погрешность реального результата и его математического ожидания, помноженного на количество бросков, будет уменьшаться все сильнее.
Теперь суть того, что я, собственно, хотел рассказать: математические подсчеты довольно хорошо прогнозируют разные события, если они напрямую не зависят от выбора человека. Если же вмешивается антропогенный фактор, то строить какие-то планы, опираясь только на теорию вероятности нужно с осторожностью. Приведу пару простых примеров. Возможно они немного надуманные, но зато простые и понятные.
Монетка
Случай раз
Вам во время пары в универе (урока в школе, рабочего дня) стало скучно и Вы предложили соседу по парте (коллеге по работе) сыграть в следующую игру: подбрасываете монетку; если выпал орел — Ваш друг платит вам 5 рублей, если же выпала решка, то Вы платите 5 рублей. От скуки человек может и согласиться. Вы будете играть так весь день, а в конечном итоге оба останетесь практически при тех же деньгах, что были изначально. Вероятность выпадения любой стороны монетки 1/2 и, как следствие, математическое ожидание Вашего выигрыша равно нулю. Так что в среднем выигрыш/проигрыш будет в районе плюс-минус 10 рублей. Ну, может быть, немногим больше. В любом случае, для бюджета не критично.
Случай два
Ситуация та же, но вы предложили за проигрыш платить не по 5, а по 1000 рублей. Скорее всего ваш друг/коллега откажется. Ибо не хочется просто так потерять ощутимую сумму денег.
Что же изменилось? Математическое ожидание выигрыша по-прежнему равно нулю. С точки зрения математики все практически то же самое. А тут уже вмешался человеческий фактор, и Ваш план скоротать скучный день провалился.
Лотерея
Вы меняете условия и делаете лотерею практически благотворительной. Теперь выигрыш 25 рублей. Математическое ожидание выигрыша минус стоимость билета — 2.5 рубля! Вы даже останетесь в убытке! Но народ в большинстве своем по-прежнему не будет жаловать Вашу лотерею, ибо выигрыш немногим больше цены билета. В лотерею будут играть разве что школьники, которым не хватает мелочи на мороженное.
Читатель может решить, что дело просто в количественном размере выигрыша. Но это далеко не обязательно. Приведу еще один довольно надуманный, но показательный пример:
Очень крупная лотерея
Вам предлагают подарок неслыханной щедрости. «Супер-лотерею». Одну из двух, на выбор. Сыграть в нее можно только один раз. В первой «лотерее» Вам гарантированно выплачивают миллион долларов. А во второй с 50% шансом Вы получите 2 миллиона, с 40% шансом миллион и с 10% шансом уйдете ни с чем. Математическое ожидание выигрыша в первой «лотерее» 1 миллион. Во второй — 1.4 миллиона. Но что же Вы выберете? Может кто-то и выберет второй вариант, но проведение опроса среди некоторого количества людей покажет, что большинство наверняка выберет первый вариант. Ведь, как говорится, лучше синица в руках… Тем более, если синица — это миллион, а во второй «лотерее» есть шанс не получить ничего. И гипотетические 2 миллиона ничего не решают.
Последний пример
Ну и что в итоге?
В итоге, с одной стороны, математические подсчеты могут дать не совсем очевидные с точки зрения математики результаты. Человек может из почти одинаковых условий выбирать строго одно, а среди нескольких предложений брать более невыгодное для себя. Почему? Так устроен человек. Выгода одного конкретного человека не всегда может быть просто так подсчитана.
С другой стороны, если смотреть с точки зрения различных фирм, корпораций и т.д., то имея множество клиентов, можно получать неплохие деньги, даже если с точки зрения математики предложение для клиента не самое выгодное. Именно поэтому существуют банки, лотереи, страховые компании. И люди берут кредиты под дикие проценты, покупают сомнительные лотерейные билеты и страхуют вещи, с которыми, скорее всего, все будет в порядке.
А значит, пытаясь применить по отношению к людям какие-то подсчеты «в тупую», мысля как робот, скорее всего, ничего путного и полезного не выйдет. Но ежели действовать с умом, представить себя на месте других людей, то можно горы свернуть и миллиарды заработать с помощью математики.
В общем, думайте как люди, но про математику тоже не забывайте.
математическое ожидание
Смотреть что такое «математическое ожидание» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
Математическое ожидание
1.14 Математическое ожидание
* Если это выражение существует в смысле абсолютной сходимости
Смотри также родственные термины:
1.18. математическое ожидание (случайной величины)
а) Для дискретной случайной величины X, принимающей значения xi с вероятностями pi, математическое ожидание, если оно существует, определяют формулой
где суммируют все значения xi, которые может принимать случайная величина X;
b) Для непрерывной случайной величины X, имеющей плотность f (x), математическое ожидание, если оно существует, определяют формулой
где интеграл берут по всему интервалу (интервалам) изменения Х
3.11 математическое ожидание (совокупности) [(population) mean] μ: Для непрерывной случайной величины Х с плотностью распределения f(x)математическое ожидание (среднее) равно интегралу от х по области определения переменной X:
6. Математическое ожидание случайного процесса
Функция времени, для каждого значения аргумента равная математическому ожиданию случайной величины
5. Математическое ожидание случайной величины
Математическое ожидание функции случайного процесса
Полезное
Смотреть что такое «Математическое ожидание» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание
Полезное
Смотреть что такое «Математическое ожидание» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (среднее значение) случайной величины числовая характеристика случайной величины. Если случайная величина, заданная на вероятностном пространстве (см. Вероятностей теория), то её M. о. MX (или EX )определяется как интеграл Лебега: где … Физическая энциклопедия
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
где 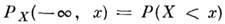
или имеет непрерывное распределение с плотностью вероятностей 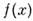
Аналогично определяют M. о. и для случайных величин со значениями в векторных пространствах.
Операция вычисления M. о. линейна и монотонна, для неслучайной величины X получим
Если величины 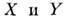
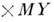
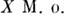
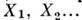
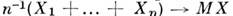
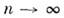
С помощью математического ожидания определяют многие важные характеристики случайной величины, напр, моменты (в т. ч. дисперсию), характеристическую функцию.
Лит.:Fеллер В., Введение в теорию вероятностей и ее приложения, пер. с англ., [4 изд.], т. 1-2, M., 1984.
Полезное
Смотреть что такое «МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ» в других словарях:
математическое ожидание — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] математическое ожидание Одна из численных характеристик случайной величины, часто называемая ее теоретической средней. Для дискретной случайной величины X математическое… … Справочник технического переводчика
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — (expected value) Среднее значение распределения экономической переменной, которые она, может принимать. Если рt – цена товара в момент времени t, ее математическое ожидание обозначается – Ept. Для указания момента времени, к которому относится… … Экономический словарь
Математическое ожидание — среднее значение случайной величины. Математическое ожидание является детерминированной величиной. Среднее арифметическое значение из реализаций случайной величины представляет собой оценку математического ожидания. Среднее арифметическое… … Официальная терминология
Математическое ожидание — [expected value] одна из численных характеристик случайной величины, часто называемая ее теоретической средней Для дискретной случайной величины X математическое ожидание равно сумме произведений возможных значений этой величины на их… … Экономико-математический словарь
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — англ. expected value; нем. Erwartung mathematische. Стохастическая средняя или центр рассеивания случайной величины. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Математическое ожидание — (Population mean) Математическое ожидание – это распределение вероятностей случайной величины Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет,… … Энциклопедия инвестора
Математическое ожидание — См. также: Условное математическое ожидание Математическое ожидание среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей.[1] В англоязычной литературе и в математических… … Википедия
Математическое ожидание — 1.14 Математическое ожидание Е (X) где xi значения дискретной случайной величины; р = Р (Х = xi); f(x) плотность непрерывной случайной величины * Если это выражение существует в смысле абсолютной сходимости Источник … Словарь-справочник терминов нормативно-технической документации
Математическое ожидание – это распределение вероятностей случайной величины
Математическое ожидание, определение, математическое ожидание дискретной и непрерывной случайных величин, выборочное, условное матожидание, расчет, свойства, задачи, оценка матожидания, дисперсия, функция распределения, формулы, примеры расчета
Структура публикации
Математическое ожидание – это одно из важнейших понятий в математической статистике и теории вероятностей, характеризующее распределение значений или вероятностей случайной величины. Обычно выражается как средневзвешенное значение всех возможных параметров случайной величины. Широко применяется при проведении технического анализа, исследовании числовых рядов, изучении непрерывных и продолжительных процессов. Имеет важное значение при оценке рисков, прогнозировании ценовых показателей при торговле на финансовых рынках, используется при разработке стратегий и методов игровой тактики в теории азартных игр.
Математическое ожидание – это мера среднего значения случайной величины в теории вероятности. Математическое ожидание случайной величины x обозначается M(x).
Математическое ожидание – это число, вокруг которого сосредоточены значения случайной величины.
Математическое ожидание – это в теории вероятности средневзвешенная величина всех возможных значений, которые может принимать эта случайная величина.
Математическое ожидание – это сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Математическое ожидание – это средняя выгода от того или иного решения при условии, что подобное решение может быть рассмотрено в рамках теории больших чисел и длительной дистанции.
Математическое ожидание – это в теории азартных игр сумма выигрыша, которую может заработать или проиграть игрок, в среднем, по каждой ставке. На языке азартных игроков это иногда называется «преимуществом игрока» (если оно положительно для игрока) или «преимуществом казино» (если оно отрицательно для игрока).
Математическое ожидание – это процент прибыли на выигрыш, умноженный на среднюю прибыль, минус вероятность убытка, умноженная на средний убыток.
Математическое ожидание случайной величины в математической теории
Термин «математическое ожидание» введён Пьером Симоном маркизом де Лапласом (1795) и произошёл от понятия «ожидаемого значения выигрыша», впервые появившегося в 17 веке в теории азартных игр в трудах Блеза Паскаля и Христиана Гюйгенса. Однако первое полное теоретическое осмысление и оценка этого понятия даны Пафнутием Львовичем Чебышёвым (середина 19 века).
Закон распределения случайных числовых величин (функция распределения и ряд распределения или плотность вероятности) полностью описывают поведение случайной величины. Но в ряде задач достаточно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный вопрос. Основными числовыми характеристиками случайных величин являются математическое ожидание, дисперсия, мода и медиана.
Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности. Иногда математическое ожидание называют взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего. Математическое ожидание случайной величины есть неслучайная (постоянная) величина.
Математическое ожидание имеет простой физический смысл: если на прямой разместить единичную массу, поместив в некоторые точки некоторую массу (для дискретного распределения), или «размазав» её с определенной плотностью (для абсолютно непрерывного распределения), то точка, соответствующая математическому ожиданию, будет координатой «центра тяжести» прямой.
Среднее значение случайной величины есть некоторое число, являющееся как бы её «представителем» и заменяющее её при грубо ориентировочных расчетах. Когда мы говорим: «среднее время работы лампы равно 100 часам» или «средняя точка попадания смещена относительно цели на 2 м вправо», мы этим указываем определенную числовую характеристику случайной величины, описывающую её местоположение на числовой оси, т.е. «характеристику положения».
Из характеристик положения в теории вероятностей важнейшую роль играет математическое ожидание случайной величины, которое иногда называют просто средним значением случайной величины.
Рассмотрим случайную величину Х, имеющую возможные значения х1, х2, …, хn с вероятностями p1, p2, …, pn. Нам требуется охарактеризовать каким-то числом положение значений случайной величины на оси абсцисс с учетом того, что эти значения имеют различные вероятности. Для этой цели естественно воспользоваться так называемым «средним взвешенным» из значений xi, причем каждое значение xi при осреднении должно учитываться с «весом», пропорциональным вероятности этого значения. Таким образом, мы вычислим среднее случайной величины X, которое мы обозначим M |X|:
Это среднее взвешенное значение и называется математическим ожиданием случайной величины. Таким образом, мы ввели в рассмотрении одно из важнейших понятий теории вероятностей – понятие математического ожидания. Математическим ожиданием случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений.
Математическое ожидание случайной величины Х связано своеобразной зависимостью со средним арифметическим наблюденных значений случайной величины при большом числе опытов. Эта зависимость того же типа, как зависимость между частотой и вероятностью, а именно: при большом числе опытов среднее арифметическое наблюденных значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию. Из наличия связи между частотой и вероятностью можно вывести как следствие наличие подобной же связи между средним арифметическим и математическим ожидание. Действительно, рассмотрим случайную величину Х, характеризуемую рядом распределения:
Пусть производится N независимых опытов, в каждом из которых величина X принимает определенное значение. Предположим, что значение x1 появилось m1 раз, значение x2 появилось m2 раз, вообще значение xi появилось mi раз. Вычислим среднее арифметическое наблюденных значений величины Х, которое, в отличие от математического ожидания М|X| мы обозначим M*|X|:
При увеличении числа опытов N частоты pi будут приближаться (сходиться по вероятности) к соответствующим вероятностям. Следовательно, и среднее арифметическое наблюденных значений случайной величины M|X| при увеличении числа опытов будет приближаться (сходится по вероятности) к её математическому ожиданию. Сформулированная выше связь между средним арифметическим и математическим ожиданием составляет содержание одной из форм закона больших чисел.
Мы уже знаем, что все формы закона больших чисел констатируют факт устойчивости некоторых средних при большом числе опытов. Здесь речь идет об устойчивости среднего арифметического из ряда наблюдений одной и той же величины. При небольшом числе опытов среднее арифметическое их результатов случайно; при достаточном увеличении числа опытов оно становится «почти не случайным» и, стабилизируясь, приближается к постоянной величине – математическому ожиданию.
Свойство устойчивости средних при большом числе опытов легко проверить экспериментально. Например, взвешивая какое-либо тело в лаборатории на точных весах, мы в результате взвешивания получаем каждый раз новое значение; чтобы уменьшить ошибку наблюдения, мы взвешиваем тело несколько раз и пользуемся средним арифметическим полученных значений. Легко убедиться, что при дальнейшем увеличении числа опытов (взвешиваний) среднее арифметическое реагирует на это увеличение все меньше и меньше и при достаточно большом числе опытов практически перестает меняться.
Следует заметить, что важнейшая характеристика положения случайной величины – математическое ожидание – существует не для всех случайных величин. Можно составить примеры таких случайных величин, для которых математического ожидания не существует, так как соответствующая сумма или интеграл расходятся. Однако для практики такие случаи существенного интереса не представляют. Обычно случайные величины, с которыми мы имеем дело, имеют ограниченную область возможных значений и, безусловно, обладают математическим ожиданием.
Модой случайной величины называется её наиболее вероятное значение. Термин «наиболее вероятное значение», строго говоря, применим только к прерывным величинам; для непрерывной величины модой является то значение, в котором плотность вероятности максимальна. На рисунках показана мода соответственно для прерывной и непрерывной случайных величин.
Если многоугольник распределения (кривая распределения) имеет более одного максимума, распределение называется «полимодальным».
Иногда встречаются распределения, обладающие посередине не максимумом, а минимумом. Такие распределения называют «антимодальными».
В общем случае мода и математическое ожидание случайной величины не совпадают. В частном случае, когда распределение является симметричным и модальным (т.е. имеет моду) и существует математическое ожидание, то оно совпадает с модой и центром симметрии распределения.
Часто применяется еще одна характеристика положения – так называемая медиана случайной величины. Этой характеристикой пользуются обычно только для непрерывных случайных величин, хотя формально можно её определить и для прерывной величины. Геометрически медиана – это абсцисса точки, в которой площадь, ограниченная кривой распределения, делится пополам.
В случае симметричного модального распределения медиана совпадает с математическим ожиданием и модой.
Математическое ожидание может быть вычислено и как интеграл Лебега от х по распределению вероятностей рх величины X:
Естественным образом можно определить понятие случайной величины с бесконечным математическим ожиданием. Типичным примером служат времена возвращения в некоторых случайных блужданиях.
С помощью математического ожидания определяются многие числовые и функциональные характеристики распределения (как математическое ожидание соответствующих функций от случайной величины), например, производящая функция, характеристическая функция, моменты любого порядка, в частности дисперсия, ковариация.
Математическое ожидание дискретной случайной величины
Пусть есть некоторая случайная величина, которая может принять одно из нескольких числовых значений (допустим, количество очков при броске кости может быть 1, 2, 3, 4, 5 или 6). Часто на практике для такой величины возникает вопрос: а какое значение она принимает «в среднем» при большом количестве тестов? Каков будет наш средний доход (или убыток) от каждой из рискованных операций?
Теперь обобщим наши примеры:
Обратимся к только что приведённой картинке. Слева табличка распределения случайной величины. Величина X может принимать одно из n возможных значений (приведены в верхней строке). Никаких других значений не может быть. Под каждым возможным значением снизу подписана его вероятность. Справа приведена формула, где M(X) и называется математическим ожиданием. Смысл этой величины в том, что при большом количестве испытаний (при большой выборке) среднее значение будет стремиться к этому самому математическому ожиданию.
Посчитаем математическое ожидание для выше описанной лотереи. Табличка будет выглядеть вот так:
Тогда математическое ожидание составит, как мы установили выше.:
Другое дело, что так же «на пальцах», без формулы, было бы трудновато, если бы имелось больше вариантов. Ну скажем, имелось бы 75% проигрышных билетов, 20% выигрышных билетов и 5% особо выигрышных.
Теперь некоторые свойства математического ожидания.
Математическое ожидание является линейным. Доказать это просто:
Постоянный множитель допускается выносить за знак математического ожидания, то есть:
Это является частным случаем свойства линейности математического ожидания.
Другое следствие линейности математического ожидания:
то есть математическое ожидание суммы случайных величин равно сумме математических ожиданий случайных величин.
Это тоже несложно доказать) Произведение XY само представляет собой случайную величину, при этом если исходные величины могли принимать n и m значений соответственно, то XY может принимать nm значений. Вероятность каждого из значений вычисляется исходя из того, что вероятности независимых событий перемножаются. В итоге получаем вот что:
Математическое ожидание непрерывной случайной величины
Если известна плотность распределения, то математическое ожидание ищется так:
Пусть, например, есть равномерное распределение:
Найдём математическое ожидание:
Это вполне соответствует интуитивному пониманию. Скажем, если мы получаем при равномерном распределении много случайных действительных чисел, каждое из отрезка |0; 1|, то среднее арифметическое должно быть около 0,5.
Взаимосвязь математического ожидания с другими статистическими показателями
В статистическом анализе наряду с математическим ожиданием существует система взаимозависимых показателей, отражающих однородность явлений и устойчивость процессов. Часто показатели вариации не имеют самостоятельного смысла и используются для дальнейшего анализа данных. Исключением является коэффициент вариации, который характеризует однородность данных, что является ценной статистической характеристикой.
Степень изменчивости или устойчивости процессов в статистической науке может измеряться с помощью нескольких показателей.
Наиболее важным показателем, характеризующим изменчивость случайной величины, является Дисперсия, которая самым тесным и непосредственным образом связана с математическим ожиданием. Этот параметр активно используется в других видах статистического анализа (проверка гипотез, анализ причинно-следственных связей и др.). Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.
Формула для расчета дисперсии выглядит так:
Однако в чистом виде, как, например, средняя арифметическая, или индекс, дисперсия не используется. Это скорее вспомогательный и промежуточный показатель, который используется для других видов статистического анализа. У нее даже единицы измерения нормальной нет. Судя по формуле, это квадрат единицы измерения исходных данных.
Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?
Или будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию Mx. В данном случае Mx = 3,5.
Каким образом получилась эта величина? Пусть в N испытаниях n1 раз выпало 1 очко, n2 раз – 2 очка и так далее. Тогда количество исходов, в которых выпало одно очко:
Аналогично для исходов, когда выпало 2, 3, 4, 5 и 6 очков.
Математическое ожидание Mx случайной величины x равно:
Математическое ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают.
Вероятность р1 того, что случайная величина х окажется меньшей х1/2, и вероятность р2 того, что случайная величина x окажется большей х1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.
Пример. В условиях испытаний при стрельбе по мишени вычислить дисперсию и среднеквадратическое отклонение случайной величины:
Размах вариации (R) представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности. Этот показатель дает самое общее представление о колеблемости изучаемого признака, так как показывает разницу только между предельными значениями вариантов. Зависимость от крайних значений признака придает размаху вариации неустойчивый, случайный характер.
Среднее линейное отклонение представляет собой среднее арифметическое из абсолютных (по модулю) отклонений всех значений анализируемой совокупности от их средней величины:
Математическое ожидание в теории азартных игр
Математическое ожидание – это среднее количество денег, которое игрок в азартные игры может выиграть или проиграть на данной ставке. Это очень существенное понятие для игрока, потому что оно является основополагающим для оценки большинства игровых ситуаций. Математическое ожидание – это также оптимальный инструмент для анализа основных карточных раскладов и игровых ситуаций.
Ваш часовой выигрыш равен нулю. Часовой выигрыш – это то количество денег, которое вы ожидаете выиграть за час. Вы можете кидать монету 500 раз в течение часа, но вы не выиграете и не проиграете, т.к. ваши шансы ни положительны, ни отрицательны. Если смотреть, с точки зрения серьезного игрока такая система ставок неплоха. Но это попросту потеря времени.
Каждый раз, делая ставку с лучшим исходом (ставка, которая может оказаться выгодной на длинной дистанции), когда шансы в вашу пользу, вы обязательно что-то выигрываете на ней, и не важно теряете ли вы ее или нет в данной раздаче. И напротив, если вы сделали ставку с худшим исходом (ставка, которая невыгодна на длинной дистанции), когда шансы не в вашу пользу, вы что-то теряете независимо от того, выиграли вы или проиграли в данной раздаче.
Вы делаете ставку с лучшим исходом, если матожидание у вас положительно, а оно является положительным, если шансы на вашей стороне. Делая ставку с худшим исходом, у вас отрицательное матожидание, которое бывает, когда шансы против вас. Серьезные игроки делают ставки только с лучшим исходом, при худшем – они пасуют. Что означает шансы в вашу пользу? Вы можете в итоге выиграть больше, чем приносят реальные шансы. Реальные шансы на то, что выпадет решка 1 к 1, но у вас выходит 2 к 1 за счет соотношения ставок. В данном случае шансы в вашу пользу. Вы точно получаете лучший исход с положительным ожиданием в 50 центов за одну ставку.
Игрок, который собирается выиграть больше, чем ставит, как в примере выше, – ловит шансы. И напротив, он губит шансы, когда предполагает выиграть меньше, чем ставит. Игрок, делающий ставку может иметь либо положительное, либо отрицательное матожидание, которое зависит от того, ловит он или губит шансы.
Математическое ожидание при игре в Покер
Игра в Покер является наиболее показательным и наглядным примером с точки зрения использования теории и свойств математического ожидания.
Математическое ожидание (англ. Expected Value) в Покере – средняя выгода от того или иного решения при условии, что подобное решение может быть рассмотрено в рамках теории больших чисел и длительной дистанции. Успешная игра в покер заключается в том, чтобы всегда принимать ходы только с положительным математическим ожиданием.
Математический смысл математического ожидания при игре в покер заключается в том, что мы часто сталкиваемся со случайными величинами при принятии решения (мы не знаем, какие именно карты на руках у оппонента, какие карты придут на последующих кругах торговли). Мы должны рассматривать каждое из решений с точки зрения теории больших чисел, которая гласит, что при достаточно большой выборке среднее значение случайной величины будет стремиться к её математическому ожиданию.
Среди частных формул для вычисления математического ожидания, в покере наиболее применима следующая:
Ожидание говорит вам о том, что вы можете ожидать (прибыль или убыток) на каждый рискуемый вами доллар. Казино зарабатывают деньги, поскольку математическое ожидание от всех игры, которые практикуются в них, в пользу казино. При достаточно длинной серии игры можно ожидать, что клиент потеряет свои деньги, поскольку «вероятность» в пользу казино. Однако профессиональные игроки в казино ограничивают свои игры короткими промежутками времени, тем самым увеличивая вероятность в свою пользу. То же самое касается и инвестирования. Если ваше ожидание является положительным, вы можете заработать больше денег, совершая много сделок в короткий период времени. Ожидание это ваш процент прибыли на выигрыш, умноженный на среднюю прибыль, минус ваша вероятность убытка, умноженная на средний убыток.
Покер также можно рассмотреть с точки зрения математического ожидания. Вы можете предположить, что определенный ход выгоден, но в некоторых случаях он может оказаться далеко не лучшим, потому что выгоднее другой ход. Допустим, вы собрали фулл-хаус в пятикарточном покере с обменом. Ваш соперник делает ставку. Вы знаете, что если повысите ставку, он ответит. Поэтому повышение выглядит лучшей тактикой. Но если вы все же поднимите ставку, оставшиеся двое игроков, точно сбросят карты. Но если вы уравняете ставку, то будете полностью уверены, что двое других игроков после вас поступят также. При повышении ставки вы получаете одну единицу, а просто уравнивая – две. Таким образом, уравнивание дает вам более высокое положительное математическое ожидание, и будет являться наилучшей тактикой.
Другой важной причиной для понимания сути математического ожидания является то, что оно дает вам чувство спокойствия независимо от того, выиграли вы ставку или нет: если вы сделали хорошую ставку или вовремя спасовали, вы будете знать, что вы заработали или сберегли определенное количество денег, которое игрок слабее не смог уберечь. Гораздо сложнее сбросить карты, если вы расстроены тем, что соперник на обмене собрал более сильную комбинацию. При всем при этом, деньги, которые вы сберегли, не играя, вместо того, чтобы ставить, прибавляются к вашему выигрышу за ночь или за месяц.
Просто помните, что если поменять ваши руки, ваш соперник ответил бы вам, и как вы увидите в статье «фундаментальная теорема покера» это лишь одно из ваших преимуществ. Вы должны радоваться, когда это случится. Вам даже можно научиться получать удовольствие от проигранной раздачи, потому что вы знаете, что другие игроки на вашем месте проиграли бы гораздо больше.
За большой промежуток времени суммарный выигрыш игрока составляет сумму его математических ожиданий в отдельных раздачах. Чем больше вы играете с положительным ожиданием, тем больше выигрываете, и наоборот, чем больше раздач с отрицательным ожиданием вы сыграете, тем больше вы проиграете. Вследствие этого, следует отдавать предпочтение игре, которая сможет максимально увеличить ваше положительное ожидание или сведет на нет отрицательное, чтобы вы смогли поднять до максимума ваш часовой выигрыш.
Положительное математическое ожидание в игровой стратегии
Если вы знаете, как считать карты, у вас может быть преимущество перед казино, если они не заметят этого и не выкинут вас вон. Казино обожают пьяных игроков и не переносят считающих карты. Преимущество позволит вам со временем выиграть большее число раз, чем проиграть. Хорошее управление капиталом при использовании расчетов математического ожидания может помочь извлечь больше прибыли из вашего преимущества и сократить потери. Без преимущества вам лучше отдать деньги на благотворительность. В игре на бирже преимущество дает система игры, создающая большую прибыль, чем потери, разница цен и комиссионные. Никакое управление капиталом не спасет плохую игровую систему.
Положительное ожидание определяется значением, превышающим ноль. Чем больше это число, тем сильнее статис¬тическое ожидание. Если значение меньше нуля, то математическое ожидание также будет отрицательным. Чем больше модуль отрица¬тельного значения, тем хуже ситуация. Если результат равен нулю, то ожидание является безубыточным. Вы можете выиграть только тогда, когда у вас положительное математическое ожидание, разумная система игры. Игра по интуиции приводит к катастрофе.
Математическое ожидание и биржевая торговля
Математическое ожидание – достаточно широко востребованный и популярный статистический показатель при осуществлении биржевых торгов на финансовых рынках. В первую очередь данный параметр используют для анализа успешности торговли. Не сложно догадаться, что чем больше данное значение, тем больше оснований считать изучаемую торговлю успешной. Конечно, анализ работы трейдера не может производиться только лишь с помощью данного параметра. Тем не менее, вычисляемое значение в совокупности с другими способами оценки качества работы, может существенно повысить точность анализа.
Математическое ожидание часто вычисляется в сервисах мониторингов торговых счетов, что позволяет быстро оценивать работу, совершаемую на депозите. В качестве исключений можно привести стратегии, в которых используется “пересиживание” убыточных сделок. Трейдеру может некоторое время сопутствовать удача, а потому, в его работе может не оказаться убытков вообще. В таком случае, ориентироваться только по матожиданию не получится, ведь не будут учтены риски, используемые в работе.
В торговле на рынке математическое ожидание чаще всего применяют при прогнозировании доходности какой-либо торговой стратегии или при прогнозировании доходов трейдера на основе статистических данных его предыдущих торгов.
В отношении управления капиталом очень важно понимать, что при совершении сделок с отрицательным ожиданием нет схемы управления деньгами, которая может однозначно принести высокую прибыль. Если вы продолжаете играть на бирже в этих условиях, то независимо от способа управления деньгами вы потеряете весь ваш счет, каким бы большим он ни был в начале.
Эта аксиома верна не только для игры или сделок с отрицательным ожиданием, она истинна также для игры с равными шансами. Поэтому единственный случай, когда у вас есть шанс получить выгоду в долгосрочной перспективе, — это заключение сделок с положительным математическим ожиданием.
Различие между отрицательным ожиданием и положительным ожиданием — это различие между жизнью и смертью. Не имеет значения, насколько положительное или насколько отрицательное ожидание; важно только то, положительное оно или отрицательное. Поэтому до рассмотрения вопросов управления капиталом вы должны найти игру с положительным ожиданием.
Если у вас такой игры нет, тогда никакое управление деньгами в мире не спасет вас. С другой стороны, если у вас есть положительное ожидание, то можно, посредством правильного управления деньгами, превратить его в функцию экспоненциального роста. Не имеет значения, насколько мало это положительное ожидание! Другими словами, не имеет значения, насколько прибыльна торговая система на основе одного контракта. Если у вас есть система, которая выигрывает 10 долларов на контракт в одной сделке (после вычета комиссионных и проскальзывания), можно использовать методы управления капиталом таким образом, чтобы сделать ее более прибыльной, чем систему, которая показывает среднюю прибыль 1000 долларов за сделку (после вычета комиссионных и проскальзывания).
Имеет значение не то, насколько прибыльна система была, а то, насколько определенно можно сказать, что система покажет, по крайней мере, минимальную прибыль в будущем. Поэтому наиболее важное приготовление, которое может сделать трейдер, — это убедиться в том, что система покажет положительное математическое ожидание в будущем.
Для того чтобы иметь положительное математическое ожидание в будущем, очень важно не ограничивать степени свободы вашей системы. Это достигается не только упразднением или уменьшением количества параметров, подлежащих оптимизации, но также и путем сокращения как можно большего количества правил системы. Каждый параметр, который вы добавляете, каждое правило, которое вы вносите, каждое мельчайшее изменение, которое вы делаете в системе, сокращает число степеней свободы. В идеале, вам нужно построить достаточно примитивную и простую систему, которая постоянно будет приносить небольшую прибыль почти на любом рынке. И снова важно, чтобы вы поняли, — не имеет значения, насколько прибыльна система, пока она прибыльна. Деньги, которые вы заработаете в торговле, будут заработаны посредством эффективного управления деньгами.
Торговая система — это просто средство, которое дает вам положительное математическое ожидание, чтобы можно было использовать управление деньгами. Системы, которые работают (показывают, по крайней мере, минимальную прибыль) только на одном или нескольких рынках или имеют различные правила или параметры для различных рынков, вероятнее всего, не будут работать в режиме реального времени достаточно долго. Проблема большинства технически ориентированных трейдеров состоит в том, что они тратят слишком много времени и усилий на оптимизацию различных правил и значений параметров торговой системы. Это дает совершенно противоположные результаты. Вместо того, чтобы тратить силы и компьютерное время на увеличение прибылей торговой системы, направьте энергию на увеличение уровня надежности получения минимальной прибыли.
И здесь нам, работающим трейдерам, неплохую помощь может оказать математическое ожидание. Данный термин в теории вероятности является одним из ключевых. С его помощью можно дать усредненную оценку некоторому случайному значению. Математическое ожидание случайной величины подобно центру тяжести, если представить себе все возможные вероятности точками с различной массой.
Что означает данное число? Оно говорит о том, что, следуя правилам данной системы, в среднем мы будет получать 1,708 доллара от каждой закрытой сделки. Поскольку полученная оценка эффективности больше нуля, то такую систему вполне можно использовать для реальной работы. Если же в результате расчета математическое ожидание получится отрицательным, то это уже говорит о среднем убытке и такая торговля приведет к разорению.
Размер прибыли на одну сделку может быть выражен также и относительной величиной в виде %. Например:
В этом случае математическое ожидание составит:
То есть, средняя сделка принесет 1,96%.
Можно разработать систему, которая несмотря на преобладание убыточных сделок будет давать положительный результат, поскольку ее МО>0.
Впрочем, одного ожидания мало. Сложно заработать, если система дает очень мало торговых сигналов. В этом случае ее доходность будет сопоставима с банковским процентом. Пусть каждая операция дает в среднем всего лишь 0,5 доллара, но что если система предполагает 1000 операций в год? Это будет очень серьезная сумма за сравнительно малое время. Из этого логически вытекает, что еще одним отличительным признаком хорошей торговой системы можно считать короткий срок удержания позиций.