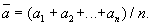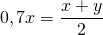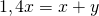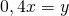Что такое среднее арифметическое чисел
Что такое среднее арифметическое чисел
Что такое среднее арифметическое чисел
Средне-арифметическое – что это значит?
Не только в различных математических науках, но и в повседневной жизни возникают случаи, когда нужно рассчитать средний показатель чего-либо. Например, среднюю стоимость огурцов на рынке, средний рост ребенка, среднюю стоимость проживания в гостинице и пр.
Всему этому уже давно было придумано научное название – «среднее арифметическое». Данный показатель активно применяется в статистике для обобщения результатов. К примеру, средний возраст для рождения детей, средний возраст смерти среди мужчин и женщин, средняя заработная плата по регионам и по России в целом.
К примеру, при принятии закона о повышении пенсионного возраста, власти как раз исходили из среднего возраста смерти в нашей стране.
Разберемся, что же представляет собой данный показатель.
Среднее арифметическое – это усредненный показатель всех имеющихся значений. Для его расчета необходимо суммировать все участвующие в операции числа, после чего разделить на их общее количество.
К примеру, в 2017 году полное среднее образование получили дети разных возрастов : 16, 17 и 18 лет. Среднее арифметическое будет рассчитано, как сумма всех возрастов, деленная на три. Итого средний возраст ребёнка, окончившего 11 класс, составил 17 лет.
В данном примере показан примитивный расчет на примере трех детей. По факту суммировать нужно все данные, имеющиеся в наличии. То есть если речь будет идти о пяти детях, то мы суммируем их возраст, к примеру, 17+17+18+16+17 и делим полученное на пять.
Аналогично производится расчет любого среднего арифметического для какой-либо операции. То есть, если, например, нужно подсчитать средний возраст матерей, родивших первого ребенка в 2017 году, то сначала нужно будет суммировать все показатели возраста, после чего поделить на общее число родительниц.
То есть в общем виде формулу можно представить так:
Среднее арифметическое = (сумма всех имеющихся значений)/общее число значений, что участвуют в операции.
Таким образом, расчет довольно прост, даже для школьников. Затруднения могут возникнуть лишь по причине большого количества респондентов, участвующих в операции.
Важно понимать, что средний показатель не является просто числом. Он имеет особый физический смысл, который уже долгие годы применяется в реальном мире на практике.
Неправильным было бы использование среднего арифметического лишь на бумаге, в тетради или в компьютерных программах. В противном случае, можно получить множество бессмысленных и просто нереальных значений.
Средних, на самом деле, существует несколько. Однако в каждом случае, только одно из них верное. В каждой из операций, нужно использовать только тот вид среднего, который необходим, иначе будет допущена огромная ошибка.
Какие виды средних используются на практике? Самые распространенные средние – это:
Эти значения наиболее часто используются, как в повседневной жизни, так и в науках. Наиболее часто, конечно же, рассчитывается первый показатель.
Зачастую данный показатель в реальных условиях применяется и рассчитывается неверно. Почему так происходит? Фактически, базой среднего арифметического выступает применение закона о больших числах. Кроме того, применяется и допущение, согласно которому исходная величина является нормально определенной.
Это означает, что вокруг представленного в ряде значений, имеется наиболее частое отклонение в какую-либо сторону. То есть. В большую или меньшую. Например, в ряду чисел 8,8,9,8,9,8,8, отклонение будет в меньшую сторону, так как больше восьмерок. А в ряде: 17,17, 20,20,20,20,20, отклонение, наоборот, будет в большую сторону, так как в этом случае больше все же «двадцаток».
Однако в большинстве случаев, такие отклонения являются небольшими и обычно равными по вероятности. Суть проблемы в том, что в бизнесе, как и в реальной жизни, нормальность распределения на практике можно встретить крайне редко.
То есть, к примеру, время обслуживания одного клиента, время, которое клиенту ожидают этого обслуживания, сумма, на которую они потом заключат контракт, рыночная доля, прирост доходов и прочее, являются теми показателями, что не распределяются равномерно и нормально. Их усреднять в некоторых случаях нежелательно именно при помощи среднего арифметического. Потому что это было бы неправильно.
На практике нормальность распределения часто можно встретить при наличии большого количества значений, начиная с сотен и тысяч. К примеру, количество обращений в техническую поддержку крупной компании может быть распределено нормально, как на бумаге, так и фактически.
Тем не менее, только лишь количества не будет достаточно, ведь в каждой конкретной ситуации нужно следить и за правильностью распределения. Только так можно будет правильно в итоге рассчитать значение среднего арифметического.
Среднее арифметическое
Средняя оценка: 4.1
Всего получено оценок: 114.
Средняя оценка: 4.1
Всего получено оценок: 114.
Среднее арифметическое чисел – это первый параметр ряда, который изучают ученики 5 класса. Все понятия, связанные с рядами достаточно непривычны для юных математиков, поэтому возникают вопросы и ошибки. Разберемся в теме подробнее, чтобы избежать ошибок в будущем.
Для начала разберемся в том, что такое ряд. Рядом называют несколько чисел. Ряды могут быть конечными и бесконечными. В конечном ряду всегда определенное количество числе. Это может быть 2, 3 или 10 миллионов чисел – все равно ряд будет считаться конечным.
Произвольно записанные на листе числа будут являться конечным числовым рядом.
Логично возникает вопрос, если числовой ряд бесконечен, как узнать следующий член ряда? Ничего сложного в этом нет. У бесконечных рядов всегда есть формула следующего члена ряда и начальное число.
Функцию нельзя считать числовым рядом, так как в нее можно подставить любое число, то есть не существует первого члена ряда.
С бесконечными рядами учат работать в старших классах, а среднее арифметическое чаще всего ищут для конечных рядов.
Что такое среднее арифметическое?
Среднее арифметическое – это среднее значение ряда. В высшей математике такое значение называют тенденцией, то есть усредненным значением ряда.
Для того, чтобы найти среднее арифметическое нужно сложить все члены ряда и поделить сумму на число членов в ряду. Значит, если ряд бесконечный то найти среднее арифметическое всего ряда нельзя, так как невозможно узнать число членов ряда. Но можно узнать значение среднего арифметического на каком-то отрезке.
Зачем нужно среднее арифметическое?
Среднее арифметическое редко используется в математике, зато крайне часто применяется в реальной жизни. Приведем несколько примеров:
Это лишь единичные примеры. На деле среднее арифметическое используется практически в любой отрасли человеческой жизни. Умение правильно находить среднее арифметическое и понимание того, что скрывается под этим понятием необходимо для любой профессии.
Нужно различать понятия среднее арифметическое и среднее геометрическое. Среднее геометрическое высчитывается по другой формуле и гораздо чаще встречается в математике. Нужно понимать, что это две разные характеристики ряда.
Что мы узнали?
Мы поговорили о числовых рядах. Выделили конечные и бесконечные ряды. Поговорили отдельно о каждом из видов. Рассказали о том, что такое среднее арифметическое и как находится значение среднего арифметического. Привели примеры использования этого показателя в реальной жизни.
Среднее арифметическое
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.
Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).
Содержание
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (
, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E<xi> есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры
Непрерывная случайная величина
Для непрерывно распределённой величины 
среднее арифметическое на отрезке 
определяется через определённый интеграл:
Некоторые проблемы применения среднего
Отсутствие робастности
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.
В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост 
, то есть 8,2 % в год.
Направления
Особую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:
В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).
Что такое среднее арифметическое?
Среднее арифметическое набора чисел определяется как их сумма, деленная на их количество. То есть сумма всех чисел набора делится на количество чисел в этом наборе.
Сре́днее арифмети́ческое (в математике и статистике) — одна из наиболее распространенных мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, деленную на их количество.
У этого термина существуют и другие значения, см. среднее значение.
Сре́днее арифмети́ческое (в математике и статистике) — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, делённую на их количество.
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1].
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
Содержание [показать]
Введение [править | править вики-текст]
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (\bar
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E
На практике разница между μ и \bar
Обе эти величины вычисляются одним и тем же способом:
\bar
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры [править | править вики-текст]
Для трёх чисел необходимо сложить их и разделить на 3:
\frac
Для четырёх чисел необходимо сложить их и разделить на 4:
\frac
Или проще 5+5=10, 10:2. Потому что мы складывали 2 числа, а значит, сколько чисел складываем, на столько и делим.
Непрерывная случайная величина [править | править вики-текст]
Для непрерывно распределённой величины f(x) среднее арифметическое на отрезке [a;b] определяется через определённый интеграл: Некоторые проблемы применения среднего Отсутствие робастности [править Основная статья: Робастность в статистикеХотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическ
среднее арифметическое
3.1 среднее арифметическое; среднее (arithmetic mean / average): Сумма значений, деленная на их число.
[ИСО 3534-1:1993, 2.26]
2.26. среднее арифметическое
Сумма значений, деленная на их число.
Смотри также родственные термины:
3.7.2 среднее арифметическое (значение результата геодезических измерений)
Оценка значения геодезической величины из многократных равноточных измерений, получаемая по формуле
20. Среднее арифметическое отклонение профиля
Среднее арифметическое из абсолютных значений отклонений профиля в пределах базовой длины
Полезное
Смотреть что такое «среднее арифметическое» в других словарях:
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ — англ. mean arithmetical; нем. Mittel, arithmetisches. Сумма нек рого набора мат. величин, деленная на число этих величин. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
среднее арифметическое — aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
СРЕДНЕЕ, АРИФМЕТИЧЕСКОЕ — Сумма набора значений, поделенная на число значений. Это – наиболее часто используемое и наиболее полезное измерение центральной тенденции, так как в отличие от медианы и моды оно использует все данные распределения и служит основой для измерения … Толковый словарь по психологии
среднее арифметическое — vidurkis statusas T sritis Kūno kultūra ir sportas apibrėžtis Dydis, gaunamas padalijus įvairių dydžių sumą iš jų skaičiaus. atitikmenys: angl. average vok. Durchschnitt, m rus. среднее арифметическое … Sporto terminų žodynas
Среднее арифметическое взвешенное — набора вещественных чисел с вещественными весами определяется как Часто подразумевают, что сумма весов равна 1, тогда формула выглядит следующим образом: В том случае, если все веса равны между собой, среднее арифметическое взвешенное будет равно … Википедия
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ — (arithmetic mean) Средняя величина, полученная путем сложения всех членов числового ряда и деления суммы на число членов. Например, среднее арифметическое значение 7, 20, 152 и 305 равно 484/4 = 121. Однако средняя величина не позволяет судить о… … Словарь бизнес-терминов
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ — (arithmetic mean) Средняя величина, полученная путем сложения всех членов числового ряда и деления суммы на число членов, например среднее арифметическое значение 7, 20, 107 и 350 равно 484/4 = 121. Однако средняя величина не позволяет судить о… … Финансовый словарь
среднее арифметическое значение — aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m; arithmetisches Mittel, n rus. арифметическое среднее, n; среднее арифметическое значение, n … Fizikos terminų žodynas
Среднее арифметическое
Предложена (наряду со средним геометрическим и средним гармоническим) еще пифагорейцами [1] и является одной из наиболее распространенных мер центральной тенденции.
Частными случаями среднего арифметического являются генеральное среднее ( генеральной совокупности) и выборочное среднее ( выборки).
Содержание
Введение
Обозначим множество данных X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной (, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E<xi> есть математическое ожидание этой выборки.
На практике разница между μ и в том, что μ является типичной ненаблюдаемой переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Заметим, что имеется несколько других «средних» значений, в том числе среднее степенное, среднее Колмогорова, гармоническое среднее, арифметико-геометрическое среднее и различные средне-взвешенные величины.
Примеры
Непрерывная случайная величина
Для непрерывно распределённой величины среднее арифметическое на отрезке определяется через определённый интеграл:
Некоторые проблемы применения среднего
Отсутствие робастности
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только 8,2 %.
В общем, сложный процент даёт 90 % * 130 % = 117 % общий рост, а годовой прирост , то есть 8,2 % в год.
Направления
Особую осторожность нужно иметь при расчёте циклических данных, таких как фазы или углы. Наивное вычисление среднего арифметического 1° и 359° даёт результат 180°. Это неверно по двум причинам:
В целом применение такого рассмотрения средней величины ведёт к искусственному сдвигу его к середине числового диапазона. Решение этой проблемы заключается в использовании оптимальной формализации (а именно, определение среднего в качестве центральной точки, то есть точки, от которой наименьшая дисперсия), а также переопределение вычитания как модульного расстояния (то есть как расстояние от окружности; в частности, модульное расстояние между 1° и 359° — это 2°, а не 358°).
Среднее арифметическое
Определение. нескольких величин — это отношение суммы величин к их количеству.
Примером среднего арифметического служат такие показатели, как урожайность, производительность, посещаемость, скорость движения на определенном участке. Вычисление среднего арифметического и его составляющих производится по следующему простом правилу.
Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.
Пример 1. У Васи было 2 яблока, у Кати — 10 яблок, а у Саши — 6. Среднее количество яблок:
Пример 2. Средняя посещаемость зала в столовой за неделю высчитывается из посещаемости в течение 7 дней: 145 человек в 1-й день; 152 человека во 2-й день; 158 человек в 3-й лень; 162 человека в 4-й день; 164 человека в 5-й день; 161 человек в 6-й день и 157 человек в 7-й день.
Найдем среднее арифметическое (посещаемость) за
неделю:
Xсреднее = (145 + 152 + 158 + 162 + 164 + 161 + 157) : 7 = 157.
Можно определить среднюю посещаемость и как 1099 : 7 = 157 человек (1099 человек за 7 дней). Т. с. можно фиксировать общее количество посетителей за неделю без учета посещаемости по дням. Но тогда мы не будем знать, что наибольшее количество посетителей в день — 164 человека, а наименьшее — 145 человек, что в этом примере важно (кухня должна ориентироваться на максимальное посещение, от количества посетителей зависит выручка столовой н т. д.).
Во втором примере мы вели статистический учет, следовательно, среднее арифметическое — показатель и в статистике. Но вычисление среднего арифметического имеет смысл только в определенных пределах (небольших промежутках). Нам ничего не даст, например, среднее-мировое количество жителей в одной стране. Стран в мире более 200, а число жителей Индии и Китая совершенно несоизмеримо с количеством жителей Нидерландов или Люксембурга. Полученная средняя численность проживающих в одной стране не будет объективной характеристикой каждой из стран (из-за большого расхождения в числах).
Среднее арифметическое
Сре́днее арифмети́ческое (в математике и статистике) множества чисел — число, равное сумме всех чисел множества, делённое на их количество. Является одной из наиболее распространённых мер центральной тенденции.
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.
Содержание
Введение
Обозначим множество чисел X = (x1, x2, …, xn), тогда выборочное среднее обычно обозначается горизонтальной чертой над переменной ( x ¯ <\displaystyle <\bar 
, произносится «x с чертой»).
Для обозначения среднего арифметического всей совокупности чисел обычно используется греческая буква μ. Для случайной величины, для которой определено среднее значение, μ есть вероятностное среднее или математическое ожидание случайной величины. Если множество X является совокупностью случайных чисел с вероятностным средним μ, тогда для любой выборки xi из этой совокупности μ = E<xi> есть математическое ожидание этой выборки.
На практике разница между μ и x ¯ <\displaystyle <\bar в том, что μ является типичной переменной, потому что видеть можно скорее выборку, а не всю генеральную совокупность. Поэтому, если выборку представлять случайным образом (в терминах теории вероятностей), тогда x ¯ <\displaystyle <\bar (но не μ) можно трактовать как случайную переменную, имеющую распределение вероятностей на выборке (вероятностное распределение среднего).
Обе эти величины вычисляются одним и тем же способом:
Если X — случайная переменная, тогда математическое ожидание X можно рассматривать как среднее арифметическое значений в повторяющихся измерениях величины X. Это является проявлением закона больших чисел. Поэтому выборочное среднее используется для оценки неизвестного математического ожидания.
В элементарной алгебре доказано, что среднее n + 1 чисел больше среднего n чисел тогда и только тогда, когда новое число больше чем старое среднее, меньше тогда и только тогда, когда новое число меньше среднего, и не меняется тогда и только тогда, когда новое число равно среднему. Чем больше n, тем меньше различие между новым и старым средними значениями.
Примеры
Непрерывная случайная величина
Некоторые проблемы применения среднего
Отсутствие робастности
Хотя среднее арифметическое часто используется в качестве средних значений или центральных тенденций, это понятие не относится к робастной статистике, что означает, что среднее арифметическое подвержено сильному влиянию «больших отклонений». Примечательно, что для распределений с большим коэффициентом асимметрии среднее арифметическое может не соответствовать понятию «среднего», а значения среднего из робастной статистики (например, медиана) может лучше описывать центральную тенденцию.
Классическим примером является подсчёт среднего дохода. Арифметическое среднее может быть неправильно истолковано в качестве медианы, из-за чего может быть сделан вывод, что людей с большим доходом больше, чем на самом деле. «Средний» доход истолковывается таким образом, что доходы большинства людей находятся вблизи этого числа. Этот «средний» (в смысле среднего арифметического) доход является выше, чем доходы большинства людей, так как высокий доход с большим отклонением от среднего делает сильный перекос среднего арифметического (в отличие от этого, средний доход по медиане «сопротивляется» такому перекосу). Однако, этот «средний» доход ничего не говорит о количестве людей вблизи медианного дохода (и не говорит ничего о количестве людей вблизи модального дохода). Тем не менее, если легкомысленно отнестись к понятиям «среднего» и «большинство народа», то можно сделать неверный вывод о том, что большинство людей имеют доходы выше, чем они есть на самом деле. Например, отчёт о «среднем» чистом доходе в Медине, штат Вашингтон, подсчитанный как среднее арифметическое всех ежегодных чистых доходов жителей, даст на удивление большое число из-за Билла Гейтса. Рассмотрим выборку (1, 2, 2, 2, 3, 9). Среднее арифметическое равно 3.17, но пять значений из шести ниже этого среднего.
Сложный процент
Если числа перемножать, а не складывать, нужно использовать среднее геометрическое, а не среднее арифметическое. Наиболее часто этот казус случается при расчёте окупаемости инвестиций в финансах.
Например, если акции в первый год упали на 10 %, а во второй год выросли на 30 %, тогда некорректно вычислять «среднее» увеличение за эти два года как среднее арифметическое (−10 % + 30 %) / 2 = 10 %; правильное среднее значение в этом случае дают совокупные ежегодные темпы роста, по которым годовой рост получается только около 8,16653826392 % ≈ 8,2 %.
Направления
При расчёте среднего арифметического значений некоторой переменной, изменяющейся циклически (например, фаза или угол), следует проявлять особую осторожность. Например, среднее чисел 1° и 359° будет равно 1 ∘ + 359 ∘ 2 = <\displaystyle <\frac <1^<\circ >+359^<\circ >><2>>=> 180°. Это число неверно по двум причинам.
Среднее значение для циклической переменной, рассчитанное по приведённой формуле, будет искусственно сдвинуто относительно настоящего среднего к середине числового диапазона. Из-за этого среднее рассчитывается другим способом, а именно, в качестве среднего значения выбирается число с наименьшей дисперсией (центральная точка). Также вместо вычитания используется модульное расстояние (то есть, расстояние по окружности). Например, модульное расстояние между 1° и 359° равно 2°, а не 358° (на окружности между 359° и 360°==0° — один градус, между 0° и 1° — тоже 1°, в сумме — 2°).
Арифметическое среднее
Смотреть что такое «Арифметическое среднее» в других словарях:
арифметическое среднее — aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
арифметическое среднее — aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m; arithmetisches Mittel, n rus. арифметическое среднее, n; среднее арифметическое значение, n … Fizikos terminų žodynas
АРИФМЕТИЧЕСКОЕ, СРЕДНЕЕ — См. среднее арифметическое … Толковый словарь по психологии
арифметическое среднее — Простое среднее, полученное делением суммы двух или более показателей на число этих показателей … Финансово-инвестиционный толковый словарь
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ — число а, получаемое делением суммы нескольких чисел на их число п … Математическая энциклопедия
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ — число а, получаемое делением суммы неск. чисел а, a i. an на п их число: а=(a1+a1+. +an):п … Большой энциклопедический политехнический словарь
Материал из Википедии — свободной энциклопедии
Tell your friends about Wikiwand!
Gmail Facebook Twitter Link
Suggest as cover photo
Would you like to suggest this photo as the cover photo for this article?
Thank you for helping!
Your input will affect cover photo selection, along with input from other users.
Thanks for reporting this video!
This browser is not supported by Wikiwand 🙁
Wikiwand requires a browser with modern capabilities in order to provide you with the best reading experience.
Please download and use one of the following browsers:
An extension you use may be preventing Wikiwand articles from loading properly.
If you’re using HTTPS Everywhere or you’re unable to access any article on Wikiwand, please consider switching to HTTPS (https://www.wikiwand.com).
An extension you use may be preventing Wikiwand articles from loading properly.
If you are using an Ad-Blocker, it might have mistakenly blocked our content. You will need to temporarily disable your Ad-blocker to view this page.
Помимо математики и статистики, среднее арифметическое часто используется во многих различных областях, таких как экономика, антропология и история, и в той или иной степени он используется почти во всех академических областях. Например, доход на душу населения это средний арифметический доход населения страны.
Хотя среднее арифметическое часто используется для отчета центральные тенденции, это не надежная статистика, что означает, что на него сильно влияют выбросы (значения, которые намного больше или меньше большинства значений). В частности, для перекошенные распределения, такой как распределение доходов для которых доходы некоторых людей значительно превышают доходы большинства людей, среднее арифметическое может не совпадать с понятием «среднего» и надежной статистикой, такой как медиана, может дать лучшее описание центральной тенденции.
Содержание
Определение
Например, рассмотрим ежемесячную зарплату 10 сотрудников фирмы: 2500, 2700, 2400, 2300, 2550, 2650, 2750, 2450, 2600, 2400. Среднее арифметическое:
Мотивирующие свойства
Среднее арифметическое имеет несколько свойств, которые делают его полезным, особенно в качестве меры центральной тенденции. К ним относятся:
Контраст с медианой
У этого явления есть приложения во многих областях. Например, с 1980-х годов средний доход в США увеличивался медленнее, чем среднее арифметическое дохода. [5]
Обобщения
Средневзвешенное
Непрерывные распределения вероятностей
Если числовое свойство и любая выборка данных из него могут принимать любое значение из непрерывного диапазона, а не, например, только целые числа, тогда вероятность числа, попадающего в некоторый диапазон возможных значений, можно описать интегрированием непрерывное распределение вероятностей в этом диапазоне, даже когда наивная вероятность для номера выборки, выбирающего одно определенное значение из бесконечного множества, равна нулю. Аналог средневзвешенного значения в этом контексте, в котором существует бесконечное количество возможностей для точного значения переменной в каждом диапазоне, называется среднее значение распределения вероятностей. Наиболее распространенное распределение вероятностей называется нормальное распределение; он обладает тем свойством, что все меры его центральной тенденции, включая не только среднее значение, но также вышеупомянутую медиану и Режим (три М [7] ), равны между собой. Это равенство не выполняется для других распределений вероятностей, как показано для логнормальное распределение здесь.
Особую осторожность следует проявлять при использовании циклических данных, таких как фазы или углы. Наивное взятие среднего арифметического 1 ° и 359 ° дает результат 180 °. Это неверно по двум причинам:
Символы и кодировка
В некоторых текстах, например PDF-файлы, символ x можно заменить на цент (¢) символ (Unicode & # 162), при копировании в текстовый процессор, например Microsoft Word.
Среднее арифметическое
Преподаватель: Платонова Татьяна Евгеньевна
Математическая статистика
Лекция 1
Основные понятия математической статистики
Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.
В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей — свойства и взаимосвязи этих величин (распределений).
Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.
При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину — как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?
Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?
Часто бывает возможно высказать некие предположения о распределении, спрятанном в «черном ящике», или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения («гипотезы»). При этом надо помнить, что ответ «да» или «нет» может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента — например, о наличии функциональной зависимости между наблюдаемыми величинами, о нормальности распределения, о его симметричности, о наличии у распределения плотности или о его дискретном характере, и т.д.
Итак, о (математической) статистике имеет смысл вспоминать, если
· имеется случайный эксперимент, свойства которого частично или полностью неизвестны,
· мы умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое (а лучше — какое угодно) число раз.
Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.
Лекция 2.
Первичная обработка результатов эксперимента
Среднее арифметическое
Дисперсия и среднее квадратическое отклонение
Интервальный ряд и гистограмма
Первичная обработка результатов эксперимента
Явления, происходящие в природе и обществе, сложны и разнообразны. Ученые изучают разные стороны этих явлений, причем каждая наука вырабатывает свои методы исследования. Например, преступность изучают юристы, социологи, психологи, медики. Есть тут серьезная работа и для математиков. Их задача – подвергнуть математической обработке огромный статистический материал – отчеты органов внутренних дел и прочее – содержащий различные числовые данные. Цель этой работы – выделить наиболее существенные сведения об интересующем явлении.
Результаты обработки представляются в виде таблиц, диаграмм, графиков и различных числовых характеристик, которые называются параметрами. Важнейшие из них – среднее арифметическое и дисперсия.
Среднее арифметическое
Понятие среднего значения используется для описания разнообразных явлений природы и общественной жизни: средняя температура воздуха, средняя зарплата, средняя продолжительность жизни. Например, для изучения общественного мнения проводят опрос не всех избирателей, а лишь небольшой части населения. По результатам прогнозируют популярность кандидатов у различных групп населения в разных регионах. При грамотной математической обработке результатов опроса выводы будут достаточно точно отражать реальную ситуацию.
Средней величиной обычно называют среднее арифметическое.
Пусть 
— некоторые числа. Их средним арифметическим называется число
(1)
Пример. Количество ДТП на улицах города в первую декаду декабря:
6 8 10 7 6 11 9 8 7 11.
Среднее арифметическое этих чисел
показывает среднее число ДТП в день.
В сводке за следующие 10 дней такие данные: 0 5 7 7 12 11 14 13 7 6.
Их среднее арифметическое
Отсюда видно, что средние значения 8,3 и 8,2 отличаются друг от друга значительно меньше, чем число ДТП за каждый день. Поэтому среднее число ДТП можно прогнозировать, причем достаточно точно. Этот факт подтверждается и отчетами ГАИ за много лет. Из них также видно, что чем больше срок отчетности (декада, месяц, квартал, …), тем устойчивее средняя величина.
Такое свойство средних значений представляет собой одно из важнейших проявлений закона больших чисел, открытого знаменитым русским математиком П.Л.Чебышевым.
Если исходные данные содержат несколько десятков чисел, то составляют таблицу, в которой указывают для каждой величины, сколько раз она наблюдалась.
Пример. Число правонарушений в городе, совершенных подростками за первые 20 дней сентября: 8 6 13 4 13 13 12 9 7 6 12 14 13 12 17 6 8 12 7 12. По этим данным составим таблицу:
 |
 |
Здесь — число дней с одинаковым количеством правонарушений, — число правонарушений за день. В первой строке значения расположены в порядке возрастания, а если сложить все числа второй строки, то получится общее число дней, т.е. 20.
Среднее число правонарушений в день:
.
Отсюда формулу (1) можно переписать так:
(2)
Здесь 
— различные среди заданных n чисел.
При этом 
(3)
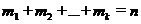
Таблицу 1 можно переписать так, чтобы во второй строке вместо числа дней стояла доля, которую это число составляет от числа всех дней, т.е. частота:
| | |||||||||
 | 0,05 | 0,15 | 0,1 | 0,1 | 0,05 | 0,25 | 0,2 | 0,05 | 0,05 |
Используя понятие частоты, подсчитаем среднее значение 
иным способом:
Таким образом, среднее арифметическое равно сумме произведений чисел, взятых из первой строки таблицы 2, на их частоты.
Преобразуем таким же способом формулу (2). Возьмем частоты:
; 
;…; 
Отсюда 
(4)
Этой формулой можно пользоваться и в том случае, когда не известны величины 
, но известны значения частот.
Пример. В некотором городе каждому пассажиру междугородного автобуса вручают страховой полис на 50000 руб., взимая за это 50 руб. Какова средняя прибыль страховой компании от продажи одного полиса, если несчастные случаи происходят в среднем с одним пассажиром из 10000?
Решение. Прибыль может принимать 2 значения: 50 руб., если несчастного случая не произошло, и – 49950 руб. при гибели пассажира. Составим таблицу частот:
| Прибыль | -49950 | |
| Частота | 0,9999 | 0,0001 |
Отсюда среднее значение прибыли:
(руб.)
Среднее арифметическое. Среднее значение величины
Средним арифметическим нескольких чисел называют частное от деления суммы этих чисел на количество слагаемых.
Говоря о значениях каких − то величин, часто имеют в виду их средние значения. Например, когда говорят, что с 1 га поля собрали 38 ц пшеницы, то это не означает, что с каждого гектара поля было собрано именно такое количество центнеров пшеницы. Эту величину получили, разделив массу всего урожая, выраженную в центнерах, на площадь всего поля, выраженную в гектарах. Величина 38 ц является средней урожайностью с 1 га данного поля.
Еще один пример. Если автомобиль проехал 120 км за 1,5 ч, то, разделив длину пути на время, получим среднюю скорость движения автомобиля. Она равна 80 км/ч. При этом автомобиль мог останавливаться, ехать со скоростью большей либо меньшей, чем 80 км/ч.
Средний возраст футболиста команды, средняя за один матч результативность футболиста, среднее количество молока, потребляемое одним жителем России в год, и т.п. также являются примерами средних величин.
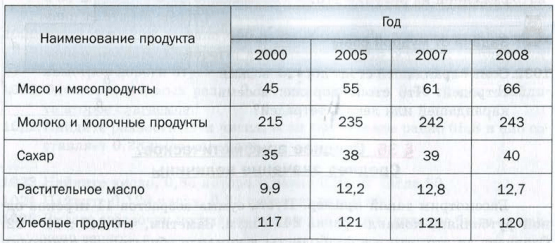
В повседневной жизни мы часто встречаемся со средними значениями величин. Например, приведем таблицу потребления некоторых продуктов питания в России (в килограммах на человека в год).
Такую таблицу могут использовать, например, экономисты и диетологи в своих исследованиях, крупные производители и поставщики сельхозпродукции при планировании своей деятельности.
1 ) 54 * 4 = 216 (км) − проехал автомобиль со скоростью 54 км/ч.
2 ) 60 * 2 = 120 (км) − проехал автомобиль со скоростью 60 км/ч.
3 ) 216 + 120 = 336 (км) − весь путь, пройденный автомобилем.
4 ) 4 + 2 = 6 (ч) − общее время движения автомобиля.
5 ) 336 : 6 = 56 (км/ч) − средняя скорость движения автомобиля.
1 ) 2,4 + 3,6 = 6 (кг) − печенья купила мама.
2 ) 73 * 6 = 438 (р.) − стоит все печенье.
3 ) 55 * 2,4 = 132 (р.) − стоит печенья первого вида.
4 ) 438 − 132 = 306 (р.) − стоит печенье второго вида.
5 ) 306 : 3,6 = 85 (р.) − цена 1 кг печенья второго вида.
Среднее арифметическое
Содержание
Часто в жизни для исследования и анализа разной информации о явлениях в природе или в нашем обществе, для решения многих задач используют среднее арифметическое предоставленных чисел.
Этим плотно занимается наука под названием «Статистика». Она получила своё имя от известного всем пользователям соцсетей латинского слова «status». Слово в переводе обозначает «состояние (или положение) вещей».
Ранее вы, вероятно, уже слышали о статистике и в предыдущих классах изучали понятие среднего арифметического. В данном уроке разберем тему подробнее, а также узнаем, что такое в статистике «мода», «размах» и «медиана».
Где используется среднее арифметическое число? Например:
Пример использования в расчетах
Рассмотрим сразу задание на вычисление среднего арифметического.
В результате отличной подготовки ему удалось выиграть соревнования. Тренеру нужно было рассчитать, сколько примерно необходимо пробегать другим спортсменам в день в среднем (бегая по 5 дней в неделю), чтобы достигать аналогичных результатов.
Показать решение и ответ
Решение:
Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых
Уже сейчас вы можете использовать эту методику подсчета, чтобы, например, узнать, сколько времени в среднем вы тратите в день на выполнение домашнего задания. Для этого записывайте каждый день потраченное на уроки время в течение недели-двух и самостоятельно посчитайте среднее арифметическое. Полученная информация будет вам полезна для планирования своего времени.
Среднее арифметическое — методы и примеры расчетов
Нахождение среднего арифметического изучается на уроках математики в 5 классе. Однако ученики иногда не понимают эту тему. Изучение материала самостоятельно по учебнику не всегда дает положительный эффект. Специалисты позаботились об этом и разработали специальный алгоритм, который поможет восполнить «пробелы» в знаниях, а также добиться успехов в других физико-математических дисциплинах.
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Как вычислить среднее арифметическое двух чисел
Среднее арифметическое — это число, равное сумме всех чисел множества, делённой на их количество.
Среднее арифметическое двух чисел вычисляется по формуле:
Xср — среднее арифметическое 2-х чисел;
X1 — первое число;
X2 — второе число.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета среднего арифметического двух чисел (среднее между двумя числами). С помощью этого калькулятора вы в один клик сможете рассчитать среднее арифметическое 2-х чисел, если известны исходные числа.
Что такое среднее арифметическое
Средним арифметическим нескольких величин является отношение суммы этих величин к их количеству.
Среднее арифметическое определенного ряда чисел называется сумма всех этих чисел, поделенная на количество слагаемых. Таким образом, среднее арифметическое является средним значением числового ряда.
Чему равно среднее арифметическое нескольких чисел? А равно они сумме этих чисел, которая поделена на количество слагаемых в этой сумме.
Как найти среднее арифметическое число
В вычислении или нахождении среднего арифметического нескольких чисел, нет ничего сложного, достаточно сложить все представленные числа, а полученную сумму разделить на количество слагаемых. Полученный результат и будет средним арифметическим этих чисел.
Рассмотрим этот процесс более подробно. Что же нам нужно сделать для вычисления среднего арифметического и получения конечного результата этого числа.
Во-первых, для его вычисления нужно определить набор чисел или их количество. В этот набор могут входить большие и маленькие числа, и их количество может быть каким угодно.
Во-вторых, все эти числа нужно сложить и получить их сумму. Естественно, если числа несложные и их небольшое количество, то вычисления можно произвести, записав от руки. А если же набор чисел впечатляющий, то лучше воспользоваться калькулятором или электронной таблицей.
И, в-четвертых, полученную от сложения сумму необходимо разделить на количество чисел. В итоге мы получим результат, который и будет средним арифметическим числом этого ряда.
Для чего нужно среднее арифметическое
Среднее арифметическое может пригодиться не только для решения примеров и задач на уроках математики, но для других целей, необходимых в повседневной жизни человека. Такими целями может служить подсчет среднего арифметического для расчета среднего расхода финансов в месяц, или для подсчета времени, которое вы тратите на дорогу, также для того чтобы узнать посещаемость, производительность, скорость движения, урожайность и много другого.
Так, например, давайте попробуем рассчитать, сколько времени вы тратите на дорогу в школу. Идя в школу или возвращаясь, домой вы каждый раз тратите на дорогу разное время, так как когда вы спешите, то вы идете быстрее, и поэтому дорога занимает меньше времени. А вот, возвращаясь, домой вы можете идти не спеша, общаясь с одноклассниками, любуясь природой и поэтому времени на дорогу займет больше.
Поэтому, точно определить время, затраченное на дорогу у вас не получиться, но благодаря среднему арифметическому вы сможете приблизительно узнать время, которое вы тратите на дорогу.
Припустим, что в первый день после выходных, вы потратили на путь от дома до школу пятнадцать минут, на второй день ваш путь занял двадцать минут, в среду вы прошли расстояние за двадцать пять минут, за такое же время составил ваш путь и в четверг, а в пятницу вы никуда не торопились и возвращались целых пол часа.
Давайте найдем среднее арифметическое, прибавив время, за все пять дней. Итак,
15 + 20 + 25 + 25 + 30 = 115
Теперь разделим эту сумму на количество дней
Благодаря такому способу вы узнали, что путь от дома до школы вы приблизительно тратите двадцать три минуты своего времени.
Домашнее задание
1.Путем нехитрых вычислений найдите среднее арифметическое число посещаемости учеников вашего класса за неделю.
2. Найдите среднее арифметическое:
3. Решите задачу:
Тема среднего арифметического и среднего геометрического входит в программу математики 6-7 классов. Так как параграф довольно прост для понимания, его быстро проходят, и к завершению учебного года школьники его забывают. Но знания в базовой статистике нужны для сдачи ЕГЭ, а также для международных экзаменов SAT. Да и для повседневной жизни развитое аналитическое мышление никогда не помешает.
Как вычислить среднее арифметическое и среднее геометрическое чисел
Допустим, имеется ряд чисел: 11, 4, и 3. Средним арифметическим называется сумма всех чисел, поделенная на количество данных чисел. То есть в случае чисел 11, 4, 3, ответ будет 6. Как образом получается 6?
Решение: (11 + 4 + 3) / 3 = 6
В знаменателе должно стоять число, равное количеству чисел, среднее которых нужно найти. Сумма делится на 3, так как слагаемых три.
Теперь надо разобраться со средним геометрическим. Допустим, есть ряд чисел: 4, 2 и 8.
Средним геометрическим чисел называется произведение всех данных чисел, находящееся под корнем со степенью, равной количеству данных чисел.То есть в случае чисел 4, 2 и 8 ответом будет 4. Вот каким образом это получилось:
Решение: ∛(4 × 2 × 8) = 4
В обоих вариантах получились целые ответы, так как для примера были взяты специальные числа. Так происходит отнюдь не всегда. В большинстве случаев ответ приходится округлять или оставлять под корнем. Например, для чисел 11, 7 и 20 среднее арифметическое ≈ 12,67, а среднее геометрическое — ∛1540. А для чисел 6 и 5 ответы, соответственно, будут 5,5 и √30.
Может ли так произойти, что среднее арифметическое станет равным среднему геометрическому?
Конечно, может. Но только в двух случаях. Если имеется ряд чисел, состоящий только либо из единиц, либо из нулей. Примечательно также то, что ответ не зависит от их количества.
Доказательство с единицами: (1 + 1 + 1) / 3 = 3 / 3 = 1 (среднее арифметическое).
∛(1 × 1 × 1) = ∛1 = 1(среднее геометрическое).
Доказательство с нулями: (0 + 0) / 2=0 (среднее арифметическое).
√(0 × 0) = 0 (среднее геометрическое).
Другого варианта нет и быть не может.
Под понятием среднего арифметического чисел подразумевается результат несложной последовательности расчётов средней величины для ряда чисел, определённых заранее. Необходимо отметить, что такое значение в данное время широко применяется специалистами ряда отраслей. Например, известны формулы при проведении расчётов экономистами или работниками статистической отрасли, где требуется иметь значение данного типа. Кроме этого, этот показатель активно используют и в ряде других отраслей, которые являются смежными с вышеуказанными.
Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сможет любой желающий. Для этого не надо иметь специальное образование. Часто нет необходимости применять и вычислительную технику.
В качестве ответа на вопрос как найти среднее арифметическое рассмотрим ряд ситуаций.
Самым простым вариантом расчёта данной величины есть подсчёт её для двух чисел. Процедура проведения расчёта в этом случае является очень простой:
Формула
Таким образом, формула для подсчёта требуемой величины в случае с двумя будет выглядеть следующим образом:
В этой формуле применяется следующее обозначение:
А и В – это заранее выбранные числа, для которых необходимо находить значение.
Нахождение значения для трёх
Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет сильно отличаться от предыдущего варианта:
Формула
Тем самым формула, необходимая при проведении расчётов арифметического трёх, будет выглядеть так:
В данной формуле принято следующее обозначение:
А, В и С – это числа, к которым необходимо будет находить среднее арифметическое.
Вычисление среднего арифметического четырёх
Как уже видно по аналогии с предыдущими вариантами вычисление данного значения для количества, равного четырём, будет носить следующий порядок:
Формула
Из описанной выше последовательности действий по нахождению среднего арифметического для четырёх, можно получить следующую формулу:
В данной формуле переменные имеют следующее значение:
А, В, С и Е – это те, к которым необходимо найти значение среднего арифметического.
Применяя данную формулу, всегда можно будет вычислять требуемое значение для данного количества чисел.
Подсчёт среднего арифметического пяти
Выполнение данной операции потребует проведения определённого алгоритма действий.
Формула
Тем самым аналогично с ранее рассмотренными вариантами получаем такую формулу для подсчёта среднего арифметического:
В данной формуле переменные имеют такое обозначение:
А, В, С, Е и Р – это числа, для которых необходимо получить среднее арифметическое.
Универсальная формула вычисления
Поэтому практичнее будет применять общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов может быть очень большой. Поэтому разумнее будет использовать универсальную формулу и не выводить каждый раз индивидуальную технологию для расчёта данной величины.
Главным при определении формулы является принцип расчёта среднего арифметическог о.
Данный принцип как было видно из приведённых примеров, выглядит таким образом:
Таким образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет выглядеть следующим образом:
Данная формула содержит следующие переменные:
А и В – это числа, которые выбраны заранее для расчёта их среднего арифметического.
N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.
Подставляя каждый раз в данную формулу выбранные числа, мы всегда сможем получить требуемое значение среднего арифметического.
Как видно, нахождение среднего арифметического является несложной процедурой. Однако надо внимательно относиться к проводимым вычислениям и проводить проверку полученного результата. Такой подход объясняется тем, что даже в самых простых ситуациях существует вероятность получения ошибки, которая может повлиять потом на дальнейшие расчёты. В связи с этим рекомендуется применять вычислительную технику, которая способна произвести подсчёты любой сложности.
В математике среднее арифметическое значение чисел (или просто среднее) — это сумма всех чисел в данном наборе, разделенная на их количество. Это наиболее обобщенное и распространенное понятие средней величины. Как вы уже поняли, чтобы найти нужно суммировать все данные вам числа, а полученный результат разделить на количество слагаемых.
Что такое среднее арифметическое?
Давайте рассмотрим пример.
Для начала найдем сумму всех данных чисел.
Теперь разделим получившуюся сумму на количество слагаемых. Так как у нас слагаемых три, соответственно, мы будем делить на три.
Следовательно, среднее значение чисел 6, 7 и 11 — это 8. Почему именно 8? Да потому, что сумма 6, 7 и 11 будет такая же, как трех восьмерок. Это отлично видно на иллюстрации.
Среднее значение чем-то напоминает «выравнивание» ряда чисел. Как видите, кучки карандашей стали одного уровня.
Рассмотрим еще один пример, чтобы закрепить полученные знания.
Пример 2. Даны числа: 3, 7, 5, 13, 20, 23, 39, 23, 40, 23, 14, 12, 56, 23, 29. Нужно найти их среднее арифметическое значение.
3 + 7 + 5 + 13 + 20 + 23 + 39 + 23 + 40 + 23 + 14 + 12 + 56 + 23 + 29 = 330
Делим на количество слагаемых (в этом случае — 15).
Следовательно, среднее значение данного ряда чисел равно 22.
Зная это, рассмотрим еще один пример.
Находим сумму чисел.
3 + (-7) + 5 + 13 + (-2) = 12
Так как слагаемых 5, разделим получившуюся сумму на 5.
В наше время технологического прогресса гораздо удобнее использовать для нахождения среднего значения компьютерные программы. Microsoft Office Excel — одна из них. Искать среднее значение в Excel быстро и просто. Тем более, эта программа входит в пакет программ от Microsoft Office. Рассмотрим краткую инструкцию, значение с помощью этой программы.
Чтобы было более понятно, опробуем полученные знания.
Очень удобно использовать эту функцию для ведения учета, накладных или когда вам просто нужно найти среднее значение из очень длинного ряда чисел. Поэтому ее часто используют в офисах и крупных компаниях. Это позволяет сохранять порядок в записях и дает возможность быстро посчитать что-либо (например, средний доход за месяц). Также с помощью Excel можно найти среднее значение функции.
Ответ: каждому досталось по 4 груши.
Пример 2. На курсы английского языка в понедельник пришло 15 человек, во вторник — 10, в среду — 12, в четверг — 11, в пятницу — 7, в субботу — 14, в воскресенье — 8. Найти среднюю посещаемость курсов за неделю.
Решение: Найдем среднее арифметическое:
| 15 + 10 + 12 + 11 + 7 + 14 + 8 | 77 | 7 | 7 |
Ответ: в среднем на курсы английского языка приходило 11 человек в день.
Пример 3. Гонщик ехала два часа со скоростью 120 км/ч и час со скоростью 90 км/ч. Найдите среднюю скорость автомобиля во время гонки.
Решение: Найдем среднее арифметическое скоростей автомобиля за каждый час пути:
| 120 + 120 + 90 | 330 | 3 | 3 |
Ответ: средняя скорость автомобиля во время гонки была 110 км/ч.
Пример 4. Среднее арифметическое 3 чисел равно 6, а среднее арифметическое 7 других чисел равно 3. Чему равно среднее арифметическое этих десяти чисел?
Решение: Так как среднее арифметическое 3-х чисел равно 6 то их сумма равна 6 · 3 = 18, аналогично сумма оставшихся 7-ми чисел равна 7 · 3 = 21.
Значит сумма всех 10-ти чисел будет 18 + 21 = 39, а среднее арифметическое равно
Как найти среднее арифметическое чисел? Повторим правило и рассмотрим его применение на конкретных примерах.
Чтобы найти среднее арифметическое чисел, надо:
1) сложить эти числа;
2) результат разделить на количество слагаемых:
Найти среднее арифметическое чисел:
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат поделить на 2:
2) 12,6, 14,7 и 16,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3:
(12,6 + 14,7 + 16,5):3=14,6.
3) 40,52, 44,63, 52,34 и 58,29.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4:
(40,52 + 44,63 + 52,34 + 58,29):4=48,945.
4) 17,4. 21,6, 25,2, 28,7 и 30,1.
Чтобы найти среднее арифметическое пяти чисел, надо сложить эти числа и результат разделить на 5:
(17,4 + 21,6 + 25,2 + 28,7 + 30,1):5=24,6.
66 Comments
КЛАСС Я ВСЁ ПОНЯЛ!
Все ясно,просто моментально вспомнила
Я понял но это не точно
Я ВООБЩЕ ВСЕ ПОНЯЛА. Д/З НА 10 СДЕЛАЛА. ( ПРИМЕРЫ ЛИШНЕЕ )
Если каждую новую тему постараться разобрать сразу же, не откладывая на «когда-нибудь потом», то оказывается, что математика — не такой уж сложный предмет.
Поля, желаю Вам дальнейших успехов в учебе!
Среднее арифметическое 4 чисел равно 7.6, а среднее арифметическое 10 других чисел равно 3.6. Найдите значение среднего арифметического этих 14 чисел. Помогите решить, пожалуйста.
Как найти среднее арифметическое число 5,24
Данил, Вы имеете в виду среднее арифметическое чисел 5 и 24? Чтобы найти среднее арифметическое 5 и 24, надо сумму этих чисел разделить на количество слагаемых: (5+24):2=29:2=14,5.
Количество чисел — три. Чтобы найти среднее арифметическое этих чисел, надо их сложить и сумму разделить на 3: (-3+0+9):3=2.
как найти среднее арифметическое чисел с дробями?
Валерия, так же, как и с другими числами: найти их сумму и разделить на количество слагаемых.
Спасибо за статью!Статья очень помогла!
Непомогло у меня числа
5, 7, 10, 12, 16
Как решить-среднее арифметическое семи чисел равно 10,2,а среднее арифметическое трёх других чисел-6,8.Найдите среднее арифметическое этих десяти чисел.
Валентина, специально в ответ на аналогичный вопрос Вероники написала пост (ссылка вверху, за 27.08.2014)
Спасибо я всё понял
Все довольно понятно, но вся соль в том, что у меня 3 числа — неизвестны. :
Лол, перепутал. Не правильно прочитал Д/З, спасибо за статью!
Отличная новость, Илья! Поздравляю!
Как и любое другое среднее арифметическое чисел: сложить и поделить на их количество. Если у Вас три числа- (60+75+270)6:3. Если два — (6075+270):2.
среднее арифметическое чисел равно 47.первые три числа равны 37 6 81 найдите четвертое число
Супер!! Оказывается все ОЧЕНЬ легко!! Так мало написанно, но понятно!! 🙂
Среднее арифметическое чисел:
x; 3; 2,1; 2,1
равно 2,55
Найти x
А откуда нужно брать знаменатель?
Делим на количество слагаемых. То есть сколько чисел, среднее арифметическое которых надо найти, дано, на то и делим.
Ребят помогите вот что нам сказали сделать: среднее арефметическое 2 чисел=18.1число=350% второго числа.
Пусть x — I число, тогда II — 3,5x (так как составляет 350% от I-го). Так как их среднее арифметическое равно 18, сосавим и решим уравнение: (x+3,5x):2=18; 4,5x=18∙2; x=36:4,5; x=8. Следовательно, I число равно 8, II — 3,5∙8=28.
Дедушке Вите 90 лет. Средний возраст внуков 20. Среднее арифметическое дедушки и его внуков 22 года. Найдите кол-во внуков. Помогите решить
Пусть n — количество внуков у дедушки. Чтобы найти средний возраст внуков, надо сумму лет всех внуков и разделить на количество внуков, то есть на n. Таким образом, (сумма лет всех внуков):n=20, следовательно,
сумма лет всех внуков=20n.
Чтобы найти средний возраст дедушки и внуков, надо сложить сумму лет всех внуков и дедушки и разделить на (n+1): (сумма лет всех внуков + 90):(n+1)=22.
Значит, (20n + 90):(n+1)=22. Остаётся решить уравнение.
20n + 90=22(n+1)
20n-22n=22-90
n=34.
Ответ: 34 внука.
Повезло деду :D) 34 внука иметь)
Среднее арифметическое восьми чисел равно 4,3. После того как
из этого набора убрали некоторое число, среднее арифметическое
нового набора стало 3,7. Найдите это число. ПОМОГИТЕ РЕШИТ))
1) Среднее арифметическое восьми чисел равно частному от деления суммы этих восьми чисел на 8. По условию, среднее арифметическое этих восьми чисел равно 4,3. Значит, сумма восьми чисел равна 4,3∙8=34,4.
2) Среднее арифметическое семи чисел равно частному от деления суммы семи чисел на 7. По условию, среднее арифметическое семи чисел равно 3,7. Значит, сумма семи чисел равна 3,7∙7=25,9.
3) Разность между суммой восьми чисел и суммой семи чисел и есть то число, которое убрали:
34,4-25,9=8,5.
Спасибо большое все легко и понятно)
Очень благодарна вам и вашему сайту)
Удачи вам в дальнейшем)
Спасибо, Полина! И Вам удачи и успехов в учёбе!
средняя арифметическая 9и чисел равно 16и. если один из этих чисел равен 0 тогда сколько будет ср.арифметическая остальных?
Среднее арифметическое 9 чисел (а1+а2+…+а8+0):9=16.Отсюда а1+а2+…+а8+0=16∙9=144.
Значит, среднее арифметическое оставшихся восьми чисел (а1+а2+…+а8):8=144:8=18.
Среднее арифметическое трёх чисел 15. Найти эти числа, если второе число число в 1,4 раза,а третье в 1.2 раза больше первого.
Пусть первое из чисел равно х, тогда второе — 1,4х, а третье — 1,2х. Так как их среднее арифметическое равно 15, составим и решим уравнение:(х+1,4х+1,2х):3=15.
Светлана Ивановна, если я правильно вас поняла то в моём случае:записать формулу среднего арифметического трёх чисел одно из ко орых в 3 раза больше другого и в 2 раза меньше третьего, это записываем так(х+3х+3х×2):3,заранее спасибо за ответ
Елена, всё верно.
Среднее арифметическое двух чисел равно 14 одно из чисел 12,4 как найти другое число
(х+12,4):2=14. Отсюда х=28-12,4=15,6.
Среднее арифметическое двух положительных чисел на 30% меньше большего из этих чисел. На сколько процентов оно больше меньшего из этих чисел? (Ответ запишите числом). Помогите, пожалуйста решить!
Примем большее из данных двух положительных чисел за x, а меньшее — за y. Тогда среднее арифметическое этих чисел равно 0,7x.Имеем:
Отсюда x=y:0,4; x=2,5y. Соответственно, среднее арифметическое 0,7x=0,7∙2,5y=1,75y составляет 175% от меньшего числа y. А значит, среднее арифметическое на 75% больше меньшего из чисел.
Плиз,помогите не могу сообразить.Я считаю показатель с 9 утра до 9 вечера,и с 9 вечера до 9 утра,то есть днём допустим у меня показатель 121руб,а вечером 221,среднее получается 171,но если я беру общий показатель за день,то он 141руб.А как мне из дневного и вечернего показателя высчитать общий?А показатель считается так:Я беру выручку и делю на количество.
Олеся, извините, но я не понимаю, о каком показателе Вы говорите.
Светлана Михайловна доброго времени! Подскажите пожалуйста как определить среднее арифметическое нескольких углов. результат нужен в градусах. Спасибо. Сергей
Наверное, просто найти среднее арифметическое градусных мер и результат округлить до градусов (в 1 градусе 60 минут. Соответственно, до 30 минут округляем с недостатком, от 30 и более — с избытком).
Большое спасибо за ответ.
Здравствуйте, как найти среднее арефметическое в таком примере,с двух сторон не известные числа
Пример: …14,18,25,44,30…
Нужно найти какие цифры нужно вставить по краям
Артём, условие неполное, данных недостаточно.
Здравствуйте помогите найти средеарифметическое двух чисел 1,536 и 1,540
Здравствуйте, не могли бы вы помочь… совсем забыла математику. задача:среднее для серии из 70 значений 30. Какова сумма этих значений?
Среднее арифметическое нескольких чисел равно сумме этих чисел, делённой на количество слагаемых. Следовательно, чтобы найти сумму, надо известное среднее арифметическое умножить на количество слагаемых: 30∙70=2100.
А если в ряду есть отрицательные и положительные числа, как тогда?
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ
Смотреть что такое «СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ» в других словарях:
Среднее арифметическое — У этого термина существуют и другие значения, см. среднее значение. В математике и статистике среднее арифметическое одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех наблюденных значений деленную на их… … Википедия
среднее арифметическое — 3.1 среднее арифметическое; среднее (arithmetic mean / average): Сумма значений, деленная на их число. [ИСО 3534 1:1993, 2.26] Источник … Словарь-справочник терминов нормативно-технической документации
среднее арифметическое — aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
СРЕДНЕЕ, АРИФМЕТИЧЕСКОЕ — Сумма набора значений, поделенная на число значений. Это – наиболее часто используемое и наиболее полезное измерение центральной тенденции, так как в отличие от медианы и моды оно использует все данные распределения и служит основой для измерения … Толковый словарь по психологии
среднее арифметическое — vidurkis statusas T sritis Kūno kultūra ir sportas apibrėžtis Dydis, gaunamas padalijus įvairių dydžių sumą iš jų skaičiaus. atitikmenys: angl. average vok. Durchschnitt, m rus. среднее арифметическое … Sporto terminų žodynas
Среднее арифметическое взвешенное — набора вещественных чисел с вещественными весами определяется как Часто подразумевают, что сумма весов равна 1, тогда формула выглядит следующим образом: В том случае, если все веса равны между собой, среднее арифметическое взвешенное будет равно … Википедия
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ — (arithmetic mean) Средняя величина, полученная путем сложения всех членов числового ряда и деления суммы на число членов. Например, среднее арифметическое значение 7, 20, 152 и 305 равно 484/4 = 121. Однако средняя величина не позволяет судить о… … Словарь бизнес-терминов
СРЕДНЕЕ АРИФМЕТИЧЕСКОЕ ЗНАЧЕНИЕ — (arithmetic mean) Средняя величина, полученная путем сложения всех членов числового ряда и деления суммы на число членов, например среднее арифметическое значение 7, 20, 107 и 350 равно 484/4 = 121. Однако средняя величина не позволяет судить о… … Финансовый словарь
среднее арифметическое значение — aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m; arithmetisches Mittel, n rus. арифметическое среднее, n; среднее арифметическое значение, n … Fizikos terminų žodynas
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ
Смотреть что такое «АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ» в других словарях:
арифметическое среднее — aritmetinis vidurkis statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
арифметическое среднее — aritmetinis vidurkis statusas T sritis fizika atitikmenys: angl. arithmetic average; arithmetic mean; arithmetical mean vok. arithmetischer Mittelwert, m; arithmetisches Mittel, n rus. арифметическое среднее, n; среднее арифметическое значение, n … Fizikos terminų žodynas
АРИФМЕТИЧЕСКОЕ, СРЕДНЕЕ — См. среднее арифметическое … Толковый словарь по психологии
арифметическое среднее — Простое среднее, полученное делением суммы двух или более показателей на число этих показателей … Финансово-инвестиционный толковый словарь
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ — число а, получаемое делением суммы нескольких чисел на их число п … Математическая энциклопедия
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ — число а, получаемое делением суммы неск. чисел а, a i. an на п их число: а=(a1+a1+. +an):п … Большой энциклопедический политехнический словарь
Изучаем статистику: средние значения
Один из разделов описательной статистики посвящен знакомству с характеристиками числового набора: минимальное значение, максимальное значение, размах, среднее арифметическое и медиана. Ученики должны научиться определять их для набора чисел, заданного списком, таблицей или диаграммой рассеивания.
Мы изучали этот материал в течение трех уроков. На первых двух были введены новые понятия и решались задачи из учебного пособия (авт. Ю.Н. Тюрин, А.А. Макаров, И.Р. Высоцкий, И.В. Ященко). Например. Найдите наибольшее и наименьшее значение, размах, среднее значение и медиану набора чисел: 12; 7; 25; 3; 19; 15. (Ответ: 25; 3; 22; 13,5; 13,5).
Однако естественно показать учащимся, зачем мы все это изучаем. На третьем уроке мы решали задачи, в которых требуется выбрать такое среднее, которое наилучшим образом отражает особенности данного набора чисел в соответствии с их природой и требованиями задачи. В одних задачах не сказано, какую характеристику надо искать, поэтому, чтобы ответить на вопрос задачи, приходится примерять к поставленной задаче поочередно разные средние и выяснять, какое подходит больше других. В этом случае ответом к задаче является не число, а название подходящей характеристики. В других задачах присутствует необходимость правильно интерпретировать полученные результаты, отнестись к ним критически, попытаться найти здравое зерно даже там, где, на первый взгляд, «все сделано неверно». И наконец, предложен и третий вид задач, в которых природа данных накладывает определенные дополнительные требования на найденное значение среднего: например, оно должно быть целым.
Тем самым мы не только продолжаем закреплять навык подсчета среднего, но и демонстрируем возможности применения изученного в реальных жизненных ситуациях. Ведь для учащихся важным фактором освоения нового является осознание необходимости знания этого нового, то есть не только как найти, но и зачем находить.
Данная статья состоит из двух частей. В первой дается описание наиболее употребительных средних. Во второй части предлагается набор задач для решения в классе и для самостоятельной работы учащихся.
Знакомимся со средними
Наибольшее и наименьшее значения
Слова «минимальный», «максимальный», «меньший», «больший» интуитивно понятны учащимся, поэтому первые две характеристики: наибольшее и наименьшее значения оставим без определения. Скажем, что в наборе, упорядоченном по возрастанию, наименьшее число стоит на первом месте, а наибольшее — на последнем.
В пособии имеются задания, в которых требуется найти наибольшее или наименьшее значения среди чисел, указанных в таблице. К ним добавим задания с другой формой представления данных — в виде диаграммы рассеивания.
Задание. Имеется диаграмма 1 рассеивания, показывающая взаимосвязь роста и веса 15 опрошенных юношей. Найти рост самого высокого и рост самого низкого юноши (т.е. определить минимальное и максимальное значения набора чисел, заданного диаграммой рассеивания).
Для этого будем использовать следующее: минимальный рост соответствует абсциссе точки, расположенной левее других, а максимальный — абсциссе крайней точки справа. Получим:
min ≈ 167 см, max ≈ 181 см.
Интересно, что остальные 13 точек участия в «обсуждении» вообще не принимают. Их можно стереть — результат от этого не изменится (см. диаграмму 2).
Вторая особенность получаемого результата в том, что, в отличие от работы с таблицей, данные, получаемые с помощью графиков и диаграмм, являются не точными, а приближенными, то есть ответы могут отличаться.
Аналогично находим минимальное и максимальное значения веса, как ординаты самой нижней и самой верхней точек.
Диаграмма 2
С каким же видом представления данных удобнее работать?
Преимущество таблицы заключается в точности получаемых результатов, но работа с ней требует концентрации внимания на протяжении длительного времени: нельзя пропустить искомое число, а оно может попасть в любой исследуемый столбец. И если таблица содержит не 15 чисел, а 5000, то этот аргумент становится решающим в пользу наглядного представления данных. Оно дает менее точные результаты, зато обработка такой информации происходит за считанные секунды. Даже если диаграмма будет содержать 5000 точек, нас будут интересовать только две крайние, на остальные мы даже не посмотрим.
Размах
В отличие от предыдущих понятий, размах — это незнакомая учащимся характеристика набора. Он показывает протяженность набора вдоль числовой оси, меру его разброса.
Определение. Размах набора чисел (R) — это разность между наибольшим и наименьшим числом набора.
Например, в предыдущем задании размах равен: R = 181 – 167 = 14 см.
Что показывает размах значений?
Сравним диаграммы 3 и 4:
Точки, изображенные на диаграмме 3, расположены ближе друг к другу, соответственно, и максимальное и минимальное значение отличаются друг от друга меньше, чем на диаграмме 4. Таким образом, размах показывает, сильно ли отличаются числа набора друг от друга.
Маленький размах показывает, что исследуемая величина принимала практически одинаковые значения. Большой размах показывает, что некоторая величина принимает значительно отличающиеся друг от друга значения, то есть нестабильность. Иногда большой размах свидетельствует о наличии грубой ошибки измерений, о том, что какое-то из чисел попало в список случайно.
Если вычислить полусумму наименьшего и наибольшего значений набора и обозначить ее с, а половину размаха обозначить 
то можно утверждать, что все числа набора содержатся в промежутке 
На бытовом уровне размах (а точнее, полуразмах) дает информацию о точности информации: расстояние от дома до дачи (100 ± 5) км, цена на хлеб (14 ± 2) р. и т.д.
Среднее арифметическое
Определение. Средним арифметическим нескольких чисел (
) называется частное от деления суммы этих чисел на количество чисел.
Например, средним арифметическим чисел 4; 6; 11 является число 
Зачастую среднее арифметическое называют просто «средним» в силу его наибольшей популярности. Говорят о среднем балле аттестата, среднегодовом потреблении населением фруктов. «Потребительская корзина» для определенного слоя граждан рассчитывается исходя из средних показателей.
Рассмотрим следующий пример. На олимпиаде по математике предлагалось решить пять задач по 4 балла за каждую. В протоколе указана сумма баллов каждого из восьми участников этой олимпиады:
12; 14; 14; 16; 17; 18; 19; 200.
Для ускорения подсчета имеется автоматизированная система обработки данных, которая находит среднее арифметическое любых введенных чисел. Какой средний балл набрали участники олимпиады?
У данного набора среднее равно 38,75. Однако такую сумму баллов никто из участников набрать не мог. К тому же семь чисел из данных восьми намного меньше его. Все значения этого набора, кроме крайнего правого, достаточно кучно попадают в интервал [12; 19], а 38,75 в него не попадает. Все это говорит о том, что полученное среднее арифметическое не только не передает особенностей данного набора чисел, но и вообще противоречит здравому смыслу. Значит, либо в условие, либо в решение вкралась ошибка! Посмотрим еще раз на данные числа. Теперь, получив явно бессмысленный результат, мы сможем более критически отнестись к условию: первые семь чисел вполне реальны, а вот последнее. Откуда оно взялось?! Видимо, оно случайно попало в этот список: возможно, в результате описки. Однако обнаружение ошибки в условии не избавляет нас от необходимости довести решение до конца. Можно, конечно, посоветовать комиссии снова переписать результаты учащихся и ввести числа из нового, «правильного» протокола. Но где гарантия, что в нем снова не будет опечатки?
Когда все результаты более или менее кучно располагаются на числовой оси, кроме, быть может, нескольких ненадежных значений, анализировать результаты можно! Достаточно высокую точность полученных значений будет гарантировать применение других средних — в частности, урезанного среднего. Для его нахождения сначала упорядочивают набор по возрастанию, а затем отбрасывают слева и справа равное небольшое количество чисел. При этом «выбросы» (или ошибки наблюдений) в дальнейших вычислениях не участвуют. У полученного «урезанного» набора обычным образом находят среднее арифметическое. Оно и является урезанным средним исходного набора.
Вернемся к задаче. Если отбросить по одному числу с каждой стороны, то есть числа 12 и 200, то у оставшегося набора из шести чисел среднее равно
Это и есть урезанное среднее. Оно неплохо передает реальное среднее количество баллов, набранных юными математиками.
Некоторая аналогия с нахождением урезанного среднего просматривается в правилах судейства во многих видах спорта. Например, в соревнованиях по прыжкам с трамплина технику каждого прыжка оценивают 5 судей. Чтобы получить объективные оценки, две из них — высшую и низшую — отбрасывают, а для трех оставшихся находят сумму. Такой подход не дает возможности судьям повышать баллы своим соотечественникам, а спортсменам затрудняет нечестный путь к медалям.
Медиана
Медианой числового набора является число, которое разделяет этот набор на две одинаковые по части.
Если набор упорядочен и в нем имеется нечетное количество чисел (2n + 1), то медиана стоит посередине этого набора, на (n + 1)-м месте. Если упорядоченный набор состоит из четного количества чисел (2n), то медианой является любое число, находящееся между двумя числами, которые стоят в середине (под номерами n и n + 1). Обычно берется их полусумма.
В наборе 12; 14; 14; 16; 17; 18; 19; 200 медианой является любое число из интервала (16; 17), например, 16,5. Напомним, что урезанное среднее равнялось 16,3. Похоже!
Перейдем к решению задач.
Вычисляем средние
1. Про отличника. У отличника Коли были отметки по математике «5», «5», «5», «5».
И вдруг в конце четверти он получил «2». Он знает, что учитель математики выставляет четвертную отметку как среднее всех отметок, имеющихся у ученика, и не признает пересдач. Какое среднее было бы предпочтительнее для Коли, если он, естественно, надеется на пятерку в четверти?
Решение. 1. Попробуем начать с такого очень распространенного способа выставления четвертных отметок, как нахождение среднего арифметического:
Естественно, что любой учитель округлит этот результат в меньшую сторону и выставит итоговую отметку «4». Значит, это среднее Колю не устраивает.
Мы видим, что один неудачный ответ на балл снизил четвертную отметку. Ведь до этого среднее арифметическое равнялось 5.
2. Помочь Колиной мечте сбыться может другое среднее, и не одно! Например, если в качестве среднего учитель Коли возьмет медиану или урезанное среднее, то в четверти Коле обеспечена пятерка:
— медиана набора 2, 5, 5, 5, 5 равна 5;
— урезанное среднее набора 5, 5, 5, равно
Ответ: медиана или урезанное среднее.
2. Про лодку. Рыбаки собираются порыбачить на озере. Но не везде им обеспечен хороший улов. Чтобы найти рыбное место, они решили воспользоваться лодкой с мотором. На лодке установлен мотор, который можно регулировать по высоте, поднимая или глубже погружая его. Известно, что мотор работает надежно и не перегревается во время работы, если опустить его как можно ниже в глубь воды. Но тогда возникает опасность зацепить им за дно водоема. Мотор устанавливается на желаемую высоту на берегу, в воде менять глубину погружения нельзя. Какой информацией о глубине воды в озере надо располагать рыбакам, чтобы не повредить мотор о дно?
Решение. Рыбаки должны узнать глубину озера вдоль предполагаемого маршрута следования. Затем у полученного набора чисел надо найти минимальное значение. Оно обеспечит им удачное прохождение и других, более глубоких участков.
Ответ: минимальное значение.
3. Библиотека. Известно, что детская библиотека выдает в день в среднем 180 книг. Сколько книг выдает библиотека в среднем за неделю? за месяц? за год?
Решение. Под средним в данной задаче подразумевается среднее арифметическое. Так как библиотека работает 6 дней в неделю, значит, за неделю она выдает около 180 
6 = 1080 книг. За 26 рабочих дней месяца она выдаст 180 26 = 4700 книг. За 12 месяцев выдача составит 4680 12 = 56 000 книг.
Ответ: 1080 книг, около 4700 книг, около 56 000 книг.
Решая эту задачу, уместно обсудить вопрос точности полученных результатов. Во-первых, из условия неясно, за какой период было получено среднедневное значение. Если наблюдения велись лишь одну неделю, то к полученным вычисленным значениям нужно относиться весьма скептически. Для получения более точных результатов надо было проводить более длительное наблюдение, сопоставимое по длительности с запрашиваемым периодом. А во-вторых, возможно, наблюдатели «попали» на неделю «книжного бума», тогда результаты, распространенные на месяц и тем более на год получатся явно завышенными. Возможна и обратная картина: нам сообщили результаты, полученные в период летних каникул, значит, результаты вычислений будут заниженными. Другими словами, к полученным числам нужно относиться с большой осторожностью, если нет возможности уточнить, как было проведено исследование, и за какой период было вычислено среднее значение 180 книг.
Этот пример показывает, что для получения достоверных результатов исследований нужно соблюдать некоторые условия, следовать определенным правилам, чтобы полученным выводам можно было доверять.
4. Метание молота. Спортивный клуб должен организовать соревнования по метанию молота среди спортсменов с разной спортивной подготовкой и разными достижениями. Для этого он должен пригласить необходимое количество судей в сектор для метания. Судьи, с которыми сотрудничает клуб, точно отмечают место падения молота, если находятся не далее четырех метров от него. Спортивный клуб может запросить любую информацию о прошлых результатах приглашенных спортсменов. Какой информацией должны располагать организаторы, чтобы пригласить необходимое количество судей?
Решение. Надо запросить предыдущие результаты метания молота всех участников и найти максимальный, минимальный результаты и размах. Зная величину угла сектора для метания и максимальный результат, можно вычислить длину дуги, вдоль которой через каждые 8 м надо расставить судей.
Количество таких рядов зависит от размаха результатов. Если он окажется менее 8 м, то судьи могут стоять в один ряд. Если размах окажется бóльшим, то чтобы успешно фиксировать как более далекие, так и близкие результаты судей надо расставить в несколько рядов через каждые 8 м.
Ответ: максимальный результат, размах.
5. Отпуск на юге. Для успешной рекламы отдыха на Кипре туристическая фирма запросила данные о погоде на острове за последние 10 лет. Выяснилось, что за этот период было лишь 216 пасмурных или дождливых дней, которые были равномерно распределены по запрашиваемым годам. Сколько дней в году на острове Кипр светит солнце?
Решение. За 10 лет наблюдалось 3652 – 216 = 3436 солнечных дней. Значит, в среднем за один год — 343,6 дня. Поскольку в ответе надо писать целое число дней, то можно округлить до целых, а можно и до десятков: в рекламе круглые числа смотрятся лучше.
Ответ: около 340 дней.
Задачи для самостоятельного решения
1. а) Через речку хотят построить мост. Известно, что уровень воды в реке меняется в течение года: весной при таянии снега повышается, засушливым летом понижается. Какую характеристику уровня воды в реке надо учитывать, чтобы построенный мост был над водой?
б) Периодически в средствах массовой информации нам сообщают о стихийных бедствиях, в результате которых переполненные водой реки выходят из своих берегов и даже затопляют улицы городов. Понимая возможность подобного стихийного бедствия, не будет ли разумнее построить мост (а заодно и высокую дамбу) как можно выше, насколько это будет технически возможно? Ведь гибель людей несравнима ни с какими материальными затратами, позволяющими предупредить беду.
2. За урок учительница вызывает в среднем 5 человек из класса и каждому ставит отметку за устный ответ. Сколько отметок за устные ответы выставит эта учительница за неделю, если она проводит в этом классе 5 уроков в неделю? За четверть?
3. В забеге на 800 м принимали участие 19 спортсменов, разделенных на группы, стартующие в разное время. Как судьи определили победителя забега?
4. На зимние каникулы в одной из школ города Мурманска учительница дала детям задание: следить за погодой и найти среднюю температуру. Ежедневно в течение десяти дней в 15 часов Наташа записывала показания термометра:
–13, –10, –15, 11, –9, –9, –11, –12, –10, –11.
А затем вычислила среднее арифметическое и получила –8,9.
а) Действительно ли в период наблюдений температура колебалась вблизи этого числа?
б) Почему большинство значений (9 из 10) меньше найденного среднего?
в) Как исправить ответ, если он неверный (заново повторить наблюдение, естественно, нельзя)?
5. Имеются данные об успеваемости по химии 8 «А» и 8 «Б» : о количестве учащихся, получивших ту или иную четвертную отметку. Данные занесены в таблице: