если государство снижает налоги то в соответствии с моделью солоу

Модель Солоу

Оглавление

Общий

История происхождения

Модель

Предположения

Процесс роста

Для анализа экономик с растущим населением и для лучшей сопоставимости экономик разного размера размеры модели выражаются не в абсолютном выражении, а в расчете на душу населения, причем для размера на душу населения используются строчные буквы. Соответственно определяется:

Его развитие определяется тремя факторами:

Таким образом, изменение основного капитала на душу населения за каждый период выражается как

Фундаментальное уравнение движения модели Солоу с ростом населения:

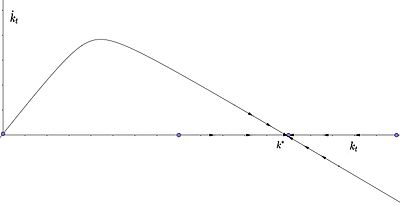
Если положительный, то основной капитал на душу населения, а вместе с ним и доход на душу населения растет. Если он отрицательный, то капитал и производство на душу населения сокращаются. Формально это означает: k ˙ т <\ displaystyle <\ dot > _> k ˙ т <\ displaystyle <\ dot > _>

(n+\delta )k_\Rightarrow <\dot >_>0>»> s ж ( k т ) > ( п + δ ) k т ⇒ k ˙ т > 0 <\ displaystyle sf (k_)> (n + \ delta) k_\ Rightarrow <\ dot > _> 0> (n + \ delta) k_\ Rightarrow <\ dot > _> 0>»> (Капиталоемкость и доход на душу населения растут) s ж ( k т ) ( п + δ ) k т ⇒ k ˙ т 0 <\ displaystyle sf (k_) (Снижение капиталоемкости и дохода на душу населения)

Сходимость к равновесию

0\;\;\forall \;\;k_k ˙ т > 0 ∀ k т k * <\ displaystyle <\ dot > _> 0 \; \; \ forall \; \; k_ 0 \; \; \ forall \; \; k_k^<*>>»> k ˙ т 0 ∀ k т > k * <\ displaystyle <\ dot > _k ^ <*>> k ^ <*>>»>

Изменения экзогенных параметров

Равновесный основной капитал для долгосрочного роста ( ) определяется, как указано выше k * <\ displaystyle k ^ <*>>

Прирост и амортизация населения

Норма сбережений и золотое правило накопления

Увеличение нормы сбережений толкает кривую сбережений экономики вверх, что приводит к увеличению равновесного роста основного капитала на душу населения и, следовательно, дохода на душу населения. Рис. 4 иллюстрирует это графически: увеличение нормы сбережений сдвигает функцию сбережений из ее исходного положения (черный) вверх, в то время как линия инвестиционных требований (красная) остается неизменной. Новое равновесие является результатом пересечения линии инвестиционных требований с новой функцией сбережений и имеет больший запас капитала и более высокий доход на душу населения. Б. <\ Displaystyle \ mathrm >

Золотое правило накопления описывает норму сбережений в экономике, которая максимизирует устойчивое потребление:

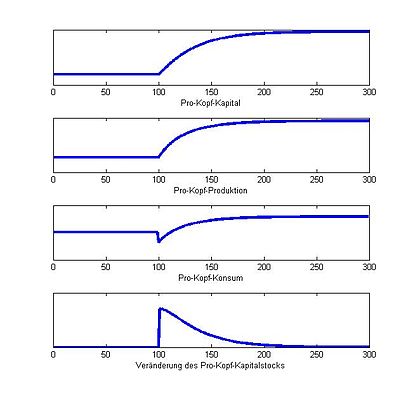
Рис. 6 и Рис. 7 графически показывают, как могут повлиять различные изменения нормы сбережений. На рис. 6 норма сбережений увеличивается на основе исходного, динамически эффективного равновесия. Увеличение приводит к положительному приросту капитала и, следовательно, к увеличению капитала и дохода на душу населения. Рост капитала снижается с увеличением накопления капитала и асимптотически приближается к нулю, экономика достигает нового равновесия с более высокими капиталом, доходом и потреблением на душу населения. Однако в начале процесса этот более высокий уровень в долгосрочной перспективе должен быть «куплен» с меньшим потреблением. Желательно ли такое изменение нормы сбережений с точки зрения национальной экономики, зависит от того, как ранние потери потребления оцениваются по сравнению с более поздними приростами потребления. На рис. 7 норма сбережений снижена из-за динамически неэффективной, то есть чрезмерно высокой нормы сбережений. Снижение приводит к отрицательному приросту капитала и, следовательно, к падению капитала и дохода на душу населения. Сокращение капитала уменьшается с увеличением накопления капитала и асимптотически стремится к нулю, экономика достигает нового равновесия с более низким капиталом и доходом на душу населения. Однако долгосрочное потребление на душу населения выше, поскольку сохраняется меньше. Основное отличие от динамически эффективной ситуации заключается в том, что потребление выше не только в долгосрочной перспективе, но и в каждый период после увеличения. Снижая норму сбережений, экономика может потреблять больше не только в долгосрочной перспективе, но и немедленно. Независимо от оценки раннего потребления по сравнению с более поздним, при норме сбережений выше «золотой» нормы сбережений снижение нормы сбережений определенно желательно с точки зрения экономики.

Технологический прогресс

Фундаментальное уравнение движения модели Солоу с ростом населения и техническим прогрессом:

˙ т знак равно s ж ( k

Долгосрочное равновесие достигается, когда запас капитала на эффективную единицу работы постоянен, то есть когда:

т ) знак равно ( δ + п + грамм ) k

Основной капитал и, следовательно, доход на эффективную единицу работы не растут в долгосрочном равновесии. Однако доход на душу населения определяется как

у т ≡ Y т / Л. т знак равно [ Y / Т т Л. т ] ⋅ Т т знак равно у

Пример: модель Солоу с производственной функцией Кобба-Дугласа

Возможной производственной функцией, которая удовлетворяет приведенным выше предположениям, является следующая функция Кобба-Дугласа :

Долгосрочное равновесие наступает, когда это изменение равно нулю и, следовательно,

и тогда это применимо к равновесной капиталоемкости

Таким образом, для равновесного дохода на душу населения следует

Кроме того, можно показать, что вышеуказанная производственная функция удовлетворяет допущениям, упомянутым в п. 1.1:

1. Постоянная отдача от масштаба:

Свойство постоянной отдачи от масштаба выполняется:

2. Положительная и убывающая маржинальная доходность:

Предельные продукты капитала и труда положительны:

3. Условия Inada выполняются:

Различные нормы сбережений

В приведенном выше примере это приводит к:

Итак, согласно модели Солоу, Корея вдвое богаче Уганды. На самом деле Корея примерно в 13 раз богаче. В результате различия в доходах можно лишь частично объяснить с помощью модели Солоу.

Эмпирические приложения

Учет роста

конвергенция

Абсолютная конвергенция

Условная сходимость

В модели Солоу экономики сходятся к различным стационарным состояниям при условии, что они имеют различия в параметрах модели. Если страны различаются по совокупной факторной производительности, норме сбережений или норме амортизации, они, следовательно, различаются своим долгосрочным равновесием (разные региональные стационарные состояния). Часто условная конвергенция эмпирическая, а не абсолютная.

эмпирические результаты

Человеческий капитал на эффективную единицу работы развивается в соответствии с уравнением движения, аналогичным уравнению движения капитала на эффективную единицу работы: ЧАС т

<\ displaystyle <\ tilde >>>

˙ знак равно s ЧАС у т

— ( п + грамм + δ ) ЧАС т

где (также экзогенная) норма инвестиций в человеческий капитал обозначает. Тогда в равновесии роста капитал и человеческий капитал на эффективную единицу работы постоянны. s ЧАС <\ displaystyle s_ >

Международные и исторические различия в доходах

Критика и дальнейшие разработки

Базовая модель Солоу предполагает закрытую экономику без государственной деятельности. Однако можно привлечь государственный сектор и международные потоки капитала.

Критики роста, такие как Герман Дейли или Николас Георгеску-Роген, критикуют, что модель Солоу не принимает во внимание роль природных ресурсов. Однако сейчас есть такие расширения, как «зеленая модель Солоу».

веб ссылки

Смотри тоже

литература

Замечания

Источник

Модель экономического роста Р. Солоу

В модели Солоу центральное место отводится технологическому прогрессу, который обеспечивает непрерывный экономический рост. К другим моделям данного направления относится однофакторная модель Домара-Харрода. В этой модели рост продукта связывается с нормой эффективностью накопления. Центральное уравнение этой модели имеет следующий вид: у=ав, где (1)

У – темп прироста продукта, а – норма накопления, в – эффективность накопления (коэффициент капиталоотдачи).

При вычислении нормы накопления (а) следует учесть, что, во-первых часть накопления осуществляется за счет амортизационного фонда и используется для возмещения выбытия основного капитала, во-вторых, из фонда накопления обеспечивается вложение не только в основной, но и в оборотный капитал, включая резервы.

Неоклассическая модель в условиях равновесия между спросом и предложением учитывает изменчивость коэффициента капиталоотдачи. Соотношение «капитал – производство» становится гибким вследствие того, что неоклассические модели учитывают не один, а два производственных фактора и допускают их взаимозаменяемость. Допуская различные комбинации производственных факторов, можно добиться роста объемов производства даже при той же технике. Среди аналитических инструментов неоклассических моделей главное место занимает производственная функция: У=f(K,L), где У- продукт, а К и L – затраты на капитал и труд. Объем и динамика продукта связывается с объемом и динамикой совокупных затрат и их эффективностью: или Y = abk+ где d – коэффициент, отражающий соотношение величин факторов К и L к величине продукта У;

b и — параметры функции, характеризующие эластичность объемов и динамики продукта от затрат факторов производства, т.е. параметры, показывающие насколько увеличится объем производства, если любой производственный фактор увеличится на 1%;

К и П — темпы роста соответственно капитала и труда.

Модель Солоу имеет возможность описать эти изменения в динамике, т.е. делает его более похожим на фильм, чем фотографию. Модель роста Солоу показывает, как сбережения, рост населения и технологический прогресс воздействуют на рост объема производства во времени.

Модель дает основу, с помощью которой можно проанализировать один из наиболее важных вопросов экономики: какая часть производственного продукта должна потребляться сегодня, и какая часть его должна сберегаться для использования в будущем. Поскольку сбережения равны инвестициям, сбережения определяют объем капитала, которым экономика будет располагать в будущем.

Предложение товаров в модели Солоу описывается с помощью известной производственной функции: Y=F (K,L), где К – капитал, L-труд.

Т.е. объем производства зависит от запасов капитала и используемого труда. Модель Солоу предполагает, что производственная функция обладает свойством постоянной отдачи от масштаба.

Производственная функция с постоянной отдачей от масштаба удобна для этой цели, потому что объем производства на одного рабочего зависит тогда от количества капитала, приходящегося на одного работника.

Производственную функцию можно записать так у=f(k), где f(k)=F (k,1). На рис. Изображена эта производственная функция

У f(k) Закон убывающей эффективности

капитал на одного работника К

Тангенс угла наклона данной производственной функции показывает, сколько дополнительного продукта на одного работника можно получить, если увеличить капиталовооруженность на одну единицу. Эта величина является предельным продуктом капитала МКР. Это можно записать так:

В модели Солоу спрос предъявляется со стороны потребителей и инвесторов. Иными словами, продукция произведенная каждым рабочим, делится между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного рабочего: У=с+I, где с – потребление, I – инвестиции.

Модель Солоу предполагает, что функция потребления принимает простую форму C = (1 – S)·у, где норма сбережения S принимает значения от 0 до 1. Эта функция означает, что потребление пропорционально доходу. Каждый год часть (1 – S) дохода потребляется и часть S сберегается.

Роль такой трактовки потребления выяснится, если мы заменим величину C величиной (1 – S)·у в тождестве национальных счетов: у =(1 – S)·у + I. После преобразования получим: I = S·у. Это уравнение показывает, что инвестиции (как и потребление) пропорциональны доходу. Если инвестиции равны сбережениям, норма сбережений S показывает, какая часть произведений продукции направляется на капитальные вложения.

Представив две главных составляющих модели Солоу – производственную функциюифункцию потребления, можно проанализировать, как накопление капитала обеспечивает экономический рост. Запасы капитала могут изменяться по двум причинам: 1. Инвестиции приводят к росту запасов капитала. 2. Часть капитала изнашивается, то есть амортизируется, что приводит к уменьшению запасов капитала. Для того, чтобы понять, как изменяются запасы капитала, необходимо найти факторы, определяющие величину инвестиций и амортизации. Инвестиции в расчете на одного работника являются частью продукта, приходящегося на одного работника (S·y). Заменив y выражением производственной функции, мы представим инвестиции на одного работника как функцию от капиталовооруженности: I = S·f(k).

Чем выше уровень капиталовооруженности k, тем выше объем производства f(k) и больше инвестиции I. Это уравнение, которое включает в себя производственную функцию и функцию потребления, связывает существующие запасы капитала k с накоплением нового капитала i. На графике показано, как норма сбережений определяет разделение продукта на потребление и инвестиции для каждого из значений k.

У Производительность f(k)

капиталовооруженность k

Норма сбережений S определяет деление производственного продукта на потребление и инвестиции. Для любого уровня капиталовооруженности kобъем производства есть f(k), инвестиции равны S·f(k), а потребление составляет f(k) – S·f (k).

Предположим, что ежегодно выбывает определенная доля капитала σ. Назовем σ нормой выбытия. Например, если капитал эксплуатируется в среднем 25 лет, то норма выбытия равна 4% в год (σ= 0,04). Таким образом, количество капитала, которое выбывает каждый год, cоставляет σ·k. На графике показано, как выбытие зависит от запасов капитала.

σ К

Выбытие

σ к

Капиталовооруженность

Влияние инвестиций и выбытия на запасы капитала можно выразить с помощью следующего уравнения:

Изменение запасов капитала =инвестиции – выбытие, т.е. к=I-σк, где к есть изменение запасов капитала, приходящихся на одного работника за год. Поскольку инвестиции равны сбережениям, изменение запасов капитала может быть записано так: к=Sf(к)- σк. Это уравнение показывает, что изменение запасов капитала равно инвестициям Sf(к) минус выбытие капитала σк.

Чем выше капиталовооруженность, тем больше объем производства и инвестиции, приходящиеся на одного работника. Однако, чем больше запасы капитала, тем больше и величина выбытия.

инвестиции как раз компенсирует выбытие капитала. Сразу после повышения нормы сбережений инвестиции увеличиваются, но запас капитала, и следовательно, выбытие остаются пока неизменными; в итоге инвестиции превышают выбытие. Капитал будет постепенно расти до тех пор, пока экономика не достигнет нового устойчивого состояния k₂ * с большой капиталовооруженностью и более высокой производительностью труда, чем в прежнем устойчивом состоянии.

Модель Солоу показывает, что норма сбережений является ключевой (определяющей) детерминантой величины устойчивой капиталовооруженности. Если норма сбережений более высока, то экономика будет иметь при прочих равных условиях больший запас капитала и более высокий уровень производства.

Более высокие сбережения ведут к более быстрому росту, но это ускорение длится не вечно. Увеличение нормы сбережений обеспечивает рост до тех пор, пока экономика не достигнет нового устойчивого состояния. Если в экономике поддерживается высокая норма сбережений, то и капиталовооруженность, и производительность будут высоки, но и сохранить высокие темпы экономического роста навечно не удастся.

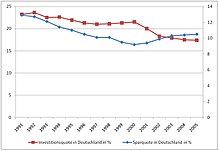
В соответствии с моделью Солоу страна, которая направляет значительную часть дохода на сбережения, будет иметь высокую устойчивую капиталовооруженность труда и, вследствие этого, высокий уровень душевого дохода. Страны с высоким уровнем инвестиций (США, Канада или Япония) обычно имеют высокий душевой доход, в то время как страны с низким уровнем инвестиций (Эфиопия, Заир, Чад) имеют низкий доход на душу населения. Международный опыт, таким образом, подтверждает предсказания модели Солоу о том, что норма сбережений является важнейшей детерминантой богатства или бедности страны.

Теперь рассмотрим вопрос: какие размеры накопления являются оптимальными.

При капиталовооруженности, соответствующей уровню Золотого правила, производственная функция и линия σk * имеют одинаковый наклон, и потребление достигает максимального уровня.

Если же устойчивый запас капитала превышает уровень Золотого правила, то рост объема капитала снижает потребление, поскольку предельный продукт капитала меньше, чем норма выбытия. Поэтому следующее условие составляет само Золотое правило МРК = σ. При капиталовооруженности на уровне Золотого правила предельный продукт капитала равен норме выбытия. Другими словами, если Золотое правило выполняется, предельный продукт за вычетом нормы выбытия, МРК = σ, равен нулю.

Базовая модель Солоу показывает, что само по себе накопление капитала не может объяснить непрерывный экономический рост. Высокий уровень сбережений временно увеличивает темпы роста, но экономика в конце концов приближается к устойчивому состоянию, при котором запасы капитала и объем производства постоянны. Для того, чтобы объяснить непрерывный экономический рост, который наблюдается в большинстве стран мира, нужно расширить модель Солоу и включить в нее два других источника экономического роста: рост населения и технологический прогресс.

Для того, чтобы экономика была в устойчивом состоянии, инвестиции S f(k), должны компенсировать последствия выбытия капитала и роста населения – (σ + n)·k, что представлено на рис. точкой двух кривых.

Рост населения дополняет исходную модель Солоу по трем направлениям. Во-первых, он позволяет приблизиться к объяснению причин экономического роста. В устойчивом состоянии экономики при растущем населении капитал и выпуск продукции на одного работника остаются неизменными, но поскольку количество работников растет с темпом n, капитал и объем производства тоже растут с темпом n. Следовательно, рост населения не может объяснить длительного роста уровня жизни, поскольку объем производства в расчете на одного работника в устойчивом состоянии остается постоянным. Однако рост населения может объяснить непрерывный рост валового выпуска продукции.

Во-вторых, рост населения позволяет дать дополнительно объяснение того, почему некоторые страны богаты, а другие – бедны.

Так модель Солоу предсказывает, что страны с более высокими темпами роста населения будут иметь более низкий ВНП на душу населения.

Инвестиции

Теперь включим в модель Солоу технологический прогресс – третий источник экономического роста. Запишем производственную функцию следующим образом: Y = F(K,L х Е), где Е представляет собой новую переменную, которую мы назовем эффективностью труда одного работника. Эффективность труда зависит от здоровья, образования и квалификации рабочей силы.

Описание технологического прогресса через приращение эффективности труда делает его аналогичным росту населения.

Уравнение, показывающее изменение к с течением времени, теперь выглядит следующим образом: Новый элемент этой формулы g, темп технологического прогресса, появляется постольку, поскольку к есть количество капитала в расчете на единицу труда с постоянной эффективностью. Если величина g велика, то общее количество единиц труда с постоянной эффективностью растет быстро, а прирост капитала на такую единицу труда сравнительно мал и может стать отрицательным.

Таким образом, с учетом технологического прогресса наша модель в конце концов может объяснить, почему уровень жизни растет из года в год. Тем самым мы показывали, что технологический прогресс может поддерживать непрерывный рост выпуска продукции на одного работника, тогда как высокий уровень сбережений ведет к высоким темпам роста только до момента достижения устойчивого состояния. Как только экономика достигает устойчивого состояния, темп роста производства на одного работника зависит только от скорости технологического прогресса. Модель Солоу показывает, что только технологический прогресс может объяснить непрерывно растущий уровень жизни.

Введение в модель технологического прогресса изменяет также условия выполнения Золотого правила. Золотое правило для накопления капитала определяет устойчивый уровень, при котором максимизируется потребление на единицу труда с постоянной эффективностью. Следует сказать, что устойчивый уровень потребления на единицу труда с неизменной эффективностью составляет: .

Устойчивый уровень потребления максимизируется, если:

МРК – σ + n + g, или МРК – σ = n + g. Таким образом, при запасе капитала по Золотому правилу чистый предельный продукт капитала (МРК – σ) равен темпу прироста объема производимой продукции n + g.

Контрольные вопросы

В модели AD-AS экономический рост может быть представлен как:

а) сдвиг влево кривой AS;

б) сдвиг вправо кривой AD;

в) сдвиг влево кривой AD.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

Обязательная

1. Агапова Т. А., Серегина С. Ф. Макроэкономика: Учебник / Под общ. ред. А. В. Сидоровича. – М.: Изд-во МГУ, 2001. – 416 с.

3. Макконнелл К. Р., Брю С. Л. Экономикс: Принципы, проблемы и полити­ка. В 2 т.: Пер с англ. – М.: Туран, 1996. –Т. І. – 400 с.

4. Менкью Г. Н. Макроэкономика. — М.: Изд-во Моск. ун-та, 1994.

5. Мікроекономіка і макроекономіка / Кол. авт. під ред. С. Будаговської. — Київ: Основи, 1998.

6. Савченко А. Г., ПухтаєвичГ.О., Тітьонко О. М. Макроекономіка: Підруч­ник. – К.: Либідь, 1999 – 288 с.

7. Сакс Д. Джеффри, Ларрен Б. Филипс. Макроэкономика. Глобальный подход. — М.: Дело, 1996.

8. Самюелсон Пол А., НордгаузВільям Д.Макроекономіка. – Київ: Основи, 1995.

Дополнительная

9. Агапова Т. Концепция рациональных ожиданий и эффектив­ность макроэкономической политики // Российский экономический журнал.—1996.— № 10.

11. Базилевич В. Д., Баластрик Л. О.Макроекономіка: Опорний конспект лекцій. – К.: Четверта хвиля, 1997.– 275 с.

12. Барановський О. Грошова маса в системі економічної безпе­ки держави // Банківська справа. – 1996. – № 4.

13. Борисова О. С. Регулирование бюджетного дефицитаФРГ // Финансы. – 1992. – № 2.

Источник