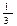если на множестве всех треугольников на плоскости рассматривается отношение подобия

Свойства отношений на множестве

Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения.

Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.

Существуют отношения, не обладающие свойством рефлексивности, например, отношение перпендикулярности отрезков: ab, ba (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе). Поэтому на графе данного отношения нет ни одной петли.

Не обладает свойством рефлексивности и отношение «длиннее» для отрезков, «больше на 2» для натуральных чисел и др.

Отношение R на множестве Х называется антирефлексивным, если для любого элемента из множества Х всегда ложно хRх: .

Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны сами себе, а точки, не лежащие на прямой l, себе не симметричны.

Граф симметричного отношения обладает следующей особенностью: вместе с каждой стрелкой, идущей от х к y, граф содержит стрелку, идущую от y к х (рис. 35).

Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.

Существуют отношения, которые не обладают свойством симметричности.

Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Граф этого отношения обладает особенностью: стрелка, соединяющая вершины, направлена только в одну сторону.

Отношение R называют антисимметричным, если для любых элементов х и y из истинности xRy следует ложность yRx: : xRyyRx.

Кроме отношения «длиннее» на множестве отрезков существуют и другие антисимметричные отношения. Например, отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др.

Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности.

Отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRzxRz.

Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z.

Свойством транзитивности обладает и отношение «длиннее» на множестве отрезков: если отрезок а длиннее отрезка b, отрезок b длиннее отрезка с, то отрезок а длиннее отрезка с. Отношение «равенства» на множестве отрезков также обладает свойством транзитивности: (а=b, b=с)(а=с).

Существуют отношения, которые не обладают свойством транзитивности. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку b, а отрезок b перпендикулярен отрезку с, то отрезки а и с не перпендикулярны!

Существует еще одно свойство отношений, которое называется свойством связанности, а отношение, обладающее им, называют связанным.

Отношение R на множестве Х называется связанным, если для любых элементов х и y из данного множества выполняется условие: если х и y различны, то либо х находится в отношении R с элементом y, либо элемент y находится в отношении R с элементом х. С помощью символов это определение можно записать так: xy xRy или yRx.

Например, свойством связанности обладает отношение «больше» для натуральных чисел: для любых различных чисел х и y можно утверждать, либо x>y, либо y>x.

На графе связанного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые не обладают свойством связанности. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и y, что ни число х не является делителем числа y, ни число y не является делителем числа х (числа 17 и 11, 3 и 10 и т.д.).

Рассмотрим несколько примеров. На множестве Х= задано отношение «число х кратно числу y». Построим граф данного отношения и сформулируем его свойства.

Про отношение равенства дробей говорят, оно является отношением эквивалентности.

Отношение R на множестве Х называется отношением эквивалентности, если оно одновременно обладает свойством рефлексивности, симметричности и транзитивности.

Примерами отношений эквивалентности могут служить: отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).

В рассмотренном выше отношении «равенства дробей», множество Х разбилось на три подмножества: <; ; >, <; >, <>. Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеем разбиение множества на классы.

Итак, если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно непересекающиеся подмножества – классы эквивалентности.

Так, мы установили, что отношению равенства на множестве
Х= <;; ; ; ; > соответствует разбиение этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.

Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики. Почему?

Во-первых, эквивалентный – это значит равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемы. Так, дроби, оказавшиеся в одном классе эквивалентности <; ; >, неразличимы с точки зрения отношения равенства, и дробь может быть заменена другой, например . И эта замена не изменит результата вычислений.

Во-вторых, поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. свойства, присущие некоторому классу, рассматриваются на одном его представителе.

В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее, что имеют параллельные прямые между собой.

Другим важным видом отношений являются отношения порядка. Рассмотрим задачу. На множестве Х=<3, 4, 5, 6, 7, 8, 9, 10> задано отношение «иметь один и тот же остаток при делении на 3». Это отношение порождает разбиение множества Х на классы: в один попадут все числа, при делении которых на 3 получается в остатке 0 (это числа 3, 6, 9). Во второй – числа, при делении которых на 3 в остатке получается 1 (это числа 4, 7, 10). В третий попадут все числа, при делении которых на 3 в остатке получается 2 (это числа 5, 8). Действительно, полученные множества не пересекаются и их объединение совпадает с множеством Х. Следовательно, отношение «иметь один и тот же остаток при делении на 3», заданное на множестве Х, является отношением эквивалентности.

Возьмем еще пример: множество учащихся класса можно упорядочить по росту или возрасту. Заметим, что это отношение обладает свойствами антисимметричности и транзитивности. Или всем известен порядок следования букв в алфавите. Его обеспечивает отношение «следует».

Отношение R на множестве Х называется отношением строгого порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности. Например, отношение «х Просмотров 151 133 Комментариев 0

Источник

Математика и информатика (стр. 4 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

При создании нового множества элементы первого множества должны стоять на первом месте, элементы второго множества должны стоять на втором месте. Множество, элементами которого являются упорядоченные пары чисел, называется декартовым произведением.

В упорядоченных парах компоненты могут находиться в какой-то связи, т. е. отношении. Если рассматривают отношения между объектами, то это: «больше», «меньше», «равно». Например: x>y; z y, z 0. Можно построить новое множество, которое соответствует данному отношению: <(1,0); (2,1); (3,2)>. Данное множество состоит из упорядоченных пар, каждая из которых удовлетворяет заданному отношению.

3. Отношения строгого порядка (зависимости). Примеры отношений зависимости: табличная, функциональная y=f(x). График функции есть множество упорядоченных пар: G=<(x, y)|xÎX; yÎf(x)>.

Рассмотрим различные виды отношений на примерах.

Источник

Дискретная математика- бесплатные ответы на тест Синергия

Если на множестве всех треугольников на плоскости рассматривается отношение
подобия, то данное отношение является отношением …
толерантности
порядка
эквивалентности+

Матрица смежности для графа

Полный неориентированный граф с числом вершин, равным n, имеет …ребер

Если на множестве М задано отношение А «х знаком с у», тогда на основе данного соотношения нельзя разбить множество М на непересекающиеся классы, потому что
отношение А …
нерефлексивно
несимметрично
нетранзитивно+
не антирефлексивно

Пустое множество θ … подмножеством некоторого множества
будет собственным
будет несобственным+
не будет никаким
не всегда является

Количество «нулевых» значений таблицы истинности формулы XYZvXYZvXYZ составляет…

0
5+
3

Если на множестве М задано отношение А «х знаком с у», тогда на основе данного соотношения нельзя разбить множество М на непересекающиеся классы, потому что
отношение А …
нерефлексивно
несимметрично
нетранзитивно+
не антирефлексивно

Бинарное отношение, заданное на множестве натуральных чисел соотношением X =
Y(mod3) (остатки отделения на 3 равны), является отношением …
толерантности
порядка
эквивалентности+

Значение X, определяемое уравнением

Если выразите конъюнкцию АvВ через импликацию и отрицание, получим:

Если заданы два нечетких отношения R1 и R2 :

, то результат операции пересечения равен

Конечное множество, состоящее из n элементов, имеет …
1 несобственное подмножество+
2 несобственных подмножества
n несобственных подмножеств
n2 несобственных подмножеств

Граф … обладает эйлеровым циклом

G1
G2
G3+
G4

Отношение |x-y|

Хроматическое число графа равно

Дистрибутивные законы булевой алгебры и алгебры действительных чисел …
совпадают+
не совпадают
совпадают в частном случае

Логической функции f (0,0,0) = f(0,0,l) = f (1,0,0) = 1
соответствует формула алгебры высказываний

Отношение ««быть старше»: «х старше у»» является …
рефлексивным
симметричным
транзитивным+
антисимметричным

Пусть А=1.В = 1. С = 1. К = (А —>В)лС л(А С) тогда

Выражение S=(A→B)Λ(B→С)->(A→C)… высказыванием

является тождественно истинным+
является тождественно ложным
является переменным
не является

является тождественно истинным
является тождественно ложным+
является переменным
не является

Количество «единичных» значений таблицы истинности формулы
(Xv YvZXXv YvZXXv Y vZ)

0
5+
3

Граф … содержит эйлерову цепь, соединяющую две различные вершины

Преобразовывая формулу S-AnBuCnBuA
1 (An(BuC)nB)uA
2 (AnB)u(Cn(BuA))
3 AH(BU(COB)UA)
4 (AnB)u(CnBM
, нужно производить операции в следующем порядке:

Если заданы два нечетких отношения R1 и R2 :

то результат операции, дополнения R1 равен

1
2+
3

Высказывание «Произведение целых чисел а и b не делится на 2 в том и только в том случае, если а или b

1 С АлВ 2 C AvB 3 А АВ —> С 4 А лВ vC нечетное» в символической форме имеет вид

Высказывание «Неверно, что первым пришел Петр или Павел» может быть интерпретировано как сложное
1 AvBl
2 AvB
3 АлВ
4 АлВ
высказывание и записано формулой «…»

Можем решить этот и любой другой тест Синергия. Для заказ необходимо обратиться к менеджеру. Все контакты указаны на сайте, можете выбрать любой удобный

Другие тесты Синергии:

Наша команда профессионально занимаемся сдачей тестов, выполнением курсовых, дипломных работ (ВКР), практик, рефератов МТИ (МОИ), Синергии (МФПУ), МФЮА, Витте, Педкампус и так далее

ИП Карасев Руслан Николаевич

helpstudent24.ru Помощь студентам дистанционного обучения” ИНН-366230965804

Источник

Свойства бинарных отношений

Мы установили, что бинарное отношение на множестве Х представляет собой множество упорядоченных пар элементов, принадлежащих декартову произведению Х´C. Это математическая сущность всякого отношения. Но, как и любые другие понятия, отношения обладают свойствами. Их удалось выделить, изучая различные конкретные отношения. Свойств достаточно много, в нашем курсе мы будем изучать только некоторые.

Рассмотрим на множестве отрезков, представленных на рисунке, отношения перпендикулярности, равенства и «длиннее».

а

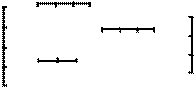
Построим графы этих отношений и будем их сравнивать.

a ·

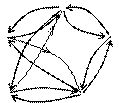
d · · c

·

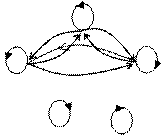
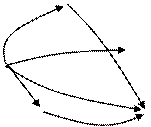
Граф отношения «длиннее»

· a

Определение.Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой.

Используя символы, это отношение можно записать в таком виде:

R рефлексивно на Х Û х R х для любого х ÎХ.

Замечание:Если отношение R рефлексивно на множестве Х, то в каждой вершине графа данного отношения имеется петля. Справедливо и обратное утверждение: граф, каждая вершина которого имеет петлю, задает отношения, обладающие свойством рефлексивности.

Примеры рефлексивных отношений:

— отношение «кратно» на множестве натуральных чисел (каждое натуральное число кратно самому себе);

— отношение подобия треугольников (каждый треугольник подобен самому себе).

Существуют отношения, которые свойством рефлексивности не обладают.

Примеры отношений, которые свойством рефлексивности не обладают:

— отношение перпендикулярности на множестве отрезков (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе);

— отношение «длиннее» для отрезков.

Обратим внимание на графы отношений перпендикулярности и равенства отрезков. Они «похожи» тем, что если есть одна стрелка, соединяющая пару элементов, то обязательно есть и другая, соединяющая те же элементы, но идущая в противоположном направлении. Эта особенность графа отражает те свойства, которыми обладают отношения параллельности и равенства отрезков:

— если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому;

— если один отрезок равен другому отрезку, то этот «другой» равен первому.

Про отношения перпендикулярности и равенства отрезков говорят, что они обладают свойством симметричности или просто симметричны.

Определение.Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у, следует, что и элемент у находится в отношении R с элементом х.

Используя символы, это отношение можно записать в таком виде:

R симметрично на Х Û( х R х Þу Rх).

Замечание.Граф симметричного отношения обладает особенностью: вместе с каждой стрелкой, идущей от х к у, граф содержит и стрелку, идущую от у к х. Справедливо и обратное утверждение. Граф, содержащий вместе с каждой стрелкой, идущей от х к у, и стрелку, идущую от у к х, является графом симметричного отношения.

Примеры симметричных отношений:

— отношение параллельности на множестве прямых (если прямая х параллельна прямой у, то прямая у параллельна прямой х);

— отношение подобия треугольников (если треугольник F подобен треугольнику Р, то треугольник Р подобен треугольнику F).

— отношение перпендикулярности на множестве отрезков (если один отрезок перпендикулярен другому отрезку, то этот «другой» перпендикулярен первому);

— отношение «длиннее» для отрезков (если один отрезок равен другому отрезку, то этот «другой» равен первому).

Рассмотрим отношение «длиннее» на множестве отрезков, которое свойством симметричности не обладает. Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Про отношения «длиннее» говорят, что оно обладает свойством антисимметричности или просто антисимметрично.

Определение. Отношение R на множестве Х называется антисимметричным, если для различных элементов х и у из множества Х выполнено условие: из того, что элемент отношении R с элементом х не находится.

Используя символы, это отношение можно записать в таком виде:

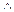
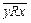
R антисимметрично на Х Û( х R у х¹у Þ ).

Замечание.Граф антисимметричного отношения обладает особенностью: если вершины графа соединены стрелкой, то эта стрелка только одна. Справедливо и обратное утверждение: граф, вершины которого соединены только одной стрелкой, есть граф антисимметричного отношения.

Примеры антисимметричных отношений:

— отношение «длиннее» на множестве отрезков;

— отношение «больше» для чисел (если х больше у, то у не может быть больше х);

— отношение «больше на 2» для чисел (если х больше у на 2, то у не может быть больше на 2 числа х).

Рассмотрим отношение «быть сестрой» на множестве детей одной семьи, которое не обладает ни свойством симметричности, ни свойством антисимметричности. Пусть в семье трое детей: Катя, Маша, и Толя. Тогда граф отношения» быть сестрой» будет таким:

К · · М

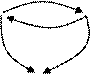
Он показывает, что данное отношение не обладает ни свойством симметричности, ни свойством антисимметричности.

Обратим внимание еще на одну особенность графа отношения «длиннее». На нем можно заметить: если стрелки проведены от е к а и от а к с, то есть стрелка от е к с; если стрелки проведены от е к в и от в к с, то есть стрелка и от е к с и т.д. Эта особенность графа отражает важное свойство отношения «длиннее»: если первый отрезок длиннее второго, а второй – длиннее третьего, то первый – длиннее третьего. Говорят, что это отношение обладает свойством транзитивности или просто транзитивно.

Определение. Отношение R на множестве Х называется транзитивным, если выполняется условие: из того, что элемент х находится в отношении R с элементом у находится в отношении R с элементомz, следует, что и элемент х в отношении R с элементом z.

Используя символы, это отношение можно записать в таком виде:

R транзитивно на Х Û( х R у уR z Þх R z).

Замечание.Граф транзитивного отношения с каждой парой стрелок, идущих от х к у и у кz, содержит стрелку, идущую от х к z. Справедливо и обратное утверждение..

Примеры транзитивных отношений:

— отношение «длиннее» на множестве отрезков;

— отношение равенства (если отрезок х равен отрезку у и отрезок у равен отрезку z, то отрезок х равен отрезку z.

Существуют отношения, которые свойством транзитивности не обладают. Таким отношением является, например, отношение перпендикулярности: если отрезок а перпендикулярен отрезку d, а отрезок d перпендикулярен отрезку b, то отрезки а и b не перпендикулярны.

Рассмотрим еще одно свойство отношений, которое называют свойством связности, а отношение, обладающее им, называют связанным.

Определение. Отношение R на множестве Х называется связанным, если для любых элементов х и у из множества Х выполнено условие: из того, что х и у различны, следует, что либо х находится в отношении R с элементом у, либо элемент у находится в отношении R с элементом х.

Используя символы, это отношение можно записать в таком виде:

R связано на множестве Х Û( х¹у Þ х R уÚ у R х).

Свойством связности обладают отношения «больше» для натуральных чисел: для различных чисел х и у можно утверждать, что х >у, либо у > х.

Замечание.На графе связного отношения любые две вершины соединены стрелкой. Справедливо и обратное утверждение.

Существуют отношения, которые свойством связности не обладают. Таким отношением, например, является отношение делимости на множестве натуральных чисел: можно назвать такие числа х и у, что ни число х не является делителем числа у, ни число у не является делителем числа х.

Выделенные свойства позволяют анализировать различные отношения с общих позиций – наличия (или отсутствия) у них тех или иных свойств.

Так, если суммировать все сказанное об отношении равенства, заданного на множестве отрезков, то получится, что оно рефлексивно, симметрично и транзитивно. Отношение «длиннее» на том же множестве отрезков антисимметрично и транзитивно, а отношение перпендикулярности – симметрично, но оно не обладает свойствами рефлексивности и транзитивности. Все эти отношения на заданном множестве отрезков связанными не являются.

Сформулировать свойства отношения «больше в 2 раза», заданного на множестве натуральных чисел.

Данное отношение не обладает свойством рефлексивности, потому что ни про одно число нельзя сказать, что оно больше самого себя в 2 раза.

Заданное отношение не транзитивно, так как из того, что число х больше числа у в 2 раза, а число у больше числа z в 2 раза, следует, что число х не может быть больше числа z в 2 раза.

Это отношение на множестве натуральных чисел свойством связности не обладает, так как существуют пары таких чисел х и у, что ни число х не больше числа у в два раза, ни число у не больше х в 2 раза. Например, это числа 7 и 3, 5 и 8 и др.

Отношение эквивалентности и порядка

Рассмотрим на множестве дробей Х = 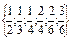отношение равенства. Это отношение:

— рефлексивно, так как всякая дробь равна сама себе;

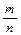
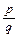
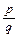
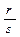
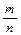
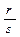
— симметрично, так как из того, что дробь равна дроби и дробь равна дроби , следует, что дробь равна дроби .

Про отношение равенства дробей говорят, что оно является отношением эквивалентности.

Определение. Отношение R на множестве Х называется отношение эквивалентности, если оно одновременно обладает свойствами рефлексивности, симметричности и транзитивности.

Примерами отношений эквивалентности могут служить отношения равенства геометрических фигур, отношение параллельности прямых (при условии, что совпадающие прямые считаются параллельными).

Почему в математике выделили этот вид отношений? Рассмотрим отношение равенства дробей, заданное на множестве Х=

· · ·

·

· ·

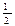
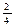
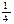
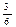
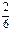
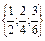
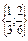
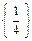
Видим, что множество разбилось на три подмножества: , , . Эти подмножества не пересекаются, а их объединение совпадает с множеством Х, т.е. имеет разбиение множества Х на классы. Это не случайно.

Замечание. Если на множестве Х задано отношение эквивалентности, то оно порождает разбиение этого множества на попарно не непересекающиеся подмножества (классы эквивалентности).

Так, мы установили, что отношению равенства на множестве дробей 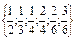соответствует разбиению этого множества на классы эквивалентности, каждый из которых состоит из равных между собой дробей.

Замечание.Верно и обратное утверждение: если какое – либо отношение, заданное на множестве Х, порождает разбиение этого множества на классы, то оно является отношением эквивалентности.

Рассмотрим на множестве Х = <1, 2, 3, 4, 5, 6, 7, 8, 9, 10>отношение «иметь один и тот же остаток при делении на 3». Оно порождает разбиение множества Х на классы: в один попадут все числа, при делении которых на 3 получается в остатке 0 (это числа 3, 6, 9), во второй – числа, при делении которых на 3 в остатке получается 1(это числа 1, 4, 7, 10), и в третий – все числа, при делении которых на 3 в остатке получается 2 (это числа 2, 5, 8). Действительно, полученные подмножества не пересекаются и их объединение совпадает с множеством Х. Следовательно, отношение «иметь один и тот же остаток при делении на 3», заданное на множестве Х, является отношением эквивалентности. Утверждения о взаимосвязи отношения эквивалентности и разбиения на классы мы принимаем без доказательства.

Если отношение эквивалентности имеет название, то соответствующее название дается и классам. Например, если на множестве отрезков задать отношение равенства (оно является отношением эквивалентности), то множество отрезков разобьется на классы равных отрезков. Множество треугольников отношением подобия разбивается на классы подобных треугольников.

Принцип разбиения множества на классы при помощи некоторого отношения эквивалентности является важным принципом математики.

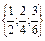
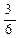
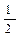
Во-первых,эквивалентный – это значит равносильный, взаимозаменяемый. Поэтому элементы одного класса эквивалентности взаимозаменяемые. Так, дроби, оказавшиеся в одном классе эквивалентности , неразличимы с точки зрения отношения равносильности, и дробь может быть заменена другой, например . И эта замена не изменит результата вычислений.

Во–вторых,поскольку в классе эквивалентности оказываются элементы, неразличимые с точки зрения некоторого отношения, то считают, что класс эквивалентности определяется любым своим представителем, т.е. произвольным элементом этого класса. Так, любой класс равных дробей можно задать, указав любую дробь, принадлежащую этому классу. Определение класса эквивалентности по одному представителю позволяет вместо всех элементов множества изучать совокупность отдельных представителей из классов эквивалентности. Например, отношение эквивалентности «иметь одинаковое число вершин», заданное на множестве многоугольников, порождает разбиение этого множества на классы треугольников, четырехугольников, пятиугольников и т.д. Свойства, присущие некоторому классу, рассматриваются на одном его представителе.

В-третьих, разбиение множества на классы с помощью отношения эквивалентности используется для введения новых понятий. Например, понятие «пучок прямых» можно определить как то общее. Что имеют параллельные между собой прямые.

Вообще любое понятие, которым оперирует человек, представляет собой некоторый класс эквивалентности. «Стол», «дом», «книга» – все эти понятия являются обобщенными представлениями о множестве конкретных предметов, имеющих одинаковое назначение.

Другим важным видом отношений являются отношения порядка.

Определение. Отношение R на множестве Х называется отношение порядка, если оно одновременно обладает свойствами антисимметричности и транзитивности.

Примеры отношений порядка:

— отношение «меньше» на множестве натуральных чисел;

— отношение «короче» на множестве отрезков.

Источник