если субъект и предикат видовое и родовое понятия такие отношения называются
Если субъект и предикат видовое и родовое понятия такие отношения называются
43. Согласно правилам определения понятий, …
*определение не должно быть сложным и непонятным
*определение должно быть последовательным
*понятие и определение должны быть в отношениях равнозначности
*результаты определения понятий не должны пересекаться
Показать полностью.
*определение должно быть соразмерным
*определение не должно быть двусмысленным
*определение должно быть полным
*определение не должно быть только отрицательным
*определение проводится по одному основанию
44. Раздел логики, возникший в древности, изучающий то, как мыслит человек, – это … логика множественная
формальная
символическая
45. Индуктивным называется умозаключение, где …
*из общего правила выводится частный случай
*на основе сходства предметов в одних признаках делается вывод об их сходстве и в других
*из частных случаев выводится общее правило
46. Совместимые понятия – это понятия, …
*в содержании которых нет ни одного общего признака
*объемы которых не имеют общих элементов и не соприкасаются
*объемы которых имеют общие элементы или соприкасаются
47. Аргумент – это …
*высказывания, используемые при обосновании
*высказывание, истинность которого обосновывается
*опровержение или подтверждение высказывания
48. Принцип однозначности в искусственных языках заключается в том, что …
*в высказываниях должно утверждаться или отрицаться нечто об объектах, представляемых именами, а не о самих этих именах
*всякое выражение должно обозначать только один предмет (этот принцип исключает омонимию) *если два выражения имеют одно и то же значение, то одно из них можно заменять другим
49. … создан искусственным путем, является универсальным средством решения познавательных задач, а имена в нем не зависят от контекста и однозначны
*Искусственный язык
*Естественный язык
*Язык логики высказываний
50. Абстрагирование – это …
*системное объединение общих и существенных признаков предмета в одну мысль
*отделение существенных признаков предмета от несущественных
*мысленное отвлечение свойств и отношений от предметов
51. Непреднамеренная ошибка в рассуждении, обусловленная нарушением законов логики, – это …
*критика
*софизм
*паралогизм
52. Собирательное понятие обозначает …
не объект, а признак
объект, состоящий из отдельных элементов
наличие чего-либо
53. Каноны индукции были разработаны …
Ф. Бэконом и Дж. Миллем
Платоном и Аристотелем
Ф. Бэконом и Б. Спинозой
54. Суждения «Солнце встает на востоке» и «Солнце не встает на востоке» являются примерами закона …
тождества
противоречия
достаточного основания
55. При логической операции умножения понятий происходит …
*объединение понятий и образуется новое понятие с объемом, охватывающим совпадающие элементы объемов исходных понятий
*раскрытие содержания понятия и имеет место изучение новых предметов на основе имеющихся знаний
*раскрытие объема понятия и имеет место разделение областей действительности на группы, части, виды и др.
56. Значение логики в современной культуре заключается в том, что логика учит …
*убеждать людей в истинности своих суждений
*человека сознательно применять законы и формы мышления
*решать практические профессиональные задачи
57. Предмет изучения логики – это …
*законы логики
*содержание мышления
*форма мышления
Если субъект и предикат видовое и родовое понятия такие отношения называются
Краткий курс логики: Искусство правильного мышления
Логика – один из обязательных предметов в высших учебных заведениях. В последнее время она также изучается в некоторых средних учебных заведениях. Практика показывает: тем, кто познакомился с логикой в школьные годы, намного легче осваивать эту науку в вузе. Книга состоит из четырёх основных глав, теста, ста занимательных задач. Первые три главы посвящены логическим формам: понятию, суждению и умозаключению, четвёртая – рассказывает о важнейших законах логики и распространённых нарушениях этих законов, которые делают наше мышление запутанным, речь – неясной, а значит, мешают полноценно общаться и понимать друг друга. Каждую тему завершают вопросы и задания для самопроверки и закрепления материала. Примеры, содержащиеся в книге, показывают практическую значимость логики для современного человека.
Тест состоит из ста заданий закрытого типа (при нескольких вариантах ответа на каждый вопрос, только один является правильным). Для выполнения теста обязательны теоретические знания по логике.
Сто занимательных логических задач, представленных в книге, различаются по типу построения и уровню сложности. Объединяет их то, что для правильного решения задач требуется нестандартный подход и творческая работа мысли. Задачи направлены на развитие мышления, памяти, внимания и воображения; они могут развлечь в часы досуга. Для решения задач не обязательны теоретические знания по логике, достаточно жизненного опыта и смекалки, т. е. интуитивной логики, которой в большей или меньшей степени обладают все люди, независимо от пола, возраста и уровня образования. Ко всем задачам приведены ответы и комментарии.
Книгу завершает список литературы, рекомендуемый для дальнейшего, более широкого изучения предмета.
Надеемся, что книга вам понравится, а изучение логики станет интересным и увлекательным.
В словаре приведены определения наиболее важных логических терминов, его можно рассматривать как конспект курса логики, построенный по алфавитно-терминологическому принципу.
Логика – наука о формах и законах правильного мышления.
Эта наука появилась приблизительно в V в. до н. э. в Древней Греции. Её создателем считается знаменитый древнегреческий философ и учёный Аристотель. Логике 2,5 тысячи лет, однако она до сих пор сохраняет своё практическое значение. Многие науки и искусства Древнего мира навсегда ушли в прошлое и представляют для нас только «музейное» значение, интересны исключительно как памятники старины, но некоторые из них пережили века, и в настоящее время мы продолжаем ими пользоваться. К их числу относится геометрия Евклида (в школе мы изучаем именно её) и логика Аристотеля. В XIX в. появилась и стала быстро развиваться символическая (математическая, современная) логика, которая является разделом высшей математики. Однако наша книга посвящена исключительно аристотелевской логике.
Так зачем нам нужна логика, какую роль она играет в нашей жизни? Логика помогает нам правильно строить свои мысли и верно их выражать, убеждать других людей и лучше понимать собеседника, объяснять и отстаивать свою точку зрения, избегать ошибок в рассуждениях.
Каждый из нас хорошо знает, что по содержанию человеческое мышление бесконечно многообразно, ведь мыслить (думать) можно о чём угодно, например, об устройстве мира и происхождении жизни на Земле, о прошлом человечества и его будущем, о прочитанных книгах и просмотренных фильмах, о сегодняшних занятиях и завтрашнем отдыхе… Но самое главное заключается в том, что наши мысли возникают и строятся по одним и тем же законам, подчиняются одним и тем же принципам, укладываются в одни и те же схемы или формы. Причём если содержание нашего мышления чрезвычайно разнообразно, то форм, в которых выражается это разнообразие, совсем немного.
Приведём простой пример. Рассмотрим три совершенно различных по содержанию высказывания: «Все караси – это рыбы», «Все треугольники – это геометрические фигуры», «Все стулья – это предметы мебели». Несмотря на различное содержание, у этих высказываний есть нечто общее, что-то их объединяющее. Что? Их объединяет форма. Отличаясь по содержанию, они сходны по форме – каждое из трёх высказываний строится по форме: «Все A – это B», где A и B – какие-либо предметы. Понятно, что само высказывание: «Все A – это B», – лишено всякого содержания. Это высказывание представляет собой чистую форму, которую можно наполнить любым содержанием, например: «Все сосны – это деревья», «Все города – это населённые пункты», «Все школы – это учебные заведения», «Все тигры – это хищники».
Другой пример: возьмём три различных по содержанию высказывания: «Если наступает осень, то опадают листья», «Если завтра пройдёт дождь, то на улице будут лужи», «Если вещество – металл, то оно электропроводно». Будучи непохожими друг на друга по содержанию, эти высказывания сходны между собой тем, что строятся по одной и той же форме: «Если A, то B». Понятно, что к этой форме можно подобрать огромное количество различных содержательных высказываний, например: «Если не подготовиться к контрольной работе, то можно получить двойку», «Если взлётная полоса покрыта льдом, то самолёты не могут взлетать», «Если слово стоит в начале предложения, то его надо писать с большой буквы».
Логика не интересуется содержанием мышления (им занимаются другие науки), она изучает только формы мышления; её интересует не то, что мы мыслим, а то, как мы мыслим, поэтому она часто называется формальной логикой. Аристотелевскую (формальную) логику также часто называют традиционной.
Если по содержанию высказывание: «Все комары – это насекомые», – является нормальным, а высказывание: «Все Чебурашки – это инопланетяне», – абсурдным, то для логики эти два высказывания равноценны, так как она занимается формами мышления, а форма у этих высказываний одна и та же: «Все A – это B».
Форма мышления – это способ выражения мыслей, или схема их построения.
Существует всего три формы мышления:
1. Понятие – это форма мышления, которая обозначает какой-либо объект или признак объекта. Примеры понятий: карандаш, растение, небесное тело, химический элемент, мужество, глупость, нерадивость.
2. Суждение – это форма мышления, которая состоит из понятий, связанных между собой, и что-либо утверждает или отрицает. Примеры суждений: «Все планеты являются небесными телами», «Некоторые школьники – это двоечники», «Все треугольники не являются квадратами».
3. Умозаключение – это форма мышления, в которой из двух или нескольких исходных суждений (посылок) вытекает новое суждение (вывод).
В логике принято располагать посылки и вывод друг под другом и отделять посылки от вывода чертой.
Любое суждение является истинным или ложным



Если суждение соответствует действительности, оно истинное, а если не соответствует – ложное. Например, суждение Все розы – это цветы является истинным, а суждение Все мухи – это птицы – ложным. Надо отметить, что понятия, в отличие от суждений, не могут быть истинными или ложными. Невозможно, например, утверждать, что понятие школа – истинное, а понятие институт – ложное, понятие звезда – истинное, а понятие планета – ложное и т. п. Но разве понятия Змей Горыныч, Кощей Бессмертный, вечный двигатель не ложные? Нет, эти понятия являются нулевыми (пустыми), но не истинными и не ложными. Вспомним, понятие – это форма мышления, которая обозначает какой-либо объект, и именно поэтому не может быть истинным или ложным. Истинность или ложность – это всегда характеристика какого-то высказывания, утверждения или отрицания, поэтому она применима только к суждениям, а не к понятиям.
4. Суждения бывают простыми и сложными.Сложные суждения состоят из простых, соединенных каким-либо союзом.
Как видим, суждение – это более сложная форма мышления по сравнению с понятием. Неудивительно поэтому, что суждение имеет определенную структуру, в которой можно выделить четыре части: субъект, предикат, связка и квантор.
Субъект (обозначается латинской буквой S ) – это то, о чем идет речь в суждении. Например, в суждении Все учебники являются книгами речь идет об учебниках, поэтому субъектом данного суждения выступает понятие учебники.
Предикат (обозначается латинской буквой Р ) – это то, что говорится о субъекте. Например, в том же суждении Все учебники являются книгами о субъекте (об учебниках) говорится, что они – книги, поэтому предикатом данного суждения выступает понятие книги.
Связка – это то, что соединяет субъект и предикат. В роли связки могут быть слова есть, является, это и т. п.
Квантор– это указатель на объем субъекта. В роли квантора могут быть слова все, некоторые, ни один и т. п.
Рассмотрим суждение Некоторые люди являются спортсменами. В нем субъектом выступает понятие люди, предикатом – понятие спортсмены, роль связки играет слово являются, а слово некоторые представляет собой квантор. Если в каком-то суждении отсутствует связка или квантор, то они все равно подразумеваются. Например, в суждении Тигры – это хищники квантор отсутствует, но он подразумевается – это слово все. С помощью условных обозначений субъекта и предиката можно отбросить содержание суждения и оставить только его логическую форму. Например, если у суждения Все прямоугольники – это геометрические фигуры отбросить содержание и оставить форму то получится: Все S есть Р. Логическая форма суждения Некоторые животные не являются млекопитающими есть Некоторые S не есть Р.
Субъект и предикат любого суждения всегда представляют собой какие-либо понятия, которые, как мы уже знаем, могут находиться в различных отношениях между собой. Между субъектом и предикатом суждения могут быть следующие логические отношения: равнозначности, пересечения, подчинения и несовместимости.
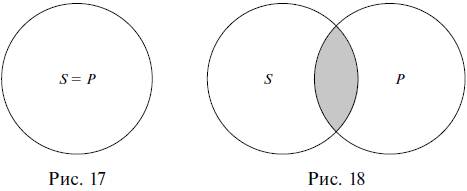
Отношение равнозначности предполагает, что субъект и предикат представляют собой равнозначные понятия. В суждении Все квадраты – это равносторонние прямоугольники субъект квадраты и предикат равносторонние прямоугольники находятся в отношении равнозначности, потому что квадрат – это обязательно равносторонний прямоугольник, а равносторонний прямоугольник – это обязательно квадрат (рис. 17).
Отношения равнозначности субъекта и предиката иллюстрируют примеры ниже:
Антарктида представляет собой ледовый материк (равнозначность).
Д. И. Менделеев – создатель Периодической системы химических элементов (равнозначность).
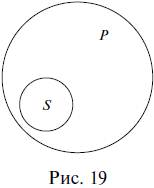
Отношение пересечения показывает, что субъект и предикат суждения являются пересекающимися понятиями. В суждении Некоторые писатели – это американцы субъект писатели и предикат американцы находятся в отношении пересечения (так как писатель может быть американцем и может им не быть, и американец может быть писателем, но также может им не быть) (рис. 18).
Отношением пересечения связаны субъект и предикат следующих суждений:
Некоторые русские писатели – это всемирно известные люди.
Некоторые ученые – древние греки.
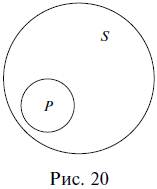
При отношении подчинения субъект и предикат суждения соотносятся как видовое и родовое понятия. В суждении Все тигры – это хищники субъект тигры и предикат хищники находятся в отношении подчинения, потому что тигр – это обязательно хищник, но хищник не обязательно тигр. Так же в суждении Некоторые хищники являются тиграми субъект хищники и предикат тигры находятся в отношении подчинения, будучи родовым и видовым понятиями.
Отношение подчинения хорошо иллюстрируют следующие суждения:
• Все бактерии являются живыми организмами.
• Солнце – это одна из звезд.
• Не все спортсмены являются олимпийскими чемпионами.
Отметим, в случае подчинения между субъектом и предикатом суждения возможны два варианта отношений: объем субъекта полностью включается в объем предиката (рис. 19), или наоборот (рис. 20).
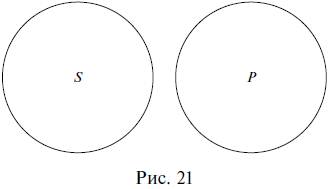
Отношение несовместимости означает, что субъект и предикат суждения являются несовместимыми (соподчиненными) понятиями. В суждении Все планеты не являются звездами субъект планеты и предикат звезды находятся в отношении несовместимости, так как ни одна планета не может быть звездой, и ни одна звезда не может быть планетой (рис. 21).
В приведенных ниже суждениях субъект и предикат находятся в отношении несовместимости:
Параллельные прямые не пересекаются (несовместимость).
Учебники не могут быть развлекательными книгами (несовместимость).
Чтобы установить, в каком отношении находятся субъект и предикат того или иного суждения, надо сначала установить, какое понятие данного суждения является субъектом, а какое предикатом. Для примера определим отношение между субъектом и предикатом в суждении Некоторые военнослужащие являются россиянами.
Сначала находим субъект суждения, – это понятие военнослужащие, затем устанавливаем его предикат, – это понятие россияне. Понятия военнослужащие и россияне находятся в отношении пересечения (военнослужащий может быть россиянином и может им не быть; и россиянин может как быть, так и не быть военнослужащим). Следовательно, в указанном суждении субъект и предикат пересекаются.
Точно так же в суждении Все планеты – это небесные тела субъект и предикат находятся в отношении подчинения, а в суждении Ни один кит не является рыбой субъект и предикат несовместимы.
Как правило, все суждения подразделяют на три вида:
Атрибутивные суждения (от лат. attributum – «неотъемлемый признак») – это суждения, в которых предикат представляет собой какой-либо существенный, неотъемлемый признак субъекта. Например, суждение Все воробьи – это птицы – атрибутивное, потому что его предикат является неотъемлемым признаком субъекта, ведь быть птицей – это главный признак воробья, его атрибут, без которого он не будет самим собой (если некий объект не птица, то он обязательно и не воробей).
Надо отметить, что в атрибутивном суждении не обязательно предикат является атрибутом субъекта, может быть и наоборот – субъект представляет собой атрибут предиката. Например, в суждении Некоторые птицы – это воробьи (как видим, по сравнению с вышеприведенным примером, субъект и предикат поменялись местами) субъект является неотъемлемым признаком (атрибутом) предиката. Однако эти суждения всегда можно формально изменить таким образом, что предикат станет атрибутом субъекта. Поэтому атрибутивными обычно называются те суждения, в которых предикат является атрибутом субъекта.
Экзистенциальные суждения (от лат. existentia – «существование») – это суждения, в которых предикат указывает на существование или несуществование субъекта. Например, суждение Вечных двигателей не бывает является экзистенциальным, так как его предикат не бывает свидетельствует о несуществовании субъекта (вернее – предмета, который обозначен субъектом).
Релятивные суждения (от лат. relativus – «относительный») – это суждения, в которых предикат выражает собой какое-то отношение к субъекту. Например, суждение Москва основана раньше Санкт-Петербурга является релятивным, потому что его предикат основана раньше Санкт-Петербурга указывает на временное (возрастное) отношение одного города и соответствующего понятия к другому городу и соответствующему понятию, представляющему собой субъект суждения.
В мышлении и языке большую часть составляют атрибутивные суждения. Они встречаются чаще, чем экзистенциальные и релятивные. Кроме того, последние, в принципе, можно представить как атрибутивные. Вернемся к экзистенциальному суждению Вечных двигателей не бывает. Его предикат (не быть или не существовать ) вполне можно рассматривать как атрибут субъекта (вечные двигатели ), ведь не существовать – это действительно неотъемлемый признак вечных двигателей, следовательно, данное суждение возможно расценивать как атрибутивное.
Теперь обратимся к релятивному суждению Москва основана раньше Санкт-Петербурга, предикат которого (быть основанным раньше Санкт-Петербурга ) вполне можно рассматривать как атрибут субъекта (Москва ), ведь быть старше Санкт-Петербурга (ранее основанным городом) – это действительно неотъемлемый признак Москвы. Таким образом, это суждение также возможно охарактеризовать как атрибутивное.
9. Краткий курс классической логики. Суждение
Суждение – это форма мышления, в которой что-либо утверждается или отрицается. Примеры суждений: «Некоторые студенты – отличники», «Все люди – смертные».
Суждения составляется из понятий, оно предоставляет собой чаще всего повествовательное предложение. В редких случаях оно бывает риторическое-восклицательное или риторическое-вопросительное предложение, которое что-то утверждает или отрицает.
Бывают простые и сложные суждения, сложные суждения складываются из двух или более простых суждений соединённых союзом.
Суждение на отмену от понятий бывают истинные и ложные, а так же имеют сложную структуру, которая складывается из таких понятий:
Субъект и предикат суждения могут состоять в отношениях:
1.Равнозначности – когда объем субъекта равен объёму предиката. «Все квадраты – равносторонние прямоугольники».
2.Подчинения – когда объем субъекта входит в объем предиката или наоборот. «Все березы – это деревья». Объем понятия деревья больше понятия березы, так как береза только одно из разновидностей деревьев.
3.Пересечения – когда объемы субъекта и предиката пересекаются частично, к примеру, «Некоторые литераторы – это лауреаты нобелевской премии». Литераторы могут быть лауреатами нобелевской премии, но могут и не быть, так же как и лауреаты нобелевской премии могут быть литераторами, но могут ими и не быть. Объем этих понятий совпадает только в некоторых случаях, потому субъект и предикат находятся в отношении пересечения.
4.Несовместимости – когда объемы субъекта и предиката не имеют общих точек соприкосновения. «Звезды – это не планеты». Чаще субъект и предикат, входя в третье более общее понятия, в нашем случае – это небесные тела.
Важно заметить, что при обращении, суждения меняют свой тип, согласно ниже приведенных примеров:
Суждения типа А:
равнозначности – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа I:
пересечения – обращается в самое себя.
подчинения – обращается в суждения типа I.
Суждения типа Е:
несовместимости – обращается в самое себя.
Суждения типа О:
пересечения – обращению не поддается.
подчинения – обращению не поддаётся.
Второе действие над суждениями — превращения. Оно заключается в том, что у суждения меняется связка, положительная на отрицательную или наоборот. При этом предикат суждения меняется на противоречащий, перед ним ставиться частица «не». Вернемся к нашему исходному суждению: «Все акулы – являются рыбами». Результатом превращения будет суждения: «Все акулы не являются не рыбами». Выглядит это суждения непривычно, однако это более короткое изречение той мысли, что если какое-то животное не являются акулой, то оно не являются и рыбой. Или, что если какое-то животное является акулой то оно обязательно должно являться рыбой, ни одна акула не может быть таким существом, которое бы не являлось при этом рыбой.
В отличие от обращения превращение не зависит от характера отношения субъекта и предиката простого суждения:
Суждения типа А всегда превращается в суждения типа Е, и наоборот.
Суждения типа I всегда превращается в суждения типа О, и наоборот.
При действии противоставления предикату суждения меняют свой тип, аналогично обращении.
В итоге, из одного суждения, мы можем получить четыре:
1. Исходное суждение: «Все акулы являются рыбами».
2. Результат обращения: «Некоторые рыбы – это акулы».
3. Результат превращения: «Все акулы не являются не рыбами».
4. Результат противоставления предикату: «Все не рыбы не являются акулами».
Если мы разобрались с этим, то совершить превращения и противоставления предикату этого суждения совсем не проблематично. Получиться, как и в первом варианте — четыре суждения:
Исходное суждение: «Идти назад – значит не идти вперед»
Обращения: «Иногда не идти вперед, значит идти назад».
Превращения: «Идти назад не означает, не идти вперед».
Противоставление предикату: «Иногда не идти вперед не означает, не идти назад».
Несовместимые суждения находятся в отношениях:
Противоположности (контарность) – суждения, в которых, так же как при отношении частичного совпадения, субъект и предикат совпадает, а связка отличается, но в этом случае суждения могут быть только общими: общеутвердительными (А) или общеотрицательными (О). «Все люди – лгут», «Все люди – не лгут». Важным признаком противоположных суждений является то, что они не могут быть одновременно истинные как несовместимые, но при этом могут быть одновременно ложными. Между этими суждениями всегда можно вставить третье, нейтральное утверждение. В нашем примере это «Некоторые люди лгут, а некоторые не лгут». Это суждение, будучи истинным, доказывает ложность двух первых.
Противоречия (контрадикторность) – это отношения между двумя суждениями в которых предикаты совпадают, связки отличаются, а субъекты находятся в родовом, видовом отношении, то есть отличаются объемами. «Все люди – являются разумными существами», Некоторые люди – не являются разумными существами». На отмену от противоположных суждений противоречивые, не могу быть одновременно ложными. Ложность одного непременно будет доказательством истинности другого, и наоборот.
Возможные отношения между простыми суждениями отображают посредством, так называемого логического квадрата:
Истинное значение суждения, связано с истинностью значений всех других сравнимых суждений. К примеру если суждения типа А: «Все акулы – являются рыбами» истинно, смотря на логический квадрат, можно определить, что суждения типа I: «Некоторые рыбы – являются акулами», тоже будет истинным. Суждения типа Е: «Все акулы – не являются рыбами», точно так же как и суждения типа О: «Некоторые акулы – не являются рыбами», будут ложными.
Еще несколько слов о сложных суждениях. В зависимости от союза, которым соединяются простые суждения в сложные, выделяют пять видов сложного суждения: