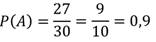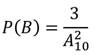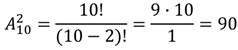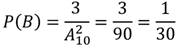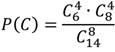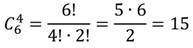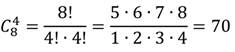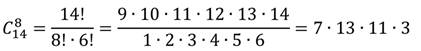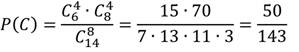Алгебра. 9 класс

Подбрасывание монеты для определения вероятности выпадения орла или решки, или бросание игрального кубика для определения выпавшего числа, всё это яркие примеры наступления вероятности некоторого случайного события.

Исходы при которых наступает ожидаемое событие называют благоприятными исходами для данного события.

При бросании игрального кубика, с очками на каждой стороне от 1 до 6 существует 6 равновозможных событий (исходов), ведь шансы выпадения любого очка от 1 до 6 абсолютно одинаковы.

Если шансы исходов любого эксперимента одинаковы, то все исходы принято считать равновозможными.

Вероятность обозначается буквой Р, от французского слова probabilité – вероятность.

Если все исходы испытания равновозможны, то вероятность наступления события в данном испытании равна отношению числа благоприятных для него исходов к числу всех равновозможных исходов.

Существует два подхода к определению вероятности.

Статистический подход требует проведения реальных экспериментов.
Классический подход требует правильного определения числа равновозможных исходов испытания и числа благоприятных исходов.

Достоверным событием называется такое событие, которое происходит всегда при проведении эксперимента.

При бросании игрального кубика определить вероятность события, при котором выпадет менее 7 очков. Каждый из шести результатов даст такой исход (1; 2; 3; 4; 5; 6), значит

Вероятность достоверного события равна единице.

Рассмотрим обратный пример.

При бросании игрального кубика определить вероятность события, при котором выпадет 7 очков. Данное событие ни при каких условиях не может произойти.

Невозможным событием называется такое событие, которое не может произойти ни при каком исходе эксперимента.

Вероятность невозможного события равна нулю.

Вероятность наступления случайного события иногда можно определить с помощью геометрических соображений, используя вероятностую шкалу.

Допустим проведено некоторое испытание с n равновозможными исходами, среди которых m исходов являются благоприятными для наступления события А. Можем записать, что

Заметим, что всегда m ≤ n, следовательно , то есть вероятность наступления события А будет P(A) ≤ 1. Но также отметим, что P(A) ≥ 0. Сделаем вывод:
0 ≤ P(A) ≤ 1.

Геометрический смысл записи состоит в том, что, чем ниже вероятность наступления события А, тем ближе к нулю располагается точка P(A), чем выше вероятность наступления события А, тем ближе к единице располагается точка P(A).

Вероятность любого события всегда находится между 0 и 1.

Алгебра. 9 класс: учеб. для общеобразоват. организаций / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б Суворова]; под ред. С. А. Теляковского. – 4-е изд. – М.: Просвещение, 2017.

Источник

Вероятность равновозможных событий

Урок 31. Алгебра 9 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Вероятность равновозможных событий»

Вернёмся к эксперименту с подбрасыванием монеты. Многие ученые проводили его и получали различные, но близкие значения.

Говоря о том, что монета однородна и имеет правильную геометрическую форму, можно сделать вывод, что случаи выпадения орла или решки имеют одинаковые шансы. Такие события называют равновозможными.

Найдём вероятность события выпадения орла.

Всего при подбрасывании монеты могут быть 2 равновозможных исхода: выпадет орёл или решка. Для нас благоприятным событием является первое. Среди всех возможных оно встречается 1 раз. Тогда получаем, что относительная вероятность выпадения орла равна: .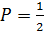

Если все исходы какого-либо испытания равновозможны, то вероятность события в этом испытании равна отношению числа благоприятных для него исходов к числу всех равновозможных исходов.

Такой способ отыскания относительной вероятности называется классическим. Но полученное значение вероятности совсем не означает, что если подбросить монету два раза, то один раз выпадет орёл.

Чтобы вычислить вероятность события классическим способом необходимо только правильно определить количество всех равновозможных исходов, а также число благоприятных для этого события исходов.

Студент не выучил 3 билета из тридцати. Какова вероятность того, что он сдаст экзамен?

Ученик записал в тетради произвольное двузначное число (не повторяя цифры). Какова вероятность того, что сумма цифр этого числа равна 6?

Определим число равновозможных исходов. Из 10 цифр можно составить различные суммы. И их количество равно .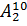

Благоприятными исходами для нашего события будут случаи, когда сумма цифр равна 6. Такую сумму дают пары (0; 6), (1; 5) и (2; 4). Пару (3; 3) мы не берём, так как цифры в числе ученик не повторял. Значит, число благоприятных исходов m=3.

Запишем формулу нахождения вероятности:

Отдельно вычислим число размещений:

Получаем, что вероятность события:

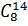
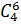
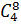
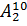
Число равновозможных исходов, n= . Число благоприятных исходов равно произведению полученных сочетаний, то есть 4 учебника из 6 можно выбрать способами, для каждого такого выбора существует способов выбора оставшихся книг, в которых 4 учебника, m=.

Найдём вероятность события:

Найдем вероятность события:

Событие, которое при проведении опыта или наблюдения происходит всегда, называют достоверным событием.

А событие, которое при проведении опыта или наблюдения не происходит никогда, называют невозможным.

Например, при бросании игрального кубика выпадает Оцените видеоурок

Источник

Теория вероятностей, формулы и примеры

Тема непростая, но если вы собираетесь поступать на факультет, где нужны базовые знания высшей математики, освоить материал — must have. Тем более, все формулы по теории вероятности пригодятся не только в универе, но и при решении 4 задания на ЕГЭ. Начнем!

Основные понятия

Французские математики Блез Паскаль и Пьер Ферма анализировали азартные игры и исследовали прогнозы выигрыша. Тогда они заметили первые закономерности случайных событий на примере бросания костей и сформулировали теорию вероятностей.

Когда мы кидаем монетку, то не можем точно сказать, что выпадет: орел или решка.

Но если подкидывать монету много раз — окажется, что каждая сторона выпадает примерно равное количество раз. Из чего можно сформулировать вероятность: 50% на 50%, что выпадет «орел» или «решка».

Теория вероятностей — это раздел математики, который изучает закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними.

Вероятность — это степень возможности, что какое-то событие произойдет. Если у нас больше оснований полагать, что что-то скорее произойдет, чем нет — такое событие называют вероятным.

Ну, скажем, смотрим на тучи и понимаем, что дождь — вполне себе вероятное событие. А если светит яркое солнце, то дождь — маловероятное или невероятное событие.

Случайная величина — это величина, которая в результате испытания может принять то или иное значение, причем неизвестно заранее, какое именно. Случайные величины можно разделить на две категории:

Вероятностное пространство — это математическая модель случайного эксперимента (опыта). Вероятностное пространство содержит в себе всю информацию о свойствах случайного эксперимента, которая нужна, чтобы проанализировать его через теорию вероятностей.

Формулы по теории вероятности

Теория вероятности изучает события и их вероятности. Если событие сложное, то его можно разбить на простые составные части — так легче и быстрее найти их вероятности. Рассмотрим основные формулы теории вероятности.

Случайные события. Основные формулы комбинаторики

Классическое определение вероятности

Вероятностью события A в некотором испытании называют отношение:

P (A) = m/n, где n — общее число всех равновозможных, элементарных исходов этого испытания, а m — количество элементарных исходов, благоприятствующих событию A

Таким образом, вероятность любого события удовлетворяет двойному неравенству:

Пример 1. В пакете 15 конфет: 5 с молочным шоколадом и 10 — с горьким. Какова вероятность вынуть из пакета конфету с белым шоколадом?

Так как в пакете нет конфет с белым шоколадом, то m = 0, n = 15. Следовательно, искомая вероятность равна нулю:

Неприятная новость для любителей белого шоколада: в этом примере событие «вынуть конфету с белым шоколадом» — невозможное.

Пример 2. Из колоды в 36 карт вынули одну карту. Какова вероятность появления карты червовой масти?

Количество элементарных исходов, то есть количество карт равно 36 (n). Число случаев, благоприятствующих появлению карты червовой масти (А) равно 9 (m).

Геометрическое определение вероятности

Геометрическая вероятность события А определяется отношением:

P(A)= m(A)/m(G), где m(G) и m(A) — геометрические меры (длины, площади или объемы) всего пространства элементарных исходов G и события А соответственно

Чаще всего, в одномерном случае речь идет о длинах отрезков, в двумерном — о площадях фигур, а в трехмерном — об объемах тел.

Пример. Какова вероятность встречи с другом, если вы договорились встретиться в парке в промежутке с 12.00 до 13.00 и ждете друг друга 5 минут?

У нас есть отличное онлайн обучение по математике для учеников с 1 по 11 классы, записывайся на пробное занятие!

Сложение и умножение вероятностей

Теорема о сложении вероятностей звучит так: вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:

P(A + B) = P(A) + P(B)

Эта теорема справедлива для любого числа несовместных событий:

Если случайные события A₁, A₂. A_n образуют полную группу несовместных событий, то справедливо равенство:

Произведением событий А и В называется событие АВ, которое наступает тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события.

Вторая теорема о сложении вероятностей: вероятность суммы совместных событий вычисляется по формуле:

P(A + B) = P(A) + P(B) − P(AB)

События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Теорема об умножении вероятностей: вероятность произведения независимых событий А и В вычисляется по формуле:

P(AB) = P(A) * P(B)

Пример. Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6; 0,7 и 0,8.

Найдем вероятности того, что формула содержится:

А — формула содержится в первом справочнике;

В — формула содержится во втором справочнике;

С — формула содержится в третьем справочнике.

Воспользуемся теоремами сложения и умножения вероятностей.

Ответ: 1 — 0,188; 2 — 0,452; 3 — 0,336.

Формула полной вероятности и формула Байеса

По теореме умножения вероятностей:

Аналогично, для остальных гипотез:

Эта формула называется формулой Байеса. Вероятности гипотез называются апостериорными вероятностями, тогда как — априорными вероятностями.

Пример. Одного из трех стрелков вызывают на линию огня, он производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго — 0,5; для третьего — 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Формула Бернулли

При решении вероятностных задач часто бывает, что одно и тоже испытание повторяется многократно, и исход каждого испытания независит от исходов других. Такой эксперимент называют схемой повторных независимых испытаний или схемой Бернулли.

Примеры повторных испытаний:

Итак, пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытаний независимы. А вероятность появления события А в каждом случае постоянна и не изменяется от испытания к испытанию.

Биномиальное распределение — распределение числа успехов (появлений события).

Пример. Среди видео, которые снимает блогер, бывает в среднем 4% некачественных: то свет плохой, то звук пропал, то ракурс не самый удачный. Найдем вероятность того, что среди 30 видео два будут нестандартными.

Опыт заключается в проверке каждого из 30 видео на качество. Событие А — это какая-то неудача (свет, ракурс, звук), его вероятность p = 0,04, тогда q = 0,96. Отсюда по формуле Бернулли можно найти ответ:

Ответ: вероятность плохого видео приблизительно 0,202. Блогер молодец🙂

Наивероятнейшее число успехов

Биномиальное распределение ( по схеме Бернулли) помогает узнать, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов k (появлений события) выглядит так:

Пример. В очень большом секретном чатике сидит 730 человек. Вероятность того, что день рождения наугад взятого участника чата приходится на определенный день года — равна 1/365 для каждого из 365 дней. Найдем наиболее вероятное число счастливчиков, которые родились 1 января.

Формула Пуассона

При большом числе испытаний n и малой вероятности р формулой Бернулли пользоваться неудобно. Например, 0.97 999 вычислить весьма затруднительно.

В этом случае для вычисления вероятности того, что в n испытаниях событие произойдет k раз, используют формулу Пуассона:

Здесь λ = np обозначает среднее число появлений события в n испытаниях.

Эта формула дает удовлетворительное приближение для p ≤ 0,1 и np ≤10.

События, для которых применима формула Пуассона, называют редкими, так как вероятность, что они произойдут — очень мала (обычно порядка 0,001-0,0001).

При больших np рекомендуют применять формулы Лапласа, которую рассмотрим чуть позже.

Пример. В айфоне 1000 разных элементов, которые работают независимо друг от друга. Вероятность отказа любого элемента в течении времени Т равна 0,002. Найти вероятность того, что за время Т откажут ровно три элемента.

P₁₀₀₀(3) = λ 3 /3! * e −λ = 2 3 /3! * e −2 ≈ 0,18.

Ответ: ориентировочно 0,18.

Теоремы Муавра-Лапласа

Кроме того, пусть P_n(k₁;k₂) — вероятность того, что число появлений события А находится между k₁ и k₂.

Локальная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Интегральная теорема Лапласа звучит так: если n — велико, а р — отлично от 0 и 1, то

Функции Гаусса и Лапласа обладают свойствами, которые пригодятся, чтобы правильно пользоваться таблицей значений этих функций:

Теоремы Лапласа дают удовлетворительное приближение при npq ≥ 9. Причем чем ближе значения q, p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность по сравнению с исходной формулой Бернулли.

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Записаться на марафон

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)

Источник

Вероятность равновозможных событий

Для того чтобы оценить вероятность интересующего нас события путем статистического исследования, необходимо провести большое число опытов или наблюдений, и только после этого можно определить приближенно вероятность этого события. В то же время в ряде случаев вероятность события можно оценить непосредственно из условий самого опыта или наблюдения путем рассуждений, не прибегая к испытаниям.

Вернемся к примеру с бросанием игрального кубика. Если кубик имеет правильную форму и сделан из однородного материала, то при его бросании шансы выпадения на его верхней грани каждого числа очков от 1 до 6 одинаковы, т. е. нет оснований считать, что какой-нибудь из исходов более возможен, чем остальные. Говорят, что существует б равновозможных исходов опыта с бросанием кубика: выпадение 1, 2, 3, 4, 5 и 6 очков.

Вообще исходы в определенном опыте или наблюдении считают равновозможными, если шансы этих исходов одинаковы.

Исходы, при которых происходит некоторое событие, называются благоприятными исходами для этого события.

Рассмотрим событие В, которое означает выпадение на кубике числа очков, кратного 3. Это событие происходит лишь при двух исходах испытания: когда выпало 3 очка и когда выпало 6 очков, т. е. для события В благоприятными являются два исхода из шести равновозможных исходов.

Отношение числа благоприятных исходов к числу всех равновозможных исходов в рассматриваемом примере равно Это отношение считают вероятностью события В и пишут:

Обозначение Р происходит от французского слова рrоbаbilité, что означает « вероятность».

В отличие от статистического подхода к вычислению вероятности такой подход называется классическим.

Что означает на практике, что вероятность рассмотренного события В равна Разумеется, это не означает, что при шести бросках кубика число очков, кратное 3, выпадет ровно 2 раза. Возможно, что оно выпадет 1 раз, 3 раза, не выпадет совсем. Однако если провести большое число испытаний, то относительная частота появления события В будет мало отличаться от т. е. от Вообще при увеличении числа испытаний со случайными исходами относительная частота появления случайного события приближается к его вероятности.

Сопоставляя статистический и классический подходы к вычислению вероятностей, можно сделать вывод, что статистический подход предполагает фактическое проведение испытания, а при классическом подходе не требуется, чтобы испытание было проведено в действительности.

Для того чтобы найти вероятность некоторого события (при классическом подходе), надо правильно определить число равновозможных исходов испытания и число благоприятных для этого события исходов.

Задача. Найдем вероятность того, что при подбрасывании двух монет на обеих монетах выпадет решка.

При одновременном бросании двух монет равновозможными являются следующие исходы:

— на обеих монетах выпадет орел;
— на первой монете выпадет орел, а на второй — решка;
— на первой монете выпадет решка, а на второй — орел;
— на обеих монетах выпадет решка.

Благоприятным для события А, состоящего в том, что на обеих монетах выпадет решка, является один исход из четырех возможных, значит,

При решении этой задачи было бы ошибкой считать, что в данном опыте имеются три равновозможных исхода:

— на обеих монетах выпадет орел;
— на одной монете выпадет орел, а на другой — решка;
— на обеих монетах выпадет решка.

Отсюда следовал бы неверный вывод, что

Приведем примеры вычисления вероятностей.

Пример 1. Из 25 экзаменационных билетов по геометрии ученик успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он не подготовил?

Пример 2. Антон и Игорь бросают белый и черный игральные кубики и подсчитывают сумму выпавших очков. Они договорились, что если при очередном бросании в сумме выпадет 8 очков, то выигрывает Антон, а если в сумме выпадет 7 очков, то выигрывает Игорь. Можно ли считать, что шансы выиграть в этой игре у мальчиков одинаковы?

При бросании кубиков на белом кубике может выпасть 1, 2, 3, 4, 5 или 6 очков. Каждому числу очков, выпавших на белом кубике, соответствует шесть вариантов числа очков, выпавших на черном кубике. Все исходы этого испытания приведены в таблице:

В каждой паре на первом месте записано число очков, выпавших на белом кубике, а на втором месте — число очков, выпавших на черном кубике. Указанные исходы испытания равновозможны. Общее число равновозможных исходов равно 36. Пусть событие А означает, что при бросании кубиков в сумме выпало 8 очков, а событие В означает, что в сумме выпало 7 очков.

Для события А благоприятными являются 5 исходов:

Для события В благоприятными являются б исходов:

Поэтому шансов выиграть у Игоря больше, чем у Антона.

Источник