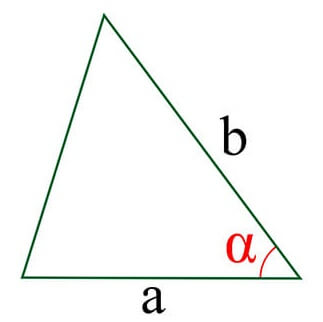
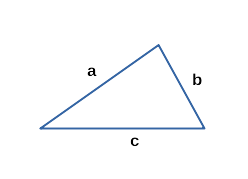
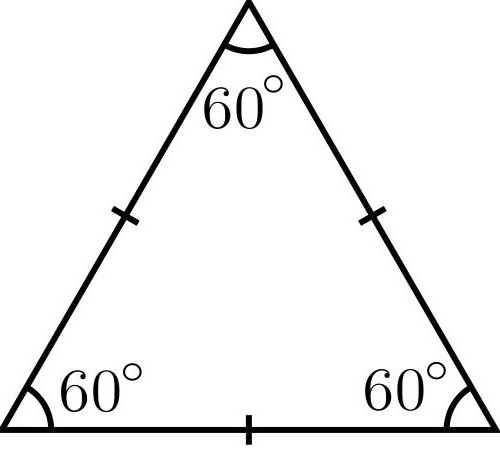
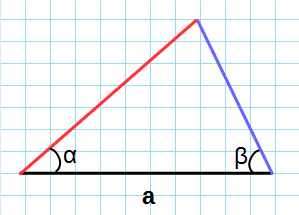
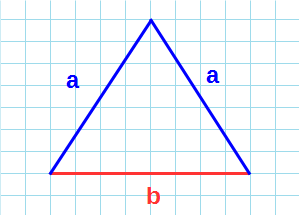
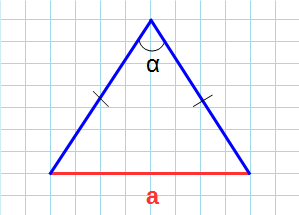
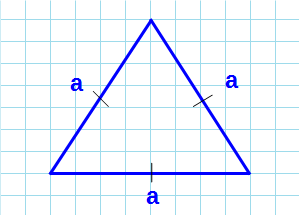
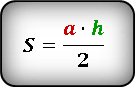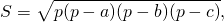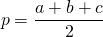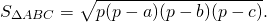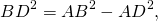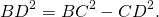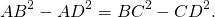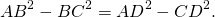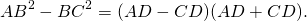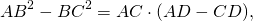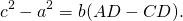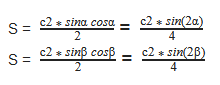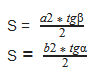Как найти площадь треугольника зная все стороны
Как найти площадь треугольника зная все стороны
Нахождение площади треугольника по трём сторонам: онлайн-калькулятор
Рассчитать площадь треугольника формулой по трем сторонам онлайн-калькулятором пригодится школьникам, студентам, преподавателям, специалистам различных специальностей. Вычисления производятся бесплатно. Пользователь сервиса получает не только готовый ответ, но и подробное решение. Используя данный способ, можно осуществлять самостоятельную подготовку к занятиям без привлечения репетиторов.
Чтобы найти площадь треугольника по трем сторонам онлайн:
В автоматических вычислениях заложена формула Герона, в которой фигурируют величины трех сторон треугольника и его полупериметра.
Как найти площадь треугольника по трем сторонам с помощью онлайн-калькулятора
Онлайн-калькулятор позволяет вычислить площадь треугольника, зная длину его сторон. При этом не важно, является ли треугольник прямоугольным, равнобедренным, равносторонним, или вообще задан произвольно.
Рассмотрим простой пример, демонстрирующий работу калькулятора. Пусть нужно вычислить площадь треугольника, со сторонами a=5 см, b=4 см и с=3 см.
Обратите внимание, стороны можно задавать в метрах, сантиметрах и миллиметрах.
Калькулятор расчета площади треугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади треугольника по разным исходным данным: через основание и высоту, три стороны, две стороны и угол между ними, три стороны и радиус вписанной или описанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.
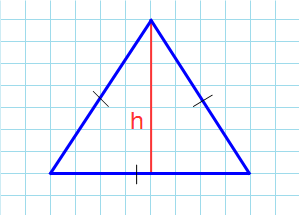
1. Через основание и высоту
Формула расчета
2. Через длину трех сторон (формула Герона)
Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).
Формула расчета:
p – полупериметр, который считается так:
3. Через две стороны и угол между ними
Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).
Калькулятор площади треугольника
Скачать, сохранить результат
Выберите способ сохранения
Информация
В современном мире не возможно представить человека, который не сталкивался с площадью треугольника. Еще в начальной школе учат этим знаниям. Особенно важны эти знания в различных сферах деятельности человека. Например, строитель (инженер, техник или проектировщик) не может не знать как искать площадь прямоугольного треугольника. Это может пригодиться при расчете размера покупки нужного количества материала для того или иного объекта.
Как найти площадь треугольника онлайн?
Для того, чтобы избавить специалистов различных отраслей от навязчивого вопроса «Как найти площадь треугольника?» и обезопасить их от допущения ошибок в процессе расчета, которые могу привести к катастрофическим последствиям, мы создали калькулятор онлайн. В наш калькулятор встроена формула для поиска площади любого треугольника по любым исходным данным. Благодаря этому инструменту, Вы можете найти площадь равнобедренного треугольника менее, чем за 5 секунд. Также калькулятор мгновенно рассчитывает площадь равностороннего треугольника, которая может находится как площадь правильного треугольника, поскольку равносторонний треугольник является правильным.
Треугольник – основная геометрическая фигура, состоящая из трех отрезков, которые соединяются в точках (вершинах) треугольника.
Существует две классификации треугольника
По углам:
По сторонам:
Калькулятор поможет рассчитать площадь через синус и сообщит Вам чему равна площадь данного треугольник, что доказывает универсальность нашего калькулятора, который является незаменимым в определенных ситуациях. В его программу внесен способ расчета площади треугольника по трем сторонам, что позволяет искать площадь Вашего треугольника через стороны.
Таким образом, созданный нами калькулятор, позволяет избавить людей от риска возникновения ошибки, которая могла бы привести к очень плохим последствиям. Экономит время, поскольку нет необходимости тратить его на самостоятельное вычисление нужного показателя. И важным преимуществом является то, что калькулятор включает в расчет площади треугольник любой его вид и применяет любую формулу.
Калькулятор площади треугольника
Существует множество способов вычисления площади треугольника: по высоте и основанию, по двум сторонам и углу между ними, по трём сторонам. В последнем случае используется, знакомая всем со школы, формула Герона. Данный метод уникален тем, что помогает произвести вычисления вне зависимости от типа фигуры. Если известно, что треугольник прямоугольный, равнобедренный или равносторонний, то для расчётов может понадобиться меньшее количество исходных данных. Площадь треугольника, построенного на векторах, вычисляется через векторное произведение этих величин. Фигура, вершины которой заданы через координаты в пространстве, рассчитывается путём нахождения расстояний между точками, а затем подстановки полученных значений в уже упомянутую формулу Герона. Онлайн-калькулятор позволит найти площадь треугольника удобным для пользователя способом в зависимости от начальных значений.
Калькулятор площади треугольника
Выберите тип треугольника:
Выберите способ расчета площади треугольника:
Округлять результат до знаков после запятой
Онлайн калькулятор. Площадь треугольника
Используя этот онлайн калькулятор, вы сможете найти площадь треугольника в зависимости от имеющихся у вас данных.
Воспользовавшись онлайн калькулятором для вычисления площади треугольника, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.
Найти площадь треугольника
Ввод данных в калькулятор для вычисления площади треугольника
В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.
Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.
Дополнительные возможности калькулятора вычисления площади треугольника
Вы можете найти площадь треугольника если знаете следующие параметры:
Теория. Площадь треугольника
Формули площади треугольника
Формула Герона
S = 1 2 a · b · sin γ
Площадь треугольника по формуле Герона (по трем сторонам)
Задача нахождения площади треугольника довольно часто встает не только перед учениками в школе, но и перед архитекторами, инженерами, проектировщиками. Один из способов расчета площади треугольника — использование формулы Герона. Для того, что бы найти площадь треугольника, необходимо знать три его стороны. Вы можете воспользоваться нашим онлайн калькулятором или же использовать формулу и произвести расчет самостоятельно.
Как найти площадь треугольника по трем сторонам
Сначала рассчитывают периметр треугольника. Напоминаем, что периметр — это сумма длин сторон. Предположим, что наш треугольник имеет стороны длиной 15, 13 и 17 сантиметров. Тогда его периметр будет равен:
P = a + b + c = 15 + 13 + 17 = 45см.
После этого находим полупериметр, т. е. делим периметр на 2:
p = P / 2 = 45 / 2 = 22,5 см.
После этого подставляем значения в формулу Герона и получаем результат:
Как найти площадь треугольника
Формулы
Примеры вычисления площади треугольника
Решение. Искомая площадь равна полупроизведению сторон на синус угла между ними, то есть
Решение. Так как площадь треугольника в два раза меньше произведения стороны на высоту, проведенную к этой стороне:
то отсюда получаем, что искомая высота
Остались вопросы?
Здесь вы найдете ответы.
Длина катета (а) = 5 см.
Длина гипотенузы (с) = 13 см.
Используя теорему Пифагора, определим длину второго катета:
Рассчитать площадь прямоугольного треугольника можно по формуле:
S = 0,5ав = 0,5*5*12 = 30
Ответ: S прямоугольного треугольника равна 30 кв.см.
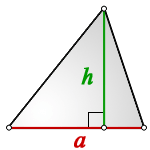
Для того чтобы вычислить площадь (S) треугольника, следует произвести умножение длины его основания (а) на длину высоты к основанию (h), а затем разделить полученное число пополам:
Если длина каждой стороны треугольника известна, то вычислить его площадь (S) можно, используя формулу Герона:
a,b,c – длина каждой из трех сторон;
р – полупериметр треугольника, который равен сумме длин всех сторон, разделенной на 2.
По условию задачи известны 3 точки, являющиеся вершинами треугольника АВС, площадь (S) которого нужно вычислить. Это точки А(1;8), В(7;8) и С(6;6).
Две из трех известных точек расположены на прямой, которая параллельна оси Х, ввиду того что координаты Ya и Yb одинаковы. Это точки А и В. Это означает, что высота треугольника (h), которая опущена на сторону АВ из вершины С (6;6), является числом, полученным в результате вычитания из координаты Ya или Yb координаты Yc:
Для того чтобы определить длину стороны АВ, нужно от координаты Xb вычесть координату Xa:
Теперь можно вычислить площадь треугольника (S):
(1/2)*AB*h = (1/2)*6*2 =6 ед.
Ответ: S = 6 ед.кв.
Формула расчета площади треугольника (S) через синус применима в случае, когда известны длины 2-х его сторон и угол, образованный между ними. При этом следует воспользоваться таблицей синусов, согласно которой синус угла в 30° = 0,5.
Ответ: S треугольника = 3 см.кв.
Зная длины двух сторон треугольника и синус угла между ними, можно рассчитать его площадь. Она будет равна ½ произведений длин его сторон, умноженной на значение синуса угла между ними:
Ответ: S треугольника = 24 см.кв.
Площадь треугольника АВС можно рассчитать, воспользовавшись формулой Герона:
Найти синус угла А можно по следующей формуле:
S=1\2 * АВ * АС * sin∠A
1\2 * 6 * 5 * sin∠A = 1215 * sin∠A = 12
Для того чтобы вычислить площадь треугольника (S), зная параметры, указанные в задаче, следует воспользоваться нижеприведенной формулой:
S= (a b sinα)/2 = (5·12·0,2)/2 =6
Ответ: S треугольника = 6 см.кв.
Для начала нужно убедиться в том, что заданная фигура с параметрами АВ=ВС=1, АС=2 действительно представляет собой треугольник.
Длины двух сторон треугольника в сумме не могут быть равны или меньше длине его третьей стороны. В данном случае:
1+1=2, то есть АВ+ВС=АС
Следует помнить, что говорить о фигуре как о треугольнике можно только в том случае, когда сумма длин двух любых его сторон больше длины третьей стороны.
Ответ: при заданных параметрах треугольника нет, и вычислить синус угла в данном случае невозможно.
Сторона треугольника, которая имеет наибольшую длину, является противоположной его наибольшему углу. В данном случае сторона АС имеет наибольшую длину (15 см), это значит, что наибольшим углом является угол В.
Перейдем к построению треугольника.
Нужно провести к стороне ВС высоту АН. Синусом наибольшего угла В является отношение АН:АВ. Теперь можно вычислить высоту из площади треугольника, рассчитанной по формуле Герона и равной 84 см:
Ответ: sin B = 0,923.
В условии говорится о том, что треугольники являются подобными. Также приведены длины двух сходственных сторон. Эти данные можно использовать, для того чтобы вычислить коэффициент подобия:
Известно, что квадрат коэффициента подобия равен отношению площадей двух треугольников, являющихся подобными. Это означает, что в заданном случае площадь второго треугольника в четыре раза превышает площадь первого из них. Зная это, можно найти площадь первого треугольника следующим образом:
Ответ: Площадь первого треугольника – 8 см.кв.
Произведение катетов прямоугольного треугольника, разделенное на два, равно его площади. Для того чтобы дать ответ на поставленный вопрос, нужно перемножить катеты (2,5*4=10) и разделить полученное число на 2 (10/2=5).
Ответ: Площадь прямоугольного треугольника равна 5 см.кв.
Для начала нужно рассчитать площадь квадрата:
Теперь можно вычислить площадь одного из получившихся в результате треугольников:
Ответ: Площадь треугольника равна 8 см.кв.
Квадраты сходственных сторон двух подобных треугольников относятся как их площади. Это значит, что:
где х – это площадь треугольника, которую нужно вычислить.
Ответ: Площадь треугольника – 81 см.кв.
Сначала нужно найти длину всего основания:
Теперь можно вычислить площадь меньшего из двух треугольников:
208 / 32 * 10 = 65 см.кв.
Ответ: Площадь меньшего треугольника составляет 65 см.кв.
Для того чтобы рассчитать площадь треугольника, нужно найти полупроизведение двух его сторон на синус угла, образованного между ними:
Площадь треугольника можно найти, если разделить на два число, полученное в результате умножения высоты (h), опущенной на его основание, на длину самого основания (а):
Как вычислить площадь треугольника по формуле 3-го класса?
В случае треугольника с прямыми углами, его площадь вычисляется по формуле:
где а и b – это стороны, которые прилегают к прямому углу.
Во всех остальных случаях рассчитать площадь треугольника можно следующим образом:
Для вычисления площади треугольника по длинам двух его сторон и находящемуся между ними углу, нужно пользоваться формулой:
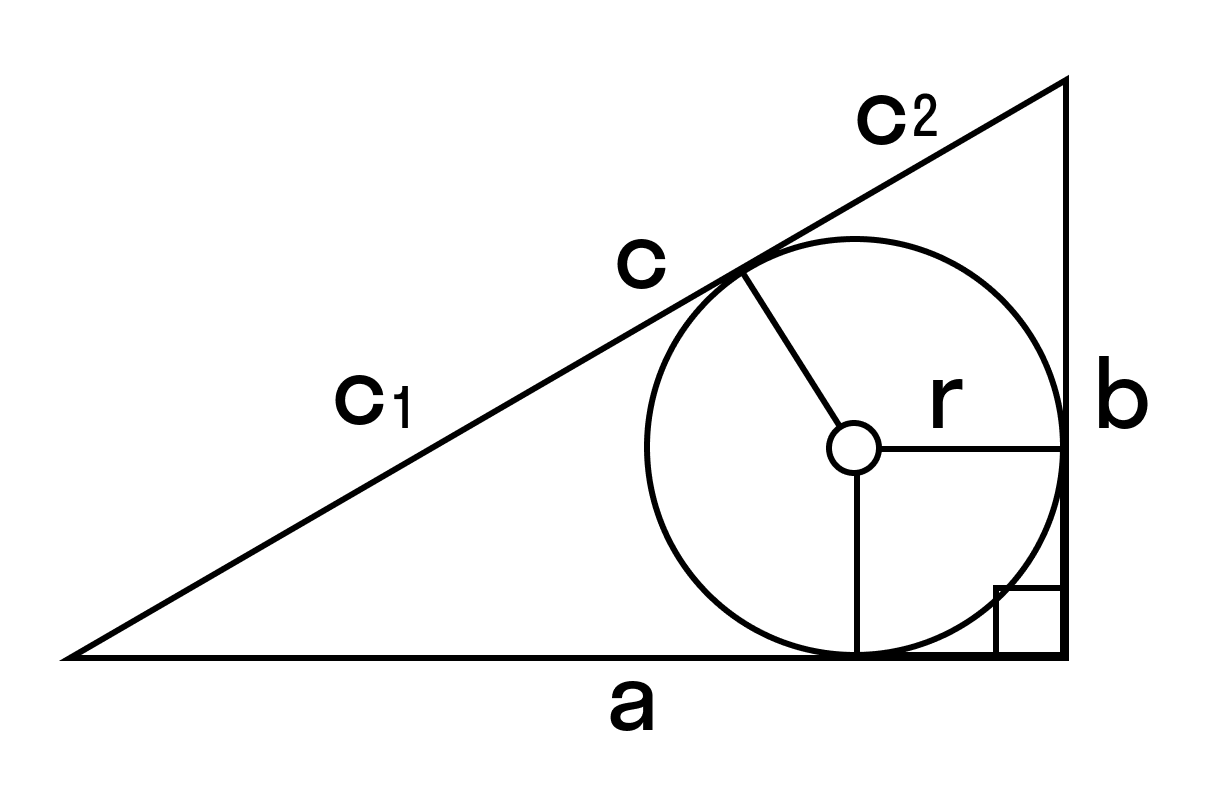
— О – центр вписанной окружности, точка пересечения биссектрис;
— Н – точка касания окружности на АВ;
Площадь ВОС рассчитывается так:
Площадь заданного треугольника АВС можно найти следующим образом:
S АВС = S АОВ + S ВОС + S АОС = 1/2АВ*ОН+1/2ВС*ОК+1/2АС*ОМ.
Тогда S АВС = 1/2*r*(АВ+ВС+АС).
Но АВ+ВС+АС= периметр Р, что означает, что
Сначала следует произвести расчет полупериметра (р):
Далее, используя формулу Герона, можно найти площадь треугольника (S):
Высота к стороне треугольника находится по формуле b*sin(C). Отсюда можно найти его площадь S = a*b*sin(C)/2. При этом следует принимать во внимание теорему синусов, согласно которой c = 2*R*sin(C); или sin(C) = c/(2*R). Тогда площадь S = a*b*c/4R. Именно это требовалось доказать.
Полагаясь на координаты, можно утверждать, что точка R лежит на оси Y и находится на расстоянии в пять единиц от начала отсчета. При этом точка F находится на оси X, на расстоянии двух единиц от начала отсчета. Заданный треугольник является прямоугольным. RO равна 5 единицам длины, FO – двум единицам длины. В этом случае площадь треугольника ROF равна:
S =RO*FO/2=5*2/2=5(единиц длины)².
Формула Герона, предназначенная для вычисления площади треугольника, выгладит так:
где а,b, с – это стороны треугольника,
р – полупериметр, рассчитываемый как Р/2.
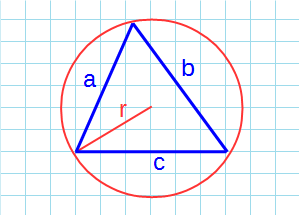
Если известны длины трех сторон треугольника (а,b, с), а также радиус описанной окружности (R), то можно рассчитать площадь треугольника (S) по следующей формуле:
В случае необходимости выразить длину одной из сторон треугольника b из формулы расчета его площади S=abc/4R, нужно произвести умножение всего выражения на 4R:
После этого нужно произвести деление всего на ac:
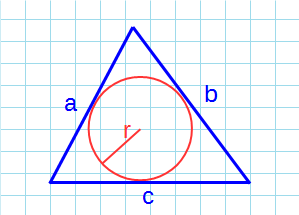
В случае соединения вершин треугольника с центром окружности, вписанной в него, в результате произойдет его деление на 3 треугольника. Радиус в точке касания будет выступать в роли высоты в каждом из них. Из этого вытекает формула:
где р – полупериметр.
Ответ на поставленный вопрос выглядит следующим образом:
Ответ: Длина стороны а равна 6 см.
Формула S=1\2 bа для прямоугольного треугольника с двумя катетами (а и b) и гипотенузой с. В представленной задаче а=3 см, b=4 см, с=5 см. Согласно таблице Пифагора с²=а²+в². В нашем случае 5²=3²+4², 25=9+16) и S=1\2*3*4=6 cм. кв.
Площадь треугольника можно рассчитать, применяя формулу Герона:
в которой р обозначает полупериметр, вычисляемый как сумма длин всех сторон треугольника, разделенная на 2: р=(16+24+32)/2=36.
В формуле стороны треугольника обозначены как a, b, c.
S=√36*20*12*4 = 48√15 cм.кв.
S = a*b*c/(4R) – это формула нахождения площади треугольника. В ней a, b и с – это его стороны, а R – это радиус окружности, которая описана вокруг данного треугольника. Каким образом можно использовать данную формулу, чтобы найти площадь треугольника, если а = 11, b = 13, с = 20 и R = 65/6?
Сначала нужно перемножить длины всех сторон треугольника:
a*b*с = 11*13*20 = 2860.
Четыре радиуса окружности равны:
Из этого следует, что площадь треугольника будет равна:
S = 2860/(130/3) = 8580/130 = 66 см. кв.
Существует несколько формул, которыми можно пользоваться для вычисления площади треугольника:
1. S = 1/2*bh, в которой b – это основание фигуры, а h – проведенная к нему высота.
3. Формула Герона: S = √(р * (р-а)(p-b)(p-c) ), в которой стороны треугольника обозначены как а,b, с. Полупериметр (Р/2) обозначен как р.
4. S=р*r, или полупериметр*радиус вписанной окружности.
5. S= 1/2*ab*sinα, где a и b – это стороны треугольника, α – угол, образованный между ними.
Площадь треугольника можно вычислить по формуле Герона:
S = √(р * (р-а)(p-b)(p-c)) = √ (48*(48-20)*(48-34)*(48-42)) = 336 см. кв.
Отсюда следует, что высота, проведенная к стороне 42 рассчитывается так:
х = 84/13; y = 176/13.
Длина большей стороны треугольника равна 16 см. Число 0,4 является разностью длин двух других его сторон. Чему равны стороны треугольника при условии, что его периметр равен 0,38 м?
Схема решения задачи:
а (большая сторона треугольника) = 16 см.
b-с = 0,4 см., b = 0,4+с.
Периметр (Р) = 38 см.
с = 21,6/2 = 10,8 см.
b = 10,8+0,4 = 11,2 см.
Для равносторонних треугольников характерно равенство длин всех трех сторон. Если одна его сторона равна а, то и обе другие тоже будут равны а. Если же все стороны треугольников равны, то это равенство соблюдается по 3 признаку.
Длины двух сторон треугольника с периметром 19 см равны 6 см и 4 см. Чему равна третья сторона данного треугольника?
Известно, что периметр треугольника является суммой длин всех его сторон и рассчитывается по формуле:
В данном случае:
Ответ: Длина третьей стороны треугольника – 9 см.
Сначала необходимо вычислить коэффициент подобия двух этих треугольников. Он равен отношению сходственных сторон:
Теперь нужно рассчитать длины других сторон первого из треугольников. Одна из них, которая является сходственной стороне второго из треугольников длиной 8 см, рассчитывается следующим образом:
Еще одна сторона первого треугольника, сходственная стороне другого из них, которая имеет длину 9 см, вычисляется так:
9*к = 9*5/2 = 22,5 см.
Следует найти отношение этих сторон:
Отношение всех сторон подобного треугольника будет таким же.
Одну из сторон подобного треугольника обозначим 4х, вторую сторону – 12х, а третью – 11х. В результате получается следующее уравнение:
x = корень 3-ей степени из 0,125 = 0,5.
Первая сторона треугольника = 4х = 4*0,5 = 2 см.
Вторая сторона треугольника = 12х = 12*0,5 = 6 см.
Третья сторона треугольника = 11х = 11*0,5 = 5,5 см.
Проверка: 2*6*5,5 = 66 см.
Имеется треугольник АВС, в котором АВ = 6 см, ВС = 8 см, ВD – медиана на АС = √46 см (2*АВ в квадрате+2*ВС в квадрате-АС в квадрате). √46 см. = ½*√(2*36+2*64-АС в квадрате), каждую часть возводим в квадрат, 4*46=72+128-АС в квадрате, АС в квадрате=16, АС=4.
Ответ: Длина третьей стороны треугольника равна 4 см.
Если предположить, что третья сторона треугольника равна 1 см, то в этом случае не получится соблюсти неравенство 1 см+1 см = 2 см. В этом случае 3 см больше 2 см, а должно быть меньше. Если длина неизвестной стороны равна 2 см, то неравенство снова не соблюдается: 2 см+1 см = 3, тогда 3 см =3 см, чего тоже не может быть ввиду того, что одна из сторон треугольника обязательно должна быть меньше суммы двух других его сторон. Если принять длину третьей стороны равной 3 см, то получается 1 см+3 см = 4 см, 3 Ответ: Третья сторона треугольника равна 3 см.
Для того чтобы рассчитать площадь треугольника (S) с прямыми углами, следует воспользоваться приведенной ниже формулой:
где a и b – катеты.
Площадь треугольника с прямыми углами равна ½ от произведения его катетов:
S = (5*4)/2=20/2=10 см. кв.
Для того чтобы получить возможность вычислить площадь треугольника, необходимо произвести замеры его основания (а) и высоты (h). Тогда площадь может быть рассчитана по следующей формуле:
Площадь треугольника через стороны
Площадь треугольника через стороны — это
площадь треугольника, которая выражена через
три стороны треугольника и полупериметр.
Полупериметр — это половина суммы
длин всех сторон треугольника.
Площадь любого треугольника можно рассчитать по
разным формулам. Одна из популярных формул:
С помощью этой формулы можно найти площадь
треугольника зная длину основания и высоту.
Но, иногда требуется найти площадь треугольника,
зная только стороны треугольника. Так, как у
каждого треугольника три стороны, то соответственно
три длины. Но, как же найти площадь?
Площадь треугольника через стороны легко рассчитать
зная Формулу Герона.Герон — греческий математик, в
честь которого и была названа эта формула. В чем суть
формулы Герона? Как найти площадь треугольника через длины сторон?
Площадь произвольного треугольника равна квадратному
корню из произведения полупериметра на разницу
между полупериметром и стороной a, полупериметром
и стороной b, полупериметром и стороной c.
Можно сделать вывод, что, чтобы рассчитать площадь треугольника
по Формуле Герона, нужно знать все стороны данного треугольника.
Формула Герона:
a, b, c — длины сторон треугольника;
p — полупериметр;
S — площадь;
Формула полупериметра:
Обобщение площади треугольника через стороны:
Подставив в вышеперечисленные формулы длины всех сторон,
можно найти площадь любого треугольника. С помощью формулы
площади треугольника через три стороны, можно также
найти не только площадь, но и периметр.
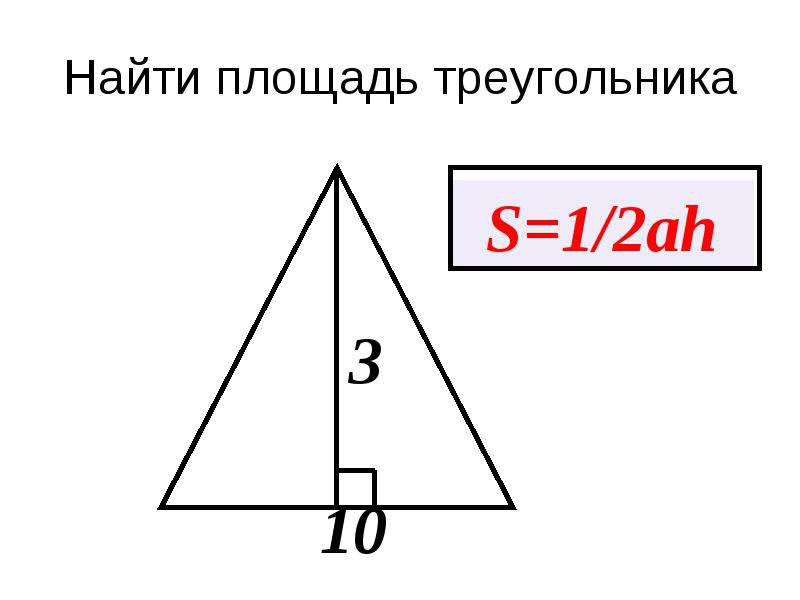
Формула расчета площади треугольника
Что бы найти площадь треугольника,
для этого надо основание умножить на высоту и разделить на два
1. Площадь разностороннего треугольника
Формула площади треугольника (S):
Калькулятор для расчета площади треугольника
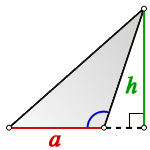
2. Площадь треугольника с тупым углом
Формула площади треугольника с тупым углом (S):
Формулы для треугольника:
Как найти площадь любого треугольника по трём сторонам
Часто бывает необходимо вычислить площадь той или иной геометрической фигуры. Если дело обстоит с прямоугольником или квадратом, то тут все более-менее ясно: формулы для их площадей интуитивно просты и понятны, а также легко запоминаются. Но как быть, если речь идет о каком-нибудь треугольнике, для вычисления площади которого простого перемножения сторон недостаточно. Тогда на помощь приходит она, госпожа Математика…
Что такое треугольник и какие бывают треугольники?
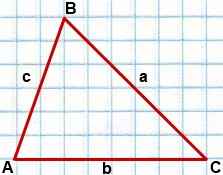
Вспомним определение из школьного курса геометрии: «Треугольником АВС называется фигура, состоящая из трех точек, не лежащих на одной прямой, и соединенных между собой отрезками». Точки А, В и С будут вершинами, а отрезки АВ, ВС и АС — сторонами треугольника. Треугольник АВС кратко записывают так: ∆ABC.
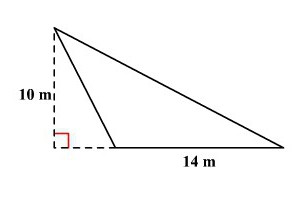
Треугольники бывают правильные, когда все их стороны равны. По-другому их еще называют равносторонними. Также есть равнобедренные, когда только две стороны одинаковы, и прямоугольные, когда один из углов — прямой.
Вычисление площади треугольника по трем сторонам. Формула Герона
Можно долго описывать свойства биссектрисы или медианы треугольника, однако, у нас другая задача: можно ли, зная длины всех сторон ∆АВС, найти его площадь? Такая необходимость возникает, если мы измерили три стороны треугольника, а углы нам неизвестны. Конечно, можно. Уже в I веке нашей эры была известна замечательная формула, позволяющая без проблем находить площади любых треугольников только по трем сторонам.
Эта формула, ныне известная как формула Герона (по имени древнегреческого ученого Герона Александрийского, жившего в I веке н. э., в чьей книге под названием «Метрика» эту формулу и обнаружили), была открыта знаменитым Архимедом. Она очень проста и сводится к следующему:
Площадь любого треугольника ABC со сторонами a, b и с определяется формулой Герона:
S=√p (p-a)(p-b)(p-c), где p=(a+b+c)/2 — полупериметр ∆ABC.
Как получить формулу Герона?
Как же была получена столь замечательная формула? Все очень просто. Если вы запасетесь небольшим терпением, то сами сможете убедиться, как же легко можно прийти к формуле Герона. Для этого поднимите из памяти на свет вашего разума известные со школьной скамьи теоремы синусов и косинусов. Как они звучат?
Теорема синусов: «Отношения сторон ∆ABC к синусам противолежащих им углов равны:
a/sin α=b/sin β=c/sin γ, где α, β и γ — углы ∆АВС, противолежащие сторонам а, b и с соответственно».
Теорема косинусов: «Квадрат стороны ∆ABC равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними: a²=b²+c²-2bc•cos α».
Используя их, вы сами придете к желаемому результату, как это сделал много веков назад знаменитый математик. Вот вам небольшая подсказка: используйте формулу площади ∆ABC подвум сторонам и углу между ними. Удачи!
Вариации формулы Герона
Существуют и другие формы записи этой формулы. Вот они:
Еще формулы для вычисления площади треугольника:
Примеры
Эти примеры помогут вам лучше освоить тему:
Пример №1
Вычислить площадь ∆АВС, если a=10, в=20, c=30. Решение. Находим полупериметр: p=(10+20+30)/2=30. Теперь по формуле Герона: S=√(30•(30−10)•(30−20)•(30−30))=0, т. е. на самом деле мы имеем дело не с треугольником, а с отрезком, у которого с=а+b=10+20=30.
Пусть а=3, в=5, c=6, тогда p=(3+5+6)/2=7. Искомая площадь S=√(7•(7−3)•(7−5)•(7−6))=√(7•4•2•1)=√56≈7,48.
Пример №2
Найти угол γ между сторонами треугольника a и в из предыдущей задачи. Решение. S=(aв/2)•sin γ, sin γ=2S/(aв)=2•√56/(3•5)=0,99778, γ=arcsin 0,99778≈86°.
Пример №3
Пусть даны координаты вершин ∆ABC: А (1,2), В (-1,3), С (2,-5). Найти его площадь по одной из формул. Решение. Находим длины его сторон: AB=√((-1−1)²+(3−2)²)=√5, BC=√((2-(-1))²+(-5−3)²)=√73, AC=√((2−1)²+(-5−2)²)=√50. Тогда S=¼•√(4•5•73-(5+73−50)²)=¼•√676=26/4=6,5.
Пример №4
Периметр равностороннего треугольника численно равен его площади. Чему равна его сторона а? Решение. Так как периметр равностороннего треугольника равен Р=3а, а его площадь S=¼•a²√3, то приравняв эти равенства, получим: 3а=¼•а²√3. Решив это уравнение, найдем: а=4√3.
Пример №5
Площадь круга радиусом R равна площади равностороннего ∆ABC. Найти радиус круга. Решение. Площадь круга S=πR² по условию задачи равна площади равностороннего ∆ABC: πR²=¼•а²√3. Из этого соотношения находим: R=а√(√3)/(2√π)≈0,3713а.
Пример №6
Сторона и два прилежащих к ней угла в ∆ABC равны соответственно а=7, β=30°, γ=60°. Чему равна его площадь? Решение. S=½•7²/(ctg 30°+ctg 60°)=(49/2)/(√3+1/√3)=49√3/8≈10,61.
Видео
Это видео поможет вам закрепить материал, изложенный в статье.
Как найти площадь треугольника
Еще в школе мы выучили, что треугольником является геометрическая фигура, которая состоит из 3 разных отрезков, соединенных между собой 3 точками и не расположенными на единой прямой. Свое название фигура получила благодаря наличию 3 углов. Хотя этой фигуре можно дать и другое определение – это так же многоугольник, у которого есть 3 угла и это тоже будет верно.
Исходя из величины углов и количества равных сторон в данной фигуре, треугольники делятся на прямоугольный, тупо- и остроугольный или равнобедренный, разно- и равносторонний. Разобравшись с определением, становится интересно, как найти площадь треугольника? Такие расчеты нередко могут потребоваться в обыденной жизни.
Как найти площадь треугольника
Различных формул, которые дают возможность вычислить площадь фигуры с тремя углами, достаточно много. Поэтому вы сами можете выбрать ту, по которой вам будет это легче сделать. Прежде чем с ними познакомиться, нужно определиться с некоторыми обозначениями:
S – так обозначается площадь фигуры;
a, b, c – обозначение его сторон;
h – значение высоты многоугольника;
p– значение полупериметра;
R – значение радиуса окружности, описанной вокруг нашей фигуры.
Это самые распространенные обозначения, которые можно встретить в формулах, используемых для расчета площади треугольника. Желательно запомнить основные из них, так как это может пригодиться не только во время подготовки к занятиям с вашим ребенком, но и в повседневной жизни. Самая простая формула:
S=1/2*b*h
Прямоугольный треугольник и расчет его площади
Таким треугольником является тот, один из углов которого прямой, то есть равен 90 градусам. Подобный угол (прямой) многоугольника образуют 2 перпендикулярных отрезка. Стоит отметить, что в треугольнике таких (прямых) углов не может быть больше одного, потому что сумма их в любом случае равна 180 градусов. Следовательно, 2 других угла в сумме будут равны 90 градусов. Это азы геометрии, о которых знает каждый школьник. Так как же найти площадь, имея перед собой именно такой прямоугольный треугольник:
Равнобедренный треугольник
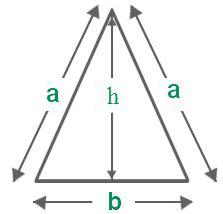
При необходимости рассчитать площадь равнобедренного треугольника, легче всего сделать это, используя классическую формулу:
S=h*c/2
Стоит помнить, что равнобедренным считается тот треугольник, в котором 2 стороны из 3 равны между собой. При этом третья сторона будет являться основанием. Но, не нужно путать его с равносторонним треугольником. Таким (равносторонним или правильным) треугольником, является тот, все стороны которого имеют равную (одинаковую) длину. Для равнобедренного треугольника так же могут быть использованы следующие формулы нахождения площади:
S=(a*c/2)*cos(y/2)=(a*c/2)*sin(β/2);
S=a²*sin(y/2)*cos(y/2)=a²*sin(α/2)*cos(α/2);
Угол α – это тот угол, который расположен между одной из боковых сторон и основанием фигуры, а угол y – тот, который расположен между боковыми (равными) сторонами.
Конечно же, чтобы использовать такие формулы, вам нужно будет иметь под рукой таблицу величин синусов, косинусов и тангенсов, поэтому их нельзя назвать удобными и общедоступными.
Найти площадь треугольника
Данный сервис поможет вам найти площадь треугольника онлайн.
Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, и соединёнными между собой. Длина каждой стороны треугольника не превосходит суммы длин двух других сторон.
В любом треугольнике сумма углов равна 180° или π радиан. Также в любом треугольнике против равных сторон лежат равные углы, а против большей стороны лежит больший угол.
Площадь треугольника можно найти по разным формулам.
Если известна хотя бы одна из сторон и высота, опущенная на это сторону, то площадь находится как половина произведения этих величин:
Формула площади треугольника по известной стороне и высоте
Если известна хотя бы одна из сторон и высота, опущенная на это сторону, то площадь находится как половина произведения этих величин:
$$S = <1\over 2>\cdot a \cdot h_a = <1\over 2>\cdot b \cdot h_b = <1\over 2>\cdot c \cdot h_c.$$
Если известны две стороны и угол между ними, то площадь треугольника можно найти, умножив эти величины и разделив на 2:
$$S = <1\over 2>\cdot a \cdot b \cdot \sin(C) = <1\over 2>\cdot a \cdot c \cdot \sin(B)=<1\over 2>\cdot b \cdot c \cdot \sin(A)$$
В данном онлайн-сервисе используется формула Герона для вычисления площади треугольника (необходимо знать длины трех сторон):
Площадь треугольника
Определение площади треугольника
Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.
Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.
Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.
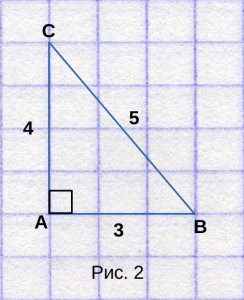
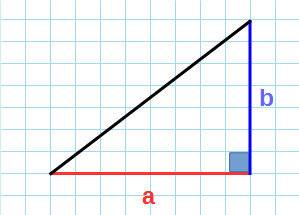
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.
Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.
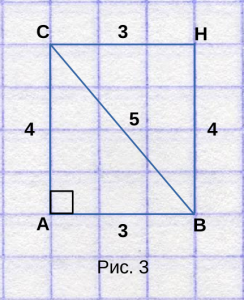
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.
Как видим, весь прямоугольник занимает 12 полных клеток.
Формула площади прямоугольника равна произведению
одной стороны на другую — \( S = ab \) ,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.
Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: \( S = \frac<1>2 ab \) .
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.
Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.
Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.
Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.
Формулы площади треугольника
Ⅰ. Через высоту и основание
a — сторона, на которую падает высота,
b — высота.
Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.
Ⅱ. Через все стороны и периметр
p — полупериметр, вычисляется по формуле: \( p = \frac
a, b, c — стороны треугольника.
Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.
Эту формулу площади также называют формулой Герона.
Ⅲ. Через две стороны и угол между ними
\[ S = \frac<1> <2>a \cdot b \cdot \sin β \]
a, b — стороны между которыми расположен угол β,
sin β — синус угла β.
Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.
Ⅳ. Через периметр и радиус вписанной окружности
\[ S = r \cdot \frac
2 \]
r — радиус вписанной окружности,
P — периметр треугольника.
Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.
Ⅴ. Через все стороны и радиус описанной окружности
abc — произведение всех сторон треугольника,
R — радиус описанной окружности.
Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.
Ⅵ. Через сторону и два прилежащих к ней угла
a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.
Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.
Найти площадь прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить площадь прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
Найти площадь прямоугольного треугольника по двум катетам
Теория
Чему равна площадь (S) прямоугольного треугольника если известны оба катета (a и b)?
Формула
Пример
К примеру найдём площадь прямоугольного треугольника у которого сторона a = 2 см, а сторона b = 4 см:
S = 2 ⋅ 4 / 2 = 8 / 2 = 4 см²
Найти площадь прямоугольного треугольника по катету и гипотенузе
Теория
Чему равна площадь (S) прямоугольного треугольника если известны его гипотенуза (c) и один из катетов (a или b)?
Формула
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 2 см, а гипотенуза c = 5 см:
Найти площадь прямоугольного треугольника по катету и прилежащему к нему острому углу
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
S = ½ ⋅ a² ⋅ tg(β) = ½ ⋅ b² ⋅ tg(α)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а прилежащий к нему ∠β = 45°:
S = ½ ⋅ 4² ⋅ tg(45) = ½ ⋅ 16 ⋅ 1 = 16 / 2 = 8 см²
Найти площадь прямоугольного треугольника по катету и противолежащему к нему острому углу
Теория
Чему равна площадь (S) прямоугольного треугольника если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого катет a = 4 см, а противолежащий к нему ∠α = 45°:
S = 4² / 2⋅ tg(45) = 16 / 2 ⋅ 1 = 8 см²
Найти площадь прямоугольного треугольника зная длину гипотенузы и один из острых углов
Теория
Чему равна площадь (S) прямоугольного треугольника если известны длина гипотенузы (c) и один из острых углов?
Формула
S = ½ ⋅ c² ⋅ sin(α) ⋅ cos(α) = ½ ⋅ c² ⋅ sin(β) ⋅ cos(β)
Пример
К примеру посчитаем чему равна площадь прямоугольного треугольника у которого гипотенуза c = 8 см, а ∠α = 45°:
S = ½ ⋅ 8² ⋅ sin(45) ⋅ cos(45) ≈ ½ ⋅ 64 ⋅ 0.7071067812 ⋅ 0.7071067812 ≈ 16 см²
Введите длину первой стороны в см (сантиметрах):
Введите длину второй стороны в см (сантиметрах):
Введите длину третьей стороны в см (сантиметрах):
Площадь треугольника равна:
Как рассчитать площадь любого треугольника по трем сторонам?
Можно воспользоваться формулой Герона:
S = √ (p (p-a) (p-b) (p-c))
p = (a+b+c) / 2
p — полупериметр треугольника;
S — площадь треугольника образованного сторонами a, b и c;
a — первая сторона треугольника;
b — первая сторона треугольника;
с — первая сторона треугольника.
Для нахождения площади любого треугольника по трем сторонам:
2. Находим площадь треугольника путем извлечения корня квадратного из произведения полупериметра умножить на полупериметр за вычетом первой стороны умножить на полупериметр за вычетом второй стороны и умножить на полупериметр за вычетом третьей стороны.
Площадь прямоугольного треугольника
площадь, 8 класс
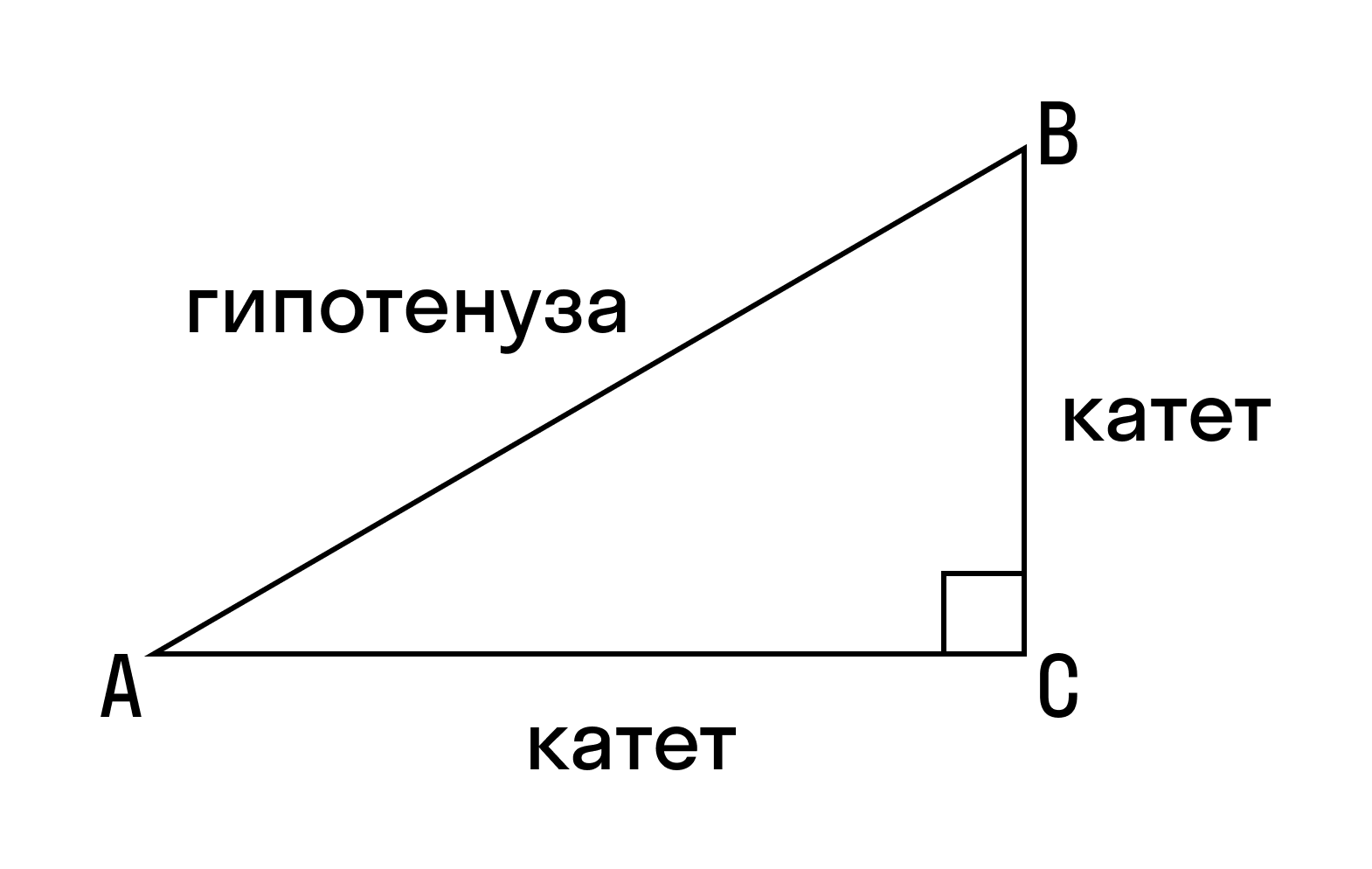
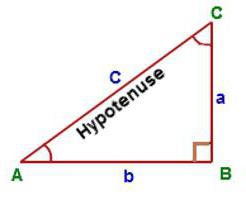
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу по формуле:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Уверены, что во всем разобрались? Закрепите знания на курсах обучения математике в онлайн-школе Skysmart!
Как найти площадь треугольника, если известно три стороны
Для того, чтобы воспользоваться формулой, необходимо знать еще одну числовую характеристику – периметр, а точнее, полупериметр треугольника. Он равен полусумме длин всех его сторон. Это требуется для того, чтобы немного упростить выражение, являющееся довольно громоздким:
Равенство всех сторон треугольника, который в этом случае называется правильным, превращает формулу в простое выражение:
Равнобедренный треугольник характеризуется одинаковой длиной двух из трех сторон АВ = ВС и, соответственно, прилежащих углов. Тогда формула Герона преобразуется в следующее выражение:
S = 1/2•AC•√((АВ + 1/2•AC)•(AC – 1/2•АВ)) = 1/2•AC•√(АВ² – 1/4•AC²), где AC – длина третьей стороны.
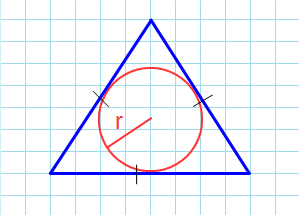
Определить площадь треугольника по трем сторонам можно не только с помощью Герона. Например, пусть в треугольник вписана окружность радиуса r. Это значит, что она касается всех его сторон, длины которых известны. Тогда площадь треугольника можно найти по формуле, тоже связанной с полупериметром и состоит в простом произведении его на радиус вписанного круга:
Калькулятор площади треугольника по трем сторонам
Удобная навигация по статье:
Калькулятор площади треугольника по трем сторонам
Как рассчитать площадь треугольника
Как известно, треугольником принято называть плоскую геометрическую фигуру, многоугольник, который ограничен минимальным количеством сторон. Также, стоит помнить, что всякий многоугольник делится на определённое количество треугольников.
Для этого необходимо соединить его вершины такими отрезками, которые не пересекали бы его стороны. Вот почему, зная как рассчитать площадь треугольника, Вы можете получить площадь большинства геометрических фигур.
Формула Герона для вычисления площади треугольника по трем сторонам
В том случае если нам известны параметры каждой стороны нашего треугольника, мы можем рассчитать площадь фигуры по формуле Герона. Для её упрощения следует применить новую величину, так называемый полупериметр, который является суммой всех сторон треугольника, которая разделена пополам.
После получения значения полупериметра, Вы можете приступать к расчёту площади по руководствуясь следующей формулой: S = sqrt(p(p-a)(p-b)(p-c)), в которой «p» — полупериметр, «a,b,c» — стороны фигуры и sqrt –квадратный корень.
Пример вычисления площади треугольника по трем сторонам
Рассмотрим на примере вычисление площади треугольника по формуле Герона.
p = ( a + b + c)/ 2 где p — половина периметра треугольника.
(Это также называется формулой Герона)
Дано:
Треугольник со сторонами a = 4, b = 5, c = 3.
Задание:
Найдите площадь треугольника
Решение:
Используйте формулу половинного периметра:
p = ( 3 + 4 + 5)/ 2 = 6
Полученные значения подставляем в формулу Герони:
S = √ 6 ( 6 — 3 ) ( 6 — 4 ) ( 6 — 5 ) =
√ 6 ⋅ 3 ⋅ 2 ⋅ 1 = √ 36 = 6
Ответ: 6
Историческая справка
Формула приписывается Герону, живущему в Александрии, который был греческим инженером и математиком в 10 — 70 годах нашей эры
Среди прочего, он разработал первый известный паровой двигатель, но его рассматривали как игрушку!
Как вычислить площадь треугольника. Видео.
Площади фигур. Площадь треугольника.
Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей
одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь
будет равна числу этих квадратов.
Треугольник образуется соединением отрезками трех точек, не лежащих на одной прямой. Точки
Воспользуйтесь нашим калькулятором для расчета площади треугольника.
Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.
Ниже приведены основные формулы, по которым можно найти площадь треугольника:
1. Площадь треугольника равна половине произведения длины стороны треугольника на длину
проведенной к этой стороне высоты.
2. Формула площади треугольника по трем сторонам. Формула Герона.
3. Формула площади треугольника по двум сторонам и углу между ними.
Площадь треугольника равна половине произведения двух его сторон, умноженного на синус угла между
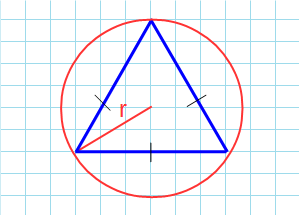
4. Формула площади треугольника по трем сторонам и радиусу описанной окружности.
5. Формула площади треугольника по трем сторонам и радиусу вписанной окружности. Площадь
треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.
Площадь треугольника
У геометрической фигуры — треугольника — 3 стороны и 3 вершины. Треугольник получается, если три точки, которые не лежат на одной прямой, соединить отрезками.
Для названия треугольника используются большие латинские буквы, при этом соблюдается последовательность вершин, но начинать название можно с любой вершины.
Иногда используют знак Δ. 
В зависимости от величин углов треугольника выделяют:
Площадь треугольника
Прямоугольный треугольник легко представить как половину прямоугольника. 
Если площадь прямоугольника равна произведению длин сторон, то для определения площади треугольника необходимо это произведение разделить на 2.
Допустим, RP = a, TP = b;
SRPT=(ab)/2.
Если треугольник не имеет прямого угла, можно построить два прямоугольника, как показано на рисунке. 
Допустим, MA=BD=NC = h, AC = a.
SABC=SABD+SCBD=h⋅AD/2+h⋅DC/2=h⋅AC/2=h⋅a/2.
Как видно, достаточно в треугольнике от одной вершины провести отрезок под прямым углом к противолежащей стороне и использовать длины отрезка для определения площади треугольника.
Отрезок называют высотой треугольника. 
Свойства треугольника
Пример. Можно ли построить треугольник из отрезков с длинами: 3 см, 7 см, 4 см?
Пример. Можно ли построить треугольник из отрезков с длинами: 16 см, 32 см, 18 см?
Пример. Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 4 см, другая сторона, которая образует прямой угол, в 2 раза меньше. Определи площадь треугольника.
Одна сторона, которая образует прямой угол прямоугольного треугольника ABD, равна 12 см, другая сторона, которая образует прямой угол, в 3 раза меньше.
Определи площадь треугольника.
Поэтому площадь можно рассчитать следующим образом:
Известно, что периметр равностороннего треугольника — 21 см. Определи периметр данного четырёхугольника, который состоит из равносторонних треугольников.
Значит, одна сторона треугольника равна 7 см.
Периметр данного четырёхугольника состоит из 4 таких сторон, значит, равен 28 см.
Дан равносторонний треугольник. 2 раза сделано следующее:
1. на всех сторонах отмечены и соединены серединные точки.
2. На сторонах внутреннего треугольника опять отмечены и соединены серединные точки.
Треугольник, который образовался на этот раз, закрашен розовым цветом. 
1. Сколько маленьких треугольников необходимо для перекрытия данного треугольника?
2. Чему равна площадь большого треугольника, если площадь розового треугольника равна 4 м²?
3. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 4 раза?
Если повторить эти действия (построить такую конструкцию) 4 раза, то общее число маленьких треугольников будет равняться 256.
4. Сколько маленьких треугольников получится, если повторить эти действия (построить такую конструкцию) 3 раза?
Если повторить эти действия (построить такую конструкцию) 3 раза, то общее число маленьких треугольников будет равняться 64.
Определи площадь данных фигур, если площадь одной клетки равна 6 см2.
1) 
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Сколько клеток образует площадь фигуры? Чему равна площадь фигуры?
Подумай, как построены данные фигуры, и определи, сколько клеток будет у следующих двух фигур, если их построить по той же закономерности.
Как находить площадь треугольника?
Стандартная формула площадь треугольника равна половине произведения его основания на высоту не полностью описывает возможности нахождения площади треугольника.
Если же наш треугольник не имеет прямого угла, то проводим перпендикуляр из любого угла, к противоположной стороне. Делим длину этого перпендикуляра на 2 и умножаем на длину той стороны к которой примкнул перпендикуляр проведенной нами из любого угла. Получаем площадь треугольника.
Стандартная формула для всех видов треугольника: площадь равна 1/2 произведения основания и высоты.
Площадь треугольника можно найти по формуле:
Иногда познания из школьной программы бывают необходимы и во взрослой жизни (как правило это такая потребность возникает во время ремонта).
Площадь треугольника можно найти различными способами, в зависимости от вида треугольника, площадь которого мы ищем. Есть обычные треугольники (плоская фигура образованная тремя пересекающимися прямыми), прямоугольные (один из его углов равен 90 градусам), равнобедренные (два из его рёбер равны) и равносторонние (все его рёбра равны).
В обычном треугольнике его площадь исчисляется как половина произведения длины основания треугольника на величину высоты, опущенной на это основание с противоположной вершины:
где S-площадь треугольника,
b-длина одной из сторон треугольника,
h-высота, опущенная к этой стороне.
Формулу легко запомнить на примере площади прямоугольного треугольника (частному случаю нахождения площади треугольника). Площадь прямоугольного треугольника – это половина площади воображаемого прямоугольника:
Существует ещё один способ расчёта площади треугольника (по формуле Герона), который применяется, если известна длина трех сторон треугольника.
Площадь равна квадратному корню из произведений полупериметра и ризниц между полупериметром и сторонами треугольника:
Площадь треугольника по двум сторонам и углу между ними: онлайн-калькулятор
Чтобы получить площадь треугольника:
После этого доступно подробное решение задачи.
Нахождение площади треугольника по двум сторонам и углу между ними
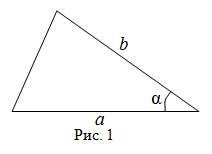
Онлайн-калькулятор позволяет найти площадь треугольника, зная значения двух его сторон и угла между ними. Для получения ответа нужно лишь задать значения сторон и указать угол, а калькулятор автоматически произведет расчет с применением формулы:
S = 1 2 a · b · sin α
Рассмотрим пример, демонстрирующий работу калькулятора. Пусть две стороны треугольника соответственно равны 5 см и 3 см, а угол между ними – 56 градусов.
Введем эти значения в соответствующие поля калькулятора: 
Мы специально выбрали произвольные значения, чтобы показать: калькулятор работает не только с табличными значениями синусов углов.
Обратите внимание: значения сторон треугольника можно задавать в миллиметрах, сантиметрах и метрах. Так же и площадь: ответ можно получить в наиболее предпочтительных единицах измерения.
После того, как все необходимые поля заполнены, нажмем «Найти»: 
Калькулятор выдаст ход решения и ответ: 
Отметим, что в калькуляторе существуют ограничения. Например, в поле для значений сторон нельзя вводить отрицательные числа. Если вы введете некорректное значение, калькулятор предупредит вас об этом.
Как найти площадь треугольника
Доброго времени суток!
Какие существуют методы, как найти площадь треугольника?
Благодарю всех, кто откликнется!
Существует четыре метода как найти площадь треугольника: если известны его основание и высота, если известны его стороны, если известна одна из сторон равностороннего треугольника и используя тригонометрические функции.
Наиболее распространенным способом вычисления площади треугольника является деление пополам результата умножения его основания и высоты. Но метод вычисления площади необходимо выбирать в зависимости от того, какие его параметры известны.
Например, если известны высота и основание треугольника, то записывают формулу площади треугольника:
и подставляют известные значения.
Если известны только две стороны треугольника, но треугольник является прямоугольным (то есть известны два его катета), то одна из сторон является и его высотой, а значит можно также воспользоваться данной формулой. В другом случае (когда известны гипотенуза и катет) можно воспользоваться теоремой Пифагора.
Если известны все стороны треугольника, то нужно найти его полупериметр и воспользоваться формулой Герона.
Для нахождения площади равностороннего треугольника достаточно знать только одну сторону (так как они все равны) и подставить ее значение в соответствующую формулу.
Если известны (или можно найти) длины двух смежных сторон, а также угол между ними, то площадь треугольника можно вычислить с помощью тригонометрических функций.
Как найти площадь треугольника зная все стороны
§2. Площадь треугольника. Метод площадей
В школьном курсе геометрии доказано несколько формул площади треугольника. Напомним их.
При вычислении площади из этих формул следует выбрать ту, которая в условиях конкретной задачи приводит к более простому решению.
Для примера, рассмотрим два треугольника:
`DeltaABC:` `AB=13`, `BC=14`, `AC=15`;
`DeltaKML:` `KL=sqrt(13)`, `LM=sqrt(14)`, `KM=sqrt(15)`;
Надо найти площадь и радиус описанной окружности.
Для треугольника `ABC` удобен ход решения такой:
`p=1/2(AB+BC+AC)=21`, по формуле Герона
`S_(ABC)=sqrt(21*6*7*8)= ul(84)` и по формуле (5)
тогда `sinM=sqrt(1-64/(210))=(sqrt(146))/(sqrt(14)*sqrt(15))` и по формуле (2):
тогда `R=(KL)/(2sinM)=ul((sqrt(13)*sqrt(14)*sqrt(15))/(2*sqrt(146)))=(sqrt(13)*sqrt7*sqrt(15))/(2*sqrt(73))` (точно также по формуле 5).
Сравнение площадей треугольников обычно опирается на одно из следующих утверждений:
$$ 2.<1>^<○>$$. Площади треугольников с одинаковой высотой относятся как длины соответствующих оснований. В частности, если точка `D` лежит на основании `AC` (рис. 6а), то
$$ 2.<2>^<○>$$. Площади треугольников с общим углом относятся как произведения сторон, заключающих этот угол (см. рис. 6б):
$$ 2.<3>^<○>$$. Площади подобных треугольников относятся как квадраты их
сходственных сторон, т. е. если `Delta ABC
DeltaA_1B_1C_1`, то `(S_(A_1B_1C_1))/(S_(ABC))=((A_1B_1)/(AB))^2`.
Все эти утверждения легко доказываются с использованием соответственно формул площади (1) и (2).
Обратим внимание на важное свойство медиан треугольника.
Три медианы треугольника разбивают его на `6` треугольников с общей вершиной и равными площадями.
Докажем, например, для треугольника `BOM`, что `S_(BOM)=1/6S_(ABC)`.
Дан треугольник `ABC`. Точка `D` лежит на стороне `AB`, `AD:DB=1:2`, точка `K` лежит на стороне `BC`, `BK:KC=3:2` (рис. 8а). Отрезки `AK` и `CD` пересекаются в точке `O`. Найти отношение площади четырёхугольника `DBKO` к площади треугольника `ABC`.
2. Через точку `D` проведём прямую `DL«|\|«AK`. По теореме о пересечении сторон угла параллельными прямыми (`/_ABC`, `DL«|\|«AK`) имеем `(BL)/(LK)=(BD)/(AD)`, откуда `LK=y`.
По той же теореме (`/_DCB`, `OK«|\|«DL`) получим `(DO)/(DC)=(LK)/(LC)`, `DO=1/3DC`.
3. Теперь находим `S_(ADO):S_(ADC)=DO:DC`, `a=1/3(1/3S)=1/9S`.
(Можно по теореме Менелая для треугольника `BCD` и секущей `CD:`
`(BK)/(KC)*(CO)/(OD)*(DA)/(AB)=1 iff 3/2*(CO)/(OD)*1/3=1 iff CO=2OD=>OD=1/3DC`).
Находим площадь: `sigma=3/5S-a=(3/5-1/9)S=22/45S`.
Найти площадь треугольника, две стороны которого равны `3` и `7`, а медиана к третьей стороне равна `4` (рис. 9).
Пусть `AB=3`, `BC=7`, `AM=MC` и `BM=4`. Достроим треугольник `ABC` до параллелограмма, для этого на прямой `BM` отложим отрезок `MD=BM` и соединим точки: `A` с `D` и `C` с `D`. Противоположные стороны параллелограмма равны: `(DC=AB)` и равны площади треугольников `ABC` и `DBC` (общее основание `BC` и равные высоты из вершин `A` и `D`).
В треугольнике `DBC` известны все три стороны: `BC=7`, `DC=3`, `BD=2BM=8`.
Находим его площадь по формуле Герона: `p=9`, `S_(BCD)=6sqrt3`.
Значит и `S_(ABC)=6sqrt3`.
В решении этой задачи дополнительным построением получен треугольник, площадь которого равна площади заданного и легко вычисляется по данным задачи. Приведём ещё одну задачу, где сначала вычисляется площадь дополнительно построенной фигуры, а затем легко находится искомая площадь.
Найти площадь треугольника, если его медианы равны `3`, `4` и `5`.
По свойству медиан `AO=2/3m_a`, `CO=2/3m_c` и `ON=1/3m_b`. В треугольнике `AOC` известны две стороны `AO` и `CO` и медиана третьей стороны `ON`. Площадь этого треугольника найдём как в предыдущей задаче.
Достроим треугольник `AOC` до параллелограмма `AOCD`, `S_(AOC)=S_(DOC)`, в треугольнике `DOC` известны три стороны:
`DO=2ON=2/3m_b`, `OC=2/3m_c`, `DC=AO=2/3m_a`.
Площадь треугольника `DOC` вычисляем по формуле Герона `S_1=S_(AOC)=S_(DOC)=8/3`. Сравним теперь площадь треугольника `ABC` (обозначим её `S`) с площадью треугольника `AOC`. Из теоремы 2 о медианах и площадях следует `S_(AOC)=S_(AON)+S_(NOC)=2*1/6S=1/3S`.
В следующей задаче докажем лемму об отношении площади треугольника к площади другого треугольника, построенного из медиан первого.
Найти отношение площади `S` треугольника к площади `S_0` треугольника, составленного из медиан первого.
Рассмотрим рис. 10. В построенном треугольнике `OCD` стороны таковы: `OC=2/3m_c`, `OD=2/3m_b`, `CD=2/3m_a`. Очевидно, что треугольник со сторонами `m_a`, `m_b`, `m_c` подобен (по третьему признаку) треугольнику со сторонами `2/3m_a`, `2/3m_b`, `2/3m_c`.
| `S_(m_am_bm_c)=3/4S_(abc)`. |
Около окружности радиуса `sqrt3` описан треугольник. Найти его площадь, если одна из его сторон точкой касания делится на отрезки `9` и `5`.
Пусть `AP=9`, `PC=5` (рис. 11) и пусть `BM=x`. По свойству касательных `AM=AP`, `CN=CP` и `BN=BM`, поэтому стороны треугольника таковы: `AC=14`, `AB=9+x`, `BC=5+x`, тогда `p=14+x`. (Заметим, что `p=AC+BM`!). По формулам площади (3) и (4) имеем: `S=pr=(14+x)sqrt3` и `S=sqrt((14+x)x*5*9)`. Приравниваем правые части, возводим в квадрат, приводим подобные члены, получаем `x=1`. Вычисляем площадь треугольника:
Приём, применённый в решении этой задачи, когда площадь фигуры выражается двумя различными способами, часто используется в задачах на доказательство.
Проведём два примера, в каждом выведем полезную формулу.
В треугольнике `ABC` угол `C` равен `varphi`, `AC=b`, `BC=a` (рис. 12). Доказать, что биссектриса `CD` равна `(2ab)/(a+b) cos varphi/2`.
Обозначим `CD=x`. Очевидно, что `S_(ABC)=S_(ACD)+S_(DCB)`. По формуле (2) `S_(ABC)=1/2 ab sin varphi`, `S_(ACD)=1/2 bx sin varphi/2`, `S_(BDC)=1/2 ax sin varphi/2`. Таким образом, имеем: `1/2 ab sin varphi=1/2(a+b)x sin varphi/2`. Используем формулу синуса двойного угла `sin varphi=2sin varphi/2 cos varphi/2`, получим:
| `x=(2ab)/(a+b)cos varphi/2`. |
называется окружность, касающаяся одной из сторон треугольника и продолжений двух других сторон. Таких окружностей, очевидно, три (рис. 13). Их радиусы обычно обозначаются `r_a`, `r_b`, `r_c` в зависимости от того, какой стороны окружность касается.
Вневписанная окружность касается стороны `a=BC` треугольника `ABC` (рис. 14). Доказать, что `S_(ABC)=r_a(p-a)`, где `2p=a+b+c`.
Считаем площадь `S_0` четырёхугольника `ABI_aC`:
`S_0=S_(ABC)+S_(BCI_a)` и `S_0=S_(ABI_a)+S_(ACI_a)`, откуда
Праздник — вот он!
Попасть на праздник? Легко! Сделай праздник сам!
Как найти площадь треугольника, если известны все стороны
Находим площадь треугольника, если известны все стороны — формулы для вычислений.
Геометрия – раздел математики, изучающий пространственные формы, а также их измерение и расположение относительно друг друга. Геометрия как наука получила своё название и систематизацию знаний в Греции (около двух с половиной тысяч лет назад).
Вычисление площадей фигур – одна из самых распространённых задач, которые решает геометрия (чаще всего вопрос определения площади становится актуальным в процессе строительства). В качестве примера попробуем найти площадь треугольника, если известны все стороны.
Для определения площади треугольника могут использоваться различные формулы, исходя из имеющихся данных. В случае, когда известны длины всех сторон треугольника, его площадь может быть вычислена по формуле Герона.
Формула Герона
Для вычисления площади треугольника по длинам его сторон используется одна из самых древнейших в геометрии формул – формула Герона, названная в честь выдающегося древнегреческого математика Герона Александрийского (I век н.э.).
Площадь треугольника по этой формуле вычисляется как корень квадратный из произведения полупериметра треугольника и разностей полупериметра с каждой из сторон треугольника:
Дан треугольник со сторонами а = 6см, b = 8см, с = 10см.
Первоначально необходимо вычислить полупериметр треугольника:
р = (6 + 8 +10) / 2 = 12см
Далее, используя площадь Герона, можно найти площадь треугольника:
S = √12(12-6)(12-8)(12-10) = √12*6*4*2 = √576 = 24 см.
Другие формулы
В зависимости от имеющихся данных, для вычисления площади треугольника могут использоваться другие формулы. Площадь треугольника равна:
Как вычислить площадь треугольника
Треугольник — хорошо знакомая всем фигура. И это, несмотря на богатое разнообразие его форм. Прямоугольный, равносторонний, остроугольный, равнобедренный, тупоугольный. Каждый из них чем-то отличается. Но для любого требуется узнавать площадь треугольника.
Общие для всех треугольников формулы, в которых используются длины сторон или высот
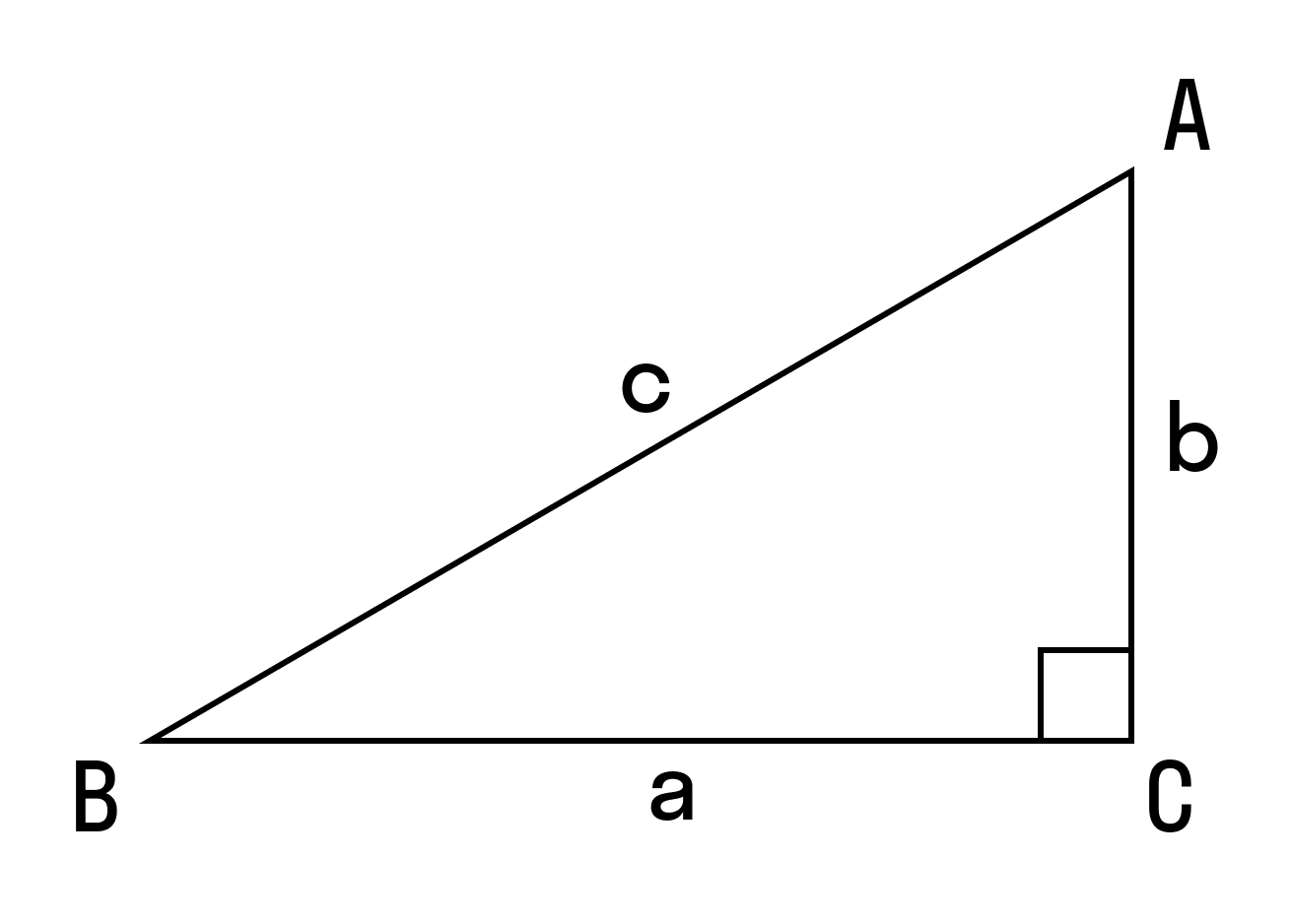
Обозначения, принятые в них: стороны — а, в, с; высоты на соответствующие стороны на, нв, нс.
1. Площадь треугольника вычисляется, как произведение ½, стороны и высоты, опущенной на нее. S = ½ * а * на. Аналогично следует записать формулы для двух остальных сторон.
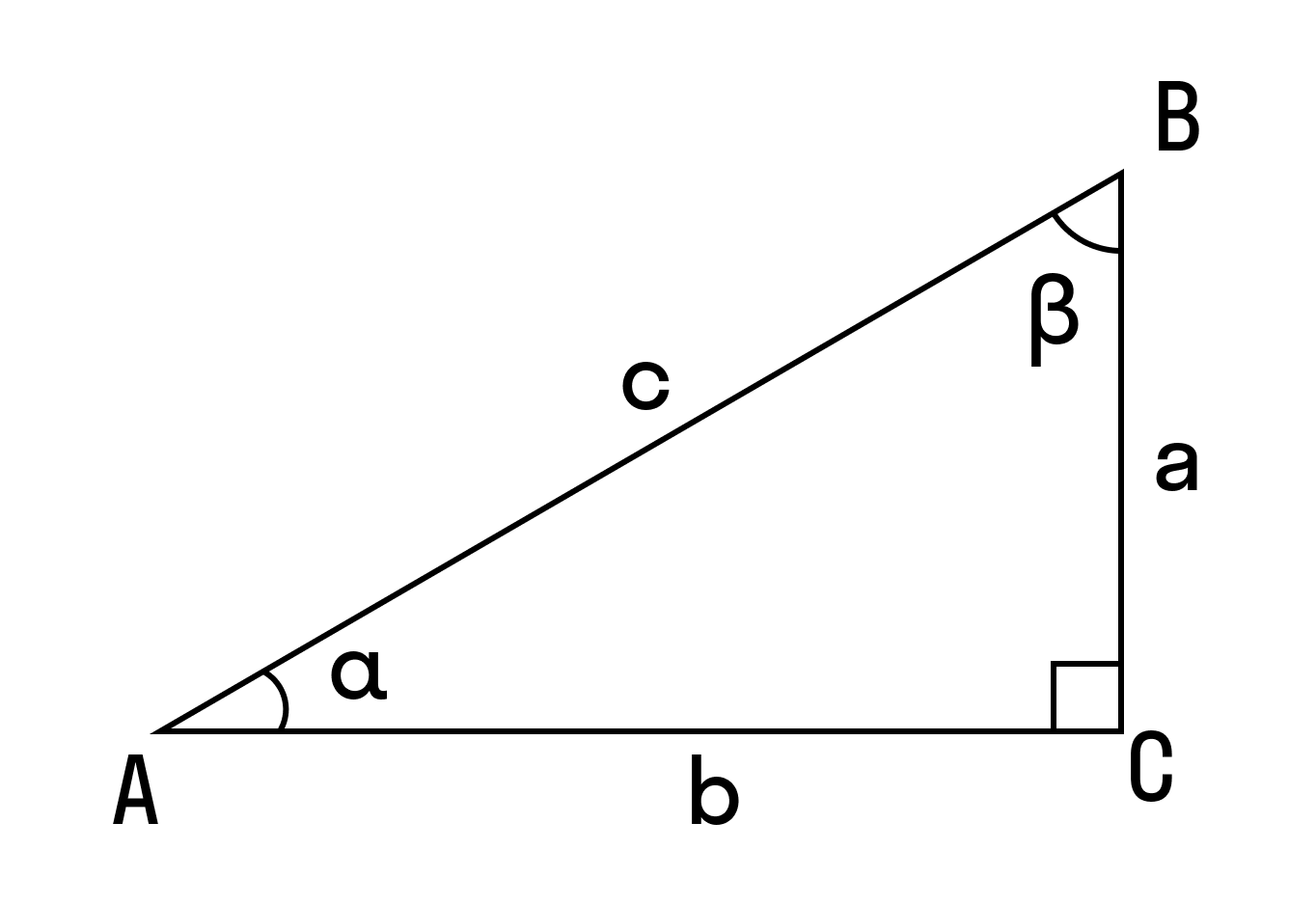
Общие формулы, в которых фигурируют углы треугольника
Обозначения, которые требуются для прочтения формул: α, β, γ — углы. Они лежат напротив сторон а, в, с, соответственно.
1. По ней половина произведения двух сторон и синуса угла между ними равна площади треугольника. То есть: S = ½ а * в * sin γ. Подобным образом следует записать формулы для двух других случаев.
2. Площадь треугольника можно вычислить по одной стороне и трем известным углам. S = (а 2 * sin β * sin γ) / (2 sin α).
3. Существует еще формула с одной известной стороной и двумя прилежащими к ней углами. Она выглядит таким образом: S = с 2 / (2 (ctg α + ctg β)).
Две последние формулы являются не самыми простыми. Запомнить их довольно сложно.
Общие формулы для ситуации, когда известны радиусы вписанных или описанных окружностей
Дополнительные обозначения: r, R — радиусы. Первый используется для радиуса вписанной окружности. Второй — для описанной.
1. Первая формула, по которой вычисляется площадь треугольника, связана с полупериметром. S = р * r. По-другому ее можно записать так: S = ½ r * (а + в + с).
2. Во втором случае потребуется перемножить все стороны треугольника и разделить их на учетверенный радиус описанной окружности. В буквенном выражении это выглядит так: S = (а * в * с) / (4R).
3. Третья ситуация позволяет обойтись без знания сторон, но потребуются значения всех трех углов. S = 2 R 2 * sin α * sin β * sin γ.
Частный случай: прямоугольный треугольник
Это самая простая ситуация, поскольку требуется знание только длины обоих катетов. Они обозначаются латинскими буквами а и в. Площадь прямоугольного треугольника равна половине площади достроенного к нему прямоугольника.
Математически это выглядит так: S = ½ а * в. Она запоминается проще всего. Потому что выглядит, как формула для площади прямоугольника, только появляется еще дробь, обозначающая половину.
Частный случай: равнобедренный треугольник
Поскольку у него две стороны равные, то некоторые формулы для его площади выглядят несколько упрощенными. Например, формула Герона, по которой вычисляется площадь равнобедренного треугольника, принимает следующий вид:
Если ее преобразовать, то она станет короче. В таком случае формула Герона для равнобедренного треугольника записывается так:
Несколько проще, чем для произвольного треугольника, выглядит формула площади, если известны боковые стороны и угол между ними. S = ½ a 2 * sin β.
Частный случай: равносторонний треугольник
Обычно в задачах про него известна сторона или ее можно как-либо узнать. Тогда формула, по которой находится площадь такого треугольника, выглядит следующим образом:
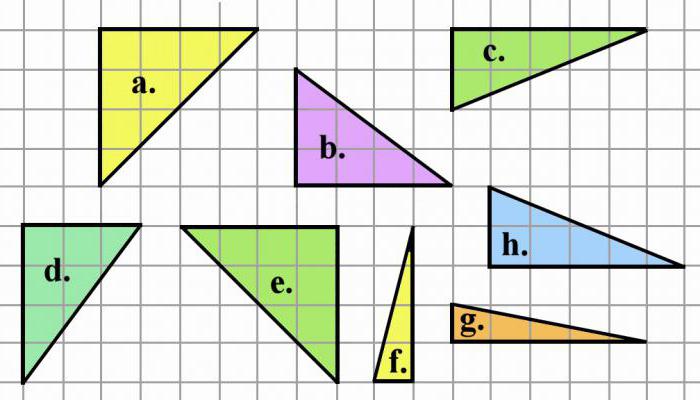
Задачи на нахождение площади, если треугольник изображен на клетчатой бумаге
Самой простой является ситуация, когда прямоугольный треугольник начерчен так, что его катеты совпадают с линиями бумаги. Тогда требуется просто посчитать число клеточек, укладывающихся в катеты. Потом перемножить их и разделить на два.
Когда треугольник остроугольный или тупоугольный, его нужно дорисовать до прямоугольника. Тогда в получившейся фигуре будет 3 треугольника. Один — тот что дан в задаче. А два других — вспомогательные и прямоугольные. Определить площади двух последних нужно по описанному выше способу. Потом сосчитать площадь прямоугольника и вычесть из него те, что вычислены для вспомогательных. Площадь треугольника определена.
Гораздо сложнее оказывается ситуация, в которой ни одна из сторон треугольника не совпадает с линиями бумаги. Тогда его нужно вписать в прямоугольник так, чтобы вершины исходной фигуры лежали на его сторонах. В этом случае вспомогательных прямоугольных треугольников будет три.
Пример задачи на формулу Герона
Условие. У некоторого треугольника известны стороны. Они равны 3, 5 и 6 см. Необходимо узнать его площадь.
Решение. Первым делом полагается сосчитать полупериметр треугольника. Составить сумму всех трех, данных в задаче, чисел и разделить ее на два. Простые вычисления приводят к числу 7. Это значение полупериметра.
Теперь можно вычислять площадь треугольника по указанной выше формуле. Под квадратным корнем оказывается произведение четырех чисел: 7, 4, 2 и 1. То есть площадь равна √(4 * 14) = 2 √(14).
Если не требуется большая точность, то можно извлечь квадратный корень из 14. Он равен 3,74. Тогда площадь будет равна 7,48.
Пример задачи с прямоугольным треугольником
Осталось вычислить второй катет: прибавить к полученному числу 31. Получается 40. Это искомые в задаче величины.
Ответ. Катеты треугольника равны 9 и 40 см.
Задача на нахождение стороны через площадь, сторону и угол треугольника
Решение. Исходя из принятых обозначений, искомая сторона «а», известная «в», заданный угол “γ”. Тогда формула площади можно переписать так:
60 = ½ а * 15 * sin 30º. Здесь синус 30 градусов равен 0,5.
После преобразований «а» оказывается равным 60 / (0,5 * 0,5 * 15). То есть 16.
Ответ. Искомая сторона равна 16 см.
Задача о квадрате, вписанном в прямоугольный треугольник
Условие. Вершина квадрата со стороной 24 см совпадает с прямым углом треугольника. Две другие лежат на катетах. Третья принадлежит гипотенузе. Длина одного из катетов равна 42 см. Чему равна площадь прямоугольного треугольника?
Решение. Рассмотрим два прямоугольных треугольника. Первый — заданный в задаче. Второй — опирается на известный катет исходного треугольника. Они подобны, так как имеют общий угол и образованы параллельными прямыми.
Тогда отношения их катетов равны. Катеты меньшего треугольника равны 24 см (сторона квадрата) и 18 см (заданный катет 42 см вычесть сторону квадрата 24 см). Соответствующие катеты большого треугольника — 42 см и х см. Именно этот «х» нужен для того, чтобы вычислить площадь треугольника.
18/42 = 24/х, то есть х = 24 * 42 / 18 = 56 (см).
Площадь треугольника по сторонам
Найти площадь треугольника по трем сторонам можно с помощью формулы Герона.
Формула Герона:
где p — полупериметр:
a, b, c — длины сторон треугольника.
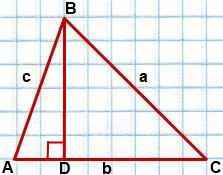
Проведем в треугольнике ABC высоту BD при условии, что углы A и C- острые
(если треугольник ABC тупоугольный либо прямоугольный, то в качестве угла B выбираем тупой либо прямой угол).
По теореме Пифагора, из прямоугольного треугольника ABD
из прямоугольного треугольника BCD —
Приравниваем правые части равенств:
BC² перенесем в правую часть, AD² — в левую:
Правую часть разложим по формуле разности квадратов:
Так как AD+CD=AC, то
Сложим эти два равенства почленно и приведем правую часть к общему знаменателю:
Площадь треугольника
Площадь треугольника. Во многих задачах по геометрии связанных с вычислением площадей используются формулы площади треугольника. Их существует несколько, здесь мы рассмотрим основные. Перечислить эти формулы было бы слишком просто и пользы ни какой. Мы разберём происхождение основных формул, тех что используются наиболее чаще.
Перед тем как ознакомиться с выводом формул обязательно посмотрите статью о площади параллелограмма. После изучения материала вы без труда сможете восстановить формулы в памяти (если вдруг они «вылетят» в нужный вам момент).
Диагональ параллелограмма разбивает его на два равных по площади треугольника:
Следовательно площадь треугольника будет равна половине площади параллелограмма:
Площадь треугольника формула
*То есть если нам будет известна любая сторона треугольника и высота опущенная на эту сторону, то мы всегда сможем вычислить площадь этого треугольника.
Как уже было изложено в статье о площади параллелограмма формула имеет вид:
Площадь треугольника равна половине его площади, значит :
*То есть если будут известны любые две стороны в треугольнике и угол между ними, мы всегда сможем вычислить площадь такого треугольника.
Формула Герона (третья)
Данную формулу выводить сложно и вам это ни к чему. Посмотрите какая она красивая, можно сказать, что сама запоминается.
*Если даны три стороны треугольника, то по данной формуле мы всегда можем вычислить его площадь.
где r – радиус вписанной окружности
*Если известны три стороны треугольника и радиус вписанной в него окружности, то мы всегда можем найти площадь этого треугольника.
где R – радиус описанной окружности.
*Если известны три стороны треугольника и радиус описанной около него окружности, то мы всегда можем найти площадь такого треугольника.
Возникает вопрос: если известны три стороны треугольника, то не проще ли его площадь найти по формуле Герона!
Да, бывает проще, но не всегда, иногда возникает сложность. Это связано с извлечением корня. Кроме того, данные формулы очень удобно применять в задачах, где дана площадь треугольника, его стороны и требуется найти радиус вписанной или описанной окружности. Такие задания имеются в составе ЕГЭ.
Давайте отдельно рассмотрим формулу:
Она является частным случаем формулы площади многоугольника, в который вписана окружность:
Рассмотрим её на примере пятиугольника:
Соединим центр окружности с вершинами данного пятиугольника и опустим из центра перпендикуляры к его сторонам. Получим пять треугольников, при чём опущенные перпендикуляры являются радиусами вписанной окружности:
Площадь пятиугольника равна:
Теперь понятно, что если речь идёт о треугольнике, то данная формула приобретает вид:
Пусть сторона треугольника равна a, из противоположной вершины к этой стороне проведён произвольный отрезок образующий с ней угол (фи):
Данная формула используется очень редко на практике, возможно вы её видите впервые, ну так просто написал, чтобы знали. Её ещё можно вывести преобразовав формулу площади четырёхугольника:
Также она является следствием из формулы:
Что добавить? Есть ещё формулы треугольника связанные с координатами вершин, векторами на которых он построен. Об этом будет статья в будущем, не пропустите!
Площадь прямоугольного треугольника. Тут всё просто — она равна половине площади прямоугольника, то есть одной второй произведения катетов.
Площадь треугольника
Вы будете перенаправлены на Автор24
На данной странице вы сможете не только ознакомиться со всеми формулами нахождения площади треугольника, но и воспользоваться достаточно удобными калькуляторами и рассмотреть примеры решения задач. Это очень рационально и полезно для того, чтобы вспомнить уже давно забывшиеся формулы и сверить свой ответ с ответом необходимого калькулятора.
Площадь треугольника по основанию и высоте
Формула площади треугольника по основанию и высоте выглядит, как
Рассмотрим наглядно на примере, в котором используется данная формула, как просто и быстро самостоятельно или с помощью калькулятора вычислить площадь в одно действие по данным элементам.
Найти: площадь треугольника.
Решение:
$S = \frac12 \cdot 6 \cdot 10$
Ответ:
Площадь треугольника по двум сторонам и углу между ними
Формула площади треугольника по двум сторонам и углу между ними выглядит следующим образом:
$S = \frac12 \cdot a \cdot b \cdot \sin (α)$, где
По радиусу описанной окружности и трем сторонам
Площадь треугольника по радиусу описанной окружности и трем сторонам вычисляется по следующей формуле:
Решение:
$S = (5 \cdot 6 \cdot 10) / (4 \cdot 6) = 12,5$ см$^2$.
Ответ:
По радиусу вписанной окружности и трем сторонам
Формула площади треугольника по радиусу вписанной окружности и трем сторонам выглядит, как:
$S = r \cdot \frac<2>$, где
Площадь равнобедренного треугольника по боковым сторонам и углу между ними
Площадь равнобедренного треугольника по боковым сторонам и углу между ними вычисляется следующим образом:
$S = \frac <1> <2>\cdot b^2 \cdot \sin (y)$
Площадь равностороннего треугольника по стороне
Площадь равностороннего треугольника по стороне вычисляется по следующей формуле:
Площадь равностороннего треугольника по высоте
Площадь равностороннего треугольника по высоте вычисляется следующим образом:
Площадь равностороннего треугольника по радиусу вписанной окружности
Площадь равностороннего треугольника по радиусу вписанной окружности вычисляется по следующей формуле:
$S = 3 \cdot \sqrt3 \cdot R^2$, где
Площадь равностороннего треугольника по радиусу описанной окружности
Формула площади равностороннего треугольника по радиусу описанной окружности выглядит следующим образом:
Площадь прямоугольного треугольника по двум катетам
Формула площади прямоугольного треугольника по двум катетам выглядит как:
$S = \frac12 \cdot a \cdot b$, где
Решение:
$S = (5 \cdot 6) / 2 = 15$ см$^2$.
Ответ:
Площадь прямоугольного треугольника по отрезкам
Формула вычисления площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность выглядит следующим образом:
$S = d \cdot e$, где
Для того, чтобы сверить свой ответ и решение с данным калькулятором и найти какие-либо свои ошибки или недочеты, будет полезно рассмотреть пример решения данной задачи на нахождение площади прямоугольного треугольника по отрезкам, на которые делит гипотенузу вписанная окружность.
Как найти площадь треугольника всеми способами
Как найти площадь треугольника
О чем эта статья:
Основные понятия
Треугольник — это геометрическая фигура, которая получилось из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере плоскости, ограниченной замкнутой геометрической фигурой.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Общая формула
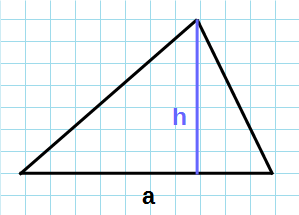
1. Площадь треугольника через две стороны и угол между ними.
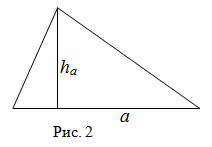
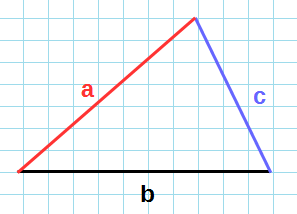
2. Площадь треугольника через основание и высоту.
S = 0,5 * a * h, где a — основание, h — высота.
3. Площадь треугольника через описанную окружность и стороны.
S = (a * b * c) : (4 * R), где a, b, c — стороны, R — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны.
S = r * (a + b + c) : 2, где a, b, c — стороны, r — радиус вписанной окружности.
Если учитывать, что (a + b + c) : 2 — это способ поиска полупериметра. Тогда формулу можно записать следующим образом:
S = r * p, где p — полупериметр.
5. Площадь треугольника по стороне и двум прилежащим углам.
S = a 2 : 2 * (sin(α)⋅sin(β)) : sin(180 — (α + β)), где a — сторона, α и β — прилежащие углы, γ — противолежащий угол.
6. Формула Герона для вычисления площади треугольника.
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
S = √ p * (p − a) * (p − b) * (p − c), где a, b, c — стороны, p — полупериметр, который можно найти по формуле: p = (a + b + c) : 2
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам.
S = 0,5 * a * b, где a, b — стороны.
Площадь треугольника по гипотенузе и острому углу.
S = 0,25 * c 2 * sin(2α), где c — гипотенуза, α — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу.
S = 0,5 * a 2 * tg(α), где a — катет, α — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и по радиусу вписанной окружности.
S = r * (r + c), где c — гипотенуза, r — радиус вписанной окружности.
Площадь треугольника вписанного в окружность.
Площадь прямого треугольника по формуле Герона.
S = (p − a) * (p − b), где a, b — катеты, p — полупериметр, который рассчитывается по формуле p = (a + b + c) : 2.
Для равнобедренного треугольника
Поиск площади через основание и сторону.
Вычисление площади через основание и угол.
S = 0,5 * a * b * sin(α), где a — боковая сторона, b — основание, α — угол между основанием и стороной.
Вычисление площади через основание и высоту.
S = 0,5 * b * h, где b — основание, h — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
S = 0,5 * a 2 * sin(α), где a — боковая сторона, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами.
S = b 2 : (4 * tgα/2), где b — основание, α — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности.
S = (3 * √ 3 * R 2 ) : 4, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности.
Площадь равностороннего треугольника через сторону.
S = (√ 3 * a 2 ) : 4, где a — сторона.
Площадь равностороннего треугольника через высоту.
S = h 2 : √ 3, где h — высота.
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь прямоугольного треугольника
О чем эта статья:
площадь, 8 класс
Основные определения
Прямоугольный треугольник — это треугольник, в котором один угол прямой, то есть равен 90˚.
Гипотенуза — это сторона, противолежащая прямому углу.
Катеты — это стороны, прилежащие к прямому углу.
Чтобы найти площадь прямоугольного треугольника, можно применить любую формулу нахождения площади треугольника — их несколько.
Формула для нахождения площади прямоугольного треугольника через катеты
Чтобы найти площадь, нужно вывести формулу:
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию.
Так как в прямоугольном треугольнике катеты перпендикулярны, то один катет — это высота, проведенная ко второму катету.
Отсюда следует, что площадь прямоугольного треугольника равна половине произведения его катетов.
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через катеты.
S = 1/2 (a × b), где a и b — катеты
Формула для нахождения площади прямоугольного треугольника через гипотенузу
Площадь прямоугольного треугольника равна половине произведения гипотенузы на высоту, проведенную к гипотенузе.
где с — гипотенуза,
Используйте эту формулу, чтобы найти площадь прямоугольного треугольника через гипотенузу.
Формула для нахождения площади прямоугольного треугольника через гипотенузу и острый угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через катет и угол
α, β — острые углы
Формулы нахождения площади прямоугольного треугольника через радиус вписанной окружности и гипотенузу
Радиус вписанной окружности выражается через катеты и гипотенузу вот так:
S прямоугольного треугольника = r (r + c) = c1 × c2
r — радиус вписанной окружности
C1 и С2 — отрезки, полученные делением гипотенузы на две части точкой касания с окружностью
Разные способы © 2022
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.