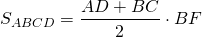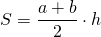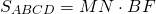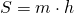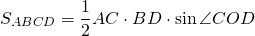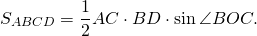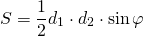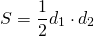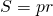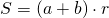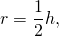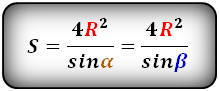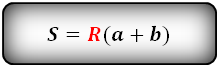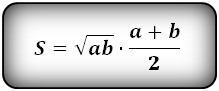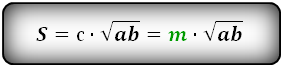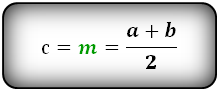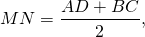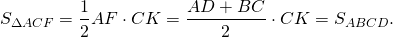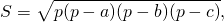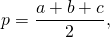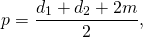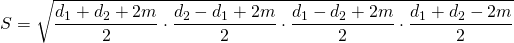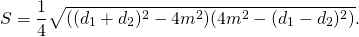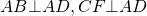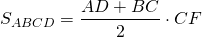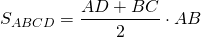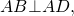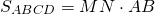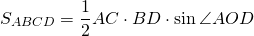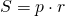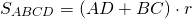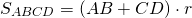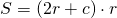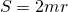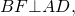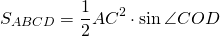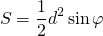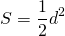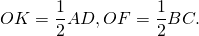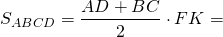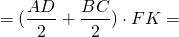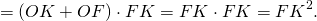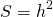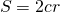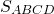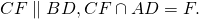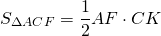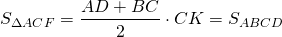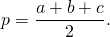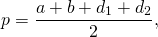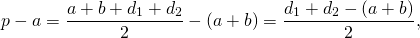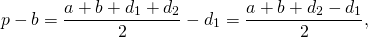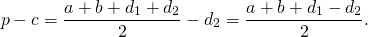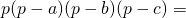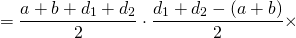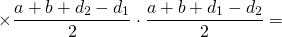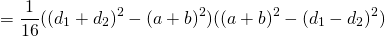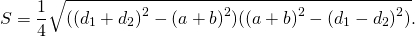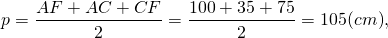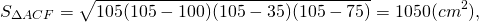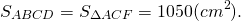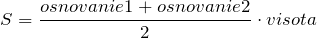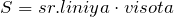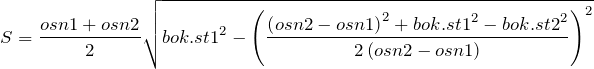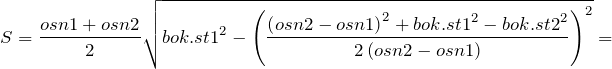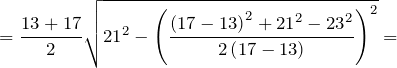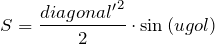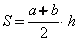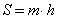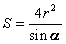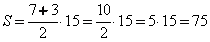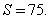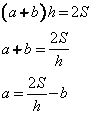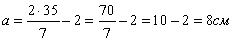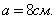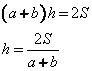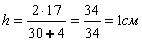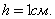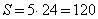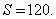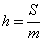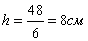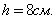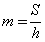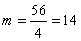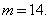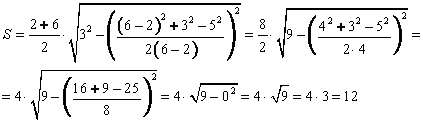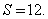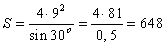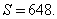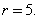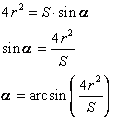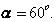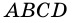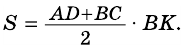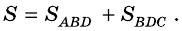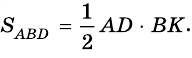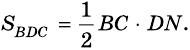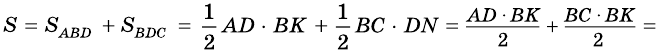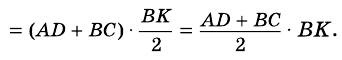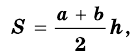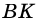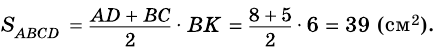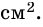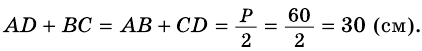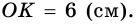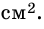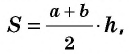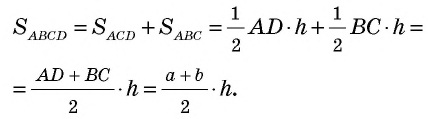Как найти площадь трапеции если известны все стороны

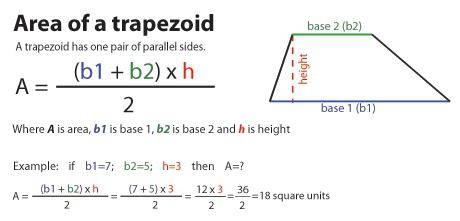
Как найти площадь трапеции

Как найти площадь трапеции? Для этого в зависимости от данных условия можно использовать несколько формул.

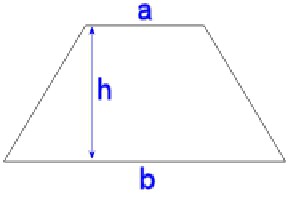
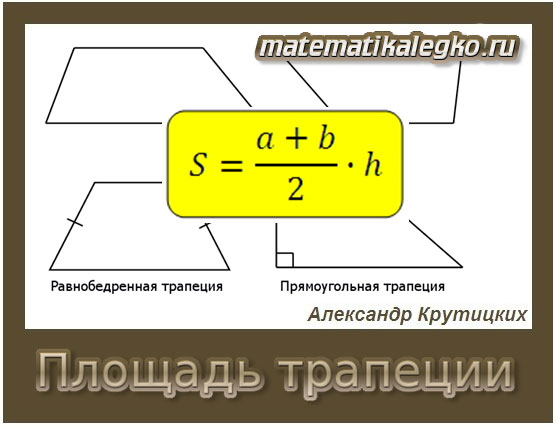
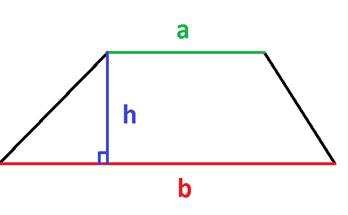
1. Площадь трапеции равна произведению полусуммы её оснований на высоту.

Для трапеции ABCD, AD ∥ BC, с высотой BF площадь равна

Если AD=a, BC=b, BF=h, формула для нахождения площади трапеции

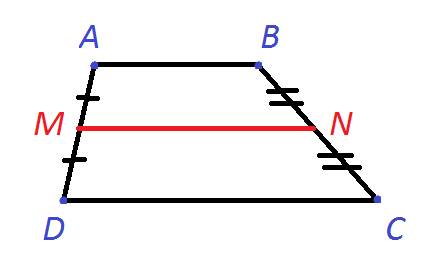
2. Площадь трапеции равна произведению её средней линии на высоту.

Если MN=m, BF=h, формула для нахождения площади трапеции через среднюю линию и высоту

3. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

Если AC=d1, BD=d2, ∠COD=φ, то формула для нахождения площади трапеции через диагонали —

Если диагонали трапеции перпендикулярны,

так как sin 90º=1,

то формула площади трапеции

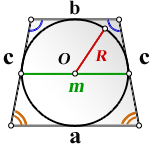
4. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

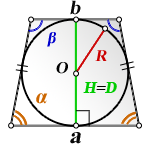
Так как в трапецию можно вписать окружность, если суммы ее противолежащих сторон равны, то AB+CD=AD+BC. Следовательно, полупериметр трапеции равен сумме её оснований: p=AD+BC или p=a+b.

Таким образом, получаем еще одну формулу для нахождения площади трапеции через радиус вписанной окружности:

(Так как радиус вписанной в трапецию окружности равен половине высоты трапеции:

то эта формула может быть получена непосредственно из формулы из пункта 1).

Источник

Площадь трапеции

Существует множество способов найти площадь трапеции. Обычно репетитор по математике владеет несколькими приемами ее вычисления, остановимся на них подробнее:
1) , где AD и BC основания, а BH-высота трапеции. Доказательство: проведем диагональ BD и выразим площади треугольников ABD и CDB через полупроизведение их оснований на высоту:

, где DP – внешняя высота в

Сложим почленно эти равенства и учитывая, что высоты BH и DP равны, получим:

Вынесем за скобку

Что и требовалось доказать.

Следствие из формулы площади трапеции:
Так как полусумма оснований равна MN — средней линии трапеции, то

2) Применение общей формулы площади четырехугольника.
Площадь четырехугольника равна половине произведения диагоналей, умноженной на синус угла между ними
Для доказательства достаточно разбить трапецию на 4 треугольника, выразить площадь каждого через «половину произведения диагоналей на синус угла между ними» (в качестве угла берется , сложить получившиеся выражения, вынести за скобку и раскладываю эту скобку на множители методом группировки получить ее равенство выражению . Отсюда

3) Метод сдвига диагонали
Это мое название. В школьных учебниках репетитор по математике не встретит такого заголовка. Описание приема можно найти только в дополнительных учебных пособиях в качестве примера решения какой-нибудь задачи. Отмечу, что большинство интересных и полезных фактов планиметрии репетиторы по математике открывают ученикам в процессе выполнения практической работы. Это крайне неоптимально, ибо школьнику нужно выделять их в отдельные теоремы и называть «громкими именами». Одно из таких – «сдвиг диагонали». О чем идет речь? Проведем через вершину B прямую параллельную к АС до пересечения с нижним основанием в точке E. В таком случае четырехугольник EBCA будет параллелограммом (по определению) и поэтому BC=EA и EB=AC. Нам сейчас важно первое равенство. Имеем:

Заметим, что треугольник BED, площадь которого равна площади трапеции, имеет еще несколько замечательных свойств:
1) Его площадь равна площади трапеции
2) Его равнобедренность происходит одновременно с равнобедренность самой трапеции
3) Верхний его угол при вершине B равен углу между диагоналями трапеции (что очень часто используется в задачах)
4) Его медиана BK равна расстоянию QS между серединами оснований трапеции. С применением этого свойства я недавно столкнулся при подготовке ученика на мехмат МГУ по учебнику Ткачука, вариант 1973 года (задача приводится внизу страницы).

Спецприемы репетитора по математике.

Иногда я предлагаю задачи на весьма хитрый путь нахождении я площади трапеции. Я отношу его к спецприемам ибо на практике репетитор их использует крайне редко. Если вам нужна подготовка к ЕГЭ по математике только в части B, можно про них и не читать. Для остальных рассказываю дальше. Оказывается площадь трапеции в два раза больше площади треугольника с вершинами в концах одной боковой стороны и серединой другой, то есть треугольника ABS на рисунке:
Доказательство: проведем высоты SM и SN в треугольниках BCS и ADS и выразим сумму площадей этих треугольников:

Так как точка S – середина CD, то (докажите это сами).Найдем cумму площадей треугольников:

Так как эта сумма оказалась равной половине площади трапеции, то — вторая ее половина. Ч.т.д.

В копилку спецприемов репетитора я бы отнес форму вычисления площади равнобедренной трапеции по ее сторонам: где p – полупериметр трапеции. Доказательство я приводить не буду. Иначе ваш репетитор по математике останется без работы :). Приходите на занятия!

Задачи на площадь трапеции:

Замечание репетитора по математике: Нижеприведенный список не является методическим сопровождением к теме, это только небольшая подборка интересных задач на вышерассмотренные приемы.

1) Нижнее основание равнобедренной трапеции равно 13, а верхнее равно 5. Найдите площадь трапеции, если ее диагональ перпендикулярна боковой стороне.
2) Найдите площадь трапеции, если ее основания равны 2см и 5см, а боковые стороны 2см и 3см.
3) В равнобокой трапеции большее основание равно 11, боковая сторона равна 5, а диагональ равна Найти площадь трапеции.
4) Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь.
5) В равнобедренной трапеции основания равны 12 и 20, а диагонали взаимно перпендикулярны. Вычислить площадь трапеции
6) Диагональ равнобокой трапеции составляет с ее нижним основанием угол . Найти площадь трапеции, если ее высота равна 6см.
7) Площадь трапеции равна 20, а одна из ее боковых сторон равна 4 см. Найдите расстояние до нее от середины противоположной боковой стороны.
8) Диагональ равнобокой трапеции делит ее на треугольники с площадями 6 и 14. Найти высоту, если боковая сторона равна 4.
9) В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований равен 2. Найти площадь трапеции (Мехмат МГУ, 1970г).

Я выбирал не самые сложные задачи (не стоит пугаться мехмата!) с расчетом на возможность их самостоятельного решения. Решайте на здоровье! Если вам нужна подготовка к ЕГЭ по математике, то без участия в этом процессе формулы площади трапеции могут возникнуть серьезные проблемы даже с задачей B6 и тем более с C4. Не запускайте тему и в случае каких-либо затруднений обращайтесь за помощью. Репетитор по математике всегда рад вам помочь.

Колпаков А.Н.
Репетитор по математике в Москве, подготовка к ЕГЭ в Строгино.

Спасибо Вам, Александр Николаевич! Вы мне очень помогли. Мой муж метролог, сейчас повышает квалификацию и мне пришлось помогать ему делать курсовик. Так вот формула вычисления площади равнобедренной трапеции по ее сторонам (а я уже многое забыла со школы) мне очень помогла, в интернете ничего подобного не нашла. Спасибо Вам большое.

Уважаемый Александр Николаевич!
Если Вам не трудно, помогите решить задачу №8 из предложеных Вами. Если я правильно поняла Вас, здесь нужно применить Ваш метод сдвига диагонали?
Буду очень признательна.
С уважением Водяева С В

Нет, диагональ трапеции трогать не нужно. Обозначьте буквой икс высоту трапеции и выразите с помощью площадей 6 и 14 ее основания. Затем проведите вторую высоту. От трапеции отсекутся два равных боковых треугольника. У каждого из них один из катетов — высота трапеции (то есть икс), а второй катет — полуразность оснований. Затем запишите теорему Пифагора для одного из боковых треугольников. Подставьте туда боковую строну 4, и полученные выражения для катетов. Ответом к задаче будет корень уравнения.

Уважаемый Александр Николаевич! Сын готовился к ГИА и не смог решить задачу, которая опубликована у Вас последней (№9). Натолкните на путь истинный, если можно, у нашего преподавателя математики пока тоже нет решения. Заранее спасибо.

Через вершину верхнего основания трапеции проведите параллельно диагонали отрезок до его пересечения с основанием. Образуется треугольник, две стороны которого будут равны диагоналям трапеции. Длина медианы, проведенной к третьей стороне данного треугольника, равна длине отрезка, соединяющего середины оснований (это не сложно доказать). Площадь треугольника, очевидно, равна площади трапеции (в моем справочнике этот факт назван теоремой о сдвиге диагонали трапеции).

Извините,Александр я не понимаю почему в 3-ем доказательстве площади трапеции площадь треугольника EBD равна площади трапеции ABCD, прежде чем такое утверждать, надо доказать что треугольник EBD=ABCD-трапеции. Не могли бы вы подсказать как это доказать?!

Не очень понял, что именно Вам не ясно. На странице опубликовано достаточно добротное доказательство. Я специально писал так, чтобы в нем можно было разобраться без всякого репетитора по математике, то есть самостоятельно. Равенство площадей следует из равенства выражений, отвечающих за площади. Изучите материал повнимательнее.

Откуда вы знаете что площадь треугольника BED равна площади трапеции ABCD? Нам формулу площади трапеции вывести надо, а выводится формула площади треугольника BED. Нет, конечно, мы знаем чему равна площадь трапеции по формуле, ну надо же формулу как-то вывести, а вы пишите,что площадь треугольника BED равна площади трапеции. Откуда вы это знаете? Вы же не доказали это! Поэтому и непонятно!

В третьем пункте не выводится ни площадь треугольника, ни площадь трапеции. Доказывается только равенство этих площадей. Формула же площади трапеции выведена в самом начале страницы. Читайте внимательнее. Советую найти хорошего репетитора по математике, чтобы он объяснил Вам все доказательства в отдельности, ибо в комментариях к странице не совсем удобно вести полноценную разъяснительную работу. Обучение математике — живой процесс!

Спасибо большое, помогла последняя формула, которую не доказывали. Буду и дальше к ГИА по математике (теперь уже к ЕГЭ) готовиться вместе с вашим сайтом.

Спасибо большое за такие подробные доказательства!

Диагональ равнобокой трапеции равна 5, а средняя линия равна 4. Найти площадь. Не могу решить. Подскажите какой формулой тут воспользоваться.

Базовой прямой формулы нет. Сделайте так: через любую вершину верхнего основания проведите прямую, параллельную одной из диагоналей до пересечения с нижним основанием. Образуется треугольник с площадью, равной площади трапеции. Легко найти все его стороны, а затем и площадь. Удачи!

Спасибо, очень пригодилось.

И как же выйти на площадь трапеции в 9 задаче? Подскажите, пожалуйста. Не могу сообразить. Заранее огромное спасибо репетитору по математике за помощь.

Воспользуйтесь методом «сдвига диагонали». Получится треугольник со сторонами, которые равны диагоналям трапеции и медианой, равной длине отрезка, соединяющего середины ее оснований. Правда последнее необходимо будет доказать. По двум сторонам и медиане найти площадь полученного треугольника несложно.

спасибо.Еще раз обращаюсь за помощью-заело с задачей:
Плот проплывает путь из А в В за 6 часов,а моторная лодка из В в А за 2 часа.За какое время моторная лодка преодолеет такое же расстояние в стоячей воде?Подскажите,пожалуйста,направление решения.Заранее признательна.

Александр, подскажите пожалуйста как во втором доказательстве площади трапеции мы можем выразить площадь 4-х треугольников? Ведь нам известны только две диагонали трапеции и угол между ними

Там вроде все внятно изложено. Выражать площади треугольников нужно через кусочки диагоналей. После всех преобразований они сложатся в полные диагонали.

Можно ли найти площадь неправильного четырёхугольника, если известны длины всех его сторон в отдельности (периметр)?

Нет, конструкция будет «плавающей». В случае правильного четырехугольника легко привести показательный пример — ромб. С неправильным ситуация аналогичная.

Уважаемый Александр Николаевич! Есть похожая на Вашу 6 задачу: Диагональ равнобокой трапеции составляет с ее нижним основанием угол 60. Найти площадь трапеции, если большее основание равно 6 см.
Натолкните, пожалуйста, на путь истинный.

Здравствуйте! Воспользуйтесь теоремой о сдвиге диагонали. Получится равносторонний треугольник (равнобедренный с углом 60 градусов), имеющий сторону 6 см. Его площадь равна площади трапеции.

Источник

Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

Формула площади равнобедренной трапеции через стороны, ( S ):

Формула площади равнобедренной трапеции через стороны и угол, ( S ):

2. Формулы площади равнобедренной трапеции если в нее вписана окружность

Формула площади равнобедренной трапеции через радиус вписанной окружности, ( S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию ( S ):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

Формула площади равнобедренной трапеции через диагонали и угол между ними, ( S ):

4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, ( S ):

5. Формула площади равнобедренной трапеции через основания и высоту

Формула площади равнобедренной трапеции через основания и высоту, ( S ):

Источник

Все варианты того, как найти площадь трапеции

Многоликая трапеция. Она может быть произвольной, равнобедренной или прямоугольной. И в каждом случае нужно знать, как найти площадь трапеции. Конечно, проще всего запомнить основные формулы. Но иногда проще воспользоваться той, которая выведена с учетом всех особенностей конкретной геометрической фигуры.

Несколько слов о трапеции и ее элементах

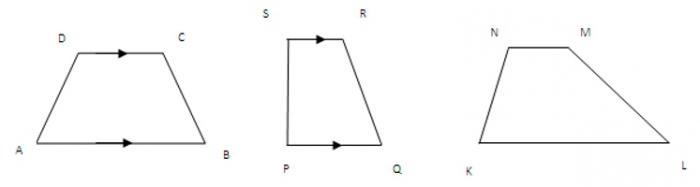
Любой четырехугольник, у которого две стороны параллельны, можно назвать трапецией. В общем случае они не равны и называются основаниями. Большее из них — нижнее, а другое — верхнее.

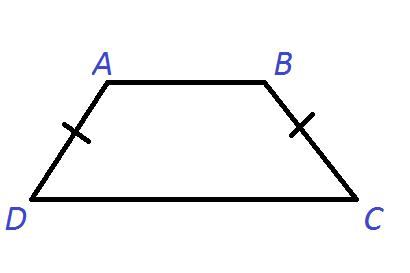
Две другие стороны оказываются боковыми. У произвольной трапеции они имеют различную длину. Если же они равны, то фигура становится равнобедренной.

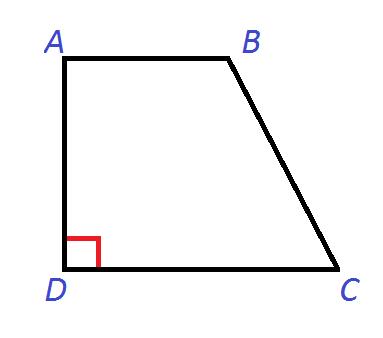
Если вдруг угол между любой боковой стороной и основанием окажется равным 90 градусам, то трапеция является прямоугольной.

Все эти особенности могут помочь в решении задачи о том, как найти площадь трапеции.

Среди элементов фигуры, которые могут оказаться незаменимыми в решении задач, можно выделить такие:

По какой формуле вычислить площадь, если известны основания и высота?

Это выражение дается основным, потому что чаще всего можно узнать эти величины, даже когда они не даны явно. Итак, чтобы понять, как найти площадь трапеции, потребуется сложить оба основания и разделить их на два. Получившееся значение потом еще умножить на значение высоты.

Если обозначить основания буквами а₁ и а₂, высоту — н, то формула для площади будет выглядеть так:

Формула, по которой вычисляется площадь, если даны ее высота и средняя линия

Если посмотреть внимательно на предыдущую формулу, то легко заметить, что в ней явно присутствует значение средней линии. А именно, сумма оснований, деленная на два. Пусть средняя линия будет обозначена буквой l, тогда формула для площади станет такой:

Возможность найти площадь по диагоналям

Этот способ поможет, если известен угол, образованный ими. Предположим, что диагонали обозначены буквами д₁ и д₂, а углы между ними — α и β. Тогда формула того, как найти площадь трапеции, будет записана следующим образом:

В этом выражении можно легко заменить α на β. Результат не изменится.

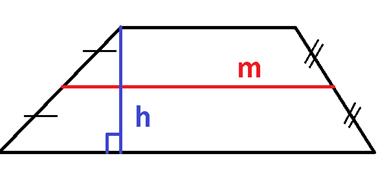
Как узнать площадь, если известны все стороны фигуры?

Бывают и такие ситуации, когда в этой фигуре известны именно стороны. Эта формула получается громоздкой и ее сложно запомнить. Но возможно. Пусть боковые стороны имеют обозначение: в₁ и в₂, основание а₁ больше, чем а₂. Тогда формула площади примет такой вид:

Способы вычисления площади равнобедренной трапеции

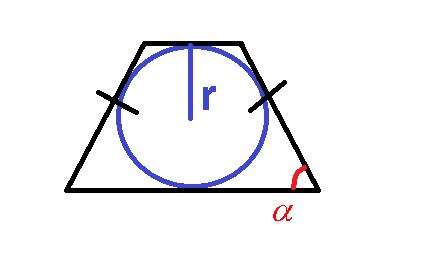
Первый связан с тем, что в нее можно вписать окружность. И, зная ее радиус (он обозначается буквой r), а также угол при основании — γ, можно воспользоваться такой формулой:

S = (4 * r 2 ) / sin γ.

Последняя общая формула, которая основана на знании всех сторон фигуры, существенно упростится за счет того, что боковые стороны имеют одинаковое значение:

Методы вычисления площади прямоугольной трапеции

Понятно, что подойдет любой из перечисленных для произвольной фигуры. Но иногда полезно знать об одной особенности такой трапеции. Она заключается в том, что разность квадратов длин диагоналей равна разности, составленной из квадратов оснований.

Часто формулы для трапеции забываются, в то время как выражения для площадей прямоугольника и треугольника помнятся. Тогда можно применить простой способ. Разделить трапецию на две фигуры, если она прямоугольная, или три. Одна точно будет прямоугольником, а вторая, или две оставшиеся, треугольниками. После вычисления площадей этих фигур останется их только сложить.

Это достаточно простой способ того, как найти площадь прямоугольной трапеции.

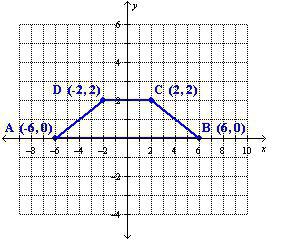
Как быть, если известны координаты вершин трапеции?

В этом случае потребуется воспользоваться выражением, которое позволяет определить расстояние между точками. Его можно применить три раза: для того, чтобы узнать оба основания и одну высоту. А потом просто применить первую формулу, которая описана немного выше.

Для иллюстрации такого метода можно привести такой пример. Даны вершины с координатами А(5; 7), В(8; 7), С(10; 1), Д(1; 1). Нужно узнать площадь фигуры.

До того как найти площадь трапеции, по координатам нужно вычислить длины оснований. Потребуется такая формула:

Верхнее основание обозначено АВ, значит, его длина будет равна √ <(8-5) 2 + (7-7) 2 >= √9 = 3. Нижнее — СД = √ <(10-1) 2 + (1-1) 2 >= √81 = 9.

Теперь нужно провести высоту из вершины на основание. Пусть ее начало будет в точке А. Конец отрезка окажется на нижнем основании в точке с координатами (5; 1), пусть это будет точка Н. Длина отрезка АН получится равной √ <(5-5) 2 + (7-1) 2 >= √36 = 6.

Осталось только подставить получавшиеся значения в формулу площади трапеции:

S = ((3 + 9) / 2) * 6 = 36.

Задача решена без единиц измерения, потому что не указан масштаб координатной сетки. Он может быть как миллиметр, так и метр.

Примеры задач

№ 1. Условие. Известен угол между диагоналями произвольной трапеции, он равен 30 градусам. Меньшая диагональ имеет значение 3 дм, а вторая больше ее в 2 раза. Необходимо посчитать площадь трапеции.

Решение. Для начала нужно узнать длину второй диагонали, потому что без этого не удастся сосчитать ответ. Вычислить ее несложно, 3 * 2 = 6 (дм).

Теперь нужно воспользоваться подходящей формулой для площади:

S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (дм 2 ). Задача решена.

Решение. Для начала нужно сделать чертеж. Поскольку значение перпендикуляра меньше стороны, к которой он проведен, то трапеция будет немного вытянутой вверх. Так ЕН окажется внутри фигуры.

Найти площадь параллелограмма можно по формуле, которая содержит произведение стороны и высоты, опущенной на нее.

Основания известны, высота сосчитана. Можно пользоваться первой формулой, которая здесь была рассмотрена для произвольной трапеции.

S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (см 2 ).

№ 4. Условие. Имеется произвольная трапеция АВСД. На ее боковых сторонах взяты точки О и Е, так что ОЕ параллельна основанию АД. Площадь трапеции АОЕД в пять раз больше, чем у ОВСЕ. Вычислить значение ОЕ, если известны длины оснований.

Решение. Потребуется провести две параллельные АВ прямые: первую через точку С, ее пересечение с ОЕ — точка Т; вторую через Е и точкой пересечения с АД будет М.

Пусть неизвестная ОЕ=х. Высота меньшей трапеции ОВСЕ — н₁, большей АОЕД — н₂.

Поскольку площади этих двух трапеций соотносятся как 1 к 5, то можно записать такое равенство:

Высоты и стороны треугольников пропорциональны по построению. Поэтому можно записать еще одно равенство:

Здесь требуется провести ряд преобразований. Сначала перемножить крест накрест. Появятся скобки, которые укажут на разность квадратов, после применения этой формулы получится короткое уравнение.

В нем нужно раскрыть скобки и перенести все слагаемые с неизвестной «х» в левую сторону, а потом извлечь квадратный корень.

Источник

Как найти площадь трапеции?

Чему равна площадь трапеции? 1. Внесите в графы значения оснований и высоты 2. Наш калькулятор найдёт площадь трапеции онлайн!

Площадь трапеции формула

Трапеция это четырёхугольная фигура, у которой две стороны параллельны, а две другие расположены произвольно.

Основания это две стороны трапеции, которые располагаются параллельно, две остальные стороны могут располагаться под произвольными углами.

Формула площади трапеции: Площадь трапеции равна половине суммы верхнего и нижнего основания, умноженного на высоту. (a+b)/2*h=S.

Высота это линия проведённая под прямым углом от одного основания к другому основанию. Высота обычно изображена выходящей из какого либо угла трапеции, но по факту она одинаковая для любой точки находящейся на основании.

У трапеции одно основание больше другого. Традиционно, трапеция изображается на чертеже меньшим основанием сверху, а большим основанием книзу. Так визуально она логично устойчива. Хотя от расположения сторон суть не меняется.

Как найти площадь трапеции?

В геометрии есть большое количество методов, как найти площадь трапеции. Самым популярным является формула, которая доказывается теоремой. Площадь трапеция равна сумме оснований, делённой пополам и умноженной на высоту.

Источник

Площадь трапеции по диагоналям и средней линии

Как найти площадь трапеции по известным диагоналям и средней линии?

Дано: ABCD, AD∥BC,

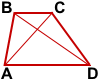
MN — средняя линия трапеции,

1) Проведём через вершину C прямую, параллельную диагонали BD. На пересечении этой прямой с прямой, содержащей основание AD, отметим точку F.

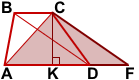
Имеем: CF∥BD (по построению),

BC∥DF(так как лежат на основаниях трапеции), следовательно, четырёхугольник BCFD — параллелограмм (по определению).

Рассмотрим треугольник ACF.

Таким образом, задача сводится к нахождению площади треугольника ACF.

В треугольнике ACF известны все стороны: AC=d₁, CF=d₂, AF=2m.

Остаётся найти площадь треугольника по формуле Герона.

Разумеется, запоминать эту формулу не нужно. Для нахождения площади трапеции через среднюю линию и диагонали достаточно провести аналогичные рассуждения.

Найти площадь трапеции, диагонали которой равны 15 и 13, а средняя линия равна 7.

Проводя аналогичные приведённым выше рассуждения, находим полупериметр и площадь треугольника ACF, площадь которого равна искомой площади трапеции:

Источник

Площадь прямоугольной трапеции

Площадь прямоугольной трапеции можно найти по любой из формул для площади произвольной трапеции. Некоторые из общих формул могут быть упрощены на основании свойств прямоугольной трапеции.

I. Площадь трапеции равна произведению полусуммы оснований на высоту.

Площадь прямоугольной трапеции ABCD,

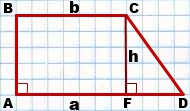
Так как меньшая боковая сторона прямоугольной трапеции перпендикулярна основаниям, то она равна высоте трапеции, то есть

Если обозначить AD=a, BC=b, CF=AB=h, то формула площади прямоугольной трапеции через основания и высоту (меньшую боковую сторону):

II. Площадь трапеции равна произведению средней линии на высоту.

Если MN — средняя линия прямоугольной трапеции ABCD,

Если обозначить среднюю линию MN=m, меньшую боковую сторону AB=h, получим формулу для нахождения площади прямоугольной трапеции через среднюю линию:

III. Площадь трапеции равна половине произведения диагоналей трапеции на синус угла между ними.

Для прямоугольной

Если AC=d1, BD=d2, ∠COD=φ, то

В частности, если диагонали трапеции перпендикулярны, то

VI. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

Обозначив AD=a, BC=b, CD=c, AB=h=2r, получим формулы площади прямоугольной трапеции через радиус вписанной окружности:

Если в трапецию вписана окружность, площадь трапеции также можно найти как удвоенное произведение радиуса и средней линии. Формула

Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.

Источник

Площадь трапеции

Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз ))

Теперь подробно и по порядку.

Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.

Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.

В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:

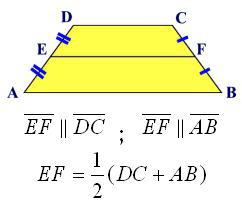
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.

Теперь давайте вникнем глубже. Почему именно так?

*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.

Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).

Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.

Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:

Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:

Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.

Теперь рассмотрим треугольник:

*Средняя линия данной трапеции и средняя линия треугольника совпадают.

Известно, что средняя линия треугольника равна половине параллельного ей основания, то есть:

Хорошо, разобрались. Теперь о площади трапеции.

Площадь трапеции формула:

Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.

То есть, получается, что она равна произведению средней линии и высоты:

Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:

То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:

Но дело тут не в записи, конечно, а в понимании.

Скачать (посмотреть) материал статьи в формате *pdf

Источник

Площадь равнобедренной трапеции

Площадь равнобедренной трапеции можно найти с помощью любой из формул для нахождения площади трапеции в общем случае. Благодаря свойствам равнобедренной трапеции некоторые из этих формул могут быть упрощены.

I Площадь трапеции равна произведению полусуммы оснований на высоту.

Как и для случая произвольной трапеции, площадь равнобедренной трапеции ABCD, AD∥BC, AB=CD,

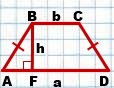
Если AD=a, BC=b, BF=h, то формула площади трапеции принимает вид

II. Площадь трапеции равна произведению её средней линии на высоту.

Это верно, в частности, для равнобедренной трапеции.

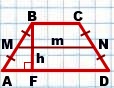
Если MN — средняя линия трапеции ABCD, BF — её высота, то площадь трапеции равна

Если MN=m, BF=h, то

III. Площадь трапеции равна половине произведения её диагоналей на синус угла между ними.

Поскольку диагонали равнобедренной трапеции равны, площадь равнобедренной трапеции равна половине произведения квадрата её диагонали на синус угла между диагоналями.

Для равнобедренной трапеции ABCD

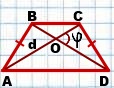
AD∥BC, AB=CD, AC∩BD=O,

VI. Площадь равнобедренной трапеции с перпендикулярными диагоналями.

1) Если диагонали равнобедренной трапеции перпендикулярны, так как sin 90º=1, предыдущая формула принимает вид:

2) Площадь равнобедренной трапеции, диагонали которой перпендикулярна, равна квадрату её высоты.

В равнобедренной трапеции ABCD

AD∥BC, AB=CD, AC∩BD=O, проведем высоту FK через точку пересечения диагоналей.

Прямоугольные треугольники AOD и BOC — равнобедренные (с основаниями AD и BC). Поэтому их высоты OK и OF являются также медианами. Следовательно, по свойству медианы, проведенной к гипотенузе

Таким образом, формула для нахождения площади равнобедренной трапеции с перпендикулярными диагоналями:

V. Площадь трапеции равна произведению её полупериметра на радиус вписанной окружности.

Так как в трапецию ABCD можно вписать окружность, то

AD+BC=AB+CD, то есть p=AD+BC или p=AB+CD=2AB.

Таким образом, площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению суммы оснований на радиус окружности.

Если обозначить основания трапеции AD=a, BC=b, то

Также площадь равнобедренной трапеции, в которую можно вписать окружность, равна удвоенному произведению боковой стороны на радиус окружности.

Если обозначить боковые стороны AB=CD=c, то формула площади трапеции в этом случае

Так как высота равнобедренной трапеции, в которую можно вписать окружность, равна среднему пропорциональному (среднему геометрическому) между её основаниями, то площадь равнобедренной трапеции, в которую можно вписать окружность, равна произведению среднего арифметического и среднего геометрического её оснований:

Источник

Площадь трапеции через основания и диагонали

Как найти площадь трапеции через ее основания и диагонали?

Площадь трапеции равна произведению полусуммы оснований на высоту. Поскольку основания известны, задача может быть сведена к нахождению высоты трапеции.

На самом деле, зная основания и диагонали, можно найти площадь трапеции и без высоты.

Дано : ABCD — трапеция,

Через точку C проведем прямую, параллельную диагонали BD. Обозначим точку пересечения этой прямой с прямой, содержащей основание AD трапеции через F:

2) В четырехугольнике BCFD AF || BC (как прямые, содержащие основания трапеции), BD || CF (по построению). Значит, BCFD — параллелограмм (по определению). Следовательно, его противоположные стороны равны: DF=BC=a, CF=BD=d₂.

3) Рассмотрим треугольник ACF. AF=AD+DF=a+b.

Все три стороны треугольника ACF известны, поэтому его площадь можно найти по формуле Герона

Вместо a, b и c подставляем a+b, d₁ и d₂. Получаем:

Таким образом, площадь трапеции через основания и диагонали может быть найдена по формуле

Запоминать её не нужно, достаточно провести аналогичные рассуждения для своей задачи и по формуле Герона вычислить площадь треугольника, стороны которого равны диагоналям трапеции и сумме её оснований.

Основания трапеции равны 10 см и 90 см, а диагонали равны 75 см и 35 см. Найти площадь трапеции.

Проводим дополнительные построения и доказываем, что площадь трапеции ABCD равна площади треугольника ACF. Затем находим его площадь по формуле Герона:

В следующий раз рассмотрим, как по основаниям и диагонали найти площадь равнобедренной трапеции.

2 Comments

По основаниям и диагонали найти площадь равнобедренной трапеции.
S=((a+b)/2)*под кв.корень(d2-((a+b)/2)**2))

Да, Nasimi, именно так для равнобедренной трапеции. Дальше есть вывод этой формулы.

Источник

Площадь трапеции по основаниям и высоте: онлайн калькулятор

Существует несколько способов нахождения параметров фигуры. Решение зависит от того, какие данные представлены в примере. Онлайн-калькулятор на этой странице предлагает следующий вариант. Площадь трапеции равна произведению половины суммы оснований на высоту.

Чтобы воспользоваться программой расчета, вам не придется вносить оплату или регистрироваться на сайте. Доступ к подробному решению получает любой желающий.

Материалы, которые помогут вам лучше разобраться в теме:

Как найти площадь трапеции через высоту и основание

Сервис автоматических подсчетов протестирован и исключает неточности, выбор неверной формулы, ошибки при переводе. Нахождение площади трапеции по высоте и основанию происходит по формуле:

S = 1 2 · ( a + b ) · h

Онлайн-калькулятором пользуются школьники для освоения непонятных материалов, быстрого получения ответов на контрольной, закрепления темы и подготовки к поступлению в ВУЗ. Студенты пользуются быстрыми подсчетами на зачетах и экзаменах. Преподаватели благодаря сервису экономят время на планирование занятий.

Если в задании другие данные, найдите подходящий калькулятор из предложенных в разделе. На сайте круглосуточно доступен онлайн-консультант на случай затруднений. По вашему запросу он подберет опытного преподавателя из нашего штата для выполнения задания или объяснения непонятной темы.

Источник

как найти площадь трапеции если все её стороны разные. к примеру а-верх 1.8; b-низ 3.7; с-лево 2.4; d-право 2.6.

Держи формулу, подставляй значения и считай.

Основные формулы нахождения площади трапеции

S= h*(a+b)/2
Где h – высота трапеции, a,b – основания. Самая часто используемая формула поиска площади трапеции выглядит как полусумма оснований, умноженная на высоту.
S = m*h
Где m – средняя линия трапеции, h – высота. Площадь трапеции также равна произведению средней линии трапеции на её высоту.
S=1/2*d1*d2*sin(d1^d2)
Где d1, d2 – это диагонали трапеции, sin(d1^d2) – это синус угла, между диагоналями трапеции.
Существуют также различные формулы, выведенные из основных, а также формула для расчёта площади трапеции, когда известны все её стороны. Однако эта формула достаточно громоздкая и используется редко, ведь, зная все стороны трапеции можно просто определить высоту или её среднюю линию. Также в равнобедренную трапецию можно вписать окружность. В этом случае площадь трапеции будет высчитываться по формуле: 8*радиус окружности в квадрате.

Как найти площадь прямоугольной трапеции

Как и говорилось ранее, прямоугольной называется та трапеция, у которой хотя бы один угол прямой. Найти площадь такой трапеции очень просто. В основном, для поиска площади прямоугольной трапеции используются те же формулы, что и для обычной трапеции. Однако стоит помнить, что одна из боковых сторон такой трапеции и будет являться высотой. Также часто решение задач поиска площади прямоугольной трапеции сводится к поиску площади прямоугольника и треугольника, образованных опущенной высотой. Такие задачи достаточно просты.

Источник

Как найти площадь и периметр трапеции? Какие есть формулы?

Как найти площадь и периметр равнобедренной трапеции?

Как найти площадь и периметр прямоугольной трапеции?

Площадь трапеции, у которой основания a1 и a2, средняя линия m = (a1 + a2)/2, а высота h.

S = (a1 + a2)*h/2 = m*h

Периметр равнобочной трапеции, у которой боковые стороны равны b

У прямоугольной трапеции одна боковая сторона перпендикулярна основаниям, то есть совпадает с высотой. Вторая равна b.

P = a1 + a2 + h + b

Геометрия интересная наука, другое дело, что не каждому она дается на изучение. Пыталась «дружить» с геометрией, конечно, не всегда все было гладко, но, если по формулам, то все удавалось. Доказывать теоремы нравилось.

Так вот трапеция, помню из курса геометрии это фигура, которая имеет разные длины сторон.Поэтому эти стороны обычно обозначают разными буквами латинского алфавита. Чтобы вычислить периметр необходимо все стороны просто сложить

Чтобы получить площадь трапеции руководствуйтесь вот этой формулой:

S = (A+B)/2*H

Ну а периметр трапеции находится как сумма всех его сторон. Если боковые стороны не известны, то пригодится теорема Пифагора как для равнобедренной трапеции, так и для прямоугольной.

Источник

Чему равна площадь трапеции

Здравствуйте!
Как узнать, чему равна площадь трапеции? При разных заданных условиях?
Спасибо!

Разберемся чему равна площадь трапеции в зависимости от того, какие данные известны из условия задачи.
Основными данными для решения задач на трапецию, и в частности на нахождение ее площади, являются высота и средняя линия.
Если известна высота трапеции и ее основания, то площадь вычисляется по формуле:

Если известна средняя линия трапеции, то ее площадь можно вычислить, исходя из предыдущей формулы и учитывая, что средняя линия равна половине суммы двух оснований трапеции:

Если известны все стороны, то можно использовать следующую формулу:

Пример.
Дана трапеция с основаниями по 13 и 17 см, боковые стороны которой равны 21 и 23 см. найдем площадь этой трапеции.

Решение.
Подставим известные данные в формулу:

(кв. см).

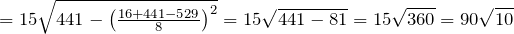
Ответ. 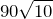(кв. см).

В случае равнобокой трапеции (или равнобедренной) ее площадь можно найти по диагонали и углу между ними:

Здесь диагональ берется в квадрате, поскольку диагонали у равнобедренной трапеции равны.

Источник

Как найти площадь трапеции, если известны диагонали

Используйте общую формулу площади для произвольного четырехугольника:

Если требуется доказать или вывести эту формулу, разбейте трапецию на 4 треугольника. Запишите формулу площади каждого из треугольников (1/2 произведения сторон на синус угла между ними). Берите тот угол, который образуется пересечением диагоналей. Далее используйте свойство аддитивности площади: запишите площадь трапеции как сумму площадей образующих ее треугольников. Сгруппируйте слагаемые, вынеся множитель 1/2 и синус за скобки (учитывая, что sin(180°-φ)=sinφ). Получите исходную формулу площади четырехугольника.

Вообще, полезно рассматривать площадь трапеции как сумму площадей составляющих ее треугольников. Зачастую это является ключом к решению задачи.

Теоремы, которые могут понадобиться, если числовое значение угла между диагоналями не задано в явном виде:

1) Сумма всех углов треугольника равна 180°.

2) Теорема синусов для треугольника со сторонами a, b и c:

3) Теорема косинусов для треугольника со сторонами a, b и c:

Обратите внимание на свойства трапеции, указанные в условии задачи. Если дана равнобедренная трапеция (боковые стороны равны), используйте то ее свойство, что диагонали в ней равны.

Если дана прямоугольная трапеция (один из углов трапеции прямой), рассмотрите прямоугольные треугольники, находящиеся внутри трапеции. Вспомните, что площадь прямоугольного треугольника равна половине произведения его сторон, образующих прямой угол, т.к. sin90°=1.

Источник

Площадь трапеции

ПЛОЩАДЬ ТРАПЕЦИИ

Выберете формулу вычисления площади трапеции, которую Вы планируете применить для решения поставленной перед Вами задачи:

Общая теория для вычисления площади трапеции.

Трапеция – это плоская фигура, состоящая из четырех точек, три из которых не лежат на одной прямой, и четырех отрезков (сторон), соединяющих попарно эти четыре точки, у которой две противоположные стороны параллельны (лежат на параллельных прямых), а две другие не параллельны.

Точки называются вершинами трапеции и обозначаются заглавными латинскими буквами.

Отрезки называются сторонами трапеции и обозначаются парой заглавных латинских букв соответственно вершинам, которые отрезки соединяют.

Две параллельные стороны трапеции называются основаниями трапеции.

Две не параллельные стороны трапеции называются боковыми сторонами трапеции.

Рисунок №1: Трапеция ABCD

AB ǁ DC – основания трапеции ABCD.

AD, BC – боковые стороны трапеции ABCD.

Угол, образованный лучами AB и AD, называется углом при вершине A. Обозначается он как ÐA или ÐBAD, или ÐDAB.

Угол, образованный лучами BA и BC, называется углом при вершине B. Обозначается он как ÐB или ÐABC, или ÐCBA.

Угол, образованный лучами CB и CD, называется углом при вершине C. Обозначается он как ÐC или ÐDCB, или ÐBCD.

Угол, образованный лучами AD и CD, называется углом при вершине D. Обозначается он как ÐD или ÐADC, или ÐCDA.

Рисунок №2: Трапеция ABCD

На рисунке №2 отрезок MN, соединяющий середины боковых сторон, называется средней линией трапеции.

Средняя линия трапеции параллельна основаниям и равна их полусумме. То есть,.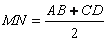

Рисунок №3: Равнобедренная трапеция ABCD

На Рисунке №3, AD=BC.

Трапеция называется равнобедренной (равнобокой), если ее боковые стороны равны.

Рисунок №4: Прямоугольная трапеция ABCD

На Рисунке №4 угол D – прямой (равен 90 о ).

Трапеция называется прямоугольной, если угол при боковой стороне прямой.

Площадью S плоской фигуры, к которым относится и трапеция, называется ограниченное замкнутое пространство на плоскости. Площадь плоской фигуры показывает величину этой фигуры.

Площадь обладает несколькими свойствами:

1. Она не может быть отрицательной.

2. Если дана некоторая замкнутая область на плоскости, которая составлена из нескольких фигур, не пересекающихся друг с другом (то есть, фигуры не имеют общих внутренних точек, но вполне могут касаться друг друга), то площадь такой области равна сумме площадей составляющих ее фигур.

3. Если две фигуры равны, то и площади их равны.

4. Площадь квадрата, который построен на единичном отрезке, равна единице.

За единицу измерения площади принимают площадь квадрата, сторона которого равна единице измерения отрезков.

При решении задач часто используются следующие формулы вычисления площади трапеции:

1. Площадь трапеции равна полусумме ее оснований умноженной на высоту:

2. Площадь трапеции равна произведению ее средней линии на высоту:

3. При известных длинах оснований и боковых сторон трапеции её площадь можно вычислить по формуле:

4. Возможно вычислить площадь равнобедренной трапеции при известной длине радиуса вписанной в трапецию окружности и известном значении угла при основании по следующей формуле:

Пример 1: Вычислить площадь трапеции с основаниями a=7, b=3 и высотой h=15.

Решение:

Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Решение:

Для нахождения стороны основания трапеции воспользуемся формулой вычисления площади:

Выразим из данной формулы сторону основания трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 3: Найти высоту трапеции с площадью S=17 см 2 и основаниями a=30 см, b = 4 см.

Решение:

Для нахождения высоты трапеции воспользуемся формулой вычисления площади:

Выразим из данной формулы высоту трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 4: Вычислить площадь трапеции с высотой h=24 и средней линией m=5.

Решение:

Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Пример 5: Найти высоту трапеции с площадью S = 48 см 2 и средней линией m=6 см.

Решение:

Для нахождения высоты трапеции воспользуемся формулой вычисления площади трапеции:

Выразим из данной формулы высоту трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 6: Найти среднюю линию трапеции с площадью S = 56 и высотой h=4.

Решение:

Для нахождения средней линии трапеции воспользуемся формулой вычисления площади трапеции:

Выразим из данной формулы среднюю линию трапеции:

Таким образом, имеем следующее:

Ответ:

Пример 7: Вычислить площадь трапеции с основаниями a=2, b=6 и боковыми сторонами c=3, d=5.

Решение:

Для нахождения площади трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Решение:

Для нахождения площади равнобедренной трапеции воспользуемся следующей формулой вычисления площади:

Таким образом, имеем следующее:

Ответ:

Решение:

Для нахождения радиуса вписанной в равнобедренную трапецию окружности воспользуемся следующей формулой вычисления площади:

Выразим из данной формулы радиус:

Таким образом, имеем следующее:

Ответ:

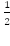
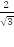
Пример 9: Вычислить угол при основании трапеции, считая, что он острый. Если радиус вписанной в равнобедренную трапецию окружности r = и площадь трапеции S=.

Решение:

Для нахождения угла при основании трапеции воспользуемся следующей формулой вычисления площади:

Выразим из данной формулы угол при основании трапеции:

Таким образом, имеем следующее:

Ответ:

Источник

Как найти площадь прямоугольной трапеции?

Площадь прямоугольной трапеции найти очень просто: достаточно вспомнить, из что представляет собой эта геометрическая фигура. Трапеция состоит из двух параллельных и двух боковых сторон, причем одна из боковых сторон имеет угол в 90 градусов.

Найти площадь трапеции можно по следующим формулам:

Площадь трапеции равна полусумме её оснований, умноженной на высоту данной трапеции:

S=(( AD+ВС) :2)хВН,

Площадь равнобедренной трапеции можно найти и по формуле:

S=4r:sina;

Площадь трапеции равна произведению средней линии трапеции и её высоты:

S=mh,

где h— это высота трапеции, m— её средняя линия.

Есть и ещё одна формула, по которой возможно найти площадь трапеции. В данной формуле:

a и b— это основания, с и d— боковые стороны трапеции.

Что такое прямоугольная трапеция?

Это фигура, у которой две стороны параллельны, третья перпендикулярна первым двум, а четвёртая расположена под определённым, не прямым углом.

Рисунок:

На рисунке вы видите прямоугольную трапецию. Две стороны у неё параллельны (a и c). Сторона b перпендикулярна, а четвёртую сторону мы даже можем не обозначать, так как она нам не понадобится для расчётов.

Теперь посмотрите, что будет, если справа достроить к четвёртой стороне два отрезка так, как изображено на рисунке красным цветом. То есть отрезки должны быть параллельны противоположной стороне трапеции. Как вы видите, получился прямоугольник большей площади, чем наша трапеция. Затем ещё проведём из правого верхнего угла трапеции вниз отрезок, перпендикулярный нижней стороне.

Площадь трапеции складывается из суммы площади левого прямоугольника и из площади треугольника:

Sтрап = Sab + Sтреуг

Площадь левого прямоугольника равна произведению a на b:

Sab = a * b

А площадь треугольника равна одной второй от площади правого прямоугольника, то есть её половине. Вертикальная сторона этого прямоугольника равна b, а горизонтальная равна разности между большей из параллельных сторон трапеции и меньшей, то есть вертикальная сторона равна c-a.

Получается, что площадь правого прямоугольника равна b(c-a).

Источник

Площади фигур. Площадь трапеции.

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей

одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь

будет равна числу этих квадратов.

Трапецией называется четырехугольник, у которого только две стороны параллельны, а две другие не

Площадь трапеции равна произведению полусуммы ее оснований a и b на высоту h.

Воспользуйтесь нашим калькулятором для расчета площади трапеции.

Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.

Площадь трапеции можно найти по следующим формулам:

1. Формула Герона для трапеции.

2. Формула площади трапеции по длине основ и высоте.

Площадь трапеции равна произведению полусуммы ее оснований на высоту

Источник

Трапеция формулы

Трапеция – это четырехугольник, у которого 2 стороны параллельны (основания), а две другие – нет (боковые стороны).

Любая трапеция характеризуется основаниями a и b, боковыми сторонами c и d, высотой h и средней линией L (см. рисунок). Именно эти характеристики используются в формулах трапеции при вычислении площади и периметра.

Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон.

Формула средней линии трапеции

Среднюю линию трапеции L можно получить, зная ее основания:

Формула периметра трапеции

Периметр P трапеции можно получить, зная все ее стороны:

Формулы площади трапеции

Площадь трапеции S можно вычислить, зная его основания и высоту h, проведенную к одному из оснований:

Также площадь трапеции S можно вычислить, зная ее среднюю линию L и высоту h:

Если в трапеции известны 2 диагонали d₁ и d₂ и угол α между ними, площадь трапеции также удастся вычислить:

Поделитесь статьей с одноклассниками «ТРАПЕЦИЯ формулы площади и периметра, средняя линия трапеции».

Источник

Высота трапеции

Что такое трапеция

Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.

Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.

Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти высоту трапеции

Через стороны

Если нам известны стороны фигуры, мы можем найти ее высоту по формуле:

Где h — высота, a — большее основание, b — меньшее основание, c и d — боковые стороны.

Через среднюю линию и площадь

Если в условии есть данные о величине средней линии и площади, можем использовать формулу:

Где m — средняя линия трапеции.

Через боковую сторону и угол

Когда нам известна величина одной из боковых сторон и угол между этой стороной и большим основанием, используем формулу:

Где \alpha — это угол между стороной c и большим основанием a.

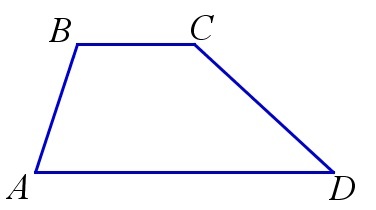
Через диагонали, угол между ними и основания

Если нам известны длины обоих диагоналей трапеции, а также угол между ними, можем найти высоту следующим образом:

Где \(d_1\) и \(d_2\) — диагонали трапеции, а \(\gamma\) — угол между ними.

Через диагонали, угол и среднюю линию

В том случае, если нам известны сразу длины диагоналей, угол между ними и величина средней линии, мы можем узнать высоту трапеции по формуле:

Через радиус вписанной окружности

Если в трапецию можно вписать окружность, то ее высота будет равна диаметру этой окружности, то есть d=h. Другими словами, высота фигуры будет равна удвоенному радиусу вписанной в нее окружности:

Где r — радиус выписанной окружности.

Примеры вычисления

Дана трапеция, в которой известны основания a и b. Они равны 4,5 см и 2,5 см. Также известны ее боковые стороны d и c, равные 2 см и \(2\sqrt2\) см соответственно. Найти высоту.

Чтобы решить эту задачу, используем формулу \(h=\sqrt^2+d^2+c^2><2\cdot(a-b)>>)^2.\)

Подставляем известные значения:

Чтобы найти высоту, нужно знать величину средней линии m. Определим ее следующим образом:

Теперь используем формулу \(h=\frac Sm\) и подставим известные значения:

Мы знаем, что сторона c трапеции равна \(\sqrt2\) см, а угол \(\alpha\) между известной стороной и основанием равен 45 градусов. Найти значение высоты.

Используем формулу \(h=c\cdot\sin\left(\alpha\right)\) и подставим значения:

Для решения задачи использует формулу \(h=\frac\cdot\sin\left(\gamma\right).\)

Источник

Нахождение высоты трапеции: формулы и примеры задач

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.

Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.

Нахождение высоты трапеции

Через длины сторон

Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:

Через боковую сторону и прилежащий угол

Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.

Через диагонали и угол между ними

Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:

Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:

Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b) /₂.

Через площадь

Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).

Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.

Примеры задач

Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.

Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:

Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.

Решение
В данном случае можно применить последнюю из рассмотренных формул:

Источник

Как найти площадь трапеции если известны все стороны

Трапеция – четырехугольная фигура, имеющая всего одну пару параллельных сторон. Их называют основаниями. Непараллельные – боковыми сторонами. Иногда трапецию определяют, как четырехугольник с противолежащими параллельными сторонами, без уточнения о двух других сторонах, поэтому в частных случаях трапецией является и параллелограмм.

Виды и элементы трапеции

Различают три вида трапеции:

Вычисление площади трапеции

Если величины оснований не известны, но известна длина средней линии и высота, то площадь фигуры будет равна произведению высоты и средней линии. Например, отрезок соединяет середины двух непараллельных сторон в точках К и М. Формула будет выглядеть, как: S=КМ х Н.

Другие элементы трапеции также могут помочь при вычислении ее площади. Зная размер диагоналей (d1 и d2) и величину угла между ними, можно вычислить площадь по формуле:(d1хd2 х sin α)/2.

Все эти формулы справедливы для трапеции любого вида.

Особенности равнобедренной трапеции

Равнобедренная трапеция обладает рядом свойств, отличающих ее от прямоугольной и разносторонней.

2. Длины диагоналей в равнобедренной трапеции равны.

3. Если провести перпендикуляр из вершины наибольшее основание (высоту), она разделит его на отрезки, первый из которых будет равен половине разности оснований (а – b)/2, а второй – половине сумме оснований(а + b) / 2.

4. Если диагонали равнобедренной трапеции перпендикулярны (как в ромбе), то можно узнать высоту по формуле: Н= (а+ b )/ 2, тоесть она составляет половину суммы оснований.

5. Если через середины оснований трапеции провести прямую, то она будет являться осью симметрии этой геометрической фигуры.

6. Доказать, что трапеция является равнобедренной можно с помощью круга. Если в нее можно вписать окружность, а также описать вокруг нее, то такая трапеция считается равнобедренной.

Площадь равнобедренной трапеции

Но если речь идет строго о равнобедренной трапеции, ток ней применимы формулы, которые не подходят для нахождения площади разносторонней или прямоугольной трапеций.

Найти площадь равнобедренной трапеции можно, вписав в нее окружность. В таком случае площадь вычисляем по формуле S =4R2 / sin α.R– радиус окружности, вписанной в трапецию. α–величина угла при основании.

Если угол равен 30 градусам, то формула будет выглядеть так: S = 8R2.

Если требуется узнать площадь равнобедренной трапеции, когда известны размеры всех сторон, используется формула:

Здесь: а и b означают основания фигуры, а c и d – ее боковые стороны.

Так как часто в геометрии и повседневной жизни приходится сталкиваться с необходимостью вычислить площадь сложных фигур, можно их разбить прямыми линиями наиболее простые, среди которых будет и трапеция. Сложив площади простых фигур, можно узнать площадь сложной, которая ими образуется.

Источник

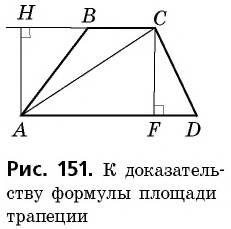
Теорема (о площади трапеции). Площадь трапеции равна произведению полусуммы ее оснований на высоту.

Доказательство:

Пусть

Докажем, что площадь 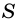трапеции можно найти по формуле:

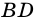
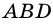
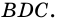
1) Диагональ разбивает трапецию на два треугольника и Поэтому

2) — высота треугольника поэтому

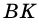
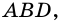
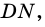
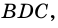
3) Проведем в трапеции высоту она является и высотой треугольника поэтому

4) (как высоты трапеции). Следовательно,

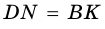
В общем виде формулу площади 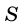трапеции можно записать так:

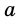
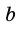
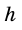
где и — основания трапеции, — ее высота.

Следствие. Площадь трапеции равна произведению ее средней линии на высоту.

Пример:

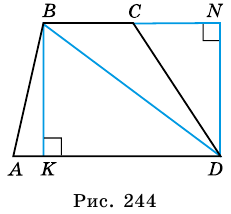
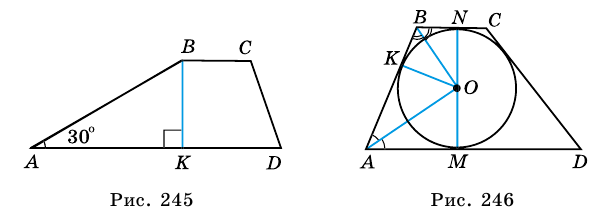
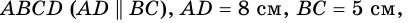
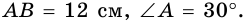
В трапеции Найдите площадь трапеции.

Решение:

1) Проведем в трапеции 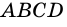высоту

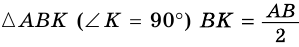
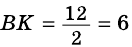
(рис. 245). В (по свойству катета, противолежащего углу 30°). Следовательно, (см).

2)

Ответ. 39

Пример:

Периметр трапеции 60 см, а одна из боковых сторон точкой касания вписанной окружности делится на отрезки 9 см и 4 см. Найдите площадь трапеции.

Решение:

1) Так как трапеция является описанной около окружности (рис. 246), то

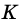
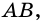
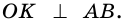
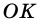
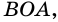
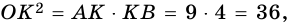
3) Точка — точка касания окружности со стороной поэтому Следовательно, — радиус окружности и высота прямоугольного треугольника проведенная к гипотенузе. По теореме о средних пропорциональных отрезках в прямоугольном треугольнике имеем: откуда

4) — диаметр окружности, а также высота трапеции, поэтому (см).

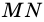
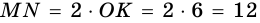
5) Следовательно,

Ответ. 180

Площадь трапеции

Часто для вычисления площади некоторого многоугольника его разбивают на несколько треугольников и находят искомую площадь как сумму площадей этих треугольников. Именно такой подход можно применить для вывода формулы площади трапеции.

Теорема (формула площади трапеции) Площадь трапеции равна произведению полусуммы ее оснований на высоту:

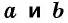
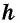
где — основания трапеции, — высота трапеции.

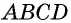
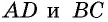
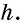
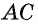
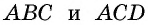
Пусть дана трапеция с основаниями и высотой Диагональ делит ее на два треугольника (рис. 151).

Проведем высоты этих треугольников 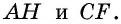Обе они являются высотами трапеции, т.е. равны Имеем:

Следствие

Площадь трапеции равна произведению средней линии на высоту.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник