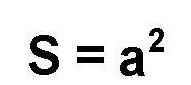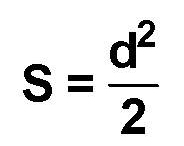Как посчитать площадь квадрата

Онлайн калькулятор. Площадь квадрата

Используя этот онлайн калькулятор, вы сможете найти площадь квадрата.

Воспользовавшись онлайн калькулятором для вычисления площади квадрата, вы получите детальное пошаговое решение вашего примера, которое позволит понять алгоритм решения таких задач и закрепить пройденный материал.

Найти площадь квадрата

Выберите известную величину:

Ввод данных в калькулятор для вычисления площади квадрата

В онлайн калькулятор вводить можно числа или дроби 3, 0.4, 5/7. Более подробно читайте в правилах ввода чисел.

Если у вас возникли трудности с преобразованием единиц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади.

Теория. Площадь квадрата

Формулы для вычисления площади квадрата

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Как определить площадь квадрата

3 класс, 8 класс

Формула нахождения площади квадрата

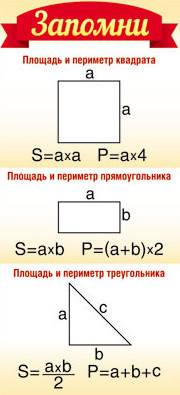
Квадрат — это фигура, которая является частным случаем прямоугольника, из-за чего можно заметить схожесть некоторых алгоритмов. Способ вычисления всегда зависит от исходных данных. Чтобы узнать площадь квадрата, необходимо знать специальные формулы, рассмотрим пять из них.

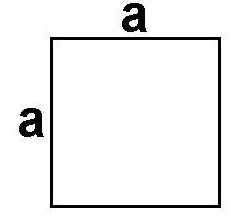
Если известна длина стороны

Умножаем ее на то же число или возводим в квадрат.

Эту формулу проходят в 3 классе. Остальные формулы третьеклассникам знать пока не нужно, но они пригодятся ученикам 8 класса.

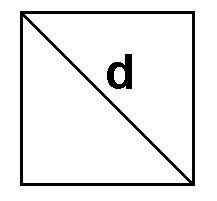
Если нам дана диагональ

Возводим ее в квадрат и делим на два.

S = d 2 : 2, где d — диагональ.

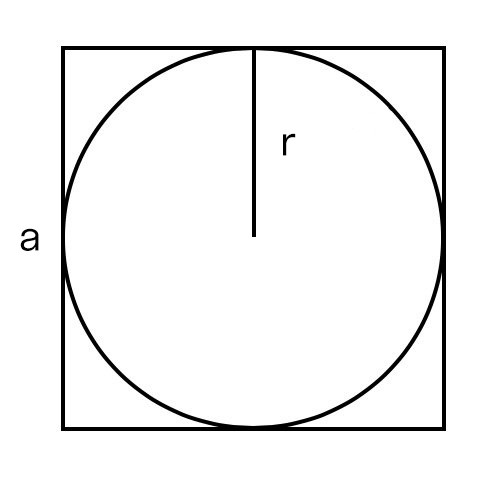
Если известен радиус вписанной окружности

Умножаем его квадрат на четыре.

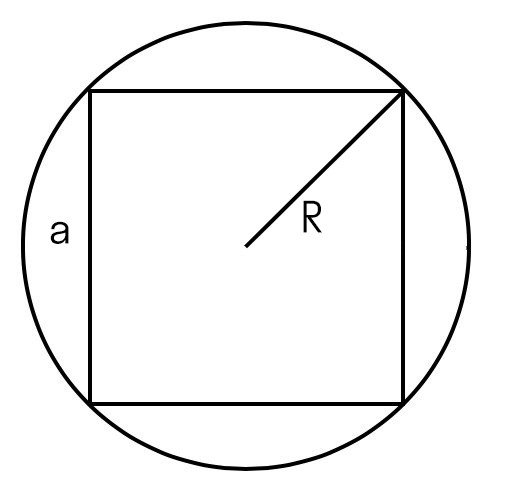
Если у нас есть радиус описанной окружности

Возведем его в квадрат и умножим на два.

У нас есть курсы обучения математике для учеников с 1 по 11 классы — записывайтесь!

Если есть периметр

Мы должны возвести его в квадрат и разделить на 16.

S = Р 2 : 16, где Р — это периметр.

Периметр любого четырехугольника равен сумме длин всех его сторон.

Популярные единицы измерения площади:

S квадрата. Решение задач

Мы разобрали пять формул для вычисления площади квадрата. А теперь давайте потренируемся!

Задание 1. Как найти площадь квадрата, диагональ которого равна 90 мм.

Воспользуемся формулой: S = d 2 : 2.

Задание 2. Окружность вписана в квадрат. Найдите площадь квадрата, если радиус окружности равен 24 см.

Если окружность вписана в квадрат, то сторона квадрата равна диаметру:
a = d

Диаметр окружности равен двум радиусам:
d = 2r

Получается, что сторона равна двум радиусам:
a = 2r

Используем формулу нахождения площади квадрата через сторону:
S = a 2

Так как из пункта 3 мы получили, что сторона равна двум радиусам, то формула площади квадрата примет вид:
S = (2r) 2
S = 4r 2

Теперь подставим значение радиуса в формулу площади:
S = 4 × 24 2 = 2304 см 2

Источник

Площадь квадрата

Как найти площадь квадрата? 1. Введите в калькулятор длину стороны квадрата. 2. Мы найдём площадь и периметр квадрата. 3. Распишем решение квадрата подробно!

Формула площади квадрата

Как мы написали выше квадрат это простейшая фигура, по этому и формула как найти площадь также очень простая! L * L = S чтобы найти площадь нужно умножить сторону саму на себя, или другими словами возвести в квадрат.

1. Вы не знаете как найти площадь квадрата, а сторона квадрата Вам известна? Тогда разберём этот вариант.

Пример: найдём площадь квадрата сторона 3 см. Для решения мы используем выше приведённую формулу площадь квадрата. Сторона 3 умножается на саму себя и получаем площадь 9. (3см х 3см = 9см)

2. Можно сделать ещё один вариант записи решения по той же формуле площади квадрата, разберём площадь квадрата сторона 2 см.

Пример решения площади квадрата: Сторона 2 см возводится во вторую степень и получается площадь квадрата для стороны 2, равная 4 см!

Чему равна площадь квадрата?

Кстати, интересен тот факт, что само название математической операции ‘возвести число в квадрат’ пошло именно из формулы площади квадрата! И это абсолютно логично! Если задуматься, получается что если мы возводим число 3, 5, 6, 8 или 1 в квадрат (или вторую степень), то тем самым мы просто узнаём площадь квадрата со стороной 3, 5, 6, 8 см, или дм, или метров )))

Наш онлайн калькулятор найдёт площадь и периметр квадрата для любой стороны, вы можете использовать его для вычисления площади в 1см, 1дм, 1м. И любых единицах длины. Мы распишем решение площади и периметра квадрата в двух вариантах и Вам останется только его переписать! Упростите процесс решения домашнего задания или вычисления для рабочих моментов.

Источник

Площади фигур. Площадь квадрата.

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей

одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь

будет равна числу этих квадратов.

Квадратом называется четырехугольник с прямыми углами и равными сторонами. Площадь квадрата равна

квадрату длины его стороны. Или половине квадрата диагонали.

Воспользуйтесь нашим калькулятором для расчета площади квадрата.

Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.

Формулы для нахождения площади квадрата:

1. Формула площади квадрата по длине его стороны

Площадь квадрата равна квадрату длины его стороны.

2. Формула площади квадрата по длине его диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

Источник

Нахождение площади квадрата: формула и примеры

Квадрат – это геометрическая фигура; правильный четырехугольник, т.е. четырехугольник, имеющий равные стороны и углы (90°).

Формула вычисления площади

1. По длине стороны:

Площадь квадрата (S) равняется квадрату длины его стороны:

S = a 2

Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:

S = a*b

2. По по длине диагонали

Площадь квадрата равняется половине квадрата длины его диагонали:

S = d 2 /2

Примеры задач

Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.

Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.

Источник

Как найти площадь квадрата?

Площадь квадрата можно вычислить двумя способами (по двум формулам).

Вот и вся геометрия!

Площадь квадрата можно найти с помощью двух основных формул:

1) Через сторону.

2) Через диагональ.

Как найти площадь квадрата, если известна его сторона.

Площадь прямоугольника равна произведению 2 его сторон:

В случае с квадратом a = b.

Таким образом, площадь квадрата будет находиться по формуле:

Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².

Как найти площадь квадрата, если известна его диагональ.

Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:

Перепишем формулу в виде:

Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.

Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².

Источник

Формула площади квадрата, как посчитать площадь

Как посчитать диагональ квадрата?

Первый способ – это всем уже известная и привычная теорема Пифагора. В квадрате все углы прямые, а значит, диагональ делит его на два равных прямоугольных треугольника и сама является их гипотенузой. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

Второй способ – это простая формула, которая свойственна исключительно квадратам, и ее нужно просто запомнить. Как известно, все стороны квадрата равны, и именно поэтому математики вычислили следующую формулу для нахождения его диагонали: она равна произведению стороны на корень из двух.

Безусловно, лучше всего просто запомнить формулу длины диагонали квадрата и пользоваться ею всегда, ведь это гораздо быстрее и удобнее. Особенно это чувствуется при решении задач в буквенном виде, где вместо целых больших подкорневых выражений можно обойтись лишь одним произведением.

Формула вычисления площади

1. По длине стороны:

Площадь квадрата (S) равняется квадрату длины его стороны:

S = a 2

Данная формула следует из того, что квадрат является частным случаем прямоугольника, площадь которого находится путем умножения его смежных сторон:

S = a*b

2. По по длине диагонали

Площадь квадрата равняется половине квадрата длины его диагонали:

S = d 2 /2

Основные свойства квадрата

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:

AC ┴ BD	AO = BO = CO = DO =	d
		2

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Площадь поверхности куба, онлайн расчет

Найти площадь поверхности куба по формуле через длину его ребра.Площадь поверхности куба, онлайн расчет

Находим площадь по стороне квадрата, формула расчёта

S- площадь квадрата

А- сторона квадрата

Пример расчёта

А= 10см
Рассчёт будет таким:
S = 10²=10×10=100
Ответ: площадь квадрата равна 100см

Как найти площадь квадрата по диагонали, формула расчёта

S- площадь квадрата

D- диагональ квадрата

Пример расчёта площади по диагонали

Диагональ D= 30см
Рассчёт будет таким:
S = 30²/2=(30×30)/2 =450см
Ответ: площадь квадрата равна 450см

Формулы для четвёртой степени

( a + b ) 4 = a 4 + 4 a 3 b + 6 a 2 b 2 + 4 a b 3 + b 4

( a – b ) 4 = a 4 – 4 a 3 b + 6 a 2 b 2 – 4 a b 3 + b 4

a 4 – b 4 = ( a – b )( a + b )( a 2 + b 2 )

Площади фигур

Расчет площади квадрата, прямоугольника, параллелограмма, треугольника, трапеции, ромба, круга (площадь фигур).Площади фигур

Формула площади квадрата через радиус описанной окружности

Примеры задач

Задание 1
Найдите площадь квадрата, сторона которого равна 7 см.

Задание 2
Найдите площадь квадрата, диагональ которого равняется 4 см.

Как найти площадь квадрата если известен периметр формулы, пример расчёта

S- площадь квадрата

P- периметр квадрата

Вычисление диагонали квадрата по известной стороне

Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.

Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.

Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.

Определения и соглашения

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Таблица с формулами площади квадрата

эскиз	формула
1	сторона
2	диагональ
3	периметр
4	отрезок проведенный из вершины квадрата к середине противоположной стороны
5	радиус вписанной окружности
6	радиус описанной окружности

Неполный квадрат разности

Это квадрат разности, который также называется полным квадратом разности относительно выражения:

которое называется неполным квадратом разности. Неполный квадрат разности двух чисел равен квадрату первого числа, минус произведение первого числа на второе, плюс квадрат второго числа. Неполный квадрат разности отличается от полного только произведением чисел, которое не удваивается.

Формула площади квадрата через радиус вписанной окружности

Площадь квадрата

Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.

Формулы определения площади квадрата

2. Формула площади квадрата через периметр квадрата:

S =	P 2
	16

3. Формула площади квадрата через диагональ квадрата:

S =	d 2
	2

5. Формула площади квадрата через диаметр описанной окружности:

S =	Do 2
	2

8. Формула площади квадрата через длину отрезка l :

S = l 2	16
	√ 5

Другие свойства диагоналей квадрата

Помимо знания того, как найти диагонали квадрата, нужно также знать и их свойства. Основные из них:

Формула площади квадрата через периметр

В любой квадрат можно вписать окружность и вокруг любого квадрата можно описать окружность. Центром вписанной и описанной окружностей есть точка пересечения диагоналей квадрата. При этом радиусы и вписанной r и описанной R окружностей связаны с длиной его стороны a следующими соотношениями:

Свойства и признаки квадрата (необходимые и достаточные условия того, что четырехугольник – квадрат)

Утверждения.

Вывод

Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.

Источник

Как рассчитать площадь квадрата через диагональ или периметр

Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Способ № 1: Расчёт площади квадрата по размеру стороны

Расчёт по стороне

Введите размер стороны квадрата

Площадь квадрата равна

Способ № 2: Найти площадь квадрата по диагонали

Расчёт по диагонали квадрата

Введите размер диагонали

Площадь квадрата равна

Способ № 3: Найти площадь квадрата зная периметр

Расчёт по диагонали квадрата

Площадь квадрата равна

Как рассчитать площадь квадрата формулы, примеры расчёта

Находим площадь по стороне квадрата, формула расчёта

S- площадь квадрата

А- сторона квадрата

Пример расчёта

А= 10см
Рассчёт будет таким:
S = 10²=10×10=100
Ответ: площадь квадрата равна 100см

Как найти площадь квадрата по диагонали, формула расчёта

S- площадь квадрата

D- диагональ квадрата

Пример расчёта площади по диагонали

Диагональ D= 30см
Рассчёт будет таким:
S = 30²/2=(30×30)/2 =450см
Ответ: площадь квадрата равна 450см

Как найти площадь квадрата если известен периметр формулы, пример расчёта

S- площадь квадрата

P- периметр квадрата

Пример расчёта

Р= 40см
Рассчёт будет таким:
S = 40/4=10×10=100
Ответ: площадь квадрата равна 100см

Источник

Квадратный метр площади помещения – это сколько и как быстро посчитать?

Отправим материал на почту

Квадратный метр – это единица измерения, обозначающая произведение двух числовых значений длины и ширины объекта. Другими словами, длину умножают на ширину. Полученный результат имеет свой математический термин – площадь или численная характеристика плоскости (в отличие от объема – количественной характеристики пространства). Чаще всего с такими параметрами сталкиваются при расчетах площади помещения, участка земли, количества расхода строительного материала. Посчитать квадратные метры можно разными способами, о которых речь пойдет ниже.

Расчет квадратных метров площади

Для вычислений понадобится сантиметровая лента или рулетка. При помощи них делают замеры сторон геометрической фигуры правильной формы (прямоугольник, квадрат и другие варианты). Затем все перемножают. После полученных результатов сантиметры необходимо перевести в метры.

3,42 х 2,15 = 7,353

Округляем до двухзначного числа после запятой – 7,35 кв. м

Часто результат не представлен в форме целого числа – в нем отражены как метры, так и сантиметры. Поэтому нужно перевести сантиметры в метры. Тогда легче будет перемножать числа. Пример: 3 метра 78 сантиметров. Один сантиметр равен 0,01 метрам. Перевод осуществляется простым приемом – переносом запятой числа «0,01» на 2 цифры назад (влево).

3 м 78 см = 3 м + 78 см = 3,78 м

Если взять метровую ленту или рулетку, конечно же, считать будет проще – не понадобится переводить полученные числовые значения в метры. Замеры длины, ширины осуществляют от одной точки (угла) до другой, противоположной точки (угла). Если получается не целое число, то считают не только метры, но и сантиметры. Пример: 3,55 м – 3 метра и 55 сантиметра.

Когда числа получаются меньше одного метра в миллиметрах, тогда делают округление к ближайшему сантиметру. Пример: 2 метра 4 сантиметра и 3 миллиметра записывают как 2,4 м. Но при установке мебельного каркаса важна абсолютная точность. Поэтому здесь выверяют все до миллиметров. Особенно это касается встраиваемых в стеновые ниши шкафов.

Конвертация других единиц измерения площади

Иностранные единицы измерения тоже обозначают квадратный метр. Только для этого их следует правильно конвертировать. Сделать это можно при помощи простого математического расчета:

Количественно футовые или ярдовые значения предстают всегда большими, чем метровые.

Вычисление площади сложной фигуры

Чтобы найти значение площади у сложной фигуры, нужно сначала ее разделить на более простые геометрические формы – треугольник, прямоугольник, квадрат. У контуров фигур должны быть четкие границы, не накладывающиеся друг на друга, а только лишь соприкасающиеся. Находят площадь каждой фигуры, а затем складывают полученные результаты вместе.

Найти площадь треугольника с прямым углом можно простым способом:

Остальные виды треугольников считать можно методом визуального черчения лини от любой вершины, образующей прямой угол с любой стороны. Отыскать площадь круга можно при помощи формулы: π х R2, где π – постоянная (3,1415926535), а R2 – цифровое значение радиуса во второй степени.

Заключение

Квадратный метр – единица измерения площади, числовой характеристики плоскости. Чтобы получить такой параметр, необходимо умножить число, обозначающее длину фигуры, на число его ширины. Правильнее выражаться «2 квадратный метра», а не «3 метра в квадрате». Тогда никто не сочтет, что одна из сторон объекта равна 3 м.

Источник

Площадь квадрата

Квадрат — это параллелограмм с равными сторонами и углами. Площадь квадрата можно рассчитать 2-мя способами: через сторону или диагональ.
1-й способ. Через сторону площадь квадрата можно рассчитать, воспользовавшись формулой:

где S — площадь; a — сторона квадрата.
Т. е. пл. квадрата равняется квадрату его стороны.

Расчет площади квадрата по стороне

2-й способ. Через диагональ площадь квадрата можно рассчитать по формуле:

где S — пл. квадрата; c — его диагональ.
Т. е. площадь квадрата равняется квадрату его диагонали, деленной пополам.
Воспользовавшись онлайн калькулятором, вы сможете быстро определить площадь квадрата.

Источник

Площадь

Рассмотрим фигуру ниже:

Вся фигура состоит из 8 квадратов со стороной 1 см каждый.

Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.

В математике для нахождения площади геометрических фигур используют специальные формулы, в которых площадь обозначается заглавной латинской буквой « S ».

Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.

Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата, равна 1 м, то его площадь равна 1 квадратному метру ( 1 м 2 ); если длина его стороны равна 1 см, то его площадь равна 1 квадратному сантиметру ( 1 см 2 ).

Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.

Как перевести квадратные единицы

Рассмотрим квадрат со стороной 1 см.

Его площадь равна:

S = 1 см · 1 см = 1см 2

Рассмотрим квадрат со стороной 1 м.

Его площадь равна:

S = 1 м · 1 м = 1 м 2

Известно, что: 1 м = 100 см

1 м 2 = 1 м · 1 м = 100 см · 100 см = 10 000 см 2

Увеличим сторону квадрата равную 1 м в 10 раз. Получим квадрат со
стороной 10 м.

Площадь такого квадрата называют ар или сотка.

S = 10 м · 10 м = 100 м 2

В одном аре — сто квадратных метров.

Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».

1 ар (сотка) = 100 м 2

Значит: 1 ар (сотка) = 100 м 2 = 100 · 10 000 см 2 = 1 000 000 см 2

Увеличим сторону квадрата равную 10 м в 10 раз. Получим квадрат со
стороной 100 м.

Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование проговаривается полностью.

Выразим гектар в квадратных метрах.

1 га = 100 м · 100 м = 10 000 м 2

Теперь определим, сколько в одном гектаре аров.

Значит: 10 000 м 2 : 100 м 2 = 100 (ар)

1 км 2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м 2

Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.

Таблица переводов квадратных единиц

Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.

Источник

Найти площадь квадрата через сторону

Главная » Учёба и наука » Математика » Найти площадь квадрата через сторону

Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны. Состоит соответственно из четырёх равных сторон, четырёх вершин и прямых углов 90°.

Как рассчитать площадь квадрата онлайн

Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.

Всё зависит от того, какие данные у вас имеются. Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон.

Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …

Источник

Как правильно и быстро посчитать квадратные метры стен, пола и потолка? Объём помещения по формуле, сложные фигуры

Проверить работу строителей, определить объёмы работ и материалов легко, зная как посчитать квадратные метры пола или стен помещения с помощью простых геометрических формул, несложных вычислений и нехитрых приёмов.

В строительстве и отделочных работах почти все расценки на работы сведены к стоимости за квадратный метр. Квадратура поверхностей нужна и для подсчёта расхода материала (смотрите еще: советы для дома).

Метр квадратный это сколько?

Квадратным метром называется единица измерения площади, принятая в международной системе единиц, СИ. 1м² равен площади квадрата со стороной 1 м.

Знание простых правил и нескольких геометрических формул для подсчёта количества квадратных метров стен, полов, потолка позволит избежать ошибок в вычислениях и правильно определить нужные величины.

Инструменты для подсчёта

Для замера и расчёта понадобятся следующие предметы и инструменты:

Угольником размечают перпендикуляры – линии, пересекающиеся под прямым углом.

Площадь комнаты

Знание метража комнаты пригодится для определения стоимости полового покрытия, отделки потолка, количества и мощности осветительных приборов. Замеряя квадратуру помещения, проверяют соответствие площади, заявленной по проекту.

Измерения стен удобнее производить снизу, на уровне плинтуса. Сомнения в правильной форме помещения устраняют при помощи измерения диагоналей. Если диагонали комнаты равны, то углы – прямые, а помещение – прямоугольное.

Квадрат или прямоугольник

Самая распространенная форма комнаты в плане – квадратная или прямоугольная. Подсчёт квадратуры по полу при этом не составит особого труда:

При этом площадь потолка считают по тому же принципу, то есть умножают длину на ширину за вычетом технологических проемов, если таковые имеются.

[stextbox квадратные метры помещений и сложив их, можно узнать площадь всего дома.[/stextbox]

Помещение неправильной формы

Эркеры, мансарды и комнаты домов со сложной архитектурой в плане часто имеют неправильную форму. Метраж нестандартной комнаты с полукругами, выступами, множеством углов подсчитать сложнее. Облегчают задачу, используя принцип деления сложных фигур на простые.

Пол, представляя как составную фигуру мысленно или отображая на бумаге, разделяют на стандартные геометрические элементы. Затем вычисляют площадь элементов по одному и складывают полученные величины.

Г-образные, Т-образные формы помещения в плане разбивают на прямоугольники и квадраты. Полукруглые поверхности принимают как часть круга.

Количество квадратных метров пола комнаты, в основе которой лежит трапеция, можно высчитать двумя способами:

Для подсчёта по формуле измеряют две противоположные длинные стены, эти размеры дадут значения оснований. Значение высоты определяют путём замера перпендикуляра, проведённого от одного из углов меньшего основания к большему.

Формула площади трапеции S=1/2(А+В)*Н, где:

Площадь трапециевидной комнаты – половина суммы числовых значений оснований, умноженных на высоту.

Объем комнаты

Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты.

Объём измеряется в кубических метрах. Единица записывается как 1 м³.

С точки зрения геометрии, помещение как фигура представляет собой шестигранник.

Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.

Объём помещения сложной формы вычисляют следующим путём:

Как посчитать квадратуру стен?

Размер стены в квадратных метрах нужен для подсчёта количества отделочных материалов, размещения полок, зеркал или навесных шкафов.

Сплошная стена

Квадратура стены рассчитывается аналогично площади пола – длина, высота стены после обмера перемножаются между собой. Учитывают все впадины и выступы, если такие есть. Стены мансардных помещений под крышей часто ломаной формы, сегменты находятся в разных плоскостях.

В этом случае участки стены измеряют по отдельности, переносят на бумагу. Подсчитывают площадь каждой отдельной геометрической фигуры и суммируют числа.

С окном

Определяя количество квадратных метров стены, оконные проёмы, как правило, исключают.

Торцевые грани стен возле окна называют откосами, их размеры также не входят в метраж стены и считаются отдельно, например при подсчёте штукатурных работ или шпаклёвки.

С дверью

Квадратуру дверного проёма из площади стены при расчёте вычитают. Откосы при необходимости измеряют отдельно.

Измеряем площадь неправильной фигуры

Высчитывая метраж декоративных арочных проёмов или стрельчатых окон, поступают по тому же принципу, разбивая сложную фигуру на несколько простых элементов.

С квадратами и прямоугольниками совмещают части круга и треугольники.

Окружность

Целый круг в интерьере встречается достаточно редко. Полностью круглым может быть окно, колонны, центральная часть многоуровневого потолка. В основном дело приходится иметь с частями круга: половиной или сегментами.

Рулеткой снимают размер между двумя противоположными точками круга. Этот отрезок будет называться диаметром. Радиус круга равен половине диаметра.

Подсчёт площади круга производят по формуле S = π*R², где:

Числовое значение площади полукруга получают делением полученного результата на 2.

Квадратура сектора круга равна произведению половины длины дуги сектора на радиус круга, вычисляется по формуле S = 1/2 L*R.

Треугольник

Формула площади треугольника S=1/2*Н*А, где:

Высоту треугольника получают, измеряя рулеткой перпендикуляр от угла, противоположного к стороне.

Посмотрите на видео ниже полезные советы для быстрого и правильного подсчета квадратуры стен и пола:
[yvideo number=»9ulNrvMoO30″]
Используя простые формулы из школьного курса геометрии, можно подсчитать любую нужную величину для строительства или ремонта.

Статья полезна? Сохраните закладку или отметьте для друзей!

Источник

Как рассчитать квадратные метры помещения

Во время ремонта или отделки помещения часто возникает вопрос о том, как посчитать квадратные метры покрытия: обоев, ламината и т.п. Для этого нужно определить размер стен, пола или потолка.

Сколько в квадратном метре сантиметров

Узнать, сколько в квадратном метре сантиметров, можно с помощью простейших вычислений. Известно, что 1 м = 100 см. Поскольку кв.м. – это единица измерения площади, то 1 м² = Д х Ш, где Д = 100 см – это длина, а Ш = 100 см – ширина метрового участка. Таким образом, 1 м² = 100 см х 100 см = 10 000 см2.

Что такое погонный метр

Погонный метр – это единица измерения длины, обозначение, которым пользуются в строительстве и некоторых других отраслях.

Применение этого термина удобно и необходимо:

Как пересчитать в квадратные метры

Сравнивать между собой можно только аналогичные единицы измерения одного и того же параметра. В погонных метрах обозначают длину изделия, т.е. линейную величину. В квадратных измеряют плоскостную характеристику.

Чтобы найти квадратуру поверхности, достаточно знать ее длину в погонных метрах и ширину (высоту). Например, площадь кухонных фасадов равна их общей длине в погонных метрах, умноженной на высоту шкафов.

Пepeвoд квaдpaтныx caнтимeтpoв в квaдpaтныe мeтpы

Иногда размер поверхности выражен в квадратных сантиметрах. Чтобы перевести значение в квадратуру, нужно знать, что 1 м² равен 10 000 см².

Например: известно, что S = 3 000 см². Поэтому 3 000 / 10 000 = 0,3 м².

Формулы для расчета площади помещения в квадратных метрах

Приведенные выше формулы подскажут, как узнать площадь комнаты. При определении размера помещения пользуются математическими расчетами с учетом конфигурации места.

Все величины должны быть выражены в одних и тех же единицах – в данном случае в квадратных метрах:

Как рассчитывать площадь комнат разных форм

Чтобы узнать, как посчитать площадь пола, нужно замерить размеры комнаты. Требуемые параметры зависят от ее конфигурации. Важно произвести замеры правильно.

Размеры помещения или его отдельных частей могут отличаться от указанных в чертежах, т.к. схематичные изображения не учитывают толщины отделочных материалов – штукатурки, линолеума и т.п. Не учтены и небольшие смещения стен и потолка от вертикальной и горизонтальной осей.

Чтобы знать, как рассчитать площадь комнаты, нужно определить ее конфигурацию.

Для измерения можно пользоваться рулеткой или лазерным дальномером. Последний более точен, но не всегда возможен. С помощью лазерного устройства можно замерить только ровную поверхность. Если на пути измерения встречаются выступы или другие неровности, лучше воспользоваться металлической рулеткой.

Выполняя линейные замеры, нельзя пользоваться деревянным, пластиковым или другим мягким инструментом, т.к. со временем он усыхает и коробится.

Прямоугольная

Легче всего рассчитать площадь комнаты прямоугольной формы. Для этого замеряют длину и ширину поверхности в квадратных метрах, а затем перемножают полученные величины. При вертикальных стенах и их одинаковой высоте размеры пола и потолка одинаковы. В противном случае придется высчитывать величину каждого участка отдельно.

Трапециевидная

Площадь помещения трапециевидной формы легко посчитать, условно выделив ее центральную часть, представляющую прямоугольник, и 2 участка треугольной формы, прилегающих к его сторонам. Для расчета используют формулы, приведенные ранее.

Легче всего узнать квадратуру трапециевидной комнаты правильной формы, когда треугольные части одинаковы.

Круглое помещение

Для определения метража круглого помещения находят его самую широкую часть. Разделив этот отрезок пополам, легко найти центр круга – его диаметр. 1/2 этой величины является радиусом. Воспользовавшись приведенной формулой для определения площади круга, можно рассчитать квадратуру всей комнаты.

Помещение неправильной формы

Чтобы найти величину помещения неправильной формы, нужно условно разбить его на участки простых геометрических форм – прямоугольники, треугольники и т.п. Их размер легко посчитать, используя приведенные формулы.

В этом случае лучше сделать чертеж комнаты, замерив все нужные параметры.

Треугольная

Величину треугольного участка определяют путем измерения одной из его сторон и высоты, т.е. размера линии, проведенной к ней из противоположного угла под прямым углом, как показано на рисунке:

Далее по формуле можно узнать величину треугольника.

Кaк выcчитaть квaдpaтypy кoмнaты

Площадь всех стен комнаты узнают, просуммировав их величину. Это часто бывает необходимо при покупке обоев или других отделочных материалов.

Неровности, изгибы поверхности могут привести к неточностям в измерении. Поэтому предварительно лучше проверить вертикальность стен с помощью строительного уровня. Если она в точности не выдержана, высоту и ширину лучше измерять в нескольких местах – снизу и сверху – либо с учетом искривлений.

При расчете площади отделки нужно учесть проемы: окна, двери, ниши, арки. Это можно сделать 2 способами.

Также при расчете площади стен учитывают ниши под батареи отопления, двери и т.п. Нужно обдумать и электрическую проводку, ведь при прокладке короба и других нюансах отделка может не потребоваться.

Как посчитать объем комнаты

Объем помещения равен произведению всех величин: ширины, высоты и длины, выраженных в одинаковых единицах измерения.

Чтобы высчитать кубатуру помещения сложной формы, нужно:

Калькулятор квадратных метров

Инструменты позволяют узнать величину комнаты любой формы. В калькулятор вносят значения из приведенных формул, расчет происходит автоматически.

Источник

Как правильно и быстро посчитать квадратные метры стен, пола и потолка? Объём помещения по формуле, сложные фигуры

Во время выполнения ремонта и при приобретении строительных, отделочных материалов необходимо правильно рассчитать площадь комнат и поверхностей. Для этого необходимо знать, сколько в квадратном метре сантиметров, как правильно определять площадь каждой конструкции. Также эту величину называют квадратурой – от названия единиц измерения площади. Важно разобраться, что представляет собой квадратный метр, и как работать с замерами площадей.

Ремонт предусматривает определение площади помещения

Как посчитать квадратуру комнаты, стен, потолка, пола

Периодически нам требуется знать площадь и объем комнаты. Эти данные могут понадобиться при проектировании отопления и вентиляции, при закупке стройматериалов и еще во многих других ситуациях. Также периодически требуется знать площадь стен. Все эти данные вычисляются легко, но предварительно придется поработать рулеткой — измерять все требуемые габариты. О том, как посчитать площадь комнаты и стен, объем помещения и пойдет речь дальше.

Часто требуется посчитать кубатуру комнаты, ее объем

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту. Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный.

В этом случае порядок вычислений такой:

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка. Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Площадь квадрата

Из известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– ) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I2S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

Способ № 1

Расчет на основании значения площади происходит следующим образом:

Ширина обойных полотен – 50 см (0,50 м), метраж – 15 м.

Высота комнаты – 2,7 м, параметры – 4 × 2,8 м, окно и дверь стандартных размеров.

Вспоминаем формулу расчета площади комнаты: квадратный метр – это сколько и как измерить

При проведении ремонтных работ возникает вопрос: квадратный метр – это сколько необходимо материалов, чтобы его покрыть.

Чтобы не потратить лишние деньги, лучше для начала произвести расчет квадратных метров комнаты и только потом отправляться в магазин с конкретными требованиями.

На упаковках с красками, штукатуркой, грунтовкой обязательно обозначено, на какой размер помещения рассчитано данное количество смеси.

Главный вопрос – сколько необходимо упаковок или банок, чтобы хватило на площадь стен или пола.

[править] Источники

Основные единицыАмпер · Кандела · Кельвин · Килограмм · Метр · Моль · СекундаПроизводные единицыБеккерель · Ватт · Вебер · Вольт · Генри · Герц · Градус Цельсия · Грей · Джоуль · Зиверт · Катал · Кулон · Люкс · Люмен · Ньютон · Ньютон-метр · · Паскаль · Радиан · Сименс · Стерадиан · Тесла · ФарадПринятые для использования с СИАнгстрем · Астрономическая единица · Гектар · Градус дуги (Минута дуги, Секунда дуги) · Дальтон (Атомная единица массы) · Децибел · Квадратный метр · Литр, Кубический километр · Микрограмм (Миллиграмм) · Микросекунда (Миллисекунда, Наносекунда) · Микрометр (Нанометр, Миллиметр, Сантиметр, Фемтометр, Километр) · Непер · Сутки (Час, Минута) · Тонна · Электронвольт Атомная система единиц · Естественная система единицСм. такжеИзмерение · История метрической системы · Квантовая система единиц · Новые определения СИ · Планковская длина · Преобразование единиц · Приставки СИ · Произвольная единица · Система физических величин

Что такое квадратный метр

Для начала надо определиться, что из себя представляет квадратный метр. Люди, которые плохо учили в школе математику, все равно рано или поздно сталкиваются с проблемой подсчета количества строительных материалов. Поэтому квадратный метр – основная точка отсчета при определении площади помещения.

Если нарисовать квадрат (это геометрическая фигура с одинаковыми сторонами), и сторона будет равна 100 см, то при умножении на 100 получим число 10000 см. это означает, что размер данной фигуры 10000 см2. Можно проще. Посчитать в метрах: 100 см – это 1 м. Применяем формулу подсчета площади – перемножаем две стороны, то есть 1 умножаем на 1, получаем 1 м. Значит, размер квадрата 1 кв.м.

См. также

Смотреть что такое «Квадратный метр» в других словарях:

квадратный метр — — [https://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN square metersq m … Справочник технического переводчика

квадратный метр — kvadratinis metras statusas T sritis Standartizacija ir metrologija apibrėžtis Ploto, lygiaverčio paviršiaus arba objekto ploto, skerspjūvio, lėtinimo, difuzijos ir migravimo ploto, atominio silpimo koeficiento matavimo vienetas: m². atitikmenys … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр — kvadratinis metras statusas T sritis fizika atitikmenys: angl. square metre vok. Quadratmeter, n rus. квадратный метр, m pranc. mètre carré, m … Fizikos terminų žodynas

квадратный метр — мера площадей метрической системы = 100 кв. дециметрам = 1,19599 англ. кв. ярда = 0,21967 кв. сажени = 1,97704 кв. аршина; узаконенное в СССР сокращенное обозначение квадратного метра: русское “m2” или “кв. м”, латинское “m2” … Справочный коммерческий словарь

квадратный метр на джоуль — kvadratinis metras džauliui statusas T sritis Standartizacija ir metrologija apibrėžtis Spektrinio skerspjūvio matavimo vienetas: m²/J. atitikmenys: angl. square metre per joule vok. Quadratmeter durch Joule, m rus. квадратный метр на джоуль, m… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр на килограмм — kvadratinis metras kilogramui statusas T sritis Standartizacija ir metrologija apibrėžtis Masinio energijos perdavos ir masinio silpimo koeficiento matavimo vienetas: m²/kg. atitikmenys: angl. square metre per kilogram vok. Quadratmeter durch… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр на моль — kvadratinis metras moliui statusas T sritis Standartizacija ir metrologija apibrėžtis Molinio sugerties koeficiento ir molinio silpimo koeficiento matavimo vienetas: m²/mol. atitikmenys: angl. metre squared per mole; square metre per mole vok.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр на секунду — kvadratinis metras per sekundę statusas T sritis Standartizacija ir metrologija apibrėžtis Difuzijos koeficiento, kinematinės klampos koeficiento ar kinematinės klampos, temperatūrinio laidžio matavimo vienetas: m²/s. atitikmenys: angl. square… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр на стерадиан — kvadratinis metras steradianui statusas T sritis Standartizacija ir metrologija apibrėžtis Kampinio skerspjūvio matavimo vienetas: m²/sr. atitikmenys: angl. square meter per steradian vok. Quadratmeter durch Steradiant, m rus. квадратный метр на… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

квадратный метр-кельвин на ватт — kvadratinis metras iš kelvino vatui statusas T sritis Standartizacija ir metrologija apibrėžtis Šiluminės izoliacijos koeficiento matavimo vienetas: m² · K/W. atitikmenys: angl. square metre kelvin per watt vok. Quadratmeterkelvin durch Watt, n… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Формула подсчета квадратных метров

Чтобы рассчитать площадь, необходимо применить формулу квадратного метра А X B, где число А – это длина одной стороны, а число В – длина второй стороны. Они могут быть одинаковы, если форма пола или стены квадратная.

Чаще всего она не квадратная, а прямоугольная, то есть число А будет иметь одно значение, а число В – другое. Их необходимо будет перемножить в уме, или по таблице умножения, или на калькуляторе. И полученное число будет площадью, которую надо будет покрывать краской или еще чем-нибудь.

Это интересно! Иногда нужно знать как правильно высчитываются размеры. Сколько же дюймов в мм? Об этом можно прочесть в нашей статье.

Бывает, что форма пола не стандартная, а, например, трапециевидная. Тогда сложнее, особенно тем людям, кто не знает, что такое треугольник (такое тоже есть в природе). Чтобы рассчитать размер трапеции, необходимо посчитать сначала площадь прямоугольника в середине, потом величину каждого треугольника по бокам

, потом эти три числа сложить. Не легче ли сразу позвать бригаду рабочих? Пускай они думают, как рассчитать квадратные метры комнаты.

Если на этом этапе возникло непонимание, то лучше сразу позвать учителя математики и попросить подсчитать, сколько кв. метров имеет комната.

Расчёт погонного метра

Для мебели

Часто необходимо произвести расчёт погонного метра для корпусной мебели.

Так же погонный метр необходим при покупке уже готовой мебели, при помощи него сможете определиться с количеством тумб и других необходимых деталей.

Рассчет стоимости

Цена погонного метра мебели будет зависеть от материала, взятого для ее изготовления, так же от применяемой фурнитуры, дизайна и размеров. Например, чтобы рассчитать стоимость погонного метра кухонного гарнитура, необходимо его стоимость разделить на длину.

В том случае, если в торговой точке есть цена уже готового гарнитура, то цену одного погонного метра вы сможете вычислить самостоятельно.

Когда вы будете знать какая длина мебели вам понадобиться, вы можете умножить полученное число на количество метров, так вы узнаете стоимость мебели для комнаты.

Необходимо учитывать, то что в цену кухонного гарнитура не входит цена мойки, варочной поверхности. Часто продавцы в магазинах не включают в цену погонного метра ручки, и другие аксессуары. Вот по этой причине за погонный метр готового изделия приходиться платить больше, чем изначально. Лучше всего такие нюансы заранее оговаривать с продавцом.

труба прямошовная б/у

труба бесшовная б/у

труба спиральношовная б/у

труба круглая нержавеющая

труба профильная нержавеющая

Если Вам нужно узнать вес погонного метра трубы, арматуры или другого проката, то наиболее удобным и простым решением является наш калькулятор металла.

Сначала Вы выбираете номенклатуру, по которой хотите произвести расчет метров в тонны.

Площадь пола или потолка

Потолка и пол в обычной квартире одинаковые. Как посчитать квадратные метры? Очень просто. Если помещение мансардное, тогда потолка там нет – есть только пол и стены.
Этап № 1. Измерить длину комнаты и записать полученное число на бумаге. Если число целое, тогда пишем просто цифру. Например, 5 (м). Если число больше 5, но меньше 6, тогда придется вспомнить десятичные дроби и написать, к примеру, 5,5 (м).

Этап № 2. Измерить ширину комнаты и записать аналогично. К примеру – 3м.

Этап № 3. Теперь необходимо перемножить эти два числа. Пример: 5 x 3 = 15м. Итак, площадь пола – 15 кв. м. Следовательно, размер потолка также будет равняться 15 кв. м. Записать это число отдельно и обвести ручкой.

Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.
В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах.

Размеры и виды напольного плинтуса

Сегодня на рынке представлен широкий ассортимент плинтусов, различающихся по форме, материалу изготовления и размеру. Каждый из материалов имеет свои преимущества и особенности, а также характерные типовые размеры.

Материал изготовления плинтуса	Преимущества	Особенности	Типовой размер напольного плинтуса, мм
ширина	высота
Массив дерева	Хорошо сочетается с паркетом и ламинатом. Безопасный, экологичный, эстетичный и респектабельный вид	Непластичный материал, слабая устойчивость к повреждениям, неустойчив к высокой влажности и перепадам температур, необходимость в периодическом окрашивании (лакировании)	15 — 25	40 — 120
МДФ	Большой выбор форм, расцветок, фактур; относительно низкая стоимость; несложный монтаж; большая вариативность в сочетании с разным напольным покрытием	Слабая устойчивость к повышенной влажности, к физическому износу	15 — 25	40 — 120
Пробка	Экологичность, гибкость по небольшому радиусу, хорошая адгезия с поверхностью стены	Легко повреждается при физическом воздействии, высокая гигроскопичность, невысокая стилистическая универсальность	10-20	40-100
ПВХ	Универсальность, легкий вес, удобство в монтаже, дешевизна, практичность в уходе, гибкость, устойчивость к влаге	Хрупкость, нереспектабельный вид, вероятность выделения вредных веществ при повышенной температуре, неустойчивость к УФ-лучам	22-23	50-65, с кабель каналом до 85 мм
Полистирол	Повышенная прочность, доступная цена, безопасность, практичность в уходе, пластичность, устойчивость к влаге и ультрафиолету	Выделяют вредные летучие вещества несколько месяцев, ограниченность в стилистическом сочетании	22-23	50-65, с кабель каналом до 85 мм
Полиуретан	Устойчивость к износу и влаге, легкий вес, разнообразие структур (жесткие и гибкие виды), готовность к окрашиванию	Требуют окрашивания составами только на водной основе, поперечная (линейная) укладка формирует щели, требующие периодического заполнения	15-30	70-150
Дюрополимер	Прочность, износостойкость, экологичность, готовность к окрашиванию, не дает усадки, устойчив к влаге, плесени	Высокий вес и плотность, сложность в разрезании, ограниченность форм и профилей	15-30	70-150
Металл	Повышенная устойчивость к износу, оригинальный внешний вид, поддержка для гипсокартона	Ограниченность в использовании, высокий вес	Подбирается с учетом конструкции кабель-канала	35 — 120
Керамический плинтус	Повышенная устойчивость к влаге	Применяются только для напольного покрытия из плитки, высокая хрупкость	60-80	До 40
Керамогранит	Высокие эстетические качества, повышенная прочность, устойчивость к влаге, долгий срок эксплуатации	Тяжелый вес, сложный монтаж, высокая цена	16-90	Подбирается индивидуально

Как посчитать квадратные метры стены с дверью

Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.

Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.

Что не так с этими стенами?

Казалось бы, измерили длину и ширину пола, взяли материала впритык, а его не хватило или, наоборот, что-то слишком много осталось. В чем проблема?

Во-первых, никогда не берите материал четко по полученной квадратуре. Во-вторых, понимайте, что речь идёт не об идеальном прямоугольнике, а о реальном, то есть с погрешностями. Ошибки при вычислениях или специфика поверхности могут быть таковы, что лучше взять немного запаса. Плюс материал может испортиться: сломаться, прорваться, отколоться или что-то в этом роде, смотря о каком покрытии идет речь. Хорошо, если останется лишнее, но вот если не хватит каких-то 40 сантиметров обоев или ламината, будет очень обидно. Замечательно, если в магазине найдётся такой же материал и его не раскупят до вашего прихода или как раз завезут новый, аналогичный. А если купили через интернет? Заказывать вновь одну штуку и ждать неделю доставки?

Работа встала, все злые – нет, это не наш вариант. Мы учтем все моменты того, как правильно считать квадратные метры, и не попадем в такую ситуацию.

Измеряем площадь сложных фигур

Круг и треугольник – сложные фигуры для самостоятельного вычисления

. Как измерить квадратные метры окружности, если нет математического или инженерного образования? Опять-таки по формуле.

Как измерить размер окружности

Существует формула вычисления площади круга. Есть такое постоянное число – отношение длины окружности к ее диаметру. Оно одинаково для всех размеров круга. Называется оно пи и равняется 3,14. Вот это число и используют при подсчетах.
Этап № 1. Замеряем диаметр (это линия, которая проходит через центр круга от одного края окружности к другому). Пускай диаметр будет равняться 3 м. Далее находим радиус – это половина длины диаметра. То есть 1,5 м. Записываем радиус на бумагу.

Этап № 2. Производим расчеты по формуле S = ПR2, где S – это площадь круга, П – постоянное число, а R – радиус окружности. Получается 3,14 x (1,5 x 1,5) = 7, 065. Площадь данного круга – 7,065 кв. м.

Но это площадь целого круга. Арка над дверью – это половина круга. Значит, еще нужно разделить данное число на два и далее прибавить к прямоугольной площади двери. 7,065 : 2 = 3,53 м2.

Как измерить площадь треугольника

Если предыдущий хозяин квартиры был математик, то он вполне мог сделать на потолке треугольные фигуры, которые приходится реставрировать и выделять другим цветом или штукатуркой. Придется считать, чтобы не переплачивать.

Расчет метра квадратного в треугольной фигуре начинается с внимательного осмотра этой фигуры.

Необходимо найти основание треугольника, то есть линию, на которую опираются две других (как крыша на доме). Далее провести линию из противоположной верхушки к основанию. Эти два числа записать.

Как самостоятельно рассчитать площадь дома

Не забывайте о том, что каждый «лишний» квадратный метр несет в себе как материальные, так и трудовые затраты: уборка и ремонт.

Ваша задача – найти оптимальный размер дома, строительство которого не ударит по карману, а уход за ним не будет обременителен.

Безусловно, метраж дома зависит от финансовых возможностей, однако, обязательно высчитайте минимальную полезную общую площадь на всех членов семьи с учетом того, что у каждого должно быть свое независимое пространство.

Для комфортного проживания 1 взрослого человека, достаточно 30 м2, а для ребенка – 12м2. Отсюда можно высчитать площадь, необходимую для небольшой семьи: по подсчетам, это как минимум 80 – 90 м2.

При подсчете рекомендуется учитывать размер минимальной площади на каждого члена семьиИсточник moranie.com.br

Советы и рекомендации

Таким образом можно высчитать площадь всей квартиры и расписать, что и каким цветом красить. Размеры всех стен и потолка сложить – получится число, на которое надо будет ориентироваться при покупке стройматериалов.

При расчетах лучше пригласить еще одного человека в помощь. Одна голова хорошо, а две надежнее.

Дело за малым – пойти в магазин и купить материалы. Здесь еще придется считать, так как не все упаковки предназначены для больших помещений. К примеру, размер потолка на кухне 3 x 3. Сколько квадратных метров штукатурки понадобится, если одной упаковкой можно покрыть 3 кв. м? Считаем: размер потолка 9 кв. м. Одна упаковка уходит на 3 кв. м. Следовательно, на весь потолок необходимо 3 пачки.

Если на упаковке написано, что расход на 12 квадратных метров, это означает, сколько материала надо, чтобы покрыть стену размером 3 x 4 м.

Или другой пример. Стена в квартире 6 на 4. Сколько квадратных метров необходимо закрасить? Умножаем 6 на 4, получаем 24 квадратных метра. Это сколько нужно банок краски по 3 л, если каждая банка расходуется на 6 кв. м? Считаем: 24 делим на 6. Получается 4. Значит, необходимо купить 4 трехлитровых банки краски для покрытия всей стены.

Для ремонтных работ всегда лучше взять немного больше материалов, чтобы потом не идти лишний раз в магазин.

В будущем, если придется что-то подкрасить или подбелить, остатки материалов могут здорово выручить.

Немного теории

Как найти площадь различных фигур, проходили еще в начальной школе. Было это давно, так что «обновить» информацию может быть полезно. Будем рассматривать только то, что может иметь отношение к полу. Итак, начнем с самого простого — единиц измерения.

Чтобы посчитать площадь комнаты в квадратных метрах, нужен будет карандаш, рулетка и некоторый багаж знаний

Что такое 1 см² и 1 м²

Площадь любой фигуры измеряется в квадратных метрах или в квадратных сантиметрах. Обозначение см² или м², может встречаться написание кв.м, кв. см., кв. метры, кв. сантиметры и другие вариации.

Что такое один квадратный сантиметр

Один квадратный сантиметр — это площадь квадрата со стороной 1 см. Если нарисовать такой квадрат, стороны которого равны 1 см, то заштрихованная часть (на рисунке красным или синим) и будет один квадратный сантиметр. Соответственно, квадрат со стороной один метр — 1 м — имеет площадь один квадратный метр. Тот самый «квадрат площади». То есть, это квадратный участок пола (или стены) со стороной в один метр — 1 м². В одном квадратном метре десять тысяч квадратных сантиметров: 1 м² = 10000 см².

Формулы

Это то, что касалось единиц измерения и их соответствия. Но наши помещения, слава богу, больше чем один квадратный метр. Как посчитать площадь комнаты? Сколько в ней квадратных метров? Обычно комната имеет форму прямоугольника, реже — квадрата. Значит, надо будет вспомнить формулы нахождения площади квадрата и прямоугольника.

При помощи очень простых формул, можно рассчитать площадь прямоугольника и квадрата

Надо длины сторон прямоугольника перемножить. Получим искомую площадь. Давайте потренируемся.

В случае с квадратом длину стороны можно возвести в квадрат — получится одно и то же. Но можно не морочить голову. Проще помнить, что надо стороны умножить.

Число соток в 1 га

При очень большой площади земли использовать размер в сотках неудобно. На аграрных земельных участках размеры наделов меряют в гектарах. Один гектар эквивалентен ста соткам, или равен десяти тысячам м2. Стоит отметить, что в документах участки регистрируют в гектарах.

1 гектар – это сколько м2?

Крупные территории земель совхозов или фермерских хозяйств бывают габаритами в десятки квадратных километров. Определим, сколько это в сотках. Но стоит оговориться заранее, что такие размеры в метрах или сотках считать неудобно. Удобнее использовать гектары.

Для определения размеров земельного надела в сотках нужно найти площадь 1 км2 в метрах квадратных. Умножая 1 тысячу на 1 тысячу метров, получаем 1 миллион квадратных метров.

В данном случае измерять площади в гектарах удобнее, чем это делать в сотках или в метрах квадратных. Стоит отметить, что в некоторых других западных странах используют для измерений акр.

Как посчитать площадь комнаты в квадратных метрах

Рассчитать площадь комнаты, часто надо при закупке материалов для строительства или ремонта. Например, некоторые виды напольного покрытия продают на квадраты (то есть, на квадратные метры). Чтобы правильно рассчитать его количество, надо знать площадь пола (часто говорят квадратура комнаты, что по сути одно и то же).

Можно найти площадь комнаты зная длину и ширину

Измерения

Берем рулетку, листок бумаги, карандаш и калькулятор. На бумаге рисуем план комнаты. При помощи рулетки измеряем длины всех стен. Измерения проводим на уровне пола — если постройка старая, велика вероятность того, что стены «завалены» в ту или другую сторону. Тем более что определяем площадь пола, так что логичнее измерять вплотную к стенам, но мерную ленту тянуть по полу.

На схеме проставляем измерения. Лучше всего в метрах. Точность измерений — до сантиметра. Это понадобится при покупке материалов, которые продаются на погонные метры — линолеум, ковролин или другие рулонные покрытия. Чтобы посчитать площадь комнаты в квадратных метрах, тоже желательна такая точность. Хоть можно, конечно, и округлить. Но лучше это сделать уже получив результат.

Как высчитать квадратуру комнаты

Имея длину и ширину комнаты прямоугольной формы, цифры надо просто перемножить. На рисунке выше такая комната нарисована справа. Длинная стена равна 7 м, короткая — 4 метрам. Перемножаем 7*4 = 28 квадратных метров. Это и есть площадь этого помещения, пола. Другими словами, мы нашли квадратуру. Используя эту цифру, можно покупать напольное покрытие. Но надо иметь в виду, что требуется некоторый запас — на подгонку, подрезку. Чем сложнее схема укладки и чем больше фрагменты напольного покрытия, тем запас должен быть больше.

Часто комната не прямоугольная, а имеет более сложную форму. Чтобы посчитать площадь такой комнаты в квадратных метрах, ее разбивают на простые фигуры. Если удается — на прямоугольники или квадраты. Например, Г-образную комнату разбивают на два прямоугольника. Затем считают площадь каждого прямоугольника отдельно, потом их складывают.

Как найти площадь комнаты сложной формы

При покупке материалов, проще пользоваться округленными значениями. Чаще всего говорят, что в этом помещении 28,4 квадрата.

Если помещение имеет участок «срезанной» стены, как на рисунке ниже, проще всего дорисовать прямоугольник так, чтобы косая делила его на два треугольника. В этом случае снова-таки получаем Г-образную комнату. Как высчитать ее площадь уже знаем.

Получается, ищем площадь трех прямоугольников

А недостающий участок — это половина маленького прямоугольника. То есть, находим площадь этого маленького прямоугольника, делим ее пополам и прибавляем к размерам Г-образного участка.

Приведем пример расчета подставляя произвольные значения:

Такая методика — разбиение на простые фигуры — самый удобный и простой метод. Всегда стоит стараться преобразовать сложную фигуру в набор простых. Правда, измерений может потребоваться больше.

Объем комнаты

Кубатура помещения, или объём в строительстве используется при подсчёте необходимой мощности отопления, вентиляции, кондиционирования комнаты.
Объём измеряется в кубических метрах. Единица записывается как 1 м³.

С точки зрения геометрии, помещение как фигура представляет собой шестигранник.

Измерив длину, ширину и высоту комнаты прямоугольной формы, перемножив полученные измерения, получают объём простого помещения.

Объём помещения сложной формы вычисляют следующим путём:

Рекомендуем: Как просто и правильно вырезать угол на потолочном плинтусе? Методы зарезания и стыковки углов своими руками

Площадь квартиры

Так как ремонт — это «бедствие», которое периодически нас посещает, лучше сделать план всей квартиры с подробными замерами. На этом же плане проставьте площади каждого помещения. После того, как рассчитаете квадратуру всех комнат, сложите цифры и получите метраж квартиры.

Для плана лучше рассчитать метраж каждой комнаты

Один вариант может быть как на рисунке выше — для того, чтобы знать именно площади каждого помещения. Это потребуется для закупки материалов. Но нужен будет еще план, на котором будут все длины. Простенки, ширина окон, дверей и т.д. Это потребуется, например, для разработки схем укладки ламината, напольной плитки или других покрытий. Нужен будет такой план и при планировании теплого пола.

Есть, кстати, приложение-калькулятор для телефона, при помощи которого все вычисления сделать очень просто.

Источник

Как найти площадь и периметр квадрата

Квадрат, свойства и формулы, площадь и периметр

Квадрат – это правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.

Видео

Площадь квадрата

Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см

Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.

Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см

В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:

Как найти площадь квадрата?

Вычисление площади данной фигуры можно просто и легко объяснить на примере:

Площадь геометрической фигуры

Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.

Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.

Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.

Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.

Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:

Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.

Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:

Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:

Допустим, потребовалось измерить площадь следующей комнаты:

Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:

Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:

Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.

Свойства квадрата:

1. Длины всех сторон равны.

2. Противоположные стороны квадрата параллельны.

3. Все углы квадрата прямые. Каждый из них равен 90°.

4. Сумма углов квадрата равна 360 градусам.

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°.

5. Диагонали квадрата равны между собой.

6. Диагонали квадрата взаимно перпендикулярны.

7. Диагонали квадрата точкой пересечения делятся пополам.

8. Угол между диагональю и стороной квадрата равен 45 градусам.

9. Диагонали квадрата являются биссектрисами углов и делят углы пополам.

10. Каждая из диагоналей делит квадрат на два равных равнобедренных прямоугольных треугольника.

11. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности.

Источник

Площадь квадрата

Свойства

Зная площадь квадрата, легко найти его сторону. Для этого из заданного значения площади необходимо извлечь квадратный корень. S=a^2 a=√S

Периметр квадрата получится равным четырем таким корням. P=4a=4√S

Для того чтобы найти диагональ квадрата, зная площадь, необходимо так же подставить вместо стороны полученное выражение. d=√2 a=√2S

Углы пересечения диагоналей со сторонами и друг с другом останутся неизменными. (рис. 69.1) m(

Радиус вписанной в квадрат окружности через площадь квадрата можно найти, подставив в формулу вместо стороны квадратный корень из площади. r=a/2=√S/2

Для того чтобы найти радиус описанной окружности через площадь квадрата, нужно разделить сторону не на два, а на корень из двух. Тем самым, корни объединятся, и получится, что радиус равен корню из половины площади. R=a/√2=√S/√2=√(S/2)

Источник

Геометрия

План урока:

Понятие площади многоугольника

Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.

Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м 2 ):

Аналогично можно определить такие величины, как квадратный сантиметр (см 2 ), квадратный километр (км 2 ), квадратный миллиметр (мм 2 ) и т.д.:

Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.

Общепринято, что площадь фигуры обозначается буквой S.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m 2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R 2 ):

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Соотношение между единицами измерения площадей

Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:

В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:

Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см 2 равен 100 мм 2 :

Площадь прямоугольника

Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.

Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):

Итак, мы доказали следующее утверждение:

Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?

Решение. Просто перемножаем эти числа:

Задание. Найдите площадь фигуры, изображенной на рисунке:

Решение. Необходимо разбить фигуры на несколько прямоугольников:

Далее считаем площадь каждого отдельного прямоугольника:

Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?

Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:

Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:

Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно

Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.

Решение. Запишем формулу площади прямоугольника:

Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.

Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел

Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна

Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:

Это обычное квадратное уравнение, решаемое с помощью:

Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна

Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:

Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:

Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:

В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.

Источник