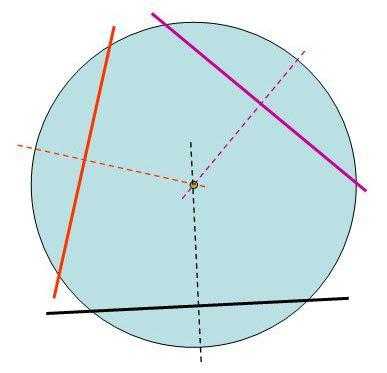
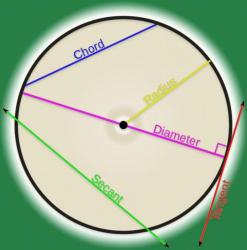
Как рассчитать хорду окружности
Как рассчитать хорду окружности
Длина хорды окружности
В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром.
Определение длины хорды окружности
Формула расчёта длинны хорды
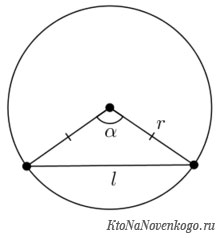
Длина хорды окружности может быть определена по формуле:
r – радиус окружности
O – центр окружности
α – центральный угол
Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения.
Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты. Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий.
Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды. При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника.
Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры).
Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | ||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность |  | |||||||||||||||||||||||||||||||||||||||||||||||||
| Круг | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Конечная часть плоскости, ограниченная окружностью | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Радиус | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Отрезок, соединяющий центр окружности с любой точкой окружности | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Хорда | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Отрезок, соединяющий две любые точки окружности | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Диаметр | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Хорда, проходящая через центр окружности. Диаметр является самой длинной хордой окружности | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Касательная | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Прямая, имеющая с окружностью только одну общую точку. Касательная перпендикулярна к радиусу окружности, проведённому в точку касания | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Секущая | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Прямая, пересекающая окружность в двух точках Свойства хорд и дуг окружности
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Диаметр, проходящий через середину хорды | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Равные хорды | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Хорды, равноудалённые от центра окружности | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Две хорды разной длины | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Большая из двух хорд расположена ближе к центру окружности. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Равные дуги | ||||||||||||||||||||||||||||||||||||||||||||||||||
 У равных дуг равны и хорды. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Параллельные хорды | ||||||||||||||||||||||||||||||||||||||||||||||||||
 Дуги, заключённые между параллельными хордами, равны. Теоремы о длинах хорд, касательных и секущих
Произведения длин отрезков, на которые разбита каждая из хорд, равны: Касательные, проведённые к окружности из одной точки | Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны. Касательная и секущая, проведённые к окружности из одной точки | Доказательства теорем о длинах хорд, касательных и секущихТогда справедливо равенство откуда и вытекает требуемое утверждение. Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство откуда и вытекает требуемое утверждение. Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство Точка B – точка касания. В силу теоремы 2 справедливы равенства откуда и вытекает требуемое утверждение. Теорема о бабочкеВоспользовавшись теоремой 1, получим Воспользовавшись равенствами (1) и (2), получим откуда вытекает равенство что и завершает доказательство теоремы о бабочке. Хорда в геометрииКаждая хорда имеет свою длину. Ее можно определить с помощью теоремы синусов. То есть длина хорды окружности зависит от радиуса и вписанного угла, опирающегося на данный отрезок. Формула для определения длины выглядит следующим образом: B*A = R*2 * sin α, где R — радиус, AB — это хорда, α — вписанный угол. Также длину можно вычислить через другую формулу, которая выводится из теоремы Пифагора: B*A = R*2 * sin α/2 , где AB — это хорда, α — центральный угол, который опирается на данный отрезок, R — радиус. Если рассматривать хорды в совокупности с дугами, то получаются новые объекты. Например, в кругу можно дополнительно выделить две области: сектор и сегмент. Сектор образуется с помощью двух радиусов и дуги. Для сектора можно вычислить площадь, а если он является частью конуса, то еще и высоту. Сегмент, в свою очередь, это область, состоящая из отрезка и дуги. Для того чтобы проверить правильность своего решения в нахождении длины, можно обратиться к онлайн-калькуляторам в интернете. Они представлены в виде таблицы, в которую нужно вписать только известные параметры, а программа сама выполнит необходимые вычисления.
Свойства отрезка окружностиДля решения геометрических задач необходимо знать свойства хорды окружности. Для нее характерны такие показатели:
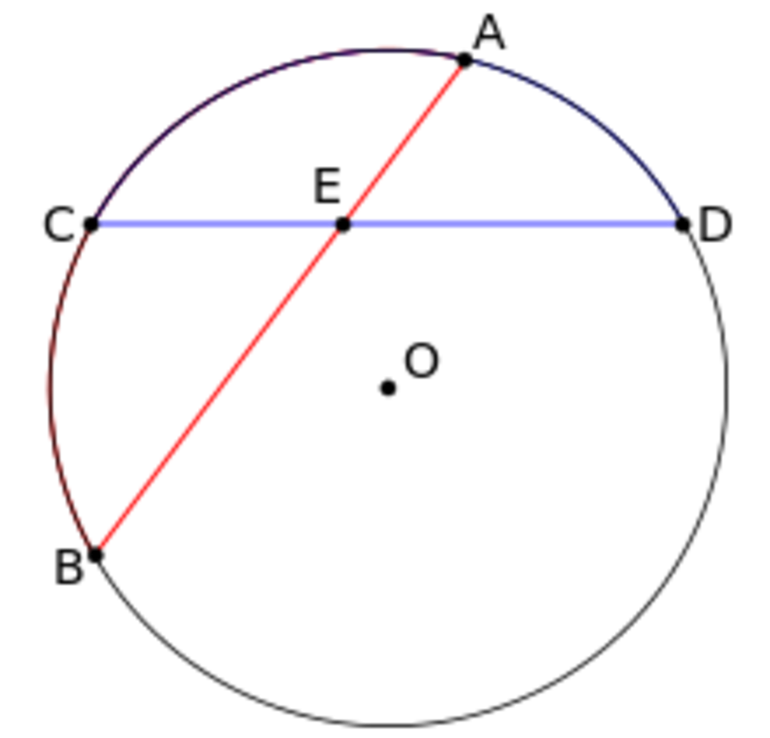
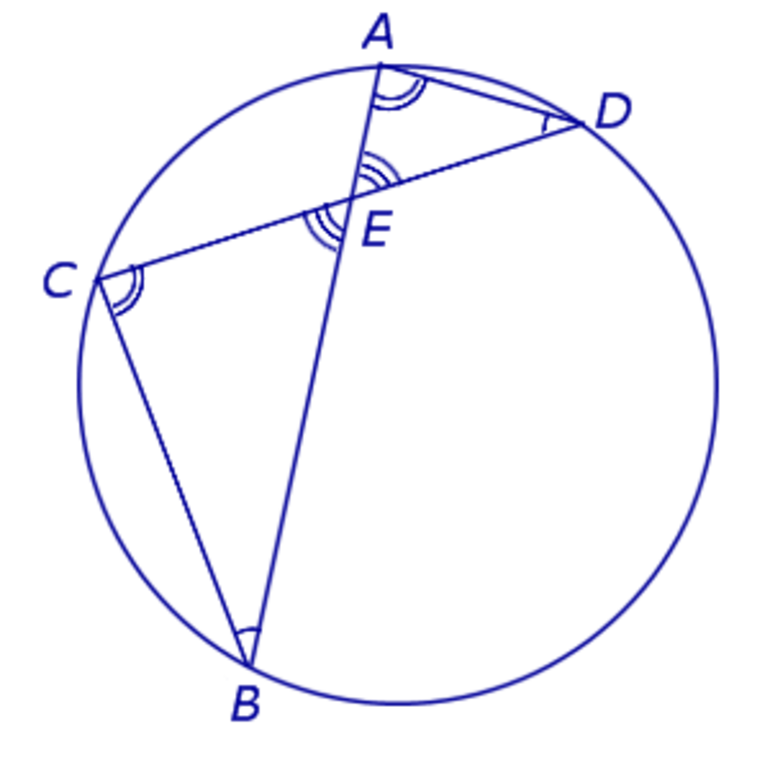
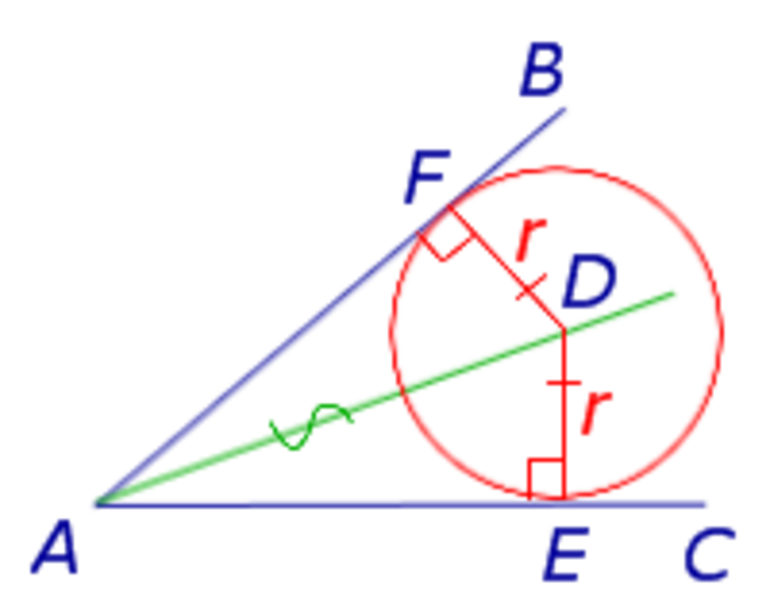
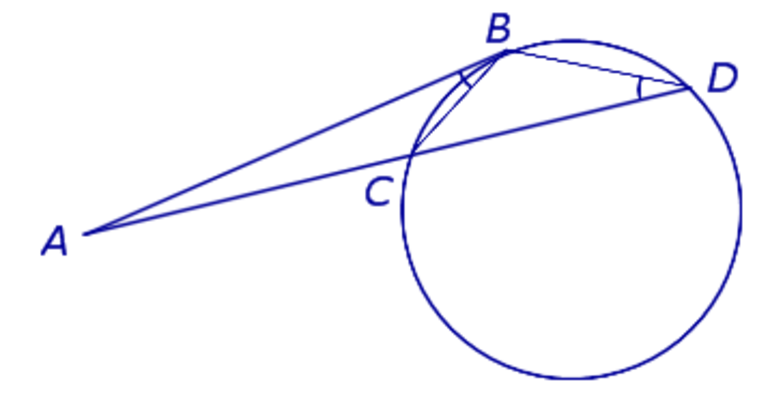
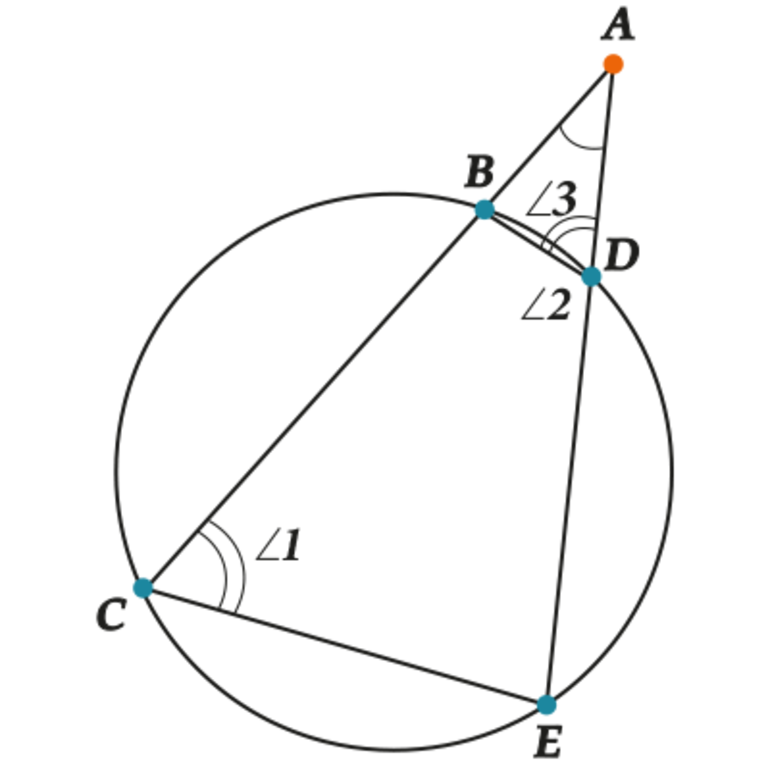
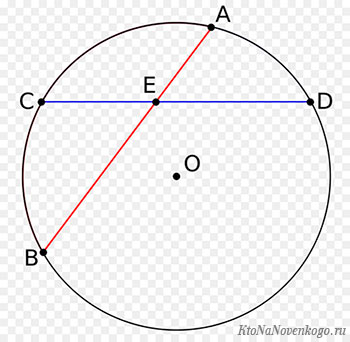
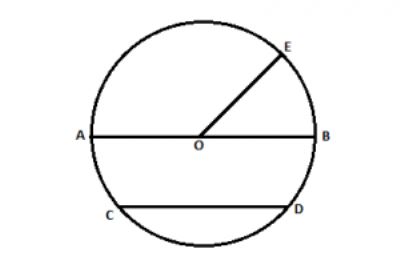
Ключевая теоремаИмеется круг с центром в точке O и радиусом R. Для теоремы нужно в круг вписать две прямые, пускай это будут хорды BA и CD, которые пересекаются в точке E. Перед тем как перейти к доказательству, нужно сформулировать определение теоремы. Оно звучит следующим образом: если хорды пересекаются в некоторой точке, которая делит их на отрезки, то произведения длин отрезков первой хорды равно произведению длин отрезков второй хорды. Для наглядности можно записать эту формулу: AE*BE= EC*ED. Теперь можно перейти к доказательству. Проведем отрезки CB и AD. Рассмотрим треугольники CEB и DEA. Известно, что углы CEB и DEA равны как вертикальные углы, DCB и BAD равны за следствием с теоремы про вписанные углы, которые опираются на одну и ту же дугу. Треугольники CEB и DEA подобны (первый признак подобия треугольников). Тогда выходит пропорциональное соотношение BE/ED = EC/EA. Отсюда AE*BE= EC*ED. Помимо взаимодействия с внутренними элементами окружности, для хорды еще существуют свойства при пересечении с секущейся и касательными прямыми. Для этого необходимо рассмотреть понятия касательная и секущая и определить главные закономерности. Касательная — это прямая, которая соприкасается с кругом только в одной точке. И если к ней провести радиус круга, то они будут перпендикулярны. В свою очередь, секущая — это прямая, которая проходит через две точки круга. При взаимодействии этих прямых можно заметить некоторые закономерности. Касательная и секущаяСуществует теорема о двух касательных, которые проведены с одной точки. В ней говорится о том, что если есть две прямые OK и ON, которые проведены с точки O, будут равны между собой. Перейдем к доказательству теоремы. Рассмотрим два прямоугольных треугольника AFD и AED. Поскольку катеты DF и DE будут равны как радиусы круга, а AD — общая гипотенуза, то между собой данные треугольники будут равны за признаком равенства треугольников, с чего выходит, что AF = AE.
Предположим у нас есть касательная AB и секущая AD, которые берут начало с одной точки A. Обратим внимание на угол ABC, он спирается на дугу BC, значит, за свойством значение его угла будет равно половине градусной меры дуги, на которую он опирается. За свойством вписанного угла, величина угла BDC также будет равно половине дуги BC. Таким образом, треугольники ABD и ABC будут подобны за признаком подобия треугольников, так как угол A — общий, а угол ABC равен углу BDC. Опираясь на теорию, получаем соотношение: AB/CA = DA/AB, переписав это соотношение в правильную форму, получаем равенство AB 2 = AD*AC, что и требовалось доказать. Как есть теорема про две касательные, так есть и теорема про две секущие. Она так же просто формулируется, как и остальные теоремы. Поэтому рассмотрим доказательство и убедимся, что AB*AC = AE*AD. Проведем две прямые через точку A, получим две секущие AC и AE. Дорисуем две хорды, соединяя точки C и B, B и D. Получим два треугольника ABD И CEA. Обратим внимание на вписанный четырехугольник BDCE. За свойством вписанных четырехугольников узнаем, что значения углов BDE и ECB в сумме будут давать 180 градусов. И сумма значений углов BDA и BDE также равна 180, за свойством смежных углов. Отсюда можно получить два уравнения, из которых будет выведено, что углы ECB и BDA будут равны: BDA + BDE = 180; BDE + ECB = 180. Все это записываем в систему уравнений, отнимаем первое от второго, получаем результат, что ECB = BDA.
Решение задачПри решении задач, связанных с окружностью, хорда часто выступает главным элементом, опираясь на который можно найти остальные неизвестные элементы. В каждой второй задаче задаются два параметра, чтобы найти третий неизвестный. В задачах, которые, связанные с кругом, хорда — это обязательный элемент:
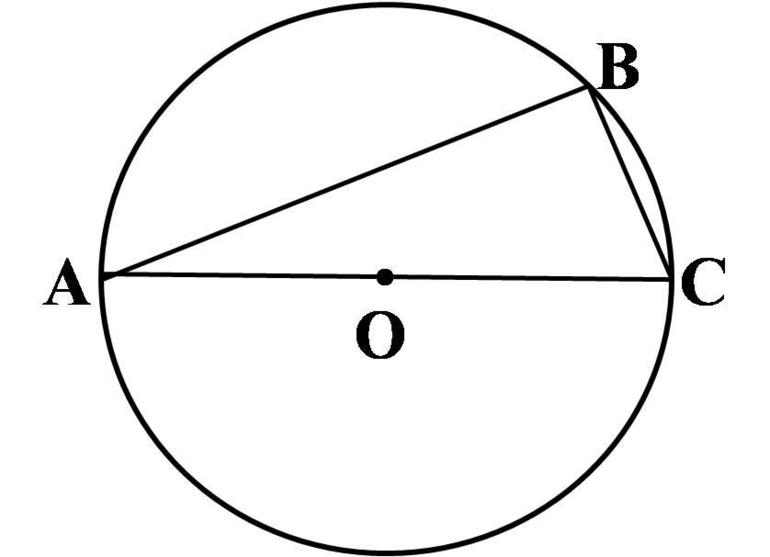
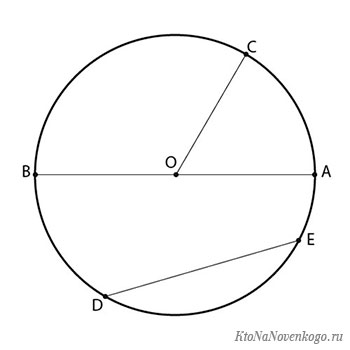
Хорда — это геометрическая струнаЗдравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы подробно расскажем, что такое ХОРДА. Слово это имеет древнегреческие корни и переводится как «струна». Это очень точно характеризует ее внешний вид, так как хорда представляет собой прямую линию. Хорда — это.Термин ХОРДА применяется сразу в нескольких областях: В геометрии хорда – это часть прямой, которая проходит между двумя точками на окружности или эллипсе; Но в рамках этой статьи мы подробно рассмотрим первый вариант значения термина ХОРДА. Тот, который применяют в геометрии, и который школьники подробно изучают в 7 классе. Что такое хорда в геометрииХорда – это отрезок прямой, которая проходит через две точки на любой кривой линии. Это могут быть окружность, эллипс, гипербола или парабола. Выглядит хорда вот так: На этом рисунке изображены сразу две хорды – AB и CD. А есть еще частный случай, когда хорда проходит через центр окружности. Такая хорда, на данном рисунке это отрезок AB, будет являться диаметром окружности. И как нетрудно догадаться, это самая длинная хорда, которая может быть для данного примера. Свойства хордыЕсли сравнивать хорду с другими частями окружности, то можно вывести целый ряд закономерностей. Например, хорда и радиус: Хорда и диаметр: Хорда и центр окружности: И еще одно свойство хорд в окружности. Если взять уже знакомый нам рисунок расположенный сразу под определением, то при пересечении хорд получается вот такая зависимость – произведение частей одной хорды равна произведению частей другой: Как рассчитать длину хордыДлина хорды – это расстояние от одной точки пересечения с окружностью до другой. Чаще всего она обозначается латинской буквой «L». Чтобы рассчитать длину хорды, надо знать значение радиуса и центрального угла. Формула выглядит так: Вот и все, что мы хотели рассказать о ХОРДЕ. Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru Эта статья относится к рубрикам: Комментарии и отзывы (1)Не знаю, что делать школьникам с этими знаниями, вот мне эти хорды нигде не пригодились, далеко не всю геометрию можно направить в практическое русло. Как найти хорду окружности?Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой. Для любой точки L, лежащей на окружности, действует равенство OL=R. (Длина отрезка OL равняется радиусу окружности). Окружность. Длина окружности. Касательная, дугаОтрезок, который соединяет две точки окружности, является ее хордой. Хорда, проходящая прямо через центр окружности, является диаметром этой окружности (D). Диаметр можно вычислить по формуле: D=2R Длина окружности вычисляется по формуле: C=2pi R Площадь круга: S=pi R^ Дугой окружности называется та ее часть, которая располагается между двух ее точек. Эти две точки и определяют две дуги окружности. Хорда CD стягивает две дуги: CMD и CLD. Одинаковые хорды стягивают одинаковые дуги. Центральным углом называется такой угол, который находится между двух радиусов. Длину дуги можно найти по формуле: Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам. В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой. ANcdot NB = CN cdot ND Касательная к окружностиКасательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью. Если же у прямой есть две общие точки, ее называют секущей. Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности. Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке. Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. Можно сделать вывод: произведение целого отрезка первой секущей на его внешнюю часть равняется произведению целого отрезка второй секущей на его внешнюю часть. AC cdot BC = EC cdot DC Углы в окружностиГрадусные меры центрального угла и дуги, на которую тот опирается, равны. angle COD = cup CD = alpha ^ Вписанный угол — это угол, вершина которого находится на окружности, а стороны содержат хорды. Вычислить его можно, узнав величину дуги, так как он равен половине этой дуги. angle AOB = 2 angle ADB Опирающийся на диаметр, вписанный угол, прямой. angle CBD = angle CED = angle CAD = 90^ Вписанные углы, которые опираются на одну дугу, тождественны. angle ADB = angle AEB = angle AFB Опирающиеся на одну хорду вписанные углы тождественны или их сумма равняется 180^ angle ADB + angle AKB = 180^ angle ADB = angle AEB = angle AFB На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием. Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов. angle DMC = angle ADM + angle DAM = frac<1> <2>left ( cup DmC + cup AlB ight ) Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла. angle M = angle CBD — angle ACB = frac<1> <2>left ( cup DmC — cup AlB ight ) Вписанная окружностьВписанная окружность — это окружность, касающаяся сторон многоугольника. В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр. Окружность может быть вписанной не в каждый многоугольник. Площадь многоугольника с вписанной окружностью находится по формуле: p — полупериметр многоугольника, r — радиус вписанной окружности. Отсюда следует, что радиус вписанной окружности равен: Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны. В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности. Радиус вписанной окружности вычисляется по формуле: Описанная окружностьЕсли окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника. В точке пересечения серединных перпендикуляров сторон этой фигуры будет находиться центр описанной окружности. Радиус можно найти, вычислив его как радиус окружности, которая описана около треугольника, определенного любыми 3-мя вершинами многоугольника. Есть следующее условие: окружность возможно описать около четырехугольника только, если сумма его противоположных углов равна 180^< circ>. angle A + angle C = angle B + angle D = 180^ Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника. Радиус описанной окружности можно вычислить по формулам: Теорема ПтолемеяПод конец, рассмотрим теорему Птолемея. Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника. Секущая и хорда окружностиЗачем что-то знать о секущих и хордах в окружности? Как обычно, знание свойств и закономерностей сильно облегчает жизнь. Зная свойства секущих и хорд в окружности и закономерности (формулы), мы сможем решить многие задачи на ЕГЭ! Секущая и хорда окружности — коротко о главномСекущая окружности Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках. Хорда окружности Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности. Длина хорды Пусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle AСB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\). Тогда: \( \displaystyle AB=2R\sin \alpha\). Произведение длин отрезков хорд и секущих Для любых двух хорд, проходящих через некоторую точку \( \displaystyle A\), выполняется: \( \displaystyle AB\cdot AC=AD\cdot AE\). Теорема о секущей и касательной Для любых секущей и касательной, проходящих через точку \( A\), верно: \( \displaystyle A< А теперь подробнее… Определения секущей и хорды окружностиДавай прежде всего вспомним, что такое секущая и хорда. Смотри на картинки. Здесь \( \displaystyle AC\) – секущая окружности – начинается снаружи окружности и пересекает её в двух точках. Здесь \( \displaystyle BC\) – хорда окружности – отрезок, соединяющий две точки на окружности. Кстати, заметил ли ты, что на первом рисунке хорда \( \displaystyle BC\) является кусочком секущей \( \displaystyle AC\)? Вот так всегда и бывает: если есть секущая, то один её кусок – хорда, а второй называется внешняя часть, ну, как у нас \( \displaystyle AB\) – она же снаружи, верно? Что же мы должны знать о секущей и хорде окружности? Всего-то 2-3-4 утверждения. Давай начнём с того, что ты, возможно, уже читал в разделе «Теорема синусов» и «Теорема косинусов» — с длины хорды в окружности. Длина хорды окружностиПусть \( \displaystyle AB\) – хорда, \( \displaystyle R\) – радиус, \( \displaystyle \angle ACB\) – любой вписанный угол, опирающийся на хорду \( \displaystyle AB\). Тогда \( \Large\frac Узнал теорему синусов? Значит, длину хорды окружности можно найти по формуле: Открыть ответы…Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз: Произведение длин отрезков хорд и секущихСейчас мы сформулируем очень важное, пожалуй, даже основное свойство хорд и секущих окружности. Словами это свойство формулировать неудобно – получается длинно и некрасиво, поэтому ограничимся буквами. Произведение длин отрезков хорд окружности
Произведение длин отрезков секущих окружности
Вопрос первый: Почему мы сформулировали утверждения друг под другом столбиком? Ответ: Утверждения очень похожи – если закрыть картинки и слова, то получится просто одно и то же – удивительно, не правда ли? Ну, и это сходство гораздо лучше видно, когда утверждения стоят рядом. Вопрос второй: Как не перепутать, что на что умножать? Хорда окружностиНа одном из последних заказов пришлось освежить свои знания геометрии. Давайте сделаем это вместе. Что такое хорда Хорду окружности можно определить как отрезок прямой, соединяющий любые две точки на окружности. Следует отметить, что диаметр является самой длинной хордой окружности, которая проходит через центр окружности. На рисунке ниже изображен круг и его хорда. В данном круге с O в качестве центра, AB представляет диаметр круга (самая длинная хорда), OE обозначает радиус круга и CD представляет собой хорду круга. Формула длины хорды Существует две основные формулы для нахождения длины хорды круга:
Расчет длины хорды окружности – Формула длины хорды окружностиДлина хорды окружностиВ элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром. Определение длины хорды окружности Длина хорды окружности может быть определена по формуле: r – радиус окружности O – центр окружности α – центральный угол Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения. Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты. Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий. Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды. При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника. Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры). Формула высоты сегмента кругаСегмент — часть круга ABC, отсеченная хордой AC h — высота сегмента ABC L — хорда AC R — радиус кружности O — центр окружности α — центральный угол AOC Формула высоты через радиус и центральный угол, (h): Сегмент круга — расчет параметров онлайнДанный калькулятор считает параметры сегмента круга, а именно: Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента: 1) сегмент круга решается с помощью радиуса (R) и угла (A). 2) сегмент круга находим с помощью высоты и длины хорды. The field is not filled. ‘%1’ is not a valid e-mail address. Please fill in this field. The field must contain at least% 1 characters. The value must not be longer than% 1 characters. Field value does not coincide with the field ‘%1’ An invalid character. Valid characters:’%1′. It is expected a positive number. It is expected a positive integer. The ‘% 1’ is already present in the set of valid characters. The first character must be a letter of the Latin alphabet. An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3 Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,). Wrong file format. Only the following formats: %1 Please leave your phone number and / or email. Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. |
Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. При пользовании таблицей при радиусах, не равных 1, следует умножить l, h и C на величину радиуса, а площадь сегмента умножить на квадрат радиуса. Центральный угол в градусах Длина дуги lo Стрелка h 1/h Длина хорды с Площадь сегмента | |||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 0,0175 | 0,0000 | 458,36 | 0,0175 | 0,00000 | |||||||||||||||||||||||||||||||||||||||||||||
| 2 | 0,0349 | 0,0002 | 229,19 | 0,0349 | 0,00000 | |||||||||||||||||||||||||||||||||||||||||||||
| 3 | 0,0524 | 0,0003 | 152,79 | 0,0524 | 0,00001 | |||||||||||||||||||||||||||||||||||||||||||||
| 4 | 0,0698 | 0,0006 | 114,60 | 0,0698 | 0,00003 | |||||||||||||||||||||||||||||||||||||||||||||
| 5 | 0,0873 | 0,0010 | 91,69 | 0,0872 | 0,00006 | |||||||||||||||||||||||||||||||||||||||||||||
| 6 | 0,1047 | 0,0014 | 76,41 | 0,1047 | 0,00010 | |||||||||||||||||||||||||||||||||||||||||||||
| 7 | 0,1222 | 0,0019 | 64,01 | 0,1221 | 0,00015 | |||||||||||||||||||||||||||||||||||||||||||||
| 8 | 0,1396 | 0,0024 | 56,01 | 0,1395 | 0,00023 | |||||||||||||||||||||||||||||||||||||||||||||
| 9 | 0,1571 | 0,0031 | 50,96 | 0,1569 | 0,00032 | |||||||||||||||||||||||||||||||||||||||||||||
| 10 | 0,1749 | 0,0038 | 45,87 | 0,1743 | 0,00044 | |||||||||||||||||||||||||||||||||||||||||||||
| 11 | 0,1920 | 0,0046 | 41,70 | 0,1917 | 0,00059 | |||||||||||||||||||||||||||||||||||||||||||||
| 12 | 0,2094 | 0,0055 | 38,23 | 0,2091 | 0,00076 | |||||||||||||||||||||||||||||||||||||||||||||
| 13 | 0,2269 | 0,0064 | 35,28 | 0,2264 | 0,00097 | |||||||||||||||||||||||||||||||||||||||||||||
| 14 | 0,2443 | 0,0075 | 32,78 | 0,2437 | 0,00121 | |||||||||||||||||||||||||||||||||||||||||||||
| 15 | 0,2618 | 0,0086 | 30,60 | 0,2611 | 0,00149 | |||||||||||||||||||||||||||||||||||||||||||||
| 16 | 0,2793 | 0,0097 | 28,04 | 0,2783 | 0,00181 | |||||||||||||||||||||||||||||||||||||||||||||
| 17 | 0,2967 | 0,0110 | 27,01 | 0,2956 | 0,00217 | |||||||||||||||||||||||||||||||||||||||||||||
| 18 | 0,3142 | 0,0123 | 25,35 | 0,3219 | 0,00257 | |||||||||||||||||||||||||||||||||||||||||||||
| 19 | 0,3316 | 0,0137 | 24,17 | 0,3301 | 0,00302 | |||||||||||||||||||||||||||||||||||||||||||||
| 20 | 0,3491 | 0,0152 | 22,98 | 0,3473 | 0,00352 | |||||||||||||||||||||||||||||||||||||||||||||
| 21 | 0,3665 | 0,0167 | 21,95 | 0,3645 | 0,00408 | |||||||||||||||||||||||||||||||||||||||||||||
| 22 | 0,3840 | 0,0184 | 20,90 | 0,3816 | 0,00468 | |||||||||||||||||||||||||||||||||||||||||||||
| 23 | 0,4014 | 0,0201 | 20,00 | 0,3987 | 0,00535 | |||||||||||||||||||||||||||||||||||||||||||||
| 24 | 0,4189 | 0,0219 | 19,17 | 0,4158 | 0,00607 | |||||||||||||||||||||||||||||||||||||||||||||
| 25 | 0,4363 | 0,0237 | 18,47 | 0,4329 | 0,00686 | |||||||||||||||||||||||||||||||||||||||||||||
| 26 | 0,4538 | 0,0256 | 17,71 | 0,4499 | 0,00771 | |||||||||||||||||||||||||||||||||||||||||||||
| 27 | 0,4712 | 0,0276 | 17,06 | 0,4669 | 0,00862 | |||||||||||||||||||||||||||||||||||||||||||||
| 28 | 0,4887 | 0,0297 | 16,45 | 0,4838 | 0,00961 | |||||||||||||||||||||||||||||||||||||||||||||
| 29 | 0,5061 | 0,0319 | 15,89 | 0,5008 | 0,01087 | |||||||||||||||||||||||||||||||||||||||||||||
| 30 | 0,5236 | 0,0341 | 15,37 | 0,5176 | 0,01180 | |||||||||||||||||||||||||||||||||||||||||||||
| 31 | 0,5411 | 0,0364 | 14,88 | 0,5345 | 0,01301 | |||||||||||||||||||||||||||||||||||||||||||||
| 32 | 0,5585 | 0,0387 | 14,42 | 0,5513 | 0,01429 | |||||||||||||||||||||||||||||||||||||||||||||
| 33 | 0,5760 | 0,0412 | 13,99 | 0,5680 | 0,01566 | |||||||||||||||||||||||||||||||||||||||||||||
| 34 | 0,5934 | 0,0437 | 13,58 | 0,5847 | 0,01711 | |||||||||||||||||||||||||||||||||||||||||||||
| 35 | 0,6109 | 0,0463 | 13,20 | 0,6014 | 0,01864 | |||||||||||||||||||||||||||||||||||||||||||||
| 36 | 0,6283 | 0,0489 | 12,84 | 0,6180 | 0,02027 | |||||||||||||||||||||||||||||||||||||||||||||
| 37 | 0,6458 | 0,0517 | 12,50 | 0,6346 | 0,02198 | |||||||||||||||||||||||||||||||||||||||||||||
| 38 | 0,6632 | 0,0545 | 12,17 | 0,6511 | 0,02378 | |||||||||||||||||||||||||||||||||||||||||||||
| 39 | 0,6807 | 0,0574 | 11,87 | 0,6676 | 0,02568 | |||||||||||||||||||||||||||||||||||||||||||||
| 40 | 0,6981 | 0,0603 | 11,58 | 0,6840 | 0,02767 | |||||||||||||||||||||||||||||||||||||||||||||
| 41 | 0,7156 | 0,0633 | 11,30 | 0,7004 | 0,02976 | |||||||||||||||||||||||||||||||||||||||||||||
| 42 | 0,7330 | 0,0664 | 11,04 | 0,7167 | 0,03195 | |||||||||||||||||||||||||||||||||||||||||||||
| 43 | 0,7505 | 0,0696 | 10,78 | 0,7330 | 0,03425 | |||||||||||||||||||||||||||||||||||||||||||||
| 44 | 0,7679 | 0,0728 | 10,55 | 0,7492 | 0,03664 | |||||||||||||||||||||||||||||||||||||||||||||
| 45 | 0,7854 | 0,0761 | 10,32 | 0,7654 | 0,03915 | |||||||||||||||||||||||||||||||||||||||||||||
| 46 | 0,8029 | 0,0795 | 10,10 | 0,7815 | 0,04176 | |||||||||||||||||||||||||||||||||||||||||||||
| 47 | 0,8203 | 0,0829 | 9,80 | 0,7975 | 0,04448 | |||||||||||||||||||||||||||||||||||||||||||||
| 48 | 0,8378 | 0,0865 | 9,69 | 0,8135 | 0,04731 | |||||||||||||||||||||||||||||||||||||||||||||
| 49 | 0,8552 | 0,0900 | 9,50 | 0,8294 | 0,05025 | |||||||||||||||||||||||||||||||||||||||||||||
| 50 | 0,8727 | 0,0937 | 9,31 | 0,8452 | 0,05331 | |||||||||||||||||||||||||||||||||||||||||||||
| 51 | 0,8901 | 0,0974 | 9,14 | 0,8610 | 0,05649 | |||||||||||||||||||||||||||||||||||||||||||||
| 52 | 0,9076 | 0,1012 | 8,97 | 0,8767 | 0,05978 | |||||||||||||||||||||||||||||||||||||||||||||
| 53 | 0,9250 | 0,1051 | 8,80 | 0,8924 | 0,06319 | |||||||||||||||||||||||||||||||||||||||||||||
| 54 | 0,9425 | 0,1090 | 8,65 | 0,9080 | 0,06673 | |||||||||||||||||||||||||||||||||||||||||||||
| 55 | 0,9599 | 0,1130 | 8,49 | 0,9235 | 0,07039 | |||||||||||||||||||||||||||||||||||||||||||||
| 56 | 0,9774 | 0,1171 | 8,35 | 0,9389 | 0,07417 | |||||||||||||||||||||||||||||||||||||||||||||
| 57 | 0,9948 | 0,1212 | 8,21 | 0,9543 | 0,07808 | |||||||||||||||||||||||||||||||||||||||||||||
| 58 | 1,0123 | 0,1254 | 8,07 | 0,9696 | 0,08212 | |||||||||||||||||||||||||||||||||||||||||||||
| 59 | 1,0297 | 0,1296 | 7,94 | 0,9848 | 0,08629 | |||||||||||||||||||||||||||||||||||||||||||||
| 60 | 1,0472 | 0,1340 | 7,81 | 1,0000 | 0,09059 | |||||||||||||||||||||||||||||||||||||||||||||
| 61 | 1,0647 | 0,1384 | 7,69 | 1,0151 | 0,09502 | |||||||||||||||||||||||||||||||||||||||||||||
| 62 | 1,0821 | 0,1428 | 7,56 | 1,0301 | 0,09958 | |||||||||||||||||||||||||||||||||||||||||||||
| 63 | 1,0996 | 0,1474 | 7,46 | 1,0450 | 0,10428 | |||||||||||||||||||||||||||||||||||||||||||||
| 64 | 1,1170 | 0,1520 | 7,35 | 1,0598 | 0,10911 | |||||||||||||||||||||||||||||||||||||||||||||
| 65 | 1,1345 | 0,1566 | 7,24 | 1,0746 | 0,11408 | |||||||||||||||||||||||||||||||||||||||||||||
| 66 | 1,1519 | 0,1613 | 7,14 | 1,0893 | 0,11919 | |||||||||||||||||||||||||||||||||||||||||||||
| 67 | 1,1694 | 0,1661 | 7,04 | 1,1039 | 0,12443 | |||||||||||||||||||||||||||||||||||||||||||||
| 68 | 1,1868 | 0,1710 | 6,94 | 1,1184 | 0,12982 | |||||||||||||||||||||||||||||||||||||||||||||
| 69 | 1,2043 | 0,1759 | 6,85 | 1,1328 | 0,13535 | |||||||||||||||||||||||||||||||||||||||||||||
| 70 | 1,2217 | 0,1808 | 6,76 | 1,1472 | 0,14102 | |||||||||||||||||||||||||||||||||||||||||||||
| 71 | 1,2392 | 0,1859 | 6,67 | 1,1614 | 0,14683 | |||||||||||||||||||||||||||||||||||||||||||||
| 72 | 1,2566 | 0,1910 | 6,58 | 1,1756 | 0,15270 | |||||||||||||||||||||||||||||||||||||||||||||
| 73 | 1,2741 | 0,1961 | 6,50 | 1,1896 | 0,15889 | |||||||||||||||||||||||||||||||||||||||||||||
| 74 | 1,2915 | 0,2014 | 6,41 | 1,2036 | 0,15514 | |||||||||||||||||||||||||||||||||||||||||||||
| 75 | 1,3090 | 0,2066 | 6,34 | 1,2175 | 0,17154 | |||||||||||||||||||||||||||||||||||||||||||||
| 76 | 1,3265 | 0,2120 | 6,26 | 1,2312 | 0,17808 | |||||||||||||||||||||||||||||||||||||||||||||
| 77 | 1,4339 | 0,2174 | 6,18 | 1,2450 | 0,18477 | |||||||||||||||||||||||||||||||||||||||||||||
| 78 | 1,3614 | 0,2229 | 6,11 | 1,2586 | 0,19160 | |||||||||||||||||||||||||||||||||||||||||||||
| 79 | 1,3788 | 0,2284 | 6,04 | 1,2722 | 0,19859 | |||||||||||||||||||||||||||||||||||||||||||||
| 80 | 1,3963 | 0,2340 | 5,97 | 1,2856 | 0,20573 | |||||||||||||||||||||||||||||||||||||||||||||
| 81 | 1,4137 | 0,2396 | 5,90 | 1,2989 | 0,21301 | |||||||||||||||||||||||||||||||||||||||||||||
| 82 | 1,4312 | 0,2453 | 5,83 | 1,3221 | 0,22045 | |||||||||||||||||||||||||||||||||||||||||||||
| 83 | 1,4486 | 0,2510 | 5,77 | 1,3252 | 0,22804 | |||||||||||||||||||||||||||||||||||||||||||||
| 84 | 1,4661 | 0,2569 | 5,71 | 1,3383 | 0,23578 | |||||||||||||||||||||||||||||||||||||||||||||
| 85 | 1,4735 | 0,2627 | 5,65 | 1,3512 | 0,24367 | |||||||||||||||||||||||||||||||||||||||||||||
| 86 | 1,5010 | 0,2686 | 5,59 | 1,3640 | 0,25171 | |||||||||||||||||||||||||||||||||||||||||||||
| 87 | 1,5184 | 0,2746 | 5,53 | 1,3767 | 0,25990 | |||||||||||||||||||||||||||||||||||||||||||||
| 88 | 1,5359 | 0,2807 | 5,47 | 1,3893 | 0,26825 | |||||||||||||||||||||||||||||||||||||||||||||
| 89 | 1,5553 | 0,2867 | 5,42 | 1,4018 | 0,27675 | |||||||||||||||||||||||||||||||||||||||||||||
| 90 | 1,5708 | 0,2929 | 5,36 | 1,4142 | 0,28540 | |||||||||||||||||||||||||||||||||||||||||||||
| 91 | 1,5882 | 0,2991 | 5,31 | 1,4265 | 0,29420 | |||||||||||||||||||||||||||||||||||||||||||||
| 92 | 1,6057 | 0,3053 | 5,26 | 1,4387 | 0,30316 | |||||||||||||||||||||||||||||||||||||||||||||
| 93 | 1,6232 | 0,3116 | 5,21 | 1,4507 | 0,31226 | |||||||||||||||||||||||||||||||||||||||||||||
| 94 | 1,6406 | 0,3180 | 5,16 | 1,4627 | 0,32152 | |||||||||||||||||||||||||||||||||||||||||||||
| 95 | 1,6580 | 0,3244 | 5,11 | 1,4746 | 0,33093 | |||||||||||||||||||||||||||||||||||||||||||||
| 96 | 1,6755 | 0,3309 | 5,06 | 1,4863 | 0,34050 | |||||||||||||||||||||||||||||||||||||||||||||
| 97 | 1,6930 | 0,3374 | 5,02 | 1,4979 | 0,35021 | |||||||||||||||||||||||||||||||||||||||||||||
| 98 | 1,7104 | 0,3439 | 4,97 | 1,5094 | 0,36008 | |||||||||||||||||||||||||||||||||||||||||||||
| 99 | 1,7279 | 0,3506 | 4,93 | 1,5208 | 0,37009 | |||||||||||||||||||||||||||||||||||||||||||||
| 100 | 1,7453 | 0,3572 | 4,89 | 1,5321 | 0,38026 | |||||||||||||||||||||||||||||||||||||||||||||
| 101 | 1,7628 | 0,3639 | 4,84 | 1,5432 | 0,39050 | |||||||||||||||||||||||||||||||||||||||||||||
| 102 | 1,7802 | 0,3707 | 4,80 | 1,5543 | 0,40104 | |||||||||||||||||||||||||||||||||||||||||||||
| 103 | 1,7977 | 0,3775 | 4,76 | 1,5652 | 0,41166 | |||||||||||||||||||||||||||||||||||||||||||||
| 104 | 1,8151 | 0,3843 | 4,72 | 1,57,60 | 0,42242 | |||||||||||||||||||||||||||||||||||||||||||||
| 105 | 1,8326 | 0,3912 | 4,68 | 1,5867 | 0,43333 | |||||||||||||||||||||||||||||||||||||||||||||
| 106 | 1,8500 | 0,3982 | 4,65 | 1,5973 | 0,44439 | |||||||||||||||||||||||||||||||||||||||||||||
| 107 | 1,8675 | 0,4052 | 4,61 | 1,6077 | 0,45560 | |||||||||||||||||||||||||||||||||||||||||||||
| 108 | 1,8850 | 0,4122 | 4,57 | 1,6180 | 0,46695 | |||||||||||||||||||||||||||||||||||||||||||||
| 109 | 1,9024 | 0,4193 | 4,54 | 1,6282 | 0,47845 | |||||||||||||||||||||||||||||||||||||||||||||
| 110 | 1,9199 | 0,4264 | 4,50 | 1,6383 | 0,49008 | |||||||||||||||||||||||||||||||||||||||||||||
| 111 | 1,9373 | 0,4336 | 4,47 | 1,6483 | 0,50187 | |||||||||||||||||||||||||||||||||||||||||||||
| 112 | 1,9548 | 0,4408 | 4,43 | 1,6581 | 0,51379 | |||||||||||||||||||||||||||||||||||||||||||||
| 113 | 1,9722 | 0,4481 | 4,40 | 1,6678 | 0,52586 | |||||||||||||||||||||||||||||||||||||||||||||
| 114 | 1,9897 | 0,4554 | 4,37 | 1,6773 | 0,53807 | |||||||||||||||||||||||||||||||||||||||||||||
| 115 | 2,0071 | 0,4627 | 4,34 | 1,6868 | 0,55041 | |||||||||||||||||||||||||||||||||||||||||||||
| 116 | 2,0246 | 0,4701 | 4,31 | 1,6961 | 0,56389 | |||||||||||||||||||||||||||||||||||||||||||||
| 117 | 2,0420 | 0,4775 | 4,28 | 1,7053 | 0,57551 | |||||||||||||||||||||||||||||||||||||||||||||
| 118 | 2,0595 | 0,4850 | 4,25 | 1,7143 | 0,58827 | |||||||||||||||||||||||||||||||||||||||||||||
| 119 | 2,0769 | 0,4925 | 4,22 | 1,7233 | 0,60116 | |||||||||||||||||||||||||||||||||||||||||||||
| 120 | 2,0944 | 0,5000 | 4,19 | 1,7321 | 0,61418 | |||||||||||||||||||||||||||||||||||||||||||||
| 121 | 2,1118 | 0,5076 | 4,16 | 1,7407 | 0,62734 | |||||||||||||||||||||||||||||||||||||||||||||
| 122 | 2,1293 | 0,5152 | 4,13 | 1,7492 | 0,64063 | |||||||||||||||||||||||||||||||||||||||||||||
| 123 | 2,1468 | 0,5228 | 4,11 | 1,7576 | 0,65404 | |||||||||||||||||||||||||||||||||||||||||||||
| 124 | 2,1642 | 0,5305 | 4,08 | 1,7659 | 0,66759 | |||||||||||||||||||||||||||||||||||||||||||||
| 125 | 2,1817 | 0,5387 | 4,05 | 1,7740 | 0,68125 | |||||||||||||||||||||||||||||||||||||||||||||
| 126 | 2,1991 | 0,5460 | 4,03 | 1,7820 | 0,69505 | |||||||||||||||||||||||||||||||||||||||||||||
| 127 | 2,2166 | 0,5538 | 4,00 | 1,7899 | 0,70897 | |||||||||||||||||||||||||||||||||||||||||||||
| 128 | 2,2340 | 0,5616 | 3,98 | 1,7976 | 0,72301 | |||||||||||||||||||||||||||||||||||||||||||||
| 129 | 2,2515 | 0,5695 | 3,95 | 1,8052 | 0,73716 | |||||||||||||||||||||||||||||||||||||||||||||
| 130 | 2,2689 | 0,5774 | 3,93 | 1,8126 | 0,75144 | |||||||||||||||||||||||||||||||||||||||||||||
| 131 | 2,2864 | 0,5853 | 3,91 | 1,8199 | 0,76584 | |||||||||||||||||||||||||||||||||||||||||||||
| 132 | 2,3038 | 0,5933 | 3,88 | 1,8277 | 0,78034 | |||||||||||||||||||||||||||||||||||||||||||||
| 133 | 2,3213 | 0,6013 | 3,86 | 1,8341 | 0,79497 | |||||||||||||||||||||||||||||||||||||||||||||
| 134 | 2,3387 | 0,6093 | 3,84 | 1,8410 | 0,80970 | |||||||||||||||||||||||||||||||||||||||||||||
| 135 | 2,3562 | 0,6173 | 3,82 | 1,8478 | 0,82454 | |||||||||||||||||||||||||||||||||||||||||||||
| 136 | 2,3736 | 0,6254 | 3,80 | 1,8545 | 0,83949 | |||||||||||||||||||||||||||||||||||||||||||||
| 137 | 2,3911 | 0,6335 | 3,77 | 1,8608 | 0,85455 | |||||||||||||||||||||||||||||||||||||||||||||
| 138 | 2,4086 | 0,6416 | 3,75 | 1,8672 | 0,86971 | |||||||||||||||||||||||||||||||||||||||||||||
| 139 | 2,4160 | 0,6498 | 3,73 | 1,8733 | 0,88497 | |||||||||||||||||||||||||||||||||||||||||||||
| 140 | 2,4435 | 0,6580 | 3,71 | 1,8794 | 0,90034 | |||||||||||||||||||||||||||||||||||||||||||||
| 141 | 2,4609 | 0,6662 | 3,69 | 1,8853 | 0,91580 | |||||||||||||||||||||||||||||||||||||||||||||
| 142 | 2,4784 | 0,6744 | 3,67 | 1,8910 | 0,93135 | |||||||||||||||||||||||||||||||||||||||||||||
| 143 | 2,4958 | 0,6827 | 3,66 | 1,8966 | 0,94700 | |||||||||||||||||||||||||||||||||||||||||||||
| 144 | 2,5133 | 0,2910 | 3,64 | 1,9021 | 0,96274 | |||||||||||||||||||||||||||||||||||||||||||||
| 145 | 2,5307 | 0,6993 | 3,62 | 1,9074 | 0,97858 | |||||||||||||||||||||||||||||||||||||||||||||
| 146 | 2,5482 | 0,7076 | 3,60 | 1,9126 | 0,99449 | |||||||||||||||||||||||||||||||||||||||||||||
| 147 | 2,5656 | 0,7160 | 3,58 | 1,9176 | 1,01050 | |||||||||||||||||||||||||||||||||||||||||||||
| 148 | 2,5831 | 0,7244 | 3,57 | 1,9225 | 1,02658 | |||||||||||||||||||||||||||||||||||||||||||||
| 149 | 2,6005 | 0,7328 | 3,55 | 1,9273 | 1,04275 | |||||||||||||||||||||||||||||||||||||||||||||
| 150 | 2,6180 | 0,7412 | 3,53 | 1,9319 | 1,05900 | |||||||||||||||||||||||||||||||||||||||||||||
| 151 | 2,6354 | 0,7496 | 3,52 | 1,9363 | 1,07532 | |||||||||||||||||||||||||||||||||||||||||||||
| 152 | 2,6429 | 0,7581 | 3,50 | 1,9406 | 1,09171 | |||||||||||||||||||||||||||||||||||||||||||||
| 153 | 2,6704 | 0,7666 | 3,48 | 1,9447 | 1,10818 | |||||||||||||||||||||||||||||||||||||||||||||
| 154 | 2,6878 | 0,7750 | 3,47 | 1,9487 | 1,12472 | |||||||||||||||||||||||||||||||||||||||||||||
| 155 | 2,7053 | 0,7836 | 3,45 | 1,9526 | 1,14132 | |||||||||||||||||||||||||||||||||||||||||||||
| 156 | 2,7227 | 0,7921 | 3,44 | 1,9563 | 1,15799 | |||||||||||||||||||||||||||||||||||||||||||||
| 157 | 2,7402 | 0,8006 | 3,42 | 1,9598 | 1,17472 | |||||||||||||||||||||||||||||||||||||||||||||
| 158 | 2,7576 | 0,8092 | 3,41 | 1,9633 | 1,19151 | |||||||||||||||||||||||||||||||||||||||||||||
| 159 | 2,7752 | 0,8178 | 3,39 | 1,9665 | 1,20835 | |||||||||||||||||||||||||||||||||||||||||||||
| 160 | 2,7925 | 0,8264 | 3,38 | 1,9696 | 1,22525 | |||||||||||||||||||||||||||||||||||||||||||||
| 161 | 2,8100 | 0,8350 | 3,37 | 1,9726 | 1,24221 | |||||||||||||||||||||||||||||||||||||||||||||
| 162 | 2,8274 | 0,8436 | 3,35 | 1,9754 | 1,25921 | |||||||||||||||||||||||||||||||||||||||||||||
| 163 | 2,8449 | 0,8522 | 3,34 | 1,9780 | 1,27626 | |||||||||||||||||||||||||||||||||||||||||||||
| 164 | 2,8623 | 0,8608 | 3,33 | 1,9805 | 1,29335 | |||||||||||||||||||||||||||||||||||||||||||||
| 165 | 2,8798 | 0,8695 | 3,31 | 1,9829 | 1,31049 | |||||||||||||||||||||||||||||||||||||||||||||
| 166 | 2,8972 | 0,8781 | 3,30 | 1,9851 | 1,32766 | |||||||||||||||||||||||||||||||||||||||||||||
| 167 | 2,9147 | 0,8868 | 3,28 | 1,9871 | 1,34487 | |||||||||||||||||||||||||||||||||||||||||||||
| 168 | 2,9322 | 0,8955 | 3,27 | 1,9890 | 1,36212 | |||||||||||||||||||||||||||||||||||||||||||||
| 169 | 2,9496 | 0,9042 | 3,26 | 1,9908 | 1,37940 | |||||||||||||||||||||||||||||||||||||||||||||
| 170 | 2,9671 | 0,9128 | 3,25 | 1,9924 | 1,39671 | |||||||||||||||||||||||||||||||||||||||||||||
| 171 | 2,9845 | 0,9215 | 3,24 | 1,9938 | 1,41404 | |||||||||||||||||||||||||||||||||||||||||||||
| 172 | 3,0020 | 0,9302 | 3,23 | 1,9951 | 1,43140 | |||||||||||||||||||||||||||||||||||||||||||||
| 173 | 3,0194 | 0,9390 | 3,22 | 1,9963 | 1,44878 | |||||||||||||||||||||||||||||||||||||||||||||
| 174 | 3,0369 | 0,9477 | 3,20 | 1,9973 | 1,46617 | |||||||||||||||||||||||||||||||||||||||||||||
| 175 | 3,0543 | 0,9564 | 3,19 | 1,9981 | 1,48359 | |||||||||||||||||||||||||||||||||||||||||||||
| 176 | 3,0718 | 0,9651 | 3,18 | 1,9988 | 1,50101 | |||||||||||||||||||||||||||||||||||||||||||||
| 177 | 3,0892 | 0,9738 | 3,17 | 1,9993 | 1,51845 | |||||||||||||||||||||||||||||||||||||||||||||
| 178 | 3,1067 | 0,9825 | 3,16 | 1,9997 | 1,53589 | |||||||||||||||||||||||||||||||||||||||||||||
| 179 | 3,1241 | 0,9913 | 3,15 | 1,9999 | 1,55334 | |||||||||||||||||||||||||||||||||||||||||||||
| 180 | 3,1416 | 1,0000 | 3,14 | 2,0000 | 1,57080 | |||||||||||||||||||||||||||||||||||||||||||||
Пример 1.
Вычислить радиус окружности, у которой при стрелке h=2 мм длина дуги l=10 мм.
Находим l/h=10/2=5. Из таблицы определяем lo≈ 1,6930, r=l/ lo=10/1,6930=5,9 мм.
Пример 2.
Вычислить стрелку h дуги окружности радиусом r=50 мм при центральном угле α=30 o
Из таблицы находим h=0,0341*50=1,705 мм.





































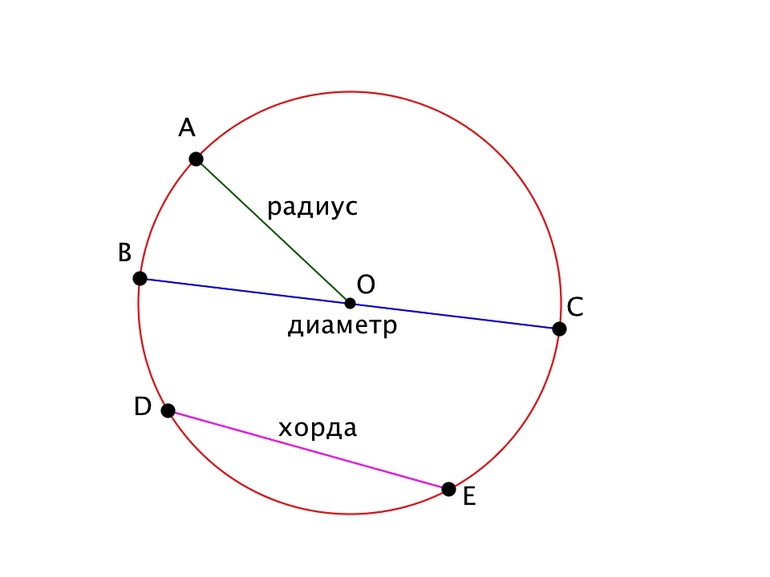

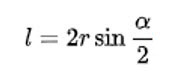










 заметки, математика, геометрия
заметки, математика, геометрия









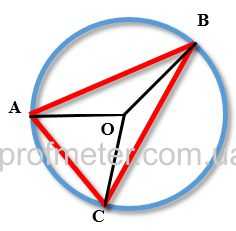
 Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.
Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.