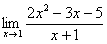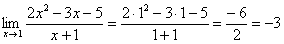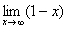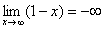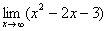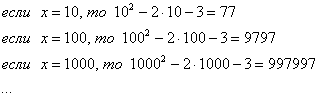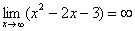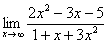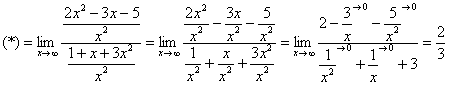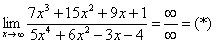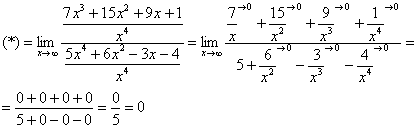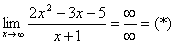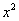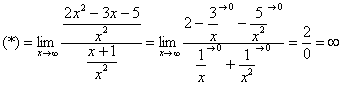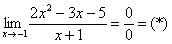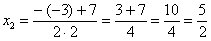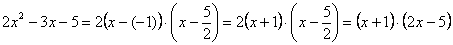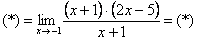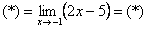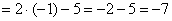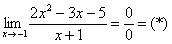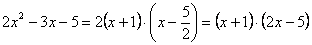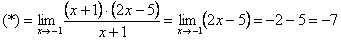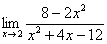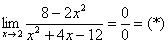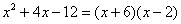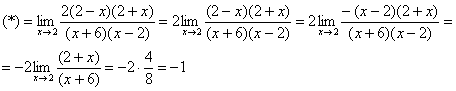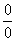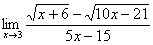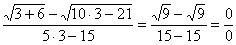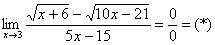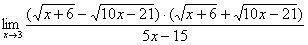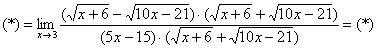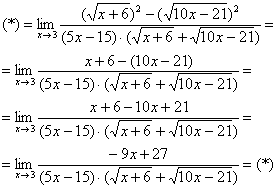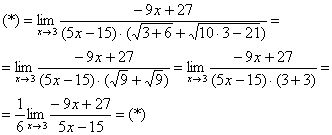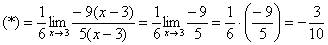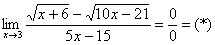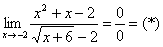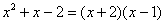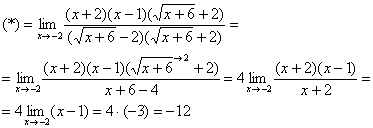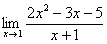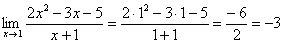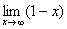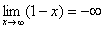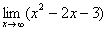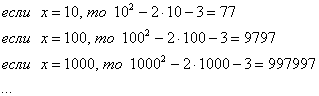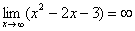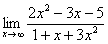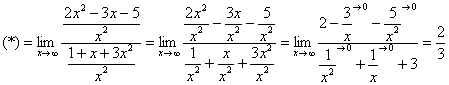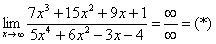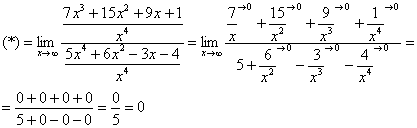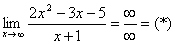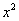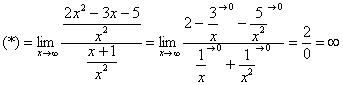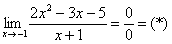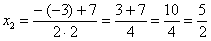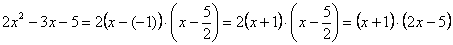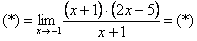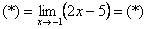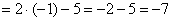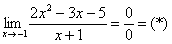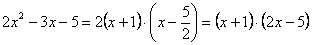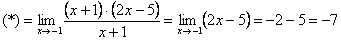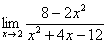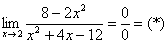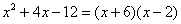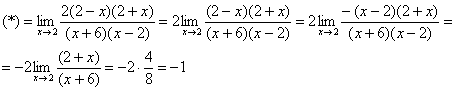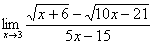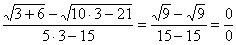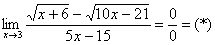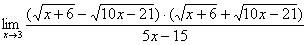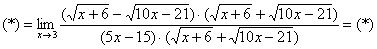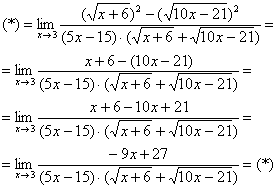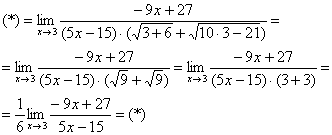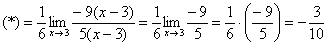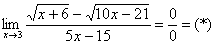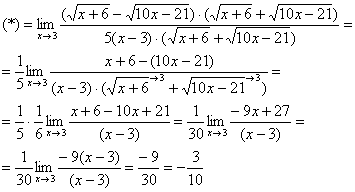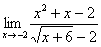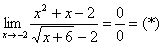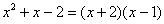Как решать пределы функции
Как решать пределы функции
Что такое предел функции
В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.
Определение предела функции
Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.
Запись предела:
Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):
Читается как “предел функции при икс, стремящемся к единице”.
x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).
Решение пределов
С заданным числом
Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):
Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).
С бесконечностью
В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:
Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:
Другой более сложный пример
Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.
Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.
С неопределенностью (икс стремится к бесконечности)
В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.
Пример: давайте вычислим предел ниже.
Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:
Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:
1. Находим x в старшей степени для числителя (в нашем случае – это два).
2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).
3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.
4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.
С неопределенностью (икс стремится к конкретному числу)
И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.
В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.
Пример: Найдем предел функции ниже.
1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.
2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
Знаменатель () изначально является простым.
3. Получаем вот такой видоизмененный предел:
4. Дробь можно сократить на ():
5. Остается только подставить число 1 в выражение, получившееся под пределом:
Предел функции.
Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Или другими словами, число A является пределом функции y = f (x) в точке x0, если для всякой последовательности точек из области определения функции, не равных x0, и которая сходится к точке x0 (lim xn = x0), последовательность соответствующих значений функции сходится к числу A.
График функции, предел которой при аргументе, который стремится к бесконечности, равен L:
Предел функции по Гейне.
Значение А является пределом (предельным значением) функции f (x) в точке x0 в случае, если для всякой последовательности точек 

Предел функции по Коши.
Ответ
Необходимо рассчитать предел
Таким образом, числитель будет таким:
Далее сокращаем числитель и знаменатель на (x – 1):
Ответ
Решение пределов функции.
Чтобы решить пределы, следуйте правилам:
Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.
Пределы функций. Примеры решений
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который дал строгие определения многим понятиям матана и заложил его основы. Надо сказать, этот уважаемый математик снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причём одна теорема убойнее другой. В этой связи мы пока не будем рассматривать определение предела по Коши, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
Любой предел состоит из трех частей:
1) Всем известного значка предела 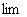
2) Записи под значком предела, в данном случае 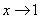
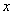
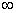
3) Функции под знаком предела, в данном случае 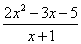
Сама запись 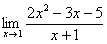
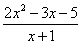
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 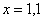

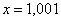
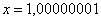
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 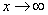
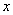
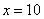
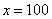
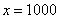
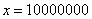
А что в это время происходит с функцией 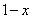
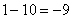
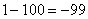
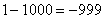
Итак: если 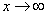
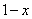
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 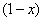
Еще один пример с бесконечностью:
Опять начинаем увеличивать 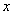
Вывод: при 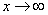
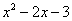
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
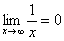
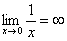
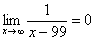
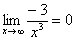
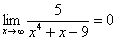
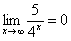
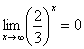
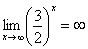
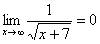
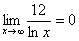
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 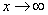
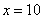
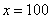
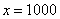
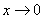
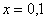
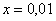
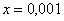
! Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: 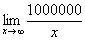
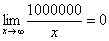
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как 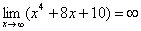
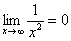
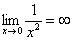
Более того, у предела есть очень хороший геометрический смысл. Для лучшего понимания темы рекомендую ознакомиться с методическим материалом Графики и свойства элементарных функций. После прочтения этой статьи вы не только окончательно поймете, что такое предел, но и познакомитесь с интересными случаями, когда предела функции вообще не существует!
На практике, к сожалению, подарков немного. А поэтому переходим к рассмотрению более сложных пределов. Кстати, по этой теме есть интенсивный курс в pdf-формате, который особенно полезен, если у Вас ОЧЕНЬ мало времени на подготовку. Но материалы сайта, разумеется, не хуже:
Пределы с неопределенностью вида 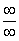
Сейчас мы рассмотрим группу пределов, когда 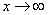
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 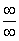
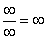
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 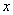
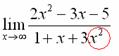
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 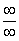
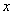
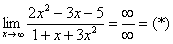
Разделим числитель и знаменатель на 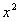
Вот оно как, ответ 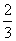
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 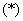
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: 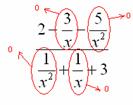
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Найти предел 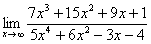
Снова в числителе и знаменателе находим 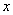
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 
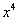
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Найти предел 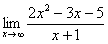
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( 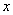
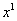
Для раскрытия неопределенности 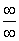
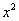
Разделим числитель и знаменатель на
Под записью 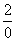
Таким образом, при раскрытии неопределенности вида 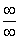
Пределы с неопределенностью вида 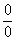
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 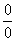
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: 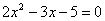
Сначала находим дискриминант: 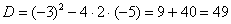
И квадратный корень из него: 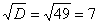
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни: 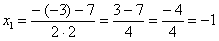
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель 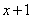
Очевидно, что можно сократить на 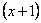
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители. 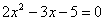
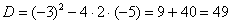
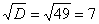
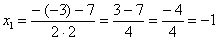
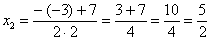
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: 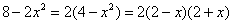
Знаменатель: 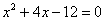
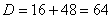
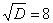
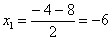
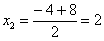
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида 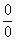
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 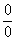
Вспоминаем нашу нетленную формулу разности квадратов: 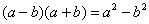
И смотрим на наш предел: 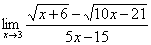
Что можно сказать? 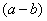
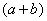
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 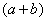
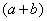
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу 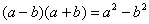
Неопределенность 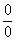
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители: 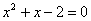
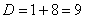
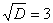
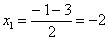
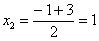
Умножим числитель и знаменатель на сопряженное выражение
Спасибо за внимание.
Помимо рассмотренных типов пределов на практике часто встречаются так называемые Замечательные пределы. После освоения двух базовых уроков, рекомендую изучить статью Методы решения пределов, материалы которой позволят выйти на «твёрдую четвёрку»!
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Предел функции: примеры решений
Обновлено: 24 Октября 2021
Рассмотрим понятие и определение предела, разберем основные решения пределов.
Разбор записи предела на математическом языке
Любой предел состоит из трех частей:
Данная запись читается так: «предел функции \(\lim_
Понятие предела, в отличие от большинства известных математических понятий, динамическое, то есть нет какого-то статичного, неменяющегося числа или тождества в качестве его определения. Построим последовательность:
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»? Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность:
Все данные значения x и разница между ними настолько малы и близки к одной точке (в данном случае к единице), что можно сказать, что «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают. Это и означает «икс стремится к единице».
Предел последовательности: определение и свойства
Предел последовательности, как и предел функции, является одним из основных понятий математического анализа. По сути, каждое вещественное число может быть представлено в виде последовательности максимально приближенных к нему чисел.
Вещественные (действительные) числа обозначаются как ε (эпсилон) и принадлежат множеству R, которое включает в себя все натуральные, целые, рациональные и иррациональные числа.
Теперь обратимся к определению предела последовательности и разберем, что же оно означает.
Для лучшего восприятия понятия «окрестность» рассмотрим следующее изображение:
Окрестностью в данном случае являются интервалы слева и справа от x0, причем окрестность может быть проколотой (третий случай), то есть сама точка x0 не входит в заданный интервал.
На математическом языке данное определение записывается следующим образом:
Свойства
1. Постоянный множитель c можно выносить за знак предела. На математическом языке данное утверждение выглядит так:
\(\lim_
где \(a_n\) — бесконечно малая величина. Очевидно, что:
где \(\alpha_n\) и \(\beta_n\) — некоторые бесконечно малые величины.
Тогда \(x_n\pm y_n=(A\pm B)+(\alpha_n\pm\beta_n)\)
Учитывая, что \((\alpha_n\pm\beta_n)\) — бесконечно малая величина, получаем:
\(\lim_<>(x_n\pm y_n)=(A\pm B)=\lim_<>(x_n)\pm\lim_<>(y_n) \) Аналогично:
\(x_n\times y_n=(A\pm\alpha_n)(B\pm\beta_n)=AB+(B\alpha_n+A\beta_n+\alpha_n\beta_n)\)
Осталось распознать в выражении \( (B\alpha_n+A\beta_n+\alpha_n\beta_n)\) бесконечно малую величину, что влечет за собой:
\(\lim_<>(x_n\times y_n)=AB=\lim_<>x_n\times\lim_<>y_n\\\\ \)
Далее покажем, что отношение \(\frac
Что и требовалось доказать.
Определенного доказательства данного свойства нет, однако интуитивно мы можем провести следующие умозаключения.
Пусть \(\underset<><\lim\;>y_n=A,\) тогда:
\(y_n=A+\alpha_n\)
где \( \alpha_n\) – некоторая бесконечно малая величина.
Что и требовалось доказать.
Предел функции
Обратимся сразу к определению.
Постоянное число А называется пределом функции f(x) при x→a, если, задав некоторое произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству 0 \(\lim_
Для того, чтобы функция являлась непрерывной, обязательно должны выполнятся 3 условия:
Существуют и другие определения, которые, как и в случае с определением пределов по Коши и по Гейне, различаются по формулировке для наиболее удобного использования.
Если функция y=f(x) непрерывна в каждой точке некоторого промежутка, то её называют непрерывной на данном промежутке.
Также можно дать определение непрерывности справа или слева от точки.
Функция f(x) называется непрерывной справа/слева в точке x0, если она определена на некоторой правосторонней/левосторонней окрестности \(U(x_0+0)/U(x_0-0)\) этой точки, и если правый/левый предел в точке x0 равен значению функции в x0.
Вычисление пределов
Рассмотрим примеры вычисления пределов.
Простейшие пределы
Для начала обратимся к простейшему пределу, который был рассмотрен в самом начале: \(\lim_
В данном случае можно попробовать просто подставить единицу (так как предел стремится к единице) в выражение. Тогда:
Да, это работает только с простейшими пределами, которые, на самом деле, на практике встречаются не редко, так что попробовать просто подставить икс в выражение — одно из возможных решений.
Теперь попробуем сделать то же самое с пределом, который стремится к бесконечности.
Икс стремится к бесконечности \((x\rightarrow\infty)\) означает, что икс неограниченно возрастает (например, х=10, х=100, х=1000, х=10000 и так далее).
Рассмотрим предел \(\lim_
Даже если числитель функции в пределе, стремящимся к бесконечности, кажется очень большим — миллион, миллиард и т. п., весь предел все равно будет равен нулю, так как знаменатель, зависящий от бесконечности, в какой-то момент начнет принимать значения, гораздо большие, чем числитель. То есть:
Итак, когда мы видим простейший предел, сначала нужно попробовать подставить в функцию «х».
Выражения для самостоятельного решения:
Пределы с неопределенностью вида \(\frac\infty\infty\)
Неопределенность вида \(\frac\infty\infty\) появляется, когда мы пытаемся подставить «х» в предел стремящийся к бесконечности и имеющий дробную функцию:
Для начала находим и в числителе, и в знаменателе старшую степень икса, а затем выбираем наибольшую из них. В данном случае старшие степени числителя и знаменателя равны, однако это частный случай.
Теперь мы должны и числитель, и знаменатель разделить на х в старшей степени:
Затем анализируем дроби с иксом, мысленно подставляя вместо х бесконечность. Получается, что все эти дроби стремятся к нулю, соответственно, их можно принять за ноль. Значит:
Однако, ответом при решении предела, стремящегося к бесконечности, может быть как любое число — в том числе и ноль, — так и сама бесконечность.
Рассмотрим еще 2 примера, чтобы в этом убедиться.
Поделив числитель и знаменатель на \(x^4\) и подставив бесконечность в получившиеся дроби (для закрепления материала лучше высчитать это самостоятельно), получаем:
Пределы с неопределенностью вида \(\frac00\)
Сразу же возникает логичный вопрос: почему мы делим на ноль, если каждый школьник знает, что на ноль делить нельзя? Если обратиться к определению предела, все встанет на свои места: дело в том, что мы работаем не с самим нулем, а с бесконечно малыми числами и функциями, однако для удобства записываем «0».
Рассмотрим конкретные примеры и научимся решать подобные пределы.
Теперь запомним правило:
Почти всегда для этого необходимо решить квадратное уравнение и/или использовать ФСУ (формулы сокращенного умножения).
В знаменателе мы имеем x+1, это уже простейшая функция, так что знаменатель мы не трогаем.
Применяя стандартные операции для решения квадратного уравнения, раскладываем числитель и получаем (x+1)(5x-7).
Два важных момента, на которые стоит обратить внимание при вычислении дискриминанта:
Очевидно, что (х+1) в числителе и знаменателе можно сократить.
Очень важно при разложении на множители замечать формулы сокращенного умножения! Они могут быть видны не сразу, а после проведения одного или нескольких шагов, например, вынесения числа за скобку.
Чтобы облегчить процесс решения, всегда сразу выносите число за скобку, если это условие это позволяет. Кроме того, часто целесообразно выносить такие числа и за знаки предела, так как они не будут мешаться во время вычислений. Однако нужно быть крайне внимательным, чтобы не потерять в какой-то момент число или знак.
Теперь, для того, чтобы упростить выражение, нужно избавиться от корней. Вообще, в математике стараются избавляться от иррациональности в любом случае, когда это возможно, — так гораздо проще жить.
Что же это за метод? А основан он на всей известной формуле разности квадратов:
Теперь, учитывая формулу в числителе дроби, проводим ряд преобразований и получаем:
Да, избавившись от иррациональности в числителе, мы обрели ее в знаменателе, однако оперировать суммой корней, которую мы получили, гораздо легче. И, вообще, можно сразу подставить в корни тройку и вынести полученное число за знак предела, как упоминалось об это ранее.
А теперь просто раскладываем дробь на множители и получаем конечный ответ:
Примеры для самостоятельного решения:
Мы рассмотрели основное понятие пределов функции и последовательности и разобрали классические варианты решения пределов.
Если же быстро разобраться в этой сложной теме не получается, а сдача важной работы не за горами, вы всегда можете обратиться к авторам ФениксХелп, которые помогут с решением.
Предел функции: основные понятия и определения
В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.
Понятие предела
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.
Что такое предел функции
В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.
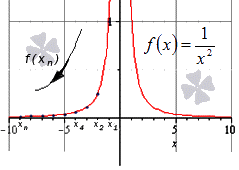
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).
Решение
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.
Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:
Ответ: Верность данного в условии равенства подтверждена.
Решение
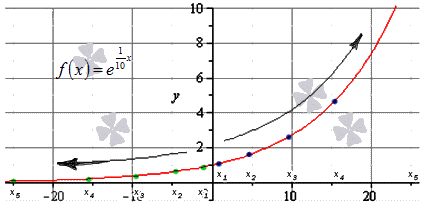
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞
Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными – отрицательных.
Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.
Теперь сформулируем, что такое предел функции справа.
Теперь мы разъясним данные определения, записав решение конкретной задачи.
Решение
Значения функции в этой последовательности будут выглядеть так:
Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.
Как решать пределы?
В данной статье вы узнаете о том, как решать пределы?
Решение пределов является одним из важных разделов математического и вычислительного анализа. Многие ученики и учащиеся вузов справляются с данной проблемой свободно, когда другие постоянно задают один и тот же вопрос: «Как решать пределы?». Нахождение пределов тема актуальная. Существует множество способов решения пределов. Идентичные пределы можно найти согласно закону Лопиталя и без его помощи. Однако сначала нам следует разобраться, что же такое предел?
Предел имеет три части
Первая — это всем известный значок lim, вторая, это то, что написано под ним.
Третья часть это сама функция, которая стоит после знака lim.
Хотелось бы уточнить, значение икс стремится к 1, это то значение x, при котором х принимает определенные значения, которые близки к единице или почти с ней совпадают.
Решать пределы, дело легкое, если в них разобраться.
Первое правило решения пределов
В случае если предоставлена нам функция, попросту подставьте число в функцию. Это элементарные пределы, которые действительно встречаются в примерах и очень часто.
Есть пределы, где х->? Тогда бесконечность это та функция, где икс бесконечно возрастает. Значение такой функции является (1-х). Чтобы решить данный предел, нам необходимо следуя нашему первому правилу подставить значение (1-х) в функцию и получить ответ.
Из вышесказанного, для того чтобы обучиться решать наиболее непростые пределы, вы обязаны помнить правила решение элементарных пределов.
Как только вы это поймете, то сразу начнете замечать элементарные пределы и сможете их решить. Вот мы и научились решать легкие пределы. Теперь ознакомимся с решением более сложных пределов.
Такая функция возможна, когда х->?, а предел выражен в виде дроби.
Многие интересуются, просто ли решить такой предел?
Первое, что вы должны запомнить, вам необходимо найти в числителе х по старшинству, т.е. в самой большей степени из всех х, которые есть в числителе.
Мы видим, что старшая степень в числителе это 2
Теперь, нам необходимо сделать тоже самое только со знаменателем. В знаменателе старшая степень тоже 2.
Теперь рассмотрим, решение самых сложных пределов. Это вид 0/0.
Подобные пределы очень напоминают нам решение пределов вида бесконечность на бесконечность. Но есть отличие, которое важно помнить при решении. Когда икс стремится к бесконечности, то он бесконечно увеличивается, а тут он равен 0, т.е. конечному числу.
Чтобы разрешить подобную функцию, нам следует, и числители и знаменатель разложить на множители. Чтобы получить элементарный дискриминант, известный нам с 6 класса. Вычисляем дискриминант и подставляем ответы в нашу функцию. Находим конечный ответ.
Правило: если в числителе или знаменателе можно некое число вынести за данную скобку, то мы, не думая, обязательно выносим.
Существует множество разных способов решения более сложных пределов. Одним из них является метод замены. Заменить любую переменную легче, чем постоянно раскладывать на множители. Очень часто такой способ применяется для того, чтобы из сложного предела сделать первый замечательный предел.
Давайте рассмотрим детальнее на примере
Мы видим в пределе арктангенс, нехорошая функция, от которой нам необходимо избавиться. Очень комфортно нам будет, если мы арктангенс превратим в одну простую и легкую букву.
Сделаем замену: arctg заменим на у. И в процессе решения арктангенс будем именовать как у. Если наш икс стремится к нулю, арктангенс мы заменили на у, тогда записываем, что у тоже стремится к нулю. Все, что нам осталось в знаменателе выразить икс через игрек. Для этого в обе части равенства мы добавляем tg
Выражения приобретёт такой вид:
tg ( arctg4x)=tgy
С левой стороны две функции мы убираем, они взаимообратные и пропадают.
4х = tgу, отсюда: х= tgy/4
А теперь осталось самое элементарное:
Дальше решаем первый замечательный предел.
Следует запомнить, что как только наш предел оказывается в степени, это главный знак того, что такое выражение нам поможет решить второй замечательный предел. Сейчас мы подробнее остановимся на примере, который встречается очень часто, советую его изучить детально.
Этот предел вида (?/?)^?Второй замечательный предел такой вид не решает, как мы знаем, он решает вид 1^?, для этого нашу функцию необходимо преобразить в другой вид. В знаменателе мы видим х+1, значит, в числителе тоже должно быть х+1
Хочу поздравить вас, дорогие читатели, вы научились решать пределы. Надеюсь, моя статья была познавательной, увлекательной и интересной!
Как решать пределы функции
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Начнем с самого понятия предела. Но сначала краткая историческая справка. Жил-был в 19 веке француз Огюстен Луи Коши, который заложил основы математического анализа и дал строгие определения, определение предела, в частности. Надо сказать, этот самый Коши снился, снится и будет сниться в кошмарных снах всем студентам физико-математических факультетов, так как доказал огромное количество теорем математического анализа, причем одна теорема отвратительнее другой. В этой связи мы не будем рассматривать строгое определение предела, а попытаемся сделать две вещи:
1. Понять, что такое предел.
2. Научиться решать основные типы пределов.
Прошу прощения за некоторую ненаучность объяснений, важно чтобы материал был понятен даже чайнику, что, собственно, и является задачей проекта.
Итак, что же такое предел?
А сразу пример, чего бабушку лохматить….
Любой предел состоит из трех частей:
1) Всем известного значка предела 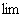
2) Записи под значком предела, в данном случае 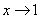
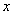
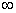
3) Функции под знаком предела, в данном случае 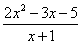
Сама запись 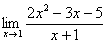
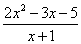
Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 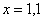
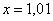
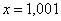
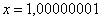
То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 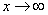
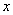
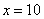
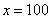
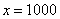
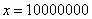
А что в это время происходит с функцией 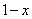
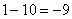
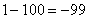
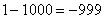
Итак: если 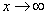
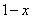
Грубо говоря, согласно нашему первому правилу, мы вместо «икса» подставляем в функцию 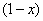
Еще один пример с бесконечностью:
Опять начинаем увеличивать 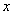
Вывод: при 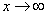
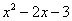
И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:
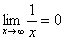
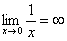
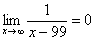
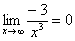
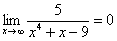
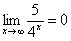
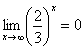
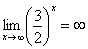
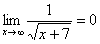
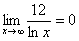
Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 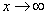
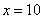
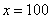
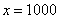
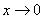
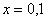
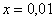
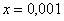
Примечание: строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: 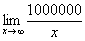
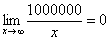
Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как 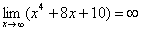
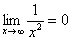
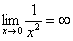
Пределы с неопределенностью вида 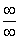
Сейчас мы рассмотрим группу пределов, когда 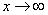
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 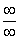
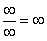
Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 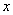
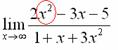
Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 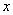
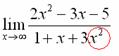
Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 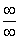
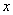
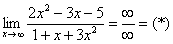
Разделим числитель и знаменатель на 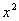
Вот оно как, ответ 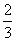
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: 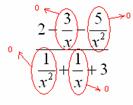
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Найти предел 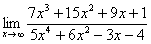
Снова в числителе и знаменателе находим 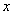
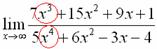
Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 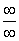
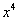
Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Найти предел 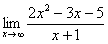
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( 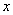
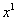
Для раскрытия неопределенности 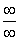
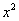
Разделим числитель и знаменатель на
Под записью 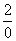
Таким образом, при раскрытии неопределенности вида 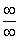
Пределы с неопределенностью вида 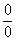
Предвосхищаю вопрос от чайников: «Почему здесь деление на ноль? На ноль же делить нельзя!». Смысл записи 0:0 будет понятен позже, после ознакомления с четвёртым уроком о бесконечно малых функциях. А пока всем начинающим изучать математический анализ предлагаю читать далее.
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 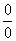
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения. Если данные вещи позабылись, тогда посетите страницу Математические формулы и таблицы и ознакомьтесь с методическим материалом Горячие формулы школьного курса математики. Кстати его лучше всего распечатать, требуется очень часто, да и информация с бумаги усваивается лучше.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: 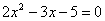
Сначала находим дискриминант: 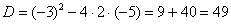
И квадратный корень из него: 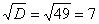
В случае если дискриминант большой, например 361, используем калькулятор, функция извлечения квадратного корня есть на самом простом калькуляторе.
! Если корень не извлекается нацело (получается дробное число с запятой), очень вероятно, что дискриминант вычислен неверно либо в задании опечатка.
Далее находим корни: 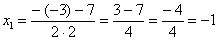
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель 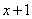
Очевидно, что можно сократить на 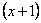
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители. 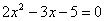
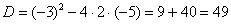
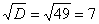
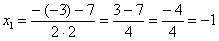
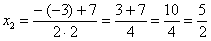
Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: 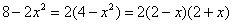
Знаменатель: 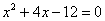
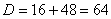
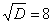
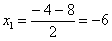
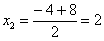
Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
Вообще, я заметил, что чаще всего в нахождении пределов данного типа приходится решать два квадратных уравнения, то есть и в числителе и в знаменателе находятся квадратные трехчлены.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида 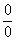
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 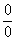
Вспоминаем нашу нетленную формулу разности квадратов: 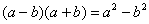
И смотрим на наш предел: 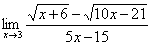
Что можно сказать? 
Умножаем числитель на сопряженное выражение:
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 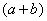
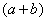
То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу 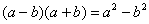
Неопределенность 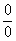
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители, собственно, это следовало сделать раньше.
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители: 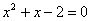
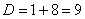
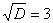
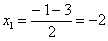
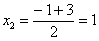
Умножим числитель и знаменатель на сопряженное выражение
Пределы функций. Примеры решений.
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
Пределы функций. Примеры решений.
Теория пределов – это один из разделов математического анализа. Вопрос решения пределов является достаточно обширным, поскольку существуют десятки приемов решений пределов различных видов. Существуют десятки нюансов и хитростей, позволяющих решить тот или иной предел. Тем не менее, мы все-таки попробуем разобраться в основных типах пределов, которые наиболее часто встречаются на практике.
Итак, что же такое предел?
Любой предел состоит из трех частей :
1) Всем известного значка предела 
2) Записи под значком предела, в данном случае 


3) Функции под знаком предела, в данном случае 
Сама запись 

Разберем следующий важный вопрос – а что значит выражение «икс стремится к единице»? И что вообще такое «стремится»?
Понятие предела – это понятие, если так можно сказать, динамическое. Построим последовательность: сначала 



То есть выражение «икс стремится к единице» следует понимать так – «икс» последовательно принимает значения, которые бесконечно близко приближаются к единице и практически с ней совпадают.
Как решить вышерассмотренный пример? Исходя из вышесказанного, нужно просто подставить единицу в функцию, стоящую под знаком предела:
Итак, первое правило: Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
Мы рассмотрели простейший предел, но и такие встречаются на практике, причем, не так уж редко!
Пример с бесконечностью:
Разбираемся, что такое 





А что в это время происходит с функцией 



Итак: если 

Еще один пример с бесконечностью:
Опять начинаем увеличивать 
Вывод: при 

И еще серия примеров:
Пожалуйста, попытайтесь самостоятельно мысленно проанализировать нижеследующее и запомните простейшие виды пределов:










Если где-нибудь есть сомнения, то можете взять в руки калькулятор и немного потренироваться.
В том случае, если 







Примечание : строго говоря, такой подход с построением последовательностей из нескольких чисел некорректен, но для понимания простейших примеров вполне подойдет.
Также обратите внимание на следующую вещь. Даже если дан предел с большим числом вверху, да хоть с миллионом: 

Что нужно запомнить и понять из вышесказанного?
1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
2) Вы должны понимать и сразу решать простейшие пределы, такие как 


Пределы с неопределенностью вида 
Сейчас мы рассмотрим группу пределов, когда 
Вычислить предел
Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида 

Как решать пределы данного типа?
Сначала мы смотрим на числитель и находим 

Старшая степень в числителе равна двум.
Теперь смотрим на знаменатель и тоже находим 

Старшая степень знаменателя равна двум.
Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.
Итак, метод решения следующий: для того, чтобы раскрыть неопределенность 


Разделим числитель и знаменатель на 
Вот оно как, ответ 
Что принципиально важно в оформлении решения?
Во-первых, указываем неопределенность, если она есть.
Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак 
В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: 
Для пометок лучше использовать простой карандаш.
Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?
Найти предел 
Снова в числителе и знаменателе находим 

Максимальная степень в числителе: 3
Максимальная степень в знаменателе: 4
Выбираем наибольшее значение, в данном случае четверку.
Согласно нашему алгоритму, для раскрытия неопределенности 

Полное оформление задания может выглядеть так:
Разделим числитель и знаменатель на
Найти предел 
Максимальная степень «икса» в числителе: 2
Максимальная степень «икса» в знаменателе: 1 ( 

Для раскрытия неопределенности 

Разделим числитель и знаменатель на
Под записью 
Таким образом, при раскрытии неопределенности вида 
Пределы с неопределенностью вида 
Следующая группа пределов чем-то похожа на только что рассмотренные пределы: в числителе и знаменателе находятся многочлены, но «икс» стремится уже не к бесконечности, а к конечному числу.
Общее правило : если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 
Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.
Итак, решаем наш предел
Разложим числитель и знаменатель на множители
Для того чтобы разложить числитель на множители, нужно решить квадратное уравнение: 
Сначала находим дискриминант: 
И квадратный корень из него: 
Далее находим корни: 
Таким образом:
Всё. Числитель на множители разложен.
Знаменатель. Знаменатель 
Очевидно, что можно сократить на 
Естественно, в контрольной работе, на зачете, экзамене так подробно решение никогда не расписывают. В чистовом варианте оформление должно выглядеть примерно так:
Разложим числитель на множители. 




Вычислить предел
Сначала «чистовой» вариант решения
Разложим числитель и знаменатель на множители.
Числитель: 
Знаменатель: 




Что важного в данном примере?
Во-первых, Вы должны хорошо понимать, как раскрыт числитель, сначала мы вынесли за скобку 2, а затем использовали формулу разности квадратов. Уж эту-то формулу нужно знать и видеть.
Рекомендация: Если в пределе (практически любого типа) можно вынести число за скобку, то всегда это делаем.
Более того, такие числа целесообразно выносить за значок предела. Зачем? Да просто чтобы они не мешались под ногами. Главное, потом эти числа не потерять по ходу решения.
Обратите внимание, что на заключительном этапе решения я вынес за значок предела двойку, а затем – минус.
Метод умножения числителя и знаменателя на сопряженное выражение
Продолжаем рассматривать неопределенность вида
Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.
Найти предел
Сначала пробуем подставить 3 в выражение под знаком предела
Еще раз повторяю – это первое, что нужно выполнять для ЛЮБОГО предела. Данное действие обычно проводится мысленно или на черновике.
Получена неопределенность вида 
Как Вы, наверное, заметили, у нас в числителе находится разность корней. А от корней в математике принято, по-возможности, избавляться. Зачем? А без них жизнь проще.
Когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 
Вспоминаем нашу нетленную формулу разности квадратов: 
И смотрим на наш предел: 
Что можно сказать? 

Умножаем числитель на сопряженное выражение :
Обратите внимание, что под корнями при этой операции мы ничего не трогаем.
Хорошо, 

То есть, мы умножили числитель и знаменатель на сопряженное выражение.
В известной степени, это искусственный прием.
Умножили. Теперь самое время применить вверху формулу 
Неопределенность 
Число, как уже отмечалось ранее, лучше вынести за значок предела.
Теперь осталось разложить числитель и знаменатель на множители и сократить «виновников» неопределённости, ну а предел константы – равен самой константе:
Как должно выглядеть решение данного примера в чистовом варианте?
Примерно так:
Умножим числитель и знаменатель на сопряженное выражение.
Найти предел
Сначала попробуйте решить его самостоятельно.
Окончательное решение примера может выглядеть так:
Разложим числитель на множители: 




Умножим числитель и знаменатель на сопряженное выражение
Простейшие виды пределов:












Пример 1. 
Разделим числитель и знаменатель на 
Пример 2.
Разделим числитель и знаменатель на
Пример 3.
Разделим числитель и знаменатель на
Правило 2: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 
Пример 1.
Разложим числитель на множители. 




Пример 2.
Разложим числитель и знаменатель на множители.
Числитель: 
Знаменатель: 




Правило 3: когда в числителе (знаменателе) находится разность корней (или корень минус какое-нибудь число), то для раскрытия неопределенности 
Пример 3.
Умножим числитель и знаменатель на сопряженное выражение.