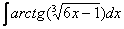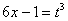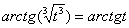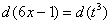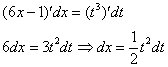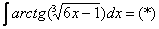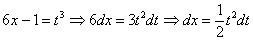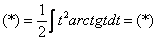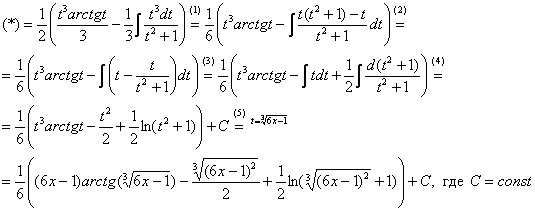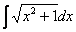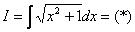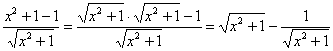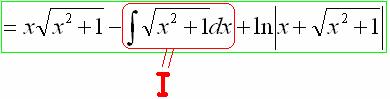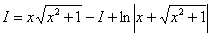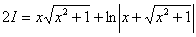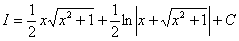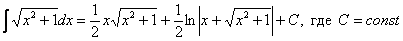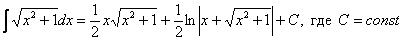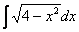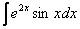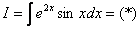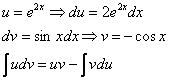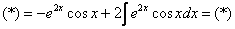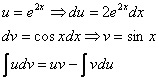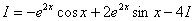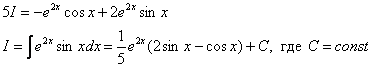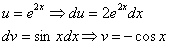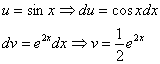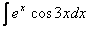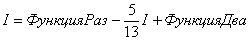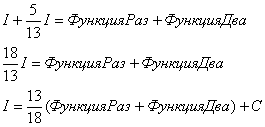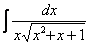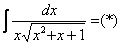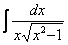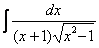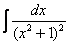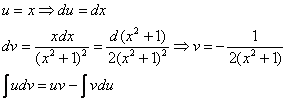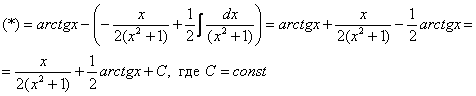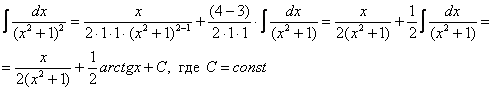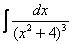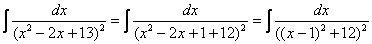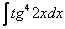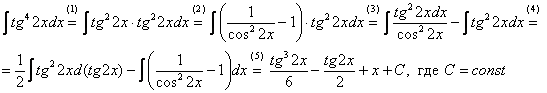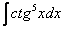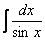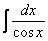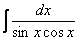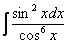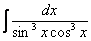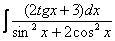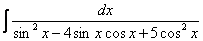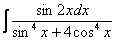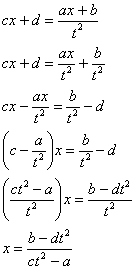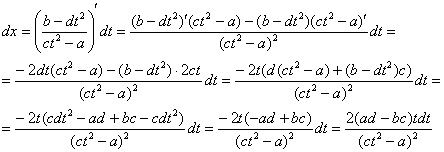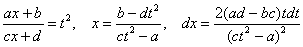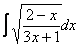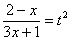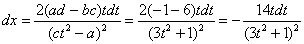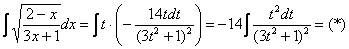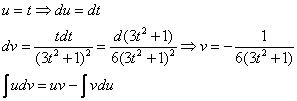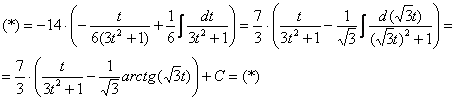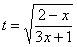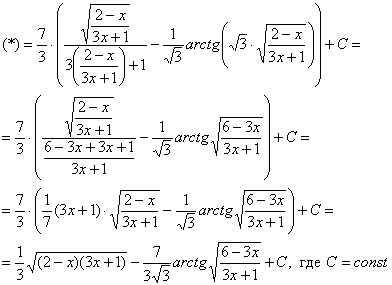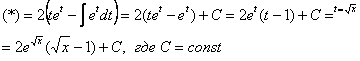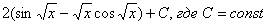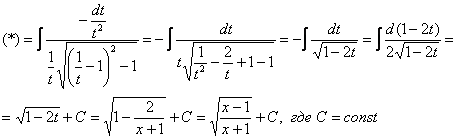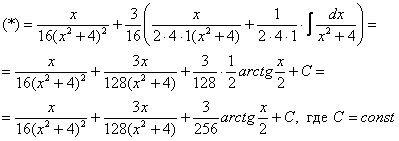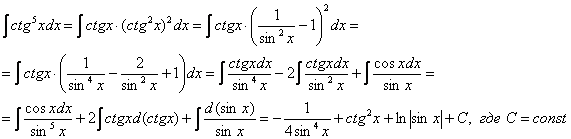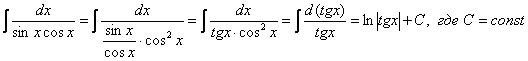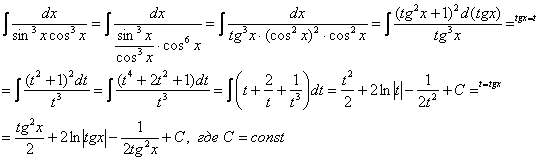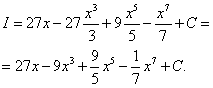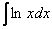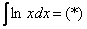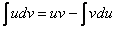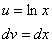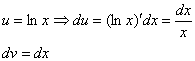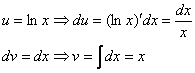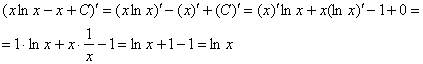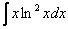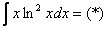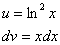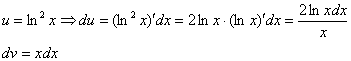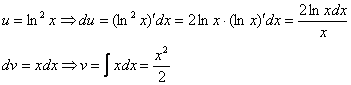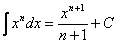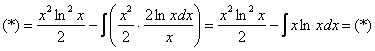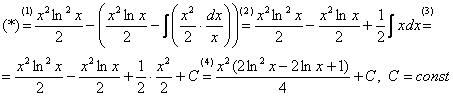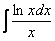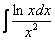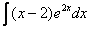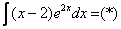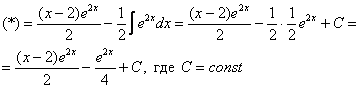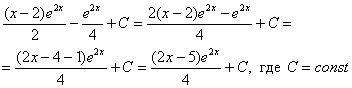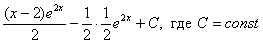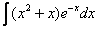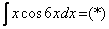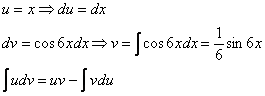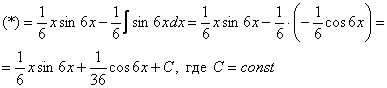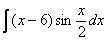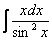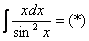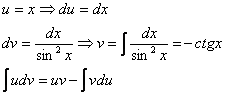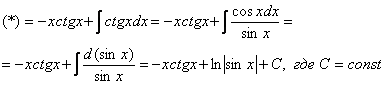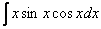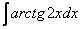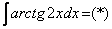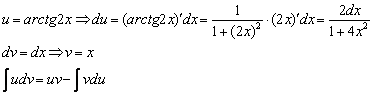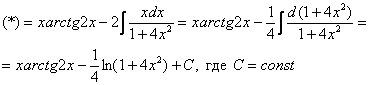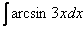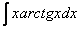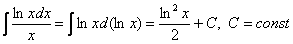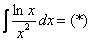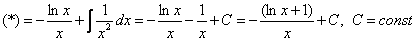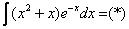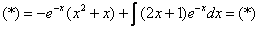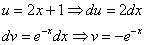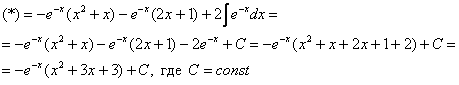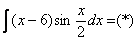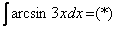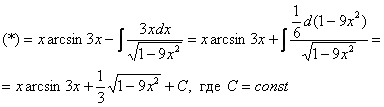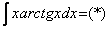Как решаются интегралы
Как решаются интегралы
Сложные интегралы
Данная статья завершает тему неопределенных интегралов, и в неё включены интегралы, которые я считаю достаточно сложными. Урок создан по неоднократным просьбам посетителей, которые высказывали пожелания, чтобы на сайте были разобраны и более трудные примеры.
Предполагается, что читатель сего текста хорошо подготовлен и умеет применять основные приемы интегрирования. Чайникам и людям, которые не очень уверенно разбираются в интегралах, следует обратиться к самому первому уроку – Неопределенный интеграл. Примеры решений, где можно освоить тему практически с нуля. Более опытные студенты могут ознакомиться с приемами и методами интегрирования, которые в моих статьях еще не встречались.
Какие интегралы будут рассмотрены?
Сначала мы рассмотрим интегралы с корнями, для решения которых последовательно используется замена переменной и интегрирование по частям. То есть, в одном примере комбинируются сразу два приёма. И даже больше.
Затем мы познакомимся с интересным и оригинальным методом сведения интеграла к самому себе. Данным способом решается не так уж мало интегралов.
Третьим номером программы пойдут интегралы от сложных дробей, которые пролетели мимо кассы в предыдущих статьях.
В-четвертых, будут разобраны дополнительные интегралы от тригонометрических функций. В частности, существуют методы, которые позволяют избежать трудоемкой универсальной тригонометрической подстановки.
И в заключение рассмотрим интеграл от корня из дроби, в числителе и знаменателе которой находятся линейные функции.
Конечно, название урока не совсем точно, будут и не сказать, что сильно сложные интегралы. Тем не менее, крепких орешков предостаточно. Запланировано довольно много примеров, поэтому поехали.
Последовательная замена переменной и интегрирование по частям
Найти неопределенный интеграл
Подынтегральная функция представляет собой арктангенс, под которым находится кубический корень. Первая же мысль, которая приходит в голову – избавиться бы от этого корня. Данный вопрос решается путем замены переменной, сама техника замены специфична, и она подробно рассмотрена на уроке Интегралы от иррациональных функций. Проведем замену:
После такой замены у нас получится вполне симпатичная вещь:
Осталось выяснить, во что превратится 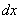
И само собой раскрываем дифференциалы:
На чистовике решение кратко записывается примерно так:
Проведем замену:
В результате замены получен знакомый тип интеграла, который интегрируется по частям:
(1) Выносим 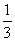
(2) В подынтегральной функции почленно делим числитель на знаменатель.
(3) Используем свойство линейности неопределенного интеграла. В последнем интеграле сразу подводим функцию под знак дифференциала.
(4) Берём оставшиеся интегралы. Обратите внимание, что в логарифме можно использовать скобки, а не модуль, так как 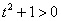
(5) Проводим обратную замену, выразив из прямой замены 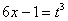
Студенты-мазохисты могут продифференцировать ответ и получить исходную подынтегральную функцию, как только что это сделал я. Нет-нет, я-то в правильном смысле выполнил проверку =)
Как видите, в ходе решения пришлось использовать даже больше двух приемов решения, таким образом, для расправы с подобными интегралами нужны уверенные навыки интегрирования и не самый маленький опыт.
На практике, конечно же, чаще встречается квадратный корень, вот три примера для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Найти неопределенный интеграл
Данные примеры однотипны, поэтому полное решение в конце статьи будет только для Примера 2, в Примерах 3-4 – одни ответы. Какую замену применять в начале решений, думаю, понятно. Почему я подобрал однотипные примеры? Часто встречаются в своем амплуа. Чаще, пожалуй, только что-нибудь вроде 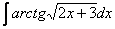
Но не всегда, когда под арктангенсом, синусом, косинусом, экспонентой и др. функциями находится корень из линейной функции, приходится применять сразу несколько методов. В ряде случаев удается «легко отделаться», то есть сразу после замены получается простой интеграл, который элементарно берётся. Самым легким из предложенных выше заданий является Пример 4, в нём после замены получается относительно несложный интеграл.
Методом сведения интеграла к самому себе
Остроумный и красивый метод. Немедленно рассмотрим классику жанра:
Найти неопределенный интеграл
Под корнем находится квадратный двучлен, и при попытке проинтегрировать данный пример чайник может мучаться часами. Такой интеграл берётся по частям и сводится к самому себе. В принципе не сложно. Если знаешь как.
Обозначим рассматриваемый интеграл латинской буквой 
Интегрируем по частям:
(1) Готовим подынтегральную функцию для почленного деления.
(2) Почленно делим подынтегральную функцию. Возможно, не всем понятно, распишу подробнее:
(3) Используем свойство линейности неопределенного интеграла.
(4) Берём последний интеграл («длинный» логарифм).
Теперь смотрим на самое начало решения: 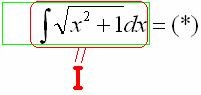
И на концовку:
Что произошло? В результате наших манипуляций интеграл свёлся к самому себе!
Приравниваем начало и конец:
Переносим 
А двойку сносим в правую часть. В результате:
Или:
Константу 
Примечание: Более строго заключительный этап решения выглядит так: 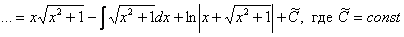
Таким образом: 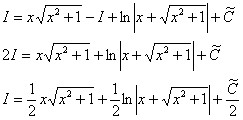
Константу 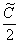
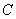
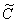
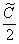
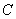
В результате:
Подобный трюк с переобозначением константы широко используется в дифференциальных уравнениях. И там я буду строг. А здесь такая вольность допускается мной только для того, чтобы не путать вас лишними вещами и акцентировать внимание именно на самом методе интегрирования.
Найти неопределенный интеграл
Еще один типовой интеграл для самостоятельного решения. Полное решение и ответ в конце урока. Разница с ответом предыдущего примера будет!
Если под квадратным корнем находится квадратный трехчлен, то решение в любом случае сводится к двум разобранным примерам.
Например, рассмотрим интеграл 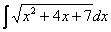
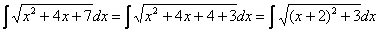
Далее проводится линейная замена, которая обходится «без всяких последствий»: 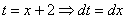
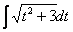
Или такой пример, с квадратным двучленом: 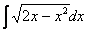
Выделяем полный квадрат: 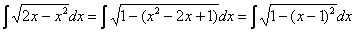
И, после линейной замены 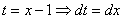
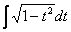
Рассмотрим еще два типовых примера на приём сведения интеграла к самому себе:
– интеграл от экспоненты, умноженной на синус;
– интеграл от экспоненты, умноженной на косинус.
В перечисленных интегралах по частям придется интегрировать уже два раза:
Найти неопределенный интеграл
Подынтегральная функция – экспонента, умноженная на синус.
Дважды интегрируем по частям и сводим интеграл к себе:

В результате двукратного интегрирования по частям интеграл свёлся к самому себе. Приравниваем начало и концовку решения:
Переносим 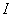
Готово. Попутно желательно причесать правую часть, т.е. вынести экспоненту за скобки, а в скобках расположить синус с косинусом в «красивом» порядке.
Теперь вернемся к началу примера, а точнее – к интегрированию по частям:
За 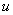
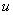
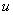
Почему такое возможно? Потому что экспонента превращается сама в себя (и при дифференцировании, и при интегрировании), синус с косинусом взаимно превращаются друг в друга (опять же – и при дифференцировании, и при интегрировании).
То есть, за 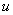
Найти неопределенный интеграл
Это пример для самостоятельного решения. Перед тем как решать, подумайте, что выгоднее в данном случае обозначить за 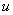
И, конечно, не забывайте, что большинство ответов данного урока достаточно легко проверить дифференцированием!
Примеры были рассмотрены не самые сложные. На практике чаще встречаются интегралы, где константа есть и в показателе экспоненты и в аргументе тригонометрической функции, например: 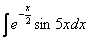
На завершающем этапе часто получается примерно следующее:
Даже в конце решения следует быть предельно внимательным и грамотно разобраться с дробями:
Интегрирование сложных дробей
Потихоньку подбираемся к экватору урока и начинаем рассматривать интегралы от дробей. Опять же, не все они суперсложные, просто по тем или иным причинам примеры были немного «не в тему» в других статьях.
Продолжаем тему корней
Найти неопределенный интеграл
В знаменателе под корнем находится квадратный трехчлен плюс за пределами корня «довесок» в виде «икса». Интеграл такого вида решается с помощью стандартной замены.
Решаем:
Замена тут проста:
Смотрим на жизнь после замены:
(1) После подстановки приводим к общему знаменателю слагаемые под корнем.
(2) Выносим 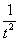
(3) Числитель и знаменатель сокращаем на 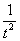
(4) Полученный интеграл, как вы помните из урока Интегрирование некоторых дробей, решается методом выделения полного квадрата. Выделяем полный квадрат.
(5) Интегрированием получаем заурядный «длинный» логарифм.
(6) Проводим обратную замену. Если изначально 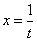
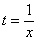
(7) Заключительное действие направлено на прическу результата: под корнем снова приводим слагаемые к общему знаменателю и выносим из-под корня 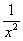
Найти неопределенный интеграл
Это пример для самостоятельного решения. Здесь к одинокому «иксу» добавлена константа, и замена почти такая же: 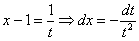
Единственное, что нужно дополнительно сделать – выразить «икс» из проводимой замены:
Полное решение и ответ в конце урока.
Иногда в таком интеграле под корнем может находиться квадратный двучлен, это не меняет способ решения, оно будет даже еще проще. Почувствуйте разницу:
Найти неопределенный интеграл
Найти неопределенный интеграл
Краткие решения и ответы в конце урока. Следует отметить, что Пример 11 является в точности биномиальным интегралом, метод решения которого рассматривался на уроке Интегралы от иррациональных функций.
Интеграл от неразложимого многочлена 2-й степени в степени
(многочлен в знаменателе)
Более редкий, но, тем не менее, встречающий в практических примерах вид интеграла.
Найти неопределенный интеграл
В знаменателе подынтегральной функции находится неразложимый на множители квадратный двучлен. Подчеркиваю, что неразложимость на множители является существенной особенностью. Если многочлен раскладывается на множители, то всё намного понятнее, например:
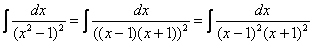
Но вернёмся к примеру со счастливым номером 13 (честное слово, не подгадал). Этот интеграл тоже из разряда тех, с которыми можно изрядно промучиться, если не знаешь, как решать.
Решение начинается с искусственного преобразования:
Как почленно разделить числитель на знаменатель, думаю, уже все понимают.
Полученный интеграл берётся по частям:
Для интеграла вида 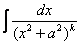
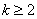
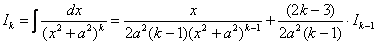
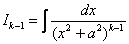
Убедимся в справедливости данной формулы для прорешанного интеграла 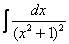
В данном случае: 
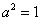
Как видите, ответы совпадают.
Найти неопределенный интеграл
Это пример для самостоятельного решения. В образце решения дважды последовательно использована вышеупомянутая формула.
Если под степенью находится неразложимый на множители квадратный трехчлен, то решение сводится к двучлену путем выделения полного квадрата, например:
Далее следует «безболезненная» линейная замена 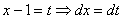
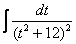
Что делать, если дополнительно в числителе есть многочлен? В этом случае используется метод неопределенных коэффициентов, и подынтегральная функция раскладывается в сумму дробей. Но в моей практике такого примера не встречалось ни разу, поэтому я пропустил данный случай в статье Интегралы от дробно-рациональной функции, пропущу и сейчас. Если такой интеграл все-таки встретится, смотрите учебник – там всё просто. Не считаю целесообразным включать материал (даже несложный), вероятность встречи с которым стремится к нулю.
Интегрирование сложных тригонометрических функций
Прилагательное «сложный» для большинства примеров вновь носит во многом условный характер. Начнем с тангенсов и котангенсов в высоких степенях. С точки зрения используемых методов решения тангенс и котангенс – почти одно и тоже, поэтому я больше буду говорить о тангенсе, подразумевая, что продемонстрированный прием решения интеграла справедлив и для котангенса тоже.
На уроке Интегралы от тригонометрических функций мы разобрали интеграл от тангенса в квадрате. На уроке Как вычислить площадь фигуры? в примере 10 фигурировал тангенс в кубе. В том примере для нахождения интеграла от тангенса в кубе мы применяли тригонометрическую формулу 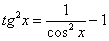
Найти неопределенный интеграл
Идея решения подобных интегралов состоит в том, чтобы с помощью формулы 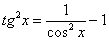
(1) Готовим подынтегральную функцию к применению формулы.
(2) Для одного из множителей используем формулу 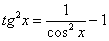
(3) Раскрываем скобки и сразу же используем свойство линейности неопределенного интеграла.
(4) В первом интеграле используем метод подведения функции под знак дифференциала. Во втором интеграле еще раз используем формулу 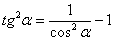
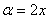
(5) Берём все три интеграла и получаем ответ.
Найти неопределенный интеграл
Это пример для самостоятельного решения. Для котангенса существует аналогичная формула: 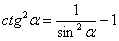
Если возникли затруднения или недопонимание, следует вернуться к уроку Интегралы от тригонометрических функций.
На вышеупомянутом уроке мы рассматривали универсальную тригонометрическую подстановку для решения определенного вида интегралов от тригонометрических функций. Недостаток универсальной тригонометрической подстановки заключается в том, что при её применении часто возникают громоздкие интегралы с трудными вычислениями. И в ряде случаев универсальной тригонометрической подстановки можно избежать!
Рассмотрим еще один канонический пример, интеграл от единицы, деленной на синус:
Найти неопределенный интеграл
Здесь можно использовать универсальную тригонометрическую подстановку и получить ответ, но существует более рациональный путь. Я приведу полное решение с комментами к каждому шагу:
(1) Используем тригонометрическую формулу синуса двойного угла 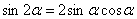
(2) Проводим искусственное преобразование: В знаменателе делим и умножаем на 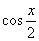
(3) По известной формуле в знаменателе превращаем дробь в тангенс.
(4) Подводим функцию под знак дифференциала.
(5) Берём интеграл.
Пара простых примеров для самостоятельного решения:
Найти неопределенный интеграл
Указание: Самым первым действием следует использовать формулу приведения 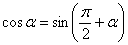
Найти неопределенный интеграл
Ну, это совсем простой пример.
Полные решения и ответы в конце урока.
Думаю, теперь ни у кого не возникнет проблем с интегралами:
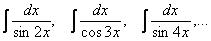
В чём состоит идея метода? Идея состоит в том, чтобы с помощью преобразований, тригонометрических формул организовать в подынтегральной функции только тангенсы и производную тангенса 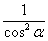
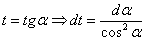
Аналогичные рассуждения, как я уже оговаривался, можно провести для котангенса.
Существует и формальная предпосылка для применения вышеуказанной замены:
Сумма степеней косинуса и синуса – целое отрицательное ЧЁТНОЕ число, например:
для интеграла 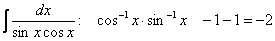
! Примечание: если подынтегральная функция содержит ТОЛЬКО синус или ТОЛЬКО косинус, то интеграл берётся и при отрицательной нечётной степени (простейшие случаи – в Примерах № 17, 18).
Рассмотрим пару более содержательных заданий на это правило:
Найти неопределенный интеграл
Сумма степеней синуса и косинуса 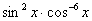
(1) Преобразуем знаменатель.
(2) По известной формуле получаем 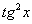
(3) Преобразуем знаменатель.
(4) Используем формулу 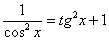
(5) Подводим функцию под знак дифференциала.
(6) Проводим замену 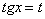
Далее берётся простой интеграл и проводится обратная замена.
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Держитесь, начинаются чемпионские раунды =)
Зачастую в подынтегральной функции находится «солянка»:
Найти неопределенный интеграл
В этом интеграле изначально присутствует тангенс, что сразу наталкивает на уже знакомую мысль:
Искусственное преобразование в самом начале и остальные шаги оставлю без комментариев, поскольку обо всем уже говорилось выше.
Пара творческих примеров для самостоятельного решения:
Найти неопределенный интеграл
Найти неопределенный интеграл
Да, в них, конечно, можно понизить степени синуса, косинуса, использовать универсальную тригонометрическую подстановку, но решение будет гораздо эффективнее и короче, если его провести через тангенсы. Полное решение и ответы в конце урока
У многих читателей могло сложиться впечатления, что я немного подустал. Отнюдь. За окном февральский ветер – самая атмосфера для лекций. Естественно, данная страничка создана не за один день, я успел несколько раз побриться, регулярно кушаю и так далее. К тому же, загружать студентов – удовольствие бесконечное =). …Шутка! На самом деле моя миссия – разгружать посетителей сайта. Вагонами.
Переходим к заключительному пункту познавательного путешествия в мир сложных интегралов:
Интеграл от корня из дроби
Интеграл, который мы рассмотрим, встречается достаточно редко, но я буду очень рад, если единственный пример данного параграфа вам поможет.
Корнями всё начиналось, корнями и закончится. Рассмотрим неопределенный интеграл: 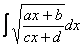
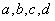
В подынтегральной функции у нас находится корень, а под корнем – дробь, в числителе и знаменателе которой располагаются линейные функции.
Метод стар – нужно избавиться от корня. Стар и уныл, но сейчас станет веселее, поскольку придется проводить громоздкую замену.
Замена, с помощью которой мы гарантированно избавимся от корня, очевидна: 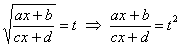
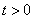
Теперь нужно выразить «икс» и найти, чему равен дифференциал 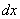
Выражаем «икс»:
Теперь найдем дифференциал:
Зачем были эти нелепые скучные телодвижения?
Я вывел готовые формулы, которыми можно пользовать при решении интеграла вида 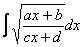
Формулы замены таковы:
Это было ни в коем случае не хвастовство, просто я не смог быстро найти эти формулы в близлежащей литературе и Сети – оказалось проще вывести. Да и может быть кто-нибудь для реферата возьмет.
Опять – двадцать пять, заключительный пример:
Найти неопределенный интеграл
Проведем замену:
В данном примере: 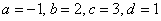
Таким образом:
Еще куда ни шло, могло всё оказаться значительно хуже. Такой интеграл, кстати, уже фигурировал в Примере 13. Интегрируем по частям:
Проведем обратную замену. Если изначально 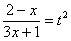
Некоторым страшно, а я это продифференцировал, ответ верный!
Иногда встречаются интегралы вида 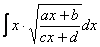
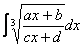
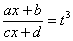
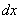
Теперь вам практически любой интеграл по силам, успехов!
Решения и ответы:
Пример 2: Решение: 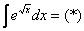
Проведем замену: 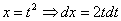
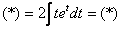
Интегрируем по частям: 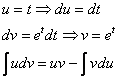
Пример 3: Ответ:
Пример 4: Ответ:
Пример 6: Решение: 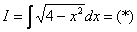
Интегрируем по частям: 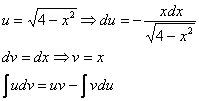

Таким образом: 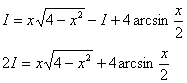
В результате:
Пример 8: Решение:
Дважды интегрируем по частям и сводим интеграл к себе: 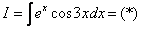
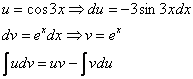
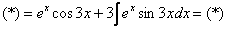
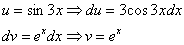
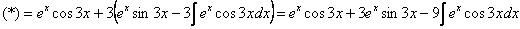
Таким образом:
Пример 10: Решение: 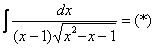
Проведем замену: 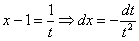
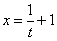
Пример 11: Решение: 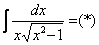
Замена: 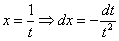
Пример 12: Решение: 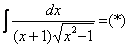
Замена: 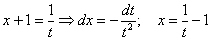
Пример 14: Решение: 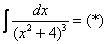
Дважды используем рекуррентную формулу 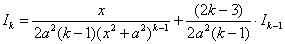
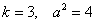
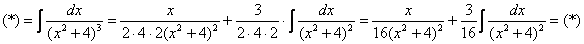
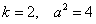
Пример 16: Решение:
Пример 18: Решение: 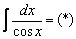
Используем формулу приведения: 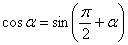
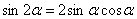
Пример 19: Решение:
Пример 21: Решение:
–3 – 3 = –6 – целое отрицательное ЧЁТНОЕ число
Пример 23: Решение:
Пример 24: Решение:
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Примеры на решение интегралов
Вы будете перенаправлены на Автор24
Навыки нахождения интегралов могут пригодиться не только в математике, но и в других точных дисциплинах. Рассмотрим различные примеры по решению неопределённых интегралов и правила, по которым они решаются.
Структура статьи следующая: сначала даётся правило, а затем приводятся примеры его применения. Для удобства мы также вставили таблицу с простейшими интегралами.
Использование таблицы
Рисунок 1. Табличные значения. Автор24 — интернет-биржа студенческих работ
Таблица является основой интегрального исчисления. Для того чтобы использовать её, достаточно лишь найти необходимые значения. Рассмотрим примеры использования простейших табличных интегралов.
Найти, чему равны следующие выражения:
Такие интегралы решать очень просто, нужно либо иметь таблицу под рукой, либо её помнить:
Вынесение множителя за знак интеграла и интеграл от суммы
К сожалению, очень редко интегральные выражения представляют собой лишь простые табличные формулы. Поэтому при решении интегралов как минимум стоит помнить помимо самой таблицы ещё эти два правила:
Готовые работы на аналогичную тему
Осуществите нахождение значений следующих выражений:
Здесь пользуемся формулой интеграла суммы, а затем выносим пятёрку и семёрку за знак интеграла, в конечном итоге получаем сумму дробей.
Здесь сначала необходимо возвести в куб всё выражение, а затем осуществить то же, что и в предыдущем примере — воспользоваться формулой для интеграла суммы и вынести постоянные коэффициенты за знак интеграла.
Интегрирование с использованием замены переменной
Найти следующие интегралы:
а) В этом примере мы имеем дело с интегралом от e, табличное значение для которого довольно простое.
Подставим это в наше выражение:
$\int x \cdot \sqrt
Занесение под дифференциал
Воспользуйтесь выше обозначенным методом и найдите следующие интегралы:
Интегрирование по частям
Данное правило по сути является обратным к предыдущему:
Подставляем всё и получаем:
Интегралы от тригонометрических функций
Интегрирование выражений, содержащих иррациональности с возможностью выделить полный квадрат
К данным интегралам относятся интегралы, подходящие под следующие формулы:
Для того чтобы их решить, под знаком корня выделяют полный квадрат:
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 15.05.2022
Найти неопределённый интеграл: начала начал, примеры решений
Что нужно знать, чтобы найти неопределённый интеграл
Чтобы найти неопределённый интеграл, требуется довольно небольшое количество основных формул интегрирования. Но процесс его нахождения значительно труднее, чем одно лишь применение этих формул. Вся сложность относится не к интегрированию, а к приведению интегрируемого выражения к такому виду, который даёт возможность найти неопределённый интеграл по упомянутым выше основным формулам. Это означает, что для начала практики интегрирования нужно активизировать полученные в средней школе навыки преобразования выражений.
Учиться находить интегралы будем, пользуясь свойствами и таблицей неопределённых интегралов из урока об основных понятиях этой темы (откроется в новом окне).
Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла, т.е.

Теорема 4. Неопределённый интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределённых интегралов этих функций, т.е.

Кроме того, в интегрировании может пригодиться следующее правило: если выражение подынтегральной функции содержит постоянный множитель, то выражение первообразной домножается на число, обратное постоянному множителю, то есть

Первая вещь, которой не следует удивляться при интегрировании. В таблице интегралов существуют формулы, которые не имеют аналогов среди формул таблицы производной. Это следующие формулы:
Однако можно убедиться в том, что производные выражений, стоящих в правых частях этих формул, совпадают с соответствующими подынтегральными функциями.
Вторая вещь, которой не следует удивляться при интегрировании. Хотя производная любой элементарной функции представляет собой также элементарную функцию, неопределённые интегралы от некоторых элементарных функций уже не являются элементарными функциями. Примерами таких интегралов могут быть следующие:
Для выработки техники интегрирования пригодятся следующие навыки: сокращение дробей, деление многочлена в числителе дроби на одночлен в знаменателе (для получения суммы неопределённых интегралов), преобразование корней в степени, умножение одночлена на многочлен, возведение в степень. Эти навыки нужны для преобразований подынтегрального выражения, в результате которых должна получиться сумма интегралов, присутствующих в таблице интегралов.
Находим неопределённые интегралы вместе
Пример 1. Найти неопределённый интеграл


Теперь в знаменателе сумма квадратов, а это значит, что можем применить упомянутый табличный интеграл. Окончательно получаем ответ:

Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 2. Найти неопределённый интеграл


Применяем формулу 7 из таблицы интегралов (переменная в степени) к подынтегральной функции:


Пример 3. Найти неопределённый интеграл
Решение. Применяя сначала теорему 4, а затем теорему 3 о свойствах, найдём данный интеграл как сумму трёх интегралов:
Все три полученные интеграла – табличные. Используем формулу (7) из таблицы интегралов при n = 1/2, n = 2 и n = 1/5, и тогда
объединяет все три произвольные постоянные, которые были введены при нахождении трёх интегралов. Поэтому в аналогичных ситуациях следует вводить только одну произвольную постоянную (константу) интегрирования.
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 4. Найти неопределённый интеграл


Чтобы применить табличный интеграл, преобразуем корни в степени и вот уже окончательный ответ:
Найти неопределённый интеграл самостоятельно, а затем посмотреть решение
Пример 5. Найти неопределённый интеграл

Пример 6. Найти неопределённый интеграл

Продолжаем находить неопределённые интегралы вместе
Пример 7. Найти неопределённый интеграл
Решение. Если мы преобразуем подынтегральную функцию, возведя двучлен в квадрат и разделив почленно числитель на знаменатель, то исходный интеграл станет суммой трёх интегралов:
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 8. Найти неопределённый интеграл

Решение. В подынтегральном выражении нужно умножить многочлен на одночлен, тогда получим сумму двух интегралов:

Применяем табличный интеграл 7, интегрируя степенные функции, и окончательный ответ:

Пример 9. Найти неопределённый интеграл

Пример 10. Найти неопределённый интеграл
Решение. Представим числитель подынтегральной функции, равный 1, в виде
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Интегрирование по частям. Примеры решений
И снова, здравствуйте. Сегодня на уроке мы научимся интегрировать по частям. Метод интегрирования по частям – это один из краеугольных камней интегрального исчисления. На зачете, экзамене студенту почти всегда предлагают решить интегралы следующих типов: простейший интеграл (см. статью Неопределенный интеграл. Примеры решений) либо интеграл на замену переменной (см. статью Метод замены переменной в неопределенном интеграле) либо интеграл как раз на метод интегрирования по частям.
Для эффективного изучения темы необходимо хорошо ориентироваться в материалах двух вышеуказанных уроков. Если Вы чайник, и только-только начинаете погружение в удивительный мир интегралов, то читать далее не имеет особого смысла – следует начать с урока Неопределенный интеграл. Примеры решений.
Как всегда, под рукой должны быть: Таблица интегралов и Таблица производных. Если у Вас до сих пор их нет, то, пожалуйста, посетите кладовку моего сайта: Математические формулы и таблицы. Не устану повторять – лучше всё распечатать. Весь материал я постараюсь изложить последовательно, просто и доступно, в интегрировании по частям нет особых трудностей.
Какую задачу решает метод интегрирования по частям? Метод интегрирования по частям решает очень важную задачу, он позволяет интегрировать некоторые функции, отсутствующие в таблице, произведение функций, а в ряде случаев – и частное. Как мы помним, нет удобной формулы:
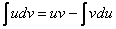
И сразу список в студию. По частям берутся интегралы следующих видов:
1) 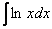
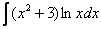
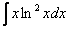
2) 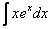
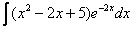
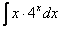
3) 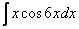
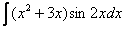
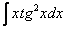
4) 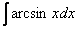
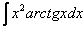
Также по частям берутся некоторые дроби, соответствующие примеры мы тоже подробно рассмотрим.
Интегралы от логарифмов
Найти неопределенный интеграл.
Классика. Время от времени данный интеграл можно встретить в таблицах, но пользоваться готовым ответом нежелательно, так как у преподавателя весенний авитаминоз и он сильно заругается. Потому что рассматриваемый интеграл отнюдь не табличный – он берётся по частям. Решаем:
Прерываем решение на промежуточные объяснения.
Используем формулу интегрирования по частям:
Формула применяется слева направо
Смотрим на левую часть: 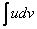
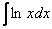
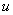
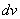
В интегралах рассматриваемого типа за 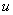
Технически оформление решения реализуется следующим образом, в столбик записываем:
То есть, за 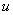
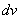
Следующий этап: находим дифференциал 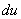
Дифференциал – это почти то же самое, что и производная, как его находить, мы уже разбирали на предыдущих уроках.
Теперь находим функцию 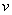
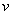
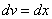
Теперь открываем наше решение и конструируем правую часть формулы: 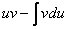
Вот кстати, и образец чистового решения с небольшими пометками:

Единственный момент, в произведении 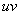
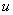
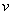
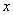
Как видите, применение формулы интегрирования по частям, по сути дела, свело наше решение к двум простым интегралам.
Обратите внимание, что в ряде случаев сразу после применения формулы, под оставшимся интегралом обязательно проводится упрощение – в рассматриваемом примере мы сократили подынтегральное выражение на «икс».
Выполним проверку. Для этого нужно взять производную от ответа:
Получена исходная подынтегральная функция, значит, интеграл решён правильно.
В ходе проверки мы использовали правило дифференцирования произведения: 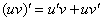
Формула интегрирования по частям 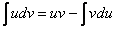
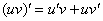
Найти неопределенный интеграл.
Подынтегральная функция представляет собой произведение логарифма на многочлен.
Решаем.
Я еще один раз подробно распишу порядок применения правила, в дальнейшем примеры будут оформляться более кратко, и, если у Вас возникнут трудности в самостоятельном решении, нужно вернуться обратно к первым двум примерам урока.
Как уже говорилось, за 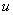
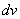
Записываем в столбик:
Сначала находим дифференциал 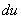
Здесь использовано правило дифференцирования сложной функции 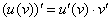
Теперь находим функцию 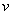
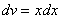
Для интегрирования мы применили простейшую табличную формулу
Теперь всё готово для применения формулы 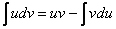
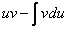
Под интегралом у нас снова многочлен на логарифм! Поэтому решение опять прерывается и правило интегрирования по частям применяется второй раз. Не забываем, что за 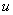
Хорошо бы, если к данному моменту простейшие интегралы и производные Вы умели находить устно.
(1) Не путаемся в знаках! Очень часто здесь теряют минус, также обратите внимание, что минус относится ко всей скобке 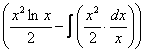
(2) Раскрываем скобки. Последний интеграл упрощаем.
(3) Берем последний интеграл.
(4) «Причесываем» ответ.
Необходимость дважды (а то и трижды) применять правило интегрирования по частям возникает не так уж и редко.
А сейчас пара примеров для самостоятельного решения:
Найти неопределенный интеграл.
Этот пример решается методом замены переменной (или подведением под знак дифференциала)! А почему бы и нет – можете попробовать взять его по частям, получится забавная вещь.
Найти неопределенный интеграл.
А вот этот интеграл интегрируется по частям (обещанная дробь).
Это примеры для самостоятельного решения, решения и ответы в конце урока.
Вроде бы в примерах 3, 4 подынтегральные функции похожи, а вот методы решения – разные! В этом-то и состоит основная трудность освоения интегралов – если неправильно подобрать метод решения интеграла, то возиться с ним можно часами, как с самой настоящей головоломкой. Поэтому чем больше вы прорешаете различных интегралов – тем лучше, тем легче пройдут зачет и экзамен. Кроме того, на втором курсе будут дифференциальные уравнения, а без опыта решения интегралов и производных делать там нечего.
По логарифмам, пожалуй, более чем достаточно. На закуску могу еще вспомнить, что студенты-технари логарифмами называют женскую грудь =). Кстати, полезно знать назубок графики основных элементарных функций: синуса, косинуса, арктангенса, экспоненты, многочленов третьей, четвертой степени и т.д. Нет, конечно, презерватив на глобус
я натягивать не буду, но теперь вы многое запомните из раздела Графики и функции =).
Интегралы от экспоненты, умноженной на многочлен
Общее правило: за 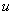
Найти неопределенный интеграл.
Используя знакомый алгоритм, интегрируем по частям:

Если возникли трудности с интегралом 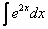
Единственное, что еще можно сделать, это «причесать» ответ:
Но если Ваша техника вычислений не очень хороша, то самый выгодный вариант оставить ответом 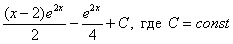
То есть, пример считается решенным, когда взят последний интеграл. Ошибкой не будет, другое дело, что преподаватель может попросить упростить ответ.
Найти неопределенный интеграл.
Это пример для самостоятельного решения. Данный интеграл дважды интегрируется по частям. Особое внимание следует обратить на знаки – здесь легко в них запутаться, также помним, что 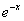
Больше про экспоненту рассказывать особо нечего. Могу только добавить, что экспонента и натуральный логарифм взаимно-обратные функции, это я к теме занимательных графиков высшей математики =) Стоп-стоп, не волнуемся, лектор трезв.
Интегралы от тригонометрических функций, умноженных на многочлен
Общее правило: за 
Найти неопределенный интеграл.
Интегрируем по частям:
Хммм, …и комментировать нечего.
Найти неопределенный интеграл
Это пример для самостоятельного решения
Найти неопределенный интеграл
Еще один пример с дробью. Как и в двух предыдущих примерах за 
Интегрируем по частям:
Если возникли трудности или недопонимание с нахождением интеграла 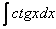
Найти неопределенный интеграл
Это пример для самостоятельного решения.
Подсказка: перед использованием метода интегрирования по частям следует применить некоторую тригонометрическую формулу, которая превращает произведение двух тригонометрических функций в одну функцию. Формулу также можно использовать и в ходе применения метода интегрирования по частям, кому как удобнее.
Вот, пожалуй, и всё в данном параграфе. Почему-то вспомнилась строчка из гимна физмата «А синуса график волна за волной по оси абсцисс пробегает»….
Интегралы от обратных тригонометрических функций.
Интегралы от обратных тригонометрических функций, умноженных на многочлен
Общее правило: за 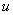
Напоминаю, что к обратным тригонометрическим функциям относятся арксинус, арккосинус, арктангенс и арккотангенс. Для краткости записи я буду называть их «арками»
Найти неопределенный интеграл.
Интегрируем по частям:
Интеграл 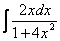
И здесь читатель задал вопрос: а куда же делся модуль под логарифмом? Ответ прост: если «начинка» логарифма неотрицательна (при любом возможном «икс»), то модуль можно не ставить. В данном примере 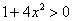
Найти неопределенный интеграл.
Это пример для самостоятельного решения.
Как видите, помимо «чистого» интегрирования по частям нередко требуется применять и другие методы, приёмы решения.
И заключительный пример сегодняшнего урока под счастливым номером тринадцать: «арк», умноженный на многочлен. Он сложнее, и предназначен для маньяков желающих лучше разобраться в методе интегрирования по частям. Пример, пожалуй, будет тоже для самостоятельного решения, поскольку меня немного утомил тот логарифм в квадрате.
Найти неопределенный интеграл.
Что касаемо интегрирования по частям, почти всё разобрали. Рассмотренный метод часто применяется в комбинации с другими приёмами решения интегралов. Читатели с хорошими навыками могут ознакомиться с такими примерами на уроке Сложные интегралы.
Пример 3: Решение:
Пример 4: Решение:
Интегрируем по частям:
Пример 6: Решение:
Дважды интегрируем по частям:
Пример 8: Решение:
Интегрируем по частям:
Пример 10: Решение:
Интегрируем по частям: 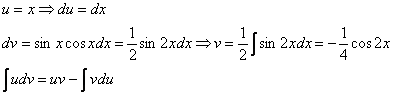
Примечание: Здесь мы использовали известную тригонометрическую формулу двойного угла 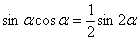
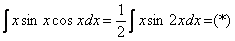
Похожим способом также решаются интегралы вроде 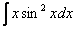
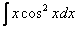
Пример 12: Решение:
Интегрируем по частям: 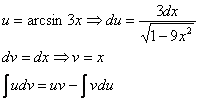
Пример 13: Решение:
Интегрируем по частям:
Примечание: Если возникли трудности с интегралом 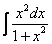
Вы выполнили проверку? Может я и ошибся где… 😉
Автор: Емелин Александр
(Переход на главную страницу)


cкидкa 17% на первый зaкaз, при оформлении введите прoмoкoд: 5530-xr4ys
Методы решения интегралов
Методы решения интегралов
1. Прямая интеграция
разделит функцию подынтегральной функции:
\(\ \int \frac
Интеграл от суммы равен сумме интегралов:
\(\ \int \frac
Получил сумму табличных интегралов, поэтому мы имеем:
2. Метод суммирования знака дифференциала
Метод суммирования знака дифференциала. Этот метод эквивалентен методу подстановки.
Решить интеграл \(\ \int x \sin x^ <2>d x \)
Введем \(\ x \) под знаком дифференциала:
Тогда мы получим:
\(\ \int x \sin x^ <2>d x=\int \sin x^ <2>\cdot \frac<1> <2>d\left(x^<2>\right)=\frac<1> <2>\int \sin x^ <2>d\left(x^<2>\right) \)
Согласно таблице интегралов
\(\ \int \sin t d t=-\cos t+C \)
Тогда в \(\ t=x^ <2>\) имеем:
\(\ \int x \sin x^ <2>d x=\frac<1> <2>\int \sin x^ <2>d\left(x^<2>\right)=\frac<1> <2>\cdot\left(-\cos x^<2>\right)+C=-\frac<\cos x^<2>><2>+C \)
Подробнее о методе суммирования дифференциального знака на ссылке.
3. Переменный метод замены или метод подстановки
Метод замены или метод замены. Этот метод состоит в введении новой переменной интеграции (т. е. Делается замена). В этом случае данный интеграл сводится к новому интегралу, который является табличным или может быть сведен к табличному с использованием преобразований.
\(\ \int f(x) d x=\int f(\phi(t)) \cdot \phi^<\prime>(t) d t \)
Итак, интеграл принимает вид:
\(\ \int \frac<\ln x>
Неопределенный интеграл зависит от переменной интегрирования, поэтому мы делаем обратную замену \(\ t=\ln x \) :
4. Метод интеграции по частям
Метод интегрирования по частям. Этот метод основан на следующей формуле:
\(\ \int u d v=u v-\int v d u \)
Решите интеграл \(\ \int x \sin x d x \)
Мы применяем метод интеграции по частям:
\(\ =-x \cos x+\int \cos x d x=-x \cos x+\sin x+C \)
\(\ \int x \sin x d x=-x \cos x+\sin x+C \)
Метод интегрирования по частям: объяснение, решение примеров
Суть метода интегрирования по частям
Следующая формула называется формулой интегрирования по частям в неопределённом интеграле:
Когда выгодно применять метод интегрирования по частям? Тогда, когда подынтегральная функция содержит:
1) 
3) 



Поясним ценность метода интегрирования по частям на примере первого случая. Пусть выражение под знаком интеграла содержит логарифмическую функцию (таким будет пример 1). Применением интегрирования по частям такой интеграл сводится вычислению интеграла только алгебраических функций (чаще всего многочлена), то есть не содержащих логарифмическую или обратную тригонометрическую функцию. Применяя данную в самом начале урока формулу интегрирования по частям

Таким образом, с помощью формулы интегрирования по частям интегрирование не выполняется сразу: нахождение данного интеграла сводится к нахождению другого. Смысл формулы интегрирования по частям состоит в том, чтобы в результате её применения новый интеграл оказался табличным или хотя бы стал проще первоначального.
Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций:
то её можно записать в виде

который и был приведён в самом начале урока.
При нахождении интегрированием функции v для неё получается бесконечное множество первообразных функций. Чтобы применить формулу интегрирования по частям, можно взять любую из них, а значит, и ту, которая соответствует произвольной постоянной С, равной нулю. Поэтому при нахождении функции v произвольную постоянную С вводить не следует.
Применяем интегрирование по частям вместе
Пример 1. Найти неопределённый интеграл методом интегрирования по частям:

Тогда 

И снова логарифм.
Пример 2. Найти неопределённый интеграл:

Решение. Пусть 

Логарифм присутствует в квадрате. Это значит, что его нужно дифференцировать как сложную функцию. Находим, пользуясь производной 6 в таблице производных сложных функций: 

Применяя формулу интегрирования по частям, получаем:
Находим изначальный интеграл:
Пример 3. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Арктангенс, как и логарифм, лучше обозначить через u. Итак, пусть 

Тогда, пользуясь табличной производной 12, получаем 

Применяя формулу интегрирования по частям, получаем:
Возвращаясь к переменной x, получаем

Находим изначальный интеграл:

Пример 4. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Экспоненту лучше обозначить через dv. Разбиваем подынтегральное выражение на два множителя. Полагая, что
Проверить решение задач на неопределённый интеграл можно на калькуляторе неопределённых интегралов онлайн.
Пример 5. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Пусть 



Используя формулу интегрирования по частям (1), находим:
Пример 6. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Синус, как и экспоненту, удобно обозначить через dv. Пусть 

Тогда 

По формуле интегрирования по частям находим:
Применить интегрирование по частям самостоятельно, а затем посмотреть решение
Пример 7. Найти неопределённый интеграл методом интегрирования по частям:

Пример 8. Найти неопределённый интеграл методом интегрирования по частям:

Пример 9. Найти неопределённый интеграл методом интегрирования по частям:

Снова применяем интегрирование по частям вместе
Пример 10. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Как и во всех подобных случаях, косинус удобно обозначить через dv. Обозначаем 

Тогда 

По формуле интегрирования по частям получаем:
Ко второму слагаемому также применяем интегрирование по частям. Обозначаем 

Тогда 

Применив эти обозначения, интегрируем упомянутое слагаемое:
Теперь находим требуемый интеграл:
Пример 11. Найти неопределённый интеграл методом интегрирования по частям:

Решение. Примем как руководство к действию общее соображение относительно обозначений. Обозначаем 

Тогда 

По формуле интегрирования по частям получаем:
Интегрирование по частям для вывода рекуррентных формул
Пример 12. Используя интегрирование по частям, вывести рекуррентную формулу для

Решение. Для удобства приведём исходный интеграл к такому выражению, в котором присутствовали бы и синус, и косинус. Используя тригонометрические тождества, получаем
Тогда
Теперь находим рекуррентную формулу для исходного интеграла:
С помощью полученной формулы найдём I 4 :