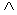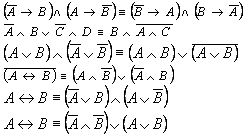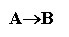Как сделать импликацию в excel
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
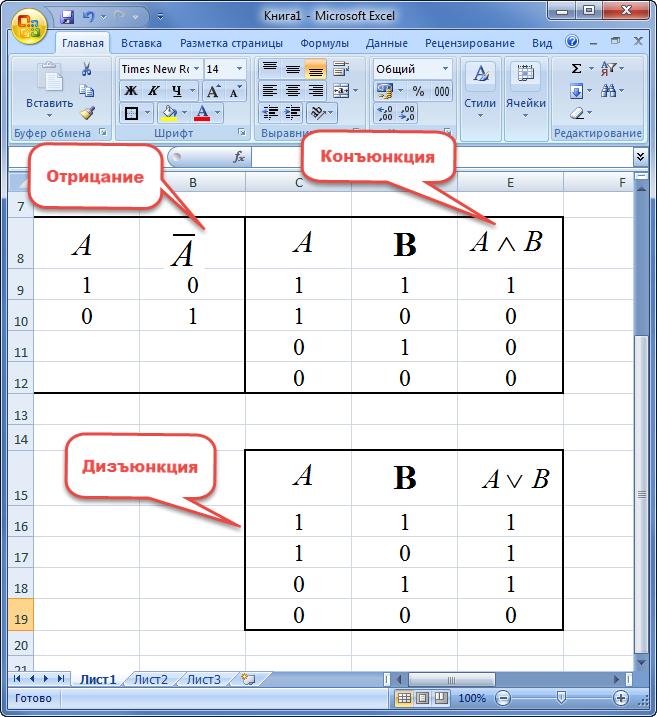
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
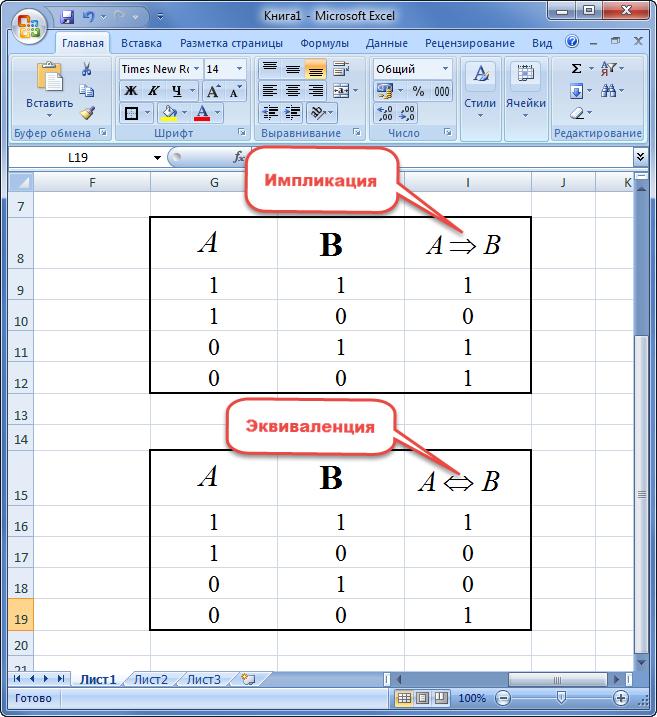
Импликацией двух переменных называют новое предложение, в котором:
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
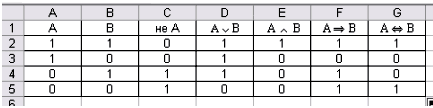
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
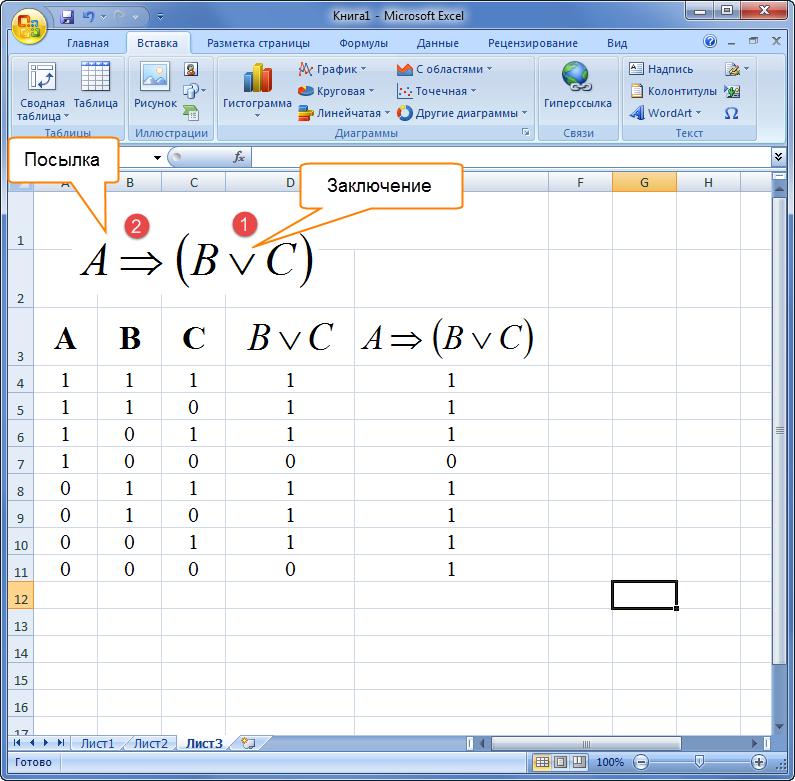
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Логические функции в excel с примерами их использования
Логические функции в Excel проверяют данные и возвращают результат «ИСТИНА», если условие выполняется, и «ЛОЖЬ», если нет.
Рассмотрим синтаксис логических функций и примеры применения их в процессе работы с программой Excel.
Использование логических функций в Excel
| Название функции | Значение | Синтаксис | Примечание |
| ИСТИНА | Не имеет аргументов, возвращает логическое значение «ИСТИНА». | =ИСТИНА () | Редко используется в качестве самостоятельной функции. |
| ЛОЖЬ | Не имеет аргументов, возвращает логическое выражение «ЛОЖЬ». | =ЛОЖЬ () | ——-//——- |
| И | Если все заданные аргументы возвращают истинный результат, то функция выдает логическое выражение «ИСТИНА». В случае хотя бы одного ложного логического значения вся функция выдает результат «ЛОЖЬ». | =И (Лог_знач. 1; Лог_знач. 2;…) | Принимает до 255 аргументов в виде условий или ссылок. Обязательным является первый. |
| ИЛИ | Показывает результат «ИСТИНА», если хотя бы один из аргументов является истинным. | =ИЛИ (Лог_знач.1; Лог_знач. 2;…) | ——-//——- |
| НЕ | Меняет логическое значение «ИСТИНА» на противоположное – «ЛОЖЬ». И наоборот. | #ИМЯ? | Обычно сочетается с другими операторами. |
| ЕСЛИ | Проверяет истинность логического выражения и возвращает соответствующий результат. | #ИМЯ? | «Логическое_выражение» при вычислении должно иметь результат «ИСТИНА» или «ЛОЖЬ». |
| ЕСЛИОШИБКА | Если значение первого аргумента истинно, то возвращает сам аргумент. В противном случае – значение второго аргумента. | #ИМЯ? | Оба аргумента обязательны. |
Логические функции в Excel и примеры решения задач
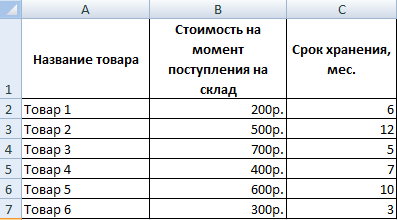
Задача 1. Необходимо переоценить товарные остатки. Если продукт хранится на складе дольше 8 месяцев, уменьшить его цену в 2 раза.
Сформируем таблицу с исходными параметрами:
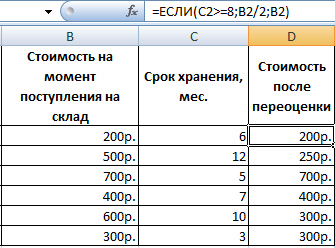
Чтобы решить поставленную задачу, воспользуемся логической функцией ЕСЛИ. Формула будет выглядеть так: =ЕСЛИ(C2>=8;B2/2;B2).
Логическое выражение «С2>=8» построено с помощью операторов отношения «>» и «=». Результат его вычисления – логическая величина «ИСТИНА» или «ЛОЖЬ». В первом случае функция возвращает значение «В2/2». Во втором – «В2».
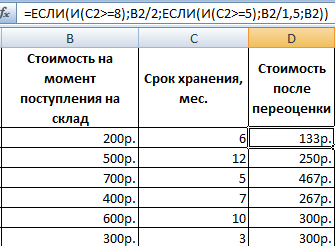
Усложним задачу – задействуем логическую функцию И. Теперь условие такое: если товар хранится дольше 8 месяцев, то его стоимость уменьшается в 2 раза. Если дольше 5 месяцев, но меньше 8 – в 1,5 раза.
Формула приобретает следующий вид: =8);B2/2;ЕСЛИ(И(C2>=5);B2/1,5;B2))’ >.
В функции ЕСЛИ можно использовать в качестве аргументов текстовые значения.
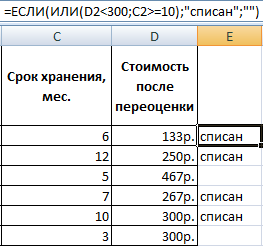
Задача 2. Если стоимость товара на складе после уценки стала меньше 300 р. или продукт хранится дольше 10 месяцев, его списывают.
Для решения используем логические функции ЕСЛИ и ИЛИ: =10);»списан»;»»)’ >. Условие, записанное с помощью логической операции ИЛИ, расшифровывается так: товар списывается, если число в ячейке D2 = 10.
При невыполнении условия функция ЕСЛИ возвращает пустую ячейку.
В качестве аргументов можно использовать другие функции. К примеру, математические.
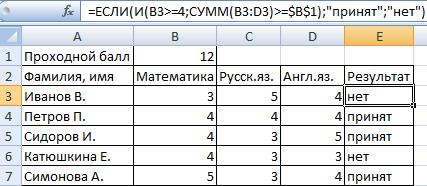
Задача 3. Ученики перед поступлением в гимназию сдают математику, русский и английский языки. Проходной балл – 12. По математике для поступления нужно получить не менее 4 баллов. Составить отчет о поступлении.
Составим таблицу с исходными данными:
Нужно общее количество баллов сравнить с проходным баллом. И проверить, чтобы по математике оценка была не ниже «4». В графе «Результат» поставить «принят» или «нет».
Введем формулу вида: =4;СУММ(B3:D3)>=$B$1);»принят»;»нет»)’ >. Логический оператор «И» заставляет функцию проверять истинность двух условий. Математическая функция «СУММ» используется для подсчета итогового балла.
Функция ЕСЛИ позволяет решать многочисленные задачи, поэтому используется чаще всего.
Статистические и логические функции в Excel
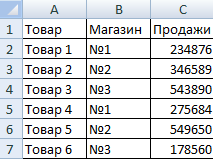
Задача 1. Проанализировать стоимость товарных остатков после уценки. Если цена продукта после переоценки ниже средних значений, то списать со склада этот продукт.
Работаем с таблицей из предыдущего раздела:
Составим таблицу с исходными данными:
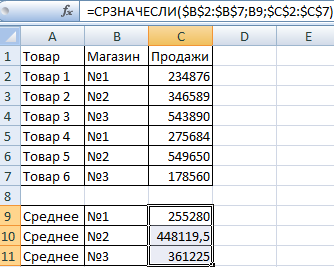
Необходимо найти среднее арифметическое для ячеек, значение которых отвечает заданному условию. То есть совместить логическое и статистическое решение.
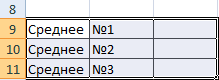
Чуть ниже таблицы с условием составим табличку для отображения результатов:
Функция СРЗНАЧЕСЛИ сопоставляет значение ячейки В9 (№1) со значениями в диапазоне В2:В7 (номера магазинов в таблице продаж). Для совпадающих данных считает среднее арифметическое, используя числа из диапазона С2:С7.
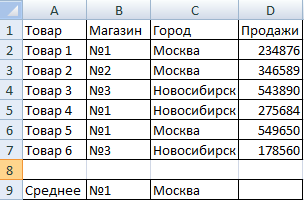
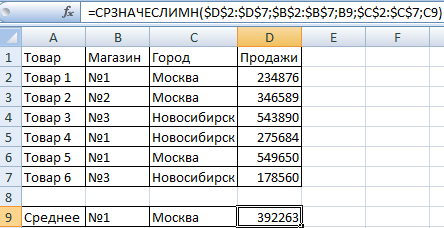
Задача 3. Найти средние продажи в магазине №1 г. Москва.
Видоизменим таблицу из предыдущего примера:
Третий аргумент – В9 – первое условие. Четвертый и пятый аргумент – диапазон для проверки и второе условие, соответственно.
Функция учитывает только те значения, которые соответствуют всем заданным условиям.
Как сделать таблицу истинности в excel?
Функция ИСТИНА в Excel предназначена для указания логического истинного значения и возвращает его в результате вычислений.
Функция ЛОЖЬ в Excel используется для указания логического ложного значения и возвращает его соответственно.
Функция НЕ в Excel возвращает противоположное указанному логическому значению. Например, запись =НЕ(ИСТИНА) вернет результат ЛОЖЬ.
Примеры использования логических функций ИСТИНА, ЛОЖЬ и НЕ в Excel
Пример 1. В таблице Excel хранятся телефонные номера различных организаций. Звонки на некоторые из них являются бесплатными (с кодом 8800), на остальные – платные по тарифу 1,5 руб/мин. Определить стоимость совершенных звонков.
В столбце «Бесплатный» отобразим логические значения ИСТИНА или ЛОЖЬ по следующему условию: является ли код номера телефона равным «8800»? Введем в ячейку C3 формулу:
Аналогично определим является ли звонок бесплатным для остальных номеров. Результат:
Для расчета стоимости используем следующую формулу:
Мы получили суммарную стоимость вех совершенных звонков по всем организациям.
Как посчитать среднее значение по условию в Excel
Пример 2. Определить средний балл за экзамен для группы студентов, в составе которой есть студенты, которые его провалили. Так же необходимо получить среднюю оценку успеваемости только лишь для тех студентов, которые сдали экзамен. Оценка студента, не сдавшего экзамен, должна учитываться как 0 (нуль) в формуле для расчета.
Для заполнения столбца «Сдал» используем формулу:
Создадим новый столбец, в который перезапишем оценки при условии, что оценка 2 интерпретируется как 0 с использованием формулы:
Определим средний балл по формуле:
Теперь получим средний балл успеваемости, для студентов, которые допущены к следующим экзаменам. Для этого воспользуемся еще одной логической функцией СРЗНАЧЕСЛИ:
Как получить значение по модулю числа без использования функции ABS
Пример 3. Реализовать алгоритм определения значения модуля числа (абсолютную величину), то есть альтернативный вариант для функции ABS.
Для решения используем формулу массива:
=ЕСЛИ(НЕ(A3:A100, функция НЕ будет возвращать ЛОЖЬ.
Если единственным аргументом функции НЕ является текстовая строка, функция вернет код ошибки #ЗНАЧ!. В вычислительной технике используется специальный логический тип данных (в программировании имеет название «булев» тип или Boolean в честь известного математика Джорджа Буля). Этот тип данных оперирует всего двумя значениями: 1 и 0 (ИСТИНА, ЛОЖЬ). В Excel истинному логическому значению также соответствует число 1, а ложному логическому значению – также числовое значение 0 (нуль). Функции ИСТИНА() и ЛОЖЬ() могут быть введены в любую ячейку или использоваться в формуле и будут интерпретированы в качестве логических значений соответственно. Обе рассмотренные выше функции необходимы для обеспечения совместимости с другими программными продуктами, предназначенными для работы с таблицами. Функция НЕ позволяет расширить возможности функций, предназначенных для выполнения логической проверки. Например, при использовании данной функции в качестве аргумента лог_выражение функции ЕСЛИ, можно обеспечить проверку сразу нескольких условий.
Они могут принимать значения «истина» или «ложь» (1 или 0). Для функции, содержащей две переменные, наборов значений переменных всего четыре:
Значения логических функций определяются с помощью таблица истинности.
Таблицы истинности для основных двоичных логических функций
1. Конъюнкция (логическое умножение) – сложное логическое выражение, которое является истинным только в том случае, когда истинны оба входящих в него простых выражения.
Обозначение:
2. Дизъюнкция (логическое сложение) – это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно, если оба простых логических выражения ложны.
Обозначение:
3. Импликация (логическое следствие) – это сложное логическое выражение, которое является ложным тогда и только тогда, когда условие истинно, а следствие ложно.


Обозначение:
4. Эквиваленция – это сложное логическое высказывание, которое является истинным только при одинаковых значениях истинности простых выражений, входящих в него.
Обозначение:
5. Логическое отрицание (инверсия) делает истинное высказывание ложным и, наоборот, ложное – истинным.
Обозначение:
6. Штрих Шеффера – операция, отрицающая конъюнкцию, т.е. значение ложно тогда и только тогда, когда оба простых выражения истинны.
Обозначение:
7. Стрелка Пирса – операция, отрицающая конъюнкцию, т.е. значение истинно тогда и только тогда, когда оба простых выражения ложны.
Обозначение:
Порядок выполнения логических операций
При построении таблицы истинности необходимо учитывать порядок выполнения логических операций:
Для последних двух операций приоритет не определен.
Замечание. Если необходимо изменить указанный порядок выполнения логических операций используются скобки.
Примеры решения задач
по теме «Построение таблиц истинности с помощью электронных таблиц Excel»
Цель работы: познакомиться с логическими функциями Excel, научиться строить таблицы истинности сложных высказываний.
Порядок выполнения работы.
1.Найдите обозначения логических функций, которые имеются в Excel
Импликация в excel формула
Использование MS Excel при изучении математической логики
В настоящее время применение информационных технологий становится неотъемлемой частью образовательного процесса. Компьютер наиболее полно удовлетворяет дидактическим требованиям и позволяет адаптировать процесс обучения к индивидуальным особенностям учащихся.
Компьютерные технологии активно внедряются в процесс обучения и диагностики, позволяют упростить процесс отработки навыков и умений и оценки знаний учащихся.
В данной работе рассматривается применение табличного процессора MS Excel при изучении основ логики.
Существует множество задач, в которых исходные и результатные данные должны быть представлены в табличной форме. Электронные таблицы представляют собой удобный инструмент для автоматизации таких вычислений. Решения многих вычислительных задач на ЭВМ, которые раньше можно было осуществить только путем программирования, стало возможно реализовать. Использование математических формул в электронных таблицах позволяет представить взаимосвязь между различными параметрами некоторой реальной системы. Основное свойство электронных таблиц – мгновенный пересчет формул при изменении значений входящих в них операндов. Благодаря этому свойству, таблица представляет собой удобный инструмент для организации численного эксперимента:
В электронных таблицах предусмотрен также графический режим работы, который дает возможность графического представления (в виде графиков, диаграмм) числовой информации, содержащейся в таблице.
В процессе изучения алгебры логики учащиеся знакомятся с такими понятиями как: высказывание, таблицы истинности, логические функции и логические операции. Алгебра логики является разделом математической логики, в которой изучаются методы доказательства истинности (1) или ложности (0) сложных логических конструкций, составленных из простых высказываний, на основе истинности или ложности последних. Для закрепления полученных знаний возможно использование табличного процессора MS Excel и его функций.
Для реализации функций булевой алгебры используются логические функции: ЕСЛИ, И, ИЛИ, НЕ, ИСТИНА и ЛОЖЬ. При работе с функциями в MS Excel используется мастер функций (Вставка 
Рисунок 1. Окно мастера функций
Первоначально следует создать таблицу основных логических операций:
Рисунок 2. Таблица истинности основных логических операций
При составлении таблицы истинности используются следующие формулы:
В последующей работе данная таблица может использоваться учащимися как основа для выполнения заданий лабораторной работы.
Учащимся может быть предложена следующая работа.
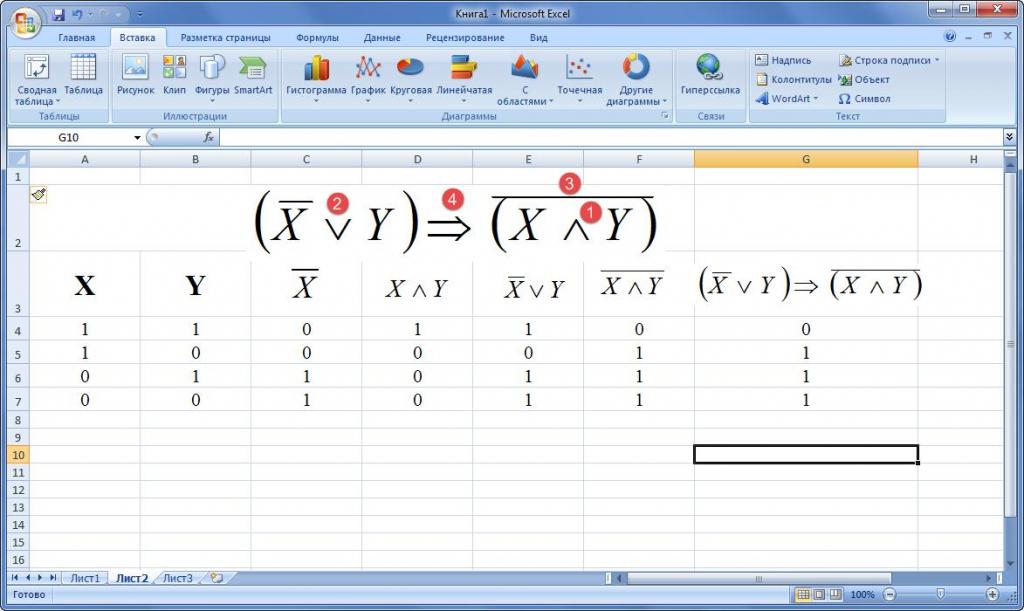
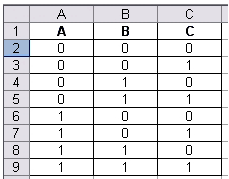
Задание: Построить таблицу истинности для формулы (A 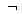
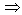

Рисунок 3. Исходные данные
Для этого в ячейку D2 ввести формулу: =ЕСЛИ(B2=1;0;1);
в E2: =ЕСЛИ(И(A2=1;D2=1);1;0);
в F2: =ЕСЛИ(И(E2=1;C2=0);0;1);
Заполнение остальных строк произвести путем копирования введенной формулы.
Рисунок 4. Результат выполнения работы
Табличный процессор может быть использован для закрепления не только материала математической логики, но и для основ теории вероятностей и математической статистики.
Задачи для самостоятельного решения
Определить с помощью таблиц истинности равносильность формул.
Определить являются ли формулы тавтологиями.
Примеры вычислений с использованием стандартных функций
СУММ(А) – функция суммирования, где: А — список от 1 до 30 аргументов суммирования.
СУММЕСЛИ(диапазон; критерий; диапазон_суммирования) – суммирования ячеек диапазона, удовлетворяющих заданным условиям, где:
· диапазон — диапазон адресов вычисляемых ячеек;
· критерий — критерий в виде числа, выражения или текста, определяющего суммируемые ячейки. Например, критерий может быть выражен как 24, «>22»;
· диапазон_суммирования — фактические ячейки для суммирования.
ЕСЛИ(логическое_выражение; значение_если_истина; значение_если_ложь) – проверяет, выполняется ли логическое выражение, если да, то выводит значение если истина, нет – значение если ложь;
Ошибки в формулах Excel.Если формула построена неправильно, Excel формирует соответствующую ошибку, основными причинами появления которых следующие:
· #ЗНАЧ! — используется недопустимый тип аргумента;
· #ДЕЛ/0! — в формуле выполняется деление на ноль;
· #ИМЯ? — Excel не может определить используемое в формуле имя;
· #ССЫЛКА! — используется недопустимая ссылка на ячейку;
· #Н/Д — неопределенные данные, при некорректном определении аргументов функции;
· #ПУСТО! — задано пересечение двух областей, не имеющих общих ячеек.
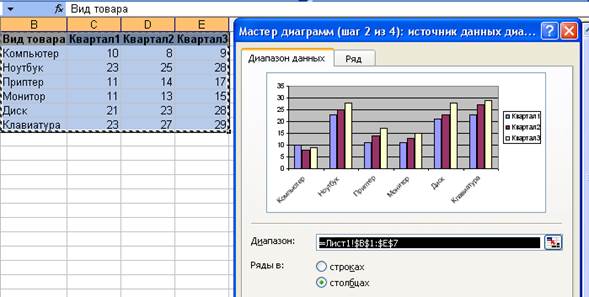
2.3 Построение диаграмм и графиков в Excel
Наиболее удобным способом создания диаграммы является использование Мастера диаграмм,вызываемый нажатием кнопки Мастер диаграмм 
1. Выбор типа и вида диаграммы.После вызова Мастера диаграммв диалоговом окне Мастер диаграмм (шаг 1 из 4): тип диаграммы следует выбрать тип и вид диаграммы. Диалоговое окно имеет две вкладки: Стандартные и Нестандартные. Во вкладке Стандартные расположены стандартные типы диаграмм Excel и их разновидности. Для просмотра внешнего вида выбранной диаграммы следует нажать и удерживать кнопку Просмотр результата. Выбранный тип и вид диаграммы можно будет изменить в последующем при редактировании и оформлении диаграммы.
2. Выбор источника данных.В диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы необходимо выбрать источник данных для диаграммы (рис.4.22), диалоговое окно имеет две вкладки: Диапазон данных и Ряд.
Рис. 4.22. Выбор источника данных диаграммы
Если перед началом создания диаграммы на листе были выделены ячейки с данными, то во вкладке Диапазон данных в поле Диапазон указан диапазон ячеек листа, для которого создается диаграмма, а на листе этот диапазон обведен «бегущим» пунктиром. При необходимости можно очистить поле Диапазон и, не закрывая диалогового окна, на листе выделить другой диапазон ячеек.
Как правило, независимо от размещения данных на листе, Excel правильно выбирает вариант построения рядов данных (по строкам или по столбцам выделенного диапазона) и устанавливает соответствующий переключатель (на строках или на столбцах), имена рядов данных показываются в легенде.
Содержание вкладки Ряд зависит от типа выбранной диаграммы, а также от выбора варианта построения рядов данных.
По окончании работы с источниками данных диаграммы в диалоговом окне Мастер диаграмм (шаг 2 из 4): источник данных диаграммы следует нажать кнопку Далее.
3. Выбор параметров диаграммы.Выполняется на 3-емшаге вокне Мастер диаграмм (шаг 3 из 4 ): параметры диаграммы. На данном шаге мастером предлагается определить заголовок создаваемой диаграммы, использовать линии сетки, включить легенду в любом месте диаграммы, дать имена осям Х и У, определить подписи данных и щелкнуть Далее для перехода на последний четвертый шаг.
4. Размещение диаграммы. Выполняется в окне Мастер Диаграмм (шаг 4 из 4): размещение диаграммы.На этом шаге пользователь определяет, где поместить диаграмму: на текущем рабочем листе или на отдельном листе книги. После нажатия кнопки Готово Excel создаст диаграмму. Затем пользователь может внести изменения данных в исходной таблице, что автоматически отразится на построенной диаграмме.
Определим логические функции:
1) Инверсия (отрицание) — это логическое не.
Говорят, что имея суждение А, можно образовать новое суждение, которое читается как «не А» или «неверно, что А»
Для обозначения отрицания суждения употребляется символ или– над переменной.
Запись А читается как «не А».
2) Коньюкция — это логическое умножение.
3) Дизьюкция — это логическое сложение.
4) Эквиваленция — это функция тождества.
Выбираем обозначение А = В. («тогда и только тогда»).
Запись А = В читается как «А эквивалентно В».
5) Импликация — это логическое следование.
Импликация двух высказываний А и В соответствует союзу «ЕСЛИ…ТО».
Она обозначается символом->
Читается как «из А следует В»
Обозначение:
Импликация устроена немного сложнее других функций. В импликации существенное значение имеет порядок аргументов. Первый называется посылкой, а второй следствием. Можно сказать, что первое высказывание является как бы причиной второго, а второе как бы вытекает из первого.
Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация 

Таблицы истинности:
прямая импликация (от a к b) (материальная импликация, материальный кондиционал)
если 
«Житейский» смысл импликации. Для более лёгкого понимания смысла прямой импликации и запоминания ее таблицы истинности может пригодиться житейская модель: А — начальник. Он может приказать «работай» (1) или сказать «делай что хочешь» (0). В — подчиненный. Он может работать (1) или бездельничать (0). В таком случае импликация — не что иное, как послушание подчиненного начальнику. По таблице истинности легко проверить, что послушания нет только тогда, когда начальник приказывает работать, а подчиненный бездельничает.
Условная функция. Общий вид условной функции следующий:
Условие — это логическое выражение, которое может принимать значениеИСТИНА илиЛОЖЬ. и могут быть числами, формулами или текстом.
Построить таблицу истинности в Excel: основные понятия и примеры
Алгебра высказываний – точная наука, не дающая компромиссов. Чтобы решить примеры с конъюнкцией, дизъюнкцией, импликацией и т. д., можно построить таблицу истинности в прикладной программе Excel. Она оснащена набором логических функций, позволяющих автоматизировать и облегчить процесс нахождения результата.
Математическая логика: основные понятия
Основателем формальной логики считают Аристотеля. В XVII в. Г. Лейбниц предложил вводить символы для определения высказываний. Д. Буль закрепил усвоенные знания и впервые обозначил предложения символами.
Схематически «ИСТИНА» замещается 1, а «ЛОЖЬ» – 0.
Под высказыванием понимают любое повествовательное предложение, дающее какую-либо информацию и способное принимать значение истинности или ложности. В алгебре логики отвлекаются от смысловой нагрузки предложений и рассматривают только логические значения.
Под отрицанием понимают новое выражение, принимающее значение истины в случае его ложности и наоборот.
Конъюнкцией двух переменных называют новое предложение, принимающее значение истинности в случае одновременного обозначения «1» и ложности в остальных ситуациях.
Под дизъюнкцией двух высказываний понимают новое выражение, принимающее значение «ЛОЖЬ» только при одновременном наличии «0» и «ИСТИНА» в остальных вариациях.
Импликацией двух переменных называют новое предложение, в котором:
Под эквиваленцией двух переменных понимают новое высказывание, принимающее значение истинности только в случае одинаковости элементов. Иначе предложение равняется «0».
Логические значения выражений принято оформлять в табличном виде. Есть и другое название у такого рода информации. Говорят, для высказывания нужно построить таблицу истинности. В ней указываются первоначальные значения для всех переменных, а потом вычисляется результат всего выражения.
Алгоритм реализации вычислений в логических операциях
Чтобы построить таблицу истинности, необходимо знать, в каком порядке выполняются действия. В выражении, где несколько операндов, вычисление осуществляется в следующем порядке:
Существуют еще две операции, но для них приоритет не определен:
Алгоритм вычислений меняется, если выражение заключено в скобки.
Порядок построения табличной формы для логических операндов в Excel
Прежде чем находить значение выражения, нужно изучить понятие формулы алгебры логики. Определение гласит, что это сложное выражение, состоящее из простейших высказываний, соединенных между собой логическими операндами.
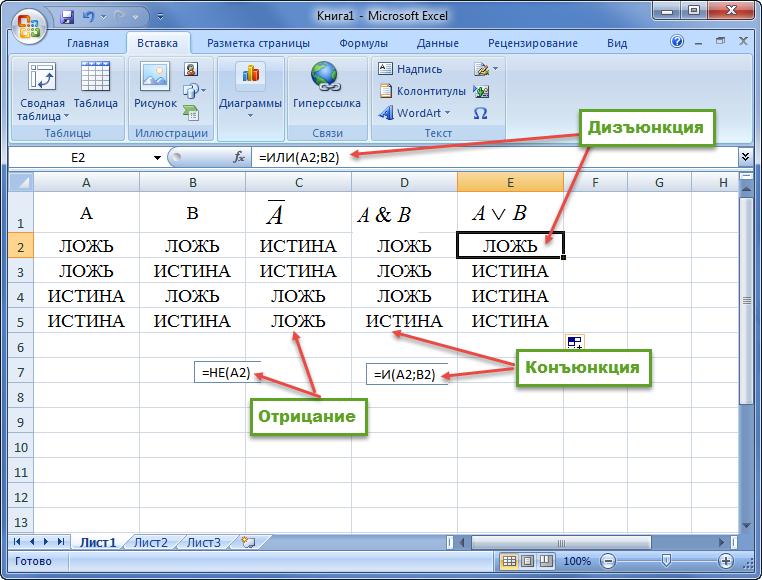
Пример 1. Построить таблицу истинности для конъюнкции, дизъюнкции и отрицания.
Пример 2. Дана формула алгебры логики. Построить таблицу истинности. Примеры в качестве образца даны ниже.
Пример 3. Как построить таблицу истинности в Excel, если дана формула алгебры логики в словесном описании. Высказывание: «Если треугольник – равносторонний, то все его ребра равны или все его углы равны».
Для начала необходимо разобрать составное предложение на минимальные элементы:
После этого составляется выражение и решается в программном пакете Excel.
При составлении таблиц истинности важно помнить о порядке выполнения операций.
Использование логических функций в Excel
Табличный редактор Эксель – очень гибкий и мощный инструмент для структурированной работы с данными. Среди большого количества его эффективных инструментов стоит отдельно выделить логические операторы, в основе использования которых лежит признание выражения истинным или ложным. Эти функции эффективно встроены в инструментарий формул и позволяют создавать гибкие условия для различных вычислений или заполнения ячеек на основе логических выражений. В данной статье будут описаны основные используемые функции, а также приведен практический пример использования логических операторов в Excel.
Основные логические функции, используемые в Эксель
Перечень наиболее часто используемых логических операторов можно ограничить следующим набором:
В большинстве случаев их достаточно для построения сложных логических конструкций и задания условий.
Для каждого из указанных выше операторов существуют аргументы (за исключением функций ИСТИНА и ЛОЖЬ) – это могут быть как цифровые или текстовые значения, так и ссылки на данные, содержащиеся в других ячейках.
Операторы ИСТИНА и ЛОЖЬ
Функция ИСТИНА не имеет собственных аргументов и практически всегда используется, как структурный компонент для других логических выражений, так как принимает одно конкретно заданное значение.
Функция ЛОЖЬ, напротив, может принимать любые значения, не являющиеся истинными. Как и ИСТИНА, практически всегда используется, как структурный компонент для других сложных выражений.
Операторы И и ИЛИ
Синтаксис оператора И выглядит следующим образом:
=И(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.
Оператор И используется в качестве элемента-связки для нескольких условий логического выражения. Важно, чтобы все аргументы оператора имели значение ИСТИНА (если в выражении их несколько), в противном случае вся логическая цепочка будет возвращать значение ЛОЖЬ.
Синтаксис оператора ИЛИ:
=ИЛИ(лог_значение1; лог_значение2; …), возможное количество используемых аргументов – от 1 до 255.
В отличие от И, функция ИЛИ будет возвращать значение ИСТИНА даже в случае, когда хотя бы один из используемых аргументов ему соответствует, а все остальные – ложные.
Оператор НЕ
Синтаксис функции НЕ: =НЕ(лог_значение).
Количество аргументов оператора НЕ – всегда один. Соответственно, результат функции (ИСТИНА/ЛОЖЬ) полностью зависит только от значения аргумента.
Операторы ЕСЛИ и ЕСЛИОШИБКА
Общий синтаксис функции ЕСЛИ представляет собой конструкцию:
=ЕСЛИ(логическое_выражение;значение_если_истина;значение_если-ложь).
Оператор ЕСЛИ используется для построения сложных развернутых логических цепочек. Суть функции – в проверке внесенного в качестве логического выражения условия. Если условие выполняется, и оно истинно, то в качестве результата функции возвращается одно выражение, если же логическое выражение ложно, то в качестве результата функции возвращается другое условие.
Синтаксис оператора ЕСЛИОШИБКА имеет вид:
=ЕСЛИОШИБКА(значение;значение_если_ошибка).
Функция проверяет истинность логического выражения для первого аргумента, и если он соблюдается, то возвращает в качестве результата его значение. Если же выражение ложно, то в качестве результата выдается значение второго аргумента, указанное в функции.
Операторы ЕОШИБКА и ЕПУСТО
Оператор ЕОШИБКА имеет следующую структуру:
=ЕОШИБКА(значение)
Он позволяет осуществить проверку корректности уже заполненных ячеек (одной или диапазона), и, если ячейка некорректно заполнена, возвращает результат ИСТИНА, в противном случае – ЛОЖЬ.
Примеры значений в некорректно заполненных ячейках:
Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.
Формула функции ЕПУСТО выглядит следующим образом:
=ЕПУСТО(значение)
Функционал оператора проверяет ячейку или диапазон ячеек и возвращает ИСТИНА, если в ячейке/диапазоне ячеек нет данных, и ЛОЖЬ, если в ячейке/диапазоне ячеек присутствуют данные. Аргумент функции – адрес конкретной ячейки или ссылка на диапазон ячеек.
Практический пример использования логических функций
В примере ниже попробуем частично использовать описанные выше функции для решения задачи, приближенной к реальной ситуации с расчетом премии, зависящей от определенных условий.
В качестве исходных данных – таблица со сведениями о работниках, в которой указан их пол и возраст.
Нам необходимо произвести расчет премии. Ключевые условия, от которых зависит размер премии:
Выполним необходимые расчеты, используя логические функции.
Заключение
Логические операторы используются практически во всех сложных формулах, в которых значение в ячейке зависит от соблюдения одного или нескольких условий и позволяют строить гибкие конструкции, объединяя простые функции и расчеты в одной ячейке. Это дает возможность значительно сократить время на обработку данных и повысить эффективность работы, так как снимает большое количество промежуточных шагов в расчетах и вычислениях.