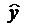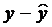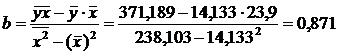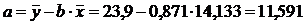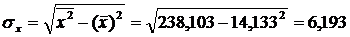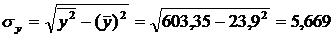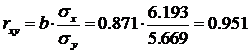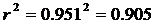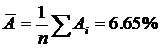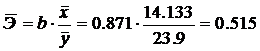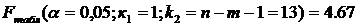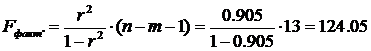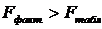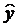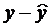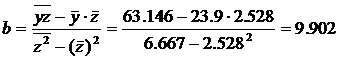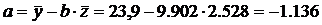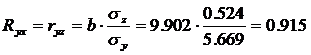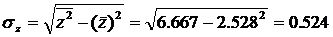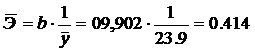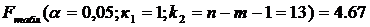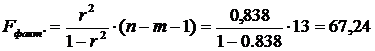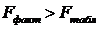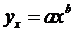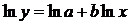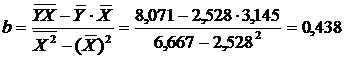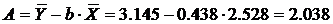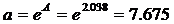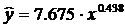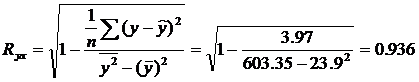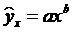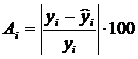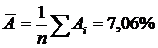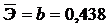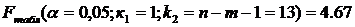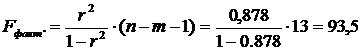Как сделать корреляционное поле
Корреляционный анализ в Excel. Пример выполнения корреляционного анализа
Корреляционный анализ – это распространённый метод исследования, применяемый для определения уровня зависимости 1-й величины от 2-й. В табличном процессоре есть особый инструмент, который позволяет реализовать данный тип исследования.
Суть корреляционного анализа
Он необходим для определения зависимости между двумя разными величинами. Иными словами, происходит выявление того, в какую сторону (меньшую/большую) меняется величина в зависимости от изменений второй.
Назначение корреляционного анализа
Важно! При 0-м коэффициенте зависимости между величинами нет.
Расчет коэффициента корреляции
Разберем расчёт на нескольких образцах. К примеру, есть табличные данные, где по месяцам описаны в отдельных столбцах траты на рекламное продвижение и объём продаж. Исходя из таблицы, будем выяснять уровень зависимости объема продаж от денег, затраченных на рекламное продвижение.
Способ 1: определение корреляции через Мастер функций
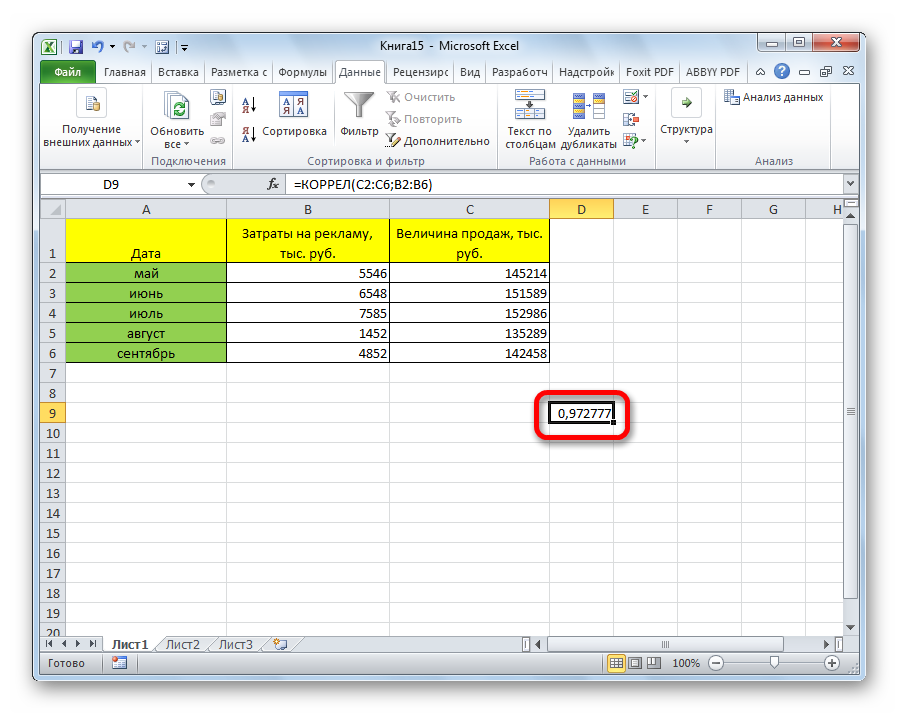
КОРРЕЛ – функция, позволяющая реализовать корреляционный анализ. Общий вид – КОРРЕЛ(массив1;массив2). Подробная инструкция:
Коэффициент отобразился в той ячейке, которая была указана в начале наших действий. Полученный результат 0,97. Этот показатель отображает высокую зависимость первой величины от второй.
Способ 2: вычисление корреляции с помощью Пакета анализа
Существует еще один метод определения корреляции. Здесь используется одна из функций, находящаяся в пакете анализа. Перед ее использованием нужно провести активацию инструмента. Подробная инструкция:
Вывелись итоговые показатели. Результат такой же, как и в первом методе – 0,97.
Определение и вычисление множественного коэффициента корреляции в MS Excel
Для выявления уровня зависимости нескольких величин применяются множественные коэффициенты. В дальнейшем итоги сводятся в отдельную табличку, именуемую корреляционной матрицей.
Коэффициент парной корреляции в Excel
Разберем, как правильно проводить коэффициент парной корреляции в табличном процессоре Excel.
Расчет коэффициента парной корреляции в Excel
К примеру, у вас есть значения величин х и у.
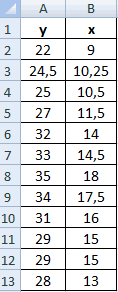
Х – это зависимая переменна, а у – независимая. Необходимо найти направление и силу связи между этими показателями. Пошаговая инструкция:
Матрица парных коэффициентов корреляции в Excel
Разберем, как проводить подсчет коэффициентов парных матриц. К примеру, есть матрица из четырех переменных.
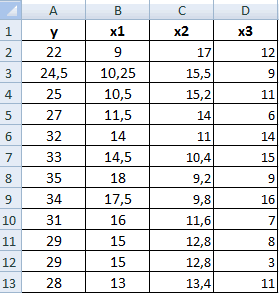
Функция КОРРЕЛ для определения взаимосвязи и корреляции в Excel
КОРРЕЛ – функция, применяемая для подсчета коэффициента корреляции между 2-мя массивами. Разберем на четырех примерах все способности этой функции.
Примеры использования функции КОРРЕЛ в Excel
Алгоритм расчёта выглядит следующим образом:
Отображенный показатель близок к 1. Результат:
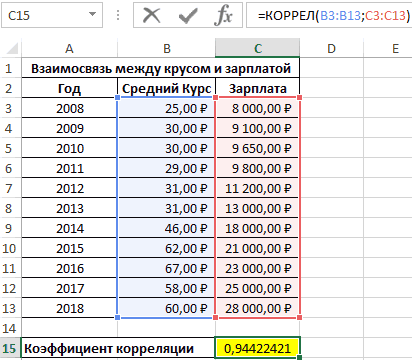
Определение коэффициента корреляции влияния действий на результат
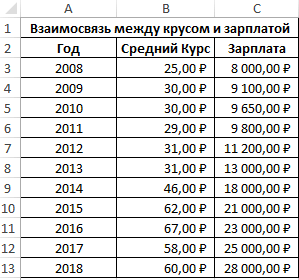
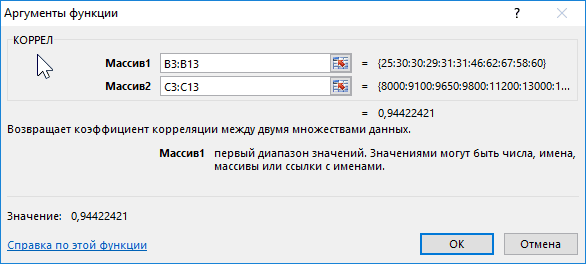
Второй пример. Два претендента обратились за помощью к двум разным агентствам для реализации рекламного продвижения длительностью в пятнадцать суток. Каждые сутки проводился социальный опрос, определяющий степень поддержки каждого претендента. Любой опрошенный мог выбрать одного из двух претендентов или же выступить против всех. Необходимо определить, как сильно повлияло каждое рекламное продвижение на степень поддержки претендентов, какая компания эффективней.
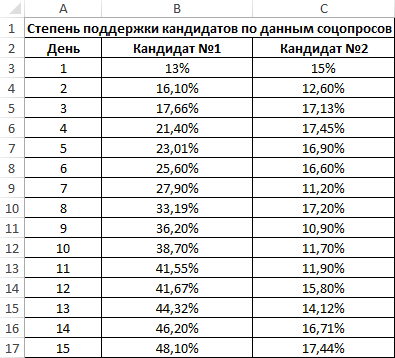
Используя нижеприведенные формулы, рассчитаем коэффициент корреляции:
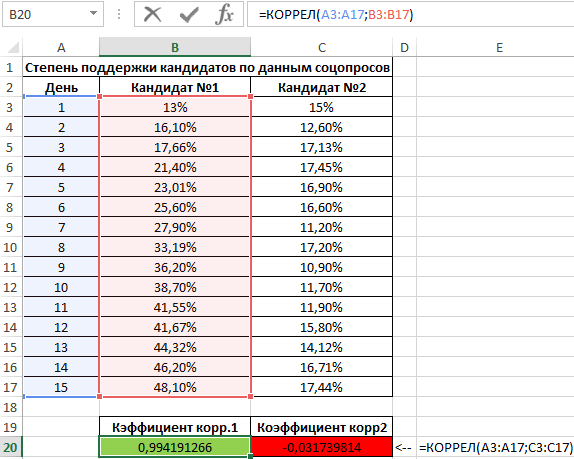
Из полученных результатов становится понятно, что степень поддержки 1-го претендента повышалась с каждыми сутками проведения рекламного продвижения, следовательно, коэффициент корреляции приближается к 1. При запуске рекламы другой претендент обладал большим числом доверия, и на протяжении 5 дней была положительная динамика. Потом степень доверия понизилась и к пятнадцатым суткам опустилась ниже изначальных показателей. Низкие показатели говорят о том, что рекламное продвижение отрицательно повлияло на поддержку. Не стоит забывать, что на показатели могли повлиять и остальные сопутствующие факторы, не рассматриваемые в табличной форме.
Анализ популярности контента по корреляции просмотров и репостов видео
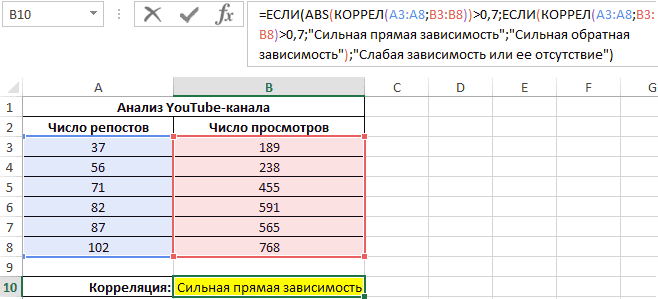
Третий пример. Человек для продвижения собственных роликов на видеохостинге Ютуб применяет соцсети для рекламирования канала. Он замечает, что существует некая взаимосвязь между числом репостов в соцсетях и количеством просмотров на канале. Можно ли про помощи инструментов табличного процессора произвести прогноз будущих показателей? Необходимо выявить резонность применения уравнения линейной регрессии для прогнозирования числа просмотров видеозаписей в зависимости от количества репостов. Табличка со значениями:
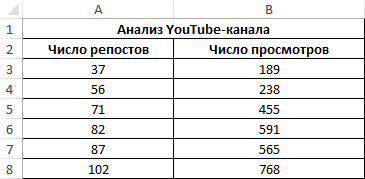
Теперь необходимо провести определение наличия связи между 2-мя показателями по нижеприведенной формуле:
0,7;ЕСЛИ(КОРРЕЛ(A3:A8;B3:B8)>0,7;”Сильная прямая зависимость”;”Сильная обратная зависимость”);”Слабая зависимость или ее отсутствие”)’ >
Если полученный коэффициент выше 0,7, то целесообразней применять функцию линейной регрессии. В рассматриваемом примере делаем:
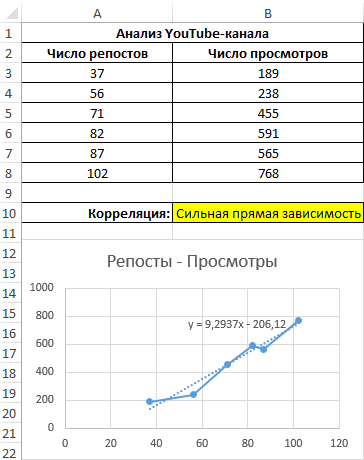
Теперь производим построение графика:
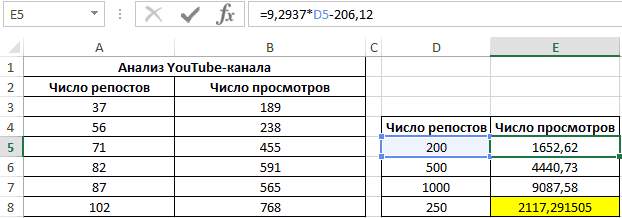
Применяем это уравнение, чтобы определить число просматриваний при 200, 500 и 1000 репостов: =9,2937*D4-206,12. Получаем следующие результаты:
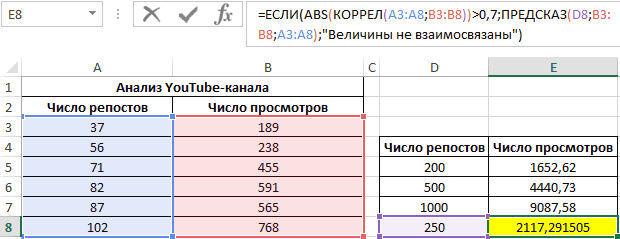
Функция ПРЕДСКАЗ позволяет определить число просмотров в моменте, если было проведено, к примеру, двести пятьдесят репостов. Применяем: 0,7;ПРЕДСКАЗ(D7;B3:B8;A3:A8);”Величины не взаимосвязаны”)’ >. Получаем следующие результаты:
Особенности использования функции КОРРЕЛ в Excel
Данная функция имеет нижеприведенные особенности:
Оценка статистической значимости коэффициента корреляции
При проверке значимости корреляционного коэффициента нулевая гипотеза состоит в том, что показатель имеет значение 0, а альтернативная не имеет. Для проверки применяется нижеприведенная формула:
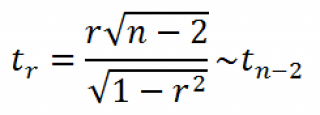
Заключение
Корреляционный анализ в табличном процессоре – это простой и автоматизированный процесс. Для его выполнения необходимо знать всего лишь, где находятся нужные инструменты и как их активировать через настройки программы.
Строим поле корреляции.



Содержание отчета
2. Краткие теоретические сведения.
3. Порядок выполнения работы.
4. Исходные данные для разработки математической модели.
5. Результаты разработки математической модели.
6. Результаты исследования модели. Построение прогноза.
В задачах 2-4 можно использовать ППП Excel для расчетов характеристик модели.
Работа № 1.
Построение моделей парной регрессии. Проверка остатков на гетероскедастичность.
По 15 предприятиям, выпускающим один и тот же вид продукции известны значения двух признаков:
| x | y |
| 5,3 | 18,4 |
| 15,1 | 22,0 |
| 24,2 | 32,3 |
| 7,1 | 16,4 |
| 11,0 | 22,2 |
| 8,5 | 21,7 |
| 14,5 | 23,6 |
| 10,2 | 18,5 |
| 18,6 | 26,1 |
| 19,7 | 30,2 |
| 21,3 | 28,6 |
| 22,1 | 34,0 |
| 4,1 | 14,2 |
| 12,0 | 22,1 |
| 18,3 | 28,2 |
Требуется:
1. Построить поле корреляции и сформулировать гипотезу о форме связи.
2. Построить модели:
Линейной парной регрессии.
Полулогарифмической парной регрессии.
2.3 Степенной парной регрессии.
Для этого:
Рассчитать параметры уравнений.
2. Оценить тесноту связи с помощью коэффициента (индекса)
корреляции.
3. Оценить качество модели с помощью коэффициента (индекса)
детерминации и средней ошибки аппроксимации.
4. Дать с помощью среднего коэффициента эластичности
сравнительную оценку силы связи фактора с результатом.
5. С помощью F-критерия Фишера оценить статистическую надежность результатов регрессионного моделирования.
По значениям характеристик, рассчитанных в пунктах 2-5 выбрать лучшее уравнение регрессии.
Используя метод Гольфрельда-Квандта проверить остатки на гетероскедастичность.
8. Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 5% от его среднего уровня. Для уровня значимости 
Строим поле корреляции.
2.1. Модель линейной парной регрессии.
2.1.1. Рассчитаем параметры a и b линейной регрессии у=а+bх.
Строим расчетную таблицу 1.
Параметры a и b уравнения
определяются методом наименьших квадратов:
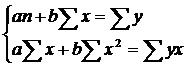
Разделив на n и решая методом Крамера, получаем формулу для определения b:
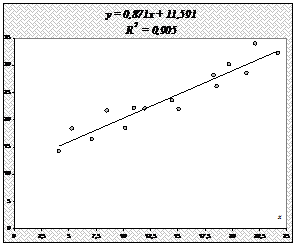
С увеличением выпуска продукции на 1 тыс. руб. затраты на производство увеличиваются на 0,871 млн. руб. в среднем, постоянные затраты равны 11,591 млн. руб.
2.1.2. Тесноту связи оценим с помощью линейного коэффициента парной корреляции.
Предварительно определим средние квадратические отклонения признаков.
Средние квадратические отклонения:
Между признаками X и Y наблюдается очень тесная линейная корреляционная связь.
2.1.3. Оценим качество построенной модели.
Определим коэффициент детерминации:
т. е. данная модель объясняет 90,5% общей дисперсии у, на долю необъясненной дисперсии приходится 9,5%.
Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации Аi .
Предварительно из уравнения регрессии определим теоретические значения 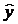
Ошибка аппроксимации Аi, i=1…15:
Средняя ошибка аппроксимации:
Ошибка небольшая, качество модели высокое.
2.1.4. Определим средний коэффициент эластичности:
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,515%.
2.1.5. Оценим статистическую значимость полученного уравнения.
Проверим гипотезу H0, что выявленная зависимость у от х носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α=0,05. Найдем табличное (критическое) значение F-критерия Фишера:
Найдем фактическое значение F— критерия Фишера:
следовательно, гипотеза H0 отвергается, принимается альтернативная гипотеза H1: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.
Построим полученное уравнение.
2.2. Модель полулогарифмической парной регрессии.
2.2.1. Рассчитаем параметры а и b в регрессии:
Линеаризуем данное уравнение, обозначив:
Параметры a и b уравнения
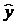
определяются методом наименьших квадратов:
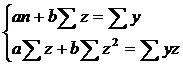
Рассчитываем таблицу 2.
Разделив на n и решая методом Крамера, получаем формулу для определения b:
2.2.2. Оценим тесноту связи между признаками у и х.
Т. к. уравнение у = а + bln x линейно относительно параметров а и b и его линеаризация не была связана с преобразованием зависимой переменной _у, то теснота связи между переменными у и х, оцениваемая с помощью индекса парной корреляции Rxy, также может быть определена с помощью линейного коэффициента парной корреляции ryz
среднее квадратическое отклонение z:
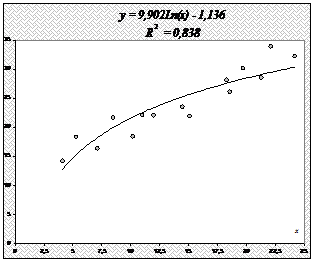
Значение индекса корреляции близко к 1, следовательно, между переменными у и х наблюдается очень тесная корреляционная связь вида 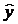
2.2.3. Оценим качество построенной модели.
Определим коэффициент детерминации:
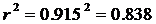
т. е. данная модель объясняет 83,8% общей вариации результата у, на долю необъясненной вариации приходится 16,2%. Следовательно, качество модели высокое.
Найдем величину средней ошибки аппроксимации Аi .
Предварительно из уравнения регрессии определим теоретические значения 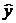
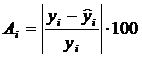
Средняя ошибка аппроксимации:
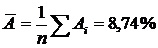
Ошибка небольшая, качество модели высокое.
2.2.4.Определим средний коэффициент эластичности:
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,414%.
2.2.5. Оценим статистическую значимость полученного уравнения.
Проверим гипотезу H0, что выявленная зависимость у от х носит случайный характер, т.е. полученное уравнение статистически незначимо. Примем α=0,05.
Найдем табличное (критическое) значение F-критерия Фишера:
Найдем фактическое значение F-критерия Фишера:
следовательно, гипотеза H0 отвергается, принимается альтернативная гипотеза H1: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.
Построим уравнение регрессии на поле корреляции
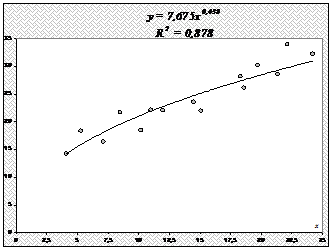
2.3. Модель степенной парной регрессии.
2.3.1. Рассчитаем параметры а и b степенной регрессии:
Расчету параметров предшествует процедура линеаризации данного уравнения:
и замена переменных:
определяются методом наименьших квадратов:
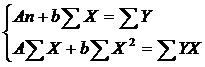
Рассчитываем таблицу 3.
Построим уравнение регрессии на поле корреляции:
2.3.2. Оценим тесноту связи между признаками у и х с помощью индекса парной корреляции Ryx.
Предварительно рассчитаем теоретическое значение 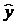
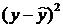
Значение индекса корреляции Rxy близко к 1, следовательно, между переменными у и х наблюдается очень тесная корреляционная связь вида:
2.3.3. Оценим качество построенной модели.
Определим индекс детерминации:
т. е. данная модель объясняет 87,6% общей вариации результата у, а на долю необъясненной вариации приходится 12,4%.
Качество модели высокое.
Найдем величину средней ошибки аппроксимации.
Ошибка аппроксимации Аi, i=1…15:
Средняя ошибка аппроксимации:
Ошибка небольшая, качество модели высокое.
2.3.4. Определим средний коэффициент эластичности:
Он показывает, что с увеличением выпуска продукции на 1% затраты на производство увеличиваются в среднем на 0,438%.
2.3.5.Оценим статистическую значимость полученного уравнения.
Проверим гипотезу H0, что выявленная зависимость у от х носит случайный характер, т. е. полученное уравнение статистически незначимо. Примем α=0,05.
табличное (критическое) значение F-критерия Фишера:
фактическое значение F-критерия Фишера:
следовательно, гипотеза H0 отвергается, принимается альтернативная гипотеза H1: с вероятностью 1-α=0,95 полученное уравнение статистически значимо, связь между переменными x и y неслучайна.