Как сделать статистическую обработку данных
Статистическая обработка данных с помощью Excel



Многие задачи статистического анализа можно решить, не прибегая непосредственно к законам распределения случайных величин, а используя лишь их статистические характеристики. Под случайной величиной понимают такую величину, значения которой изменяются случайным образом от одного испытания к другому, причем каждое из этих значений реализуется с той или иной вероятностью. Например, ежедневное количество покупателей в магазине изменяется случайно изо дня в день, принимая любые натуральные значения в некотором интервале. Наиболее часто при описании случайных величин используют такие статистические характеристики, как среднее значение, дисперсия, среднеквадратичное отклонение, мода, медиана и скос. Среднее значение случайной величины X вычисляют по формуле
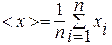
Важно также знать, как сильно значения изучаемой величины отличаются от ее среднего, или, иначе говоря, насколько широк разброс случайной величины. Рассеивание случайной величины вокруг ее среднего характеризует дисперсия D[X]. Чем больше дисперсия, тем «случайнее» случайная величина. Для приближенного значения дисперсии дискретной случайной величины X используют следующую формулу:
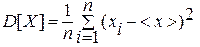
На практике часто используют и другую характеристику рассеивания – среднеквадратичное отклонение sx, вычисляемое по формуле 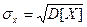
Для вычисления этих и многих других статистических характеристик Excel располагает широким набором статистических функций. Их полный список можно получить, выбрав команду Функция из меню Вставка. Применение этих функций позволяет существенно упростить статистический анализ данных различного типа.
Excel предусматривает также применение 18 статистических инструментов анализа, в том числе такие, как описательная статистика, гистограмма, генерация случайных чисел, корреляция, ковариация и ряд других. Эти инструменты позволяют автоматизировать анализ данных и статистических параметров. Доступ к ним можно получить, выбрав в меню Сервис команду Анализ данных. Затем в диалоговом окне Инструменты анализа следует выбрать нужный инструмент и задать входной и выходной интервалы, а также другие требуемые параметры. Например, инструмент анализа Описательная Статистика создает список одномерных статистических характеристик для данных во входном интервале. Инструмент Описательная Статистика генерирует, в частности, следующие выходные значения: дисперсию выборки, среднеквадратичное отклонение, медиану, моду и скос. Подробнее об этих функциях можно прочитать в соответствующих разделах встроенной Справки.
Возможно, в Вашей системе не установлены инструменты анализа статистических данных. В этом случае следует выбрать команду Сервис Þ Надстройки, далее в появившемся диалоговом окне нужно установить флажок в окне Список надстроек для строки Пакет анализа и щелкнуть по кнопке ОК.
Лабораторная работа № 8.
Создание простых таблиц, автоматическое заполнение, автосуммирование. Форматирование в Excel
Цель работы: научиться осуществлять перемещение по таблице, ввод/удаление данных в таблицу; изучить возможности форматирования и автозаполнения; производить автосуммирование.
Перед выполнением лабораторной работы необходимо изучить следующие разделы:
— создание, открытие, закрытие, сохранение книги;
— добавление, переименование рабочего листа книги;
— ввод чисел и формул в ячейку;
— форматирование содержимого ячейки, блока ячеек;
— автозаполнение числами, формулами;
— относительные и абсолютные ссылки;
— использование функций и формул в таблице;
— работа с данными из разных книг;
— скрытие и отображение блока столбцов (строк).
Первичная статистическая обработка данных



Лабораторная работа №3. Статистическая обработка данных в системе MatLab
Общая постановка задачи
Основной целью выполнения лабораторной работы является ознакомление с основами работы со статистической обработкой данных в среде MatLAB.
Теоретическая часть
Первичная статистическая обработка данных
Статистическая обработка данных основывается на первичных и вторичных количественных методах. Цель первичной обработки статистических данных является структурирование полученных сведений, подразумевающее группировку данных в сводные таблицы по различным параметрам. Первичные данных должны быть представлены в таком формате, чтобы человек смог провести приближенную оценку полученной совокупности данных и выявить информацию о распределении данных полученной выборки данных, например, однородность или компактность данных. После первичного анализа данных применяются методы вторичной статистической обработки данных, на основании которых определяются статистические закономерности в имеющемся наборе данных.
Проведение первичного статистического анализа над массивом данных позволяет получить знания о следующем:
— Какое значение наиболее характерно для выборки? Для ответа на данный вопрос определяются меры центральной тенденции.
— Велик ли разброс данных относительно этого характерного значения, т. е. какова «размытость» данных? В данном случае определяются меры изменчивости.
Стоит отметить тот факт, что статистические показатели меры центральной тенденции и изменчивостиопределяются только на количественных данных.
Меры центральной тенденции– группа величин, вокруг которых группируются остальные данные.Таким образом, меры центральной тенденции обобщают массив данных, что делает возможным формирование умозаключений как о выборке в целом, так и проведение сравнительного анализа разных выборок друг с другом.
Допустим имеется выборка данных 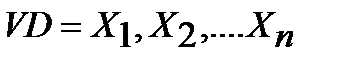
1. Выборочное среднее– это результат деления суммы всех значений выборки на их количество.Определяется по формуле (3.1).
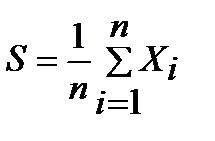
где 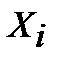
n – количество элементов выборки.
Выборочное среднее позволяет получить наибольшую точность в процессе оценки центральной тенденции.
Допустим имеется выборка из 20 человек. Элементами выборки являются сведения о среднем ежемесячном доходе каждого человека. Предположим, что 19 человек имеют средний ежемесячный доход в 20 т.р. и 1 человек с доходом в 300 т.р. Суммарный ежемесячный доход всей выборки составляет 680 т.р. Выборочное среднее в данном случае S=34.
2. Медиана– формирует значение, выше и ниже которого количество отличающихся значений одинаково, т. е. это центральное значение в последовательном ряду данных. Определяется в зависимости четности/нечетности количества элементов выборке по формулам (3.2) или (3.3).Алгоритм оценки медианы для выборки данных 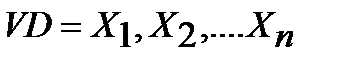
— Первым делом данные ранжируются (упорядочиваются) по убыванию/возрастанию 
— Если в упорядоченной выборке нечетное число элементов, то медиана совпадает с центральным значением.
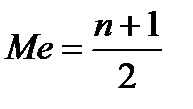
— В случае четного числа элементов медиана определяется как как среднее арифметическое двух центральных значений.
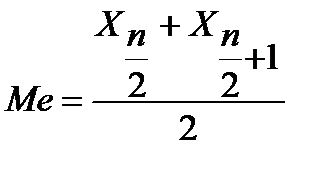
где 
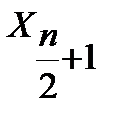

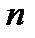
-В том случае, если все элементы выборки различны, то ровно половина элементов выборки больше медианы, а другая половина меньше. Например, для выборки <1, 5, 9, 15, 16>медиана совпадает с элементом 9.
В статистическом анализе данных медиана позволяет определить элементы выборки, которые сильно влияют на значение выборочного среднего.
Допустим имеется выборка из 20 человек. Элементами выборки являются сведения о среднем ежемесячном доходе каждого человека. Предположим, что 19 человек имеют средний ежемесячный доход в 20 т.р. и 1 человек с доходом в 300 т.р. Суммарный ежемесячный доход всей выборки составляет 680 т.р. Медиана, после упорядочивания выборки, определяется как среднеарифметическое десятого и одиннадцатого элементов выборки) и равняется Ме=20 т.р. Данный результат интерпретируется следующим образом: медиана делит выборку на две группу, таким образом, что можно сделать заключение о том, что в первой группе у каждого человека средний ежемесячный доход не более 20 т.р., а во второй группе не менее 20 т.р. В данном примере можно говорить о том, что медиана характеризуется тем, сколько зарабатывает «средний» человек. В то время как значение выборочного среднего значительно превышено S=34, что указывает на неприемлемость данной характеристики при оценке среднего заработка.
Таким образом, чем больше различие между медианой и выборочным средним, тем больший разброс данных выборки (в рассмотренном примере, человек с заработком в 300 т.р. явно отличается от среднестатистических людей конкретной выборки и оказывает существенное влияние на оценку среднего дохода). Что делать с подобными элементами решается в каждом индивидуальном случае. Но в общем случае для обеспечения достоверности выборки они изымаются, так как оказывают сильное влияние на оценку статистических показателей.
3. Мода (Мо) – формирует значение, наиболее часто встречающееся в выборке, т. е. значение с наибольшей частотой.Алгоритм оценки моды:
-В том случае, когда выборка содержит элементы, встречающиеся одинаково часто, то говорят, что мода в подобной выборке отсутствует.
— Если два соседних элемента выборки имеют одинаковую частоту, являющуюся больше частоты остальных элементов выборки, то мода определяется как среднее этих двух значений.
— Если два элемента выборки имеют одинаковую частоту, являющуюся больше частоты остальных элементов выборки, и при этом данные элементы не являются соседними, то говорят, что в данной выборке две моды.
Мода в статистическом анализе используется в ситуациях, когда необходимо проведение быстрой оценки меры центральной тенденции и не требуется высокая точность. Например, моду (по показателю размер либо бренд) удобно применять для определения одежды и обуви, которая пользуется наибольшим спросом у покупателей.
Меры разброса (изменчивости)– группа статистических показателей, характеризующих различия между отдельными значениями выборки. Основываясь на показателях мер разброса можно оценивать степень однородности и компактности элементов выборки. Меры разброса, характеризуются следующим набором показателей:

Где 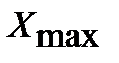

2.Среднее отклонение– среднеарифметическая разница (по абсолютной величине) между каждым значением в выборке и ее выборочным средним. Среднее отклонение определяется по формуле (3.5).

где 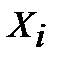

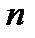
Модуль 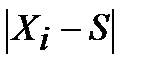
3. Дисперсия — мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Вычисляется как сумма квадратов отклонений каждого элемента выборки от средней величины. В зависимости от размера выборки дисперсия оценивается разными способами:
— для больших выборок (n>30) по формуле (3.6)
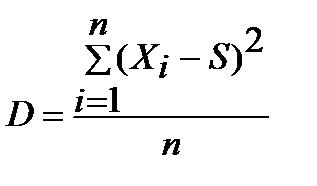
Первичная статистическая обработка данных
Все методы количественной обработки принято подразделять на первичные и вторичные. Первичная статистическая обработка нацелена на упорядочивание информации об объекте и предмете изучения. На этой стадии «сырые» сведения группируются по тем или иным критериям, заносятся в сводные таблицы. Первично обработанные данные, представленные в удобной форме, дают исследователю в первом приближении понятие о характере всей совокупности данных в целом: об их однородности – неоднородности, компактности – разбросанности, четкости – размытости и т.д. Эта информация хорошо считывается с наглядных форм представления данных и дает сведения об их 
В ходе применения первичных методов статистической обработки получаются показатели, непосредственно связанные с производимыми в исследовании измерениями.
К основным методам первичной статистической обработки относятся: вычисление мер центральной тенденции и мер разброса (изменчивости) данных.
Первичный статистический анализ всей совокупности полученных в исследовании данных дает возможность охарактеризовать ее в предельно сжатом виде и ответить на два главных вопроса: 1) какое значение наиболее характерно для выборки; 2) велик ли разброс данных относительно этого характерного значения, т.е. какова «размытость» данных. Для решения первого вопроса вычисляются меры центральной тенденции, для решения второго – меры изменчивости (или разброса). Эти статистические показатели используются в отношении количественных данных, представленных в порядковой, интервальной или пропорциональной шкале.
Меры центральной тенденции –это величины, вокруг которых группируются остальные данные. Данные величины являются как бы обобщающими всю выборку показателями, что, во-первых, позволяет судить по ним обо всей выборке, а во-вторых, дает возможность сравнивать разные выборки, разные серии между собой. К мерам центральной тенденции в обработке результатов психологических исследований относятся: выборочное среднее, медиана, мода.
Выборочное среднее (М) – это результат деления суммы всех значений (А) на их количество (N).
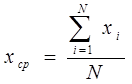 |
Медиана (Me) –это значение, выше и ниже которого количество отличающихся значений одинаково, т.е. это центральное значение в последовательном ряду данных. Медиана не обязательно должна совпадать с конкретным значением. Совпадение происходит в случае нечетного числа значений (ответов), несовпадение – при четном их числе. В последнем случае медиана вычисляется как среднее арифметическое двух центральных значений в упорядоченном ряду.
Мода (Мо) –это значение, наиболее часто встречающееся в выборке, т.е. значение с наибольшей частотой. Если все значения в группе встречаются одинаково часто, то считается, что моды нет. Если два соседних значения имеют одинаковую частоту и больше частоты любого другого значения, мода есть среднее этих двух значений. Если то же самое относится к двум несмежным значениям, то существует две моды, а группа оценок является бимодальной.
Обычно выборочное среднее применяется при стремлении к наибольшей точности в определении центральной тенденции. Медиана вычисляется в том случае, когда в серии есть «нетипичные» данные, резко влияющие на среднее. Мода используется в ситуациях, когда не нужна высокая точность, но важна быстрота определения меры центральной тенденции.
Вычисление всех трех показателей производится также для оценки распределения данных. При нормальном распределении значения выборочного среднего, медианы и моды одинаковы или очень близки.
Меры разброса (изменчивости) –это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, его компактности, а косвенно и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в психологических исследованиях показатели: среднее отклонение, дисперсия, стандартное отклонение.
Размах (Р) – это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Среднее отклонение (МД) – это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним.
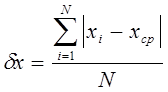 |
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но если не взять их по абсолютной величине, то их сумма будет равна нулю и мы не получим информации об их изменчивости. Среднее отклонение показывает степень скученности данных вокруг выборочного среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции – моду или медиану.
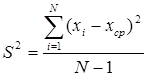
Стандартное отклонение (σ). Из-за возведения в квадрат отдельных отклонений dпри вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию – из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим, или стандартным, отклонением:
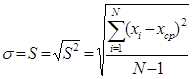 |
МД, D иσ применимы для интервальных и пропорционных данных. Для порядковых данных в качестве меры изменчивости обычно берут полуквартильное отклонение (Q), именуемое еще полуквартильным коэффициентом.
Дата добавления: 2014-01-15 ; Просмотров: 1860 ; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет


