Как сделать степень в кумире
Основные понятия и команды в программе КУМИР
Содержимое разработки
Тема урока : Основные понятия и команды в программе КУМИР
Подготовил преподаватель Бурдин А.Б.
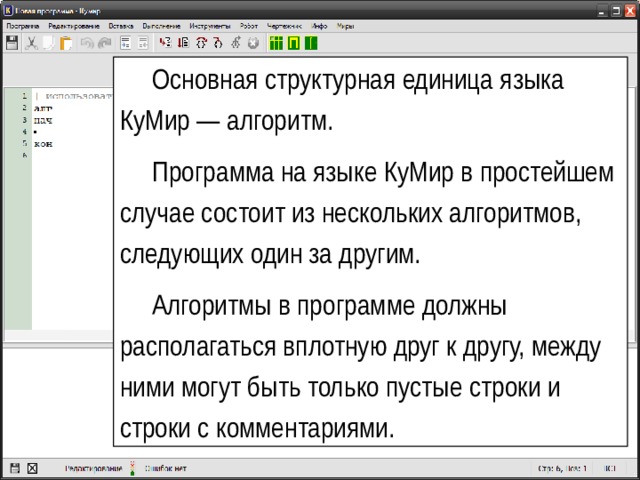
Основная структурная единица языка КуМир — алгоритм.
Программа на языке КуМир в простейшем случае состоит из нескольких алгоритмов, следующих один за другим.
Алгоритмы в программе должны располагаться вплотную друг к другу, между ними могут быть только пустые строки и строки с комментариями.
Разработчики языка «КуМир» преследовали цель создать простой язык для начального курса информатики, отвечающий современной технологии программирования и допускающий производственное использование. За основу был взят школьный алгоритмический язык.
В разных языках программирования такие единицы называются по-разному, в КуМире такая единица называется «Исполнитель».
Переменная – именованная область памяти, используемая для хранения значения, которое можно изменить при выполнении программы.
Константа – именованная область памяти, используемая для хранения фиксированного значения, которое невозможно изменить при выполнении программы.
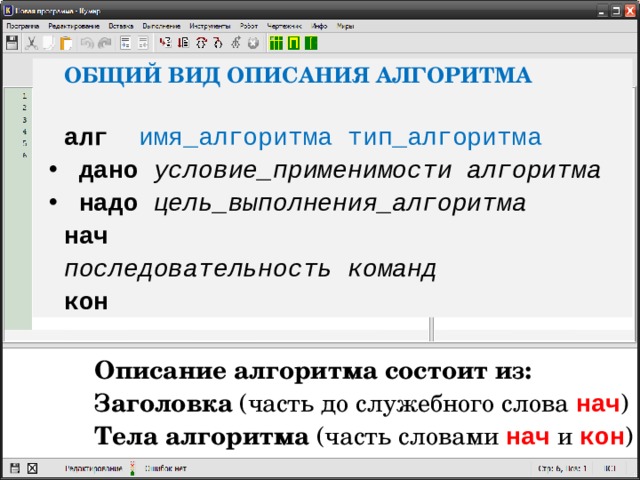
ОБЩИЙ ВИД ОПИСАНИЯ АЛГОРИТМА
алг имя_алгоритма тип_алгоритма
Описание алгоритма состоит из:
Заголовка (часть до служебного слова нач )
Тела алгоритма (часть словами нач и кон )
ТИПЫ ВЕЛИЧИН ИСПОЛЬЗУЕМЫХ В ПРОГРАММЕ
Как пишутся в программе
В записи имен переменных могут быть использованы любые символы русского и латинского алфавита, а так же цифры. Имя не должно начинаться с цифры. На длину имен в системе КуМир строгих ограничений не накладывается, но для удобства редактирования и во избежание переполнения строк переменным и алгоритмам не стоит давать слишком длинные имена. Обычно имя подбирается так, чтобы можно было понять, для чего предназначен алгоритм. При редактировании программ также следует помнить о том, что русские и латинские буквы, сходные по написанию, различаются ЭВМ. Например, если при описании переменной с именем А пользователь набрал «А» на латинском алфавите, а в тексте алгоритма пытается обратиться к этой переменной, набирая ее имя на русском алфавите, то в данной строке на «полях» появится сообщение «имя не определено».
Арифметические операции и стандартные функции для работы с числами
Как пишутся в программе
Возведение в степень

ОПЕРАЦИИ СРАВНЕНИЯ ЧИСЕЛ
Как пишутся в программе
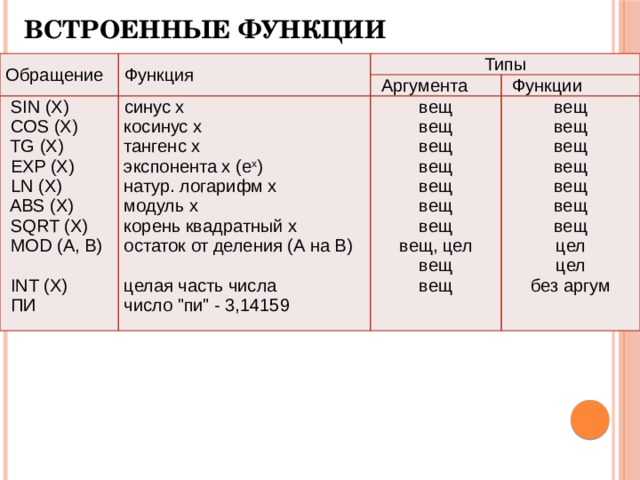
SIN (X) COS (X) TG (X) EXP (X) LN (X) ABS (X) SQRT (X) MOD (A, B) INT (X) ПИ
вещ вещ вещ вещ вещ вещ вещ вещ, цел вещ вещ
вещ вещ вещ вещ вещ вещ вещ цел цел без аргум
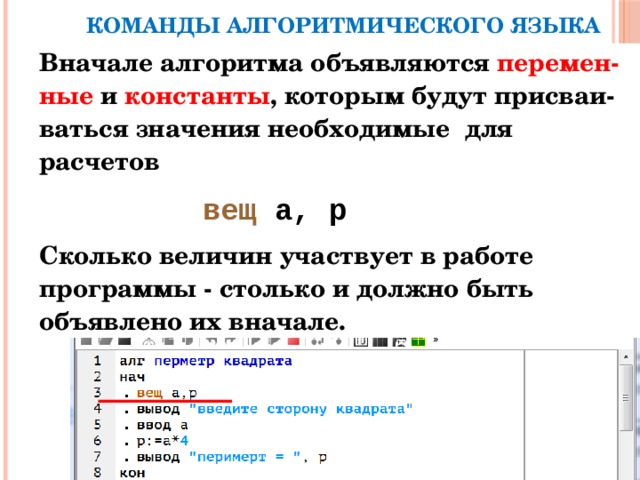
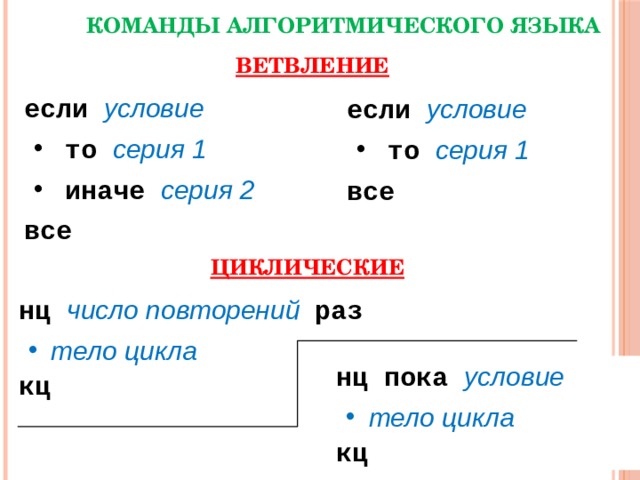
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
Вначале алгоритма объявляются перемен-ные и константы , которым будут присваи-ваться значения необходимые для расчетов
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
Вывод “введите сторону квадрата”
в процессе работы программы будет отображаться в нижнем окне:
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
после нажатия клавиши Enter будет отображена в правом окне,
то есть в буфере обмена (в памяти) программы.
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
в процессе работы программы будет отображаться в нижнем окне,
то есть будет выводиться результат работы программы.
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
Ветвление бывает полное и неполное.
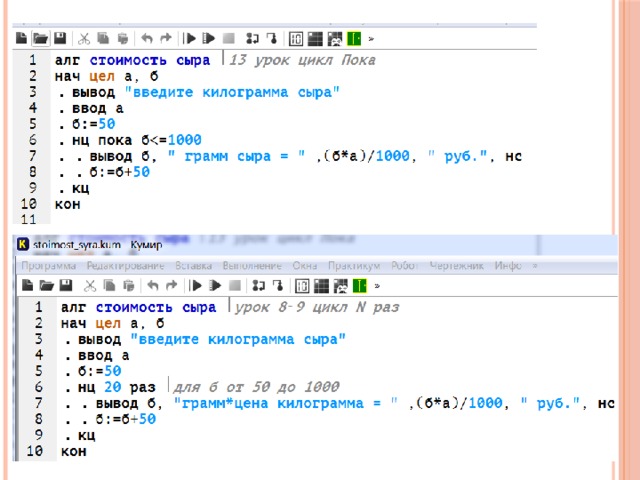
КОМАНДЫ АЛГОРИТМИЧЕСКОГО ЯЗЫКА
Служебное слово ( новая строка ) указывает ЭВМ, что информация должна выводиться на новую строку.
Система «КуМир»
2. Имена и типы величины. Операции КуМира
присваивание
сложение
вычитание
умножение
возведение в степень
деление
3. Встроенные функции языка КуМир
Приведем пример встроенных функций:
Пример записи арифметических выражений на алгоритмическом языке:
Запись на алг. языке
sinXcosY + cosXsinY
I2R
x1x2 + x1x3 + x2x3
sin(X)*cos(Y) + cos(X)*sin(Y)
(I**2)*R или I**2*R
x1*x2 + x1*x3 + x2*x3
4. Команды ВВОДА / ВЫВОДА информации
Служебное слово НС (новая строка) указывает ЭВМ, что информация должна выводиться на новую строку.
5. Команда присваивания. Создание и редактирование программ линейной структуры
ИМЯ ВЕЛИЧИНЫ : = ВЫРАЖЕНИЕ
Знак » : = » (двоеточие, а потом равенство) называется знаком присваивания и читается как «присвоить» (например, команда » n : = e» читается » n присвоить е»). При выполнении команды присваивания ЭВМ сначала вычисляет записанное в правой части выражение (заменяя имена величин на их значения), а потом полученное значение выражения записывает в память.
При выполнении команды присваивания «n : = 0»
ЭВМ запишет значение выражения (т. е. 0) внутрь
прямоугольника величины «n» (старое значение,
каково бы оно ни было, будет затерто).
Таким образом, после выполнения команды «n : = 0»
величина n будет иметь значение 0
Другими словами, после выполнения команды
«n : = n + 1» значение величины n будет увеличено на 1
Алгоритмы, представляющие собой простую последовательность действий, называются алгоритмами линейной структуры.
Рассмотрим процесс создания линейного алгоритма на примере вычисления выражения:
1. Вычислить сумму двух чисел
2. Написать программу нахождения гипотенузы прямоугольного треугольника по двум данным катетам
3. Найти объем куба, если известна его сторона
6. Создание и редактирование программ разветвляющейся структуры
Графическая схема выполнения конструкции «если«
7. Виды циклов в системе программирования КуМир
Алгоритмы, отдельные действия которых многократно повторяются, называются алгоритмами циклической структуры. Совокупность действий алгоритма, связанную с повторением, называют циклом.
Команда цикла обеспечивает повторное выполнение последовательности команд (тела цикла) по некоторому условию.
Для программирования алгоритмов циклической структуры в системе программирования КуМир предусмотрено два вида циклов: цикл с предусловием (цикл пока) и цикл с параметром (цикл для).
Цикл с предусловием (цикл пока)
При его выполнении ЭВМ циклически повторяет следующие действия:
а) проверяет записанное после слова пока условие;
б) если условие не соблюдается (условие ложно), то выполнение цикла завершается и ЭВМ начинает выполнять команды, записанные после КЦ. Если же условие соблюдается (условие истинно), то ЭВМ выполняет тело цикла, снова проверяет условие и т. д.
Если условие в цикле пока не соблюдается с самого начала, то тело цикла не выполняется ни разу.
Замечание. Выполнение цикла пока может и не завершиться, если условие все время будет истинным (эту ситуацию принято называть зацикливанием). Поэтому во избежание подобных ситуаций в теле цикла должны содержаться команды изменения условия.
Работа с прямоугольными таблицами (матрицами)
Как и линейная таблица, матрица занимает место в памяти ЭВМ, имеет имя, значение и тип. В КуМире используются таблицы целого (целтаб) и вещественного (вещтаб) типов.
Задача. В заданной таблице В определить индекс и значение максимального элемента.
Найдите разность двух чисел
Решение:
Методика преподавания основ алгоритмизации на базе системы «КуМир». Лекция 6
Мы находимся на финальной прямой изучения алгоритмического языка.
Но это не очень удобно, так как можно забыть о присваивании начального значения перед циклом или увеличении величины i внутри цикла. Поэтому цикл для вводится здесь просто, как компактная форма записи.
При работе с табличными величинами циклы для встречаются очень часто. К табличным величинам мы сейчас и перейдем.
Лекция 2. Практическое знакомство с системой “КуМир”: исполнитель Робот. Понятие алгоритма. Управление исполнителем Робот с помощью пульта. Линейные алгоритмы. Запись алгоритма. Отступление: Карел-Робот в начальном курсе программирования Стэнфордского университета.
Лекция 3. Методы “визуальной” записи алгоритма. Программное управление Роботом. Цикл “n раз”. Использование вспомогательных алгоритмов. Запись алгоритмов на алгоритмическом языке.
Контрольная работа № 1.
Лекция 4. Арифметические выражения и правила их записи. Алгоритмы с “обратной связью”. Команда “пока”. Условия в алгоритмическом языке. Команды “если” и “выбор”. Команды контроля. “Визуальное” представление команд. Отступление: правила и форма записи арифметических выражений в Фортране XXI века.
Лекция 5. Величины в алгоритмическом языке. Команды ввода/вывода информации. Команда присваивания. Вспомогательные алгоритмы. Алгоритмы с результатами и алгоритмы-функции. Цикл “для”. Табличные величины. Логические, символьные и литерные величины.
Контрольная работа № 2.
Лекция 6. Методы алгоритмизации. Рекуррентные соотношения. Метод итерации. Инвариант цикла. Рекурсия.
Общий вид цикла для :
нц для i от i1 до i2
Общий вид цикла для с шагом :
нц для i от i1 до i2 шаг i3
Линейные таблицы соответствуют классической модели памяти ЭВМ. Фактически у самой ЭВМ основным хранилищем информации служит одна большая линейная таблица байтов.
являются правильными. Размерность таблицы и границы изменения индексов указываются после имени каждой величины.
Здесь k — линейная таблица, состоящая из 11 элементов целого типа. Индексы элементов принимают значения от –5 до 5. Этот пример не типичный. Чаще всего элементы таблицы нумеруют, начиная с 1, как в языке Паскаль, или начиная с 0, как в языке Си.
Табличная величина имеет одно общее для всех ее элементов имя, а элементы таблицы отдельных имен не имеют. Именно этим табличная величина отличается от просто набора из нескольких величин. За счет этого мы можем компактно описать большое количество “элементарных” величин. Так, например, запись
нц для i от 1 до 1000
Выполняя этот фрагмент, ЭВМ присваивает значение 0 тысяче элементов таблицы, то есть изменяет большой объем информации — целую тысячу чисел. А ведь в приведенном фрагменте программы всего три строчки. Таким образом, использование табличных величин позволяет составлять компактные алгоритмы, обрабатывающие огромное количество информации, задействовать не только быстродействие, но и объем памяти ЭВМ.
Поле Робота можно рассматривать как таблицу, в каждой клетке которой записаны два числа — радиация и температура. Для лучшего усвоения понятия таблицы можно использовать аналогии с соответствующими фрагментами поля Робота. Так, горизонтальный коридор на поле Робота с заданной в каждой клетке коридора радиацией аналогичен линейной таблице с вещественными элементами (см. пример). А все поле Робота с заданной в каждой клетке температурой — это аналог прямоугольной таблицы, то есть аналог массива с двумя измерениями. Такие массивы на бумаге и на “доске” изображаются обычно в виде прямоугольных таблиц, откуда и название.
Предположим, что Робот находится в левом конце горизонтального коридора из 16 клеток, и требуется провести “радиационную разведку” этого коридора, то есть измерить радиацию в каждой клетке коридора и подсчитать какие-то характеристики измеренных данных: суммарную радиацию, максимальную радиацию, номер клетки с минимальным значением радиации и т.п.
Для решения подобных задач применимы два разных подхода. При первом подходе Робот перемещается по коридору, для каждой клетки проводит измерение уровня радиации в каждой клетке и немедленно проводит все требуемые подсчеты. При таком подходе нет необходимости запоминать все измеренные значения уровня радиации, обработка данных проводится “на ходу”. Второй подход состоит в том, чтобы разделить во времени этап получения информации и этап ее последующей обработки. При втором подходе Робот идет по коридору, измеряет уровень радиации в каждой клетке и “накапливает” где-то полученную информацию. Далее Робот “отдыхает”, а накопленная информация обрабатывается нужным образом, то есть с этой информацией ЭВМ проводит требуемое вычисление. При этом на этапе проведения вычисления совершенно неважно, откуда взялись исходные данные для этого вычисления: в процессе измерения радиации Роботом или в результате каких-то других действий. Важно только, чтобы эти данные были представлены в какой-то стандартизованной форме. В школьном алгоритмическом языке таких форм две. Данные можно накапливать в таблицах или в файлах.
Для определенности далее мы рассмотрим задачу подсчета суммарной радиации коридора с сохранением “накопленной” информации в линейной таблице.
Составляя алгоритм, можно рассуждать так. Перед началом перемещения по коридору Робот побывал только в одной клетке коридора — в самой левой, и нужно запомнить в S значение радиации в этой клетке:
Далее Робот должен сместиться вправо, измерить значение радиации в следующей клетке и добавить его к S :
вправо; S := S + радиация
Этот процесс нужно продолжать до тех пор, пока коридор не кончится, то есть пока справа от Робота свободно. Для описания такого повторяющегося процесса используется цикл “пока справа свободно”. Тем самым мы получаем такой алгоритм:
| известно, что Робот находится
| в самой левой клетке
| требуется найти суммарную радиацию
| во всех клетках коридора
| и запомнить ее в S
нц пока справа свободно
При таком подходе нам не нужно знать длину коридора, алгоритм будет успешно работать для коридора любой длины.
Применим теперь второй подход и будем запоминать информацию, получаемую Роботом, в линейной таблице. Длина таблицы должна быть задана в момент ее описания, так что в этом случае нам важно знать, что длина коридора равна 16, чтобы создать таблицу, в которой уместится вся информация о радиации в коридоре:
| известно, что Робот в самой левой клетке
| горизонтального коридора длины 16
| требуется измерить радиацию во всех
| клетках коридора и
| запомнить ее в вещтаб r[1:16]
| Робот находится в клетке номер 1:
нц для i от 2 до 16
На этом сбор информации, в котором активно участвовал Робот, закончился. Вся информация об уровнях радиации в клетках исследуемого коридора собрана в памяти ЭВМ. Остальную работу можно выполнить без помощи Робота. Даже если Робот после сбора информации сломается, ЭВМ, располагая данными измерений радиации, сумеет завершить работу.
Теперь нам нужно проделать вычислительный этап работы, найти суммарную радиацию. Для этого с линейной таблицей r нужно проделать стандартную процедуру обработки информации — найти сумму элементов этой таблицы. Это делается так:
нц для i от 1 до 16
Замечание. Подсчет суммы элементов вещественной линейной таблицы — это часто встречающаяся операция, и обычно такие операции оформляют как универсальные программы. Поэтому мы составим универсальный вспомогательный алгоритм-функцию сумма, которым и воспользуемся для решения задачи.
Составим теперь полный алгоритм подсчета суммарной радиации в коридоре, включая универсальный алгоритм-функцию
Настало время снова вернуться к простым величинам. Мы познакомились с числовыми величинами и встречали в примерах литерные величины. В алгоритмическом языке существуют еще логические и символьные величины.
Для деления с остатком на положительное целое число в “КуМире” встроены две функции:
| частное от деления m
| остаток от деления m
В отличие от многих других языков программирования, где допускаются отрицательные остатки, в алгоритмическом языке остаток никогда не бывает отрицательным, при делении на положитель-
ное число n остаток может прини-
мать только значения от 0 до n–1. В функциях div и mod второй аргумент должен быть положителен.
Числа можно сравнивать, в алгоритмическом языке есть обозначения для 6 операций сравнения: “ ”, “ =”, “=” и “<>”. Операции сравнения “=” и “<>” в алгоритмическом языке применимы к значениям любого типа, остальными операциями сравнения можно без опаски пользоваться для числовых величин и с некоторой опаской для текстовых величин, так как результат сравнения текстовых величин не соответствует алфавитному упорядочению. Наконец, целочисленная величина может появиться в левой части команды присваивания
Величины логического типа можно использовать в условиях в алгоритмическом языке. Для примера рассмотрим такую задачу. От горизонтального коридора на поле Робота кое-где вверх отходят тупики разной высоты. Надо отметить клетки коридора напротив тех тупиков, высота которых больше трех клеток (мы их назвали “длинными тупиками”). Если мы начнем решать эту задачу, т.е. составлять алгоритм, у нас, конечно, будет цикл, потому что неизвестно, сколько клеток в коридоре. Условием окончания цикла служит условие “справа стена”. Внутри цикла надо идти по коридору вправо и, если сверху обнаружится “длинный” тупик, то соответствующую клетку коридора закрасить.
Теперь, после введения величин логического типа, мы, в соответствии с методом последовательного уточнения, эту изложенную выше идею решения можем записать прямо на алгоритмическом языке:
алг отметить клетку
дано | выше клетки имеется
надо | закрасить входную клетку тупика,
| если «сверху длинный тупик»
если сверху длинный тупик
Здесь условие “сверху длинный тупик” — вызов вспомогательного алгоритма-функции, значением которого является логическое значение. Многие конструкции в алгоритмическом языке вводятся именно для того, чтобы, произнеся нормальную человеческую фразу типа “если сверху длинный тупик, то закрасить клетку коридора”, мы могли бы ее примерно в таком же нормальном виде записать в алгоритм, но уже в виде фрагмента алгоритма на алгоритмическом языке. После того как мы написали этот фрагмент, мы должны еще написать вспомогательный алгоритм-функцию, который будет анализировать, есть ли сверху “длинный” тупик.
И, наконец, скажем несколько слов о символьных и литерных величинах. Значением символьной величины может быть любой символ, всего имеется 256 символов. Некоторые символы можно найти на клавиатуре или увидеть на экране, а другие символы называются “непечатными” и увидеть их нельзя. Зато у каждого символа имеется код — целое число от 0 до 255, и есть встроенные функции “КуМира”, преобразующие символ в код и обратно. Попробуем напечатать все символы с кодами от 32 до 127:
Мы видим, что среди этих символов есть цифры, латинские буквы, знаки препинания и спецзнаки, но нет русских букв. Это и неудивительно, символы с кодами от 0 до 127 — это символы американской кодировки ASCII. Чтобы увидеть русские буквы, нужно напечатать символы с кодами от 128 до 255 (так называемые “символы кодировки KOI-8r”) — см. скриншот.
Литерная величина строится из символьных. Для литерных величин и их значений часто используется термин строка. С некоторой натяжкой литерную величину можно представлять себе в виде линейной таблицы, элементами которой являются символы, к которым можно обращаться по номеру, как к элементам таблицы. Но в отличие от числовых линейных таблиц длина литерной строки (т.е. количество “элементов таблицы”) может меняться в ходе выполнения алгоритма, а при задании литерной величины длина не указывается.
Вторая строка пуста, в ней нет ни одного символа. В “КуМир” встроена функция
подсчитывающая длину строки:
длин(стр1) = 8, длин(стр2) = 0
нц для i от 1 до длин(стр)
В отличие от линейных таблиц над литерными величинами определены еще две операции: “вырезка” куска строки и добавление одной строки в конец другой. Приведем ровно один пример. Пусть
Тогда стр1[1:4] = «паро» и стр1+стр2 = «пароход»
Вырезка из строки снова является строкой и обозначается так:
вырезка := строка[старт : финиш]
В отличие от арифметических, логических операций и операций сравнения операция вырезки из строки имеет целых три аргумента:
лит строка, цел старт, цел финиш
лит строка, вырезка
При изучении величин литерного типа можно сформулировать достаточное количество задач, в которых аргументами и/или результатами являются строки. Эта область подобна играм с шифровкой и дешифровкой, которые так любят многие дети. Наверняка в классе найдутся ученики, которым работа со словами понравится больше, чем управление Роботом. Связать эти два непохожих внешне клас-
са задач можно следующим образом. Закодируем
5 команд Робота буквами
Закодируем программу управления Роботом в виде строки путь из этих пяти букв. Тогда можно будет поставить несколько задач, в которых результат выполнения Роботом данной программы нужно определить, анализируя строку путь и не используя массивы.
Легкая задача. По строке путь определить, вернулся ли Робот в исходное положение.
Средняя по трудности задача. Робот начал движение на пустом поле. В строке путь ровно две буквы “З”. Определить, сколько клеток закрасил Робот.
Трудная задача. Робот начал движение на пустом поле. В строке путь не менее одной буквы “З”. Определить, закрасил ли Робот более одной клетки.
И, наконец, еще об одних командах в алгоритмическом языке — командах контроля.
Все три команды выполняются так. Проверяется условие. Если условие не соблюдается (равно нет), то “КуМир” прекращает выполнение алгоритма и сообщает, что возник отказ. Если же условие соблюдается, то выполнение алгоритма нормально продолжается так, как если бы команды контроля не было вовсе.
В этих командах может быть либо записано так называемое контрольное условие, либо не написано ничего, либо написан только комментарий. Последний случай — самый частый в примерах, когда дано и надо используются для пояснения алгоритмов ученику, а не для формальной проверки условий в ходе выполнения алгоритма ЭВМ:
дано |Робот в начале горизонтального
|Вверх от коридора отходят тупики
надо |Закрасить клетки коридора напротив
|тех тупиков, высота которых больше
Для простоты в начале освоения “КуМира” можно считать эти конструкции “предназначенными для комментариев” и объяснение их реального смысла пропустить.
“НЕ открывайте дверь лифта, пока не убедитесь, что кабина находится перед вами. Это может привести к падению в шахту”.
Очевидно, что такая проверка спасла от серьезных травм не одного человека. Игнорирование этого требования, например, в скоростных лифтах главного здания МГУ на Ленинских горах в Москве привело к ряду трагедий.
В системе “КуМир” школьник, пишущий программу, естественно, не подвержен такой опасности.
В программе, как и в жизни, — если контрольное условие выполнено, то надо просто продолжать дальше выполнять алгоритм. Убедились, что все в порядке, — и работаем дальше. Если же контрольное условие не выполнено (лифта нет!), значит, где-то есть ошибка: либо алгоритм неверен, либо он применяется в недопустимой для него ситуации.
С содержательной точки зрения значимость дано и надо состоит в том, что в них описываются условия, которым должны удовлетворять состояние Робота, значения величин и пр.
Даже если условия записаны в виде комментариев, они позволяют понять, что должен делать алгоритм, не разбираясь с тем, как он это делает. Это полный аналог формулировки теоремы в математике, средство, позволяющее нам структурировать и накапливать знания (алгоритмы). Аналогично, если команда утв используется для комментариев, пояснения алгоритма, то некоторые его части становится возможным понимать статически, понимать, что делает данный фрагмент алгоритма. Это отличается от анализа и восприятия того, какие действия происходят при выполнении алгоритма.
1 В производственных языках программирования вместо термина “таблица” используется термин “массив” (массив данных, массив информации). “Линейные таблицы” называются “одномерными массивами”, “прямоугольные таблицы” — “двумерными массивами”, а также существуют трех-, четырех-, пяти- и пр. “мерные массивы”.