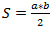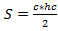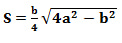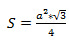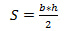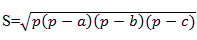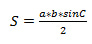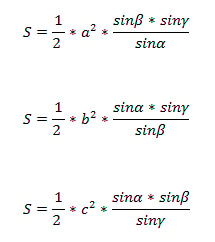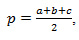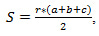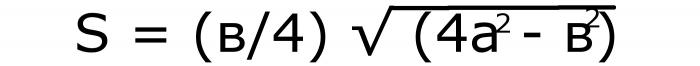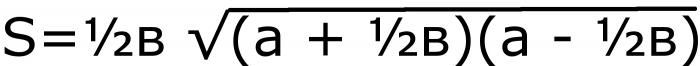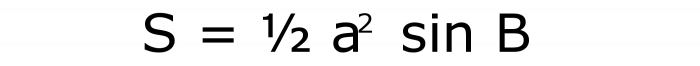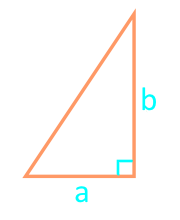Как вычислить площадь равнобедренного треугольника
Как вычислить площадь равнобедренного треугольника
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
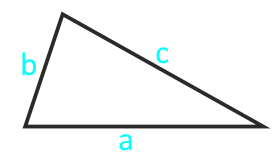
По формуле Герона
Формула Герона для нахождения площади треугольника:
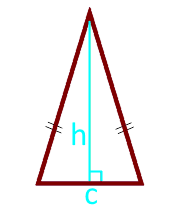
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
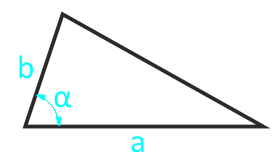
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Формула нахождения площади прямоугольного треугольника через катеты:
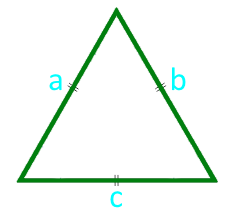
Площадь равнобедренного треугольника через стороны
Формула нахождения площади равнобедренного треугольника через две стороны:
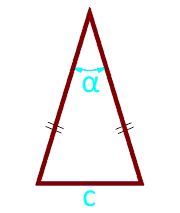
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
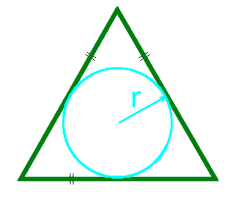
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
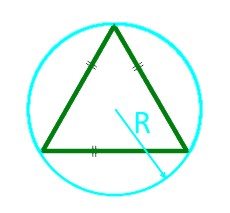
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
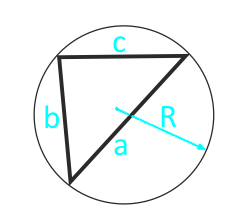
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
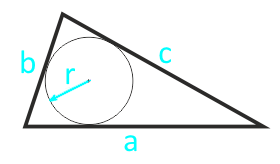
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Как посчитать площадь равнобедренного треугольника
Онлайн калькулятор
Чтобы вычислить площадь равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
Введите их в соответствующие поля и узнаете площадь равнобедренного треугольника (S).
Как посчитать площадь равнобедренного треугольника зная длину основания и высоту
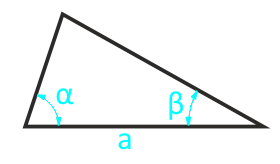
Какова площадь равнобедренного треугольника (S) если известны длина основания (b) и высота (h)?
Формула
Пример
Если основание b = 5 см, а высота h = 10 см, то:
S = ½⋅5⋅10 = 50/2 = 25 см 2
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между ними (β)
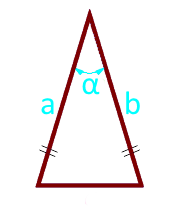
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между ними (β)?
Формула
Пример
Если сторона а = 10 см, а ∠β = 30°, то:
S = ½⋅10 2 ⋅sin30° = ½ ⋅100⋅0.5= 50/2 = 25 см 2
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и угол между стороной и основанием (α)
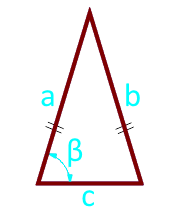
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и угол между стороной и основанием (α)?
Формула
Пример
Если сторона а = 10 см, а ∠α = 75°, то:
S = ½⋅10 2 ⋅sin(180-2⋅75)° = ½ ⋅100⋅0.5 = 50/2 = 25 см 2
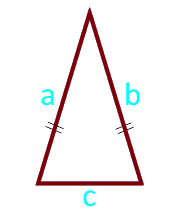
Как посчитать площадь равнобедренного треугольника зная длину двух равных сторон (a) и длину основания (b)
Какова площадь равнобедренного треугольника (S) если известны длина двух равных сторон (a) и длина основания (b)?
Формула
Пример
Если сторона а = 10 см, а основание b = 5, то:
Как найти площадь треугольника
8 класс, 9 класс
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Популярные единицы измерения площади:
квадратный миллиметр (мм 2 );
квадратный сантиметр (см 2 );
квадратный дециметр (дм 2 );
квадратный метр (м 2 );
квадратный километр (км 2 );
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
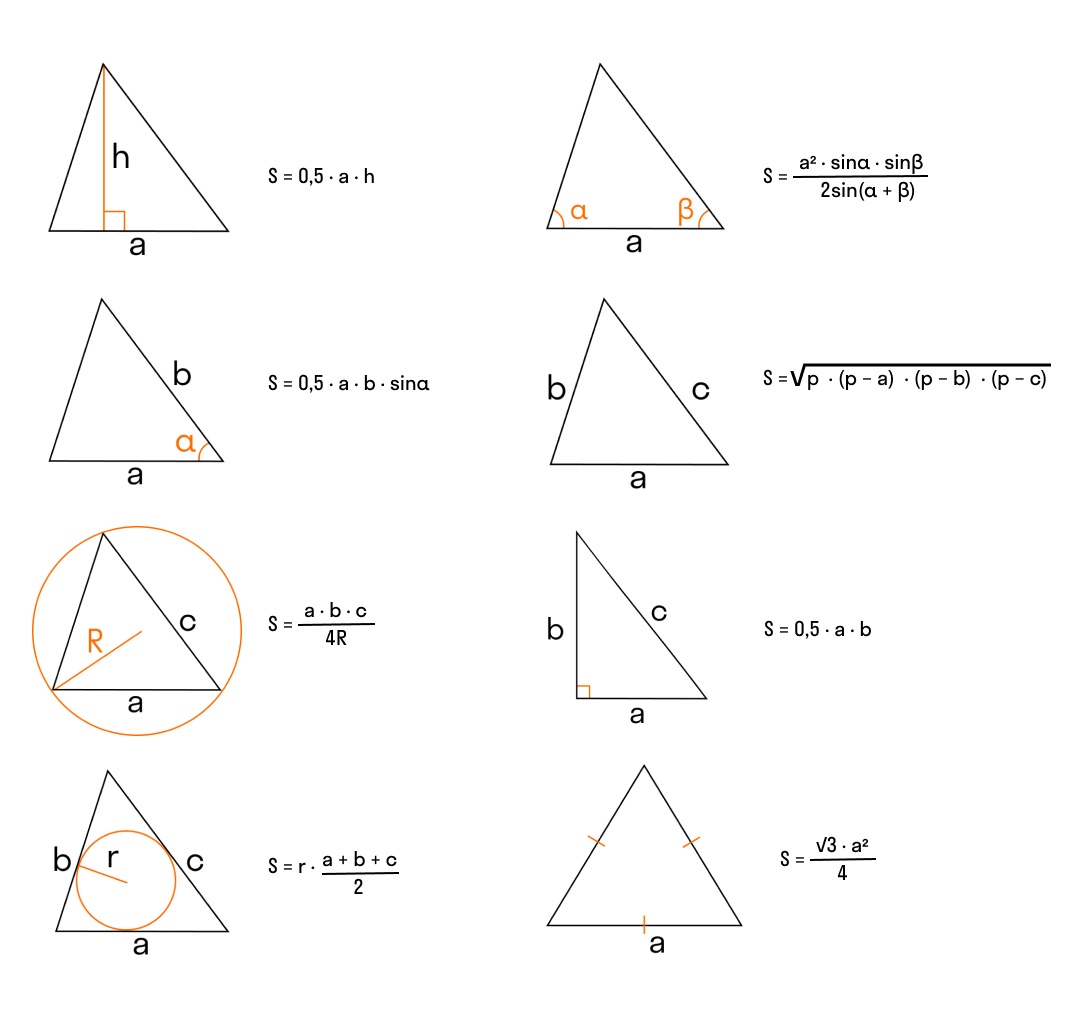
Формулы площади для любого треугольника
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними.
3. Площадь треугольника через описанную окружность и стороны
4. Площадь треугольника через вписанную окружность и стороны.
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Для прямоугольного треугольника
Для прямоугольного треугольника чаще всего используют одну формулу — половину произведения катетов. Потому что их всегда можно найти с помощью правил тригонометрии или теоремы Пифагора.
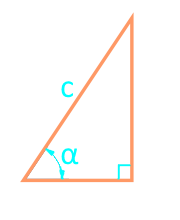
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
Площадь прямоугольного треугольника по формуле Герона
Для равнобедренного треугольника
Ниже мы покажем разные формулы для площади равнобедренного и равностороннего треугольника, их редко используют, но их легко вывести самому. Попробуйте сделать это самостоятельно.
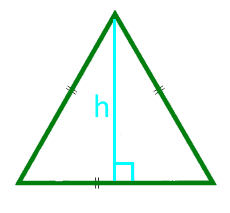
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними.
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
В задачах встречаются разные фигуры, и кажется, что нужны разные формулы. Но на самом деле, зная всего несколько формул для треугольника и пользуясь теоремами и свойствами геометрии, можно найти площадь любой фигуры.
Бесплатный онлайн-фестиваль для родителей
8 октября в 12:00
14 экспертов ответят на главные вопросы об обучении и воспитании детей
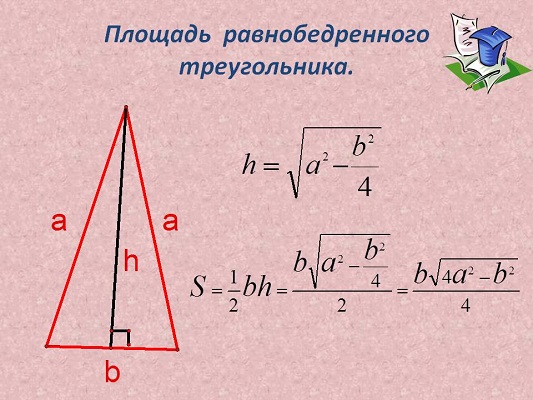
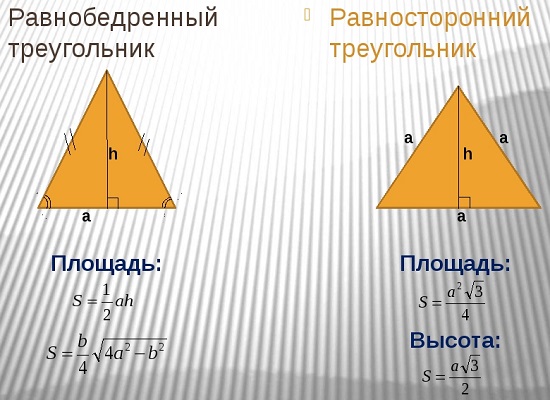
Площадь равнобедренного треугольника
Равнобедренный треугольник — это треугольник, в котором две стороны равны между собой по длине. Боковыми называются равные стороны, а последняя неравная им сторона — основанием.
Любой правильный (равносторонний) треугольник также является равнобедренным, но обратное утверждение неверно.
Используя этот онлайн калькулятор, вы сможете найти площадь равнобедренного треугольника, зная его сторону и основание.
Как найти площадь равнобедренного треугольника?
Далее приведены формулы нахождения площади равнобедренного треугольника: через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д.
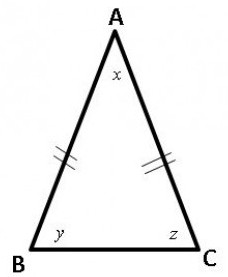
Обозначения, которые были применены в формулах на рисунке:
1. Площадь равнобедренного треугольника можно найти, зная его сторону и основание.
3. Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине.
4. Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны)
6. Шестая формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора.
Площадь равнобедренного треугольника: онлайн-калькулятор
Равнобедренным называется треугольник, у которого равны длины двух сторон. Для расчета площади используются значения длины двух неравных сторон a и b :
Площадь равнобедренного треугольника по формуле в онлайн-калькуляторе высчитывается просто. Для получения ответа:
Расчет площади равнобедренного треугольника онлайн-калькулятором предполагает получение подробного решения и не требует оплаты.
Как найти площадь равнобедренного треугольника с помощью онлайн-калькулятора
Для нахождения площади равнобедренного треугольника нужно знать значения его двух неравных сторон.
Рассмотрим пример нахождения площади равнобедренного треугольника с помощью онлайн-калькулятора. Пусть нужно найти площадь такого треугольника со сторонами 4 см и 5 см соответственно:
Площадь равнобедренного треугольника
Площадь равнобедренного треугольника — это часть плоскости, заключенной внутри данной геометрической фигуры.
Параметры для расчета
Рассчитать площадь можно с помощью нескольких способов. Для начала приведем обозначения, которые будут использоваться в последующих формулах.
Особенности вычислений, зная длину основания и высоту
Рассмотрим треугольник ABC. Если опустить из вершины В высоту, то мы получим два прямоугольных треугольника. Тогда \(S=\frac
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Задача
Боковая сторона равнобедренного треугольника ABC равна 13 см, а основание равно 10 см.
Найти: площадь равнобедренного треугольника.
Решение
Применим теорему Пифагора. Опустим из вершины B на основание AC высоту BK. Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна:
Высота с половиной основания и стороной образует прямоугольный ΔABK. В нем нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Тогда можно узнать высоту:
Площадь исходного ΔABC будет равна площади ΔABK и ΔCBK, образованных боковыми сторонами, высотой и половинами основания равнобедренного треугольника. Оба треугольника равны между собой. Гипотенузы — это стороны равнобедренного треугольника, поэтому они равны, один из катетов — общий, а поскольку BK одновременно является и биссектрисой, и высотой, то соответствующие углы тоже равны. Поэтому нам будет достаточно измерить площадь одного из них и умножить полученное число на два.
Применив формулу площади прямоугольного треугольника, получим:
Поскольку в составе ΔABC два равных ΔABK и ΔCBK, то общая площадь равнобедренного треугольника ABC составит:
Площадь равнобедренного треугольника по трём сторонам
Для нахождения S с помощью сторон, нужно воспользоваться формулой Герона:
Для этого равенства важно знать полупериметр:
Задача
Вычислить S ΔOMN, если OM=3 MN=3 NO=3.
Решение
Как посчитать, зная длину двух равных сторон и угол между ними
В таком случае S будет находиться, как половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами.
Полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту.
То есть формула будет такая же, как и в первом способе:
Задача
Найти: третью сторону.
Решение
Площадь треугольника равна половине произведения его сторон на синус угла между ними, то есть:
Отсюда находим, что6
Возможны два случая: \(\alpha=45^\circ\) или \(\alpha=135^\circ.\)
В каждом из них найдём третью сторону по теореме косинусов:
Следовательно, \(a=\sqrt<29>\) или \(a=\sqrt5.\)
Ответ: \(a=\sqrt<29>\) или \(a=\sqrt5.\)
Формула для расчета, зная длину основания и угол при основании
Тогда S рассчитывается как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами.
Если присмотреться, то станет очевидно, что половина основания, умноженная на tg, даст нам высоту треугольника. Поскольку высота в равнобедренном треугольнике является одновременно биссектрисой и медианой, то tg — это отношение половины основания к высоте \(\frac<<\displaystyle\frac12>b>h.\)
В итоге формула снова будет сведена к более простой:
Задача
В ΔABC AC=2, а \(\angle\alpha=45^\circ.\)
Решение
Подставим данные значения в формулу и получим:
Как посчитать площадь равнобедренного треугольника через одну сторону и прилежащие к ней углы
Если известна одна сторона треугольника и два прилежащих к ней угла, то площадь данного треугольника вычисляется, как половина квадрата данной стороны умноженная на дробь, в числителе которой, произведение синусов прилежащих углов, а в знаменателе синус угла, который лежит напротив.
Противолежащий угол можно сосчитать по формуле:
Тогда площадь будет равна:
Задача
В ΔCDE CE=4, \(\angle\alpha=45^\circ,\;\angle\gamma=45^\circ.\)
Решение
Так как сумма углов в треугольнике равна 180°, то чтобы найти оставшийся угол, нужно из 180° вычесть 45° и 45°.
Получим 90°. Следует вписать данные значения в формулу, и тогда мы получим:
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
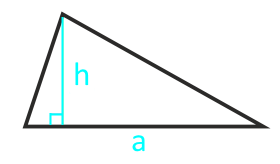
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
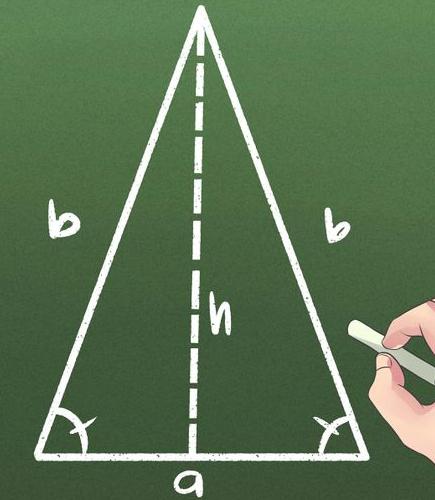
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Если известны три стороны и радиус описанной окружности
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Площадь равнобедренного треугольника
Вы будете перенаправлены на Автор24
В данной статье приведены различные формулы нахождения площади равнобедренного треугольника: через его основание и высоту, через основание и сторону, через равные стороны и угол и через основание и угол.
Также прилагаются различные калькуляторы для вычисления площади рб. треугольника.
Для тех, кто сомневается, нужна ли ему эта страница или другая, напомним определение равнобедренного треугольника:
Равнобедренный треугольник — это треугольник, 2 стороны которого равны.
Для того чтобы воспользоваться онлайн-калькуляторами, введите значения величин из вашей задачи в поля для ввода.
Рассмотрим подробно, как вычислить площадь равнобедренного треугольника.
Площадь равнобедренного треугольника, зная основание и высоту
$S = \frac12 \cdot AC \cdot h$, где
$AC$ — основание равнобедренного треугольника;
$h$ — высота равнобедренного треугольника (перпендикуляр, опущенный из угла, лежащего напротив основания).
Дано:
Как найти площадь равнобедренного треугольника
Формула
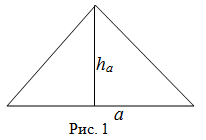
Чтобы найти площадь равнобедренного треугольника (рис. 1), необходимо вычислить произведение половины основания этого треугольника на его высоту:
Примеры вычисления площади равнобедренного треугольника
Решение. Искомая площадь равна произведению высоты на основание, деленному на два:
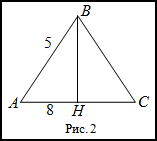
Задание. Найти площадь равнобедренного треугольника, боковая сторона которого равна 5 см, а основание 8 см.
Решение. Сделаем чертеж (рис. 2).
А тогда искомая площадь
Остались вопросы?
Здесь вы найдете ответы.
Обозначим через х катет имеющегося равнобедренного треугольника, имеющего прямой угол. В этом случае его площадь будет представлять собой ½ длины его катета, возведенную в квадратную степень. Это значит, что квадрат катета равен двум площадям треугольника (2S). В нашем случае это:
2S = 2*16 = 32 см кв.
Для того чтобы найти длину катета, нужно извлечь корень квадратный из числа 32:
Теперь можно высчитать длину гипотенузы, которая будет равна:
Ответ: Длина гипотенузы равна 8 см.
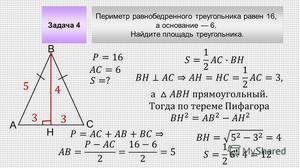
Дан треугольник АВС, в котором АВ=ВС и АС=32 см.
Проведем к основанию треугольника высоту ВН, также являющуюся медианой.
Площадь треугольника равна половине произведения длины его основания на высоту:
Из этой формулы можно выразить ВН:
Известно, что в равнобедренном треугольнике две стороны равны:
Теперь можно высчитать периметр (Р) треугольника АВС, который будет равен сумме длин его сторон:
Ответ: Периметр равнобедренного треугольника АВС равен 72 см.
Обозначим буквой х катет имеющегося треугольника. Тогда по теореме Пифагора:
12²=x² + x², что равно 144=2х²
Отсюда находим значение х:
Зная длину катета равнобедренного треугольника, можно найти его площадь (S):
S = √72 * √72/2 = 36 см кв.
Ответ: Площадь треугольника равна 36 см кв.
Разберемся с первым из треугольников. Так как он является равнобедренным, то оба угла при его основании будут равны. Зная о том, что сумма всех углов треугольника равна 180 градусом, мы можем найти третий угол треугольника, находящийся при его вершине:
Переходим ко второму треугольнику. Известно, что угол при его вершине равен 230 градусом. Исходя из этого можно рассчитать величины его углов, расположенных в основании фигуры:
Очевидно, что треугольники являются подобными на основании равенства углов.
Следует определить коэффициент подобия двух треугольных фигур. Квадрат коэффициента подобия будет равен отношению площадей треугольников:
Отсюда выражаем k:
Коэффициент подобия представляет собой отношение основания первой подобной треугольной фигуры ко второй. Это значит, что:
Ответ: Отношение оснований двух треугольников равно 7/4.
Площадь (S) треугольника с прямым углом составляет ½ часть произведения его катетов. Принимая во внимание тот факт, что треугольник является равнобедренным, можно утверждать, что длины его катетов равны. Их можно обозначить через х. В этом случае формулу для расчета площади треугольника можно записать в следующем виде:
Согласно теореме Пифагора, действительной для прямоугольного треугольника:
Подставим в формулу площади получившееся равенство:
Ответ: Площадь равнобедренного треугольника равна ¼с² см кв.
Площадь (S) любой треугольной фигуры рассчитывается путем деления пополам произведения длины его основания (с) и высоты (h):
Площадь каждого треугольника, в том числе и равнобедренного, рассчитывается как половина, взятая от произведения длины высоты треугольника и его основания. Формула имеет следующий вид:
Пусть а = 150 см.
Проводим высоту к основанию треугольника. Она же будет являться и медианой по той причине, что треугольник равнобедренный. В результате образовался треугольник с прямым углом и гипотенузой, длина которой равна 85 см. Один из катетов треугольника равен h, а второй рассчитывается как а/2:
Теперь можно рассчитать длину второго катета (на основании теоремы Пифагора):
Когда все необходимые для расчета площади треугольника величины известны, можно найти ее значение:
S=1/2 *a*h=1/2 *150*40=3000 см.
Вычислим длину боковой стороны равнобедренного треугольника, отняв от его периметра длину основания и разделив полученное число на 2:
Тогда площадь равнобедренного треугольника с заданными параметрами будет равна:
S=b/4*√(4a²-b²)=12*√(2704-2304)=12*20=240 cм кв.
К основанию равнобедренного треугольника проведем высоту, делящую его на две равные треугольные фигуры, каждая из которых имеет угол 90 градусов и катет длиной 12/2 = 6 см. Гипотенуза подобных треугольников имеет длину 10 см.
В случае с прямоугольным треугольником может быть применима теорема Пифагора, которая поможет найти катет, являющийся высотой треугольника:
Избавимся от квадратов:
Тогда площадь треугольника будет равна:
S = 12 * 8 : 2 = 48 см кв.
Введем условные обозначения, согласно которым х – это длина одного из катетов равнобедренного треугольника. В этом случае длина второго катета тоже будет равна х. Зная длину гипотенузы, можно записать формулу теоремы Пифагора для имеющегося треугольника:
Отсюда можем найти значение х:
Найдя длину катета равнобедренного треугольника, можно вычислить его площадь (S), равную ½ произведения длин его катетов:
S = √968*√968/2 = 484 см кв.
Располагая сведениями о длине основания (b) и стороны (a) треугольной фигуры с равными катетами, возможно рассчитать площадь (S) этой фигуры. С этой целью следует пользоваться приведенной ниже формулой:
Информация о длине боковых сторон (а) треугольной фигуры с катетами равной длины и размере угла (α), который образован этими катетами, позволит определить площадь этой фигуры. В этом поможет следующая формула:
Для расчета площади треугольной фигуры с катетами равной длины, при условии, что известна их длина (а), основание (b) и угол, который образован основанием и одним из катетов(α), используется следующая формула:
S = ½ * a * b * sin(α)
Примем неизвестную длину основания равнобедренного треугольника за х. В данном случае длина каждой из боковых сторон, которые в равнобедренном треугольнике равны, будет составлять (х-3). Известно, что периметр (Р) треугольника равен 30 см. Тогда:
Отсюда можно вывести х:
Ответ: Длина основания равна 12 см.
Примем х за длину основания равнобедренного треугольника. Тогда длина его боковой стороны будет составлять (х-15). Высота, проведенная в треугольнике с прямым углом, также представляет собой его медиану, которая делит его на две равных треугольных фигуры. Следует рассмотреть одну из образовавшихся треугольных фигур. Для начала вычислим ее основания, используя теорему Пифагора:
с2 = а2 + b2 = (15)²+(0,5x)²=(x-15)²
Из этого получается:
Очевидно, что сторона треугольной фигуры не может иметь длину, равную 0см. Поэтому можно сделать вывод о том, что ее длина составляет 40 см.
Для ответа на поставленный вопрос следует провести высоту из вершины того угла равнобедренного треугольника, который является противоположным его основанию. После этого длину проведенной высоты (а) нужно умножить на длину основания фигуры (b), а затем разделить полученное значение на два. Формула расчета площади треугольной фигуры, которая является равнобедренной, выглядит следующим образом:
S=a*b/2, или S=1/2a* b.
Вычислим половину длины основания данного равнобедренного треугольника:
Имеется треугольник с прямым углом и катетами, длины которых равны 1,2 см и 1,6 см. Требуется определить длину его гипотенузы. Ее можно вычислить, используя теорему Пифагора:
с² = 1,2² + 1,6² = 1,44 + 2,56 = 4
Осталось только извлечь корень квадратный из 4:
Ответ: Длина боковой стороны равнобедренного треугольника равна 2 см.
Известно, что углы, расположенные у основания равнобедренного треугольника, всегда являются острыми, иначе сумма всех трех углов превышала бы 180 градусов. Исходя из этого, можно сделать вывод о том, что тупой угол расположен у вершины данной треугольной фигуры.
Доказанным фактом является то, что та сторона фигуры, которая расположена напротив тупого угла, имеет большую длину, чем сторона, лежащая против острого угла треугольника. Это позволяет утверждать, что длина основания данного треугольника больше длины его боковой стороны. По причине того, что треугольная фигура является равнобедренной, и известны длины двух ее сторон (8 см и 14 см), можно говорить о том, что неизвестная сторона будет составлять 8 см или 14 см. Если предположить, что длина неизвестной стороны равна 14 см, тогда длина основания будет составлять 8 см, что невозможно, так как противоречит утверждению о расположении больших сторон напротив тупых углов. Это означает, что длина третьей стороны треугольника равна 8 см, а основание в данном случае составляет 14 см.
Для решения данной задачи следует воспользоваться теоремой Пифагора:
Отсюда можно выразить квадрат длины неизвестной стороны, который будет равен разности квадратов известной стороны и высоты:
Для того чтобы узнать длину основания равнобедренного треугольника, нужно извлечь корень квадратный из числа 400, а затем умножить полученное число на 2:
√400*2 = 20*2 = 40 см.
Ответ: Длина основания равнобедренного треугольника равна 40 см.
Площадь равнобедренного треугольника — формулы вычисления
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.
Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
b — размер основания;
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:
При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
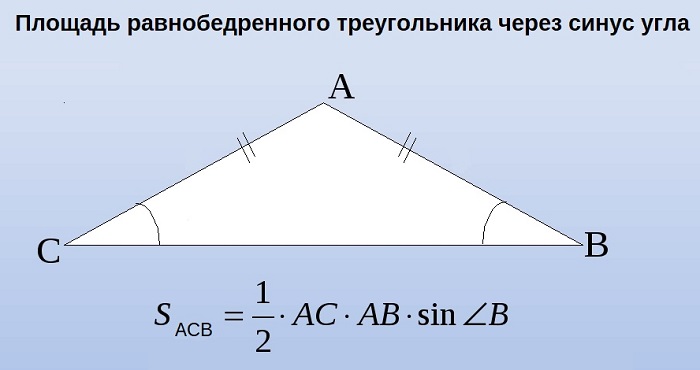
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:
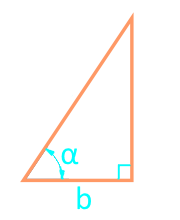
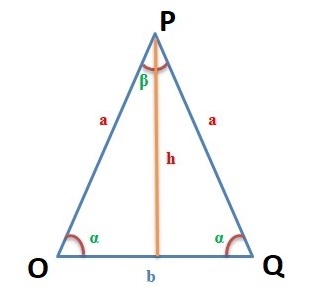
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 90 0 — угол OPQ.
SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Площадь равнобедренного треугольника важна для вычисления многих геометрических и математических задач. Например, определение площади любого многоугольника связано с его разделением на ряд треугольников и расчетом площади каждого из них.
Геометрическое тело, обладающее двумя равными сторонами и углами – есть частный случай простого разностороннего многоугольника.
Каждая из идентичных линий называется боковой, а третья – основанием.
Если в таком треугольнике опустить среднюю линию из его вершины на 3-ю сторону, то образовавшиеся два плоских тела будут идентичны (так как имеют все признаки подобия).
Площадь (S) фигуры с тремя углами возможно установить:
по двум сторонам и высоте;
через угол между двумя сторонами и величину одной из них;
по двум сторонам;
через синус противолежащего основанию угла;
зная синус прилежащего угла и др.
Площадь равнобедренного треугольника через высоту
Вычисление площади треугольника с использованием его высоты и параметров основания – самый актуальный вариант, на базе которого строятся многие другие методы решения.
У планиметрической фигуры с двумя тождественными углами и боковыми отрезками высота может рассматриваться, как медиана и биссектриса. То есть линия, проведенная из вершины, делит планиметрический объект на два эквивалентных прямоугольных треугольника.
И общая их площадь сводится к:
Требуется рассчитать S тупоугольного равнобедренного многоугольника. Его h=3 см, а длина b = 8 см.
Вычисления выглядят следующим образом:
Площадь равнобедренного треугольника через стороны
Найти S планиметрического тела с двумя одинаковыми чертами, зная их параметры, возможно.
Для этого необходима теорема Пифагора, формулы которой видны на картинке,
и формула для отыскания S через биссектрису S = ½ * b * h.
После проведения медианы к середине 3-его отрезка, в равнобедренном треугольнике образуются 2 единообразных плоских тела с h между 2-мя катетами.
Таким образом, используя свойство сторон прямоугольного треугольника, выводим формулу, которая показана на картинке:
При высчитывание S равностороннего треугольника это выражение примет другой вид. Сравнить формулы нахождения площади равностороннего и равнобедренного треугольников можно, взглянув на картинку:
У остроугольного равнобедренного треугольника даны габариты боковины b = 3 см и базиса a = 2 см. Надлежит найти его S:
Площадь равнобедренного треугольника через синус угла
В геометрии встречаются задания по отысканию площади многоугольника с тремя схожими краями через данный угол и длину прилегающей стороны.
В этой ситуации определение размера h будет осуществляться с использованием угла, прилегающего к измеренной грани. Таким образом выводится выражение, которое хорошо иллюстрирует следующая картинка:
Посмотрим на рисунок, приведенный выше. Известно, что ∠ACB фигуры 30 градусов, а величина его боковой стороны AC = AB равняется 4 см. Требуется вычислить её S.
Формула площади равнобедренного треугольника через тангенс угла
Как правило, в планиметрии нередко встречаются задания по нахождению S треугольника, в котором определено значение стороны и угол.
Разнообразные равенства для решения задач, в том числе и нахождения S через тангенс угла, можно увидеть ниже:
Прежде всего посмотрим, как найти нам требуемую величину и какую применить формулу. Остановим свой выбор на формуле нахождения площади S по тангенсу угла.
Зная, что у нас равнобедренный треугольник, у которого углы у основания равны, найдем третий угол:
180 — 45 — 45 = 90 0 — угол OPQ.
SOPQ = 5 2 /4 * tg 45° = 25/4 * 1 = 6, 25 см 2
Вот так, используя прежде всего знания о свойствах фигур, можно получать самые разнообразные способы вычисления той величины, какая требуется в задаче.
Как вычислить площадь равнобедренного треугольника

\(a\) — боковая сторона
\(\alpha\) — угол между боковыми сторонами

\(a\) — боковая сторона
\(\alpha\) — угол между основанием и ребром

\(\alpha\) — угол между боковыми сторонами
Формула Герона для равнобедренного треугольника

Площадь равнобедренного треугольника
Равнобедренным треугольником называется фигура с двумя равными сторонами. В этом случае третья сторона считается основанием, а равные стороны – боковыми.

Равнобедренный треугольник отличается следующими свойствами:
Существует множество способов нахождения площади равнобедренного треугольника. Для начала рассмотрим классический метод, для которого потребуется высота и основание. Зная эти параметры можно применить формулу площади равнобедренного треугольника:
То есть площадь равнобедренного треугольника равняется произведению высоты на половину длины основания.
| Высота треугольника = | Основание треугольника = |
| Ответ: Площадь треугольника= 10.000 | |
Также найти площадь можно по формуле площади через три стороны, или как еще говорят – формуле Герона. Во многих случаях это значение находится через радиус вписанной окружности.
Найти площадь фигуры через стороны, применив метод Герона, можно по этой формуле.
Это выражение можно преобразовать в сокращенную формулу:
Для вычислений можно использовать две равные стороны и угол между ними.
Площадь равнобедренного треугольника
Равнобедренным называется треугольник с равными боковыми сторонами. Боковыми считаются две равные стороны, а третья сторона — основанием. Если у треугольника все стороны равны, его называют правильным, он тоже является равнобедренным. Определить площадь треугольника можно, воспользовавшись другой формулой, через его стороны:
В данной формуле a и b — стороны треугольника, а S — его площадь.
Расчет площади равнобедренного треугольника, зная основание и сторону
Чтобы узнать пл. равнобедренного треугольника, высоту треугольника умножают на половину длины его основания, где b является основанием треугольника, а h — высота.
Подставив в формулу данные основания треугольника и его высоту, с помощью калькулятора онлайн вы легко сможете определить площадь заданного треугольника.
Как быстро найти площадь равнобедренного треугольника
Сегодня мы с вами поговорим о том, как найти площадь равнобедренного треугольника. Ведь это может понадобиться как студентам и школьникам, так и другим людям. В данной статье вы узнаете формулы и хитрости, с помощью которых можно найти площадь равнобедренного треугольника. Итак, поехали!
Как найти площадь равнобедренного треугольника
Давайте сначала освежим в памяти, что же такое равнобедренный треугольник? Это фигура, имеющая три угла и три стороны, две из которых имеют одинаковую длину.
Для нахождения площади равнобедренного треугольника достаточно знать длину его основания, и высоту. Если мы их знаем, то достаточно перемножить эти две величины. После чего, необходимо произведение этих двух величин разделить на два.
Чаще всего, в задачах школьной программы, какая-то из этих необходимых составляющих нам неизвестна. Давайте разберёмся более подробно с каждым из таких случаев.
Допустим, что нам неизвестна высота. Но нам известны длины всех сторон треугольника. Для нахождения высоты нам необходимо воспользоваться теоремой Пифагора. А именно извлечь квадратный корень из разности квадратов боковой стороны и половины основания. Когда высота станет нам известной, мы можем смело пользоваться формулой, о которой только что говорили выше.
Этот вариант чисто логический. До этого может додуматься далеко не каждый школьник. Да что уж греха таить, даже не каждый взрослый. Поэтому для того, чтобы не ломать голову, существует специальная формула для такого случая. Необходимо перемножить сумму и разность между боковой стороной и половиной основания. После чего, извлечь из этого произведения квадратный корень. А потом, получившийся результат умножить на половину основания. Теперь давайте поговорим о других возможных вариантах нахождения площади равнобедренного треугольника.
Варианты нахождения площади равнобедренного треугольника
Сейчас мы рассмотрим возможные варианты школьных задач, где требуется определить площадь, и расскажем как их решать:
Итак, вначале необходимо найти тангенс половины угла при вершине. Найти его мы можем, зная угол при основании. После того, как вы нашли этот тангенс, необходимо разделить квадрат основания на 4 тангенса, полученного угла. Полученный результат и будет являться площадью нашего равнобедренного треугольника.
А теперь мы вам объясним, как все получается. Основной момент — это понять и заметить, что произведение половины основания на тангенс половины угла при вершине даёт нам высоту треугольника, опущенную на основание. Когда мы перемножим значение этой высоты на основание, и разделим пополам, то определим площадь. Формула даётся именно в таком виде, чтобы расчёт производился одним коротким действием, вместо длительных расчётов.
Кстати, треугольник, у которого все стороны равны тоже считается равнобедренным. Его площадь определить очень легко. Высота ищется по теореме Пифагора, после чего умножается на длину основания, и делится на два.
Дополнительные рекомендации
Чтобы научиться быстро решать подобные задачи, необходимо делать следующее:
Взрослым также не рекомендуется забывать эти формулы. Иногда они пригождаются в реальной жизни при выполнении, например, ремонтных или хозяйственных работ.
Теперь вы знаете, как можно легко и просто найти площадь равнобедренного треугольника. В случае чего, вы можете помочь вашему ребёнку разобраться с этой темой, или решить домашнее задание.
Школьная геометрия — это очень легко. Поэтому рекомендуется посвятить два вечера решению большого количества подобных задач, и тогда, ваш ребёнок сможет решать их очень быстро.
Видео
В нашем видео вы найдете решение интересных задач о равнобедренных треугольниках.
Как найти площадь равнобедренного треугольника?
Чтобы найти площадь равнобедренного треугольника, надо половину его основания умножить на высоту, проведённую к этому основанию:
где S — площадь равнобедренного треугольника;
b — длина основания;
Чтобы найти площадь равнобедренного треугольника, достаточно его основание умножить на высоту, проведённую к этому основанию. Вообще, это очень простая задача и её решение также можно вывести из теоремы Пифагора.
Произвести вычисление площади равнобедренного треугольника можно используя следующий формулы.
Формулы вычисления площади равнобедренного треугольника:
Вычислить площадь равнобедренного треугольника онлайн можно здесь.
Площадь треугольника
Теперь вам не нужно тратить время на долгие вычисления, прежде чем вы сможете узнать площадь треугольника. Зная методы расчета, используемые для расчета площади треугольника, вы легко сможете это сделать самостоятельно. Действительно, всегда лучше знать формулы площади треугольника. Треугольники могут быть разными и вы это знаете, но как найти площадь треугольника если вам практически ничего неизвестно о треугольнике? И что нужно знать из размеров треугольника, чтобы найти его площадь. Давайте разбираться. При этом тема не так проста как кажется на первый взгляд, наверное, поэтому задачи нахождения площади треугольника есть и в ОГЭ и в ЕГЭ по математике.
Что такое треугольник
Треугольник — это геометрическая фигура. По определению, это многоугольник, имеющий три стороны. Следовательно, треугольник также должен иметь три угла.
Сумма трех углов треугольника должна быть равна 180°.
Чтобы иметь возможность вычислить площадь треугольника, мы должны сначала знать меру его основания, а также высоту. Основание треугольника представляет одну из его сторон. Высота, с другой стороны, представляет собой каждую из трех прямых линий, которые проходят через одну из вершин треугольника и перпендикулярны стороне, лежащей напротив принятой вершины (то есть перпендикулярно основанию).
Прежде всего, помните, что треугольник состоит из трех сторон и трех углов. Это значит, что у него должно быть три вершины. Треугольник, вершинами которого являются A, B и C, может быть представлен как: ΔABC. Существуют разные виды треугольников. Они могут быть классифицированы двумя различными способами: либо по свойству его сторон, либо по свойству его углов.
Различные типы треугольников в зависимости от длины их сторон
Разносторонний треугольник
Мы узнаем разносторонний треугольник по трем сторонам, которые имеют разную длину. Эта треугольная форма может быть построена только с тремя разными углами. Кроме того, один из них может быть прямым углом (или углом 90 °). В общем, название «произвольный треугольник» используется для разностороннего треугольника.
Равнобедренный треугольник
Мы говорим, что треугольник равнобедренный, если он имеет две стороны одинаковой длины и два равных угла при основании. Равнобедренный треугольник также можно узнать по тому факту, что его высота представляет его ось симметрии, его медиану и биссектрису.
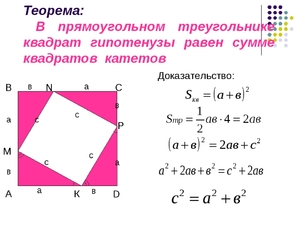
Прямоугольный треугольник
Прямоугольный треугольник обязательно имеет прямой угол. Другими словами, сумма двух других его углов должна быть равна 90°. Прямоугольный треугольник также имеет гипотенузу.
Это противоположная сторона вершине с прямым углом. Прямой треугольник может быть разносторонним (или любым), если его три стороны имеют разную длину.
Кроме того, он может быть равнобедренным в том случае, если он имеет два одинаковых катета.
Равносторонний треугольник
Треугольник называется равносторонним, если он имеет три стороны одинаковой длины. Поэтому все его углы также равны и каждый по 60°. В равностороннем треугольнике любая высота также выступает в качестве медианы и биссектрисы.
Площадь треугольника
Площадь разностороннего треугольника
Вычисляем площадь треугольника без особенностей — все его стороны разные и все углы разные.
Если известны две стороны треугольника и угол между ними, то площадь разностороннего треугольника вычисляется по формуле «площадь треугольника через две стороны и угол между ними»:
Если известны высота в треугольнике и основание, то используется формула площади треугольника через основание и высоту:
Формула Герона определения площади треугольника
Если известны стороны любого треугольника, то его площадь можно определить по формуле Герона.
, где
Площадь равнобедренного треугольника
Площадь треугольника через основание и сторону можно найти, если известны сторона и основания равнобедренного треугольника.
К равнобедренному треугольнику также применима формула площади треугольника через основание, сторону и угол между ними:
Найти площадь равнобедренного треугольника можно также через боковые стороны и угол между ними.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами:
Площадь прямоугольного треугольника
Приведем формулы площади прямоугольного треугольника. Формула площади прямоугольного треугольника через катет и прилежащий угол:
Площадь прямоугольного треугольника по радиусу вписанной окружности и гипотенузе
Площадь прямоугольного треугольника, если в него вписана окружность:
Площадь равностороннего треугольника
Площадь равностороннего треугольника можно найти через радиус описанной окружности.
Если дан радиус вписанной окружности, то площадь равностороннего треугольника можно найти по формуле:
Площадь равностороннего треугольника, если известна высота треугольника:
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь треугольника
Необходимость вычисления площади различных фигур, в том числе и треугольных, возникла за несколько веков до нашей эры. Над этим задумывались ученые и астрономы Древнем Египте.
В жизни иногда встречаются ситуации, когда требуется искать в закромах памяти знания из далеких школьных лет: подошла очередь ремонта в доме и нужно рассчитать количество необходимого материала, или потребовалось узнать площадь земельного участка в виде треугольника.
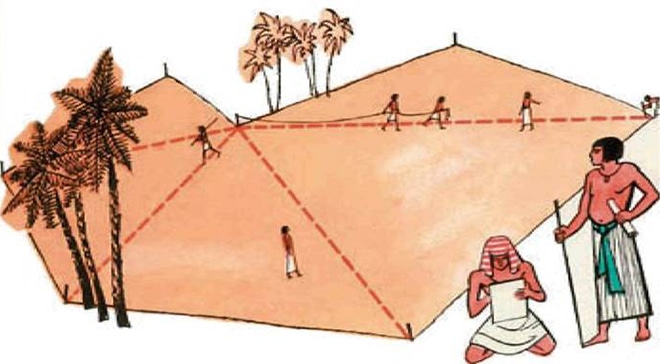
Человеческая память не может сразу воспроизвести убранные за ненадобностью школьные знания, что вполне естественно. Поэтому здесь собраны основные методы для расчета площади большинства видов треугольника.
Вычислить площадь треугольника можно различными вариантами, применяя определенные формулы. Методы расчета зависят от типов треугольных фигур и от того, какие вычислительные данные известны.
Треугольник: определение и виды фигуры
Из курса геометрии известно, что треугольник представляет собой многоугольную фигуру, которая имеет три лежащие на разных линиях точки, соединенные между собой отрезками. Размер площади треугольника выражается количеством заключенных в ней квадратных единиц и представляет собой положительное число, которое показывает размер фигуры, в части поверхности, ограниченной тремя отрезками в замкнутый контур.
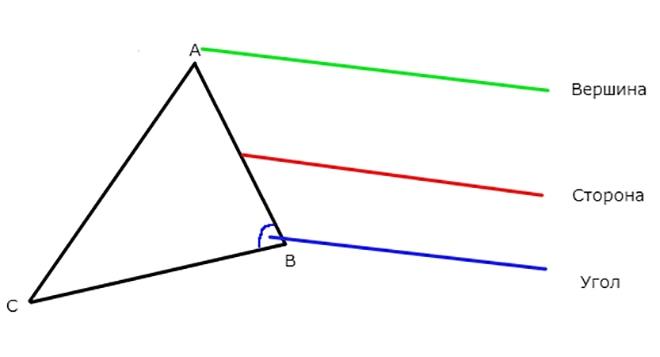
В зависимости от длины сторон и величины угла выделяется несколько разновидностей треугольников:
Для расчета площади каждого типа треугольной фигуры используется специальная формула.
Как вычислить площадь треугольника?
Классические формулы расчета площади треугольных фигур соотносятся с видами треугольников. Приведенные ниже формулы определения площади произвольного треугольника подойдут для установления площади, вне зависимости от его характеристик, углов или размеров.
Прямоугольный треугольник
Прямоугольный треугольник характеризуется наличием прямого угла. Две его стороны, образующие этот угол носят название катетов. Противоположная прямому углу сторона треугольника именуется гипотенузой.
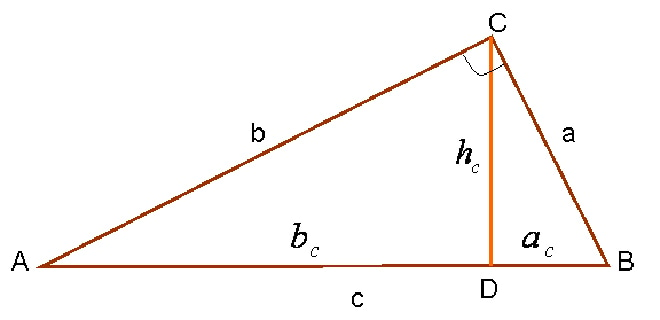
Основная формула расчета площади прямоугольного треугольника основывается на значениях катетов фигуры.
где a, b – катеты треугольника.
Вычислить площадь прямоугольного треугольника можно по другой формуле, где за основу берется величина гипотенузы и высота, проведенная к ней.
где c – гипотенуза, hc – высота, проведенная к гипотенузе.
Равнобедренный треугольник
В равнобедренном треугольнике две боковые стороны равны по значению, отличающаяся размерами сторона называется основанием.
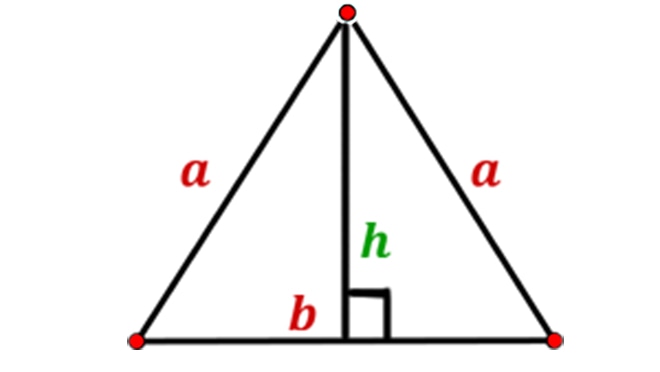
Площадь равнобедренного треугольника рассчитывается по формуле:
где а – равные стороны треугольника, b – основание.
Равносторонний треугольник
Частным случаем равнобедренного треугольника является равносторонний, отличающийся тем, что все стороны и углы фигуры равны по значению.
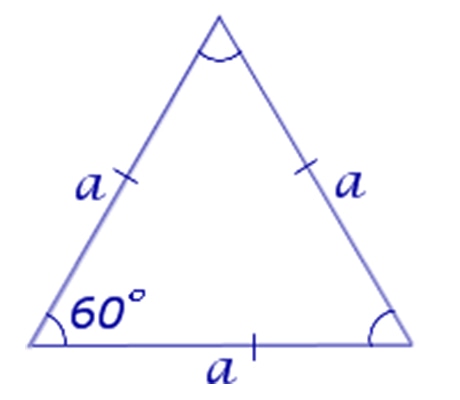
Площадь равностороннего треугольника определяется по формуле:
где a – сторона равностороннего треугольника.
Определение площади треугольника с неизвестными данными
Классические формулы расчета площади треугольника могут выручить не всегда. Существует ряд ситуаций, когда неизвестны необходимые для подстановки в формулу величины. При этом используют другие методы для расчета площади треугольника, напрямую зависящие от того, какие данные известны. Все варианты предусматривают конкретную формулу и определенный порядок проведения расчетов.
Известны основание и высота
Площадь треугольника определяется как половина произведения высоты фигуры и длины основания, то есть той стороны треугольника, к которой проведена высота.
где b – длина основания; h – высота.
Известны величины трех сторон
Площадь треугольника рассчитывается по формуле Герона. Для облегчения формулы метод предусматривает предварительный расчет величины полупериметра.
где p – величина полупериметра; a, b, c – значения длины сторон треугольника.
Известны две стороны и угол между ними
Площадь треугольника рассчитывается как произведение двух сторон, умноженное на синус угла, расположенного между этими сторонами. Угол – геометрическая фигура, полученная из двух лучей, исходящих из одной точки (вершины угла).
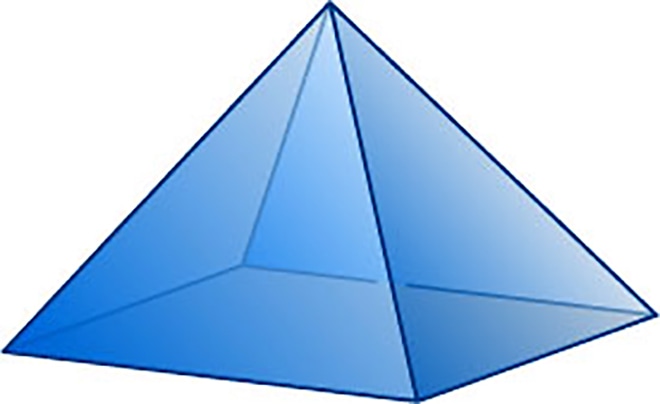
где a, b – стороны треугольника, C – угол между сторонами.
Известны одна сторона и прилежащие к ней углы
Площадь подобного треугольника равна половине квадрата известной стороны, умноженной на дробь, с числителем, выражающим произведение синусов прилежащих углов, и знаменателем, указывающим синус противолежащего угла.
Известны радиус вписанной окружности и полупериметр
Площадь треугольника определяется как произведение радиуса вписанной окружности на его полупериметр. Окружность называется вписанной, если имеет одну общую с многоугольником точку с каждой стороны фигуры. Центральная точка вписанной в треугольник окружности всегда располагается в точке, где пересекаются биссектрисы его внутренних углов.
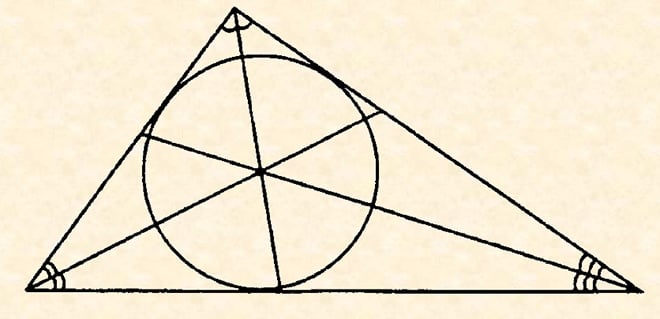
S = p * r, где p – полупериметр треугольника, r – радиус вписанной окружности.
1. Полупериметр определяется как половина суммы всех сторон треугольника по формуле:
где a, b, c – стороны треугольника.
2. Перемножаются полупериметр треугольника и радиус вписанной окружности.
Известны радиус описанной окружности и периметр
Треугольник называется описанным вокруг окружности, если его стороны соприкасаются с кругом, а сам он находится снаружи. Площадь треугольника определяется как половина произведения периметра треугольника и радиуса описанной окружности.

где r – радиус описанной окружности, a, b, c – стороны треугольника.
Знание формул вычисления площади треугольника поможет при определении площади объемных фигур, в основе граней которых лежат треугольные фигуры, таких, как например, пирамида.
Как найти площадь равнобедренного треугольника?
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь, нужно решать задачи и примеры, чертить схемы и рисунки, доказывать теоремы.
Путь к пониманию геометрии лежит через решение задач. Отличным примером могут служить задания, в которых нужно найти площадь равнобедренного треугольника.
Что такое равнобедренный треугольник, и в чем его отличие от других?
Чтобы не пугаться терминов «высота», «площадь», «основания», «равнобедренного треугольника» и прочих, потребуется начать с теоретических основ.
Сначала о треугольнике. Это плоская фигура, которая образована из трех точек — вершин, в свою очередь, соединенных отрезками. Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.
Существует частный случай равнобедренного треугольника — равносторонний, когда и третья сторона равна двум боковым.
Свойства фигуры
Они оказываются верными помощниками в решении задач, которые требуют найти площадь равнобедренного треугольника. Поэтому знать и помнить о них необходимо.
Как в задаче распознать равнобедренный треугольник?
Если при решении задания встает вопрос о том, как найти площадь равнобедренного треугольника, то сначала нужно понять, что он относится к этой группе. А в этом помогут определенные признаки.
Обозначения величин, принятые в рассматриваемых формулах
Для упрощения того, как находить площадь равнобедренного треугольника по формулам, введена замена его элементов на буквы.
| Буква в формуле | Название |
| а | боковая сторона |
| в | длина основания |
| н | высота к основанию |
| А | угол при основании |
| В | величина угла, лежащего между боковыми сторонами |
| общепринятое обозначение | площадь |
Внимание! Важно не путать «а» с «А» и «в» с «В». Это разные величины.
Формулы, которыми можно воспользоваться в разных задачах
Известны длины сторон, и требуется найти площадь равнобедренного треугольника.
В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Пусть она будет записана под №1.
Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.
Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:
Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.
Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:
В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.
Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Порядковый номер формулы — 4.
В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.
Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:
Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.
Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:
Примеры задач
Совет: как полюбить математику
Решая задачи по геометрии и определяя, как найти площадь равнобедренного треугольника, можно получить неоценимый опыт. Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.
Площадь равнобедренного треугольника

Средняя оценка: 4.6
Всего получено оценок: 240.
Средняя оценка: 4.6
Всего получено оценок: 240.
В 7 классе в курсе математики изучаются различные виды треугольников, в том числе и равнобедренный. Равнобедренный треугольник — это треугольник у которого равны две стороны, называемые боковыми, и третья сторона называется основанием: в равнобедренном треугольнике углы при основании равны. Что такое площадь равнобедренного треугольника, по какой формуле необходимо производить расчеты – об этом говорим в статье.
Определение
Треугольник это фигура, состоящая из трех, соединенных между собой точек. Элементами треугольника являются три стороны и три угла. Сумма углов в треугольнике всегда равна 180 градусам.

Треугольник может быть:
В равнобедренном треугольнике медиана, проведенная к основанию, совпадает с основанием и высотой. Именно это свойство мы и будем использовать при нахождении специализированной формулы площади равнобедренного треугольника.
Формула площади равнобедренного треугольника
Выведем формулу площади равнобедренного треугольника. Существует два варианта равнобедренного треугольника: через боковую сторону и основание или по классической формуле.
Классическая формула это простейший вариант. Площадь любого треугольника равна половине произведения основания на высоту. И равнобедренный треугольник не исключение:
$S=<1\over<2>>*a*h$, где а – основание треугольника, а h – высота, проведенная к этому основанию.
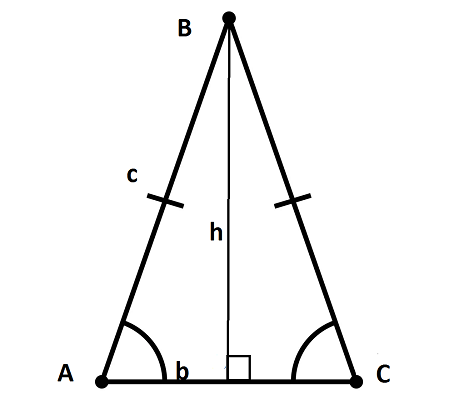
Существует формула через боковую сторону и основание. Для того, чтобы вывести ее обратим внимание на рисунок.
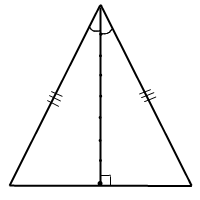
Обозначим высоту буквой h, боковую сторону а, основание в. Тогда высоту можно найти, как катет получившегося прямоугольного треугольника через теорему Пифагора:
Получившуюся формулу подставим вместо высоты и получим специальную формулу для равнобедренного треугольника:
Можно найти площадь через угол, как половину произведения синуса угла между сторонами на эти стороны.
Подобный способ, когда равнобедренный треугольник рассматривают, не как целую фигуру, а как два равных между собой прямоугольных треугольника, часто используют для вычислений. Эти треугольники получаются в результате проведения высоты к основанию равнобедренного треугольника. Важно понимать, что в равнобедренном треугольнике только высота, проведенная к основанию, имеет специфические свойства.
Что мы узнали?
Из статьи мы узнали, что площадь произвольного треугольника можно легко найти, подставив в формулу значение высоты и основания, к которому опустили эту высоту. Однако нужно учитывать тип треугольника. Для равнобедренных, равносторонних и прямоугольных треугольников можно упростить нахождение площади, воспользовавшись специфическими треугольниками.
Калькулятор расчета площади треугольника
Площадь треугольника можно найти, если известны:
Предлагаем простой и удобный калькулятор для расчета площади треугольника в режиме онлайн. Он может оказаться полезным не только для школьников, изучающих базовый курс геометрии, но и для строителей, дизайнеров, архитекторов и многих других специалистов, чья работа так или иначе связана с проектированием и изготовлением различных инженерных конструкций. Вы можете посчитать площадь произвольного треугольника, зная основные размеры, однозначно определяющие его конфигурацию.
Формула расчета площади треугольника по стороне и высоте, проведенной из противолежащей вершины
Зная длину одной из сторон треугольника (основания) и высоту, проведенную к этой стороне, его площадь можно посчитать, перемножив эти величины друг на друга и разделив результат на 2. То есть площадь треугольника — это полупроизведение основания на высоту. Это наиболее известная формула, она применима к любым треугольникам.
Площадь треугольника по трем сторонам, формула Герона
Одна из самых полезных на практике формул, незаслуженно обойденная вниманием во многих популярных источниках. Она позволяет рассчитать площадь треугольника, зная длины трех его сторон. В реальных условиях очень часто трудно провести измерения углов или каких-то линейных размеров конструкций, требующие дополнительных геометрических построений. Что же касается сторон, то они, как правило, или известны, или относительно легко поддаются измерению, поэтому площадь треугольника во многих случаях рассчитывают именно этим способом.
Для определения площади необходимо рассчитать полупериметр треугольника — сумму его сторон, деленную на 2. Далее из него поочередно вычитают длину каждой стороны, а результаты перемножают. Затем полученное значение умножают на полупериметр и из итогового числа извлекают квадратный корень. Это довольно сложный расчет, но с помощью нашего калькулятора вы проделаете его всего за несколько мгновений, введя длины сторон треугольника в предназначенные для этого поля.
Как рассчитать площадь треугольника, если известны две стороны и угол между ними
Эта формула также имеет широкое практическое применение. Например, с ее помощью можно посчитать площадь треугольного фронтона в доме с двускатной крышей. Угол наклона скатов и их длины обычно известны, их достаточно подставить в формулу и получить результат. Наш онлайн-калькулятор сделает это для вас моментально. Алгоритм расчета следующий: площадь треугольника вычисляется как половина произведения длин известных сторон на синус угла, который находится между ними.
Формула площади треугольника по его известной стороне и двум прилежащим углам
Наш калькулятор посчитает площадь треугольника и по этим параметрам. В расчете применяется довольно громоздкая формула, использовать которую при ручном подсчете довольно затруднительно. Поэтому, если вы знаете только эти характеристики треугольника, открывайте нужную вкладку и вводите значения в соответствующие поля калькулятора. Это поможет вам сэкономить время и избежать ошибок, исправлять которые будет сложно и дорого.
Как найти площадь треугольника по его периметру и радиусу вписанной окружности
Если вы знаете длины всех сторон треугольника, лучше использовать приведенную выше формулу Герона. Но если известен только полный периметр (сумма сторон, а не длины каждой из них по отдельности), площадь можно рассчитать как произведение радиуса вписанной окружности на половину периметра. Дизайнеры и проектировщики довольно часто помещают в треугольные фигуры круглые детали, при этом радиусы окружностей обычно бывают известны.
Формула площади произвольного треугольника по трем сторонам и радиусу описанной окружности
Радиус описанной окружности — избыточный параметр. Если длины всех трех сторон треугольника известны, его площадь определяется по формуле Герона. Тем не менее есть возможность несколько упростить расчет: нужно перемножить длины сторон друг на друга и разделить результат на учетверенный радиус описанной окружности. Наш онлайн-калькулятор при необходимости вычисляет площадь фигуры и по этой формуле.
Расчет площади прямоугольного треугольника
Площадь равнобедренного треугольника
Формулы для равностороннего треугольника
Если у треугольника все стороны равны, вычисление его площади еще больше упрощается. Достаточно знать длину стороны a или измерить радиус вписанной окружности r. Калькулятор использует одну из следующих формул:
В основе расчета площади треугольника во всех случаях лежит довольно простая математика. Но при этом часто требуется вычислять тригонометрические функции, радикалы и произведения больших чисел. Поэтому самое простое решение — снять все необходимые размеры и воспользоваться нашим калькулятором. Это быстро, точно и бесплатно. Никаких ограничений на количество расчетов и требований по авторизации у нас нет. Если у вас появятся вопросы, вы можете задать их в комментариях.
Формула площади равнобедренного треугольника
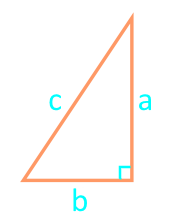
Площадь равнобедренного треугольника ABC (рис 1) с боковой стороной a и основанием b можно вычислить, используя следующие формулы:
1. Полупроизведение стороны на высоту, проведенную к этой стороне:
2. Площадь равна квадрату боковой стороны на синус угла при вершине:
3. Так как полупериметр равнобедренного треугольника равен
то в этом случае формула Герона примет вид:
4. Через радиус описанной окружности:
где \(R\) – радиус описанной окружности.
5. Через радиус вписанной окружности и полупериметр:
где r – радиус вписанной окружности.
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
О сайте
На нашем сайте вы найдете множество полезных калькуляторов, конвертеров, таблиц, а также справочных материалов по основным дисциплинам.
Самый простой способ сделать расчеты в сети — это использовать подходящие онлайн инструменты. Воспользуйтесь поиском, чтобы найти подходящий инструмент на нашем сайте.
calcsbox.com
На сайте используется технология LaTeX.
Поэтому для корректного отображения формул и выражений
пожалуйста дождитесь полной загрузки страницы.
© 2022 Все калькуляторы online
Копирование материалов запрещено
Площадь равнобедренного треугольника
Площадь равнобедренного треугольника — это число, характеризующее равнобедренный треугольник в единицах измерения площади.
Равнобедренный треугольник — это треугольник у которого равны две стороны, называемые боковыми, и третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны.
[править] Обозначения
b — боковая сторона;
ha — высота, опущенная на сторону a;
α — угол напротив стороны a;
p — полупериметр треугольника;
r — радиус вписанной окружности;
R — радиус описанной окружности;
SравнобедрΔ — площадь равнобедренного треугольника.
[править] Формулы
[править] Другие многоугольники
Персональные инструменты
Пространства имён
Варианты
Просмотры
Действия
Поиск
Навигация
Инструменты
Текст страницы доступен по условиям лицензии GNU Free Documentation License. Материалы могут быть скопированы при условии указания активной ссылки на источник копирования в теле статьи (на той же странице). В отдельных случаях могут действовать условия лицензии Creative Commons Attribution-ShareAlike (CC BY-SA 3.0), информацию об этом можно просмотреть на странице обсуждения или в истории правок. В частности, условия лицензии CC BY-SA 3.0 действуют в отношении статей, перенесенных из Википедии (указание на факт переноса всегда есть в истории правок статьи или на ее странице обсуждения).
В текстах могут упоминаться организации, признанные на территории Российской Федерации террористическими и/или в отношении которых судом принято вступившее в законную силу решение о запрете деятельности — см. полный список, а также деятельность которых запрещена по решению суда — см. полный список.
Площадь треугольника — все формулы, калькулятор онлайн
Площадь треугольника — это численная характеристика, показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц. В зависимости от типа треугольника и известных исходных данных, площадь треугольника можно рассчитать по различным формулам. Приведенные калькуляторы площади треугольника используют все известные методики и упрощают процесс вычислений.
Треугольник — это геометрическая фигура, образованная соединением отрезков трех точек, не лежащих на одной прямой. Точки называются вершинами треугольника, а отрезки — его сторонами.
Площадь треугольника — калькуляторы для всех видов
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными. Рассмотренные в данном пункте калькуляторы и формулы подходят для всех видов треугольников.
Зная сторону треугольника (основание) и высоту проведенную к основанию, можно найти его площадь. Площадь треугольника будет равна половине произведения основания на высоту. Основанием треугольника может быть выбрана любая из сторон треугольника.
Площадь треугольника по основанию и высоте — калькулятор онлайн:











































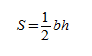
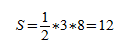
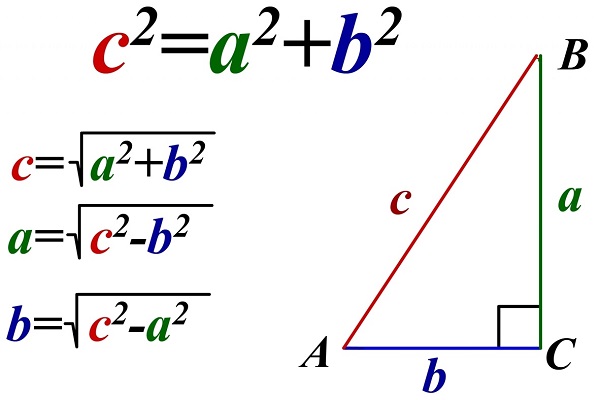
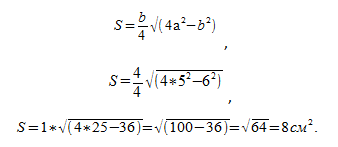
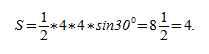
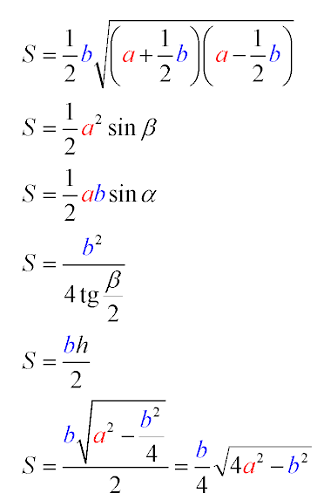
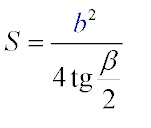



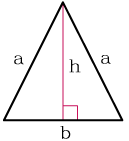
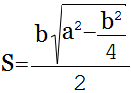











 , где
, где