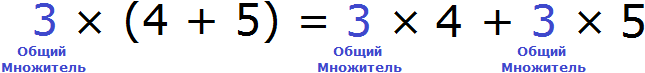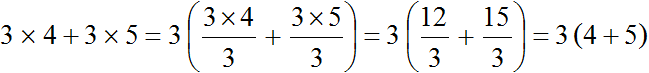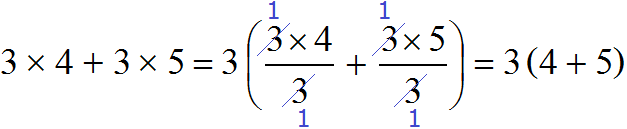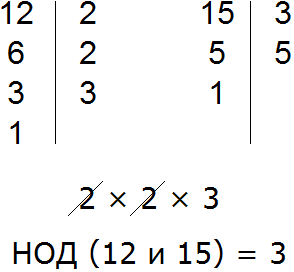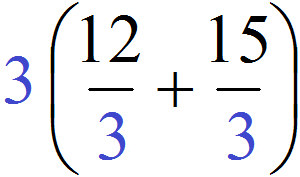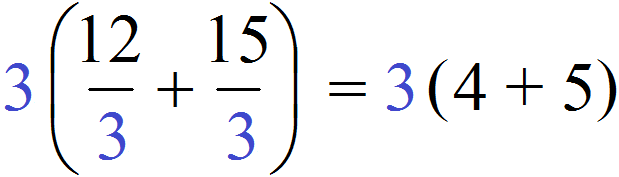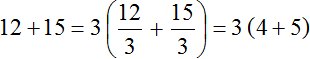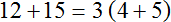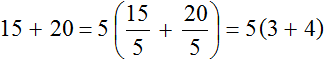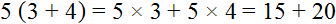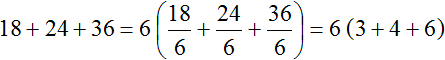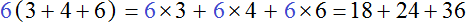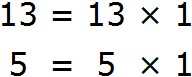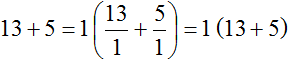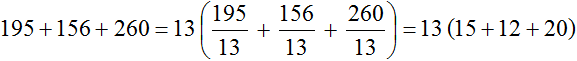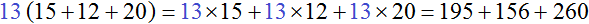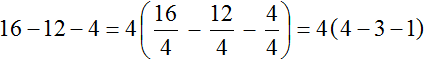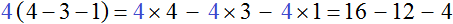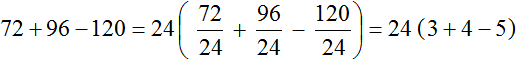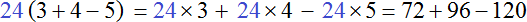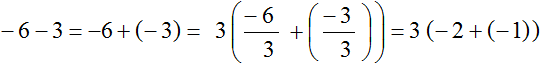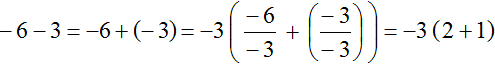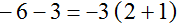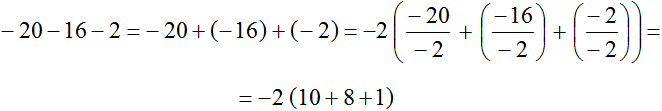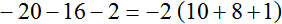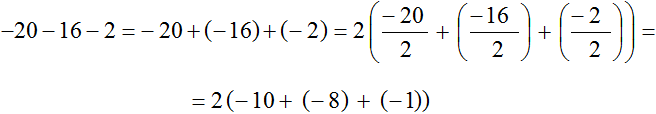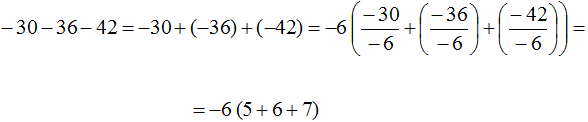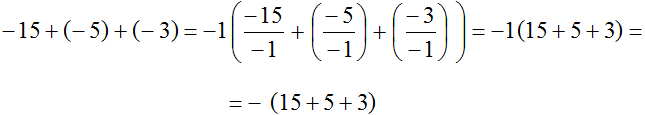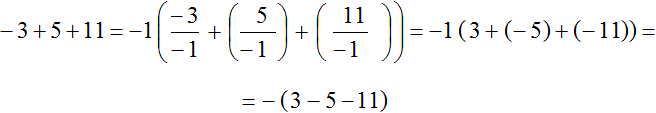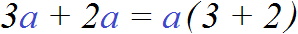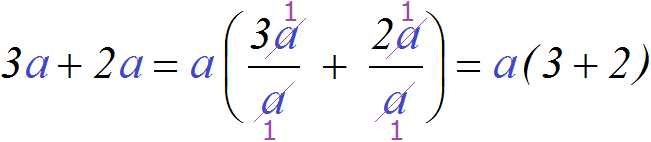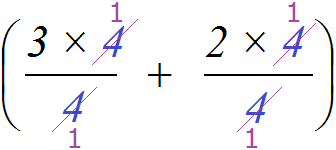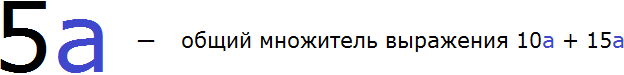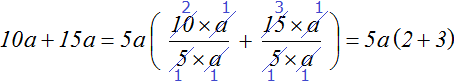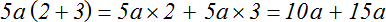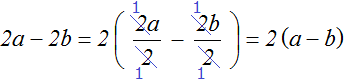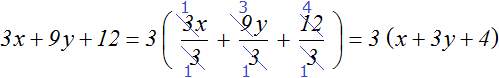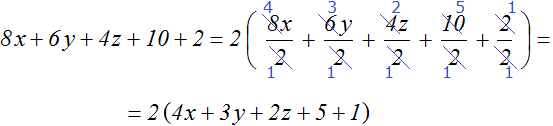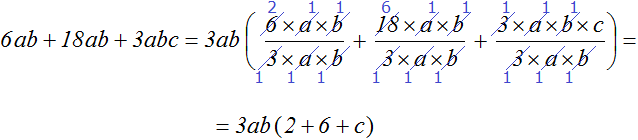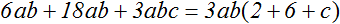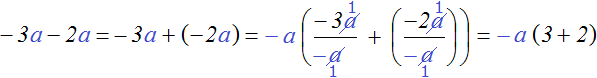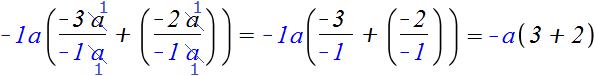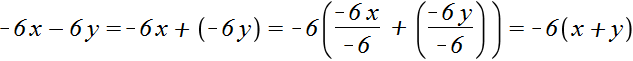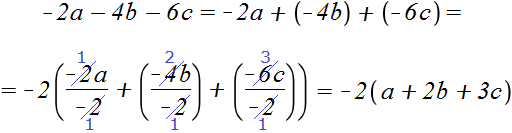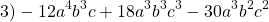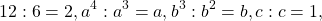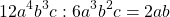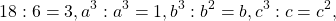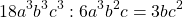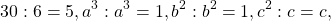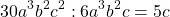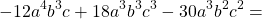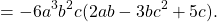Как выносить общий множитель за скобки
Как выносить общий множитель за скобки
Вынесение общего множителя за скобки
5 класс, 6 класс, 7 класс
Понятие вынесения множителя за скобки
Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.
Есть несколько способов разложения многочлена на множители. Один из них — вынесение общего множителя за скобки.
Вынести общий множитель за скобки можно в выражениях, которые представляют из себя суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один одинаковый для всех множитель. Он так и называется — общий множитель.
Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево.
Формула вынесения общего множителя за скобки:
Покажем метод вынесения общего множителя за скобки на примере с цифрами:
Определение общего множителя для всех членов многочлена производится пошагово:
Если нам дано произведение 6 · 2 и 6 · 5, то мы можем вынести за скобки общий множитель 6. В чем состоит данное преобразование? Мы представляем исходное выражение как произведение общего множителя и выражения в скобках, которое содержит сумму всех исходных слагаемых, кроме общего множителя.
Итак, вынесем общий множитель 6 в 6 · 2 и 6 · 5 и получим 6 · (2 + 5).
Итоговое выражение — это произведение общего множителя 6 на выражение в скобках, которое является суммой исходных слагаемых без 6.
Так и получается: 6 · 2 + 6 · 5 = 6 · (2 + 5).
Правило вынесения общего множителя за скобки
Чтобы вынести за скобки общий множитель, нужно записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Алгоритм вынесения общего множителя за скобки:
Важно! В скобках должно быть столько одночленов, сколько их было в многочлене.
Это и есть итог нашего преобразования. Запись всего решения выглядит так:
Определить сразу, какой множитель является общим, получается не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Вынесение минуса за скобки
Еще один случай, на котором следует обратить внимание — это вынесение за скобки минуса. Только мы выносим не сам знак, а минус единицу. Часто это помогает упростить выражение и сделать его проще.
Чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые с противоположными знаками:
Найдем решение для каждого выражения:
Поэтому между выражениями можно поставить знак равенства, потому что они равны одному и тому же значению:
Ставим минус и рядом в скобках записываем выражение с противоположным знаком у каждого слагаемого:
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица.
Вынесение общего множителя за скобку
Вынесение общего множителя – один из основных способов разложения на множители. По сути является действием обратным раскрытию скобок.
Главное правило вынесения за скобку:
Выносить за скобку можно только те множители, которые есть во всех слагаемых (одночленах).
К примеру, в выражении \(3ab+5bc-abc\) за скобку можно вынести только \(b\), потому что лишь оно есть во всех трех слагаемых. Процесс вынесения общих множителей за скобку представлен на схеме ниже:
Правила вынесения за скобки
В математике принято выносить сразу все общие множители.
Пример: \(3xy-3xz=3x(y-z)\)
Обратите внимание, здесь мы могли бы разложить и вот так: \(3(xy-xz)\) или так: \(x(3y-3z)\). Однако это были бы неполные разложения. Выносить надо и тройку, и икс.
Иногда общие члены сразу не видны.
Пример: \(10x-15y=2·5·x-3·5·y=5(2x-3y)\)
В этом случае общий член (пятерка) была скрыта. Однако разложив \(10\) как \(2\) умножить на \(5\), а \(15\) как \(3\) умножить на \(5\) – мы «вытащили пятерку на свет Божий», после чего легко смогли вынести ее за скобку.
Если одночлен выносится полностью – от него остается единица.
Пример: \(5xy+axy-x=x(5y+ay-1)\)
Мы за скобку выносим \(x\), а третий одночлен и состоит только из икса. Почему же от него остается единица? Потому что если любое выражение умножить на единицу – оно не изменится. То есть этот самый \(x\) можно представить как \(1\cdot x\). Тогда имеем следующую цепочку преобразований:
Более того – это единственно правильный способ вынесения, потому что если мы единицу не оставим, то при раскрытии скобок мы не вернемся к исходному выражению. Действительно, если сделать вынесение вот так \(5xy+axy-x=x(5y+ay)\), то при раскрытии мы получим \(x(5y+ay)=5xy+axy\). Третий член – пропал. Значит, такое вынесение некорректно.
За скобку можно выносить знак «минус», при этом знаки членов с скобке меняются на противоположные.
Пример: \(x-y=-(-x+y)=-(y-x)\)
По сути здесь мы выносим за скобку «минус единицу», которая может быть «выделена» перед любым одночленом, даже если минуса перед ним не было. Мы здесь используем тот факт, что единицу можно записать как \((-1) \cdot (-1)\). Вот тот же пример, расписанный подробно:
Скобка тоже может быть общим множителем.
Таким образом, получаем:
Вынесение общего множителя за скобки
Разложить многочлен на множители можно несколькими способами. Один из них называется вынесение общего множителя за скобки.
Разложить многочлен на множители — значит представить его в виде произведения двух и более многочленов.
Как вынести общий множитель за скобки
Чтобы вынести общий множитель за скобки нужно выполнить следующие действия.
Рассмотрим пример вынесения общего множителя за скобки.
Сначала определим число, на которое без остатка делятся все числовые коэффициенты одночленов. Для этого выпишем все числовые коэффициенты в таблицу ниже.
| Одночлен | Числовой коэффициент | Вывод |
|---|---|---|
| 6a 2 | 6 | Все числовые коэффициенты делятся без остатка на число « 3 ». |
| −3a | −3 | |
| 12ab | 12 |
Определим буквенные множители, которые повторяются во всех одночленах.
В многочлене « 6a 2 − 3a + 12ab » — только буквенный множитель « a » присутствует во всех одночленах. Наименьшая степень буквенного множителя « a » среди всех одночленов — первая.
Теперь перемножим выбранный числовой коэффициент и буквенный множитель.
Получим « 3a » и вынесем его за скобки.
Теперь вычислим оставшийся многочлен в скобках. Для этого составим таблицу ниже, где будем к каждому одночлену задавать вопрос:
«На что нужно умножить « 3а », чтобы получить данный одночлен?»
| Вопрос | Полученный одночлен |
|---|---|
| На что нужно умножить « 3а », чтобы получить « 6а 2 »? | На « 2а ». |
| На что нужно умножить « 3а », чтобы получить « −3a »? | На « −1 ». |
| На что нужно умножить « 3а », чтобы получить « 12ab »? | На « 4b ». |
Запишем полученный ответ.
Всегда проверяйте полученный результат вынесения общего множителя.
Для этого раскройте скобки в полученном результате по правилу умножения многочлена на одночлен.
Если вы вынесли общий множитель правильно, то вы должны получить исходный многочлен.
Проверим, правильно ли мы вынесли общий множитель за скобки.
При раскрытии скобок мы получили исходный многочлен, значит мы правильно вынесли общий множитель за скобки.
Действие обратное вынесению общего множителя за скобки называется раскрытием скобок.
Примеры вынесения общего множителя за скобки
Вынесение общего многочлена за скобки
Иногда есть возможность вынести многочлен за скобки целиком.
В таком случае оставшиеся одночлены просто записываются в скобки друг за другом вместе со знаком, который стоял слева от них.
Как правильно выносить общий множитель за скобки в алгебре
Понятие вынесения общего множителя за скобки
Разложить многочлен на множители — значит, преобразовать многочлен в произведение, которое равно этому многочлену.
Существует несколько методов в алгебре, позволяющих разложить многочлен на отдельные множители. Одним из наиболее распространенных способов является вынесение общего множителя за скобки. Такая методика часто встречается на уроках в средних классах.
Вынесение общего множителя за скобки представляет собой применение распределительного правила умножения с целью преобразования многочлена и получения в результате произведения.
В процессе вынесения множителя за скобки двучлен (ab + ac) примет вид произведения: a*(b + c)
Как происходит вынесение общего множителя за скобки
Определить общий множитель для каждого из членов, которые входят в состав многочлена, достаточно просто. Нужно следовать следующему алгоритму действий:
В качестве показательного примера можно разобрать порядок разложения многочлена на множители с помощью вынесения общего множителя за скобки:
В первую очередь обратим внимание на коэффициенты 20, 10 и 15 для определения наибольшего общего делителя. Таковым является число 5. Значит, 5 является общим множителем для каждого из коэффициентов.
Далее можно приступить к вычислению многочлена, который остался в скобках. При группировке требуется разделить каждый из членов начального многочлена на определенный ранее общий множитель с учетом его знака:
20 a 2 b c 2 5 a 2 c = 4 b c
10 a 3 c 5 a 2 c = 2 a
15 a 2 b 2 c 5 a 2 c = 3 b 2
В результате проделанной работы получим:
При вынесении общего множителя за скобки совершается действие, которое является обратным умножению одночлена на многочлен:
Основное правило
Основное правило, которое применимо при вынесении общего множителя за скобки: вынесение общего множителя за скобки заключается в записи начального выражения, как произведения общего множителя и скобок, содержащих начальную сумму за исключением общего множителя.
В результате вынесения общего множителя за скобки в них остается такое же количество одночленов, которое содержалось в исходном многочлене.
Например, имеется некое выражение:
Заметим, что это сумма из трех слагаемых и общего множителя в виде числа 4. Руководствуясь правилом вынесения общего множителя за скобки, преобразуем выражение:
Преобразование выполнено, запишем итоговый результат:
Не во всех случаях получается определить общий множитель. Например, перед вынесением общего множителя может потребоваться замена чисел и выражений на произведения, которые тождественно им равны.
Попробуем разложить на множители многочлен:
Пояснение на примерах
В числовом выражении требуется вынести общий множитель за скобки:
В первую очередь следует определить максимально возможный общий множитель для двух слагаемых 15 и 20. Таковым будет являться число 5. Исключим его из скобок:
15 + 20 = 5 ( 15 5 + 20 5 ) = 5 * ( 3 + 4 )
Выполним проверку. В процессе необходимо выполнить умножение общего множителя в виде числа 5 на каждое из слагаемых. В том случае, когда ответ верный, выражение примет вид 15 + 20:
5 * ( 3 + 4 ) = 5 × 3 + 5 × 4 = 15 + 20
Вынести за скобки общий множитель в выражении:
Заметим, что в условии задания записана сумма простых чисел 13 и 5. В связи с этим, такие числа можно разложить на единицу и самих себя:
Такие слагаемые не имеют общих множителей, за исключением единицы. С другой стороны, число 1 бессмысленно выносить за скобки. Выполним преобразования:
13 + 5 = 1 ( 13 1 + 5 1 ) = 1 ( 13 + 5 )
Ответ: 1 * ( 13 + 5 )
Дано выражение, в котором требуется вынести общий множитель за скобки:
Выполним замену вычитания на сложение:
−20 − 16 − 2 = −20 + (−16) + (−2)
Ответ можно записать в сокращенном виде:
Заметим, что если бы мы вынесли за скобки общий множитель в виде числа 2 без минуса, то получили бы ответ правильный, но не аккуратный:
Дано выражение, в котором требуется вынести за скобки общий множитель:
Выполним замену вычитания на сложение:
Выполним преобразования согласно правилу вынесения общего множителя за скобки:
Вынесение за скобки общего множителя: правило, примеры
В рамках изучений тождественных преобразований очень важна тема вынесения общего множителя за скобки. В данной статье мы поясним, в чем именно заключается такое преобразование, выведем основное правило и разберем характерные примеры задач.
Понятие вынесения множителя за скобки
Чтобы успешно применять данное преобразование, нужно знать, для каких выражений оно используется и какой результат надо получить в итоге. Поясним эти моменты.
В чем состоит данное преобразование? В ходе него мы представляем исходное выражение как произведение общего множителя и выражения в скобках, содержащего сумму всех исходных слагаемых, кроме общего множителя.
Правило вынесения общего множителя за скобки
Используя все сказанное выше, выведем основное правило такого преобразования:
Чтобы вынести за скобки общий множитель, надо записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Определить сразу, какой множитель является общим, возможно не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.
В выводах отметим, что преобразование путем вынесения общего множителя за скобки очень часто применяется на практике, например, для вычисления значения рациональных выражений. Также этот способ полезен, когда нужно представить выражение в виде произведения, например, разложить многочлен на отдельные множители.
Разложение многочленов на множители: вынесение общего множителя за скобки
Содержание
Часто при решении задач и уравнений необходимо упростить многочлен, то есть разложить его на множители. Вынесение общего множителя за скобки — один из способов такого разложения.
Разложение многочлена на множители — это представление многочлена в виде произведения двух или нескольких многочленов.
Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения.
Рисунок 1
Пример 1
Рассмотрим многочлен:
Пример 2
Разложим следующий многочлен на множители тем же способом:
Пример 3
Разложим на множители многочлен:
Алгебра
План урока:
Вынесение общего множителя за скобки
В предыдущем уроке мы изучили умножение многочлена на одночлен. Например, произведение монома a и полинома b + c находится так:
Однако в ряде случае удобнее выполнить обратную операцию, которую можно назвать вынесением общего множителя за скобки:
Например, пусть нам надо вычислить значение полинома ab + bc при значениях переменных a = 15,6, b = 7,2, c = 2,8. Если подставить их напрямую в выражение, то получим
ab + bc = 15.6 * 7.2 + 15.6 * 2.8
что, скорее всего, не получится посчитать в уме. Если же вынести a за скобки, то получим иную запись:
ab + bc = a(b + c) = 15.6 * (7.2 + 2.8) = 15.6 * 10 = 156
В данном случае мы представили полином ab + bc как произведение двух множителей: a и b + с. Данное действие называют разложением многочлена на множители.
При этом каждый из множителей, на которые разложили многочлен, в свою очередь может быть многочленом или одночленом.
Видно, что у обоих многочленов есть общий множитель 7b. Значит, его можно вынести за скобки:
Проверить правильность вынесения множителя за скобки можно с помощью обратной операции – раскрытия скобки:
Важно понимать, что часто полином можно разложить несколькими способами, например:
5abc + 6bcd = b(5ac + 6cd) = c(5ab + 6bd) = bc(5a + 6d)
Обычно стремятся вынести, грубо говоря, «наибольший» одночлен. То есть раскладывают полином так, чтобы из оставшегося полинома больше нечего нельзя было вынести. Так, при разложении
5abc + 6bcd = b(5ac + 6cd)
в скобках осталась сумма одночленов, у которых есть общий множитель с. Если же вынести и его, то общих множителей в скобках не останется:
b(5ac + 6cd) = bc(5a + 6d)
Разберем детальнее, как находить общие множители у одночленов. Пусть надо разложить сумму
8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10
Она состоит из трех слагаемых. Сначала посмотрим на числовые коэффициенты перед ними. Это 8, 12 и 16. В 3 уроке 6 класса рассматривалась тема НОД и алгоритм его нахождения.Это наибольший общий делитель.Почти всегда его можно подобрать устно. Числовым коэффициентом общего множителя как раз будет НОД числовых коэффициентов слагаемых полинома. В данном случае это число 4.
Далее рассмотрим буквенную часть. В ней должны быть переменные, которые есть во ВСЕХ слагаемых. В данном случае это a и b, а переменная c общей не является, так как не входит в первое слагаемое.
8a 3 b 4 + 12a 2 b 5 v + 16a 4 b 3 c 10 = 4a 2 b 3 (2ab + 3b 2 c + 4a 2 c 10 )
В результате у оставшихся слагаемых 2ab, 3b 2 c, 4a 2 c 10 нет ни одной общей буквенной переменной, а у их коэффициентов 2, 3 и 4 нет общих делителей.
Выносить за скобки можно не только одночлены, но и многочлены. Например:
Еще один пример. Необходимо разложить выражение
Решение. Напомним, что знак минус меняет знаки в скобках на противоположные, поэтому
Значит, можно заменить (3x – 8y) на – (8y – 3x):
Ответ: (8y – 3x)(5t – 2s).
Запомним, что вычитаемое и уменьшаемое можно поменять местами, если изменить знак перед скобками:
Верно и обратное: минус, уже стоящий перед скобками, можно убрать, если одновременно переставить местами вычитаемое и уменьшаемое:
Этот прием часто используется при решении заданий.
Способ группировки
Рассмотрим ещё один способ разложения многочлена на множители, который помогает раскладывать полином. Пусть есть выражение
Вынести множитель, общий для всех четырех мономов, не получается. Однако можно представить этот полином как сумму двух многочленов, и в каждом из них вынести переменную за скобки:
Теперь можно вынести выражение b – 5:
Мы «сгруппировали» первое слагаемое со вторым, а третье с четвертым. Поэтому описанный метод называют способом группировки.
Пример. Разложим полином 6xy + ab– 2bx– 3ay.
Решение. Группировка 1-ого и 2-ого слагаемого невозможна, так как у них нет общего множителя. Поэтому поменяем местами мономы:
Разности 3y – b и b – 3y отличаются только порядком переменных. В одной из скобок его можно изменить, вынеся знак минус за скобки:
Используем эту замену:
В результате получили тождество:
Ответ: (3y – b)(2x – a)
Группировать можно не только два, а вообще любое количество слагаемых. Например, в полиноме
можно сгруппировать первые три и последние 3 одночлена:
Теперь рассмотрим задание повышенной сложности
Пример. Разложите квадратный трехчлен x 2 – 8x +15.
Решение. Данный полином состоит всего из 3 одночленов, а потому, как кажется, группировку произвести не получится. Однако можно произвести такую замену:
Тогда исходный трехчлен можно представить следующим образом:
Конечно, догадаться о замене – 8х = – 3х – 5х в приведенном примере нелегко. Покажем иной ход рассуждений. Нам надо разложить полином второй степени. Как мы помним, при перемножении многочленов их степени складываются. Это значит, что если мы и сможем разложить квадратный трехчлен на два множителя, то ими окажутся два полинома 1-ой степени. Запишем произведение двух многочленов первой степени, у которых старшие коэффициенты равны 1:
(x + a)(x + b) = x 2 + xa + xb + ab = x 2 + (a + b)x + ab
Здесь за a и b мы обозначили некие произвольные числа. Чтобы это произведение равнялось исходному трехчлену x 2 – 8x +15, надо подобрать подходящие коэффициенты при переменных:
С помощью подбора можно определить, что этому условию удовлетворяют числа a= – 3 и b = – 5. Тогда
в чем можно убедиться, раскрыв скобки.
Для простоты мы рассмотрели только случай, когда у перемножаемых полиномов 1-ой степени старшие коэффициенты равны 1. Однако они могли равняться, например, 0,5 и 2. В этом случае разложение выглядело бы несколько иначе:
Однако, вынеся коэффициент 2 из первой скобки и умножив его на вторую, получили бы изначальное разложение:
В рассмотренном примере мы разложили квадратный трехчлен на два полинома первой степени. В дальнейшем нам часто придется это делать. Однако стоит отметить, что некоторые квадратные трехчлены, например,
невозможно разложить таким образом на произведение полиномов. Доказано это будет позднее.
Применение разложение многочленов на множители
Разложение полинома на множители может упростить выполнение некоторых операций. Пусть необходимо выполнить вычисление значения выражения
2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9
Вынесем число 2, при этом степень каждого слагаемого уменьшится на единицу:
2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = 2(1 + 2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 )
2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8
за х. Тогда записанное выше равенство можно переписать:
Получили уравнение, решим его (см. урок уравнения):
Теперь выразим искомую нами сумму через х:
2 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 + 2 8 + 2 9 = x + 2 9 = 510 + 512 = 1022
При решении этой задачи мы возводили число 2 только в 9-ую степень, а все остальные операции возведения в степень удалось исключить из вычислений за счет разложения многочлена на множители. Аналогично можно составить формулу вычисления и для других подобных сумм.
Теперь вычислим значение выражения
Посчитать это напрямую достаточно сложно. Однако можно применить метод группировки:
Далее посмотрим, как можно использовать разложение полинома для доказательства делимости чисел. Пусть требуется доказать, что выражение
делится на 73. Заметим, что числа 9 и 81 являются степенями тройки:
81 = 9 2 = (3 2 ) 2 = 3 4
Зная это, произведем замену в исходном выражении:
Произведение 3 12 •73 делится на 73 (так как на него делится один из множителей), поэтому и выражение 81 4 – 9 7 + 3 12 делится на это число.
Вынесение множителей может использоваться для доказательства тождеств. Например, докажем верность равенства
(a 2 + 3a) 2 + 2(a 2 + 3a) = a(a + 1)(a + 2)(a + 3)
Для решения тождества преобразуем левую часть равенства, вынеся общий множитель:
(a 2 + 3a) 2 + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a) + 2(a 2 + 3a) = (a 2 + 3a)(a 2 + 3a + 2)
Далее произведем замену 3a = 2a + a:
(a 2 + 3a)(a 2 + 3a + 2) = (a 2 + 3a)(a 2 + 2a + a + 2) = (a 2 + 3a)((a 2 + 2a) + (a + 2) = (a 2 + 3a)(a(a + 2) + (a + 2)) = (a 2 + 3a)(a + 1)(a + 2) = a(a + 3)(a + z)(a + 2) = a(a + 1)(a + 2)(a + 3)
Ещё один пример. Докажем, при любых значениях переменных x и у выражение
не является положительным числом.
Решение. Вынесем общий множитель х – у:
Обратим внимание, что мы получили произведение двух похожих двучленов, отличающихся лишь порядком букв x и y. Если бы мы поменяли местами в одной из скобок переменные, то получили бы произведение двух одинаковых выражений, то есть квадрат. Но для того, чтобы поменять местами x и y, нужно перед скобкой поставить знак минус:
Тогда можно записать:
Разложение полинома помогает решать некоторые уравнения. При этом используется следующее утверждение:
Если в одной части уравнения стоит ноль, а в другой произведение множителей, то каждый из них следует приравнять нулю.
Пример. Решите уравнение (s – 1)(s + 1) = 0.
Решение. В левой части записано произведение мономов s – 1 и s + 1, а в правой – ноль. Следовательно, нулю должно равняться или s – 1, или s + 1:
Каждое из двух полученных значений переменной s является корнем уравнения, то есть оно имеет два корня.
Пример. Решите уравнение 5w 2 – 15w = 0.
Решение. Вынесем 5w:
Снова в левой части записано произведение, а в правой ноль. Продолжим решение:
Пример. Найдите корни уравнения k 3 – 8k 2 + 3k– 24 = 0.
Решение. Сгруппируем слагаемые:
k 3 – 8k 2 + 3k– 24 = 0
(k 3 – 8k 2 ) + (3k– 24) = 0
Заметим, что уравнение k 2 = – 3 решения не имеет, так как любое число в квадрате не меньше нуля. Поэтому единственным корнем исходного уравнения является k = 8.
Пример. Найдите корни уравнения
Решение: Перенесем все слагаемые в левую часть, а после сгруппируем слагаемые:
Пример. Решите уравнение
Далее решим по отдельности эти уравнения:
Теперь займемся вторым уравнением. Перед нами снова квадратный трехчлен. Чтобы разложить его на множители методом группировки, нужно представить его в виде суммы 4 слагаемых. Если произвести замену – 5t = – 2t – 3t, то дальше удастся сгруппировать слагаемые:
В результате получили, что у исходного уравнения есть 4 корня.
Вынесение общего множителя за скобки
Основной принцип
Распределительный закон умножения позволяет умножить число на сумму (или сумму на число). Например, чтобы найти значение выражения 3 × (4 + 5) можно умножить число 3 на каждое слагаемое в скобках и сложить полученные результаты:
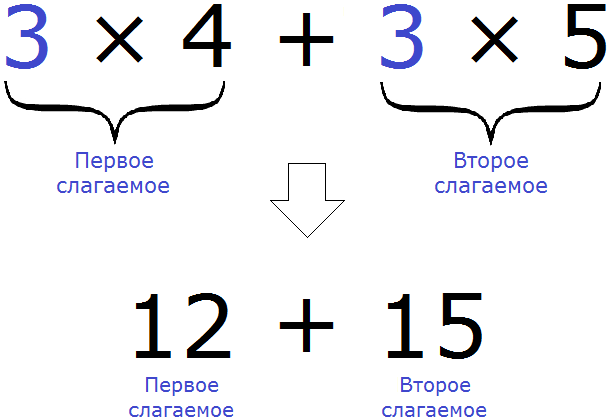
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Число 3 и выражение в скобках можно поменять местами (это следует из переместительного закона умножения). Тогда каждое слагаемое, которое в скобках, будет умножено на число 3
(4 + 5) × 3 = 4 × 3 + 5 × 3 = 12 + 15
Распределительный закон умножения иногда называют внесением множителя во внутрь скобок. В выражении 3 × (4 + 5) множитель 3 был за скобками. Умножив его на каждое слагаемое в скобках, мы по сути внесли его во внутрь скобок. Для наглядности можно так и записать, хоть и не принято так записывать:
3 (4 + 5) = ( 3 × 4 + 3 × 5)
Поскольку в выражении 3 × (4 + 5) число 3 умножается на каждое слагаемое в скобках, это число является общим множителем для слагаемых 4 и 5
3 (4 + 5) = 3 × 4 + 3 × 5
Если вычислить обе части полученного равенства, то получим тождество:
3 (4 + 5) = 3 × 4 + 3 × 5
Как происходит вынесение общего множителя за скобки
Вынесение общего множителя за скобки по сути является обратной операцией внесению общего множителя во внутрь скобок.
Если при внесении общего множителя внутрь скобок, мы умножаем этот множитель на каждое слагаемое в скобках, то при вынесении этого множителя обратно за скобки, мы должны разделить каждое слагаемое в скобках на этот множитель.
Теперь мы можем детально увидеть, как происходит вынесение общего множителя за скобки:
Видно, что общий множитель 3 сначала вынесен за скобки, затем в скобках происходит деление каждого слагаемого на этот общий множитель.
Деление каждого слагаемого на общий множитель можно выполнять не только разделяя числитель на знаменатель, как это было показано выше, но и сокращая эти дроби. В обоих случаях получится один и тот же результат:
Мы рассмотрели простейший пример вынесения общего множителя за скобки, чтобы понять основной принцип.
Но не всё так просто, как кажется на первый взгляд. После того, как число умножено на каждое слагаемое в скобках, полученные результаты складывают, и общий множитель пропадает из виду.
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Обычно при решении задач встречаются именно такие выражения, в которых общий множитель сначала нужно найти, прежде чем его выносить.
Чтобы в выражении 12 + 15 вынести общий множитель за скобки, нужно найти наибольший общий делитель (НОД) слагаемых 12 и 15. Найденный НОД и будет общим множителем.
Итак, найдём НОД слагаемых 12 и 15. Напомним, что для нахождения НОД необходимо разложить исходные числа на простые множители, затем выписать первое разложение и убрать из него множители, которые не входят в разложение второго числа. Оставшиеся множители нужно перемножить и получить искомый НОД. Если испытываете затруднения на этом моменте, обязательно повторите этот урок.
НОД слагаемых 12 и 15 это число 3. Данное число является общим множителем слагаемых 12 и 15. Его и нужно выносить за скобки. Для этого сначала записываем сам множитель 3 и рядом в скобках записываем новое выражение, в котором каждое слагаемое выражения 12 + 15 разделено на общий множитель 3
Ну и дальнейшее вычисление не составляет особого труда. Выражение в скобках легко вычисляется — двенадцать разделить на три будет четыре, а пятнадцать разделить на три будет пять:
В коротком решении пропускают запись в которой показано, как каждое слагаемое разделено на общий множитель:
Пример 2. Вынести общий множитель за скобки в выражении 15 + 20
Наибольший общий делитель слагаемых 15 и 20 это число 5. Данное число является общим множителем слагаемых 15 и 20. Его и вынесем за скобки:
Получили выражение 5(3 + 4).
Получившееся выражение 5(3 + 4) можно проверить. Для этого достаточно умножить пятёрку на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 15 + 20
Пример 3. Вынести общий множитель за скобки в выражении 18 + 24 + 36
Найдём НОД слагаемых 18, 24 и 36. Чтобы найти НОД нескольких чисел, нужно разложить эти числа на простые множители, затем найти произведение общих множителей:
НОД слагаемых 18, 24 и 36 это число 6. Данное число является общим множителем слагаемых 18, 24 и 36. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим число 6 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 18 + 24 + 36
Пример 4. Вынести общий множитель за скобки в выражении 13 + 5
Слагаемые 13 и 5 являются простыми числами. Они раскладываются только на единицу и самих себя:
Это значит, что у слагаемых 13 и 5 нет общих множителей, кроме единицы. Соответственно, нет смысла выносить эту единицу за скобки, поскольку это ничего не даст. Покажем это:
Пример 5. Вынести общий множитель за скобки в выражении 195 + 156 + 260
Найдём НОД слагаемых 195, 156 и 260
НОД слагаемых 195, 156 и 260 это число 13. Данное число является общим множителем для слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 13 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 195 + 156 + 260
Выражение, в котором требуется вынести общий множитель за скобки, может быть не только суммой чисел, но и разностью. Например, вынесем общий множитель за скобки в выражении 16 − 12 − 4. Наибольшим общим делителем чисел 16, 12 и 4 это число 4. Данное число и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим четвёрку на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 16 − 12 − 4
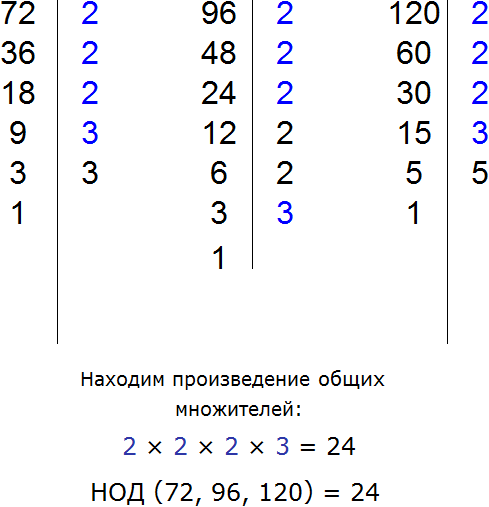
Пример 6. Вынести общий множитель за скобки в выражении 72 + 96 − 120
Найдём НОД чисел 72, 96 и 120
НОД для 72, 96 и 120 это число 24. Данное число является общим множителем слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 24 на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 72+96−120
Общий множитель, выносимый за скобки, может быть и отрицательным. Например, вынесем общий множитель за скобки в выражении −6 − 3. Вынести общий множитель за скобки в таком выражении можно двумя способами. Рассмотрим каждый из них.
Способ 1.
Заменим вычитание сложением:
Теперь находим общий множитель. Общим множителем данного выражения будет наибольший общий делитель модулей слагаемых −6 и −3.
Модуль первого слагаемого это 6. А модуль второго слагаемого это 3. НОД(6 и 3) равен 3. Данное число является общим множителем слагаемых 6 и 3. Его и вынесем за скобки:
Выражение полученное таким способом получилось не очень аккуратным. Много скобок и отрицательных чисел не придают выражению простоту. Поэтому можно воспользоваться вторым способом, суть которого заключается в том, чтобы вынести за скобки не 3, а −3.
Способ 2.
Как и в прошлый раз заменяем вычитание сложением
В этот раз мы вынесем за скобки не 3, а −3
Выражение полученное в этот раз выглядит намного проще. Запишем решение покороче, чтобы сделать его ещё проще:
Разрешать выносить отрицательный множитель за скобки связано с тем, что разложение чисел −6 и (−3) можно записать двумя видами: сначала сделать множимое отрицательным, а множитель положительным:
во втором случае множимое можно сделать положительным, а множитель отрицательным:
А значит мы вольны выносить за скобки тот сомножитель, который захотим.
Пример 8. Вынести общий множитель за скобки в выражении −20 − 16 − 2
Заменим вычитание сложением
−20 − 16 − 2 = −20 + (−16) + (−2)
Наибольшим общим делителем слагаемых −20, −16 и −2 является число 2. Это число является общим множителем этих слагаемых. Посмотрим, как это выглядит:
Запишем приведенное решение покороче:
Пример 9. Вынести общий множитель за скобки в выражении −30 − 36 − 42
Заменим вычитание сложением:
Наибольшим общим делителем слагаемых −30, −36 и −42 это число 6. Данное число является общим множителем для этих слагаемых. Но за скобки мы вынесем не 6, а −6 поскольку числа −30, −36 и −42 можно представить так:
Вынесение минуса за скобки
При решении задач иногда может быть полезным вынесение минуса за скобки. Это позволяет упростить выражение и сделать его проще.
Рассмотрим следующий пример. Вынести минус за скобки в выражении −15 + (−5) + (−3)
Для наглядности заключим данное выражение в скобки, ведь речь идёт о том, чтобы вынести минус за эти скобки
Итак, чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые, но с противоположными знаками. Знаки операций (то есть плюсы) оставляем без изменений:
−(15 + 5 + 3) = −(23) = −23
Поэтому между выражениями −15 + (−5) + (−3) и −(15 + 5 + 3) можно поставить знак равенства, потому что они равны одному и тому же значению:
−15 + (−5) + (−3) = −(15 + 5 + 3)
На самом деле при вынесении минуса за скобки опять же срабатывает распределительный закон умножения:
Если поменять местами левую и правую часть этого тождества, то получится, что сомножитель a вынесен за скобки
Тоже самое происходит, когда мы выносим общий множитель в других выражениях и когда выносим минус за скобки.
Очевидно, что при вынесении минуса за скобки, выносится не минус, а минус единица. Ранее мы говорили, что коэффициент 1 принято не записывать.
Поэтому и образуется перед скобками минус, а знаки слагаемых которые были в скобках меняют свой знак на противоположный, поскольку каждое слагаемое разделено на минус единицу.
Вернёмся к предыдущему примеру и детально увидим, как на самом деле выносился минус за скобки
Пример 2. Вынести минус за скобки в выражении −3 + 5 + 11
Ставим минус и рядом в скобках записываем выражение −3 + 5 + 11 с противоположным знаком у каждого слагаемого:
−3 + 5 + 11 = −(3 − 5 − 11)
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица. Подробное решение выглядит следующим образом:
Вынесение общего множителя за скобки в буквенном выражении
Выносить общий множитель за скобки в буквенном выражении намного интереснее.
Как и в случае с числовым выражением, здесь происходит деление каждого слагаемого на вынесенный общий множитель. Выглядит это так:
Например, если вместо переменной a подставить число 4, то конструкция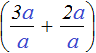 
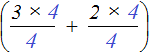
примет следующий вид: 
. Тогда четвёрки в обеих дробях можно будет сократить на 4:
Поэтому не следует пугаться при виде сокращения переменных. Переменная это полноправный множитель, пусть даже выраженный буквой. Такой множитель можно выносить за скобки, сокращать и выполнять другие действия, которые допустимы к обычным числам.
Буквенное выражение содержит не только числа, но и буквы (переменные). Поэтому общий множитель, который выносится за скобки часто бывает буквенным множителем, состоящим из числа и буквы (коэффициента и переменной). К примеру, следующие выражения являются буквенными множителями:
Прежде чем выносить такой множитель за скобки, нужно определиться, какое число будет в числовой части общего множителя и какая переменная будет в буквенной части общего множителя. Другими словами, нужно узнать какой коэффициент будет у общего множителя и какая переменная будет в него входить.
Проверим получившееся выражение. Для этого умножим 5a на каждое слагаемое в скобках. Если мы всё сделали правильно, то получим выражение 10a + 15a
Буквенный множитель не всегда можно вынести за скобки. Иногда общий множитель состоит только из числа, поскольку ничего подходящего для буквенной части в выражении не находится.
Пример 2. Вынести общий множитель выражении 3x + 9y + 12
Коэффициентами данного выражения являются числа 3, 9 и 12, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. А среди буквенных сомножителей (переменных) нет общего множителя. Поэтому окончательный общий множитель это 3
Пример 3. Вынести общий множитель за скобки в выражении 8x + 6y + 4z + 10 + 2
Коэффициентами данного выражения являются числа 8, 6, 4, 10 и 2, их НОД равен 2. Значит коэффициентом общего множителя, выносимого за скобки, будет число 2. А среди буквенных сомножителей нет общего множителя. Поэтому окончательный общий множитель это 2
Пример 4. Вынести общий множитель 6ab + 18ab + 3abc
Коэффициентами данного выражения являются числа 6, 18 и 3, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. В буквенную часть общего множителя будут входить переменные a и b, поскольку в выражении 6ab + 18ab + 3abc эти две переменные входят в каждое слагаемое. Поэтому окончательный общий множитель это 3ab
При подробном решении выражение становится громоздким и даже непонятным. В данном примере это более чем заметно. Это связано с тем, что мы сокращаем множители в числителе и в знаменателе. Лучше всего делать это в уме и сразу записывать результаты деления. Тогда выражение станет коротким и аккуратным:
Как и в случае с числовым выражением в буквенном выражении общий множитель может быть и отрицательным.
Для удобства заменим вычитание сложением
−3 a − 2 a = −3 a + (−2 a )
Пример 6. Вынести общий множитель за скобки в выражении −6x − 6y
Заменим вычитание сложением
Вынесем за скобки −6
Запишем решение покороче:
Пример 7. Вынести общий множитель за скобки в выражении −2a − 4b − 6c
Заменим вычитание сложением
Вынесем за скобки −2
Запишем решение покороче:
−2a − 4b − 6c = −2(a + 2b + 3c)
Вынесение общего множителя за скобки это очень важная тема. В данном уроке рассмотрены только азы и простейшие примеры. Мы ещё вернемся к этой теме, когда будем изучать многочлены.
Обязательно изучите данный урок, поскольку при изучении многочленов потребуется выносить за скобки сложный множитель, состоящий из степеней.
Упрощение выражений
Свойства сложения, вычитания, умножения и деления полезны тем, что позволяют преобразовывать суммы и произведения в удобные выражения для вычислений. Научимся, как можно с помощью этих свойств упрощать выражения.
В этом выражении есть числа, при сложении которых получаются «круглые» числа. Заметив это, легко провести вычисления устно. Воспользуемся переместительным законом сложения.
Также для упрощения вычисления произведений можно использовать переместительный закон умножения.
Сочетательные и переместительные свойства используются и при упрощении буквенных выражений.
Распределительный закон умножения часто применяется для упрощения вычислений.
Применяя распределительное свойство умножения относительно сложения или вычитания к выражению « (a + b) · с и (a − b) · c », мы получаем выражение, не содержащее скобки.
В этом случае говорят, что мы раскрыли (опустили) скобки. Для применения свойств не имеет значения, где записан множитель « c » — перед скобками или после.
Раскроем скобки в выражениях.
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
В таких случаях говорят, что из « ac + bc » вынесен общий множитель « с » за скобки.
Примеры вынесения общего множителя за скобки.
Вынесение общего множителя за скобки
Разложение многочлена на множители — это преобразование многочлена в произведение, равное данному многочлену.
Есть несколько способов разложения многочлена на множители. Один из них — вынесение общего множителя за скобки.
Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево:
Определение общего множителя для всех членов многочлена производится пошагово:
Рассмотрим разложение многочлена на множители методом вынесения общего множителя за скобки на примере многочлена:
В итоге мы получили следующие общие множители: 5, a 2 и c. Их произведение 5a 2 c представляет наибольший общий множитель, который будет вынесен за скобки:
Теперь надо вычислить многочлен, который должен быть в скобках. Для этого надо разделить каждый член исходного многочлена на общий множитель, который мы нашли:
Обратите внимание, что вынесение общего множителя за скобки — это действие, обратное умножению одночлена на многочлен:
Вынесение за скобки общего множителя, правило, примеры.
Продолжаем изучать тождественные преобразования, в этой статье мы остановимся на вынесении за скобки общего множителя. Для начала разберемся, в чем состоит указанное преобразование выражения. Дальше приведем правило вынесения общего множителя за скобки и подробно рассмотрим примеры его применения.
Навигация по странице.
Что значит вынести общий множитель за скобки?
Чтобы успешно справляться с вынесением общего множителя за скобки, необходимо хорошо понимать, с какими выражениями проводится это преобразование и что в результате него получается. Разберемся с этим.
Вынесение общего множителя за скобки проводится в суммах, в которых каждое из составляющих из слагаемых представляет собой произведение, причем в каждом из этих произведений присутствует одинаковый множитель. Этот одинаковый множитель и называется общим множителем, и именно он выносится за скобки.
Так в чем же заключается вынесение общего множителя за скобки? Оно состоит в представлении исходного выражения в виде произведения общего множителя и выражения в скобках, которое содержит сумму всех изначальных слагаемых, но без общего множителя.
Как выносить за скобки общий множитель?
Рассуждения из предыдущего пункта статьи приводят нас к правилу вынесения за скобки общего множителя: нужно записать произведение общего множителя и скобок, содержащих исходную сумму, но без общего множителя.
Часто в выражениях общий множитель видно не сразу. Чтобы его увидеть, приходится выполнять предварительное преобразование исходного выражения, заключающееся в замене чисел и выражений тождественно равными им произведениями.
В заключение этой статьи заметим, что вынесение за скобки общего множителя применяется очень широко. Например, с его помощью можно более рационально вычислять значения числовых выражений. Также вынесение за скобки общего множителя позволяет представлять выражения в виде произведения, в частности, на вынесении за скобки основан один из методов разложения многочлена на множители.
Вынесение общего множителя за скобки
Рассмотрим, как проводить вынесение общего множителя за скобки, на конкретных примерах.
1) 12a — 16b
Начинаем с поиска общего множителя. Сначала ищем общий множитель среди чисел. Наибольшее число, на которое делится и 12, и 16 — 4. Переменные a и b разные, общего множителя у них нет.
Таким образом, общий множитель — 4. Вынести за скобки общий множитель — значит, поделить на этот множитель каждое слагаемое, стоящее в скобках. Делим на 4 сначала 12, затем 16:
12a — 16b=4(3a — 4b).
2) 5x² + 10x
И 5, и 10 делятся на 5, следовательно, общий множитель для чисел — пять. Из степеней x² и x выносим за скобки степень с меньшим показателем, то есть x (показатель 1 не пишем).
Таким образом, в этом примере общий множитель равен 5x. Выносим его за скобки. Вынести за скобки общий множитель — значит, каждое слагаемое, стоящее в скобках, разделить на этот множитель. Отдельно делим числа 5 и 10 на 5, отдельно — степени x² и x на x. Получаем
5x² + 10x=5x(x + 2).
Начинаем с коэффициентов. Наибольшее число, на которое делятся 12, 18 и 30 — это 6. Поскольку первое слагаемое со знаком «-«, выносим минус за скобки. При этом все знаки в скобках меняются на противоположные.
Среди степеней a наименьшая a³.
Среди степеней b — b².
Среди степеней c — с в первой степени (пишем просто c).
Таким образом, общий множитель — это — 6a³b²c. Выносим его за скобки.
Каждое слагаемое, стоящее в скобках, делим на этот множитель. При этом отдельно делим число на число, отдельно — степени с одинаковыми основаниями:
Поскольку знак «минус» вынесли за скобки, все знаки в скобках меняем на противоположные. Делим каждое слагаемое, стоящее в скобках, на общий множитель:
Не забываем: сколько слагаемых было до вынесения общего множителя за скобки, ровно столько же должно остаться в скобках после вынесения. Первое слагаемое совпало с общим множителем, поэтому после вынесения общего множителя за скобки от первого слагаемого осталась единица.
Вынесение общего множителя за скобки
Преобразование математического выражения, в результате которого многочлен представлен произведением нескольких множителей и тождественен (т.е. равен) исходному, называют разложением многочлена на множители.
Чтобы вынести общий множитель за скобки, сначала нужно его найти.
Не забываем полезные лайфхаки для нахождения общего множителя:
Все четные числа делятся на два;
Число делится на три, если сумма составляющих его цифр делится на три
(например, нужно узнать, делится ли на 3 число 78;
7+8=15:3=5, соответственно, 78 делится на 3)
На 5 делятся числа, которые оканчиваются на 0 и 5
Часто в алгебраические выражения и тождества входят буквенные переменные. Например а, в, с, х, у и другие. И многоэтажные примеры в учебники алгебры из нагромождения букв и чисел приводят неподготовленного ученика в священный трепет.
Не стоит пугаться. Буквенная переменная это полноправный множитель, и с ним можно производить все действия, которые применимы к обычным числам: сокращать, выносить за скобки, складывать, возводить в степень и т.д.
Работа с многочленом ведется в определенном порядке.
1.Сначала преобразуем числовые коэффициенты. Определяем, на какое наибольшее целое число (наибольший общий делитель) делятся числовые коэффициенты каждого входящего в уравнение одночлена без остатка.
Определили, что все числовые коэффициенты делятся на 4.
2. Затем находим общие буквенные коэффициенты для всех одночленов многочлена и выносим их за скобки в наименьшей степени.
В нашем примере 8а2+12аb-4a, общим буквенным коэффициентом является а в наименьшей степени 1. Выносим за скобки общий буквенный и определенный на предыдущем этапе общий числовой коэффициенты
NB! Чтобы проверить правильность проведенных преобразований, нужно умножить вынесенный за скобки одночлен на многочлен в скобках. В результате должно получиться исходное выражение.
А сейчас, чтобы закрепить тему «Вынесение за скобки общего множителя», решим пример из учебника «Алгебра» для 7 класса под редакцией Мерзляка А. Г.
Вынесение общего множителя за скобки
Вы будете перенаправлены на Автор24
Сначала давайте вспомним правила умножения одночлена на одночлен:
Для умножения одночлен на одночлен необходимо сначала перемножить коэффициенты одночленов, затем воспользовавшись правилом умножения степеней с одинаковым основанием умножить переменные входящие в состав одночленов.
Решение:
Сначала вычислим проиведение коэффициентов
Получившийся результат оказался неправильной дробью, т. е такой, у которой числитель больше знаменателя.
Преобразуем эту дробь по средствам выделения целой части. Вспомним, что для выделения целой части необходимо неполное частное, получившиеся при делении числителя на знаменатель записать, как целую часть, остаток от деления в числитель дробной части, делитель в знаменатель.
Мы нашли коэффициент будущего произведения.
Тогда итогом умножения одночленов будет:
Тогда исходя из данного правила можно выполнить следующее задание:
Преставим каждый из одночленов,входящих в состав многолена как прозведение двух одночленов для того, чтобы выделить общий одночлен, который будет являться множителем и в первом и во втором одночлене.
Представим первый и второй одночлен, входящий в многочлен как произведение:
$<4x>^3y+8x^2=4x^2\cdot xy + 4x^2\cdot 2$
$<4x>^3y+8х^2 = 4x^2\cdot xy + 4x^2\cdot 2 = 4x^2(xy+2)$
Этот метод называется разложением на множители с помощью вынесения общего множителя.
Готовые работы на аналогичную тему
Алгоритм
Выявить переменные, которые входят в состав каждого одночлена, и выбрать переменную с наименьшим показателем степени
Одночлен, состящий из коэффициента, найденного в п.2, переменных, найденных в п.3 будет общим множителем. который можно вынести за скобки как общий множитель.
Решение:
Найдем НОД коэффициентов для этого разложим коэффициенты на простые множители
$45=3\cdot 3\cdot 5$
И найдем произведение тех, которые входят в разложение каждого:
Выявить переменные, которые входят в состав каждого одночлена, и выбрать переменную с наименьшим показателем степени
Нужны еще материалы по теме статьи?
Воспользуйся новым поиском!
Найди больше статей и в один клик создай свой список литературы по ГОСТу
Автор этой статьи Дата последнего обновления статьи: 10.05.2022
5 способов разложения многочлена на множители
Для чего нужно раскладывать многочлен на множители?
Чтобы облегчить себе жизнь! После того как ты это сделаешь, выражение станет намного проще и ты легко сможешь с ним «разобраться»!
Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
Как этому научиться?
Прочитай эту статью. Сначала мы разберем что означают все «сложные» слова.
Потом объясним все пять способов разложения многочлена на множители.
И затем разберем на примерах как это делать.
Let’s dive right in… (Поехали!) 🙂
Существует 5 основных способов разложения многочлена на множители:
Основные определения (разбираемся со «сложными» словами)
Одночлены
Одночленами могут быть числа, переменные, произведения чисел и переменных, а так же переменные в степени (если забыл, что такое степень, посмотри тему «Степень и ее свойства»)
Все это – одночлены. Видишь у них нет знаков «+» или «-«, как бы нет других членов.
Многочлены
Многочлен – это выражение, состоящее из суммы (или разности) нескольких одночленов различного вида:
Множители
Так, ну давай по порядку. Как нетрудно догадаться, слово «множитель» происходит от слова «умножать».
Возьмем, например, число \( 12\), разложить его на множители означает расписать его в виде «умножения» или, как принято говорить в математике «произведения» множителей.
Так \( 12\) мы можем получить, умножив \( 2\) на \( 6\).
А \( 6\), в свою очередь, можно представить как произведение \( 2\) и \( 3\).
Чтоб было более наглядно, обратимся к картинке:
На картинке мы видим пошаговое разложение на множители, те которые подчеркнуты – это множители, которые дальше разложить уже нельзя.
То есть их нельзя уже представить в виде произведения (можно конечно представить каждое из них как единица, умноженная на само число, но это нам ничего не дает).
Я обещал, что картинка все разъяснит, ну разве из нее не понятно, что, \( 12=2\cdot 6\), а \( 6=2\cdot 3\)?
Вот и я говорю, что элементарно!
Иными словами, \( 2\cdot 2\cdot 3=12\).
Тут \( 2\), еще раз \( 2\) и \( 3\) – это и есть множители, на которые мы раскладываем.
Зачем нужно раскладывать многочлен на множители?
Это самый главный вопрос. Я уже говорил – чтобы облегчить тебе жизнь.
Раскладывая многочлен на множители, ты упрощаешь выражение! Ты как бы делишь одну большую и сложную проблему, на несколько маленьких и простых и потом разбираешься с каждой маленькой проблемой по отдельности.
А теперь «официальное» определение.
Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. При этом каждый множитель может быть как многочленом, так и одночленом.
Для чего нужно знать все пять способов?
Потому что нет универсального способа, подходящего для всех многочленов.
Давай посмотрим на каждый из них…
5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки
2. Формулы сокращенного умножения
3. Метод группировки
Применяется если преобразование не очевидно. Здесь, например, можно переставить второй член на другое место:
Группируем члены парами, получаем:
4. Выделение полного квадрата
Можно преобразовать многочлен и привести к виду разности квадратов, например и применить формулу сокращенного умножения
5. Разложение квадратного трехчлена на множители
Квадратный трехчлен – многочлен вида
Теорема. Если квадратное уравнение \( a<
^<2>>+bx+c=0\) имеет корни \( < _<1>>,\text< >< _<2>>\), то его можно записать в виде:
Подробнее о каждом из 5-ти способов разложения на множители
1. Вынесение общего множителя за скобки
Это один из самых элементарных способов упростить выражение. Для применения этого метода давай вспомним распределительный закон умножения относительно сложения (не пугайся этих слов, ты обязательно знаешь этот закон, просто мог забыть его название).
Чтобы сумму двух чисел умножить на третье число, нужно каждое слагаемое умножить на это число и полученные результаты сложить.
Иначе говоря, \( a\left( b\text< >+\text< >c \right)\text< >=\text< >ab\text< >+\text< >ac\).
Так же можно проделать и обратную операцию, \( ab\text< >+\text< >ac\text< >=\text< >a\left( b\text< >+\text< >c \right)\).
Вот именно эта обратная операция нас и интересует. Как видно из образца, общий множитель а, можно вынести за скобку.
Подобную операцию можно проделывать как с переменными, такими как \( x\) и \( y\), например, так и с числами: \( 6\text< >+\text< >8\text< >=\text< >2\left( 3\text< >+\text< >4 \right)\).
Да, это слишком элементарный пример, так же, как и приведенный ранее пример, с разложением числа \( 12\), ведь все знают, что числа \( 6\), \( 8\) и \( 12\) делятся на \( 2\).
А как быть, если вам досталось выражение посложнее:
Как узнать на что, например, делится число \( 123\).
Нееет! С калькулятором-то любой сможет, а без него слабо?
А для этого существуют признаки делимости, эти признаки действительно стоит знать, они помогут быстро понять, можно ли вынести за скобку общий множитель.
Признаки делимости
Запомнить их не так сложно, скорее всего, большинство из них и так тебе были знакомы, а что-то будет новым полезным открытием, подробнее в таблице:
| Делится на: | Признак делимости числа на данный делитель |
|---|---|
| 2 | Оканчивается на: 0, 2, 4, 6, 8 |
| 3 | Сумма цифр делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Последняя цифра 5 или 0 |
| 7 | Разность между числом десятков и удвоенной цифрой единиц делится на семь |
| 9 | Сумма цифр делится на 9 |
| 10 | Последняя цифра – ноль |
| 11 | Разность между суммой цифр, стоящих на нечетных местах, и суммой цифр, стоящих на четных местах, делится на 11 |
Что ж, вернемся к выражению \( 3xy+123y\), может вынести за скобку \( y\) да и хватит с него?
Нет, у математиков принято упрощать, так по полной, выносить ВСЕ, что выносится!
И так, с игреком все понятно, а что с числовой частью выражения? Оба числа нечетные, так что на \( 2\) разделить не удастся.
Можно воспользоваться признаком делимости на \( 3\), сумма цифр \( 1\), \( 2\) и \( 3\), из которых состоит число \( 123\), равна \( 6\), а \( 6\) делится на \( 3\), значит и \( 123\) делится на \( 3\).
Зная это, можно смело делить в столбик, в результате деления \( 123\) на \( 3\) получаем \( 41\) (признаки делимости пригодились!).
Таким образом, число \( 3\) мы можем вынести за скобку, так же, как y и в результате имеем:
\( 3xy\text< >+\text< >123y\text< >=\text< >3y\cdot \left( x\text< >+\text< >41 \right)\).
Чтобы удостовериться, что разложили все верно, можно проверить разложение, умножением!
Также общий множитель можно выносить и в степенных выражениях.
Вот тут, например, \( 2<
У всех членов этого выражения есть иксы – выносим, все делятся на \( 2\) – снова выносим, смотрим что получилось: \( 2<
2. Формулы сокращенного умножения
Формулы сокращенного умножения уже упоминались в теории, если ты с трудом помнишь что это, то тебе стоит освежить их в памяти «Формулы сокращенного умножения».
А вот здесь можно решить вместе с нашим репетитором Алексеем Шевчуком 119 задач на формулы сокращенного умножения!
А вот здесь наше видео о том, какой навык, относящийся к формулам сокращенного умножения является самым сложным и самым важным — выделение полного кавдрата!
Справка.
Эти видео — часть нашего курса подготовки к ЕГЭ по математике. Можно провести бесплатный «тест-драйв» этого курса. Например, посетить наши пробные вебинары.
В чем суть разложения на множители с помощью формул сокращенного умножения?
Суть этого разложения в том, что бы заметить в имеющемся перед тобой выражении какую-то определенную формулу, применить ее и получить, таким образом, произведение чего-то и чего-то, вот и все разложение.
Формулы сокращенного умножения (таблица)
А теперь попробуй, разложи на множители следующие выражения, используя приведенные выше формулы:
Вот что должно было получиться:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
3. Метод группировки
А вот тебе еще примерчик:
Ну и что с ним делать будешь? Вроде бы и на \( \displaystyle 3\) что-то делится и на \( \displaystyle 5\), а что-то на \( \displaystyle x\) и на \( \displaystyle y\)
Но все вместе на что-то одно не разделишь, ну нет тут общего множителя, как не ищи, что, так и оставить, не раскладывая на множители?
Тут надо смекалку проявить, а имя этой смекалке – группировка!
Применяется она как раз, когда общие делители есть не у всех членов. Для группировки необходимо найти группки слагаемых, имеющих общие делители и переставить их так, чтобы из каждой группы можно было получить один и тот же множитель.
Переставлять местами конечно не обязательно, но это дает наглядность, для наглядности же можно взять отдельные части выражения в скобки, их ставить не запрещается сколько угодно, главное со знаками не напутать.
Не очень понятно все это? Объясню на примере:
В многочлене \( \displaystyle <
Группируем первые два члена вместе в отдельной скобке и так же группируем третий и четвертый члены, вынеся за скобку знак «минус», получаем:
А теперь смотрим по отдельности на каждую из двух «кучек», на которые мы разбили выражение скобками.
Хитрость в том, чтоб разбить на такие кучки, из которых можно будет вынести максимально большой множитель, либо, как в этом примере, постараться сгруппировать члены так, чтобы после вынесения из кучек множителей за скобку у нас внутри скобок оставались одинаковые выражения.
Из обеих скобок выносим за скобки общие множители членов, из первой скобки \( \displaystyle <
Но это же не разложение!
После разложения должно остаться только умножение, а пока у нас многочлен просто поделен на две части…
НО! Этот многочлен имеет общий множитель. Это \( \displaystyle (x-5y)\)
\( \displaystyle (x-5y)\)за скобку и получаем финальное произведение \( \displaystyle (<
Бинго! Как видишь, тут уже произведение и вне скобок нет ни сложения, ни вычитания, разложение завершено, т.к. вынести за скобки нам больше нечего.
Может показаться чудом, что после вынесения множителей за скобки у нас в скобках остались одинаковые выражения \( \displaystyle (x-5y)\), которые опять же мы и вынесли за скобку.
И вовсе это не чудо, дело в том, что примеры в учебниках и в ЕГЭ специально сделаны так, что большинство выражений в заданиях на упрощение или разложение на множители при правильном к ним подходе легко упрощаются и резко схлопываются как зонтик при нажатии на кнопку, вот и ищи в каждом выражении ту самую кнопку.
Что-то я отвлекся, что у нас там с упрощением? Замысловатый многочлен принял более простой вид: \( \displaystyle <
Согласись, уже не такой громоздкий, как был?
4. Выделение полного квадрата
Иногда для применения формул сокращенного умножения (повтори тему «Формулы сокращенного умножения») необходимо преобразовать имеющийся многочлен, представив одно из его слагаемых в виде суммы или разности двух членов.
В каком случае приходится это делать, узнаешь из примера:
Многочлен \( \displaystyle <
Возможно, поначалу тебе будет не очевидно какой член на какие разбивать, но со временем ты научишься сразу видеть формулы сокращенного умножения, даже если они не присутствуют не целиком, и будешь довольно быстро определять, чего здесь не хватает до полной формулы, а пока – учись, студент, точнее школьник.
Для полной формулы квадрата разности здесь нужно \( \displaystyle 4\) вместо \( \displaystyle 2\).
Представим третий член \( \displaystyle 2\) как разность \( \displaystyle 4-2\), получим: \( \displaystyle <
К выражению в скобках можно применить формулу квадрата разности (не путать с разностью квадратов. ), имеем: \( \displaystyle <<\left( x-2 \right)>^<2>>-2\), к данному выражению можно применить формулу разности квадратов (не путать с квадратом разности. ), представив \( \displaystyle 2\), как \( \displaystyle \sqrt<2>\), получим: \( \displaystyle (x-2-\sqrt<2>)(x-2+\sqrt<2>)\).
Не всегда разложенное на множители выражение выглядит проще и меньше, чем было до разложения, но в таком виде оно становится более подвижным, в том плане, что можно не париться про смену знаков и прочую математическую ерунду.
Ну а вот тебе для самостоятельного решения, следующие выражения нужно разложить на множители.
Примеры:
Решения:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
5. Разложение квадратного трехчлена на множители
О разложении квадратного трехчлена на множители смотри далее в примерах разложения.
Примеры 5 способов разложения многочлена на множители
1. Вынесение общего множителя за скобки. Примеры
Помнишь, что такое распределительный закон? Это такое правило: \( \displaystyle ac+bc=c\left( a+b \right)\)
Пример 1:
Разложить многочлен на множители \( \displaystyle 10<
Пример 2:
Разложи на множители \( \displaystyle 12<
Решения двух примеров:
Открыть ответы…
Чтобы открыть все задачи учебника, закрытые голубыми баннерами (как этот), зарегистрируйтесь один раз:
2. Формулы сокращенного умножения. Примеры
Чаще всего используем формулы разность квадратов, разность кубов и сумма кубов. Помнишь эти формулы? Если нет, срочно повтори тему «Формулы сокращенного умножения»!
Пример 1:
Разложите на множители выражение \( \displaystyle <
Пример 2:
Разложите на множители многочлен \( \displaystyle <
Решение примеров 1 и 2:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
3. Метод группировки. Примеры
Иногда можно поменять слагаемые местами таким образом, чтобы из каждой пары соседних слагаемых можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен превратится в произведение.
Пример:
Разложите на множители многочлен \( \displaystyle 2<
Решение:
Открыть ответы…
Мы постоянно улучшаем этот учебник и вы можете нам в этом помочь.
Оформите доступ и пользуйтесь учебником ЮКлэва без ограничений (100+ статей по всем темам ОГЭ и ЕГЭ, 2000+ разобранных задач, 20+ вебинаров-практикумов)
4. Метод выделения полного квадрата. Примеры
Если многочлен удастся представить в виде разности квадратов двух выражений, останется только применить формулу сокращенного умножения (разность квадратов).
Пример:
Разложите на множители многочлен \( \displaystyle <
Решение:
Пример:
Разложите на множители многочлен \( \displaystyle <
Решение:
5. Разложение квадратного трехчлена на множители. Пример
Квадратный трехчлен – многочлен вида \( \displaystyle a<
Значения переменной \( \displaystyle x\), которые обращают квадратный трехчлен в ноль, называются корнями трехчлена. Следовательно, корни трехчлена – это корни квадратного уравнения \( \displaystyle a<
Если не помнишь, как находить эти корни, читай тему «Квадратные уравнения».
Теорема.
Если квадратное уравнение \( \displaystyle a<
Пример:
Разложим на множители квадратный трехчлен: \( \displaystyle 2<
Сначала решим квадратное уравнение: Теперь можно записать разложение данного квадратного трехчлена на множители:
\( \displaystyle 2<
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий курсов
Добавить комментарий Отменить ответ
16 комментариев
Здравствуйте!
Помогите разложить на множители 128a⁷+b⁷.
Света, (2a)⁷+b⁷ = (2a+b)((2a)⁶ — (2a)⁵*b + (2a)⁴ * b² — (2a)³ * b³ + (2a)² * b⁴ — (2a) * b⁵ + b⁶)
Все замечательно. Но не могу разложить такое 15а^2 +14ab — 8b^2.
Ответ Алексея Шевчука:
Прекрасное изложение, спасибо! Успехов и продвижения вам!
Спасибо, Марьяна. Очень приятно слышать. И вам успехов и удачи!
1 из 100 сайтов нормальных
Спасибо, Захар. Заходите )
t^2*(t+12)^3-t*(t+12)^12*(t-6)^2 подскажите, пожалуйста, как разложить на множители
Здравствуйте, Татьяна!
Сначала давайте вынесем (t+12)^3, получим:
(t+12)^3(t^2 — t(t+12)^9(t-6)^2)
Смотрим на вторую скобку. Там у обеих частей есть t, вынесем:
t(t+12)^3(t — (t+12)^9(t-6)^2)
Я думаю, вторую скобку разложить больше не получится.
Ирина, спасибо за отзыв. Я перешлю Алексею Шевчуку ваш вопрос, но он может не ответить. Сейчас очень загружены ((
Как круто! Куб в знаменателе я тоже увидел конечно, а вот что делать с числителем не догадался ) Спасибо, Саша!
Некоторые комментарии прошлых лет к этой статье:
Гостинец
25 февраля 2018
Вау, я всю тему поняла! Поздравьте меня, подарите подарочки.
Александр (админ)
25 февраля 2018
Ну ты, крута! :)) От нас лучики счастья тебе! Хочешь понять еще лучше? Объясни кому-нибудь, кто не понимает.
Александр (Адин)
25 февраля 2018
Кстати, Гостинец, понять мало! Нужно обязательно набить руку. Нужно порешать примеры на эту тему. Причем чем быстрее ты это сделаешь, тем лучше закрепиться навык и на экзамене рука не дрогнет )) Возьми учебник и решай. Обязательно! Или можешь у нас на 100gia.ru Там все есть для подготовки к экзамену.
Геннадий
13 декабря 2018
Какой же Вы умница (без иронии!). Просто восхищаюсь. Самое ценное — с разъяснениями зачем нужно, что дает соответствующее знание.
(Админ)
28 января 2019
Спасибо, Геннадий. Поздно отвечаю, потому что поздно заметил. Но… доброе слово и кошке приятно! ) Еще раз спасибо!
Евгений
05 апреля 2019
а если сложные штуки попадутся и ни один метод не поможет.. (сложно просто догадаться будет). к примеру, y*y-x*y+4*x-7*y+12=0.. как бы не очевидно, вообще не очевидно. Сложный подход.
Александр (админ)
14 апреля 2019
Евгений, так, конечно, может быть. Но чем лучше ты подготовлен, чем больше задач решил, чем сложнее были задачи, которые ты сам решил, тем выше вероятность, что ты сможешь решить самые сложные задачи.
Когда ты находишь решение задач, ты приобретаешь навык не просто решать знакомые задачи, а находить решение сложных задач, которые ты никогда раньше не видел. И вполне возможно на экзамене именно так и случится: ты быстро решишь стандартные задачи и найдешь способ решить нестандартные в оставшееся время.
Любава
01 марта 2018
(x 2 −1 2 )(x 2 +1)мне непонятно это во 2 методе в последнем решении
Алексей Шевчук
03 марта 2018
Любава, это формула сокращённого умножения разность квадратов. Подробнее здесь: https://youclever.org/book/formuly-sokrashhennogo-umnozheniya-1#raznost-kvadratov
Рина
09 сентября 2018
4а^4+5а^2+1 Помогите пожалуйста
Александр (админ)
01 февраля 2019
Рина, это почти квадратное уравнение. Если бы уравнение было на самом деле квадратным, вот таким: 4а^2+5а+1 ты бы знала что с ним делать? А как его сделать таким? Подсказка: назови а^2 другой буквой, например b запиши новое уравнение и найди чему равно b…. Не забудь потом посчитать чему равно a.
Рина
09 сентября 2018
И спасибо!
Александр (админ)
11 февраля 2019
.
двоечник
11 февраля 2019
Что-то легко..
Александр (админ)
11 февраля 2019
Легко? В этом и цель. Спасибо.
Михаил
11 февраля 2019
Учась в школе, прорешал все задачи из задачника Сканави… Сейчас, спустя 17 лет, пытаюсь вспомнить основы 🙁
Александр (админ)
11 февраля 2019
Получается? )
Михаил
11 февраля 2019
Зачем все это нужно?
Александр (админ)
11 февраля 2019
Что «все это»? Математика?
Артем
11 февраля 2019
Завтра пробный экзамен по матану, пытаюсь вспомнить разложение на множители и формулы сокращенного умножения)
Александр (админ)
11 февраля 2019
Я так понимаю первый или второй курс университета? Да, Артем? Удачи!
Максим
11 февраля 2019
Почему в «Разложение на множители. Примеры методов разложения: 3. Метод группировки. Примеры.» после оборачивания в скобки у 3y^2 поменялся знак?
Алексей Шевчук
11 февраля 2019
Максим, за скобками знак «минус» — это значит, что мы вынесли множитель (-1). Легко проверить, правильный ли там знак: если раскроешь скобки обратно, должно получиться то, что было в начале.
Генадий
11 февраля 2019
Какой же Вы умница (без иронии!). Просто восхищаюсь. Самое ценное — с разъяснениями зачем нужно, что дает соответствующее знание.
Александр (админ)
11 февраля 2019
Спасибо, Генадий. Поздно отвечаю, потому что поздно заметил. Но… доброе слово и кошке приятно! ) Еще раз спасибо!
Ариадна
24 февраля 2019
Спасибо за материал. Действительно, ваш сайт очень помогает. Дальнейшего развития вам.
Александр (админ)
24 февраля 2019
Спасибо, Ариадна! И вам удачи во всех начинаниях!
Никита
27 февраля 2019
Здравствуйте, подскажите пожалуйста порядок решения 4 примера из примеров к подтеме «Формулы сокращенного умножения», никак не могу одолеть аналогичные уравнения.
Алексей Шевчук
27 февраля 2019
Никита, спасибо, в ответе были перепутаны знаки. На всякий случай, поясню как решать. Числитель у нас и так уже разложен на множители, осталось разложить знаменатель. Название подтемы — главная подсказка здесь: необходимо распознать и применить формулу сокращённого умножения, в данном случае это квадрат разности (4a-2b)^2. Дальше одну скобку сокращаем, затем выносим 2 за скобки в оставшихся числителе и знаменателе и сокращаем эту двойку.
Никита
28 февраля 2019
Благодарю
Алексей
09 мая 2019
a4 −12a3 +48a2 −64a это пример не на выделение полного квадрата, а на применение формулы куба разности. Поэтому этот пример лучше поместить в другой подраздел. Кроме того, хорошо бы добавить ещё одну полезную формулу сокращённого умножения: (x+a)(x+b)=x2+(a+b)x+ab.
Алексей Шевчук
23 мая 2019
Алексей, спасибо за замечание, теперь пример в нужном разделе. Формула (x+a)(x+b)=x2+(a+b)x+ab полезна, согласен, но это уже следующий уровень:) Пока что лучше эту формулу не запоминать, а использовать теорему Виета и формулу разложения квадратного трёхчлена на множители.
Сергей
09 июля 2019
Проверьте пожалуйста формулировку: Разложение многочлена на множители – тождественное преобразование, превращающее сумму в произведение нескольких множителей. Превращающее сумму… Чего? А если многочлен — разность? Может я чего-то не понял?
Алексей Шевчук
13 июля 2019
Сергей, разность всегда можно представить как сумму с отрицательным слагаемым, например: 5-3 = 5+(-3). Поэтому выражения со знаками + или — называют общим словом «сумма».
Ксения
01 октября 2019
Великолепная статья! Спасибо огромное. Все стало на свои места. Все стало понятно!
Алексей Шевчук
15 октября 2019
Спасибо за отзыв, Ксения, очень рад, что учебник вам помогает
Ксенья
06 октября 2019
как можно разложить на множители 4^179+1. Помогите пожалуйста.
Лисенок
09 октября 2019
Спасибо огромное за статью. Все понятно, и ровно столько сколько нужно, без лишней воды. Благодаря Вам я поняла наконец-то эту тему 🙂
Александр (админ)
09 октября 2019
Лисенок, как приятно слышать! И тебе спасибо! Удачи на всех экзаменах!
Алексей Шевчук
15 октября 2019
Очень рад, что статья помогла. Спасибо за отзыв!
ниважна
01 декабря 2019
ВАУ! Спасибо огромное ))просто в моем учебнике почему то не очень понятно)))а мама занята все время))))
Александр (админ)
01 декабря 2019
Мама может оставаться занятой. YouClever решает! (с) 🙂 Если серьезно, то очень приятно читать такие комментарии, Ниважна. Для того этот учебник и писали, чтобы было понятно. Удачи тебе!
Аня
03 февраля 2020
Есть у вас что нибудь на тему ЛИНЕЙНЫХ УРАВНЕНИЙ (неравенств,функций)?))) Кстати спасибо за прошлую тему.)))
Александр (админ)
04 февраля 2020
Аня, конечно есть. Вот здесь оглавление, всего, что есть. Там и линейные уравнения и неравенства и функции. https://youclever.org/book/ А что за прошлая тема? )))
brff
20 мая 2020
а как быть с примером 25a-ab^2? По статье ничего не понял..
Александр (админ)
11 июня 2020
Спасибо, Фаридун
Фаридун
11 июня 2020
Разложите на множители : a^3+b^3+c^3-3abc
Алексей Шевчук
11 июня 2020
Фаридун, классная задача! Рассмотрите (a+b+c)^3. Если раскрыть скобки, мы там увидим a^3+b^3+c^3+…+6abc (вместо троеточия ещё куча слагаемых). Вычтем и прибавим 3abc, тогда получим: (a+b+c)^3 = a^3+b^3+c^3+…+9abc — 3abc. Это значит, что можно выразить искомое выражение (обозначим его за X): X = (a+b+c)^3 — … — 9abc. В получившемся выражении можно 9abc разбить на 3 слагаемых 3abc, и тогда получится разлжить на множители группировкой. Напишите, что получилось?
Ангелина
23 июня 2020
Здравствуйте! Пожалуйста, помогите с разложением выражения на множители. 4+0,25х^2-2х. Я решила как (2-0,5х)^2, но гдз говорит (0,5х-2)^2. Не понимаю, это одно и тоже, или я что-то не понимаю… Спасибо большое заранее
Алексей Шевчук
23 июня 2020
Ангелина, это одно и то же, всё правильно.
Как выносить за скобки число?
Как выносить х за скобку?
Основное правило вынесения общего множителя за скобки
Чтобы вынести за скобки общий множитель, нужно записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.
Как выносить за скобки со степенью?
Выносить за скобки можно степень с любым показателем, но удобнее всего в качестве общего множителя вынести степень с наименьшим показателем если основание a>1, с наибольшим — при a Что значит вынести за скобки?
Вынести за скобки ( мат.) — представить многочлен в виде произведения, одним из множителей которого является общий делитель всех членов. См. также вынести.
Можно ли вынести общий множитель за скобки?
Вынести общий множитель за скобки можно в выражениях, представляющих собой суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один множитель, общий (одинаковый) для всех. Он так и называется – общим множителем. Именно его мы будем выносить за скобки.
Как вынести общий множитель за скобки примеры?
Что значит вынести минус?
Фактически вынесение минуса за скобки означает вынесение за скобки минус единицы. Для примера вынесем за скобки минус в выражении −5−12·x+4·x·y. Исходное выражение можно переписать в виде (−1)·5+(−1)·12·x−(−1)·4·x·y, откуда отчетливо виден общий множитель −1, который мы и выносим за скобки.
Как вынести квадрат за скобки?
Чтобы вынести за скобки общий множитель, необходимо каждое слагаемое алгебраической суммы разделить на этот множитель. Чтобы вынести общий множитель многочлена, возведенного в некоторую степень, необходимо этот множитель возвести в ту же степень, в которую возведен многочлен.
Что означает множитель?
МНОЖИТЕЛЬ — МНОЖИТЕЛЬ, множителя, муж. (мат.). В действии умножения число, которое показывает, сколько раз нужно повторить слагаемым какое нибудь другое число (множимое), чтобы получить произведение.
Что такое разложение на множители?
Разложить многочлен на множители — это значит представить многочлен в виде произведения двух или нескольких множителей.
Как разложить на множители многочлен?
Как разложить на множители способом группировки?
Как сделать способ группировки?
Вынесение общего множителя за скобки
Урок 27. Алгебра 7 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
Конспект урока «Вынесение общего множителя за скобки»
· показать правило вынесения общего множителя за скобки;
· подробно рассмотреть примеры вынесения общего множителя за скобки.
Давайте рассмотрим многочлен:
Обратите внимание, что каждый его член можно представить в виде произведения двух множителей:
Воспользовавшись распределительным законом умножения, мы можем представить полученное выражение в виде произведения двух множителей:
Таким образом, мы представили многочлен в виде произведения двух множителей, то есть разложили его на множители.
Такой способ разложения многочлена на множители называется вынесением общего множителя за скобки.
Рассмотрим примеры вынесения общего множителя за скобки.
Как перемножать скобки: правила, примеры
Как умножать выражения в скобках
Умножение — операция над аргументами в математике: множимым и множителем.
Множимое — повторяемое слагаемое — компонент, который умножается.
Множитель — показывает, сколько раз множимое слагаемое повторяется в выражении.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Результатом умножения является произведение.
При упрощении алгебраических выражений необходимо раскрывать скобки.
Раскрыть скобки можно с помощью:
Если выражение в скобках содержит сумму или разность переменных, то такое выражение называют многочленом. Каждый компонент многочлена является одночленом. Число перед одночленом — коэффициент. Если перед одночленом не указано число, то подразумевают один или минус один — зависит от знака.
Как вынести общий множитель за скобки
Общий множитель — наибольший общий делитель.
Операцию вынесения общего множителя за скобки используют при разложении многочлена на множители. Разложение многочлена на множители подразумевает его преобразование в равное этому многочлену произведение.
Правило вынесения общего множителя за скобки:
Чтобы вынести общий множитель, записывают исходное выражение в виде произведения общего множителя и суммы, заключенной в скобки, без общего множителя.
Для вынесения общего множителя за скобки используют распределительный закон или распределительное свойство умножения справа налево:
\(ab\pm ac=a(b\pm c)\) — сумма преобразуется в произведение.
Алгоритм нахождения общего множителя для членов многочлена:
В многочлене в скобках должно остаться столько членов, сколько было в исходном.
Метод вынесения общего множителя за скобки на примере числового выражения:
В этом выражении выносят за скобки общий множитель 3. Исходное выражение записывается как произведение общего множителя и суммы всех исходных слагаемых, кроме
Примеры вынесения общего множителя за скобки
Чтобы вынести общий множитель за скобку:
\(25kp=5\times5\times k\times p\)
\(15k^2p=3\times5\times k\times k\times p\)
Общими делителями будут 5, k, p.
\(25kp-15k^2p=\mathbf5\times5\times\boldsymbol k\times\boldsymbol p-3\times\mathbf5\times\boldsymbol k\times k\times\boldsymbol p=5kp(\frac<5\times5\times k\times p><5kp>-\frac<3\times5\times k\times k\times p><5kp>)=5kp(5-3k).\)
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Раскрытие скобок — умножение переменной или числа на выражение в скобках.
Чтобы умножить число или переменную на скобку, нужно число или переменную умножить на каждый компонент в скобках и упростить выражение.
При умножении выражения на скобку действует то же правило.
Чтобы умножить одночлен на многочлен, нужно одночлен умножить на каждый член многочлена.
\(3ab(5ac+2b-4a^2)=3ab\ast5ac+3ab\ast2b-3ab\ast4a^2=3ab\ast5ac+3ab\ast2b-3ab\ast4a^2=3\ast5a\ast abc+3\ast2ab\ast b-3\ast4a\ast a^2b=15a^2bc+6ab^2-12a^3b\)
Чтобы умножить многочлен на многочлен, нужно каждый член первого многочлена умножить на каждый член второго многочлена.
При умножении на отрицательный компонент знак меняется.
\(\mathit(a\mathit-\mathit6b\mathit)\mathit(\mathit3ab\mathit+a^<\mathit2>\mathit)\mathit=a\mathit\ast\mathit3ab\mathit+a^<\mathit2>\mathit\ast a\mathit-\mathit6b\mathit\ast\mathit3ab\mathit-\mathit6b\mathit\ast a^<\mathit2>\mathit=\mathit3a^<\mathit2>b\mathit+a^<\mathit3>\mathit-\mathit<18>ab^<\mathit2>\mathit-\mathit6a^<\mathit2>b\mathit=\mathit3a^<\mathit2>b\mathit-\mathit6a^<\mathit2>b\mathit+a^<\mathit3>\mathit-\mathit<18>ab^<\mathit2>\mathit=\mathit-\mathit3a^<\mathit2>b\mathit+a^<\mathit3>\mathit-\mathit<18>ab^<\mathit2>.\)
Чтобы решить уравнение, нужно найти все его корни или доказать, что корней нет.
Корень уравнения — значение переменной, при которой получается верное равенство.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель: